Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

1690.

Manuscrit G, f. 57r.

7 Sept. 1690. Communicata a D^o. Joh. Jacobo Spener Saxone.

Nous avons déjà résumé ces communications dans la note 3 de la p. 496 du T. IX, ainsi que dans la note 15 de la p. 540 du même Tome. Voyez sur le texte latin de quelques recettes la p. 365 qui suit. Ici nous nous contentons de donner le texte et les figures des communications suivantes:

[p. 311]

Sphaeram sulphuream Ott. Gericke¹⁷⁾ ita demum confici posse si in singulas libras addantur 13 grana salis tartari sixi.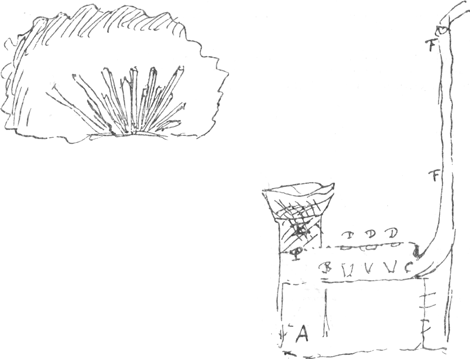

Crystallos non aliter crescere ajit quam in cavitatibus quibusdam subterraneis, in quibus est aqua, quae advehit materiam; eaque praecipitatione quadam paulatim crystalli prismata auget. Forsan inferne aqua elabitur sensim et alia succedit. Ita quoque metalli ramos non nisi in cavitatibus nasci ajit.

Furnus Chymicus Speneri. E ubi ligna imponuntur, inter BC crucibula collocat perforamina DD, quorum unum quodlibet aperire licet caeteris obturatis.

In A primum ignis accenditur usque dum calefiat tubus CFF, tum apertura ad A clauditur rursus. Magno strepitu hunc furnum ardere ajit, et omnes noxeos metalli vapores auferre.

Ad P est craticula ex lateribus concinnata quia ferrum liquesceret. Diameter ad E est 2 pedum. Tubus CF 5 vel 6 pedum.

Manuscrit G. Petite feuille séparée qui se trouve entre les f. 73 et 74 (la date du 1 janvier 1691 se trouve à la p. 78v).

In quaerendo integrali, considerandae sunt x, y, z, indefinitè pro diversis horum quantitatibus. Sed in ipso integrali ipsae x, y, z, pro maximis hoc nomine designatis accipiendae sunt.

17) Voyez la p. 611 du T. XIX.

[p. 312]

Il n'est évidemment pas toujours vrai que lorsqu'on intègre de zéro jusqu'à une certaine limite, les valeurs des variables qui correspondent à cette limite sont maximales. Il s'agit apparemment ici de certaines figures géométriques. Puisqu'il est question de trois variables, il semble que Huygens envisage le calcul des volumes des corps qu'il considère.