Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

[p. 273]

Appendice I
Aux varia academica 1666-1681.

Dans notre édition de 1934 du T. XVIII des ‘Oeuvres Complètes’ nous avons parlé de la découverte, par Huygens, de la théorie générale de l'isochronisme des vibrations harmoniques, probablement en 1673 ou 1674¹⁾. Nous y disions que, longtemps après avoir découvert et démontré l'ifochronisme des vibrations cycloïdales de différentes amplitudes, il passa, sans rien publier sur ce sujet, de la considération de ces vibrations-là à celle de vibrations harmoniques quelconques; et que rien ne prouve qu'avant (ou même après) 1687, lorsque Newton traita dans ses ‘Principia’ des vibrations harmoniques, sa pensée ait été divulguée, quoique la possibilité d'une divulgation ne puisse être niée.
Or, nous trouvons dans le Porteseuille anonyme une feuille apparemment communiquée par lui, ou du moins destinée par lui à être communiquée - voyez le dernier alinéa du texte - à un ‘clarissimus et perspicacissimus geometra’ où il indique, au lieu de la longue démonstration de l' ‘Horologium oscillatorium’ de 1673 de l'isochronisme des vibrations cycloïdales, une démonstration brève: il y commence - comme Newton le fera en 1687; p. 484 de notre T. XVIII - par parler en général de l'isochronisme d'un certain genre de vibrations grandes et petites pour dire ensuite ‘id cycloidi competere’.
Il semble donc que - quoiqu'il ne dise pas simplement que la condition de l'isochronisme, c'est que la force de rappel, donc aussi l'accélération ou retardation dans le sens du mouvement, soit proportionnelle à l'écart - il n'est nullement permis d'affirmer, pour nous servir de notre expression de la p. 483 du T. XVIII, qu'il n'a jamais ‘fait part de sa trouvaille à qui que ce soit’.
Voici cette feuille (nous divisons le texte en quatre paragraphes dont le premier est purement géométrique:

§ 1. Cum DG portio cycloidis sit aequalis duplae HD²⁾, ostendendum GF³⁾ esse duplam HD et proinde aequalem DG. Cum vero GN sit parallela⁴⁾ & proinde aequalis HD, ostendendum NF esse aequalem GN vel HD quod sic fiet. Describatur circulus CKL et ducatur ordinata FKM tum jungatur KL.

LN est aequalis arcui HE⁵⁾, est quoque aequalis KF, at KF est aequalis arcui CK ex proprietate cycloidis⁶⁾ ergo arcus HE est aequalis arcui CK, ergo LK subtensa cui

1) P. 489 et suiv. du dit Tome.

2) Voyez la l. 5 de la p. 364 du T. XIV.

3) Tangente en G à la demi-cycloïde AD.

4) D'après le théorème de la p. 375 du T. XIV.

5) Puisque LD est égale, d'après la définition de la cycloïde, à la demi-circonférence DHE, et que d'autre part ND est égale à l'arc HD (d'après le théorème CF ∞ arcui LF de la l. 12 de la p. 404 du T. XIV).

6) Théorème de la p. 347 du T. XIV.

[p. 274]

aequalis NF est aequalis et parallela subtensae HD id est GN. Ergo GF est dupla HD et proinde aequalis portioni cycloidis DG.

Ergo portio curvae AG et tangens GF usque ad cycloidem CFD est aequalis vel cycloïdi AGD vel rectae AC duplae diametri LC.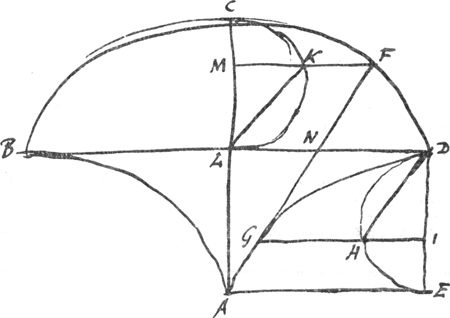

Ergo funependulum a puncto A sic coactum percurrit cycloidem DFC aut eius portionem.

[p. 275]

§ 2. Ut autem probetur aequali tempore decurri quamlibet portionem cycloidis ostendo ad id requiri ut summa velocitatum curvae percursae faciat triangulum⁷⁾.

Ostendo postea id cycloïdi competere cum velocitates sint ubique portionibus curvae proportionales⁸⁾. Nam verbi gratia velocitas puncti F quae est CK⁹⁾ est dimidia curvae FC¹⁰⁾ et sic de alijs punctis.

Suppono solum tam in diversis quam in eodem plano augmenta velocitatis proportionalia esse, nihilque proinde interturbare augmentationem velocitatis¹¹⁾.

§ 3. Eadem methodo probo minores arcus circuli citius percurri quam maiores et in qua ratione¹²⁾.

§ 4. Id longius explicare per otium non licuit¹³⁾, sed haec credo plusquam sufficient clarissimo & perspicacissimo Geometrae.

7)



Il y a lieu, nous semble-t-il, de parler ici d'une obscurité voulue..Nous croyons devoir peut-être entendre comme suit - en ayant égard à l'alinéa suivant - cette condition générale d'isochronisme de vibrations de différentes amplitudes: lorsqu'on considère ces vibrations comme se faisant simultanément suivant des lignes droites parallèles A₁O₁ et A₂O₂ (O étant le centre du mouvement, et A la position extrême), il faut que les vitesses soient telles que dans le triangle O₁A₁T (où O₁T passe par O₂ et A₁T par A₂) les droites B₁B₂ et C₁C₂ etc. qui joignent des positions atteintes simultanément, passent toutes par le sommet T.

8) Dans la figure de la note 7 les vitesses en B₁ et B₂ ou en C₁ et C₂ ou encore en O₁ et O₂ sont proportionnelles à O₁T et O₂T, donc aussi aux amplitudes O₁A₁ et O₂A₂. Pour démontrer que dans le cas de la cycloïde cette même proportionnalité existe entre les amplitudes de deux oscillations différentes, c. à. d. entre les longueurs parcourues sur la courbe dans l'un et l'autre cas, il faut e.a. faire voir que, lorsque le mobile part d'un point quelconque F, la vitesse acquise au point C est proportionnelle à la longueur de l'arc FC.

9) Cette ‘velocitas puncti F’ est apparemment celle acquise - comparez la note précédente - au point C par un mobile F commençant sa chute en partant du point F de la courbe. L'accélération de la pesanteur étant représentée par g, cette vitesse est √2g.CM. Ce que Huygens désigne par CK est la droite CK quoique celle-ci ne soit pas tracée dans la figure. Elle a la longueur √CL.CM. On peut dire que cette corde représente la vitesse acquise au point C par le mobile F, car rien n'empêche de représenter le double de l'accélération g par le diamètre CL.

10) D'après le début du § 1 - voyez la note 2 - la corde CK est la moitié de la courbe FC.

11) En d'autres termes: il est supposé que l'accélération de la pesanteur est une constante ce qui est encore admissible lorsque les oscillations cycloïdales d'amplitudes diverses ont lieu non pas dans un plan vertical mais dans un plan incliné.

12) Nous n'avons trouvé aucun calcul de Huygens sur les périodes d'oscillation d'un point parcourant des arcs de cercle de différentes amplitudes quelconques. Mais voyez sur la période correspondant à l'oscillation suivant un arc de cercle de 180^o l'Appendice II à la Première Partie de l'‘Horologium oscillatorium’ qui occupe les p. 374-387 du T. XVIII.

13) Voyez plutôt le début de la note 7 où nous parlons d'une obscurité voulue.