Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente
(1950)–Christiaan Huygens–
[pagina 126]
| |||||||||||||||||||||||||||||||||||||
LXXIV.
| |||||||||||||||||||||||||||||||||||||
[pagina 127]
| |||||||||||||||||||||||||||||||||||||
de soûmettre à votre censure. Je ne voulus pas differer neanmoins de Vous envoier le livre de Monsr. Newton, que Vous aurez sans doute receu depuis long-temps. Je l'avois addressé à Monsieur de Limeville chez les Dames de la Societé à Rotterdam. Dans une lettre qu'il m'écrivit il y a quelque temps il me marquoit que le vaisseau, où j'avois mis ce livre, n'étoit point encore arrivé. Je n'ai pas eu de ses nouvelles depuis cette fois là; mais si par malheur, Monsieur, le livre ne Vous avoit point encore eté donné, Vous avez ici le nom de mon ami, à qui Vous en pourrez demander des nouvelles. Messieurs de la Societé Roiale de Londres, qui se sont chargez du soin de l'impression de ce livre, Vous en ont voulu faire un presentGa naar voetnoot2). Comme ces Messieurs da la Societé Roiale ont resolu dans leur conseil de me proposer à l'assemblée, pour proceder à mon election, je me suis fait une obligation de rester en ces pays jusques à ce que leurs assemblées, qui ont été interrompues, recommencent: Je serai bien aise de voir une fin de cette affaire; et comme la saison est déjà avancée cela m'engagera à rester en Angleterre encore tout l'hyver. Je profiterai de ce temps là pour apprendre la langue Angloise le mieux qu'il me sera possible. Je vien d'apprendre que Messieurs de la Societé Roiale ont terminé favorablement mon élection. L'effet extraordinaire que l'on attribue à la pompe du Chevalier Gordon, n'a rien qui ne soit parfaitement d'accord avec nos connoissances de Mechanique; et cet effet ne paroît si grand, que parce qu'on n'avoit point encore trouvé de pompe qui en pût approcherGa naar voetnoot3). Douze hommes tirent en une minute de temps douze tonneaux d'eau de 2000 ℔ chacun par une même pompe, et l'on en peut avoir plus d'une dans les vaisseaux de guerre, où l'on ne manque pas de monde pour les servir. Je ne connoi point le secret de Monsr. Gordon pour la construction de sa machine; il est fort reservé là dessus et je n'ai pas seû qu'il se soit découvert à personne excepté Monsieur Boile, qui de son côté s'est engagé à garder le secret. Mais je sai en general que Monsr. Gordon se sert en même temps de la force des hommes, et de leur pesanteur, laquelle comme Vous savez ne nous coûte rien; outre que nous n'avons presque pas de peine à transporter nôtre propre corps. Dans les pompes communes le piston descend assez lentement, et touche à l'eau qui doit monter une tres grande partie du passage. Or j'ai appris que Mr Gordon remedie à ce deffaut, et que son piston laisse à l'eau beaucoup de liberté pour monter. J'ai conceu là dessus que ce piston pourroit bien être fait de la maniere suivante. Soit ac la barre du piston, que je suppose être de fer. A son extremité c elle se partage en deux branches égales b, d, qui vont à l'opposite l'une de l'autre, et qui touchent par les deux bouts le corps de pompe; ou, si l'on veut, qui ont leurs extremitez placées dans deux rainures faites le long du corps de pompe, où elles | |||||||||||||||||||||||||||||||||||||
[pagina 128]
| |||||||||||||||||||||||||||||||||||||
ont la liberté de courir. Ces deux branches b, d servent d'axe à deux demi-ellipses égales bed, bfd, qui sont couchées assez obliquement dans le corps de pompe, et qui
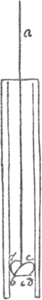 en peuvent remplir toute la largeur. Les demi-ellipses sont attachées par des charnieres à leur axe, et elles ont la liberté de se fermer vers la barre du piston. Ainsi pendant le jeu de la pompe les demi-ellipses étant fermées le piston descend librement et l'eau monte en abondance: ensuite le piston commençant à remonter les demi-ellipses s'ouvrent contre les cotez du corps de pompe, ausquels elles s'appliquent avec la derniere exactitude. Vous voiez bien Monsieur que rien ne limite ici la grosseur de la pompe sinon la force des hommes qu'on veut emploier: mais il est bon que la pompe soit unie par dedans et exactement cylindrique, et que le bord des demi-ellipfes soit arrondi et sans vive arrête. Il est aisé de construire la partie bcdef de maniere que les demi-ellipses ne s'approchent de la barre que jusqu'à un certain point, et que pendant que le piston monte il ne se perde point d'eau, et que d'abord qu'il commence à ne plus descendre les demiellipses se rouvrent promptement. Il y a d'autres choses Monsieur que l'on peut remarquer dans la construction de cette machine, mais qu'il n'est pas necessaire que je Vous ecrive. La soupape de la pompe se peut construire suivant la même idée. Vous savez bien Monsieur que sur mer il suffit d'elever l'eau, que l'on veut vuider du vaisseau, jusques à ce qu'elle soit un peu au dessus du niveau de la mer, quoi que dans un bon nombre de batimens on l'éleve jusques à dix pieds plus haut, ou environ. J'ai veu le tome sixieme de la Bibliotheque universelle, mais la réponse de Monsieur Tschirnhaus à mon écrit ne s'y trouve point. Je ne sai Monsieur si c'est parce que Monsr Ts. s'est rendu à vos raisons: mais je voi bien qu'il ne s'étoit pas donné beaucoup de peine à examiner mon écrit: sans cela il ne m'eut asseurement pas fait une reponse si foible. On m'avoit envoié de Hollande une copie de sa reponseGa naar voetnoot4). Ma replique étoit deja prête il y a longtemps, et j'avois pris soin de m'y servir dans mes raisonnemens de la ligne même, pour laquelle Monsr de T. donne sa construction, afin de l'empêcher par la de biaiser une autre fois. Cependant, Monsieur, je Vous suis tres obligé de la peine que Vous avez pris pour le detromper. Je suis fâché pour l'honneur des Mathematiques qu'il y ait des differens entre ceux qui s'attachent à ces sciences là; et en mon particulier, je serois encore plus fâché de voir durer un different où j'aurois quelque part. Si Vous avez leu le livre de Monsr Newton Vous m'obligerez beaucoup Monsieur de m'en dire vôtre sentiment. Comme j'espere de n'etre plus malade j'ose Vous promettre d'etre à l'avenir plus exact à Vous répondre. J'avois commencé de Vous écrire une lettre dans | |||||||||||||||||||||||||||||||||||||
[pagina 129]
| |||||||||||||||||||||||||||||||||||||
un temps où la moindre occupation augmentoit beaucoup mon mal. Depuis ce temps là j'ai repris deux ou trois fois cette lettre pour la continuer, et à present, que je suis un peu remis, je Vous en écris une nouvelle, qui est une des premieres que j'écris, quoi que je sois de tous cotez en arriere de bien des lettres. Je ne juge pas à propos Monsieur de Vous entretenir à present de ce que je pensois touchant le flux et le reflux de la mer. Plus je m'attache à ce sujet plus j'y trouve de difficultez, qui procedent principalement de la jonction de plusieurs causes differentes, dont les forces n'etant pas toutes connues en particulier, ce qui peut resulter de toutes ensemble est encore plus incertain. Je n'ai point encore pû me resoudre à digerer entierement ma methode de trouver l'equation de la courbe par la proprieté de la tangente: mais Monsieur je Vous l'envoie dans le meilleur ordre où je l'ai pû mettre, en la rassemblant de plusieurs papiers separez, et qui n'avoient presque pas de liaison entre eux. J'espere que les exemples éclairciront ce qu'il y a d'obscur dans les discours, et qu'au pis aller si Vous n'entendez pas ce que je dis, Vous devinerez au moins ce que je veux dire. 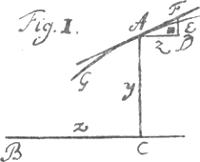 Methode de trouver les tangentes des lignes courbes par leur EquationGa naar voetnoot5). Je suppose que le point B soit donné pour le commencement de la ligne BC, que j'appelle x. Je suppose encore que la ligne CA, que j'appelle y, fasse avec BC l'angle donné BCA, et se termine à la courbe GAE en A. Enfin je suppose que l'équation de la ligne courbe GAE soit donnée par le moien des inconnues x et y et de quelques autres lettres connues. Cela étant on demande la situation de la ligne droite AF tangente de la courbe au point donné A. Soit menée AD parallele à BC et DEF parallele à CA, laquelle DEF coupe la courbe GAE au point E et la tangente AF au point F. Soit la ligne AD appellée z et la ligne DE appellée u. 1o. Si on reduit le lieu ou l'equation de la courbe aux inconnues z, et u, en regardant BC, CA ou x, y comme des grandeurs connues, on aura une nouvelle equation de la courbe, qui parmi ses termes renfermera necessairement tous ceux de la premiere equation, lesquels on pourra par consequent effacer, puis qu'ils se detruisent les uns les autres. 2o. Si par le moien de la nouvelle équation l'on determine la proportion AD, DF qui est entre les lignes z et u lors qu'elles sont infiniment petites, il est evident que l'on aura par là la situation de la ligne AF tangente de la courbe au point A. Car on peut supposer que cette tangente passe par les points de la courbe infini- | |||||||||||||||||||||||||||||||||||||
[pagina 130]
| |||||||||||||||||||||||||||||||||||||
ment voisins de A, qui sont d'un autre côté l'extremité même de l'inconnue u, lors qu'elle est infiniment petite. 3o. Si dans les operations on evite de faire ce qui ne mene pas au but, et qu'on s'attache uniquement à ce qui est essentiel on aura, dans une seule regle, la maniere la plus simple de determiner les tangentes suivant les principes dont je me sers ici, savoir en trouvant la proportion des lignes AD, DF paralleles à BC et CA. I. Pour reduire l'equation de la courbe aux inconnues z et u, il est evident qu'il ne faut que substituer par tout, dans l'equation donnée, x + z au lieu de x, et y + u au lieu de y, et de meme substituer le quarré ou cube &c de x + z, au lieu du quarré ou cube &c de x; et le quarré ou cube de y + u, au lieu du quarré ou cube &c de y. Car ce qui étoit vrai à l'égard de x dans la premiere equation doit être vrai dans la seconde à l'egard de x + z, qui n'est autre chose dans le fonds que le x de la premiere: et de même ce qui étoit vrai à l'égard de y dans la premiere équation doit être vrai dans la seconde à l'egard de y + u, qui n'est autre chose que le y de la premiere. Or il est bien evident que quand dans l'equation donnée de la courbe on substitue x + z et y + u, au lieu de x et de y, et les puissances de ces premieres quantitez au lieu des puissances des dernieres, la nouvelle equation renferme encore parmi ses termes tous ceux de la premiere. En effet si les termes de la premiere équation ne contiennent ni x ni y on les laisse dans la seconde sans les changer du tout; s'ils contiennent les lettres x ou y, ou quelques puissances de ces lettres, on substitue les quantitez x + z, ou y + u, ou les puissances correspondantes de ces quantitez, desquelles puissances correspondantes le premier terme est toujours la puissance même de x ou de y qui est renfermée dans le terme donné, et de laquelle on substitue la valeur. Il paroit donc que l'on peut effacer de la nouvelle équation tous les termes de la premiere, parce qu'ils se détruisent les uns les autres, ce qui étant fait l'égalité demeure encore entre les termes qui restent, lesquels renferment necessairement ou la lettre z ou la lettre u, ou toutes les deux. II. Mais parmi les termes de la seconde equation, qui renferment necessairement comme je vien de dire ou la lettre z ou la lettre u, il y en peut avoir qui renferment des produits de z par z, ou de z par u, ou de u par u, lesquels par consequent, à cause de l'infinie petitesse de z et de u, seront infiniment plus petits que les autres termes, qui ne renferment que la lettre z seule ou la lettre u seule. Cela étant on peut effacer tous ces termes, dont l'extreme petitesse à l'égard des autres fait qu'ils ne peuvent nullement changer la valeur de l'equation, et l'on peut dans une derniere égalité garder simplement ceux où les lettres z et u sont seules et d'une dimension. Or cette derniere egalité, dans laquelle toutes les lettres comme x, y et les autres sont connues, donne la proportion des inconnues infiniment petites z et u, ce qui suffit pour determiner la situation de la tangente AF. III. Puis que tant de produits doivent être effacez, avant que l'on n'en vienne à la derniere égalité, il paroit que l'on peut beaucoup abbreger le calcul, si on evite dabord de les ecrire. Or cela se peut aisement, parce que les produits, qui doivent rester dans | |||||||||||||||||||||||||||||||||||||
[pagina 131]
| |||||||||||||||||||||||||||||||||||||
la derniere egalité, etant seulement ceux où z et u n'ont qu'une dimension, ce sont toujours les seconds termes des differentes puissances de x + z et de y + u qu'il faut écrire, au lieu des puissances correspondantes de x et de y que l'on veut oter. Or ces seconds termes se trouvent aisement par le moien des puissances données de x et de y, comme il paroit par les tables suivantes, en multipliant la puissance de x ou de y par le nombre de ses dimensions, et en changeant un x en z ou un y en u.
On peut remarquer touchant les termes de l'equation donnée, qui ont en même temps les lettres x et y, que ceux qu'il leur faut substituer ont necessairement cette proprieté, savoir, que comme le nombre ϰ qui multiplie le produit où est z est au nombre λ qui multiplie le produit où est u, ainsi dans le terme donné le nombre des dimensions de x au nombre des dimensions de y. De tout ce qui precede je tire la regle suivante pour trouver par l'equation donnée d'une ligne courbe une autre equation qui determine la situation de la tangente. Je m'arrete dabord à tous les termes de l'équation donnée où la lettre x se rencontre, et je multiplie chacun d'eux par le nombre qu'il a de dimensions de x, changeant en meme temps un des x en z. De même je m'attache à tous les termes où la lettre y se rencontre, et je multiplie chacun d'eux par le nombre qu'il a de dimensions de y, changeant en même temps un des y en u. Aprez cela je developpe, par le moien de l'égalite que cette operation me donne, la proportion qui est entre z et u, que je suppose ici comme de m à n. Si les quantitez m et n sont toutes deux positives, ou toutes deux negatives, il faut prendre z et u comme dans la figure, c'est à dire comme des additions aux lignes x et y; on pourroit aussi les prendre comme des retranchemens des lignes x et y. Mais, si les quantitez m et n sont l'une positive et l'autre negative, il faut prendre z et u dans la figure, l'une comme une addition à x ou à y, et l'autre comme un retranchement de y ou de x. | |||||||||||||||||||||||||||||||||||||
[pagina 132]
| |||||||||||||||||||||||||||||||||||||
Methode de trouver l'equation des lignes courbes par la proprieté donnée des Tangentes.Ce probleme, qui est fort beau, et qui est extremement difficile à resoudre, si l'on prend une autre route que celle que je suivrai, n'est presque autre chose que l'inverse du probleme precedent, et se peut construire avec la même facilité a peu prez; Mais il faut pour cela que la proprieté des tangentes soit donnée, par la proportion, qui se trouve entre les lignes z et u de la figure, laquelle proportion peut toujours être donnée dans toutes les lignes geometriques, sans que z et u montent à plus d'une dimension, et sans que les lettres x et y soient enveloppées de signes radicaux, comme cela paroit assez de ce que pour toutes les lignes geometriques, dont l'equation est donnée, on trouve la proportion de z à ù d'une maniere tres simple, et par une equation d'une dimension seulement. Je suppose donc, que l'Equation des tangentes, qui vient de la proportion connue de z à u, soit donnée, et je fai mon operation comme il suit. Je rens l'equation des tangentes égale à zero, c'est à dire que j'en mets tous les termes d'un seul côté, mais avec cette precaution, que je mets de suite tous ceux où est la lettre z, et apres eux tous ceux où est la lettre u. J'examine ensuite tous les termes où est la lettre z, et en les parcourant je marque de quelque maniere ceux où la lettre y ne se trouve point. Je marque de même les termes qui ont la lettre u, lorsque x ne s'y trouve point. Chacun des termes ainsi marquez si l'on en excepte quelques cas m'en donne un autre pour l'equation de la courbe, auquel il ne se trouve qu'une des inconnues x ou y. Je trouve ces termes de l'equation de la courbe en cette maniere. Je change le z en x, et je divise le terme par le nombre des dimensions que y se trouve avoir apres ce changement. Pour ce qui regarde les signes, ils doivent etre les memes que dans les multiplications ordinaires. Les autres termes, qui n'ont point été marquez, doivent avoir necessairement les lettres z et y ou x et u, et ils ne peuvent donner dans l'equation de la courbe que quelques termes, qui contiennent en même temps les deux lettres x et y. Je pren l'un de ces termes, qui contiennent les lettres z et y, et je change le z en x, divisant en suite, comme ci dessus, par le nombre des dimensions que x se trouve avoir aprez ce changement. J'ai par la un nouveau terme de l'equation cherchée de la courbe: mais il faut qu'il y en ait encore un autre, qui lui reponde dans l'equation des tangentes, lequel ne doit plus etre consideré, parce que son generateurGa naar voetnoot6) dans l'equation de la courbe est deja connu. Cet autre terme dans l'equation des tangentes se reconnoit, en multipliant celui de l'equation cherchée par le nombre des dimensions qu'il a de y, et en changeant ensuite un y en u. Ou bien il se reconnoit par le terme même qui | |||||||||||||||||||||||||||||||||||||
[pagina 133]
| |||||||||||||||||||||||||||||||||||||
contient les lettres z et y, en le multipliant par le nombre des dimensions qu'il a de y, et en changeant le z en x, et un y en u. Ainsi tous ces termes, que je n'avois pas marqué d'abord, ne me donnent que la moitié autant de termes pour l'equation de la courbe. Il y a une observation à faire touchant ces termes qui n'ont point été marquez dabord, comme on verra plus bas. Aiant ainsi trouvé tous les termes de l'equation de la courbe, d'où ceux de l'equation des tangentes peuvent venir, il reste encore une chose fort importante à remarquer. C'est que si tous les termes trouvez pour l'equation de la courbe sont egaux ensemble à zero, cette equation est toute retrouvée; sinon ils seront tous ensemble égaux à une quantité toute connue positive ou negative, parce que l'on suppose qu'un point de la courbe est donné tout au moins, et qu'ainsi x et y sont connus, au moins pour un cas, ce qui suffit: car dans tous les cas, c'est à dire à l'égard de tous les points de la courbe, les termes composez de x et de y font toujours une même somme connue positive ou negative, par exemple a, ag, ag2, ag3 &c ou, -a.-ag, &c ou même o. Ce qui fait ordinairement trouver trois differentes lignes Geometriques, qui ont la proprieté des tangentes qui avoit été proposée. Si on reconnoit les deux termes de l'equation des tangentes, qui doivent dependre d'un seul terme de l'equation de la courbe, ce qui est ordinairement assez facile; comme si on n'a que deux termes qui n'aient point été marquez, ou s'il n'en reste plus que deux à qui on n'ait pas encore trouvé le terme correspondant [ce dernier mot a été corrigé par Huygens en: generateur, et Huygens ajoute: quoyque ces characteres ne suffisent pas tousjours] ou si on voit que deux termes aiant entre eux les lettres z et y, x et u [il y a ici des corrections de la main de Huygens: les mots ‘entre eux’ sont de lui, ainsi que les mots ‘lettres z et y, x et u’. Fatio avait écrit ‘produits zy et xu’], soient divisibles par les mêmes lettres connues et aient chacun les memes nombres de dimensions des x, comme encore le meme nombre de dimensions des y, alors on peut faire l'operation plus brievement. Car comme le nombre ϰ, qui est au devant du terme qui a la lettre z [ici Huygens a corrigé ‘zy’ en ‘la lettre z’] est au nombre λ, qui est au devant du terme qui a la lettre u [ici Huygens a corrigé ‘xu’ en ‘la lettre u’], ainsi le nombre des dimensions de x dans le terme cherché de l'equation de la courbe [Huygens ajoute: c'est a dire dans le terme generateur] au nombre des dimensions de y dans le même terme. Or il faut prendre ici les nombres ϰ et λ avec leurs signes + ou - selon que les termes de l'equation des tangentes ont ces signes; et les nombres des dimensions de x et de y sont entre eux dans la raison des nombres ϰ et λ (lesquels pour des lignes qui ne sont pas geometriques peuvent estre des quantitez analytiques, et mesme meslees d'inconnues, mais cela soit dit seulement en passant). - Toute cette parenthèse, ainsi que le mot ‘Et’ qui suit, est de la main de Huygens qui a apparemment biffé, à partir des mots ‘nombres ϰ et λ’, les lignes suivantes de Fatio: qui font ensemble une somme accommodee aux dimensions des autres termes de l'equation. Le nombre des dimensions de x et de y peut donc être aisement connu, tous les termes dans les equations des lignes geometriques, telles que je les considere, étant composez | |||||||||||||||||||||||||||||||||||||
[pagina 134]
| |||||||||||||||||||||||||||||||||||||
d'un égal nombre de lettres ou de dimensions. Mais s'il arrive que le terme de l'equation de la courbe, qui repond aux deux termes de l'equation des tangentes [qui contiennent les] produits zy et xu, ne puisse pas avoir le même nombre de dimensions que les autres, - Et il faudra faire le calcul de la maniere qui sera montrée ci dessous dans les exemples [Huygens ajoute: aux quels je voudrois qu'on s'en raportast] et changer l'equation des tangentes en une autre équation de même valeur. Enfin le terme cherché de l'equation de la courbe [Huygens ajoute: dans lequel il n'y a encore que des x et des y] doit être multiplié par un nombre [corrigé par Huygens en: une quantité] μ, qu'il est aisé de connoitre. Car on aura ce nombre [corrigé par Huygens en: cette quantité] si dans le terme qui a les lettres z et y [correction de Huygens; Fatio avait écrit: qui a le produit zy] on change le z en x, si on divise après cela tout le terme par le nombre des dimensions que x se trouve avoir apres ce changement et enfin si on divise encore ce que l'on a trouvé par les puissances de x et de y qui le multiplient, ce qui les fera entierement evanouir. Le quotient est la quantité cherchée μ [correction de Huygens; Fatio avait écrit: le nombre cherché] qui doit multiplier le terme de l'equation de la courbe, et qui se trouve bien souvent être l'unité. Il est à propos d'avertir ici qu'il vaut mieux commencer l'operation, en cherchant le terme generateur des deux termes correspondans ou gemeaux, parmi les quels peuvent etre des termes qui paroissent devoir étre marquez de quelque trait (◠), que non pas en cherchant les correspondans [corrigé par Huygens en: generateurs] des autres qui ont été marquez d'abord; parce que s'il arrivoit qu'il falût changer l'equation des tangentes, il seroit inutile d'avoir trouvé ces derniers correspondans [corrigé par Huygens en: generateurs], comme ou le comprendra facilement par la suite. On pourroit donner une telle proprieté ou équation des tangentes, qu'il seroit impossible de trouver une equation pour la courbe qui lui satisfit. En ce cas on peut être asseuré que la proprieté donnée des tangentes, si du moins elle ne peut pas être exprimée autrement [en marge, de la main de Huygens: souvent cela se peut] ne se trouve dans aucune ligne Geometrique, puis qu'il n'y a aucune equation geometrique de laquelle cette proprieté des tangentes puisse resulter. Que si dans la proprieté donnée des tangentes il y a quelques incommensurables, ou simples, c'est à dire qui ne renferment qu'un seul terme sous le signe radical, comme dans celle ci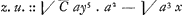 , ou composez, c'est a dire qui renferment plus d'un terme sous le signe radical, comme dans celle ci , ou composez, c'est a dire qui renferment plus d'un terme sous le signe radical, comme dans celle ci 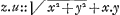 , il peut arriver que cette proprieté des tangentes appartienne neanmoins à une courbe geometrique. Mais en ce cas ou l'on peut trouver l'equation de la courbe par les mêmes regles que celles que j'ai données, comme dans la premiere proportion; ou bien la quantité incommensurable et composée, comme dans la seconde proportion , il peut arriver que cette proprieté des tangentes appartienne neanmoins à une courbe geometrique. Mais en ce cas ou l'on peut trouver l'equation de la courbe par les mêmes regles que celles que j'ai données, comme dans la premiere proportion; ou bien la quantité incommensurable et composée, comme dans la seconde proportion 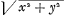 , peut toujours avoir quelques expressions commensurables, par exemple x + ½p, ou y2/p + ¼p, ou peut être quelque autre expression où les incommensurables soient simples. Et il y a quelque lieu de rechercher une valeur simple de l'incommen- , peut toujours avoir quelques expressions commensurables, par exemple x + ½p, ou y2/p + ¼p, ou peut être quelque autre expression où les incommensurables soient simples. Et il y a quelque lieu de rechercher une valeur simple de l'incommen- | |||||||||||||||||||||||||||||||||||||
[pagina 135]
| |||||||||||||||||||||||||||||||||||||
surable qui est composé, et peut etre meme de la trouver quand il est possible. Mais la proportion de z à u, dans les lignes geometriques, se peut toujours exprimer par des quantitez, qui ne renferment point d'incommensurables; et si ma methode supposoit que la proportionelle z à u fût donnée sans incommensurables et tres simple, elle ne supposeroit rien qui ne se peut saire pour toutes les lignes Geometriques et quoi qu'elle fut limitée par là [le reste de la phrase jusqu'au mot tandis est de la main de Huygens qui a biffé quelques mots] elle serviroit tousjours dans une infinité de cas, tandis qu'elle manqueroit dans [Huygens a biffé le mot ‘quelques’] autres. Mais comme la même proportion de z à u se peut exprimer d'un grand nombre [corrigé par Huygens en: d'une infinité] de manieres, même sans incommensurables, il arrive quelquefois qu'une des expressions, quoi qu'elle paroisse simple, ne peut cependant pas faire trouver d'abord l'equation de la courbe. La raison de cela paroit en ce que ma methode de trouver l'equation de la courbe par la proprieté des tangentes, telle que je l'ai donnée jusques ici, etant seulement une maniere de retourner sur ses pas lorsque cette proprieté peut être derivée de l'equation même de la courbe, il arrive de là que si on s'attache d'abord à une autre proportion entre z et u que la proportion même qui peut venir immediatement de l'equation de la courbe, il n'y a pas lieu de retrouver cette equation facilement et pied à pied. Mais quoi que cette circonstance rende quelquefois le calcul un peu plus long, neanmoins elle ne limite pas ma theorie [en marge de la main de Huygens: je trouve que si] ni ma methode, qui demeure toujours generale pour toutes les courbes geometriques; et l'on verra par les exemples que je vai joindre ici, que l'on ne manque pas de liberté pour pouvoir exprimer cette proportion de z à u de diverses manieres. | |||||||||||||||||||||||||||||||||||||
[pagina 136]
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
[pagina 137]
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
[pagina 138]
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
[pagina 139]
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
[pagina 140]
| |||||||||||||||||||||||||||||||||||||
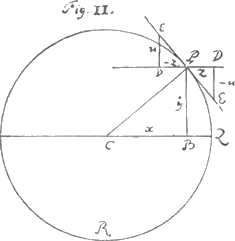
Ces exemples suffiront pour éclaircir la methode de trouver les tangentes par l'equation de la courbe, mais il est a propos d'ajouter encore quelques exemples de la methode de trouver l'equation de la courbe par la proprieté des tangentes. 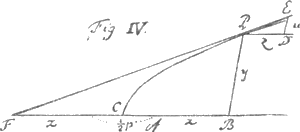 IIIGa naar voetnoot7). Dans la 4e figure la ligne AB est donnée de position, avec le point A pour le commencement des x. La ligne BP, qui est une des ordonnées y, est aussi donnée de position, et par consequent le point P est donné. Enfin une ligne droite égale à ½p est aussi donnée. On demande quelle est la ligne courbe qui passe par le point P, et dont les tangentes, comme EPF, interceptent toujours avec l'ordonnée (comme PB) sur | |||||||||||||||||||||||||||||||||||||
[pagina 141]
| |||||||||||||||||||||||||||||||||||||
la ligne BA continuée, une longueur (comme BF) égale à 2x + ½ p. Il est evident que la proprieté des tangentes est que z.u ∷ 2x + ½ p.y. L'equation des tangentes est donc zy-2ux-½ pu = 0. Je marque le terme - ½ pu d'un petit trait (◠) parce que la lettre u s'y rencontre sans la lettre x, et ce terme ne donne pas de difficulté pour determiner son correspondant, si du moins on regle bien le calcul [Huygens ajoute: c'est à dire qu'on n'introduise point de x dans ce terme]. Les deux autres termes ne peuvent point être marquez de même, parce qu'ils contiennent le produit zy ou le produit xu; et je commence l'operation en cherchant dabord leur terme correspondant, qui doit étre un seul terme contenant en même temps les lettres x et y. Je dis donc ϰ : λ ∷ 1. - 2 et le terme x/y2 peut être pris pour le correspondant cherché, ce qui paroitra davantage par les exemples qui suivront celui ci. Mais il rend les termes z/y2 - 2xu/y3, c'est à dire zy/y3- 2xu/y3, au lieu des termes zy-2xu de l'equation des tangentes. C'est pourquoi je change l'equation des tangentes en multipliant tous ses termes par 1/y3, ce qui me donne l'equation suivante zy/y3-2zu/y3-½pu/y3 = 0, de laquelle les termes correspondans sont x/y2 + ¼py/y3, lesquels avec quelque quantité connue, comme a/gg, ou plutôt -1/p sont ensemble egaux à zero. L'equation, par la nature de la parabole connue d'ailleurs, doit étre ¼p2 + px = y2. IV. Que si la proprieté des tangentes eut été reduite à celle-ci 2zy-4ux-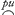 = 0, on auroit eu pour [Huygens ajoute: chercher] le correspondant des deux premiers termes, qui ne se doivent point marquer, ϰ : λ ∷ 2. ± 4 ∷ 1. ± 2 ∷ -½. + 1 [lisez ∓ 1] &c. Mais on ne peut pas prendre indifferemment pour les nombres des dimensions de x et de y tous les nombres, qui sont dans cette proportion. Par exemple si on prend x2/y4 pour le correspondant des termes qui ne sont point marquez, 2xz/y4 + 4x2u/y5 seront les termes qu'il rendra, et qui sont produits quand on multiplie les termes 2zy - 4ux de l'equation des tangentes par x/y5. C'est pourquoi pour changer l'equation des tangentes il faudra aussi multiplier le terme marqué, -pu, par x/y5. Ainsi au lieu du terme - pu, où il n'y avoit ni x ni z, mais bien la lettre u qui vient de y, on aura - pux/y5, qui contient x et y, et qui par consequent ne peut pas être seul correspondant d'un terme de la courbe. Car si ce terme de la courbe est ¼pyx/y5, il donne = 0, on auroit eu pour [Huygens ajoute: chercher] le correspondant des deux premiers termes, qui ne se doivent point marquer, ϰ : λ ∷ 2. ± 4 ∷ 1. ± 2 ∷ -½. + 1 [lisez ∓ 1] &c. Mais on ne peut pas prendre indifferemment pour les nombres des dimensions de x et de y tous les nombres, qui sont dans cette proportion. Par exemple si on prend x2/y4 pour le correspondant des termes qui ne sont point marquez, 2xz/y4 + 4x2u/y5 seront les termes qu'il rendra, et qui sont produits quand on multiplie les termes 2zy - 4ux de l'equation des tangentes par x/y5. C'est pourquoi pour changer l'equation des tangentes il faudra aussi multiplier le terme marqué, -pu, par x/y5. Ainsi au lieu du terme - pu, où il n'y avoit ni x ni z, mais bien la lettre u qui vient de y, on aura - pux/y5, qui contient x et y, et qui par consequent ne peut pas être seul correspondant d'un terme de la courbe. Car si ce terme de la courbe est ¼pyx/y5, il donne
| |||||||||||||||||||||||||||||||||||||
[pagina 142]
| |||||||||||||||||||||||||||||||||||||
bien pour correspondant dans l'equation des tangentes -pux/y5, mais il donne encore + ¼ pyz/y5. Au contraire si on prend l'unité pour le nombre des dimensions de x, alors le terme x/y2 de l'equation de la courbe donne z/y2-2xu/y3, c'est à dire zy-2xu/y3 pour l'equation des tangentes, et on doit changer l'equation donnée des tangentes en multipliant ses termes par 1/2y3 ou plustost par 1/y3 &c. cequi fait que le terme - pu se changera en -pu/2y3, qui contient les lettres u et y, mais point de x, et par consequent son correspondant se peut trouver, qui sera + ¼py/y3. Ainsi l'equation de la courbe sera x/y2 + ¼p/y2 = à une quantité toute connue qui est ici 1/p. Or on connoit ici que le nombre des dimensions de x doit être l'unité seulement, parce que dans les termes 2zy-4ux, z est d'un coté d'une dimension seulement et sans x, et x de l'autre cotéd'une dimension seulement et sans z. Les mêmes nombres de dimensions que x ou y ont dans le terme de l'equation de la courbe, ils les ont encore dans les termes correspondans de l'equation des tangentes, où je regarde la quantité z comme une puissance lineaire de x, et la quantité u, comme une puissance lineaire de y. C'est pourquoi si on veut que le changement, qui se doit faire de l'equation de la tangente, en multipliant tous ses termes par une certaine quantité, ne fasse point entrer la lettre x ou bien la lettre y dans les termes de cette equation, qui peuvent avoir été marquez dabord, il ne saut que donner à la quantité x, ou bien à la quantité y, le même nombre de dimensions qu'elle se trouve avoir dans les termes dont on cherche le correspondant. Ainsi si l'equation des tangentes étoit 2zy-4ux-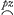 = 0, on auroit comme ci dessus ϰ : λ ∷ 2.-4 ∷ 1.-2, &c ∷ -½. 1. Mais afin que l'on puisse trouver le correspondant du terme marqué, - pz, il faut que la quantité par laquelle les termes 2zy - 4ux seront multipliez, pour changer l'equation des tangentes, ne renferme point de y. C'est pourquoi comme dans les termes 2zy-4ux on a d'un coté y d'une dimension sans u, et de l'autre u d'une dimension aussi sans y, il faut choisir pour le nombre des dimensions de y l'unité seulement, et on aura λ. ϰ ∷ - 4.2 ∷ 1.-½ : ainsi -y/√x sera le correspondant cherché. Il rend = 0, on auroit comme ci dessus ϰ : λ ∷ 2.-4 ∷ 1.-2, &c ∷ -½. 1. Mais afin que l'on puisse trouver le correspondant du terme marqué, - pz, il faut que la quantité par laquelle les termes 2zy - 4ux seront multipliez, pour changer l'equation des tangentes, ne renferme point de y. C'est pourquoi comme dans les termes 2zy-4ux on a d'un coté y d'une dimension sans u, et de l'autre u d'une dimension aussi sans y, il faut choisir pour le nombre des dimensions de y l'unité seulement, et on aura λ. ϰ ∷ - 4.2 ∷ 1.-½ : ainsi -y/√x sera le correspondant cherché. Il rend 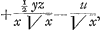 c'est à dire + c'est à dire + 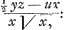 multipliant donc - pz par 1/4x √x ou si l'on vouloit par 1/x √x on a l'equation des tangentes changée en celle ci, multipliant donc - pz par 1/4x √x ou si l'on vouloit par 1/x √x on a l'equation des tangentes changée en celle ci, 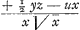 -pz/4x √x = 0, dont la correspondante est -y/√x + 2px/4x √x ± √g = 0. -pz/4x √x = 0, dont la correspondante est -y/√x + 2px/4x √x ± √g = 0.
| |||||||||||||||||||||||||||||||||||||
[pagina 143]
| |||||||||||||||||||||||||||||||||||||
Si dans la meme figure quatrieme le point P et la tangente EPF étant encore donnez de position &c, la proprieté des tangentes eut été donnée par cette proportion, z.u∷y2/p + ¼p+x.y, c'est à dire si l'equation des tangentes eut été zy- 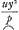 -¼ -¼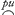 -ux=0, on auroit connu que les termes zy-ux, qui sont les seuls qui ne se doivent pas marquer, dependent d'un seul terme de l'equation de la courbe. Ces termes donnent la proportion ϰ:λ∷1. - 1. Or les termes, qui sont marquez, contiennent les lettres y et u, sans aucun melange de x ou z: c'est pourquoi afin qu'il ne faille pas multiplier ces termes marquez, ou ce qui est le même toute l'equation des tangentes, par quelque quantité, qui contienne la lettre x, je pren l'unité pour le nombre des dimensions de x dans le terme de l'equation de la courbe, parce que dans les termes zy-ux, z n'a qu'une dimension d'un côté, et x n'a aussi qu'une dimension de l'autre côté. Ainsi x/y doit être pris pour le correspondant de zy-ux; mais au lieu de zy-ux il rend z/y-ux/yy c'est à dire zy-ux/yy. Je change donc
l'equation des tangentes en multipliant tous ses termes par 1/yy, et j'ai l'equation zy-ux/yy-u/p-¼pu/yy=0, qui me donne pour l'equation de la courbe, +x/y-y/p + ¼p/y qui avec quelque quantité connue, comme a/g, sont ensemble égaux à zero. Ou, ce qui est le même, j'ai pour l'equation de la courbe, x/y-y/p + ¼p/y= toûjours à une même quantité, comme a/g, qui est connue, (parce que x et y sont donnez pour un cas par les conditions mêmes du probleme) et qui peut être égale à zero, comme dans cet exemple.
Enfin si dans la figure quatrieme on suppose que l'angle PBF soit un angle droit, et si on a cette proportion, z.u.∷ -ux=0, on auroit connu que les termes zy-ux, qui sont les seuls qui ne se doivent pas marquer, dependent d'un seul terme de l'equation de la courbe. Ces termes donnent la proportion ϰ:λ∷1. - 1. Or les termes, qui sont marquez, contiennent les lettres y et u, sans aucun melange de x ou z: c'est pourquoi afin qu'il ne faille pas multiplier ces termes marquez, ou ce qui est le même toute l'equation des tangentes, par quelque quantité, qui contienne la lettre x, je pren l'unité pour le nombre des dimensions de x dans le terme de l'equation de la courbe, parce que dans les termes zy-ux, z n'a qu'une dimension d'un côté, et x n'a aussi qu'une dimension de l'autre côté. Ainsi x/y doit être pris pour le correspondant de zy-ux; mais au lieu de zy-ux il rend z/y-ux/yy c'est à dire zy-ux/yy. Je change donc
l'equation des tangentes en multipliant tous ses termes par 1/yy, et j'ai l'equation zy-ux/yy-u/p-¼pu/yy=0, qui me donne pour l'equation de la courbe, +x/y-y/p + ¼p/y qui avec quelque quantité connue, comme a/g, sont ensemble égaux à zero. Ou, ce qui est le même, j'ai pour l'equation de la courbe, x/y-y/p + ¼p/y= toûjours à une même quantité, comme a/g, qui est connue, (parce que x et y sont donnez pour un cas par les conditions mêmes du probleme) et qui peut être égale à zero, comme dans cet exemple.
Enfin si dans la figure quatrieme on suppose que l'angle PBF soit un angle droit, et si on a cette proportion, z.u.∷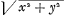 +x.y; quoi que cette proprieté soit celle des tangentes d'une parabole, dont BC est l'axe, C le sommet, et P un point, elle m'est inutile, à cause du signe radical, qui s'etend sur deux termes; et jusques ici je ne peux point juger, par ce qui precede, si cette proprieté des tangentes appartient à une ligne geometrique, ou non. Mais en general je puis être asseuré, comme je le disois tantoit, que si la quantité +x.y; quoi que cette proprieté soit celle des tangentes d'une parabole, dont BC est l'axe, C le sommet, et P un point, elle m'est inutile, à cause du signe radical, qui s'etend sur deux termes; et jusques ici je ne peux point juger, par ce qui precede, si cette proprieté des tangentes appartient à une ligne geometrique, ou non. Mais en general je puis être asseuré, comme je le disois tantoit, que si la quantité 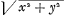 ne peut pas avoir une expression developpée de tous signes radicaux, la ligne courbe ne peut être geometrique. ne peut pas avoir une expression developpée de tous signes radicaux, la ligne courbe ne peut être geometrique.
| |||||||||||||||||||||||||||||||||||||
[pagina 144]
| |||||||||||||||||||||||||||||||||||||
Exemple sur l'Hyperbole.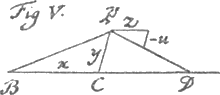 La ligne droite indesinie BCD étant donnée, avec le point P, et les lignes BC, CP, étant x, et y, on demande l'equation de la ligne courbe, qui passe par le point P, et dont les tangentes, comme PD, ont toûjours cette proprieté, que la partie de BCD interceptée entre la tangente et l'ordonnée, par exemple CD, soit égale à x. Ce qui revient à cette proportion, z.-u∷x. y. Donc zy+ux=0 est l'equation des tangentes qui donne xy-ag=0, pour l'equation de la courbe. | |||||||||||||||||||||||||||||||||||||
Exemples sur les paraboles composées.Si, dans la troisieme figure, z.u∷x.⅓y:⅓zy-ux=0 sera l'equation des tan gentes, et on aura ϰ:λ∷⅓. - 1∷1. - 3. On peut donc prendre le terme x/y3 pour le terme correspondant dans l'equation de la courbe. Il rend z/y3-3ux/y4 pour l'equation des tangentes, ce qui suffit, parce que ces quantitez sont entre elles comme ⅓zy - xu, qui font toute l'equation des tangentes, et que par consequent elles sont aussi = 0. Ainsi on a x/y3-1/ag=0 pour l'equation de la courbe. Et si dans la meme figure z.u.∷x.⅖y:⅖zy-ux=0 sera l'equation des tangentes, et on aura ϰ:λ∷2.-5: ainsi x/y5-1/ag2=0 sera l'equation de la courbe. En general si z.u.∷x.m/ny; myz-nux=0 sera l'equation des tangentes, et on aura ϰ:λ∷m. - n: ainsi xm/yn-agm-n-1=0 sera l'equation de la courbe; où xm marque la puissance de x, dont m est l'indice; et de même yn, et gm-n-1 marquent les puissances de y, et de g, dont n, et m-n-1 sont les indices. Il ne faut pas dissimuler la dissiculté suivante, qui regarde en même temps la methode de trouver les tangentes des lignes courbes par leur equation, et la methode de trouver les equations des lignes courbes par la proprieté des tangentes. C'est que si on a dans l'equation de la courbe quelque terme (par exemple x2/y) qui soit une fraction, dont le denominateur renferme quelque inconnue, x, ou y, ou toutes les deux, et qu'on veuille substituer au lieu des x, ou des y, qui peuvent être contenus dans ce terme, leurs valeurs x+z, ou y+u, pour avoir par là les termes de l'equation des tangentes, on ne trouve nullement que cette operation reussisse; et même on ne trouve | |||||||||||||||||||||||||||||||||||||
[pagina 145]
| |||||||||||||||||||||||||||||||||||||
pas qu'elle produise la même chose quand on substitue la valeur d'un même terme exprimé de deux manieres equivalentes (comme x2y/y2 et z2/y). Mais cela n'empeche point que la methode generale dont je me sers ne soit bonne; laquelle revient à substituer 2xz/y-x2u/yy au lieu de x2/y, ce qu'il suffira d'eclaircir par un seul exemple. Soit l'equation de la courbe x2/y+x-y-a=0. L'equation des tangentes selon l'analogie de la regle est 2xz/y+z-x2u/yy-u=0. Or l'equation reduite de la courbe est x2+xy-y2-ay=0. Donc l'equation des tangentes est veritablement et sans difficulté 2xz+zy+xu-2yu-au=0. Et au lieu de a substituant sa valeur x2/y+x-y, l'equation des tangentes est encore 2xz+zy+xu-2yu-x2u/y-xu+yu=0, c'est à dire 2xz+zy-yu-x2u/y=0, ou bien 2xz/y+z-u-x2u/yy=0, precisement comme en suivant l'analogie de la regle. Il en est de même pour toutes les autres equations où il y a des fractions qui renferment x ou y dans leur second terme, comme il paroit assez, et comme il se verifiera toujours par le calcul. Aussi saut il remarquer que ma methode supposant dans son origine que les fractions sont otées de l'equation, si on veut s'epargner la peine de les ôter, il faut necessairement regler le calcul de maniere qu'il soit d'accord avec celui qu'il faut faire, quand on les ôte; et par consequent, si on ne les ôte pas, il faut suivre la regle generale. | |||||||||||||||||||||||||||||||||||||
Exemple sur la courbe Logarithmique.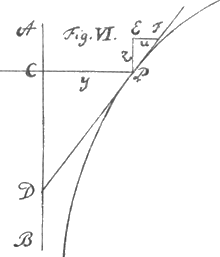 Soit ACDB dans la VIe figure l'assymptote d'une ligne, que les Geometres ont nommée ligne Logarithmique, et soit P un point dans cette ligne. Soit PC la perpendiculaire sur l'assymptote, et FPD la tangente de la courbe en P. La proprieté de cette tangente est que l'interceptée CD est toujours égale à une même ligne a. On demande si la courbe est Geometrique, et en cas qu'elle le soit, on demande son equation. Soit PE, parallele à AB, égale à z; EF, parallele à PC, égale à u, PC = y; et on a par là la proprieté des tangentes z.u∷a.y. Cette proprieté des tangentes se reduit à l'equation des tangentes au-zy=0. Le terme au étant | |||||||||||||||||||||||||||||||||||||
[pagina 146]
| |||||||||||||||||||||||||||||||||||||
marqué, parce qu'il contient la lettre u sans x, reste le terme - zy, qui est correspondant d'un terme où les lettres x et y doivent se trouver necessairement. Or ce terme, qui renferme les lettres x et y, en donne aussi necessairement pour l'equation des tangentes deux autres, qui ont les lettres z et y, et les lettres x et u. Mais comme au lieu des deux il n'y a dans cette equation des tangentes que le terme - zy, il paroit que l'on ne peut trouver d'equation geometrique ordinaire pour la courbe proposee. Ou plûtôt soit l'equation au-zy=0 changée en celle ci, au-zy-1/ωxu=0 où la quantité ω marquant un nombre infiniment grand, le terme - 1/ω xu se trouve simplement = 0, du moins supposant que la quantité 1/ω x soit infiniment petite à l'egard de a ou de y. On a donc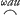 -ωzy-1 xu=0. Les deux termes qui ne sont pas marquez donnent la proportion suivante ϰ.λ∷-ω.1. Or afin qu'en changeant l'equation des tangentes l'on ne fasse pas entrer la quantité x dans le terme ωau, il faut prendre 1 pour le nombre des dimensions de x, parce que dans les termes - ωzy - 1 xu, x et z ont une dimension de part et d'autre. Ainsi on trouve par la proportion - ω. - ∷ 1. 1/ω, que le nombre des dimensions de y sera 1/ω. Or le terme - xy1/ω rend pour l'equation des tangentes -ωzy-1 xu=0. Les deux termes qui ne sont pas marquez donnent la proportion suivante ϰ.λ∷-ω.1. Or afin qu'en changeant l'equation des tangentes l'on ne fasse pas entrer la quantité x dans le terme ωau, il faut prendre 1 pour le nombre des dimensions de x, parce que dans les termes - ωzy - 1 xu, x et z ont une dimension de part et d'autre. Ainsi on trouve par la proportion - ω. - ∷ 1. 1/ω, que le nombre des dimensions de y sera 1/ω. Or le terme - xy1/ω rend pour l'equation des tangentes 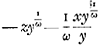 qui sont produits de ωzy-1xu multipliez par qui sont produits de ωzy-1xu multipliez par 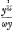 . Et l'equation des tangentes étant changée en celle ci . Et l'equation des tangentes étant changée en celle ci 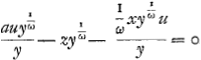 , on a pour sa correspondante
ωay1/ω-xy1/ω=±bg1/ω, qui est une equation approchée, qui exprime à peu près la proprieté de la courbe. Mais pour dire la verité des equations, où l'infini se trouve mélé dans les termes, ne font guere connoitre la nature des lignes courbes, à qui elles appartiennent, et surtout si l'une des inconnues se trouve être d'une longueur infinie. Si on suppose que ω soit égal au nombre 101000, c'est à dire à l'unité suivie de 1000 zero, l'equation sera changée en celle-ci, , on a pour sa correspondante
ωay1/ω-xy1/ω=±bg1/ω, qui est une equation approchée, qui exprime à peu près la proprieté de la courbe. Mais pour dire la verité des equations, où l'infini se trouve mélé dans les termes, ne font guere connoitre la nature des lignes courbes, à qui elles appartiennent, et surtout si l'une des inconnues se trouve être d'une longueur infinie. Si on suppose que ω soit égal au nombre 101000, c'est à dire à l'unité suivie de 1000 zero, l'equation sera changée en celle-ci, 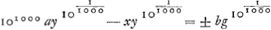 . Si cette equation étoit traittable on pourroit determiner le commencement des x par le moien de deux points donnez de la ligne courbe. Au reste, comme je ne pretens pas determiner ici tout l'usage qu'on pourroit faire de ces sortes d'equations, je ne croi pas non plus qu'on les doive regarder comme tout à fait inutiles. . Si cette equation étoit traittable on pourroit determiner le commencement des x par le moien de deux points donnez de la ligne courbe. Au reste, comme je ne pretens pas determiner ici tout l'usage qu'on pourroit faire de ces sortes d'equations, je ne croi pas non plus qu'on les doive regarder comme tout à fait inutiles.
L'equation au-zy=0 se change en z/a-u/y=0, laquelle devient fort traittable, | |||||||||||||||||||||||||||||||||||||
[pagina 147]
| |||||||||||||||||||||||||||||||||||||
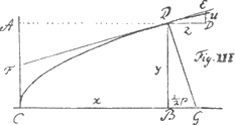
si on fait le y de cette equation égal à g+y ou bien à g-y, g marquant une quantité arbitraire. Car le terme -u/g+y ou -u/g-y se changera en une suite infinie de termes tous traittables et que j'ay trouvez extremement commodes pour rechercher les logarithmes des nombres naturelsGa naar voetnoot8). Outre la maniere qu'on vient de voir dans l'exemple precedent, pour approcher, en certains cas, de la valeur de l'equation de la courbe, il y a encore une autre maniere plus naturelle, et qui est plus d'usage, que j'ai insinuée ci dessus, dont on peut se servir en d'autres occasions, et dont il est à propos de donner un exemple. Soit A dans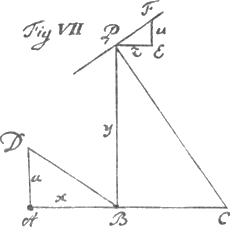 la figure VIIe le commencement des x, ABC leur tige, AB un x, BP une ordonnée y perpendiculairesur AB: on demande quelle est la courbe qui passe par le point P, et dont les tangentes ont toutes cette proprieté que z.u∷y.√x2+a2. Ou, ce qui est le meme, on demande quelle est la courbe, sur qui les perpendiculaires, comme PC, interceptent avec l'ordonnée, avec PB par exemple, la partie BC de la tige égale à √x2+a2, le point B tombant entre les points A et C. La racine de la quantité x2+a2 étant extraite par une operation algebraïque à la maniere ordinaire, qui fera approcher autant qu'on voudra de la valeur de cette racine, l'analogie precedente se change en celle ci. z.u∷y.x+a2/2x-a4/8x3+a6/16x5-5a8/128x7+7a10/256x9 &c à l'infini. Et l'equation des tangentes est - uy + zx + a2z/2x - a4z/8x3 + a6z/16x5 &c à l'infini = 0 D'où l'on deduit l'equation de la courbe - ½yy + ½x2⋆ + a4/16x2 &c à l'infini = ± ag. Comme il se rencontre ici une difficulté particuliere en ce que le terme a2z/2x de l'equation des tangentes ne peut point avoir de correspondant, ce qui procede de ce qu'il ne contient aucune dimension de x, la lettre z aiant une dimension et x aiant - 1 dimension, qui se detruisent l'une l'autre, il vaut mieux se servir de la proportion suivante, où la racine de la quantité x2 + a2 est extraite d'une autre maniere. z. u∷y. a + x2/2a - x4/4a3 + x6/16a5 - 5x8/128a7 + 7x10/256a9 &c à l'infini. | |||||||||||||||||||||||||||||||||||||
[pagina 148]
| |||||||||||||||||||||||||||||||||||||
Et l'equation des tangentes est - uy + az + x2z/2a - x4z/8a3 + x6z/16a5 - 5x8z/128a7 + 7x10z/256a9 &c à l'infini = 0. D'où l'on deduit l'equation de la courbe - ½y2 + ax + x3/6a - x5/40a3 + x7/112a5 - 5x9/1152a7-7x11/2816a9 &c à l'infini = ± ag. Mais avant que d'etre asseuré qu'il n'y ait pas d'equation plus simple de la courbe proposée, il faudroit être asseuré, qu'il n'y peut pas avoir d'expression plus simple, ou plus commode, de la proprieté des tangentes. On comprend aisement, par tout ce qui precede, que la methode de trouver l'equation des tangentes par l'equation de la courbe, et celle de trouver l'equation de la courbe par l'equation des tangentes s'etendent même aux equations, qui contiennent des incommensurables, pourvû que ces incommensurables soient simples, c'est à dire qu'il n'y ait pas plus d'un terme renfermé sous le signe radical. Ainsi l'equation de la courbe a√xy-xy-x√y3/a=0, c'est à dire l'equation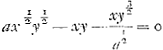 donne l'equation des tangentes ½azx½y½/x-zy-zy3/2/a½+½ax½y½u/y-xu-3/2xuy½/a½=0. Et l'equation des tangentes donne l'equation des tangentes ½azx½y½/x-zy-zy3/2/a½+½ax½y½u/y-xu-3/2xuy½/a½=0. Et l'equation des tangentes
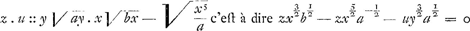 donne l'equation de la courbe ⅖x5/2b½-2/7x7/2a½-⅖y5/2a½±agg=0. Sur quoi il est bon de remarquer qu'à l'egard de toutes les equations geometriques, d'où l'on a fait evanouïr les incommensurables, la proportion des z à u pour l'equation des tangentes se trouve fort simplement, et par des quantitez toutes données, qui ne renferment point d'incommensurable. C'est pourquoi si l'equation donnée de la courbe renferme encore des incommensurables, comme dans le premier de ces deux exemples, on peut bien trouver immediatement, comme je l'ai fait, une equation des tangentes, mais elle renfermera elle même des incommensurables, et ne sera pas la plus simple que l'on auroit pû trouver, quoi qu'elle soit celle qui se presente plus aisement. Quand on a une fois reduit l'equation de la courbe à une expression simple, et sans incommensurables, la plus simple equation des tangentes se trouve aisement, et elle doit toujours avoir cette simplicité, que l'une des quantitez z ou u étant choisie d'une grandeur à discretion, l'autre se puisse determiner par une equation d'une dimension seulement, et sans l'extraction d'aucune racine. | |||||||||||||||||||||||||||||||||||||
[pagina 149]
| |||||||||||||||||||||||||||||||||||||
Il peut arriver que les equations des tangentes, soit qu'elles soient données tout à fait sans incommensurables, ou bien qu'elles soient données avec des incommensurables simples, n'aient point cependant d'equations ordinaires pour correspondantes c'est à dire dont le nombre des termes ou le nombrc des dimensions ne soit pas infini. En ce cas on ne doit pas attendre que les equations des lignes courbes se puissent facilement trouver, et même je ne voi pas qu'on puisse les rechercher toutes par approximation, quoi qu'il y ait lieu d'approcher de la veritable valeur de quelques unes. Au contraire l'equation des tangentes pourroit être donnee d'une telle maniere avec des incommensurables composez, qu'il seroit cependant facile d'approcher de la veritable valeur de l'equation de la courbe. Par exemple si on a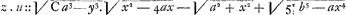 dans laquelle proportion les termes moiens ne contiennent que les lettres u et y, sans x ni z, et les extremes ne contiennent que les lettres z et x, sans y ni u, il est evident, qu'en faisant une operation algebraïque pour l'extraction de chaque racine composée, on changera cette premiere proportion en une autre, où il n'y aura plus d'incommensurables, et où au lieu de chaque racine on aura une suite infinie de termes correspondans. La suite qui resultera de dans laquelle proportion les termes moiens ne contiennent que les lettres u et y, sans x ni z, et les extremes ne contiennent que les lettres z et x, sans y ni u, il est evident, qu'en faisant une operation algebraïque pour l'extraction de chaque racine composée, on changera cette premiere proportion en une autre, où il n'y aura plus d'incommensurables, et où au lieu de chaque racine on aura une suite infinie de termes correspondans. La suite qui resultera de 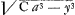 ne contiendra point d'autre lettre inconnue que y et les suites qui resulteront des autres racines ne contiendront point d'autre lettre inconnue que x: c'est pourquoi multipliant les extremes de cette nouvelle proportion l'un par l'autre, et les moiens aussi l'un par l'autre, l'equation qui resultera sera une equation qui peut approcher autant qu'on veut de la veritable equation des tangentes, et dont les termes contiendront les lettres z, x; y, u, mais sans aucun melange de z ou x, avec y ou u: de sorte que l'equation correspondante, qui sera à peu près l'equation même de la courbe, se trouvera par approximation, sans aucune difficulté pour l'ordinaire, et avec telle exactitude que l'on voudra. Or jusque ici je n'ai point rencontré d'autre
difficulté, dans les cas dont je parle, que celle qui resulte de ce que l'un des termes de l'equation des tangentes ne contient quelque fois aucune dimension de y ou de x: ces dimensions se doivent toûjours estimer en prenant z pour une dimension de x et u pour une dimension de y: mais j'ai donné ci dessus à dessein un exemple, où j'ai montré comment cette difficulté se peut lever. Que si dans un sujet si difficile on rencontroit des obstacles, que je n'ai point encore prevenus, je veux croire que ceux qui les rencontreront y pourront aussi trouver des remedes. Mais si ces remedes etoient impossibles à trouver, il seroit impossible aussi de trouver une equation d'une ligne courbe, dont les tangentes eussent la proprieté que l'on supposoit qu'elles deusfent avoir. ne contiendra point d'autre lettre inconnue que y et les suites qui resulteront des autres racines ne contiendront point d'autre lettre inconnue que x: c'est pourquoi multipliant les extremes de cette nouvelle proportion l'un par l'autre, et les moiens aussi l'un par l'autre, l'equation qui resultera sera une equation qui peut approcher autant qu'on veut de la veritable equation des tangentes, et dont les termes contiendront les lettres z, x; y, u, mais sans aucun melange de z ou x, avec y ou u: de sorte que l'equation correspondante, qui sera à peu près l'equation même de la courbe, se trouvera par approximation, sans aucune difficulté pour l'ordinaire, et avec telle exactitude que l'on voudra. Or jusque ici je n'ai point rencontré d'autre
difficulté, dans les cas dont je parle, que celle qui resulte de ce que l'un des termes de l'equation des tangentes ne contient quelque fois aucune dimension de y ou de x: ces dimensions se doivent toûjours estimer en prenant z pour une dimension de x et u pour une dimension de y: mais j'ai donné ci dessus à dessein un exemple, où j'ai montré comment cette difficulté se peut lever. Que si dans un sujet si difficile on rencontroit des obstacles, que je n'ai point encore prevenus, je veux croire que ceux qui les rencontreront y pourront aussi trouver des remedes. Mais si ces remedes etoient impossibles à trouver, il seroit impossible aussi de trouver une equation d'une ligne courbe, dont les tangentes eussent la proprieté que l'on supposoit qu'elles deusfent avoir.
Il y a quelque temps que l'illustre Monsieur Hugens me fit voir en manuscrit la maniere dont il se sert pour determiner les tangentes des lignes courbes par leur equation. Elle n'est pas beaucoup differente de la mienne, et ce n'est qu'après l'avoir veue que je suis entré dans la pensée d'où ma methode dependGa naar voetnoot9). Cependant les principes que nous emploions l'un et l'autre ne sont pas tout à fait les mêmes. Ma methode a ceci de particulier que je m'y sers de deux lettres inconnues z et u, qui répondent aux | |||||||||||||||||||||||||||||||||||||
[pagina 150]
| |||||||||||||||||||||||||||||||||||||
inconnues x et y; ce qui m'aiant donné lieu de remarquer dabord une dependance entre les termes de l'equation de la courbe et les termes de l'equation des tangentes, comme je l'appelle, je jugeai que l'equation des tangentes étant donnée, je pourrois bien remonter jusques à l'equation de la courbe. Je ne me suis étendu dans ces discours qu'autant que j'ai crû qu'il falloit le faire pour les rendre intelligibles. Mais j'ai bien mieux aimé decouvrir à fonds l'origine de cette theorie que de l'appliquer à un grand nombre d'exemples differens. On voit assez qu'elle s'étend à une infinité de cas particuliers, et quand on choisiroit dans une si grande étendue deux ou trois cens exemples, on en laisseroit à peu près autant de reste, que si l'on s'étoit contenté de deux ou trois. J'ajouterai encore un exemple, qui donne beaucoup d'ouverture pour trouver en des cas difficiles l'equation de la courbe par la proprieté des tangentes. Soit z2+u2. u2∷r2. r2-y4/r2 la proprieté des tangentes d'une ligne courbe, dont on demande l'équation. Il faut deduire de l'analogie precedente la proportion de z à u de manière que les termes moiens de cette proportion ne contiennent ni la lettre z ni la lettre x, et que les extremes ne contiennent ni la lettre u ni la lettre y. On trouve donc z2 + u2, - u2.u2∷r2, -r2+y4/r2.r2-y4/r2. C'est à dire z2.u2∷y4/r2.r2-y4/r2: Et substituant l'unité au lieu du dernier terme, r2-y4/r2 afin de rejetter tous les y dans le troisieme terme on a,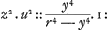 Et tirant la racine quarrée de chaque terme, Et tirant la racine quarrée de chaque terme, 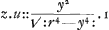 Donc Donc 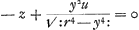 est l'equation des tangentes. A present la racine de r4-y4 se trouve par approximation, suivant les methodes connues, avec telle exactitude que l'on veut. Soit donc est l'equation des tangentes. A present la racine de r4-y4 se trouve par approximation, suivant les methodes connues, avec telle exactitude que l'on veut. Soit donc
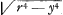 changée en cette suite changée en cette suite
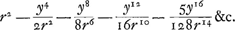 Si on ne juge pas qu'il soit necessaire de continuer cette suite plus loin on a 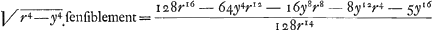 . Divisant donc y2u par cette quantité, on a . Divisant donc y2u par cette quantité, on a
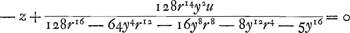 | |||||||||||||||||||||||||||||||||||||
[pagina 151]
| |||||||||||||||||||||||||||||||||||||
pour l'equation des tangentes. Et une division étant faite pour changer cette fraction en une suite infinie de termes qui deviennent traitables, on aura
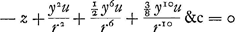 pour l'equation des tangentes, et par consequent 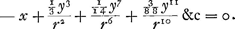 pour l'equation approchee de la courbe. Je vous rens mille graces, Monsieur, pour le present que Vous m'avez fait de vôtre Horologium, et j'espere d'avoir bientôt un nouveau sujet de Vous remerçier, quand j'aurai receu vôtre censure touchant ce que je Vous envoie. Je ne croi pas avoir fait des fautes dans mes calculs, mais si Vous en rencontrez quelques unes, Monsieur, Vous aurez bien la bonté de les pardonner, et de les attribuer ou à ma lassitude, ou a quelque inadvertance en copiant mes premiers écrits. Je crain davantage qu'il y ait peut-être quelque faute dans les exemples qui étaient dans ma premiere lettreGa naar voetnoot10), de quoi neanmoins je ne scaurois juger à present, parce que je n'en ai point ici de copie. Monsieur Boile et le Docteur Wallis m'ont chargé de Vous faire leurs complimens quand je Vous écrirois. Je suis avec un profond respect Monsieur
Votre tres humble et tres obeissant
N. Fatio de Duilliers Oxford ce 12/22 10bre 1687 Mon addresse est à Londres chez Mr. Tourton et Compagnie. |
| ||||||||||||||||||||||||||||||||||||