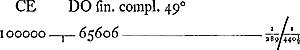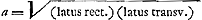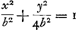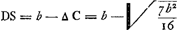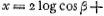Oeuvres complètes. Tome XXI. Cosmologie
(1944)–Christiaan Huygens–
[pagina 389]
| |
Considérations ultérieures sur la forme de la terre,
| |
[pagina 390]
| |
  [Fig. 103]
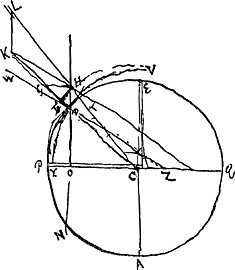
Les poles de la terre sont en P et Q.  In puncto D talis esset perpendiculi à centro C declinatio, nempe 5 min. 54″. Sed superficies liquidi ita sese hic componet ut perpendiculum ipsi sit ad angulos rectos. Producatur perpendiculum WD in Z. dabitur jam ratio CO ad OZ quae est lateris transversi ad rectum, si ellipsis est VDY.  | |
[pagina 391]
| |
§ 2. Sed secundum aequilibrium canalium ut apud NeutonumGa naar voetnoot7) debebat esse excessus [CV-CY] 1/578 meo calculo. Comme ce calcul - voyez sur le résultat le § 12 qui suit - se trouve aux p. 313 et suiv. du Manuscrit F, il paraît probable que le présent passage, emprunté à la p. 299, date d'un peu plus tard que la majeure partie du texte de cette page. Imo ... 100000/173 ∞ 578 ... correcto calculo invenio etiam 1/578. Ceci s'applique au calcul du § 1. Pour l'angle DKH ou KDW de la Fig. 103 Huygens avait pris d'abord (d'ailleurs, si nous voyons bien, sans achever le calcul) 6′ au lieu de 5′54″. Nous nous sommes contentés de reproduire dans le § 1 son ‘calculus accuratior’ où il se sert de cette dernière valeur, et où il trouve pour la fraction considérée 173/100000 c.à.d. 1/578. Ses calculs (§ 2 et § 12) lui fournissent donc l'un et l'autre la fraction 1/578. (et celui du § 4 donne le même résultat). Ergo CV - CY ∞ 1/578 ½ axis minoris CY. Ceci dans l'hypothèse - du moins dans le cas du calcul du § 1 - d'une forme sphéroidale. Mais les §§ qui suivent (§ 4, § 7, § 12) font voir que le calcul de Huygens ne conduit pas précisément à cette forme adoptée, nous l'avons dit, par hypothèse. § 3. Ut pondus absolutum ad pondus in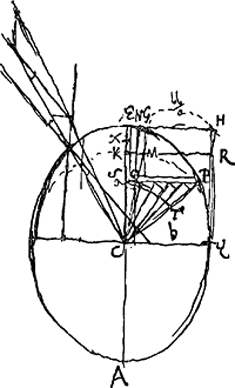 [Fig. 104]
E ita EH ad HG [Fig. 104]. 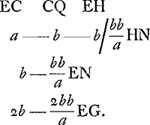 Comme EH = b, il s'ensuit que 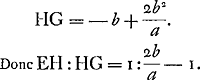 Il en résulte qu'à un rapport EH/HG = 289/288 correspond le rapport 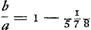 , autrement dit que , autrement dit que 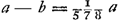 , conformément aux §§ précédents et suivants. , conformément aux §§ précédents et suivants.
| |
[pagina 392]
| |
Nous n'avons pas voulu omettre la Fig. 104 avec le petit calcul correspondant quoique nous ne voyions pas pourquoi Huygens donne au calcul cette tournure. On voit aussi dans la Fig. 104 un canal newtonien ESP (où SE = ½a). Huygens écrit: EX diminutio gravitatis in tubulo SE. Il faudrait donc écrire ensuite que cette diminution du poids, due à la force centrifuge, est telle que l'eau de la partie SE sait équilibre à celle de la partie SP, et tâcher de tirer de là une valeur pour le rapport b/a. Le calcul ébauché par Huygens et que nous ne croyons pas devoir reproduire, est apparemment incorrect et il ne peut y avoir attaché aucune valeur: ce calcul le conduit au résultat a ∞ b. § 4. Si terra esset sphaerica, tum gravitas absoluta ad vim centrifugam in E [Fig. 105] sicut 289 ad 1. Sed vis centrifuga in E ad eam quae in D est ut EC ad DO. Ergo gravitas absoluta ad vim centrifugam in D habet rationem compositam ex 289 ad 1 et ex EC ad DO. 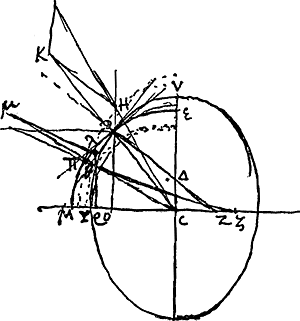 [Fig. 105]
M ou plutôt Y est un pole de la terre, V un point de l'équateur. 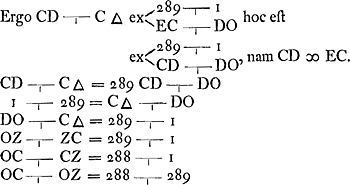 | |
[pagina 393]
| |
Ergo hinc forma ellipseos per D constituendae cognoscitur. cujus latus transversum ad rectum ut 288 ad 289, hoc est in qua CY ad CV ut √288 ad √289, hoc est ut 288½ ad 289 proxime, hoc est ut 577 ad 278, proxime [conformément au résultat du calcul du § 1: voyez le § 2]. Et punctum D in sphaeroide habebit elevationem poli 49o.5′.6″ [lisez 49o5′54″]. Est quidem punctum D et superficies liquidi ibi collocati in sphaeroide par D descripta, centrumque habente C punctum, et rationem lateris transversi ad rectum datam ac constanter eandem, sed si aliud punctum in circumferentia ED π assignatur ut π, invenietur etiam hic superficiem liquidi in sphaeroide esse, centrum C habente, et rationem lateris transversi ad rectum eandam quam sphaeroides VDY, sed non erit huic eadem sed similis, quippe quae per π transibit manente eodem centro C. Videndum ergo an posita ellipsi VDY, et proportione KD ad DH ea quae gravitatis absolutae ad vim centrifugam in D puncto, an inquam, sumto alio in ellipsi eadem puncto θ, et facto ut sicut DO ad θρ ita DH ad θλ, et θμ ∞ DK, an tunc θζ parallela μλ, occurrat ellipsi VDY ad angulos rectos. Remarque ajoutée plus tard: Hoc non poterit fieri, quia pag. 13 (numération de Huygens, correspondant à la p. 312 du Manuscrit F) inventum est lineam hanc curvam non esse ellipsin. [Fig. 106]
Sed hoc per aequilibrium canalium. Hoc tantum itaque possumus ut ostendamus, in singulis terrae sphaericae punctis, aquae superficiem componi secundum superficies sphaeroidum similium circa centrum C et axem CYM constitutorum, quarum sphaeroidum forma ac proportio axium cognoscitur. Et quia omnes vix a sphaera telluris diversae sunt, sequitur ipsam hanc sphaeram ejusmodi sphaeroidis formam affectare. quam tamen non perfecte assequitur. Fit enim alius naturae curva atque ea uno casu, cum nempe vis centrifuga sub aequatore ponitur gravitati aequalis, fit parabola [Fig. 106] ut apparet pag. 12 et 13Ga naar voetnoot8).
§ 5. Pedes ½ diam. terrae 19600000Ga naar voetnoot9). [19600000/587 = ] 33390. tot pedibus terrae semidiameter sub aequatore superat ½ diametrum ad polos. C'est apparemment par erreur que Huygens prend ici 1/587 au lieu de la fraction trouvée 1/578. Cette dernière lui aurait donné 33901 ou, si l'on veut, 33900 pieds. | |
[pagina 394]
| |
[33390/5000 = ] 6⅔ mill. anglic. [ou plutôt, pour 1/578, 6.78 mill. angl.]Ga naar voetnoot10). 12 ⫟ 5 - 6⅔/2 7/9. tot milliaribus gallicis pedum 12000 [ou plutôt 2 33/40 ou 2,825 mill. gall.] § 6. Sit VL ∞ VC [Fig. 107] referens gravitatem absolutam, VG vim centrifugam in V puncto, sive diminutionem gravitatis [l'une et l'autre évidemment en grandeur, 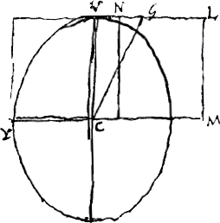 [Fig. 107]
non pas en direction]. Erit LGCM gravitas tota canalis CV. sive ▭ NM, secta VG bifariam in N. Tota vero gravitas canalis CY est ▭ VY. Ergo haec aequalia, nempe ▭ VY et ▭ NM. Ergo VN ∞ VC - CY. Ergo VG ∞ dupla differentiae VC - CY. Hinc si VC ∞ 2 CY, oportet vim centrifugam VG ipsi VL sive VC, hoc est, ipsi gravitati absolutae aequalem esse. Nulla ergo figura ex materia liquida gravi versus centrum et circa axem revoluta formari potest in qua semidiameter VC major sit quam dupla CY. Si enim esset ejusmodi, jam deberet vis centrifuga major esse gravitate absoluta. ac proinde gravia in V posita à centro C aufugerent. § 7. Cum KD ad DH [Fig. 108] ut gravitas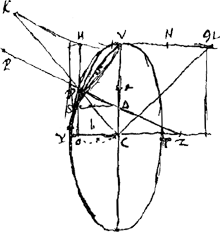 [Fig. 108]
absoluta ad vim centrifugam in D, tunc rectae KH parallelum erit perpendiculum in D, nempe PD. Ideoque superficies liquidi in D sese componet ορθογονως ad PD. DK ∞ VC. DH ∞ ½ VG. Ergo KD ad DH ut gravitas absoluta ad vim centrifugam in D. D ∆ parallela KH deberet am occurrere ellipsi ad angulos rectosGa naar voetnoot11) | |
[pagina 395]
| |
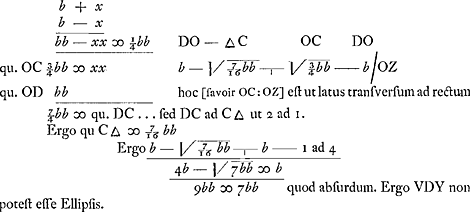 Si punctum D proxime ad Y accipiatur, apparebit facile DO fieri duplam ∆ C. nam quia vis centrifuga in V ad eam quae in D, sicut VC ad DO hoc est ut KD ad DO (nam KD sumitur ∞ VC) atque etiam ut KD ad DH, ideo DO ∞ DH. Sed ut KD ad DH ita DC ad C ∆. Et sumpto puncto D proxime ad Y fit KD dupla DC. Ergo tunc et DH dupla ∆ C, ideoque et DO dupla ∆ C. Ergo convexitas curvae ad Y erit quanta circumferentiae radio TY descriptae. Remarque apparemment ajoutée plus tard: Curvae YDV naturam aequatione expressam habemus folio ab hinc 4o.Ga naar voetnoot12) quae angulum ad V cum recta CV facit 45 gr. Et cui ad datum punctum D tangens ducitur, ponendo ut VC ad CD ita sit OZ ad CZ. Sed et aliter ut ibi ostenditur. Imo curva haec nihil aliud est quam parabola, vertice Y, axe YT. latus rectum ∞ 2CV. | |
[pagina 396]
| |
§ 8. Longueur du pendule sous le pole a celle du pendule sous l'equateur comme 289 ad 288. En laissant donc le pendule sous l'equateur de 289 au lieu de 288, il ira trop lentement, et le nombre de ses vibrations en 24 heures au nombre des vibrations qu'il feroit s'il estoit de 288, sera comme √288 ad √289. C'est a dire comme 288 à 288½ assez pres ou comme 288½ a 289 ou comme 577 a 578. 578 ⫟ 577 - 86400/86250½ 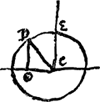 [Fig. 109]
Donc si, estant de 288, il faut 86400 vibrations en 24 heures, qui seront autant de secondes, il fera, estant de 289, 86250½ vibrations en 24 heures. C'est a dire qu'il retardera de 149½ secondes, qui sont assez pres 2½ min.
§ 9. Latitudo Paris. 48.51′50″ a Notre Dame. Ex regula. Sicut qu. EC ad qu. DO [Fig. 109] ita diminutio penduli in E ad diminutionem ejus in DGa naar voetnoot13).  | |
[pagina 397]
| |
 c numerus vibrationum AC penduli [Fig. 110]. [AC = b, AB = a]. a ⫟ √ab - c/c √ab/a numerus vibrationum AB. 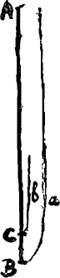 [Fig. 110]
a - a - √ab - c/c - c√ab/a Suivent des calculs sur le retardement du pendule pour toutes les latitudes de 1o à 89o. Ils sont analogues à celui pour le retardement à Paris. P.e. pour 52o: 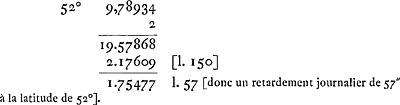 Nous avons fait mention aux p. 639 et suiv. du T. XVIII des observations de Huygens dans les pages suivantes du Manuscrit F sur le rapport de de Graaf sur l'expédition de 1686-1687 au Cap de Bonne Espérance, | |
[pagina 398]
| |
§ 10Ga naar voetnoot17). 3 Dec. 1687. Sit YC ∞ b. CV ∞ x [l'un et l'autre apparemment dans une figure analogue à la Fig. 111; dans la Fig. 112 Huygens prendra YC ∞ b]. p vis centrifuga in V aequalis gravitati absolutae. 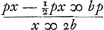
[c.à.d. CV = 2YC. Fig. 111] 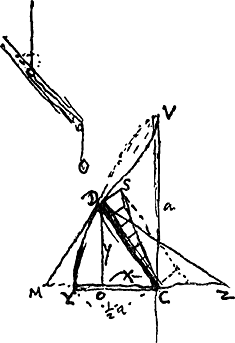 [Fig. 111]
Cum ponatur vis centrifuga in V aequalis gravitati absolutae: erit ½px vis centrifuga canalis VC. quae ablata à pondere canalis CV, quod est px, relinquitur ½px pro pressione canalis VC versus C, quae aequalis debet esse pressioni canalis VC versus C, quae aequalis debet esse pressioni canalis YC versus C, quae est bp. Hinc sit CY ∞ ½CV. Ita semper sequitur ratio CV ad CY ex data ratione vis centrifugae in V ad pondus absolutum. Sit a ∞ VC [Fig. 111]. p pondus absolutum cui aequalis vis centrifuga in V puncto. a - y - p/py/a vis centrifuga in D. Potuissem ponere a etiam pro pondere absoluto, loco p. 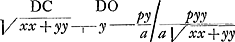 momentum gravitatis quod vis centrifuga in D, in canali DC, aufert a pondere absoluto tendente versus C. Sit DS hoc momentum ratione CV ponderis absoluti. Jam in punctis intermedij canalis DC erit hoc momentum ut applicatae in ∆o CDS. Pondus absolutum minus ½ DS ducitur in DC: tumque hoc productum efficit totum pondus aquae in canali DC, premens versus C: quod aequari debet ponderi YC canalis versus C prementis in quo nulla vis centrifuga unde hoc pondus fit ex YC ducta in p seu VCGa naar voetnoot18). Ex pressione aequali in canalibus DC, YC quaesivi punctum D in curva YDV, ponendo CO ∞ x et OD ∞ y, unde fit aequatio naturam curvae exprimens. Hui curvae tangentem ex methodo duxi MD, fit OM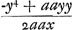 . .
| |
[pagina 399]
| |
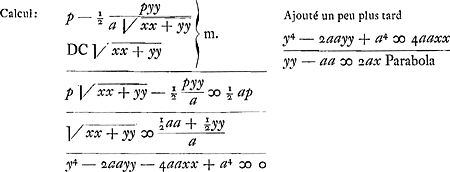 d'où se tire la soustangente OM écrite plus haut suivant la règle que Huygens démontre dans la Pièce académique de 1667Ga naar voetnoot19). 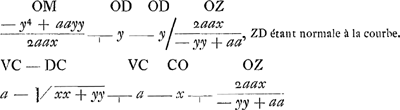 Ajouté plus tard: Haec omnia brevius poterant peragi si animadvertissem parabolam esse.
§ 11Ga naar voetnoot20). Hic quasi tota Tellus ex aqua composita esset ponimus. Et aquas canalium DC, CY [Fig. 112] sese mutuo sustinere seu aequilibres esse ut altera alteram non pellat loco. In Canali CY nulla est aquae vis centrifuga. At in canali CD; quae quantum faciat ad premendum secundum CD, et pro particularum distantia ab axe CY, consideravimus in hoc calculo. Vis centrifuga aquae in canali CD contentae aequatur necessario vi centrifugae aquae si impleatur ea canalis DO, quae est ½nyy/a (p pondus absolutum, CV ∞ a.n vis [Fig. 112]
| |
[pagina 400]
| |
centrifuga in V), ut facile apparet si imaginemur quasi particulae canalis DO singulae in suas vires centrifugas ducantur, hoc enim idem est ac si dimidia DO ducatur in vim centrifugam extremae particulae D. 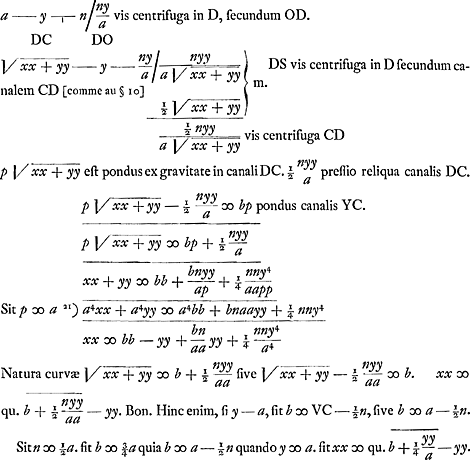 Sit y ∞ 99/100 a. yy ∞ 9801/10000 aa. fit x ∞ ⅛ a proxime. Ergo cum y fere aequalis a fit x major quam ⅛ a. Ergo figura jam tunc ad verticem V rotunditatem habet quando virtus centrifuga ∞ ½ ponderis absoluti. | |
[pagina 401]
| |
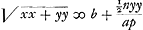 sed b ∞ a - ½an/p quia ap - ½an ∞ bp, hoc est quia pressio canalis VC debet aequilibris esse canali CY.
Ergo sed b ∞ a - ½an/p quia ap - ½an ∞ bp, hoc est quia pressio canalis VC debet aequilibris esse canali CY.
Ergo
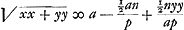 . Ita non opus est b.
Hic si n ∞ p fit . Ita non opus est b.
Hic si n ∞ p fit
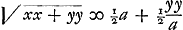 , unde parabola ut videre est pag. 12 [c.à.d.à la p. 311 du Manuscrit F, § 10 qui précède]. cujus latus rectum ∞ 2a. vertex Y, axis YC.
§ 12. , unde parabola ut videre est pag. 12 [c.à.d.à la p. 311 du Manuscrit F, § 10 qui précède]. cujus latus rectum ∞ 2a. vertex Y, axis YC.
§ 12. 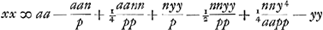 . Natura curvae melius quam pag. praecedenti. Cette équation provient de la substitution de a - ½an/p à b dans l'équation du § 11 . Natura curvae melius quam pag. praecedenti. Cette équation provient de la substitution de a - ½an/p à b dans l'équation du § 11 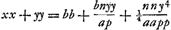 . .
Si n minima, fit xx ∞ aa - yy fere, hoc est circulus proxime. Sit n ∞ ½ p. fit xx ∞ 9/16 aa - ⅝ yy + 1/16 y4/aa. Sit y 99/100 a.xx ∞ 9/16 - 49005/80000 +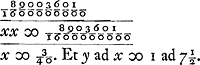 Si n/p ∞ 1/100 vel similis fractio exigua fit xx ∞ 99/100 aa - 99/100 yy proxime. Ellipsis. Si n/p ∞ 1/289 fit xx ∞ 288/289aa - 288/289yy. Ellipsis cujus latus rectum ad transversum ut 288 ad 289. Ideoque axis minor ad majorem ut 288½ ad 289 proxime, hoc est ut 577 ad 578. § 13. Pour faire une Carte Platte du demy globe de la Terre dans laquelle les degrez des meridiens seront egaux entre eux et aux degrez de 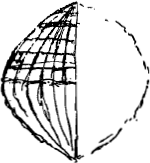 [Fig. 113]
l'Equateur. Et dans chaque parallele les degrez aussi egaux et dans la vraije proportion aux degrez de l'Equateur. On placera facilement dans cette carte [Fig. 113] chaque lieu en sa longitude et latitude. On aura sur une mesme escelle les lieues de leur longitude. Celles des Latitudes auront pour escelles la partie de leur meridien comprise entre les paralleles qui enferment ces lieuxGa naar voetnoot22). | |
[pagina 402]
| |
Les quarrez seront de 10 degrez. Cette carte pourra representer assez bien la figure des Terres. mais celle qui est avec des meridiens paralleles et les degrez de Latitude croissants suivant les secantes des latitudesGa naar voetnoot23) sont plus commodes pour prendre la longitude et latitude des lieux qui y sont marquez et ils ont les rumbsGa naar voetnoot24) exprimez par des lignes droites. 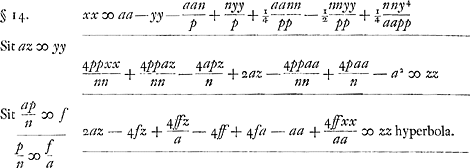 Si f ∞ a [c.àd. si la force centrifuge à l'équateur est égale à la pesanteur] fit 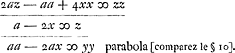 Sit n ∞ ½p. ergo a ∞ ½f, 2a ∞ f. 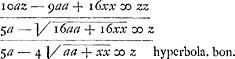 |
|