|
| |
| |
| |
| |
| |
| Page |
Au lieu de |
lisez |
| 129 ligne 2 d'en bas |
Manuscrit G, f. 47 r. Ce qui suit se rattache aux remarques sur l'ouvrage de J. van der Elst.
Ludovicus Viadana inventor Bassi Continui in Polyplectris Ao 1610. Permittit quintas et octavas continenter poni in partibus hisce, quanquam non permittat in cantu. Videndum. Quartas supra quintas, consecutive non posse poni, supra tertias posse. Potius infra cantum continendam symphoniam omnem Bassus continui quo magis emineat cantus. qui quo minus obturbetur, non idem cantus in polyplectro exponendus quem vox sequitur.
L. (Grossi) da Viadana naquit à Mantoue en 1564 et décéda à Gualtieri, probablement en 1645. On connaît beaucoup de ses compositions (messes, madrigaux, motets etc.). En 1620 parurent à Francfort ses ‘Opera omnia sacrorum concentuum etc. cum basso continuo et generali organo applicato etc.’ |
| 130 note 127 ligne 8 |
either or them |
either of them |
| 148 et 149 |
Dans la dernière colonne de la table le signe ♮ doit être remplacé par ♯. |
| 149 ligne 10 |
1) |
11) |
| 149 ligne 12 |
V2) |
V |
| 156 ligne 13 |
fixte |
sixte |
| 156 ligne 16 |
ce que |
ce qui |
| 156 ligne 8 d'en bas |
Le son |
Le ton |
| 169 ligne 8 |
♯l |
s♯l |
| 170 ligne 7 d'en bas |
De la cause des tons ... trompettes etc. - Voyez ce que Huygens dit en 1672 sur la construction de la trompette (T. XIII, p. 804) en parlant de la règle des fondeurs (T. XIX, p. 363, note 3). |
| 179 dernière ligne |
ainfi |
ainsi |
| 180 ligne 10 |
... pas d'espace absolu. - A la p. 658 du T. XVIII (dernière ligne) nous avons écrit par inadvertance, en citant la p. 215 du T. XVI: ‘nullus est mutatio loci respectu spatij mundani’. Le lecteur est prié de corriger ‘nullus’ en ‘nulla’, conformément au texte du T. XVI. |
| 190 note 1 |
La date de la Pièce que nous avons intitulée ‘Le corps, la surface, la ligne, le point’ est sans doute 1690 d'après le lieu que cette Pièce occupe dans le Manuscrit G. Il est vrai qu'on trouve exceptionnellement la date 1692 sur la f. 44: c'est la date, d'après Huygens, de la Pièce ‘Experimenta circa Electrum’ que nous avons publiée aux p. 612 et suiv. du T. XIX. Dans le T. XIX nous avons admis cette date 1692, tout en remarquant (p. 607) que c'est dans une lettre à Leibniz de novembre 1690 que Huygens parle de ses expériences sur ‘les effets de l'ambre’. Il nous semble maintenant extrêmement probable que Huygens se soit trompé en écrivant ‘1692’. C'est sans doute en décembre |
| |
| |
| Page |
Au lieu de |
lisez |
| |
1693 qu'il a inscrit cette date 1692 lorsqu'il ajouta à la relation de ses expériences de 1690 la nouvelle observation de ce mois de décembre 1693 que nous avons publiée dans le T. XIX à la fin du § 17 de la p. 615.
En 1690 parut (avec le Traité de la Lumière) le Discours de la Cause de la Pesanteur, dans lequel Huygens traite e.a. de la forme de la terre (voyez le T. XXI). Qu'elle soit sphérique ou non, il faut bien déterminer, tant sur les globes que sur les cartes, la place de chaque ville ou de chaque vaisseau par la ‘longitudo’ et la ‘latitudo’. Est-ce à cette considération que sont dus les mots biffés, sphaericae conoe .. ae (p. 190)?? |
| 201 ligne 1 |
pendre |
prendre |
| 202 dernière ligne |
.. il commença à se servir du calcul des logarithmes.. |
.. il commença à se servir couramment du calcul des logarithmes... |
| 204 dernières lignes |
.. qu'avant 1661 on ne trouve pas de calculs logarithmiques dans les manuscrits de Huygens. |
.. qu'avant 1661 on ne trouve pas de calculs logarithmiques dans les manuscrits de Huygens (ce qui toutefois n'est pas absolument exact).
En effet, avant 1661, plus précisément en 1657 et 1659, Huygens s'était servi en quelques rares occasions de logarithmes en considérant, en sa qualité d'astronome, différents triangles sphériques. Consultez dans notre T. XV les p. 528 et 531 tirées du Manuscrit K, 367-373 provenant du Manuscrit A. - La date 1657 d'après la note 6 de la p. 11 du T. XVII. |
| 204 note 32 |
1659 |
1695 |
| 206 ligne 8 et note 47 |
Mersenne a-t-il été inspiré par Roberval, comme le suppose Tannery? Voyez sur cette question les lettres de Roberval et de Huygens de 1656, Nos 324 et 329 du T. I, et aussi ce que van Schooten dit en 1650 sur Mersenne et Roberval (T. I, p. 132). |
| 209 lignes 6-10 |
Nous nous sommes trompés en écrivant ‘que le nom de Fermat ne se trouve pas chez Hérigone’ dans la ‘Propos. XXVI. De maximis & minimis’. En effet, il écrit à la p. 68 du T. VI ou Supplementum (de 1644, mais ‘acheué d'imprimer’ en juillet 1642) de son ‘Cursus mathematicus’ ou ‘Cours mathematique’: ‘nec unquam fallit haec methodus, ut asserit ejus inuentor, qui est doctissimus Fermat consiliarius in parlamento Tolosano excellens geometra, nec vlli secundus in arte |
| |
| |
| Page |
Au lieu de |
lisez |
| |
Analytica, etc.’ Comparez la note 1 de la p. 171 du T. I de 1891 des OEuvres de Fermat. |
| 218 ligne 7 d'en bas |
Pièces X et XI |
Pièces IX et X |
| 220 ligne 7 |
d'avoir |
avoir |
| 220 note 136 |
p. 188 |
p. 192 |
| 221 note 138 ligne 2 |
(T. I, p. 334) |
(T. II, p. 334) |
| 228 ligne 4 |
naximales |
maximales |
| 243 ligne 6 |
premier alinéa de la p. - |
premier alinéa de la p. 244 - |
| 257 ligne 14 |
Pièces III et VI |
Pièces III et IV |
| 289 première note |
 Lisez plutôt Lisez plutôt 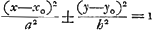 . . |
| 306 ligne 23 |
teperta |
reperta |
| 371 ligne 8 |
Nous n'avons pas voulu dire dans le texte qu'avant Aristote Archytas avait déjà dit (d'après le commentaire de Simplicius sur les Catégories d'Aristote): ἐστὶν ὁ χρόνος ϰινάσις τινος ἀριϑμός. |
| 371 note 12 |
S. Stevin a évidemment fait connaissance avec J.J. Scaliger après que celui-ci s'était établi à Leiden en 1593 comme professeur à l'université. |
| 371 note 12 ligne 8 |
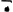 punctum punctum |
. punctum |
| |
Le petit trait horizontal au-dessus du point. ne se trouvait pas dans les épreuves. Nous n'avons donc pas pu le corriger. Il n'a aucun sens et est dû uniquement à ce qu'on appelle en néerlandais le ‘drukfoutenduivel’ (diable des fautes d'impression). Que personne ne s'imagine donc que d'après Scaliger les Arabes se servaient d'un signe 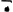 ! ! |
| 372 note 13 ligne 6 |
p. 191 |
p. 192 |
| 372 ligne 4 d'en bas |
‘Arithmetica universalis’ de 1655 |
‘Mathesis universalis sive Arithmeticum opus integrum’ de 1657 |
| |
Voyez le Cap. I (‘De Mathesi in genere’) de la ‘Mathesis universalis’. |
| 373 ligne 7 |
p. 234 |
p. 204 |
| 375 ligne 6 d'en bas |
La lettre de J. Gregory à J. Collins, où il donne la série de l'arc tangente, est de février 1670 vieux flyle, 1671 nouveau style. |
| 376 ligne 14 |
‘La versiera’. On peut consulter sur cette courbe les deux notes, se trouvant respectivement aux p. 151-152 et 251-252 du T. IV de 1912 des OEuvres de Fermat. La première, de H. Brocard, est intitulée ‘La quadrature de la versiera’, l'autre, plus explicite, de A. Aubry ‘Sur l'origine de la versiera’. Après avoir relevé les mêrites de Lalouvère (‘Quadratura circuli’, 1651) Aubry dit e.a.: ‘On terminera l'histoire de la versiera en rappelant .. que James Gregory (Geometricae pars universalis, Padoue, 1668) l'a donnée .. en montrant |
| |
| |
| Page |
Au lieu de |
lisez |
| |
que la quadrature de la versiera se ramène ... à celle du cercle ...’
Le lecteur hollandais peut aussi consulter ‘De versiera’ par E.J. Dijkster huis, article publié dans la revue ‘Euclides’, 1932/1933, Noordhoff, Groningen. |
| 388 lignes 3-2 d'en bas |
Dans ses lettres du 15 juillet et du 26 octobre 1674 à Oldenburg Leibniz n'avait pas fait connaître la forme exacte de sa série. Il se contentait d'écrire: ‘Alia mihi theoremata sunt, momenti non paulo majoris. Ex quibus illud imprimis memorabile est, cujus ope area circuli, vel sectoris ejus dati, exactè exprimi potest per seriem quandam numerorum rationalium continuè productam in infinitum’ .. ‘seriem numerorum rationalium valde simplicem & regularem’. |
| 393 ligne 2 des notes |
2. 16 x3/225 d3 √dx |
Lisez dans cette formule 525 au lieu de 225. |
| 408 ligne 6 |
En 1692 et 1693 Huygens mentionne ‘la methode des Tangentes de M. de Roberval’ (T. X, p. 352 et 440). |
| 411 ligne 6 |
À la Haye (septembre 1670-juillet 1671). |
Lisez juin au lieu de juillet. |
| 414 note 5 ligne 4 |
LVIKIL |
LVIKIL |
| 416 ligne 4 |
inutilus |
inutiles |
| 443 ligne 8 d'en bas |
aequatio x3 ∞ aay [Fig. 87] |
aequatio x3 ∞ ayy [Fig. 87] |
| 449 note 12 |
Pendulum cylindricum trichordon. Dans la note 3 de la p. 532 du T. XVIII nous avons écrit par inadvertance: ‘Caeteris paribus, le moment des forces est proportionnel à tg α, c.à.d. à fort peu près à la longueur des fils’. Le lecteur est prié de corriger cette phrase comme suit: ‘Caeteris paribus, le moment des forces est proportionnel à tg α, c.à.d. pour un même angle de rotation autour de l'axe le moment est à fort peu près inversement proportionnel à la longueur des fils’. |
| 463 ligne 4 |
AH = c, HA = m |
AH = c, HN = m |
| 472 ligne 5 d'en bas |
50 50/49 |
50/ 50/49 |
| 476 ligne 1 |
RAYON MINIMAL |
RAYON DE COURBURE MINIMAL |
| 485 ligne 5 d'en bas |
recherche |
recherches |
| 492 ligne 18 |
egaux perpendiculaires |
egaux aux perpendiculaires |
| 494 ligne 3 d'en bas |
aa ∞ bb |
aa + bb |
| 496 ligne 2 |
‘lemniscate’. Ce fut Jacques Bernoulli qui inventa en 1694 le nom de lemniscata: consultez sa ‘Constructio curvae accessus et recessus aequabilis, ope rectificationis curvae cujusdam algebraicae, addenda nuperae solutioni mensis Junii’ (Acta Eruditorum, Sept. 1694). |
| 496 ligne 4 |
d + oe/d + ooe/dx - ed/x |
d - oe/d + ooe/dx - ed/x |
| |
| |
| Page |
Au lieu de |
lisez |
| 517 ligne 2 d'en bas |
y |
y |
| 540 note 37 |
+ 1/2y |
+ /2yy |
| 552 note 1 |
L'article mathématique de Huygens (voir le T. XXI) ‘Excerpta ex epistola C.H.Z. ad G.G.L.’ (1694) ne se rapporte pas exclusivement à la courbure des voiles. |
|
-
voetnoot1)
- Voyez aussi le deuxième alinéa de la note 56 de la p. 207, où il s'agit d'une correction à apporter dans le T. XIX.
Le lecteur est prié en outre de corriger, également dans le T. XIX, dans la l. 12 de la p. 644, 4ième obiection en 11ième obiection. Et dans la l. 4 de la note 6 de la p. 104 du T. XIX il faut corriger ED en EN.
|


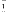 2
2 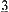 5 6 toe
5 6 toe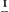 2
2  Lisez plutôt
Lisez plutôt 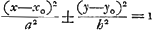 .
.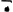 punctum
punctum