Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 467]
| |
V.
| |
[pagina 468]
| |
ST ad bT. Sed ut ▭ ex PP in OT ad ▭ ex bb in bT ita est superficies ex PP circa AB ad superficiem ex bb curva AB. Ergo illa superficies ex PP circa AB ad hanc ex bb circa AB ut ST ad bT. Atque ita tota superficies ex AOC circa AB ad superficiem ex HC circa eandem AB ut portio AXDB ad rectangulum HB. Porro quia superficies ex PP circa AB est ad superficiem ex eadem PP circa AH ut OT distantia ad distantiam OE, fiat ut OT ad OE ita ST ad IT, erit quoque ST ad IT ut superficies ex PP circa AB ad superficiem ex eadem PP circa AH. Atqui erat bT ad ST ut superficies ex bb circa AB ad superficiem ex PP circa AB. Ergo ex aequo erit bT ad IT ut superficies ex bb circa AB ad superficiem ex PP circa AH. Ideoque omnes bT, hoc est ▭ HB ad omnes IT, hoc est ad spatium hyperbolicum ALB, ut omnes superficies ex bb circa AB, ad omnes superficies ex PP circa AH. hoc est ut superficies cylindrica ex HC circa AB, vel ex HA circa CB, ad superficiem ex AC curva circa AH. Est autem I punctum ad hyperbolam descriptam, sicut et L, ut patet ex aequatione superiori. Poterit autem et superficies ex parabolica AC circa BC inveniri, posita quadratura hyperbolae. Datur enim, hac positâ quadraturâ, longitudo parabolicae ACGa naar voetnoot2). Et datur superficies ex AC circa AB. Ergo dabitur centri gravitatis curvae AC distantia ab AB. Cumque etiam detur superficies ex AC circa AH, erit ut superficies ex AC circa AB ad superficiem ex AC circa AH, ita dicta distantia centri gravitatis ad distantiam centri gravitatis ejusdem ab recta AH. Ergo datur quoque haec distantia centri gravitatis ab AH, quare et a BC. Sicut autem distantiae ejus ab AB ad distantiam ab BC ita erit superficies ex AC circa AB ad superficiem ex AC circa BC. quare et haec dabitur. |
|


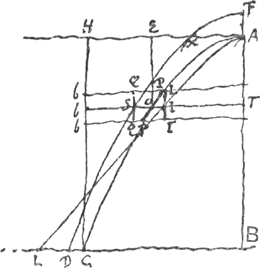
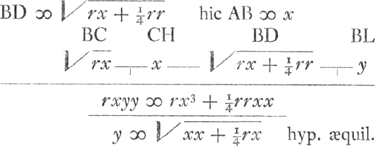
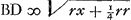 , et descripta parabola FXD cujus latus rectum erat itidem r; erit portio AXDB ad ▭ HB ut superficies parabolica conoidis ACB ad superficiem cylindricam ex conversione HC circa AB, ut notum, quia nempe rectangulum ex particula qualibet parabolae, ut PP ducta in OT distantiam suam ab AB, aequatur rectangulo ex respondente particula QQ parallela AB ducta in distantiam ST. Sed hoc rectangulum ex QQ in ST est ad rectangulum ex respondente bb particula rectae HC in bT, ut ST ad distantiam bT. Ergo et ▭ ex PP in OT est ad ▭ ex bb in bT ut
, et descripta parabola FXD cujus latus rectum erat itidem r; erit portio AXDB ad ▭ HB ut superficies parabolica conoidis ACB ad superficiem cylindricam ex conversione HC circa AB, ut notum, quia nempe rectangulum ex particula qualibet parabolae, ut PP ducta in OT distantiam suam ab AB, aequatur rectangulo ex respondente particula QQ parallela AB ducta in distantiam ST. Sed hoc rectangulum ex QQ in ST est ad rectangulum ex respondente bb particula rectae HC in bT, ut ST ad distantiam bT. Ergo et ▭ ex PP in OT est ad ▭ ex bb in bT ut