Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 463]
| |||||||
IV. Examen Curvae lineae quam Cartesius regulae et fili ductu describere docet, an sit eadem atque Ovalium ipsius primaGa naar voetnoot1). Vid. pag. 54 in Editione Geom.ae 1659Ga naar voetnoot2).
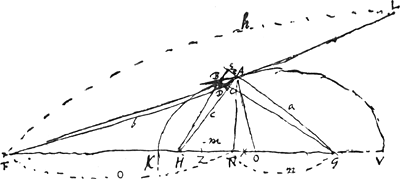
8 Sept. 1690. Curva AB [Fig. 94, où AG = a, AF = b, AH = c, HA = m, NG = n, FN = o, NO = x, AE = e; AB = élement de la courbe; AC, AD, AE = projections orthogonales de AB respectivement sur AH, AF et le prolongement de GA] ejus naturae ut si ad punctum in
| |||||||
[pagina 464]
| |||||||
Cette construction par règle et corde de Descartes s'applique, comme il le dit, au cas où l'on a [Fig. 94] FK = KG.  se trouve à la p. 275 du Manuscrit FGa naar voetnoot3): voyez, aux p. 497-500 qui suivent, les §§ 11, 13 et 16 de la Pièce I des ‘Problèmes et méthodes modernes’. 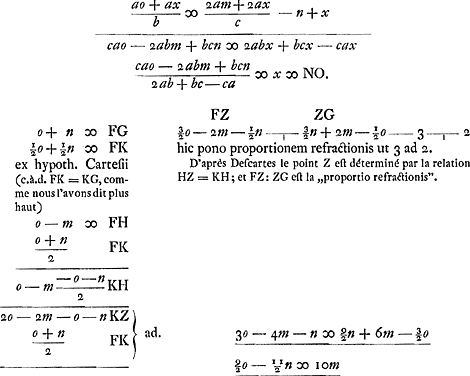 | |||||||
[pagina 465]
| |||||||
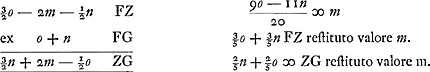 Invenitur tangens Ovalis primae Cartesij ex nostra methodo. Il s'agit de la ‘Méthode des tangentes ... pour les courbes données en coördonnées bipolaires etc.’ dont traite la Pièce I à la p. 491 qui suit. 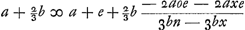 puisque d'après la première construction de Descartes, comme Huygens le dira plus loin, on
puisque d'après la première construction de Descartes, comme Huygens le dira plus loin, on 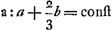 . (l'indice de réfraction étant 3/2); ceci est d'ailleurs vrai pour la première ovale même lorsqu'on n'a pas FK = KG. . (l'indice de réfraction étant 3/2); ceci est d'ailleurs vrai pour la première ovale même lorsqu'on n'a pas FK = KG.
 (Si a ∞ b, ut fit cum punctum curvae sumitur in K, fiet HK c ∞ 5/50 sive 1/10 KF vel KG, quod ita est.) Nota quod certa pars AF minus certa parte AG aequatur AHGa naar voetnoot4). | |||||||
[pagina 466]
| |||||||
Quod si haec Ovalis est eadem quam regula et filo describit Cartesius, etiam tangens utriusque facit aequale intervallum NO seu x. Hoc vero ut fiat, oportet esse 27/50 b - 22/50 a ∞ c in curva ista filari. Sed in ea est  secundum proprietatem à Cartesio suppositam, ut facile apparet.
(a + 2c + h - b ∞ d datae - d est la longueur du fil - secundum Cartesium. Sed et h - LF dans la Fig. 94 - est data. Ergo secundum proprietatem à Cartesio suppositam, ut facile apparet.
(a + 2c + h - b ∞ d datae - d est la longueur du fil - secundum Cartesium. Sed et h - LF dans la Fig. 94 - est data. Ergo 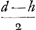 est data linea. est data linea.  ) )
Ergo in hac curva filari erit
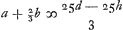 , hoc est 25/3 KZ, oportet jam, si haec curva est eadem cum illa Ovali, ut 5/3KF sit ∞ 25/3 KZ, hoc est KZ ∞ ⅕KF, quod ita est; nam FZ ad ZG ut 3 ad 2 ex constructione Cartesij; unde FG ad GZ ut 5 ad 2, et KG ad GZ [ut] 5 ad 4. Et KG seu KF ad KZ ut 5 ad 1. , hoc est 25/3 KZ, oportet jam, si haec curva est eadem cum illa Ovali, ut 5/3KF sit ∞ 25/3 KZ, hoc est KZ ∞ ⅕KF, quod ita est; nam FZ ad ZG ut 3 ad 2 ex constructione Cartesij; unde FG ad GZ ut 5 ad 2, et KG ad GZ [ut] 5 ad 4. Et KG seu KF ad KZ ut 5 ad 1.
|
|


 ,
,