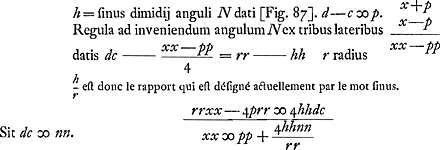Oeuvres complètes. Tome XX. Musique et mathématique

[p. 455]

II. Démonstrations de théorèmes trigonométriques.
[1687]

A. [Trigonométrie plane]. § 1. Datis trianguli duobus lateribus et angulo interjecto invenire latus tertium ipsi oppositum¹⁾.

[Fig. 87]

Jam invenienda radix summae horum duorum quadratorum per tabulas sinuum et logarithmos.

[Fig. 88]

Adde²⁾ logarithmos datorum laterum. Summae dimidiae adde logarithmum sinus

1) Manuscrit F, p. 292. Les p. 285 et 297 portent respectivement les dates août 1687 et septembre 1687.

2) Feuille collée entre les pages 182 et 183 du Manuscrit F. En marge: Vide lib. F, ce qui se rapporte sans doute à la p. 292, où l'on trouve la même règle (Adde logarithmos laterum c et d [Fig. 87] summae dimidiae. Etc.) mais sans exemple numérique. La feuille ne peut guère être antérieure à 1687: voyez la note 1 de la p. 458 qui suit.

[p. 456]

semissis anguli dati, itemque logarithmum binarij. Ab hac summa aufer logarithmum differentiae laterum. Reliquum est logarithmus tangentis anguli, cujus logarithmus sinus, ablatus ab eadem posteriore summa, dabit logarithmum lateris quaesiti.

[Fig. 89]³⁾

2.93702	log. 865	865
2.80072	log. 632	632
_____		_____
5.73774	sum.	233 diff.^a laterum [Fig. 89]
_____
2.86887	dimid.
9.92894	log. sin. ½ ang. dati sive 58^o 6½′
..30103	log. binarij
_____
s.{13.09884	summa
s.{ 2.36736	log. 233 diff.^ae laterum
_____
s.{10.73148	l. tangentis anguli cujusdum
s.{ 9.99264	cujus hic log. sinus
_____
3.10620	log. 1277 lateris nempe quaesiti.

Haec regula nostra brevior est vulgari, quae primo angulum unum quaerere praecipit atque hinc deinde latus propositum. Nostra enim tabulas logarithmicas sexies inspici postulat (nam binarij logarithmus notus est), illa vero octies. Tum in caeteris nostra quoque facilior est.

Il faut en effet consulter huit fois la table des logarithmes lorsqu'on applique d'abord la règle des tangentes pour trouver la différence des angles de la base (d'où se tire ‘angulus unus’), et ensuite celle des sinus pour trouver le ‘latus propositum’, c.à.d. la base.

3) Le triangle à côtés 632, 865, 1277 est considéré par Vlacq dans chacune des éditions de ses Tables mentionnées dans la note 5 qui suit.

[1680]

§ 2. Cette règle des tangentes est formulée et démontrée comme suit par Huygens en un endroit antérieur du même Manuscrit, datant de 1680⁴⁾ et appartenant donc, si l'on veut parler strictement, aux ‘Mathematica varia 1666-1681’:

Theorema trigonometricum utile ad inveniendam anomaliam .... etc. Huygens s'occupe de la construction de son planétaire mentionné aussi à la p. 394 qui précède. En marge: vulgo notum est hoc theorema. Vide Tabb. Vlacqui⁵⁾.

4) P. 2 du Manuscrit F, datant, nous semble-t-il, de la fin de 1680. La p. 239 du Manuscrit E porte la date du 11 mai 1680, celle du 16 novembre 1680 se trouve à la p. 39 du Manuscrit F.

5) Il existe un assez grand nombre d'éditions différentes des Tables de Vlacq. Nous mentionnons les suivantes. 1 ‘Tafels van sinus, tangentes, secantes: Ende van de logarithmi van de sinus, tangentes, Ende van de Getallen van 1 af tot 10000 toe. Nevens de maniere om door de selfde allerley Drie-hoecken, ende veele Astronomische ende Interest-Reeckeninghen te resolveren. Door A. Vlacq. In 's Graven-Hage. By Adriaen Vlacq’, MDCLXI. La III. Prop. du III. Cap. (intitulé: ‘Van de resolutie van de Rechtlinise Scheefhoeckige Drie-hoecken’) est celle-ci: ‘Bekent sijnde de twee zijden, ende een hoeck tusschen beyde, te vinden de andere hoecken’. Vlacq donne, sans la démontrer, la règle suivante: ‘Gelijck de somme van beyde de zijden, Tot het verschil der selfde; Soo is de Tangens van de halve somme der begeerde hoecken, Tot de Tangens van het halve verschil der selfde’. 2. ‘Nieuwe Konstige Tafelen sinuum, tangentium & secantium, oste, vande Hoeckmaten, Raecklijnen, en Snylijnen, met de logarithmis, der Hoeckmaten, en Raecklijnen, Als mede de Logarithmi passende op de getallen van 1 tot 10000... Met sekere aenwijzinge om door deselve alle Rechtlinische en Clootsche Driehoecken, met verscheyde Astronomische vraeg-stucken op te lossen. 't Samengestelt door A. Vlack. En vermeerdert met een nieuw uytgerekende Tafel van de vergrootende breedte, als mede de Tafel der Kromstreeckén [voyez la p. 236 du T. XVII]. Door A. de Graef [voyez sur lui la p. 27 du T. IX]. 't Amsterdam, By Hendrick Doncker, Boeck-verkooper en Graet-boogemaker [voyez sur les ‘graet-boogen’ les p. 627-628 du T. XVIII] in de Nieuwe-brug steeg’, 1665. Vlacq y donne la même règle. 3. ‘Tabulaesinuum, tangentium et secantium, et logarithmi sinuum, tangentium ... cum Methodo facillimâ, illarum ope, resolvendi omnia Triangula Rectilinea & Sphaerica, & plurimas Quaestiones Astronomicas, ab A. Vlacq. Editio ultima emendata & aucta. Amstelaedami, Apud Henricum & Viduam Theodori Boom’, MDCLXXXI. La règle (toujours dépourvue de démonstration) y a la forme suivante (p. 16): ‘Ut aggregatum datorum laterum, Ad differentiam eorundem; Sic Tangens semissis aggregati angulorum quaesitorum, Ad Tangentem semissis differentiae eorundem’.

[p. 457]

ABC [Fig. 90] triangulum. Erit ut summa laterum AB, BC, ad eorum differentiam ita tangens dimidiae summae angulorum A, C, ad tangentem dimidiae ipsorum differentiae.

[Fig. 90]

Mea demonstratio. Producatur AB, ut sit BD aequalis BC. jungaturque DC, itemque puncta E, F quae rectas AD, DC secant bifariam, et ducatur BF, ac denique BG parallela EF sive AC. Erit jam angulus DBC aequalis duobus BAC, BCA. ac proinde angulus DBF aequalis dimidiae summae ipsorum. à qua auferendo angulum DBG aequalem BCA, relinquetur GBF aequalis ½ differentiae angulorum BCA, BAC. Sumta itaque BF pro radio, oportet ostendere tangentem DF esse ad tangentem GF, sicut summa laterum AB, BC ad ipsorum differentiam, sive ut dimidia summa, quae est ED, ad dimidiam differentiam, quae est EB. Hoc autem manifestum est, quum EF, BG sint parallelae.

[p. 458]

[1687?]

B. [Trigonométrie sphérique et trigonométrie plane]. § 1. Trianguli sphaerici [Fig. 91] datis tribus lateribus invenire angulum quemlibet¹⁾.

[Fig. 91]

Vergaert de drij sijden te samen, vande helft der somme treckt elcke sijde om den begeerden hoeck. komen twee resten²⁾. Nu gelijck den radius tot sinus van eene sijde om den begeerden hoeck, alsoo sinus van d'ander sijde om den selven hoeck tot een 4^de getal. Dan voort

Gelijck dit 4^de getal tot sinus van het eene verschil, alsoo sinus van 't ander verschil tot de halve pijl van den begeerden hoeck. dese halve pijl met den radius gedeelt³⁾ en van 't product de wortel uytgetrocken sal geven sinus van den halven begeerden hoeck.

Het product van de sinus der twee resten multipliceert met het quadraet vanden radius. dit product divideert door het product van de 2 sinus der sijden aen den begeerden hoeck. de quadraetwortel uijt het product sal sijn de sinus van den halven begeerden hoeck.

Hinc regula illa per logarithmos utilissima, cujus quis sit auctor nescio⁴⁾. logarithmis των a et b adde duplum logarithmum radij. A summa omnium aufer summam logarithmorum των c et d. Reliqui semissis erit log. sinus anguli dimidij quaesiti.

Dans le tableau c et d représentent les sinus des arcs EP et ES, et a et b les sinus des termes ½ (- EP + ES + PS) et ½ (EP - ES + PS). r est l'inévitable rayon. En prenant, comme nous le faisons actuellement, les sinus comme des rapports on a sin ½ .

1) Petite feuille collée dans le Manuscrit F entre les p. 182 et 183 (comparez la note 2 de la p. 455). La feuille semble ne pas être antérieure à 1687, puisqu'à la p. 295 du Manuscrit F Huygens paraît ne pas encore connaître la démonstration de la règle ici considérée: il énonce quelques propriétés du triangle sphérique disant: ‘An hinc regula illa nota inveniri potest?’ Il est vrai que les p. 295-296 constituent aussi une feuille détachée (non collée et du format du Manuscrit).

2) Chez Vlacq (éd. de 1665, voir la note 5 de la p. 456): ‘Addeert de drie sijden te samen, en treckt elcke syde aen de bekende hoeck van de helft haerder somme, om het verschil der selfden te hebben’. Etc.

3) Pour trouver la formule √abrr/cd - voir la suite du texte - et non pas √ab/cd, il faudrait lire ‘gemultipliceert’ au lieu de ‘gedeelt’.

4) Huygens semble donc ne pas avoir consulté - nous l'avons déjà dit dans l'Avertissement - la ‘Mirifici Logarithmorum Canonis descriptio’ de 1614 de Neper.

[p. 459]

Vel addeert de arithmetische complementen van de logarithmi der sinus der sijden die den begeerden hoeck begrijpen, bij de logarithmi vande sinus der gevonden verschillen. De helft van de somme sal de logarithmus sijn vande halve begeerde hoeck.

§ 2. [Demonstratio]. ESP [Fig. 92] is de gegevene driehoeck. SEP de begeerde hoeck. Neemt EC ∞ ES. En PY ∞ PS. XW snijde CY in 2 gelijcke. Soo is EW

[Fig. 92]

de halve somme der 3 sijden. en CW is het verschil tusschen ES en dese halve somme. en PW het verschil tusschen EP en het selvige.

Sij CI en PV perpend. op EX; Soo sijn dit de sinus der boghen ES of EC en PE. CK is sinus van CW. En YQ rechthoekigh door XP treckende, die CI snijdt in Z, soo is PQ ∞ PY. En dan QC treckende; en, door het midden der selve, XOA, soo is AC ∞ AQ, en bij gevolg AP ∞ ½ CY, of CW, en CA ∞ WP. En daerom CO sinus van PW, het ander verschil. Treckt SZ. Als mede DG perpend. op

[p. 460]

XH. EN XM perp. op DH en MN paral. DG. Treckt voorts CF parall. met PX, en IF parall. met QY: soo is de ∆ CFI gelijcformigh aen PXV, als licht is te sien. Daerom XP tot PV als IC tot CF. Dat is de radius tot sinus der sijde EP als de sinus der sijde ES of EC tot een vierde linie CF. Soo moet dan voorts bewesen werden dat CF is tot CK als CO tot HN, halve pijl in den hoeck HXD of PES. En marge: pijl ipsi⁵⁾ est sinus versus.

Voorts dewijl ZT, IF parall. sijn, soo is CF tot CT als CI tot CZ. Maer HX is tot HG als CI tot CZ. volgens 't geene hier nae bewesen sal werden.

Daerom CF tot CT als HX tot HG.

Voorts dewijl den boogh AC de helft is van QAC, daerom is den hoeck AXC ∞ QYC. dat is OXC ∞ TYC. Maer de hoecken in CTY sijn recht, daerom de ∆ ^en COX, CTY gelijckformigh. En bij gevolg CT tot CY als CO tot CX. Maer wij hadden te vooren CF tot CT als HX of CX tot HG, daerom CF tot CY als CO tot HG. of CF tot CK als CO tot HN. 't welck moest bewesen werden.

Dewijl nu die hoeck XMH recht is, als oock MNH, soo is MH sinus van den halven hoeck HXD of PES, middelproportioneel tusschen NH en den radius HX. En daerom HX met HN gemultipliceert sal de wortel van 't product geven HM. 't welck noch overigh was te bewijsen.

'T geene geseght is dat HX is tot HG als CI tot CZ, werd aldus bewesen. Dewijl PS ∞ PY, soo is den boogh SY in het vlack 't welck de sphaera snijdt en rechthoeckigh is op PX. in 't welck oock YZQ sijnde, soo is oock SZ in 't selve vlack: Maer dit vlack is rechthoekigh op EHX, en soo is oock het vlack ISC. Daerom de gemeene snee SZ der vlacken ISC en YZS, sal rechthoeckigh sijn op het vlack EHX, en oock SZ perpend. op IC. en daerom parallel met DG. Soo is dan DX of HX tot XG als SI of CI tot IZ. En HX tot HG gelijck CI tot CZ, 't welck bethoont moest werden.

§ 3. Datis trianguli plani [Fig. 93] tribus lateribus invenire angulum quemlibet.

[Fig. 93]

⁶⁾

5) Vlacq, pensons-nous.

6) Les deux équations qui suivent correspondent en effet à une des deux règles données par Vlacq.

[p. 461]

√rrab/dc sinus dimidij anguli N. Ergo hic in triangulis planis eadem est regula quae in sphaericis, nisi quod in his sinus laterum et differentiarum laterum adhibentur, cum in illis latera ipsa et differentiae adhibeantur. utrobique adduntur primum tria latera, et a summae dimidio auferuntur singula latera angulum quaesitum comprehendentia ut fiant differentiae duae.