Mathematica varia 1681-1695.
I.
A propos du ‘Pendulum cylindricum trichordon’ (Sinusoïde et parabole, courbes osculatrices).
[1683]
En considérant dans le T. XVIII les calculs de Huygens qui se rapportent au ‘pendulum cylindricum trichordon’ nous avons renvoyé le lecteur (p. 530, première note et note 2) à ‘un des Tomes suivants’ pour les deux questions que voici:
1. Comment Huygens a-t-il pu dire que la ‘curva bgεq [sinusoïde ou “compagne de la roulette”, Fig. 25 de la p. 528] est aequalis curvae dimidiae Ellipsis ahb posita eh potentiâ dupla ad radium ae’?
2. Comment a-t-il calculé que la distance verticale PG entre un certain point P de la courbe BPL [Fig. 23 de la p. 527] qui devient une parabole lorsqu'on déroule sur un plan le cylindre sur lequel elle se trouve, et le point correspondant G de la courbe BGO qui par cette évolution devient une sinusoïde, est inférieure à 1/1000 AB, c.à.d. à 1/1000 du diamètre du cylindre?
1. La réponse à la première question est bien simple. Il n'est nullement besoin de considérer, comme nous le faisions dans la note 2 de la p. 530, la méthode de Pascal pour réduire ‘la dimension des lignes de toutes sortes de roulettes ... à des lignes eliptiques’. Il suffit de se rappeler ce que nous disions à la p. 511 de l'Avertissement: que Huygens savait qu'on obtient la ‘linea sinuum’ non seulement, comme dans la Pièce sur le ‘pendulum cyl. trichordon’, par l'évolution sur un plan de la ‘ligne cyclocylindrique’, mais aussi ‘par le développement sur un plan de la section elliptique obtenue en coupant un cylindre par un plan incliné à 45o’Ga naar voetnoot1). Or, dans cette section elliptique - voyez ce que Huygens dit plus haut sur la ‘potentiâ dupla’ - le grand axe est égal au produit du petit axe par √2.
2. Dans nos notes du T. XVIII nous nous sommes servis du développement du cosinus en une série. En 1683 la série du cosinus - voyez l'Avertissement - était sans doute connue, grâce à Newton, à un nombre restreint de personnes, mais Huygens ne faisait pas partie de ce cercle. C'est donc, pensons-nous, par un calcul directGa naar voetnoot2), qu'il a trouvé la fraction 1/1000 en question. Ce ne fut qu'en 1685 ou 1686Ga naar voetnoot3) qu'il apprit à connaître par l'Algèbre de Wallis quelques séries de Newton d'ailleurs dépourvues de démonstrations.
Une remarque analogue s'applique au cas du § 3 des p. 530 et suiv.; sans doute c'est par une
Auteursrecht onbekend
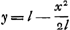se rapproche fortement de la courbe à équation 
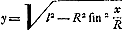(note 3 de la p. 531): l'une et l'autre courbe a, pour x = 0, c'est à dire là où les deux courbes se touchent, le rayon de courbure l (ou plutôt - l), de sorte qu'elles sont osculatrices (comme la parabole et la sinusoïde - correspondant au cas l = R - précédemment considérées) pour employer l'expression de Leibniz de 1686Ga naar voetnoot4). Ces sortes de contact entrent naturellement dans mes Evolutions de Lignes courbes, écrira Huygens en 1691Ga naar voetnoot5).