Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 405]
| |
Mathematica varia 1666-1681. | |
[pagina 407]
| |
Avertissement.Comme on peut le voir dans la suite du présent Tome, c'est surtout après sa rentrée définitive en Hollande, donc après 1681, que Huygens s'appliqua de nouveau avec ardeur, comme dans sa jeunesse, aux mathématiques puresGa naar voetnoot1): c'est surtout vers la fin du siècle que le calcul infinitésimal prit son essor triomphal. La présence de Roberval et de Frenicle de BessyGa naar voetnoot2) à l'Académie ne semble pas l'avoir fortement incité à s'occuper dans la période française de sa vie qui s'ouvre en 1666 de sujets de mathématique pure intéressant spécialement l'un ou l'autre de ces collèguesGa naar voetnoot4). Voyez toutefois le nom de Roberval dans la Pièce I, 2, B qui suit et de même dans la Pièce 1, 2, A, datant également de 1668, celui d'un autre collègue, le physicien Mariotte. Roemer, membre depuis 1672, a été mentionné dans le T. XVIIIGa naar voetnoot5) là où il était question de l'épicycloïde (année 1674); voyez aussi à la fin de la Pièce III, 4 de 1676 qui suit la ‘methodus Romeri’ rapportée par Huygens Ga naar voetnoot3) | |
[pagina 408]
| |
pour résoudre un problème planimétrique. La présence de de la Hire à l'Académie, depuis 1678, eut plus d'influence sur lui - nous parlons toujours de la mathématique pure - comme nous l'avons exposé aux p. 219-222 et dans la note 5 de la p. 335. Cette influence persista même après 1681Ga naar voetnoot6). Les Pièces III, 1 et IV, 2 sur la question des signes dans les équations de géométrie analytique (la Pièce IV, 2 de 1676 ou 1677 n'est qu'un développement un peu plus ample de celle, III, 1, de 1672) peuvent paraître bien simples. Mais ce sont précisément ces choses simples (équivalence des deux axes, celui des x et celui des y, et équivalence de leurs parties positives et négatives) qui ont de l'importance. Voyez aussi ce que nous avons dit à la p. 217 sur l'expression simple: aequatio parabolae, équation de la paraboleGa naar voetnoot7). C'est aussi une remarque simple, mais sur laquelle cependant une différence d'opinion était possible, que celle de la Pièce I, 2, B (nous avons déjà dit qu'on y trouve le nom de Roberval), d'après laquelle les équations algébriques servant à résoudre un problème déterminé fournissent souvent spontanément des solutions d'un problème plus général. Les carrés magiques, ainsi que d'autres questions sur les nombres, n'avaient pas d'attrait puissant pour HuygensGa naar voetnoot8). La composition de son article de 1668 ‘De combinationum mirandis’Ga naar voetnoot9) atteste-t-elle pourtant une certaine influence de Frenicle sur sa pensée? Nous avons déjà remarqué à la p. 20 du T XIVGa naar voetnoot10) que jadis Huygens ne s'était pas servi d'analyse combinatoire (§ 2 de la présente Pièce) dans son traité ‘Van Rekeningh in Spelen van Geluck’ de 1657. Voyez encore ce que nous disons sur Frenicle à la fin du présent Avertissement et consultez l'Appendice de la p. 419 qui suit. Au § 1 qui se rattache à sa considération de 1661 de la ligne logarithmique, Huygens établit les formules Somme des logarithmes des nombres entiers jusqu'à log n (inclus) 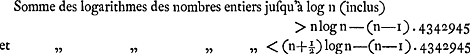 | |
[pagina 409]
| |
(où log désigne le logarithme à base 10, celui de 10 étant 10 millions); on peut donc dire, en désignant le nombre 4342945 par log e (ce qui est un anachronisme), que suivant Huygens 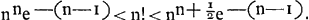
La célèbre formule de Stirling de 1730, qui peut s'écrire 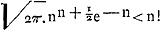
ressemble beaucoup à celle de Huygens ainsi formulée: le rapport du ‘terminus minor’ de Huygens à celui de Stirling (ce dernier étant plus exact) est e/√2πn. Quant au ‘terminus major’ de Huygens il est au ‘terminus minor’ de Stirling dans le rapport e/√2π = 1,084: c'est un ‘terminus major’ fort exact, tandis que le ‘terminus minor’ lui aussi n'est pas sans valeur.
La formule du § 2 pour le nombre de permutations possibles (‘numerus transpositionum’) lorsque les n lettres considérées ne sont pas toutes différentes, mais qu'il existe parmi elles p.e. trois groupes, aux nombres m1, m2 et m3, de lettres égales entr'elles, savoir (en notation moderne) n!/m1! m2! m3!, était loin d'être généralement connue puisqu'en 1666 Leibniz dans son oeuvre de jeunesse ‘Dissertatio de arte combinatoria’ commet une faute dans la considération d'un cas de ce genre, écrivantGa naar voetnoot11) 6! - 5! au lieu de 6! + 2! pour le nombre des permutations (‘variationes’) des syllabes ut ut re mi fa solGa naar voetnoot12). Mais cette formule n'est pas de Huygens: tout-le-monde pouvait la trouver chez Mersenne dans les ‘Harmonicorum libri’ de 1635 ou bien dans l'‘Harmonie Universelle’ de 1636. Déjà dans ‘La Vérité des Sciences’ de 1625 | |
[pagina 410]
| |
Mersenne considère les ‘combinations’ en connexion avec sa théorie des plus beaux chants, dont nous avons parlé à la p. 66 qui précède; en cette année il connaît la formule n! mais pas encore la formule n!/m1! m2! m3!. Dans son article posthume sur les combinaisons Frenicle cite au début les ‘Harmonicorum libri.’Ga naar voetnoot13) |
|

