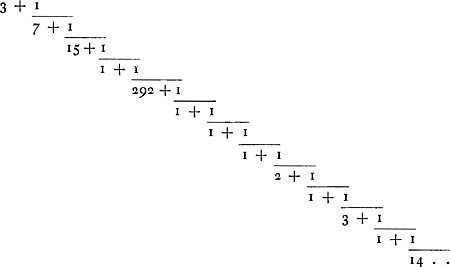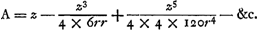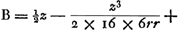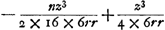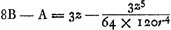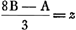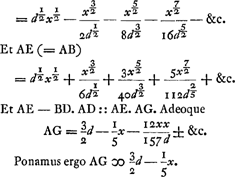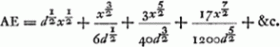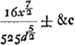1146408Ga naar voetnoot10). 1725033 a 5419351 et plusieurs autres en suite. Il nomme ces nombres incrementa. item 52746197 a 165707065.
Il se propose aussi cette proportion, 2684769 a 8376571, pour trouver la plus prochaine majeure ou mineure qui se puisse exprimer en nombres qui n'ayent que trois chifres. Et il conclut que la fraction 25/78 est la plus prochaine majeure et 308/951 la plus prochaine mineure ce qui est vray.
Huygens cite le livre de Wallis déjà à la p. 252 du Manuscrit F et calcule ensuite diverses fractions continuesGa naar voetnoot9). Notons que Brouncker avait réussi à développer en une fraction continue la formule de Wallis pour 4/π (p. 373 qui précède) ce dont Wallis traite dans son livre de 1685. A la p. 256 du Manuscrit F se trouve pour le rapport de la circonférence du cercle au diametre (notre nombre π) la valeur
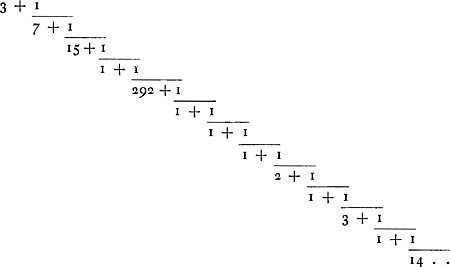
Huygens calcule même encore les dénominateurs suivants 2, 1, 1, 2, 2, 1. Sa ‘Descriptio Automati Planetarii’ (dans la présente Pièce il donne à cette construction le nom de ‘Planetologe’) auquel ce calcul était destiné - nous la publierons dans le Tome suivant - ne parut qu'en 1703 dans les ‘Opuscula postuma’. Il n'a pas jugé nécessaire de publier séparément la présente approximation du ‘numerus impossibilis’.
|
-
voetnoot1)
- Manuscrit F, p. 255. Il y a des dates de 1686 avant cette page (à la p. 239 du Manuscrit Huygens discute un article de Leibniz de septembre 1686; voyez la p. 162 du T. XIX), la date 1687 se trouve à la p. 261. Il s'agit du livre mentionné dans le catalogue de vente de 1695 des livres de Huygens: ‘A Treatise of Algebra both Historical and Practical by John Wallis, London 1685’ (Libri Mathem. in Folio, 81). Voyez sur l'édition latine du traité la note 1 de la p. 18 du T. X. Nous le citons d'après le texte latin (‘Tractatus ... auctus’) des ‘Opera mathematica’ (où l'on peut distinguer les additions du texte primitif).
-
voetnoot2)
- Cap. 83: ‘Quadratura Circuli, non designanda secundum ullum antea receptum numeros Notandi modum’.
-
voetnoot3)
- C'est dans le Scholium appartenant à la Prop. CXC de l'‘Arithmetica infinitorum’ de 1655 que Wallis s'exprime comme suit: ‘Et quidem proclivis sum ut credam (quod & ab initio suspicatus sum) rationem illam quam quaerimus talem esse ut quae non poterit numeris exprimi juxta ullum adhuc receptum notationis modum, ne quidem per latera surda; (quale quid instruit Schootenius, de radicibus Aequationum quarundam cubicarum, in ipsius Appendice ad tractatum de Organica Conicarum Sectionum Descriptione, idque ad mentem Vietaei, Cartesii, & aliorum;) ut necesse videatur aliam ejusmodi rationem explicandi modum introducere, quam vel per numeros veros, vel etiam per recepta latera surda. Atque haec quidem nostra sive sententia, sive conjectura, hinc confirmari videtur:’ Etc.
Wallis cite l'‘Appendix, de cubicarum aequationum resolutione’ de van Schooten qui suit ses ‘Commentarii’ sur les livres de Descartes dans son Recueil bien connu. Après avoir énoncé la règle dite de Cardan van Schooten parle de ‘ejus aequationis radices, aliàs numero non explicabiles’.
-
voetnoot4)
- Cap. 79 (ou plutôt LXXIX): ‘D. Fermatij Exceptionibus respondetur’. Voyez sur les démonstrations par induction, outre la note suivante, la p. 213 qui précède (avec la note 92).
-
voetnoot5)
- Dans son article ‘Sur l'oeuvre mathématique de Blaise Pascal’ (‘Revue des Questions scientifiques’, janvier et avril 1924, Louvain, Fr. Ceuterick) H. Bosmans écrit: ‘L'induction complète [expression dont Bernoulli ne se sert pas encore; il désigne donc le procédé de Wallis non pas par les mots “induction incomplète” mais, on l'a vu, simplement par l'expression “induction”, comme le fait aussi Huygens] était une méthode aussi ancienne que la Géométrie elle-même. Les Grecs la connaissaient et l'employaient souvent. Mais, de sa plume magique, Pascal lui donne un tour nouveau, lumineux, simple et alerte, qui est demeuré définitif. - Le lecteur en conclura peut-être, que la nouvelle sorme donnée à la méthode de l'induction complète fit aussitôt fortune? - Qu'il ne se hâte pas trop. Elle passa au
contraire presqu'inaperçue. Par une de ces bizarreries, dont l'histoire des mathématiques nous offre maint exemple, elle fut même si peu remarquée, que vingt et un an plus tard, dans le cahier de juillet 1686 des Acta Eruditorum, Jaques Bernoulli croyait visiblement l'inventer pour rendre rigoureux un raisonnement par induction incomplète de Wallis’.
Citons encore sur ce sujet A. Prag écrivant en 1931 dans son article ‘John Wallis (1616-1703)’ (‘Quellen und Studien zur Geschichte de Mathematik’, Abt. B. Bd. 1, Berlin, J. Springer): ‘Wallis weiss, dass Induktion in ganzen Zahlen ein Characteristikum arithmetischer Schlussweise ist [observons que Prag sait fort bien que l'induction de Wallis ne se rapporte pas seulement aux nombres entiers dont il est question dans l'article de Bernoulli; ce n'est pas en dernier lieu d'exposants fractionnaires qu'il s'agit]. Er macht sich Gedanken über die prinzipielle Zulässigkeit solcher Schlüsse ... was Wallis hier sagt ist ... barer Unsinn [?] ... aber das Problem das hinter diesen Ueberlegungen steht ist überaus wichtig ... Darstellung der Funktion durch die Tabelle, die die Zuordnung stark betont ... Sicher gehört in den Bereich funktionaler Betrachtungen dieser zweiten Art die Begründung des Verfahrens der “vollständigen” Induktion. So weit konnte Wallis nicht vordringen’.
-
voetnoot6)
- Dans le Cap. 91: ‘Doctrina Serierum Infinitarum, ulterius à D. Newtono promota’ Wallis dit: ‘Approximationes illae (in Arithmetica Infinitorum) supra memoratae (pro Circulo, Ellipsi & Hyperbola) occasionem fecerunt aliis ulterius in eam rem inquirendi; similesque approximationes exquirendi in casibus aliis. Quae jam dici coeperunt Infinitae Series, aut Series convergentes, aliisve nominibus tantundem indicantibus. Inter ea quae ego hoc in genere conspexi: Non alium video qui speculationem hanc subtilius prosecutus est & cum meliori successu, quam Vir Clar. Isaacus Newton, Matheseos Professor meritissimus in Celeberrima Academia Cantabrigiensi. Qui circa annum (ut conjicio) 1664 aut 1665 speculationem hanc magna sagacitate prosecutus est (sed eam per aliquot annos ad alia studia avocatus intermiserat speculationem). Quod innotuit mihi ex duabus Epistolis ab eo ad Clar. Virum D. Henricum Oldenburgium (Regiae Societatis Londinensis tum Secretarium) ea de re scriptis (13 Junii & 24 Augusti anni 1676), Societati Regiae Communicandis, quas inde mihi impertivit Oldenburgius; ingenue quidem scriptas & luce publica dignissimas’. Etc.
Nous avons déjà dit dans l'Avertissement (p. 374) qu'Oldenburg envoya aussi des copies de ces deux lettres de Newton à Leibniz. On les trouve aux p. 179 et 203, nos XLIII et XLV, du recueil ‘Der Briefwechsel von G.W. Leibniz mit Mathematikern’, éd. C.I. Gerhardt, I, Berlin, Mayer & Müller 1899, d'après les manuscrits conservés dans la Bibliothèque Royale de Hannovre. La date de la deuxième lettre n'est pas le 24 août, date que Wallis donne aussi dans la Préface du T. I de ses ‘Opera’ (ce Tome parut en 1695, deux ans après le T. II), mais le 24 octobre. On voit clairement qu'il ne s'agit pas de deux lettres différentes, du 24 août et du 24 octobre, mais d'une seule lettre, tant par le contenu que par le fait que Wallis écrit plus loin dans la Prop. 95 déjà citée du T. II: ‘in dicta Epistola Octob. 24. 1676’ sans qu'il ait été question d'une nouvelle lettre.
Les citations de Wallis ne sont pas absolument littérales, comme on le constate en les comparant avec le texte de l'édition des oeuvres de Newton par S. Horsley; voyez la note 36 de la p. 376 qui précède.
Cap. 92 et 93. ‘Hujus Applicatio ad Circulum & Ellipsin’. - ‘Ejusdem Applicatio ad Hyperbolam’.
Cap. 94. ‘Nova Methodus extrahendi Radices tum Simplicium tum Affectarum AEquationum’.
Cap. 95. ‘Exempla hujus Methodi exhibet multa [Newton]. Quorum ego aliquot hic transcribo’.
‘Exemplum I’. Etc.
‘Per has methodos; Quando Problema reductum fuerit ad hujusmodi Seriem, infinite continuandam; multae approximationes, usui commodae, facile obtineantur [lisez: obtinentur], & labore non magno, quae alias aegre obtineantur, magno temporis & laboris impendio. Hujus Specimen exhibet in exemplo subjecto, pro Circuli Quadratura; cum illo Clariss. Christiani Hugenii, super idem subjectum, comparando.
Exemplum X. Data cujusvis Arcus chorda A, arcusque dimidii chorda B; Invenire arcus longitudinem, proxime. Ponatur arcus = z; & circuli radius = r: tum per ea quae supra ostensa sunt habemus (duplum sinum arcus ½ z)
|
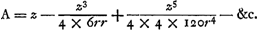 |
| Et |
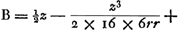 |
Tum multiplica B in n (numerum fictitium) & ex Producto deme A: & Residui secundum terminum - 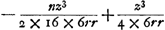 (quo evanescat) pone ∞ 0. Unde prodibit n = 8, & (quo evanescat) pone ∞ 0. Unde prodibit n = 8, & 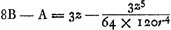 : Hoc est : Hoc est 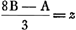 , proxime. Quippe Error (in excessu[l'édition ‘Isaaci Newtoni Opera quae exstant omnia’ de 1779 de Samuel Horsley observe, T. I, p. 323: ‘In defectu potius, sicut rectè statuit Hugenius’]) non major est quam z5/7680r4 - &c. Estque idem cum illo Hugenit Theoremate. , proxime. Quippe Error (in excessu[l'édition ‘Isaaci Newtoni Opera quae exstant omnia’ de 1779 de Samuel Horsley observe, T. I, p. 323: ‘In defectu potius, sicut rectè statuit Hugenius’]) non major est quam z5/7680r4 - &c. Estque idem cum illo Hugenit Theoremate.
Il s'agit de la Prop. VII de ‘De Circuli Magnitudine inventa’ (T. XII, p. 133).
Exemplum XI. Item. In arcus Bb [Fig. 57] sinu verso AD indefinite producto, invenire punctum G, unde, ductae rectae GB, Gb abscindant (in Tangente Ee) arcui aequalem proxime. Esto Circuli centrum C, Diameter AK = d; & sinus versus AD = x. Tum est DB (= V : dx - xx :)
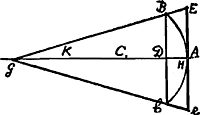
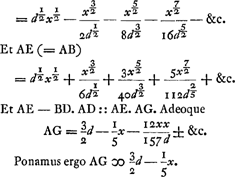
Eritque iterum, DG (= 3/2 d - 6/5 x) DB ∷ DA. AE - DB.
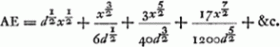
Deme hoc ex valore AE pruis invento; Residuum est error
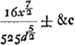
Ergo in AG, sumptis AH = 1/5 DA, & KG = HC, Rectae GBE, Gbe abscindent Ee proxime aequalem arcui Bab. Quippe error non major est quam 16x3/525d3 √ dx [lisez: 2. 16x3/225d3 √ dx, texte de Gerhardt] ± &c. Qui multo minor est quam Hugenii’.
(Etc. Cet ‘Exemplum’, comme le précédent, est emprunté à la lettre de Newton de juin 1676).
Nous trouvons en effet que lorsque l'arc BAb est la huitième partie de la circonférence, de sorte que x = r [1 - cos. 22½o] = pr, où r = ½d, l'erreur de Newton f = 4 √ 2/525 p7/2r (en ne tenant compte que de ce premier terme) a la valeur 0,00000083 r. Quant à l'erreur de Huygens, d'après le Probl. IV, Propos. XX de ‘De circuli magnitudine inventa’, où il considère le cas de l'arc dont nous venons de parler, il est de 0,0000097 r (donc 11 ou 12 fois plus grand), vu que son ‘terminus minor accuratior’ - chez Newton il s'agit également d'un terminus minor - est égal à 0,7853885 r et que ¼πr = 0,7853982 r.
-
voetnoot7)
- Cap. 10: ‘De Fractionum & Rationum Reductione ad minores terminos servato quam potest proxime valore’.
-
voetnoot8)
- Wallis parle en effet dans le sens indiqué de ‘Edwardus Davenant, S. Theologiae Doctor, & Ecclesiae Sarisburiensis tum Canonicus Residentiarius; magnae eruditionis & modestiae Vir, & in rebus Mathematicis sedulus, earumque bene gnarus’, etc. .. Problema. Cujus solutionem (ante plures annos) ad ipsum [Davenant] misi; eamque subjunxi Schediasmatis quibusdam posthumis Jeremiae Horroccii, quae meae curae commendarunt Societas Regia Londonensis, in ordinem digerenda & edenda’. Huygens possédait apparemment la première édition, celle de 1673, des ‘Opera Posthuma’ de Horrocks (T. V, p. 41, note 12) et non pas la deuxième de 1678 (T. V, p. 73, note 8) qui contient vers la sin un chapitre ‘De rationum et fractionum reductione’. Le catalogue de vente de 1695 des livres de Huygens mentionne en effet l'édition de 1673 (Libri Mathematici in Quarto, 92).
-
voetnoot9)
- On trouve déjà des fractions continues, servant au calcul des nombres des dents de différents rouages, aux p. 13 et suiv., datant de 1680, du Manuscrit F où Huygens traite de la Terrae et Mercurij periodorum proportio, etc.
-
voetnoot10)
- Et avant ceux-ci les nombres 99532 et 312689 que Huygens mentionne à la p. 253 du Manuscrit F.
-
voetnoot9)
- On trouve déjà des fractions continues, servant au calcul des nombres des dents de différents rouages, aux p. 13 et suiv., datant de 1680, du Manuscrit F où Huygens traite de la Terrae et Mercurij periodorum proportio, etc.
|