|
| |
| |
| |
VI.
Théorie de 1669Ga naar voetnoot1) du mouvement ascendant ou descendant d'un point pesant dans un milieu dont la résistance est proportionnelle au carré de la vitesse du mobile.
[Fig. 78.]
pour les montants
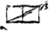
[Fig. 79.]
| |
§ 1Ga naar voetnoot2). Retardation des corps montants par l'air ou l'eau.
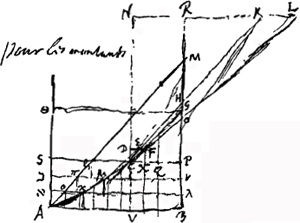
Aer, initio ascensus corporis, cum celeritate terminali, duplam resistentiam exercet ejus quam exerceretGa naar voetnoot3) in corpus ascendens eadem celeritate in medio non resistente. quia celeritas terminalis ea est quam habens corpus experitur resistentiam aeris suo ponderi aequalem.
| |
| |
Curva igitur ACG [Fig. 78]Ga naar voetnoot4) in principio A debet inclinari ad AB sicut diagonalis rectanguli αβ [Fig. 79] duplam longitudinem suae altitudinis habentisGa naar voetnoot5).
Recte autem dicitur debere esse ut qu. AB ad qu. CP ita DE ad EF, quia CP est celeritas reliqua post tempus BP ascendendo insumtumGa naar voetnoot6). DE autem representat retardationem semper eandem ex ratione gravitatis, EF vero retardationem ex resistentia medij quae ad retardationem in principio ascensus, quae ipsi DE aequalis erat, debet esse ut qu. PC reliquae nimirum celeritatis ad qu. BA primae celeritatis in ascensu.
| |
| |
Curva ACG ad G debet esse parallela AM. Sit CEH parallela AM. CF tangens in C. DEF parallela AB. Debet esse DE ad EF ut qu. AB ad qu. CP. sive ut SP ad QP, factis SP, CP, QP proportionalibus.
Spatium ACGB ad ∆ AMB ut altitudo ascensus corporis projecti celeritate terminali, ad ascensum corporis cui aer non resistit, eadem celeritate projecti; quia sumtis particulis temporis aequalibus Aא, אב, בS &c., celeritates horum initijs reliquae, ut ϰλ, μν, CP ductae in ipsa tempora Aא, אב, בS, efficiunt spatium ACGB atque etiam spatium altitudinis tempore toto AΘ vel BG, peractum. Sicut spatium AρPB est spatium altitudinis a corpore sursum jacto celeritate terminali cuique tantum gravitas sua resistit.

Ga naar voetnoot7)Ga naar voetnoot8)
Vide fig. pag. 1 [Fig. 78] ou il est parlè de la retardation des corps montants par l'air ou autre milieu qui resiste.
Hic natura curvae ACG [Fig. 79] inquiritur sumptis in AB particulis aequalibus.
| |
| |
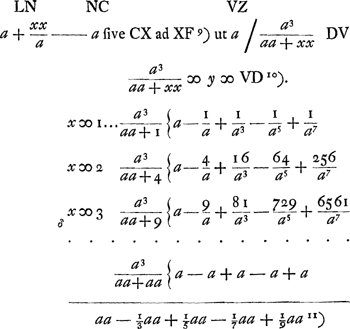
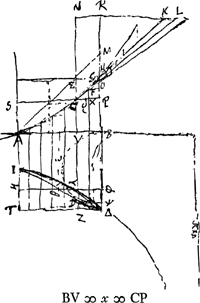
[Fig. 79.]
Ga naar voetnoot9)Ga naar voetnoot10)Ga naar voetnoot11)
Summa omnium VZ ad summam omnium DV ut summa omnium CX ad summam omnium XF. quia ponitur DI talis curva ut sicut CX ad XF ita sit ZV ad VD. Ergo ut quadratum BT ad spatium ∆IAB ita AB ad BG.
Videtur esseGa naar voetnoot12) BG ad BM ut circulus ad quadratum sibi circumscriptum, sive ut quadrans peripheriae ad diametrum.
| |
| |
Quare si mobile, celeritate terminali, sursum projiciatur in medio resistente; erit tempus ascensus totius ad tempus ascensus mobilis, eadem celeritate sursum projecti in medio non resistente, sicut circulus ad circumscriptum sibi quadratum.
[Fig 79 bis.]
[Fig. 79 ter.]
| |
| |
§ 1 bisGa naar voetnoot1).

Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)
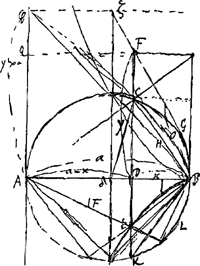
∆CDB ∞ ADEGa naar voetnoot5). Ergo spat. CBE ∞ ABE.
Spat. ABE ∞ 3 segm. BKL ut demonstravi de CissoideGa naar voetnoot6).
Ergo et spat. EBC ∞ 3 seg. BOC[H].
Sed spat. EDB ∞ spat. FGBOC, quia C[F ∞ ED]Ga naar voetnoot7).
Ergo triang. DCB + spat. FGBOC [∞] 3 segm. COBH.
Ergo spat. BGFD ∞ 4 segm. BO[CH].
Ergo spat. BGζφA aequale circulo AB. n[am] ▭ Aζ ∞ quadrato inscripto.
| |
| |
C'est bien dans le but de trouver l'aire ΔθΙ AB de la Fig. 79 (voir la note 12 de la p. 147) que Huygens a cherché la quadrature de l'aire correspondante BGζφA de la Fig. 79 ter: au revers de la feuille détachée il est question du rapport entre le tempus ascensus liberi cum celeritate inchoante PC ad tempus ascensus impediti cum eadem inchoante celeritate. Comparez sur cette feuille la note 3 de la p. 152.
| |
Spatium vero ascensus per medium resistens erit ad spatium ascensus per medium non resistens ut area ABGC ad triangulum ABM [Fig. 79].
Cum autem summa omnium XF hoc est recta BG referatur spatio BAID∆, similiterque recta CV referatur spatio VAID: patet summam omnium CV, hoc est trilineum GBA referri ungulâ solidaGa naar voetnoot9) super BAID∆ abscissa per B∆, (quia haec ungula refert summam triangularem spatiorum omnium BVAID∆, ab AI incipiendo), parallelepipedo autem aeque alto super spatio BAID∆ referri ▭ AG. Atqui si fiat ut ηφ ad θφ ita haec ad λφ erit, ducendo curvam IλΔ per omnia λ, erit inquam qu. TB ad spatium IλΔ BA ut ungula super qu.o TB abscissa per B∆ ad dictam ungulam super BAID∆ abscissam per B∆Ga naar voetnoot10).
Jam vero 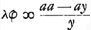 Ga naar voetnoot11) Ga naar voetnoot11). adeo ut si B φ sit y et φλ ∞ z, habeatur 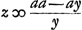 , unde liquet I λΔ esse hyperbolam.
| |
| |
SiGa naar voetnoot12) ergo qu. TB (vel ∆A) - spat. hyperb. IλΔBA ut cuneus super qu.o TB per B∆ - cuneum super BAID∆ per B∆, et invertendo erit
Spat. hyp. IλΔBA - qu. ∆A ut cun. sup. BAID∆ per B∆ - cun. sup. qu. ∆A per B∆.
Spat. hyp. IλΔBA - 2 qu. ∆A ut cun. sup. BAID∆ per B∆ - cub. sup. qu. ∆A.
Sed 2 qu. ∆A ad 2 spat. ID∆BA ut cub. qu. ∆A ad parallelepip. aeque altum super ID∆BA.
Ergo ex aequo spat. hyp. IλΔBA ad 2 spat. ID∆BA hoc est ad duplum circulum diam. AB ut cuneus super BAID∆ per B∆ ad parallelepip. super BAID∆; hoc est ut trilineum ABG ad ▭ AG, per ante dicta.
Sed duplus circulus AB est ad qu. A∆ ut dupla BG ad BM vel AB, ex ante demonstratisGa naar voetnoot13). hoc est ut ▭ AG ad triang. ABM.
Ergo ex aequo spat. hyp. IλΔBA ad qu. A∆ ut trilineum ABG ad triang. ABM. hoc est ut altitudo ascensus per medium resistens ad altitudinem ascensus per medium non resistens, positis utrobique initio ascensus celeritatibus quanta est celeritas terminalis propositi corporis per medium resistens. hoc est quam habens majorem acquirere cadendo nequit.
Hyperbola IλΔ describenda per ∆ punctum ad asymptotos ABδ, δξ posita Bδ ∞ BA. Unde spat. hyperb. IλΔBA ad qu. ∆A ex nostra quadratura sicut 693148 ad 1000000Ga naar voetnoot14).
Sed Ga naar voetnoot15) altitudo tota seu tempore BM per medium non resistens ad altitudinem per medium non resistens tempore BG, hoc ect triang. ABM ad 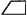 AEGB, sicut qu. A∆ ad ▭ sub GB et GB + 2 MG.
Ergo ex aequo spat. hyp. IλΔBA ad ▭ sub GB et GB + 2 MG, ut altitudo ascensus per medium resistens, nempe tempore toto BG, ad altitudinem eodem tempore medium non resistens, cum [utrumque] corpus in altum jacitur celeritate terminali.
| |
| |
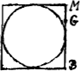
[Fig. 81.]
Est autem ▭ sub GB et GB + 2 MG aequale duplo circulo diametri AB - quadrato quadrantis circumferentiae [Fig. 80]. Est enim BG ∞ quadranti circumferentiae.
Rursus ex pag. א. Ergo ex aequo spatium hyperbolicum IλΔBA ad qu. A∆, ut trilineum ABG ad triang. ABM, hoc est ut altitudo ascensus per medium resistens ad altitudinem totam ascensus per medium non resistens, positis initio ascensus celeritatibus terminalibus.
Sed triang. ABM est ad ▭ AG hoc est qu. A∆ ad duplum rectangulum AG ut ascensus dictus per medium non resistens, ad spatium aequabili celeritate AB peractum tempore BHGa naar voetnoot1). Ergo ex aequo spatium hyperbolicum IλΔBA ad 2 ▭ AG ut altitudo per medium resistens ad spatium aequabili celeritate AB peractum tempore BHGa naar voetnoot1). Est autem 2 ▭ AG ∞ duplo circulo diametri AB.
| |
Ad pag. א quae pertinet ad pag. 1 de retardatione gravium in medio resistente.
Si mobile celeritate CP sursum projiciatur. Erit PG tempus totius ascensus quod referetur spatio VB∆D [Fig. 81]. Sit AB ∞ a ∞ 1. Item B∆ ∞ a ∞ 1. BV ∞ d. Singulae particulae aequales in quas BV divisa intelligitur, ∞ p.
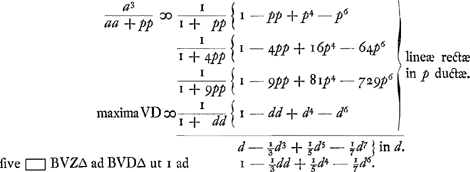
| |
| |
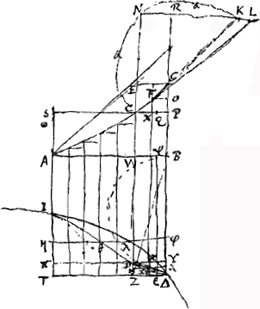
[Fig. 81.]
FE multo minor debebat esse quam in figura hac, nam FC ∞ DE [p. 150, note 7].
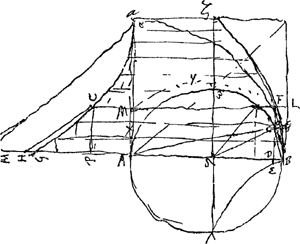
[Fig. 81 bis.]
Primae columnae summa aequalis producto ex 1 in numerum particularum ipsius BV, in p. sed numerus particularum in p, sive particulam unam, aequatur ipsi BV seu d. Ergo primae columnae summa ∞ 1 in d sive ∞ d.
Sit n numerus particularum. Secundae columnae summa ∞ ⅓dd sive ⅓ maximae toties sumtae quot sunt particulae in BV, hoc est ⅓ddn in p. Sed np ∞ d. Ergo summa secundae columnae ∞ ⅓d3 sive ⅓dd in d.
Altitudo ascensus cum celeritate initiali CP, erit trilineum CPG, quod refertur cuneo super BVD∆ abscisso per B∆. Rectang. vero PE referetur parallelepip. o super BVD∆ altitudinis BV. cujus parallelepipedi ratio ad parallelepip. super ▭ BZ, ejusdem altitudinis BV, est ea quae spatij BVD∆ ad ▭ BZ. Spatij autem hujus mensura datur ex dimensione segmenti circuli a diam. ∆B, cujus arcus dupli sagitta est ΔϒGa naar voetnoot3).
| |
| |
At ratio cunei super BVD∆ ad cuneum super ▭ BZ est ea quae componitur ex ratione cunei super BVD∆ ad cuneum super BAT∆ et ex ratione hujus cunei ad cuneum super ▭ BZ. Quarum rationum prior est ea quae spatij BψϰΔ ad qu. BT: posterior vero eadem quae quadrati AB ad qu. BV, sive quae AB ad Bψ (sunt enim proportionales πϒ, Dϒ, ϰϒ sive ψB) sive quae qu.i BT ad ▭ BψρΔ. Ergo ratio cunei super BVD#x2206; ad cuneum super ▭ BZ est ea quae spatij BψϰΔ ad ▭ BψρΔ.
| |
§ 4Ga naar voetnoot1). Accélération des corps pesants par l'air.
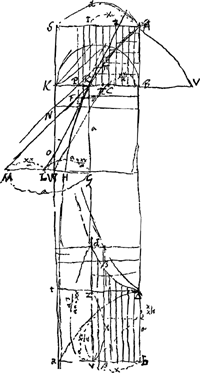
[Fig. 82.]
As [Fig. 82] maxima celeritas quam acquirere possit grave per aerem cadens exclusive. BR celeritas acquisita tempore AB. Ut KB quadratum ad BR quadratum ita resistentia aeris contra velocitatem AS, ad resistentiam contra celeritatem BR. Sed resistentia contra celeritatem AS toti ponderi gravis aequipollet, cum ab ulteriori acceleratione prohibent. Ergo resistentia contra celeritatem BR tantam partem ponderis aufert quae sit ad totum pondus ut qu. BR ad qu. BK, sive ut BC ad BK, factis KB, RB, CB proportionalibus. Ergo eadem proportione etiam acceleratio diminuitur quae est in fine temporis AB. Sit rectae AN tangenti curvam AR in A parallela RM. Et sumtâ RD minimâ, sit DF parallela AS. Ergo quum incrementum celeritatis tempore RD alioqui futurum esset DF, absque ulla aëris resistentia; jam diminuendum est quantitate FE: ut sit EF ad FD ut qu. RB ad qu. BK, sive ut BC ad BK. atque ita erit RE tangens curvae AR in puncto R, quae curva ostendet suis ordinatim applicatis celeritates acquisitas temporibus respondentibus in AB acceptis. Et spatijs suis ut ARB ostendet spatia descendendo peracta, dum spatia eodem tempore peracta absque aeris resistentia exhibentur triangulis ut APB.
| |
| |
Parallelepipedum super d∆BV [lisez d∆bV] refert ▭ RAGa naar voetnoot2), quia spat. d∆ABV [lisez d∆bV] resert maximam RI; nam in dicto parallelepipedo toties repetitur spat. d∆BV [lisez d∆bV], quoties in ▭ RA recta RI.
Rursus quia recta ππ referuntur spatijs dββV, referetur summa omnium ππ seu spat. ARB cuneo super d∆BV [lisez d∆bV] abscisso per ∆b.
On voit dans la Fig. 82 qu'en appelant x la vitesse AI du mobile après le temps AB, et a la vitesse terminale AS, Huygens trouve pour V d la formule 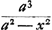 . Ce calcul, analogue à celui de la formule  du § 1, est expliqué par Huygens aux p. 25 et 26 du T. X.

Ga naar voetnoot3)
Erunt summae columnarum 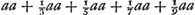 &c. (Quae summae simul sumtae efficiunt spatium γαβθKL ψδ [Fig. 83] infinite extensum). Nam progrediendo donec x sit ∞ a jam numerus ipsarum a in prima columna erit etiam a, unde
| |
| |
summa omnium a in hac columna ∞ aa. Pono autem singulos versus, hoc est singulas ηλ ductas in 1, particulam scilicet 1/10000000 totius γδ. Itaque summa aa primae columnae facit ipsum quadrantem αδ.
Secunda columna est series quadratorum ab unitate divisorum per a. Ut proinde fractiones istae omnes sint in ipsa ratione quadratorum ab unitate. maxima vero fractionum est ∞ a. Unde summa omnium aequatur trienti maximae toties sumtae quot sunt numero fractiones. Ergo summa illa ∞ ⅓aa.
Tertia columna est series proportionalium in ratione quadratoquadratorum. unde summa ipsarum aequalis ⅕ maximae toties sumtae hoc est ⅕ aa. &c.
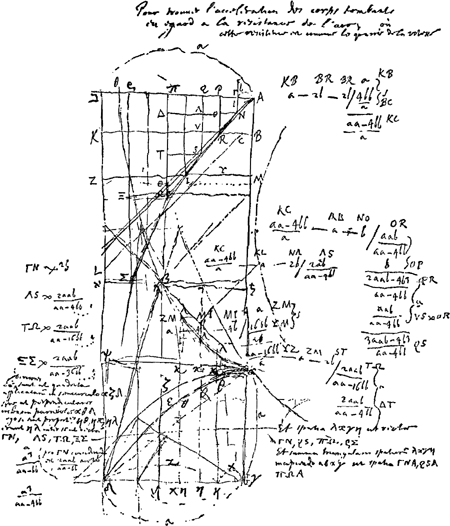
[Fig. 83.]
| |
| |
| |
§ 5Ga naar voetnoot1). Pour trouver l'acceleration des corps tombants eu egard a la resistanceGa naar voetnoot2)
de l'air, oú cette resistenceGa naar voetnoot2) est comme le quarré de la vitesse.
Nous nous contentons de reproduire une partie de la p. 80r.: la Fig. 83 est évidemment, plus encore que la Fig. 82 du § précédent, le prototype de la Fig. 1 de la p. 24 du T. X. En ce dernier endroit (c.à.d. dans le Manuscrit G) Huygens s'explique clairement, comme nous l'avons déjà dit, sur le sens de la Fig. 83 et des calculs, analogues aux précédents, qui s'y rapportent.
|
-
voetnoot1)
- Voir cependant les notes 12 de la p. 147, 12 et 15 de la p. 151.
Entre les p. 200 et 201 du Manuscrit D (la numération est postérieure à Huygens) trois feuillets ont été enlevés. Comme les feuilles 201-205 portent la numération de Huygens 6-10, le premier des feuillets enlevés doit avoir porté à son revers le numéro 1, et les deux autres respectivement les nos 2-3 et 4-5. Or, les feuillets enlevés sont apparemment les trois feuillets des ‘Chartae mechanicae’ 82v.-82r., 79 et 80v.-80r. qui satisfont à cette condition. Une des figures de la f. 82v. ressemble d'ailleurs si fortement à une figure de la feuille ‘précédente’ 200 du Manuscrit D que le doute n'est pas possible. Ces feuillets datent donc de mai ou de juin 1669: comparez aux p. 132 et 138 qui précèdent les dates des §§ 4 et 9.
À la p. 88 du Manuscrit D Huygens disait - voir la note 14 de la p. 107 qui précède - qu'on trouverait la ‘speculatio vera’ une soixantaine de feuillets plus loin, donc vers la p. 208.
Les trois feuillets paraissent avoir été enlevés par Huygens lui-même, probablement lorsqu'il rédigea, après avoir lu les ‘Principia’ de 1687 de Newton, l'Addition au Discours de la Cause de la Pesanteur (tel qu'il fut publié en 1690) qu'on ne trouve pas encore dans le présent Tome: en effet, la suscription: ‘Pour trouver l'acceleration des corps tombants eu egard a la resistance de l'air’ ‘où cette resistence est comme le quarré de la vitesse’ (p. 80r.) a apparemment été ajoutée par lui plus tard (en deux tempi, suivant les couleurs de l'encre: voyez la Fig. 83 qui suit).
Les ‘Chartae mechanicae’ contiennent en outre, se rapportant au même sujet, trois feuillets de deux pages (81, 85 et 86) et une feuille de 4 pages (83 et 84). Les p. 83v. et 84r.(ainsi que la deuxième moitié de la p. 84r.) traitent du mouvement dans un milieu dont la résistance est proportionnelle à la première puissance de la vitesse; nous en avons tiré le § 11 de la p. 118. Le reste traite du mouvement ascendant ou descendant dans l'hypothèse d'une résistance proportionnelle au carré de la vitesse. La feuille 85 est postérieure à l'apparition de l'ouvrage de Newton puisqu'elle contient des remarques sur les propositions de ce dernier. La f. 86 qui traite de la résistance d'une surface courbée nous semble également postérieure. Sur la p. 81r. qui porte l'indication א, Huygens a noté: Lib. D. Vide fig. pag. 1. ou il est parlè de la retardation des corps montants par l'air ou autre milieu qui resiste, et sur la p. 83r.: ad pag. א quae pertinet ad pag. 1 de retardatione gravium in medio resistente. La p. 84v. porte l'indication ב: elle fait suite à א. Les feuillets 81 et 83-84 ne proviennent apparemment pas du livre D. Les p. 83v. et 84r. contiennent un brouillon (déjà mentionné) qui peut fort bien dater de 1668. La deuxième moitié de la p. 84v. ou ב semble dater de 1687 ou de plus tard puisqu'on y lit: Sic fere Newtonus propos. 2. lib. 2, sans qu'on puisse voir - même dans une photographie à la lumière ultraviolette - que cette remarque ait été ajoutée après coup. Par conséquent nous ne tenons compte ici que des trois feuillets appartenant au Manuscrit D et des f. 81, 83r. et 84v. (première moitié).
Il est possible que la feuille de 4 pages (83 et 84) date entièrement de 1687 ou de plus tard.
Nous rappelons que vers 1691 Huygens s'est appliqué à bien rédiger et à compléter les ‘olim inventa’ sur le mouvement dans le cas d'une résistance proportionnelle au carré de la vitesse: nous avons publié, après Uylenbroek, sa Pièce de cette année (Manuscrit G) aux p. 23-42 du T. X.
-
voetnoot3)
- Lisez plutôt: ‘quae exerceretur’ ou ‘quam exerceret gravitas’.
-
voetnoot4)
- Comme le dit la suite du texte, BR est l'axe des temps et BA celui des vitesses. Le temps de l'ascension du corps considéré est BG.
-
voetnoot5)
- L'équation du mouvement pour la descente étant
 et celle pour l'ascension et celle pour l'ascension  , la ‘vitesse terminale’ V est déterminée par l'équation V2 = g/k, et l'on a au début de l'ascension ici considérée - dv/dt = 2g. Dans la Fig. 78 Huygens prend - dv/dt = 2. Les unités du temps t et de la vitesse v ont donc été choisies de telles manière que la retardation g de la pesanteur devient égale à l. , la ‘vitesse terminale’ V est déterminée par l'équation V2 = g/k, et l'on a au début de l'ascension ici considérée - dv/dt = 2g. Dans la Fig. 78 Huygens prend - dv/dt = 2. Les unités du temps t et de la vitesse v ont donc été choisies de telles manière que la retardation g de la pesanteur devient égale à l.
Pour un deuxième corps jeté simultanément en l'air avec la même vitesse BA et qui n'éprouve pas de résistance, le temps de l'ascension est figuré, vu le choix des unités, par une droite BM égale à BA, de sorte que la droite AM qui représente son mouvement est inclinée à 45o sur les axes.
-
voetnoot6)
- CE est une fort petite droite inclinée à 45o. DF et DE sont les diminutions gdt et (g + kv2) dt de la vitesse pendant l'élément de temps CD, respectivement pour le corps qui éprouve de la résistance et pour celui qui n'en éprouve pas.
-
voetnoot7)
- En effet, on avait [Fig. 78] DE : EF = SP : PQ, et la Fig. 79 fait voir DE : EF = NK : KL. Or, NK = SP. Donc KL = PQ.
-
voetnoot8)
- Chartae mechanicae, p. 81r. א. L'équation s'applique tant à la Fig. 78 qu'à la Fig. 79.
-
voetnoot9)
- CX : XF est la cotangente de l'angle que fait avec l'axe des vitesses BA la tangente à la courbe CFOL. Le produit y.CX étant égal à a.XF, il s'ensuit que ∑y.CX ou CX∑y = a∑XF. L'espace CX∑y ou DIAV représente donc le produit de a par l'ordonnée CV de la courbe; et l'espace ∆IAB tout entier, divisé par a, représente le temps de l'ascension totale (voir la suite du texte).
-
voetnoot10)
- D'après ce qui à été dit dans la note précédente il s'agit de déterminer ∑y, c.à.d. l'espace ∆IAB. Huygens prend donc les valeurs de y pour x = 1, 2, 3, etc., les unités étant supposées infiniment petites, et ensuite leur somme.
-
voetnoot11)
- Le temps de l'ascension totale est donc a [1 - ⅓ + ⅕ - 1/7 + 1/9 .....]. Nous rappelons, conformément au texte, que le corps auquel le milieu résiste a été lancé en l'air avec une vitesse égale à la ‘vitesse terminale’ et que les unités ont été choisies de telle manière (note 5 de la p. 146) que a représente le temps de l'ascension totale d'un deuxième corps auquel le milieu ne résiste pas et dont la vitesse initiale est la même.
-
voetnoot12)
- Les mots ‘Videtur esse’ ont été corrigés, évidemment plus tard, en ‘Ergo erit’. Huygens a de plus ajouté en cet endroit la remarque suivante: ‘Sed haec progressio arguit spat. ΔθIAB aequari circulo circa diametrum AB ex quadratura Leibnitzii quae est in libro E circa initium’; les quatre ou cinq derniers mots ont d'ailleurs été biffés et remplacés par ‘in rescissis ex libris adversariorum’. On voit en effet dans le Manuscrit E qu'une dizaine de feuilles, les premières du volume, ont été enlevées. Nous en possédons une au moins; voir la suite de la présente note. La première date qu'on trouve dans le Manuscrit E, à la p. 26, est le 19 décembre 1674. La lettre de Huygens à Leibniz du 7 novembre 1674 (T. VII, p. 393) fait voir qu'il avait appris peu avant cette date que Leibniz venait de découvrir que le rapport du cercle au carré circonscrit s'exprime par la serie 1 - ⅓ + ⅕ etc.
A propos de l'équation  , Huygens observe encore: ‘Ex hac aequatione apparet spat. ΔθIAB aequari circulo diametri AB. Ac proinde progressione Leibnitij nihil hic opus sed tantum dimensione mea Cissoidis et curva inde et ex circulo composita’. L'équation , Huygens observe encore: ‘Ex hac aequatione apparet spat. ΔθIAB aequari circulo diametri AB. Ac proinde progressione Leibnitij nihil hic opus sed tantum dimensione mea Cissoidis et curva inde et ex circulo composita’. L'équation  est en effet celle de la ‘curva’ mentionnée (note 4) et l'on a en effet est en effet celle de la ‘curva’ mentionnée (note 4) et l'on a en effet  . Ceci ne ressort pas de la quadrature de la cissoïde telle que Huygens l'avait trouvée en 1658 (T. II passim, T. XIV, p. 309-312). C'est sur une feuille détachée (Chartae mathematicae, f. 27) - apparemment un des feuillets enlevés du Manuscrit E dont il fut question plus haut: il a le format du Manuscrit et on y trouve la ‘Leibnitzij quadratura’ - que Huygens trouve l'intégrale . Ceci ne ressort pas de la quadrature de la cissoïde telle que Huygens l'avait trouvée en 1658 (T. II passim, T. XIV, p. 309-312). C'est sur une feuille détachée (Chartae mathematicae, f. 27) - apparemment un des feuillets enlevés du Manuscrit E dont il fut question plus haut: il a le format du Manuscrit et on y trouve la ‘Leibnitzij quadratura’ - que Huygens trouve l'intégrale  . Voir le § 1 bis qui suit. . Voir le § 1 bis qui suit.
-
voetnoot1)
- Voir sur le § 1 bis - datant de 1674 - le dernier alinéa de la note précédente.
-
voetnoot2)
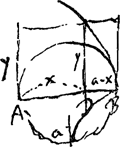
- Cette équation n'est autre, lorsqu'on intervertit les axes, que celle de la courbe
 du § 1. C'est la courbe BGF de la Fig. 79 ter, où toutefois l'origine des axes est B, tandis qu' elle était A dans la Fig. 79 bis. du § 1. C'est la courbe BGF de la Fig. 79 ter, où toutefois l'origine des axes est B, tandis qu' elle était A dans la Fig. 79 bis.
-
voetnoot3)
- Équation de la courbe BGF de la Fig. 79 ter.
-
voetnoot4)
- Ou plutôt ‘dupla curvae Leibnitzij’. Lorsqu'on prend avec Leibniz
 ou ou  , cette dernière ordonnée est la moyenne arithmétique de l'ordonnée , cette dernière ordonnée est la moyenne arithmétique de l'ordonnée  de la cissoïde et de l'ordonnée de la cissoïde et de l'ordonnée  de la circonférence de cercle des Fig. 79 bis en 79 ter. Comparez la note 3 de la p. 394 du T. VII. de la circonférence de cercle des Fig. 79 bis en 79 ter. Comparez la note 3 de la p. 394 du T. VII.
-
voetnoot5)
- Puisque
 , en vertu de l'équation de la cissoïde. , en vertu de l'équation de la cissoïde.
-
voetnoot7)
- Puisque l'ordonnée DF est la somme des ordonnées DC et DE (note 4 de la p. 149).
-
voetnoot8)
- Chartae mechanicae, p. 81r. א. Le § 2, partiellement écrit en marge, fait l'effet d'avoir été ajouté plus tard, sans doute en 1674.
-
voetnoot9)
- En marge: pro ungula deinde cuneus. Nous avons déjà remarqué à la p. 103 (note 5) que Huygens écrit parfois ‘cuneus’ où il vaudrait mieux dire ‘ungula’.
-
voetnoot10)
- La courbe IλΔ est obtenue en rabattant dans le plan de la figure - comparez le deuxième alinéa de la note 1 de de la p. 464 du T. XVI - l'onglet élevé sur l'espace BAID∆. On peut se représenter les plans obliques des onglets inclinés sous des angles de 45o. Le plan perpendiculaire au papier passant par l'horizontale quelconque ηφ coupe alors l'onglet nommé suivant un triangle rectangle isoscèle dont la surface est ½(θφ)2. Or, comme λφ, c.à.d. le triangle rabattu sous forme d'une droite, a par hypothèse la valeur (θφ)2/a,
cette surface peut s'écrire ½a.λφ, et l'onglet entier (égal au produit de a par le spat. ABG) est aussi égal au produit de ½a par l'espace IλΔBA. On a donc a2: spat. IλΔBA = ½a3: onglet nommé. C.Q.F.D.
Comparez sur la courbe des λ la p. 42 du T. X (autres lettres), où toutefois nous n'avons pas parlé d'un rabattement d'un onglet.
-
voetnoot11)
- Comme au § 1, θφ est désignée par x et l'on a
 ou ou  . Donc . Donc  . .
-
voetnoot12)
- Les alinéas qui suivent (jusqu'à ... sicut 693148 ad 1000000) sont écrits sur un morceau de papier collé sur la page 81r. ou א. Puisque Huygens y dit sans hésiter - comparez les notes 12 de la p. 147 et 1 de la p. 149 - que spat. ID∆BA = circulus diam. AB, ils doivent dater de 1674 ou de plus tard.
-
voetnoot14)
- Puisque B∆/AI = 2, on a (T. XIV, p. 435): log. IλΔBA/qu.∆A = log log 2 + 0,362216; donc IλΔBA/qu.∆A = 0,693148. C'est le rapport cherché de la hauteur atteinte par le corps auquel le milieu résiste à celle atteinte par le corps auquel il ne résiste pas, la vitesse initiale étant pour l'un et l'autre corps la ‘vitesse terminale’.
-
voetnoot15)
- Chartae mechanicae p. 84v. ou ב. On lit en marge: ‘Vide fol. א sub finem ubi signum
 ’; ce signe se trouve à l'endroit indiqué. La remarque finale de la note 12 (les neuf derniers mots) s'applique aussi au présent texte. ’; ce signe se trouve à l'endroit indiqué. La remarque finale de la note 12 (les neuf derniers mots) s'applique aussi au présent texte.
-
voetnoot1)
- Apparemment le point que Huygens désigne par H est considéré ici par lui comme identique avec le point G.
-
voetnoot1)
- Apparemment le point que Huygens désigne par H est considéré ici par lui comme identique avec le point G.
-
voetnoot2)
- Chartae mechanicae, p. 83r. Ce §, où il est question de la hauteur qu'atteint un projectile éprouvant de la résistance de la part du milieu et dont la vitesse initiale, au lieu d'être égale à la ‘vitesse terminale’, est une fraction quelconque de cette dernière, répète à peu près les raisonnements du § précédent et s'explique donc par lui.
-
voetnoot3)
- Ce dernier énoncé n'est pas clair, mais le sens se manifeste par la considération de ce que Huygens dit dans la feuille détachée, mentionnée dans le deuxième alinéa de la note 12 de la p. 147. Il y est en effet question de ce qui dans la Fig. 81 s'appelait l'espace BVD∆. Dans la Fig. 81 bis de la feuille l'espace en question s'appelle AMFB. La courbe BGFζ est identique avec BGFζ de la Fig. 79 ter, c.à.d. avec la courbe des θ de la Fig. 81 dont l'équation est
 (ou (ou  suivant le § 1 bis) et Huygens écrit: spat. FBD ∞ 4 segm. CB [T. VII, p. 394, note 3 et note 4 de la p. 149 qui précède]. segmentum CB ∞ sector δCB - ∆oδCB, hoc est ½ ▭ δB in arcum CB - CD. Ergo spat. FBD ∞ AB in differentiam arcus CB et CD. suivant le § 1 bis) et Huygens écrit: spat. FBD ∞ 4 segm. CB [T. VII, p. 394, note 3 et note 4 de la p. 149 qui précède]. segmentum CB ∞ sector δCB - ∆oδCB, hoc est ½ ▭ δB in arcum CB - CD. Ergo spat. FBD ∞ AB in differentiam arcus CB et CD.
Dans la Fig. 81 on a par conséquent: spat. DΔϒ [D∆ étant un arc de la courbe des θ; le point D n'est pas situé sur la circonférence] = le produit a. (différence de l'arc de la circonférence qui se trouve au-dessous de l'horizontale πϒ passant par le point D et de la demi-corde de cet arc). Ce que Huygens entend dans le texte du § 3 par ‘spatij hujus mensura’ est donc la différence du spat. BVD∆ et du ▭ Vϒ. Remarquons qu'en appliquant cette formule à l'espace entier, donc à spat. BAID∆ - ½▭A∆ on trouve correctement a. (¼πa - ½a); donc spat. BAID∆ = ¼πa2.
-
voetnoot1)
- Chartae mechanicae, p. 79r. Les raisonnements par lesquels débute ce § qui traite, comme le suivant, des corps tombants diffèrent peu du début du § 1 qui traitait, comme les §§ 2 et 3, des corps ascendants. Quant à la Fig. 82, on peut la comparer avec celle de la p. 24 (voyez aussi la note 4 de la p. 23) du T. X.
-
voetnoot2)
- La courbe d∆ de la partie inférieure de la Fig. 82 a été construite en prenant le rapport ββ: RI égal à la tangente de l'angle que fait avec l'axe KB la tangente à la courbe AR au point π situé sur le prolongement de ββ. Il s'ensuit, comme le dit le texte, que spat. dββV = ππ, spat. d∆bV = RI ou ∆b, etc.
Pour calculer l'espace ARB qui représente la distance parcourue par le corps tombant en un temps AB, la vitesse initiale étant nulle, Huygens représente cette distance par le tronc ou plutôt l'onglet obtenu en coupant le prisme (ou ‘parallelepipedum’) érigé sur la base d∆bV par un plan passant par ∆b.
-
voetnoot3)
- Chartae mechanicae, p. 81v. La ligne y ou Vd de la Fig. 82 correspond à ηλ de la Fig. 83 (§ 5).
-
voetnoot2)
- Comparez la fin du quatrième alinéa de la note 1 de la p. 144.
-
voetnoot2)
- Comparez la fin du quatrième alinéa de la note 1 de la p. 144.
|

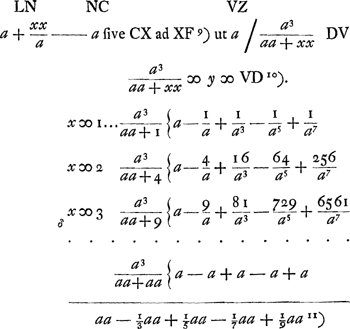




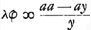 Ga naar voetnoot11). adeo ut si Bφ sit y et φλ ∞ z, habeatur
Ga naar voetnoot11). adeo ut si Bφ sit y et φλ ∞ z, habeatur 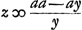 , unde liquet IλΔ esse hyperbolam.
, unde liquet IλΔ esse hyperbolam.
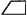 AEGB, sicut qu. A∆ ad ▭ sub GB et GB + 2 MG.
AEGB, sicut qu. A∆ ad ▭ sub GB et GB + 2 MG.

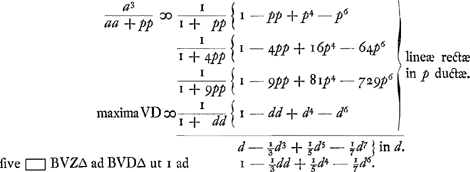



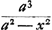 . Ce calcul, analogue à celui de la formule
. Ce calcul, analogue à celui de la formule  du § 1, est expliqué par Huygens aux p. 25 et 26 du T. X.
du § 1, est expliqué par Huygens aux p. 25 et 26 du T. X.

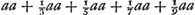 &c. (Quae summae simul sumtae efficiunt spatium γαβθKLψδ [Fig. 83] infinite extensum). Nam progrediendo donec x sit ∞ a jam numerus ipsarum a in prima columna erit etiam a, unde
&c. (Quae summae simul sumtae efficiunt spatium γαβθKLψδ [Fig. 83] infinite extensum). Nam progrediendo donec x sit ∞ a jam numerus ipsarum a in prima columna erit etiam a, unde