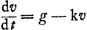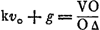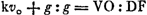Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695
(1937)–Christiaan Huygens–
[pagina 102]
| |||||||||||
IV.
| |||||||||||
[pagina 103]
| |||||||||||
Hic jam pono AFD esse lineam Logisticam de qua in libro B, et folio sequentiGa naar voetnoot6).
Sed aliter quoque et melius istarum altitudinum ratio inter se invenitur. Nam quum celeritas initio ascensus ad eam quam peracto tempore aliquo CG adhuc servat mobile R, sit ut spatium ACED ad spatium FGED, hoc est ut AB ad FH (ex demonstratione paginae praecedentisinitio) - rursus hoc ex proprietate LogisticaeGa naar voetnoot7) - patet hinc, quod si AB ponatur pro celeritate initio ascensus, reliquae celeritates sensim diminuentes per aequalia tempora representabuntur rectis in spatio ABD aequaliter inter se distantibus ac ipsi AB parallelis: ijsque in distantias interjectas hoc est in aequales temporis particulas ductis, fiet spatium ipsum ABD mensura altitudinis ad quam mobile R perveniet, triangulum vero ABP mensura altitudinis ad quam mobile N eadem celeritate | |||||||||||
[pagina 104]
| |||||||||||
projectum ascendet, quod hinc cognosciturGa naar voetnoot1), quoniam celeritates mobilis N representantur lineis in triangulo ABP parallelis ad AB, quae videlicet lineae initio decrementa subdupla habent ad decrementa parallelarum in spatio ABD; hoc enim necesse est ita se habere quia mobili N tantum una ex causa retardatio contingit, nempe ex vi gravitatis, mobili vero R ex altera praeterea isti aequali, nempe resistentia aeris, siquidem celeritate terminali mobile R projectum ponitur. Posito autem AC ∞ lateri recto, ac proinde tangente AN faciente cum AC angulum 45 graduumGa naar voetnoot2) fit ut requiritur ▭ BN ∞ spatio ACEDGa naar voetnoot3). Et ▭ proinde EP ∞ spatio ABD. Ratio autem ▭ EP ad triangulum ABP, hoc est altitudo ascensus mobilis RGa naar voetnoot4) ad altitudinem ascensus mobilis NGa naar voetnoot5), erit ea proxime quae 616 ad 1000Ga naar voetnoot6). | |||||||||||
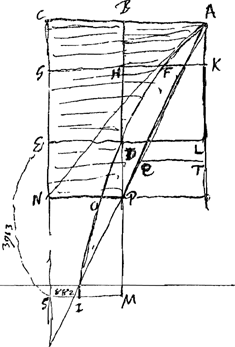
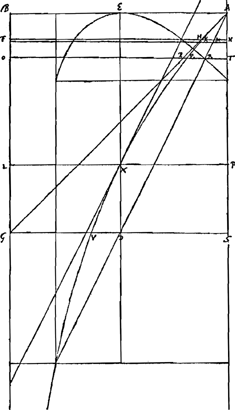
§ 2. [Mouvement vertical de haut en bas.]Ga naar voetnoot7).∆ GAS - vide fig. magnam pag. sequentis [Fig. 55]Ga naar voetnoot8) - ad spatium AVS, ut spatium descensus gravis N cui aer non obsistit ad descensum gravis R cui aer obsistit, eodem tempore peractum, cum SG est velocitas summa quam R cadendo acquirere potest, (quam velocitatem terminalem ipsius R voco). Ut autem ∆ GAS ad spatium AVS ita DG ad VG. nam spatium AVS aequatur ▭o sub BG, GV, quia spatium ABGVXA aequale rectangulo sub AS, SV, ex proprietate lineaeGa naar voetnoot9). | |||||||||||
[pagina 105]
| |||||||||||
 [Fig. 55.]
AB ∞ 4343 qualium logarithmus 2 est 0,3010. GD ∞ ½AB ∞ 2172. log. AB ∞ 3.6377898  Erit itaque spatium descensus gravis N ad spatium descensus gravis RGa naar voetnoot11) ut DG ad VG. hoc est ut 2172 ad 1597 sive ut 1000 ad 735. Ratio est petita ex eo quod applicatis ordinatim quibuscumque FKN, OPT, rectae KN, QT representant velocitates gravis R acquisitas temporibus AN, AT, dum velocitates gravis N fiunt HN, PT. Hoc inveni isto modo. | |||||||||||
§ 3. [Pourquoi la courbe considérée dans le cas du corps tombantGa naar voetnoot12) est une logarithmique.]Representavi mihi - vide fig. parvam pag. sequentis [Fig. 56] - celeritates acquisitas gravi cadenti motu naturaliter accelerato, incrementis rectangulorum | |||||||||||
[pagina 106]
| |||||||||||
 [Fig. 56.]
minimorum ab linea AB incipientium eamque latitudinem habentium, quae celeritates cum crescant sicut tempora casus, hinc temporum incrementa representavi lateribus eorum rectangulorum ut AN, AT. Itaque si AN, NT minimas temporis particulas inter se aequales esse ponamus, erunt celeritates illis temporibus acquisitae rectangula AF, NO atque ita porroGa naar voetnoot13). Rursus consideravi descensum corporis R, cui aer resistit, quod ejus incrementa celeritatis non sunt aequalia temporibus aequalibus, sicut corporis N, sed diminuuntur magis magisque, pro majori celeritate corpori R acquisita. Nam si celeritatem illi deorsum demus per aerem tantam quanta deberet esse celeritas aeris sursum flantis ad sustinendum grave R ne descendat, certum est tunc resistentiam aeris aequipollere momento gravitatis, ac proinde grave R ea celeritate descendens non acquisiturum majorem ex vi gravitatis, sed aequabili motu descensum continuaturum. Quod si vero dimidio ejus celeritatis aer sursum tendens, corpori quiescenti R, puta ex filo pendenti, occurrat, jam dimidium ei ponderis auferetGa naar voetnoot14). Unde sequitur, quod cum corpus R cadens celeritate dimidia aerem penetrabit ejus quae maxima illi acquiri potest, eo tempore incrementa celeritatis dimidia fore eorum quae habet initio descensus. Atque ita porro quanta pars erit celeritas corpori R ac- | |||||||||||
[pagina 107]
| |||||||||||
quisita celeritatis maximae acquirendae, tanta pars erit momentum resistentiae aeris, momenti ex vi gravitatisGa naar voetnoot15). quibus in contrarium nitentibus, oportet ut eorum differentia determinet gradum accelerationis ratione gradus accelerationis in principio descensus cum aer nihil adhuc resistit.
Hinc intellexi quod sicut incrementa celeritatis corporis, absque aeris resistentia descendentis, recte representantur rectangulis minimis aequalibus AF, NO, ita debere representari incrementa accelerationisGa naar voetnoot16) corporis per aerem descendentis rectangulis minimis decrescentibus ABFH, HFOP [Fig. 56], quorum omnium summa efficeret spatium quoddam ABZ, magnitudine finitumGa naar voetnoot17) (quia summa omnium graduum celeritatis certam celeritatem non debebat excedere) atque (ut putabam) etiam extensione; curvam vero AHP id spatium abscindentem debere esse ejus naturae ut sicut spatium ABFH ad ABOP ita esset NH ad TP, quia spatia ista celeritates acquisitas temporibus AN, AT referendo, simul rectangula HN, PT debent referre diminutiones graduum celeritatis qui alias absque aere aequaliter accrescerent ijsdem aequalibus temporibusGa naar voetnoot18). Hic tum mihi in mentem venit curva olim examinata in libro B, quam logarithmicam appellabam. cui proprietas ista inest, ut nempe sicut spatium ABFH ad ABOP ita sit NK ad TQ [Fig. 55], quomodocumque acceptae sint AN, AT, ut ex ibi demonstratis facile patetGa naar voetnoot19). Haec autem linea asymptoton habet BOZ [Fig. 56] | |||||||||||
[pagina 108]
| |||||||||||
 [Fig. 56.]
adeoque in infinitum extenditur, sed spatium infinitum ABZ definitam habet magnitudinem, ut hic requiri dixi; nam posita AG tangente in A, triangulum ABG aequatur dimidio dicti spatij infinitiGa naar voetnoot1). Estque BG semper ejusdem longitudinis linea, inter perpendiculum a puncto contactus et tangentem intercepta. Estque ad logarithmum binarij ut 0,43429 &c. ad 0,30103 &c. hoc est proxime ut 13 ad 9. Eam vero latus rectum hujus curvae appellabo deincepsGa naar voetnoot2). Porro cum posita hac linea viderem spatia AHFB, APOB [Fig. 56] mihi referre gradus celeritatis acquisitos in fine primi et secundi temporis, eoque spatia esse inter se ut lineae NH, TP, quarum maxima nunquam attingit longitudinem ipsius AB, intellexi gradus celeritatis crescentis temporibus aequalibus representari lineis hisce NH, TP &c.; ijsque proinde ductis in altitudines aequales NT, TS, &c. quae temporis particulas aequales referunt, necesse esse ut summae talium rectangulorum representarent altitudines descensus seu spatia peracta in datis quibuslibet temporibus, hoc est, datis exempli gratia temporibus AL, AE, areas ipsas ALR, AEV representare spatia istis temporibus peracta. Sed ut spatia haec descensus comparare possem cum spatijs à gravi, absque aeris resistentia cadente, ijsdem temporibus peractis, consideravi hujus gradus velocitatis crescentis representari ordinatim applicatis ijsdem productis usque ad tangentem AG | |||||||||||
[pagina 109]
| |||||||||||
[Fig. 55 et 56], ut a Galileo explicatum estGa naar voetnoot3), nam ita quidem ab initio casus utriusque gravis celeritas eadem incrementa sumunt [sic] ut fieri necesse est, quia aer nondum resistit, at celeritates gravis absque aeris consideratione cadentis crescunt cum temporibus aequaliter ut oportet. Atque ita ductis etiam his lineis in triangulo verbi gratia AIE [Fig. 56] applicatis in particulas aequales easdem NT, TS, quae temporis particulas aequales referunt, haberi summam eorum, triangulum nempe AIE, representantem spatium peractum tempore AE, dum area AVE representat spatium eodem tempore AE peractum à gravi per aerem cadente. Rationem autem quam inter se servant triangulum AEI et area AVE facile inveniri sciebam ex ijs quae in libro B de curva hac demonstravi. Est enim area AVE aequalis semper rectangulo sub VI et latere rectoGa naar voetnoot4). ac proinde spatium AVE ad triangulum AEI ut ▭ sub latere recto BG et sub VI ad ½▭ sub AE et EI. Hinc jam non difficile fuit problema ejusmodi resolvere, nempe | |||||||||||
§ 4. [Calcul de l'espace parcouru par le corps tombant en un certain temps.]Posito descensu duorum gravium N et R quorum N nihil retardetur ex resistentia aeris, R vero retardetur; postquam N eousque deciderit ut celeritatem acquisiverit quae maxima contingere potest corpori per aerem cadenti R, invenire quanto minus spatium eodem illo tempore peregerit R quam N. Nam ducta GK parallela BA, quae secet curvam in D, erit GK gradus celeritatis acquisitus corpori N in fine temporis AR, idemque maximus gradus celeritatis quam acquirere potest corpus R, casu aeternum durante. Itaque jam triangulum AGK referet spatium peractum corpori N, area vero ADK spatium eodem tempore peractum a corpore R. quorum planorum inter se ratio est, ex modo dictis, ea quae dimidij quadrati AK sive ▭ sub BG et dimidia GK ad rectangulum sub latere recto BG et sub DG, hoc est ea quae GD ad GQ, dimidiam GK, quae ratio reperta est initio pag. 1Ga naar voetnoot5) ea quae 1000 ad 735 proxime, et propius quantumlibet inveniri potest.
Hinc vicissim si talis proportio inveniatur spatiorum ijsdem temporibus peractorum, alterum a corpore gravissimo quod ab aeris resistentia nihil sensibiliter retardatum fuerit, alterum a corpore leviori, dicemus hujus maximam celeritatem possibilem esse eam quam habet corpus grave in fine descensus. | |||||||||||
§ 5. [Quelques propriétés géométriques de la logarithmique.] | |||||||||||
[pagina 110]
| |||||||||||
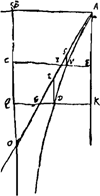 [Fig. 57.]Ga naar voetnoot1)
Ergo cum spat. AVCB sit ∞ ▭ EV, OB. Erit spatium AVE ∞ ▭ VI, OB. Et spat. ADK ∞ ▭ DG, OB. Ergo spat. AVE ad ADK ut VI ad DG, sive ut VS ad DR. 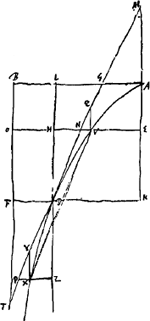 [Fig. 58.]
Quod spat. ADL [Fig. 58] ad spat. VDH ut AG ad VN sive ut AM ad VQ. GDT tangens. Ergo FT ∞ latus rectum.
spat. AVOB ∞ ▭ EV. FT. spat. ADFB ∞ ▭ KD.FT. Ergo spat. ADFB ad AVOB ut KD sive EH ad EV. Ergo per conversionem rationis spat. ADFB ad spat. VDFO ut EH sive AL ad VH.
Quia porro TF ad FD ut DL ad LG, erit ▭ TF.LG ∞ ▭ DB. Sed ▭ TF.LA ∞ spat. ADFB. Ergo spat. ADL ∞ ▭ AG.TF. Eadem ratione spat. VDH ∞ ▭ VN.TF.
Ergo spat. ADL ad VDH ut AG ad VN. vel ut AM ad VQ.
Si YX ∞ QV, erit spat. DXZ ∞ DVH. Nam ex dictis est spat. VHD ∞ ▭ TF.VN. Et spat. DXZ ∞ ▭ TF.Xφ. - Eadem ratione scilicet qua pag. 2. spatium AXVS aequale ▭ BG,GV [Fig. 55]. | |||||||||||
[pagina 111]
| |||||||||||
Sed quia QV ∞ YX, erit et VN ∞ Xφ. Ergo ▭ TF,VN ∞ ▭ TF.Xφ. hoc est spat. VDH ∞ spat. DXZ. | |||||||||||
§ 6. [Représentation graphique du rapport de la vitesse initiale quelconque de l'ascension à la ‘vitesse terminale’.]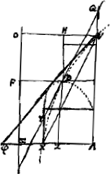 [Fig. 59.]
Sit rursus YX ∞ QV [Fig. 59]. HD tempus ascensus. DZ tempus descensusGa naar voetnoot2). VX parall. QYGa naar voetnoot3). Vφ tangens in V. DF celeritas terminalis. HV celeritas initio ascensus. φX ad XΛ ut momentum resistentiae aeris ad momentum resistentiae à gravitate. Unde ita quoque celeritas initio ascensus ad celeritatem terminalem. quae ergo etiam debet esse ut VH ad HOGa naar voetnoot4). Et facile patet quod φX ad XΛ ut VH ad HO, nam ▭ φX. O∆ ∞ spat. VXΞGa naar voetnoot5), et ▭ XΛ, O∆ ∞ spat. VOΞX. Ergo spat. VXΛ ad YOΞX ut φX ad XΛ. Sed quia spat. DZX ∞ VDH, erit ▭ HΛ ∞ spat. VXΛ. Unde spat. VXΛ ad VOΞX ut VH ad HOGa naar voetnoot6). quae itaque ut φX ad XΛ. | |||||||||||
[pagina 112]
| |||||||||||
 [Fig. 60.]
 [Fig. 61.]
| |||||||||||
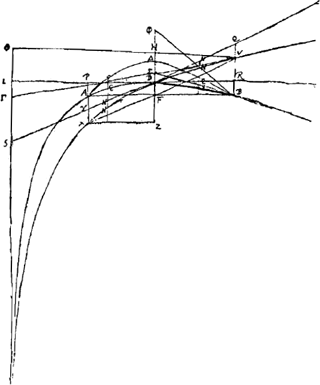
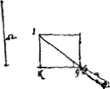
§ 7. [ConstructionGa naar voetnoot7) de la courbe de jet d'un boulet lancé en l'air sous un angle quelconque.]Sit XDV [Fig. 60] linea analogisticaGa naar voetnoot8) cujus asymptotos OS. tangens in D sit YDQ. RDP asymptoto OS ad angulos rectos. cui parallelae PX, EN, QB &c. Sumtis PA ∞ YX, EE ∞ NN, RB ∞ QV, descriptaque per puncta AEDEB curva, quam analogisticam luxatam dicemus, poterunt hujus ope determinari curvae omnium corporum projectorum quas in aere describunt, considerata videlicet aeris resistentia. Dato enim exempli gratia mobili quod projiciatur secundum rectam GI [Fig. 61] inclinatam ad horizontalem GK angulo IGK, et celeritate GI. ductâ IK perpendiculari in GK, erit KI celeritas sursum, GK celeritas prorsum, GI celeritas absoluta. | |||||||||||
[pagina 113]
| |||||||||||
Datam autam esse oportet rationem celeritatis sursum ad celeritatem terminalem dati mobîlis, hoc est ad eam quam maximam unquam ex casu habere potest, quae ratio sit ut KI ad Ω. Jam ut Ω ad IK ita sit LD, quae a vertice curvae ADB in asymptoton perpendicularis est, ad DR. VRB parall. OS occurrat curvae BDA in B et analogisticae in V. BA parall. VO in A occurrat curvae BDA, eademque secet HDZ in F. Et recta VFX occurrat curvae VDX in XGa naar voetnoot9), sitque XZ perpendicularis in HDF. Erit jam primum HD ad DZ ut tempus ascensus ad tempus descensus. VH ad ZX, sive BF ad FA ut celeritas sursum initio ascensus, ad celeritatem deorsum in fine descensus. atque item BF ad FA ut longitudo ascensus, sive sub arcu ascendente, ad longitudinem descensusGa naar voetnoot10). Curva autem in aere descripta erit B∆A, quae sic invenitur. VΣΓ tangens in V secet HZ in Σ. Haec enim tangens ducitur sumta ΟΓ ∞ lateri recto. Erit ΣB tangens in BGa naar voetnoot11). Fiat angulus FBφ ∞ KGI. Et ut FΣ ad Fφ ita sit FD ad F∆. Et secundum eandem hanc proportionem augeantur omnes parallelae ipsi FD in figura BDAB. Eritque curva per extremitates ducta B∆A quaesita, quam φB tangit in BGa naar voetnoot12). Unde apparet, dummodo ratio celeritatis initialis sursum ad celeritatem terminalem sit eadem ut hic KI ad Ω, tempora ascensus et descensus quoque in eadem ratione permanere, nempe HD ad DZGa naar voetnoot13). Itemque celeritatis in principio ascensus sursum, | |||||||||||
[pagina 114]
| |||||||||||
 [Fig. 62.]
et in fine descensus deorsum quae erant ut BF ad FA; nec non et longitudinum ascensus et descensus quae erant item ut BF ad FA. Item curvam jactus ipsi BDA proportionalem manere. Quod si tamen manente eadem celeritate sursum, celeritas in longitudinem minor ponatur, fiet amplitudo jactus proportionaliter minor, ut si celeritas in longitudinem sit tantum ⅓ GK, fiet et amplitudo jactus ∞ ⅓ BA. | |||||||||||
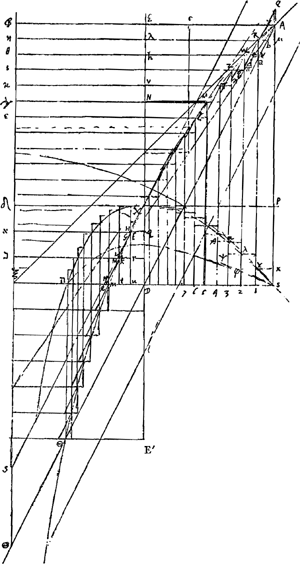
§ 8. [Mouvement horizontal avec une vitesse initiale égale à la ‘vitesse terminale’.]AXΘ [Fig. 62] est Curva Logarithmica sive Logistica, Bδs asymptotos ejus. Si corpus per medium resistens feratur super plano motu horizontali, sitque resistentia ut celeritas. temporis autem particulae aequales designentur particulis aequalibus Bη, ηθ, &c. celeritas autem corporis initio motus designetur recta BA, initio vero secundi temporis rectâ ηR. Erunt deinceps θW, ιZ celeritates initio sequentium temporum θι, ιϰ, &c. Quia sicut celeritates AB ad Rη, Wθ, ita debent esse decrementa celeritatum ob resistentiam, nempe Rμ, Vν, Zπ. quod hic contingit. nam ex proprietate curvae, proportionales continuè sunt AB, Rη, Wθ &c. unde et earum differentiae in eadem ratione decrescunt. Hinc si corpus horizontali motu impellatur, atque ea celeritate quam cadendo per medium resistens maximam acquirere potest, ac rursus idem corpus eadem hac celeritate sursum | |||||||||||
[pagina 115]
| |||||||||||
projiciatur per medium non resistens, erit spatium maximum seu totum quod horizontali motu absolvere potest (quod tamen infinito tempore non absolvet) ad spatium quo motu perpendiculari ascendet, in ratione dupla. Ducta enim tangente Aξ, referent perpendiculares aequaliter distantes in ∆lo ABξ celeritates decrescentes corporis sursum projecti. quia eadem primâ temporis particulâ Bη, tantundem celeritati initiali decedere debet ob vim gravitatis, quantum eadem temporis particula decedit celeritati horizontali propter medij resistentiam, quia posita fuit celeritas terminalis initio hujus motus, cui tantundem renititur medium quantum gravitas projecto sursumGa naar voetnoot1). | |||||||||||
§ 9. [Jet oblique suivant un angle de 45o, les vitesses initiales horizontale et verticale étant égales à la ‘vitesse terminale’. Construction de la trajectoire.]Bη, ηθ, θi &c. [Fig. 62] sunt particulae temporis aequales. Spatia BAXδ, ηRXδ sunt ut celeritates sursum in initijs temporum Bη, ηθ &c. quae spatia RAXδ, ηRXδ sunt ut AE, Rλ. AB, Rη, Wθ &c. sunt continue proportionales, ideoque et differentiae earum S1; 1, 2; 2, 3; 3, 4 &c. Quare hae representant spatia aequalibus temporibus peracta motu horizontali a mobili cui aer resistit. Dividitur autem motus projecti secundum tangentem sY in horizontalem hunc et ascendentem ipsi aequalem, hoc est aequali celeritate coeptum, quia angulus 1sY ponitur 45 graduum. In motu autem hoc horizontali si Rμ ponatur pro celeritate in prima temporis particula Bη, jam reliquae celeritates deinceps per particulas aequales erunt Wν, Zπ &c. quia et hae decrescunt eadem proportione qua AB, Rη, Wθ &c. ideoque ita ut decrescant in eadem quam inter se servant ratione. Sunt igitur S1; 1, 2; 2, 3. &c. spatia aequalibus temporibus motu projecti per saX, quatenus horizontalis ejus consideratur motus, peracta. quem motum pono incepisse celeritate terminali quam refert AB; tantamque etiam initio fuisse projecti celeritatem sursum, quam refert sA, ut proinde celeritas absoluta fuerit quam refert diagonalis quadrati. Oportet autem nunc ostendi quod rectae Y1, λφ, aψ &c.Ga naar voetnoot2) sunt ut descrescentes gradus celeritatis corporis sursum projecti, hoc est ut rectae Rλ, Wh, &c. per ea quae | |||||||||||
[pagina 116]
| |||||||||||
in praecedentibus ostensa suntGa naar voetnoot1). Sic enim eaedem Y1, λφ, aψ &c. etiam spatia referent ijs celeritatis gradibus sursum emensa, ijsdemque aequalibus temporibus, quum Y1 aequalis hic sit 1s, et utraque pari celeritate peracta, quoniam aequales celeritates sursum et in latus poscimus. Sint Aa, Rd, Wn parallelae tangenti in X sive ipsi AΘGa naar voetnoot2). eoque secent Rμ in b, Wν in e, Zπ in g. Quia igitur sicut AB, Rη, Wθ &c. ita sunt earum differentiae Rμ, Wν, Zπ. auferuntur autem a singulis prioribus aequales rectae BE, ηλ, θh &c. et à posterioribus aequales rectae μb, νe, πg, estque harum prima μb, ad Rμ à qua aufertur, sicut illarum aequalium prima EB ad AB à qua aufertur, (censendum enim est curvae particulam AR et tangentem hucusque coincidere) sequitur, sicut reliquas AE, Rλ, Wh &c. ita quoque esse reliquas Rb, We, Zg. ac proinde et earum duplas Ra, Wd, Zn, quibus ex constructione aequantur Y1, λφ, aψ &c. Ergo et hae ut celeritates decrescentes corporis quatenus sursum projecti celeritate terminali. Quare fertur per curvam SY λ a X. quod erat ostendendum.
In descensu majora paulo tempora sumsi quo minus intricata esset figura. Ijs temporibus aequalibus horizontalis motus confecit spatia Du, ut, tm &c. quibus sunt aequales qf, rk, tm. quas itaque oportet ostendere esseGa naar voetnoot3) sicut crescentes gradus celeritatis. | |||||||||||
§ 10. [Jet oblique suivant un angle quelconque et avec une vitesse quelconque. Esquisse d'une démonstration de la construction de la trajectoireGa naar voetnoot4).] | |||||||||||
[pagina 117]
| |||||||||||
 [Fig. 63.]
Sit projectio secundum ηθ inclinita sursum ad horizontalem ηϰ angulo dato θηϰ [Fig. 63]. sitque θϰ perpendicularis in ηϰ. Est ergo celeritas sursum ad celeritatem horizontalem ut θϰ ad ϰη, quae celeritas sursum sit ad celeritatem terminalem ut ϰθ ad ζ. Posita igitur curva analogistica ADZ [Fig. 64] cujus asymptotos BO, latus rectum λ, sit ut θϰ ad ϰη ita λ ad aliam, cui aequalis statuatur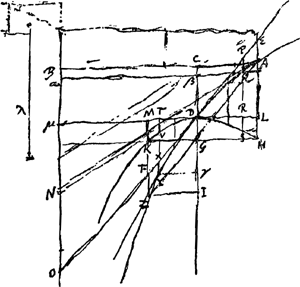 [Fig. 64.]
BA asymptoto perpendicularis et analogisticae occurrens in A. Porro ut celeritas terminalis ad celeritatem sursum, hoc est ut ζ ad θϰ, ita sit BC ad CA. Et CD parallela asymptoto secet curvam in D, ad quod punctum tangens ducatur ODE, quod fiet ducta Dμ perpendiculari ad asymptoton et sumtâ μO aequali lateri recto λ. Ducatur dictae tangenti parallela AZ occurrens curvae in Z et secans CDI asymptoto parallelam in G. et fiant AE, ZF parallelae asymptoto eaeque occurrant HGK, μDL in H, L, K et M. Jam si ductis ubivis inter EH, ZM rectis PS, ZM [lisez YT] sumantur earum partibus singulis PQ, YZ [lisez YX] inter curvam et tangentem FPE interceptis proportionales singulae RS, TV infra rectam MDL atque ita ut angulus GHS sit aequalis θηϰ [Fig. 63]Ga naar voetnoot5): perque puncta S, V et quotlibet alia hoc modo inventa transeat curva HSDVK. Dico hanc esse secundum quam [lisez plutôt eam quam] corpus projectum ascendens, ac usque in terram revertens, describet. Tempus autem ascensus ad tempus descensus erit ut CD ad DI. Celeritas perpendicularis initio ascensus ad celeritatem in fine descensus ut HG ad GK. Celeritas residua sursum in S ad celeritatem sursum ab initio in H, ut RD ad ZD. Celeritas deorsum in V ad celeritatem sursum in H ut TD ad DL. | |||||||||||
[pagina 118]
| |||||||||||
Hinc incipienda demonstratio. Sit Bμ tempus totius ascensus quod in particulas minimas aequales dividatur. et fiant singularum altitudine rectangula ad curvam ADZ terminata. ducatur CD parallela BO. sit BADμ spatium referens celeritatem totam initio ascensus. Jam hoc per rectangula illa ab AB incipiendo decrescet in temporis particulis dictis aequalibus, sicut celeritas ascendentis. per proprietatem curvae quam vide pag. 2 in libro D, ubi primum haec materia agitaturGa naar voetnoot1). Hinc et ipsae rectae AC, βQ &c. referent gradus celeritatis reliquos initio temporum aequalium respondentium in Bμ ex proprietate quam vide ibidem pag. 7Ga naar voetnoot2). Hinc in figura pag. 10 [Fig. 62] etiam rectae exiguae Rb, We, Zg eosdem gradus celeritatis decrescentis reliquos referentGa naar voetnoot3). atque etiam Ra, Wd, Zn quae ad praecedentes datam rationem habent, quam sA ad sD. sive denique etiam Y1, φλ, ψa, quas ex constructione apparet ipsis Ra, Wd, Zn esse aequales respectivè. Itaque si Ra referat primi tempusculi Bη celeritatem sursum (hoc est quae per totum tempus Bδ referatur eadem longitudine Bδ) atque adeo eadem RA [lisez Ra] ipsam altitudinem eo tempusculo peractam, reliquae deinceps φλ, ψa, &c. referent celeritates et altitudines emensas reliquis tempusculis ηθ, θ1, &c. illae ementientes totam DX sicut omnes Ra, Wd, Zn eandem DX emetiuntur, tempuscula vero ijs singulis respondentia, totam Bδ. Rursus ostendendum si primi tempusculi Bη celeritatem et spatiolum peractum referat s1 (hoc est eam quae tempore eodem Bδ peragat spatium sξ, nam sic tempus horizontalis motus fit ad ascendentem in ratione data) ostendendum inquam reliquas 12, 23, 34 &c. referre celeritates et spatiola tempusculis consecutis ηθ, θ1, &c. peracta. Unde corpus per curvam sYλ &c. incedere facile jam apparet. Faciendae propositiones plures ut huc veniaturGa naar voetnoot4).
§ 11. Les p. 83 v. et 84 r. des Chartae mechanicaeGa naar voetnoot5) se rapportent à la construction de la courbe du jet. Nous ne croyons devoir reproduire de ce brouillon que la remarque suivante: | |||||||||||
[pagina 119]
| |||||||||||
ANX tangens in A [Fig. 65] GHM angulus jactus in altum. Ut GN ad GM ita fiant singulae parallelae spatij ADZG ad respondentes parallelas spatij HQK. Erit figura jactus secundum curvam HQKGa naar voetnoot6).
Amplitudines autem ex diversis elevationis angulis ortae ex figurarum hic ortarum magnitudine non sunt aestimandae. 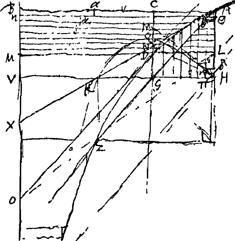 [Fig. 65.]
|
| ||||||||||