Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 29]

II.
Considérations générales sur les engins statiques.
Oct. 1676.

[Fig. 1.]⁴⁾

Hagae 1676 Oct.¹⁾.

Primum ac praecipuum Theorema Mechanicae certâ ac legitima demonstratione primus confirmavi²⁾. Nimirum brachiorum librae longitudinem contraria ratione respondere ponderum gravitati quae ab extremis brachijs suspenduntur. Nam Archimedis demonstratio quae legitur libro primo Aequipond. prop. 6³⁾ non illud evincit quod proponitur, ut à multis fuit animadversum.

Cum enim dicit [Fig. 1]: Est igitur a impositum in e, et ipsum b in d; concedi sibi tacite⁵⁾ postulat ut idem momentum librae adferant partes ponderis A, suspensae per jugi partem lg, atque cum pondus ipsi A aequale ex puncto e filo suspenditur. similiterque partes B per partem jugi gk suspensae idem efficiant ac si à puncto d pondus ipsi B aequale penderet. Proponitur enim ad demonstrandum, suspensis filo ponderibus A

4) Dans la Fig. 1 f représente la commune mesure des poids A et B.

1) Manuscrit E, p. 61-65. Comparez sur le séjour de Huygens à la Haye le note 6 de la p. 4 du T. XVIII.

2) Voir, à la p. 40 qui suit, la Pièce V, B, lue à l'Académie des Sciences de Paris en décembre 1673.

3) Τὰ σύμμετρα μεγέθεα ἰσορροπέοντι ἀπὸ μαϰέων ἀντιπεπονθότως τὸν αὐτὸν λόγον ἐχόντων τοῖς βάρεσιν (magnitudines commensurabiles aequilibritatem servant ex longitudinibus suspensae, quae in contraria proportione sunt ac pondera. - ‘Archimedis Opera omnia’, ed. J.L. Heiberg, Lipsiae, Teubner, 1913, II p. 133). La Prop. VII étend cette thèse aux grandeurs incommensurables.

5) Voyez cependant la note 5 de la p. 43 qui suit.

[p. 30]

et B à punctis e et d, fieri aequilibrium in c. Quis autem concedat eundem effectum habere respectu librae suspensae ex c, pondus A affixum per partes ad lineam lg, atque cum totum suspenditur filo ex puncto e? praesertim cum appareat partes quasdam ponderis A gravitatem exercere in brachium alterum cd. Neque enim satis est omnium partium ponderis A per lg affixarum centrum gravitatis cadere in c punctum, ut videtur voluisse Archimedes.

Stevinus, Galileus et alij mutare aliquatenus hanc demonstrationem conati sunt ac probabiliorem reddere, sed vel in similem jam dictae difficultatem incidunt, vel in alias nihilo leviores¹⁾.

Vectis²⁾ ratio, item axis in peritrochio³⁾, eaedem sunt ac librae brachiorum inaequalium.

Cochlea ad planum inclinatum refertur. Hujus⁴⁾ vero nondum aeque evidens demonstratio reperta est ac nostra illa librae quam explicuimus academicis Parisinis. Optima hucusque videtur illa Stevini qua catenam triangulo circumdat ....... voyez les p. 475-476 du T. XVIII, où nous avons publié cette partie ..... similiterque pondus catenae BC in F.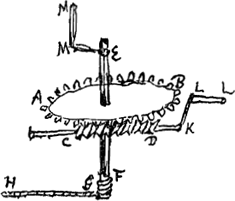

[Fig. 2.]

Cochleae [Fig. 2] quam infinitam vocant, hoc est quae aptatur dentibus rotae cujus circumferentiae adjacet, hujus inquam vis ex librae et plani inclinati rationibus constat. Caeterum ad inveniendum calculo quanta fiat virium multiplicatio cum hujusmodi machina adhibetur, nihil aliud spectare opus est, quam quanta sit celeritas ponderis moti adceleritatem potentiae moventis comparata. Quod sane in omni alio machinarum genere eodem modo se habet⁵⁾. Sit rota dentata AB 30 dentium. cochlea dentibus istis conveniens CD. cujus axi additum sit manubrium KLL. Hic, quia conversione una manubrij tantum

1) Lagrange, ‘Mécanique analytique’, Première Partie, Section I, § 1: ‘Quelques auteurs modernes, comme Stevin dans sa Statique, et Galilée dans ses dialogues sur le mouvement, ont rendu la démonstration d'Archimède plus simple.. etc.’. E. Dühring, ‘Kritische Geschichte der allgemeinen Principien der Mechanik’, 2ième éd. Leipzig, Fues, 1877, p. 75: ‘Die aüsserlichen Umgestaltungen, welche Stevin und Galilei mit dem Archimedischen Hebelbeweis vorgenommen haben, dienen einerseits zur Veranschaulichung, lassen aber andererseits die Schwächen der rein mechanischen Schlussfolgerungen noch mehr hervortreten’. La démonstration de Stevin constitue le Théorème I de la Seconde Partie des Propositions du 1^er Livre de la Statique (‘Les Oeuvres mathématiques’, éd. A. Girard, 1634). Celle de Galilée se trouve dans les ‘Discorsi e Dimostrazioni’ de 1638 (Dialogo secondo).

2) Il s'agit de la barre inflexible destinée à soulever un poids gisant à terre: comparez le deuxième alinéa de la p. 17 qui précède.

3) Voir la note 4 de la p. 23 qui précède.

4) C.à.d. de l'équilibre d'un poids placé sur un plan incliné.

5) Comparez la note 4 de la p. 23. On voit que Huygens ne tâche nullement de donner une démonstration en règle de ce principe (que nous avons appelé à la p. 15 le principe des déplacements ou des vitesses), quoiqu'il affirme que l'effet de la vis sans fin s'explique par la considération de la balance et du plan incliné. Il dira plus loin (p. 32, Fig. 4) qu'il ne faut pas expliquer l'effet des poulies par la considération de la balance ou du levier (note 4), mais qu'il faut considérer le nombre des cordes: c'est ce que fait aussi Héron dans ses Mécaniques. Dans la présente Pièce il ne s'agit que de déplacements réels; voir sur les déplacements virtuels la p. 16 qui précède et la p. 52 qui suit.

[p. 31]

unus dens in praecedentis locum succedit, ita ut rotae trigesima pars ambitus peragatur, sequitur trigecuplo validiorem esse actionem manubrij KLL quam si idem ad axem rotae AB aptatum foret ut in EMM. Quod si porro axis EF involvatur funi GH pondus quodpiam trahenti, sitque exempli gratia longitudo manubrij EM seu KL decupla ad semidiametrum ipsius axis, hinc jam decuplum insuper virium augmentum contingit, adeo ut potentiae manubrium KL circumagentis vis trecenties jam multiplicata sit. Etenim dum manus ad LL totam circumferentiam peragit radio KL descriptam, attrahitur pars chordae HG, aequalis tricesimae parti circumferentiae axis EF, quae tota circumferentia aequatur decimae parti circumferentiae radij KL. unde liquet celeritatem manus tercentuplam esse celeritatis ponderis à chordae GH agitati.

Si quis pondus centum librarum attollere velit, ac tantum potentiam unius librae habeat, oportet machinam qua utitur ita constructam esse ut dum potentia movens, quae est unius librae, movetur per intervallum pedis unius, simul pondus centum librarum moveatur tantum per unam pedis centesimam. Idque ita ut pro nihilo habeantur impedimenta ab inertia et attritu partium ipsius machinae prodeuntia. Ac qualiscunque fuerit machina, quacunque arte fabricata, semper ista potentiarum ac itinerum contraria ratio requiritur, ad effectum qui proponitur consequendum⁶⁾.

Sedet conversa hujus propositionis aeque vera est, quod mirum videri posset; nempe qualicunque constructa machina, si dum potentia movens pedis unius spatium conficit, pondus motum necessario unam centisimam pedis progreditur, non posse fieri quin ea machina vires agentis in centuplum augeat. deductis et hîc impedimentis a materia procedentibus.

6) Il s'agit bien ici (comparez la note précédente) d'un principe général indémontré et peut-être indémontrable. Comparez la note 3 de la p. 17 qui précède et la p. 80 (note 3) qui suit.

[p. 32]

Hinc omnis generis machinarum par esse virtus colligitur¹⁾, nisi quod optimae censendae quae sunt simplicissimae, quod in his minus impedimentorum accedit à materiae inertia et attritu, quodque facilius et minore sumtu construuntur.

Qui autem vera mechanicae fundamenta²⁾ ignorant inventa nova machina sperant majus quid, quam hucusque cognitis, ejus ope praestari posse, veluti ut aquas ad ingentem altitudinem, magnâ copiâ, brevi tempore, minimâ operâ perducant. Quin et ad experimenta frequenter provocant, quibus et seipsos et alios aeque imperitos perinde fallunt. Semper autem confutari possunt instituto dilligenti examine itinerum potentiae moventis ac ponderis moti, ac rursus gravitatum ipsarum considerata ratione. quo facto semper illa superius allata regula vera esse deprehendetur¹⁾.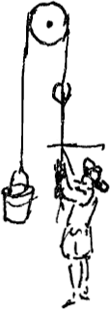

[Fig. 3.]

[Fig. 4.]

[Fig. 5.]

Si quis aquam e puteo hauriat situla ad restim alligata qui super orbiculum transeat [Fig. 3], is tantundem vel amplius etiam labore suo proficiet atque alius artificiosâ quamlibet machinâ utens, suisque ijsdem viribus annixus. Nec aliud hic ab inventione commodum adjungi queat quam ut aequilibrium concilietur situlae vacuae cum pondere resti annexo, qua parte ab homine trahitur. aut tale quippiam praeterea, ut ne retro labi possit situla ad singulos conatus quibus sursum adducta fuerit. De caetero haec omnium simplicissima est machina, cum nihil superflui ponderis impendatur.

Trochlearum ac polyspastorum³⁾ vires, qui librae aut vectis rationibus⁴⁾ explicant, errant mea sententia, cum vera demonstratio simplicissimaque ex funium multiplicatione sumatur⁵⁾. Quid enim clarius quam fune ABC [Fig. 4] pondus D sustinente à trochlea E suspenso, quam funis ambit, ita ut altero capite ad clavum A fixus sit, altero C sustineatur manu. Quid inquam manifestius quam dimidium gravitatis D incumbere digitis ad C.

1) Voir la note 6 de la p. 31.

2) Cette expression assez vague désigne apparemment en premier lieu le principe des déplacements. Voir sur la question de la grandeur finie ou infiniment petite des déplacements le dernier alinéa de la p. 16 qui précède.

1) Voir la note 6 de la p. 31.

3) Comparez la note 9 de la p. 25 qui précède.

4) Voir sur la ‘vectis’ la note 2 de la p. 31 qui précède.

5) Voir la fin de la note 5 de la p. 31.

[p. 33]

Illi vero diametrum trochleae tanquam vectem considerant. Malè. Eodem enim modo omnia se habebunt etiamsi pro trochlea fuerit annulus K [Fig. 5]. at hic jam nullus vectis erit.

Apparet autem et hic ratio illa reciproca spatiorum ac gravitatum. Nam dum manus C pede uno attollitur, pondus D tantum semipede altius fit; unde duplo augetur hic potentia agentis.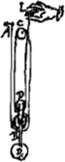

[Fig. 6.]

Similiter si funis in A affixus [Fig. 6] circumvolvatur trochleae B, atque inde ascendens super orbiculum C, cujus fixum item sit centrum, transeat, ac rursus descendens ambiat trochleam D, ipsi B connexam, tandemque ad manus L feratur. hic apparet pondus D trochleae B appensum aequaliter tendere funes quatuor, qui proinde singuli quartam ponderis partem sustinent; ac proinde una quarta incumbit manui L. Non potest autem ascendere pondus D nisi quatuor funes, e quibus pendet, tanto breviores fiant quantum est spatium ascensus istius. Quo autem breviores fiunt funes quaterni, id totum necessario cedit elevationi capitis L, utique cum caput alterum A, et orbiculus C, suo loco manere ponantur. Ergo patet necesse esse ut quatuor pedum altitudine attollatur caput L, si velimus ut uno pede afcendat pondus D. Eademque est ratio in qualibet trochlearum multitudine ac dispositione, ut nempe pro numero restium quibus pondus suspenditur, vel trahitur, augeantur vires ad extremum applicatae⁶⁾.

En marge: Quanta vis ad certam celeritatem corpori imprimendam requiratur⁷⁾.

6) Le T. VII des Registres de l'Académie se termine par un ‘Traitté de Mechanique pour expliquer les proprietés de la Poulie’ de 63 f. de Blondel, qui porte en marge la date du 18 janvier 1674.

7) Voyez sur ce sujet la Pièce IX qui suit (note 2 de la p. 160), aussi que la p. 89 de l'Avertissement sur cette Pièce.