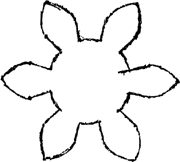
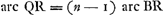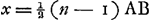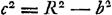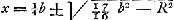Pignon quadruple de la roue de champ [Fig. 117 et 118].
[Fig. 117.]

|
-
voetnoot1)
- Les Fig. 102-106 et le texte correspondant aux trois premières ont été empruntées aux p. 1-5 du Manuscrit E, datant sans doute de 1674, puisque le Manuscrit D ne contient encore que des dates de 1673, et que la p. 26 du Manuscrit E porte la date du 19 décembre 1674.
-
voetnoot2)
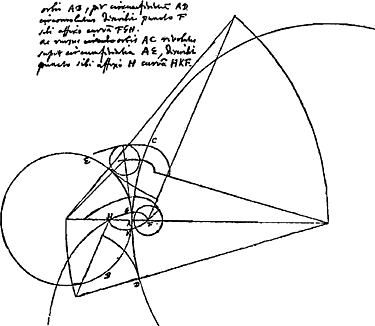
- Le point F, attaché au petit cercle EAB roulant de haut en bas sur le grand cercle immobile, décrit une épicycloïde raccourcie - nous nous servons de ce terme souvent employé pour désigner l'épicycloïde à boucles, quoique certains autres auteurs parmi lesquels Gino Loria (ouvrage cité dans la note 4 de la p. 603) parlent au contraire dans ce cas d'une épicycloïde allongée -; FGH est le demi-contour de la boucle, dont l'autre demi-contour, symétrique avec le premier par rapport à la droite HF serait obtenu par le roulement du petit cercle de bas en haut. Huygens dit, sans doute d'après Roemer, que lorsque le grand cercle roule de bas en haut sur le petit cercle immobile et que le point H est attaché au grand cercle, celui-ci décrira une épicycloïde qui viendra couper la droite HF précisément au point F. Pour voir qu'il en est ainsi, il faut remarquer que le mouvement des deux cercles l'un par rapport à l'autre est absolument le même, que ce soit le petit ou bien le grand qui roule. On peut toujours rendre le cercle roulant immobile et mettre l'autre en mouvement, par rapport à une table p.e., en donnant à l'ensemble des deux cercles un mouvement tournant approprié par rapport à cette table. Supposons, pour fixer les idées, que, dans le premier mouvement considéré le point bleu B vienne s'appliquer sur le point vert D pendant que le point bleu F décrit la ligne bleue FGH et vient donc en fin de compte coïncider avec le point vert H attaché au grand cercle immobile: il est évident que la
même coïncidence doit avoir lieu lorsque, le petit cercle bleu restant immobile et le grand cercle vert roulant sur lui également de haut en bas, le point vert D vient s'appliquer sur le point D et que le point H décrit au-dessus de la droite HF sa ligne verte. Or, si l'on considère au contraire, comme Huygens, un mouvement roulant de bas en haut du grand cercle sur le petit, il est évident que le point vert H décrira cette fois la ligne HKF symétrique par rapport à la droite HF avec la ligne verte HF supérieure.
La Fig. 102 fait fort bien voir que les lignes FGH et FKH ne sont pas symétriques par rapport à la droite FH: malgré la coïncidence des points extrêmes la ligne verte supérieure HF ne coïncide nullement avec la ligne bleue HGF, comme on pourrait le croire.
Il est évident que les mêmes coïncidences se produiront lorsque les cercles tournent chacun autour de son centre, toujours en roulant sans glisser l'un sur l'autre, puisqu'alors aussi on peut mettre l'un d'eux en repos par un mouvement rotatoire donné à l'ensemble.
Dans la Fig. 103 on reconnaît l'aire dyssymétrique HGFKH de la Fig. 102, ainsi que le point A où se touchent les deux circonférences désormais imaginaires. Supposons que la grande roue mène la petite. L'extrémité de la dent de la grande roue, correspondant au point vert H de la Fig. 102, s'appliquera constamment sur la ‘ligne HKF’, qui constitue la partie supérieure du contour d'une des dents de la petite roue, lorsque les deux circonférences imaginaires roulent l'une sur l'autre. En d'autres termes, lorsque les dents ont la forme indiquée dans la Fig. 103, que la grande roue tourne d'un mouvement uniforme et que ses dents sont toujours en contact avec celles de la petite roue, celle-ci aussi tournera uniformément.
Quant à l'expression ‘aequali vi continue in se mutuo agentes’, il est évident que, s'il n'y a aucun frottement, et que les roues tournent uniformément, ce mouvement continuera indéfiniment, sans que les dents exercent l'une sur l'autre aucune pression. Dans la pratique, où il y a des frottements et où il s'agit aussi d'accomplir un certain travail, il faudra qu'un moment agisse sur la grande roue pour maintenir son mouvement uniforme de vitesse angulaire déterminée; la grande roue exercera à son tour un moment sur la petite roue, et il faudra que ce moment, pour vaincre le moment résistant supposé constant, ait lui aussi une grandeur constante. La grande roue en mouvement uniforme ne peut donc manquer, lorsque le mouvement de la petite roue est également uniforme, c.à.d. lorsque les dents sont constamment en contact, et que la petite roue accomplit constamment le même travail, d'exercer sur elle un moment constant.
On voit que la forme des dents n'est pas entièrement déterminée: la dent de la grande roue, dans le cas considéré, n'agit que par son point extrême; quant à la dent sur laquelle elle agit, son contour supérieur seul doit avoir la forme indiquée dans la figure. Si l'on veut que la petite roue puisse aussi mener la grande, ce ne sera toujours que la partie inférieure du contour de la grande roue qui devra avoir la forme indiquée dans la figure.
Le problème peut d'ailleurs être considéré plus généralement. Pour qu'il y ait constamment contact, les mouvements des deux roues étant uniformes, les dents pourront aussi avoir d'autres formes que celles considérées jusqu'ici. Les dents d'une des roues, p.e. de la petite roue menant la grande, pourront même avoir toutes sortes de formes: il s'agit seulement de choisir convenablement les dents correspondantes de l'autre roue. Supposons p.e. que les dents de la petite roue soient de petits cercles attachés à elle, tels que le cercle à centre F de la Fig. 102 (qui peut, ou qui peut ne pas toucher la circonférence BAE). Il faudra alors remplacer la ligne HGF par la ligne indiquée dans la Fig. 102 dont tous les points se trouvent écartés de ceux de la ligne HGF à une distance égale au rayon du petit cercle à centre F. C'est ce qu'indiquent aussi la Fig. 104 et les lignes pointillées de la Fig. 103. L'extrémité de l'ancienne dent de la petite roue de la Fig. 103, qui correspondait au point F de la Fig. 102, étant maintenant remplacée par un cercle, il faudra que le contour inférieur de la dent menée de la grande roue (contour correspondant à la ligne HGF de la Fig. 102) soit remplacé par la ligne pointillée supérieure de la Fig. 103.
De la Hire dans son travail cité à la p. 602 fait une remarque du même genre: il parle de la transformation d'une cheville punctiforme d'une des roues en un cercle et de l'adaptation de la forme des dents de l'autre roue à ce changement. Il dit en général (Prop. VI du Chapitre ‘De l'Usage des Epicycloïdes dans les Mecaniques’) que l'on peut donner aux dents d'une des roues ‘quelle figure on voudra: mais alors les dents de l'autre roue dont la figure était en Epicycloïde, doivent avoir une forme composée de celle de l'Epicycloïde et de celle de la dent proposée’. Il est évident que cette composition est bien plus difficile dans tous les cas où la dent proposée n'a pas précisément la forme d'un cercle (ou partie de cercle).
Huygens n'indique pas comment ont été obtenues les Fig. 105 et 106. Cette dernière fait voir que probablement Roemer s'est aussi occupé du cas où l'une des roues est intérieure à l'autre. Comparez le dernier alinéa de la note 4 de la p. 603 qui précède.
-
voetnoot1)
- La Fig. 107 et le texte qui l'accompagne sont empruntés à la p. 167 du Manuscrit E, datant probablement de la fin de 1678, puisque la p. 165 porte la date du 3 décembre 1678 et que la p. 175 est datée 1679 (comparez la première ligne et la fin de la note 1 de la p. 400 qui précède).
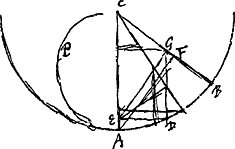
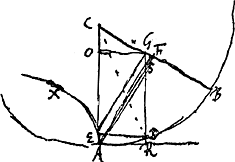
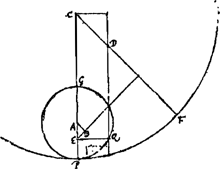
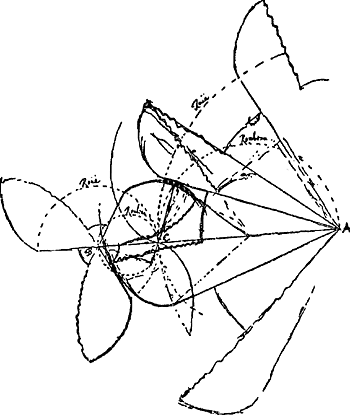
La Fig. 107 représente apparemment un pignon de trois dents (ou ailes) mené par une roue, les contours de toutes les dents étant formés par des lignes droites, des lignes épicycloïdales et des lignes quelconques. Ces dernières sont les lignes sinueuses de la figure. Quant aux épicycloïdes, contrairement au cas considéré dans le § 1, il doit s'agir ici d'épicycloïdes ordinaires. Les lignes courbes des ailes du pignon formant avec les rayons auxquels elles se rattachent des angles de 180o, sont des fragments de l'épicycloïde ordinaire décrite par un point quelconque du ‘Rouleau’ droit de diamètre CA (moitié du diamètre de la ‘Roüe’ droite) lorsque ce ‘Rouleau’ roule, de haut en bas, sur la ‘Roüe’ gauche immobile; tandis que les lignes courbes des dents de la roue, faisant également des angles de 180o avec les rayons auxquels elles se rattachent, sont des fragments de l'épicycloïde ordinaire décrite par un point quelconque du ‘Rouleau’ gauche de diamètre BC (moitié du diamètre de la ‘Roüe’ gauche) roulant de bas en haut sur la ‘Roüe’ droite immobile. Huygens a tracé les deux épicycloïdes nommées décrites par le point C considéré comme faisant partie de l'un ou de l'autre ‘Rouleau’. En effet, si les courbe sont ces formes-là, et qu'un rayon déterminé partant du centre A touche, en son point situé sur le ‘Rouleau’ droit, une des ailes du pignon, comme la figure l'indique (quoique l'on n'y distingue pas nettement la place précise du point de contact), cette même droite restera en contact
- le point de contact se trouvant toujours sur le ‘Rouleau’ droit - avec la courbe de l'aile du pignon, jusqu'au moment où le rayon qui limite l'aile considérée aura pris, en se mouvant dans le sens des aiguilles d'une montre, la positiou BC. En ce moment la courbe qui fait partie du contour de la dent de la roue commencera à presser le rayon nommé en son extrémité; elle continuera à le presser en un point situé sur le ‘Rouleau’ gauche tant qu'il y aura contact de la dent avec l'aile du pignon.
Pour le faire voir, il suffit de démontrer que le lieu des points de contact des tangentes tirées du point A aux épicycloïdes semblables plantées, non seulement en trois points mais partout, sur la ‘Roüe’ gauche, est le ‘Rouleau’ droit. Il en résultera évidemment aussi que le lieu des points de contact des tangentes partant du point B aux épicycloïdes plantées sur la ‘Roüe’ droite est le ‘Rouleau’ gauche. Or, la proposition énoncée résulte immédiatement du fait que le point C est le centre instantané de rotation - lorsque le ‘Rouleau’ droit roule sur la ‘Roüe’ gauche - correspondant à tous les points où les épicycloïdes plantées sur la ‘Roüe’ gauche coupent le ‘Rouleau’ droit: les normales aux épicycloïdes en ces points-là passent donc par le point C. Comparez la note 4 de la 401 qui précède. Et l'on voit qu'une rotation uniforme de la roue correspond à une rotation uniforme du pignon.
Les considérations de Roemer sur la Fig. 107 différaient sans doute des nôtres; voir la note 5 de la p. 613 qui suit. Il est évident que si l'on réussit à donner aux dents une forme telle, que le rapport des moments que les deux roues exercent l'une sur l'autre est constant, il s'ensuivra qu'à une rotation uniforme d'une des deux roues correspond une rotation uniforme de l'autre roue.
-
voetnoot2)
- De la Hire (‘De l'usage des épicycloïdes etc.’. Prop. VI et VIII) fait une remarque analogue: ‘On doit toujours éviter dans les dents des roues de faire qu'elles travaillent au-dessus de la ligne AC [horizontale] qui joint leurs centres, à cause que le frottement y est fort grand, & qu'au contraire il n'est pas presque considérable au-dessous ... parce que les roues ayant leur mouvement du dessus au dessous de cette ligne les faces des dents qui se rencontrent en s'écartant l'une de l'autre ne se frottent qu'en échappant ... au lieu que, lorsque le frottement se fait par la rencontre des parties que rentrent l'une sur l'autre, l'empêchement au mouvement est fort considérable’.
-
voetnoot1)
- La partie B de la Pièce II (que nous divisons, comme la partie A, en deux §§) est empruntée aux p. 39-43 du Manuscrit F.
-
voetnoot2)
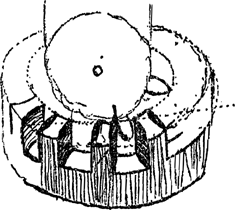
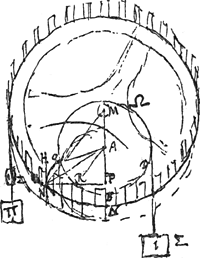
- Le cercle vertical QBD est donc une section du cylindre tournant. Ce n'est pas la section droite extrême; le point B (voir le quatrième alinéa du texte) est situé plus bas que le point ∆, ce que la Fig. 110 ne fait pas bien voir. Le cylindre à section circulaire (comparez la Fig. 108) est d'ailleurs imaginaire, tout comme les ‘roües’ circulaires des Fig. 103 et 107. Le rayon AB du cylindre est par hypothese - quatrième alinéa du texte - la distance à l'axe du pignon du point de contact des dents, lorsque le contact a lieu en B dans le plan vertical passant par M∆. Le cercle horizontal N∆ à centre M est une section de la roue de champ Ω passant par le point de contact N situé sur la dent HN. Les dents de la roue de champ sont apparemment supposées sans épaisseur.
La surface cylindrique ‘terminat dentes ... quousque plani sunt’. Apparemment les dents du pignon, lorsqu'on les parcourt en s'éloignant du centre A, sont d'abord planes, comme celles de la Fig. 107; elles possèdent deux surfaces planes passant par l'axe du pignon. C'est à partir de la génératrice du cylindre passant par le point B, donc au-dessous d'elle, que la dent du pignon dont la surface plane située à gauche se termine là, acquiert une certaine courbure qu'il s'agit de déterminer.
Nous avons parlé du point de contact B: en général il n'y a qu'un seul point de contact entre une dent du pignon et une dent de la roue de champ (supposée sans épaisseur). Toutefois dans le cas où la dent de la roue de champ se trouve précisément à l'endroit ici considéré, il est évident que la surface plane poussante de la dent du pignon la touche suivant une droite; nous voulions dire que B est le point le plus bas de cette droite de contact.
-
voetnoot3)
- Par hypothèse (fin de la phrase suivante) le rayon M∆ du cercle horizontal est le double du rayon du cylindre circulaire imaginaire.
-
voetnoot4)
- MP, partie du rayon M∆, est une droite horizontale, comme la Fig. 109 le fait bien voir.
-
voetnoot5)
- Soit F la force exercée dans le sens PN par une dent du pignon sur la dent HN, et dans le sens NP par la dent HN sur la dent du pignon; et supposons qu'il ne faille tenir compte que du contact de ce couple de dents seulement. Pour que la roue de champ soit en équilibre, il faut que les moments F.MP et Π.M∆ soient égaux. De même l'équilibre du pignon exige qu'on ait F.AP = Σ.AB. On obtient par division AP/MP = ∑/Π.AB/M∆.
Par hypothèse AB/MD = ½ (note 3). Puisque les poids Σ et Π sont égaux par hypothèse, il en résulte que l'on doit avoir, pour toute position de la dent HN, AP = ½ MP. Il s'agit de donner à la dent du pignon, qui pousse la dent HN, une forme telle que cette équation soit vérifiée. Puisque les poids Π et Σ sont constants, c.à.d. puisque le moment extérieur agissant sur le pignon est constant et qu'il en est de même du moment exercé par la roue de champ, les moments F.MP et F.AP resteront aussi constants durant le mouvement.
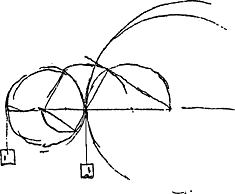 La Fig. 112 de la p. 38 du Manuscrit F semble indiquer que dans le cas des roues planes (partie A de la présente Pièce) Roemer s'était servi, comme Huygens le fait dans la Fig. 110, de la considération de poids suspendus aux contours des ‘roües’. On voit aussi des poids suspendus de cette manière dans les figures de de la Hire. La Fig. 112 montre en outre les ‘rouleaux’ de la Fig. 107.
La Fig. 112 de la p. 38 du Manuscrit F semble indiquer que dans le cas des roues planes (partie A de la présente Pièce) Roemer s'était servi, comme Huygens le fait dans la Fig. 110, de la considération de poids suspendus aux contours des ‘roües’. On voit aussi des poids suspendus de cette manière dans les figures de de la Hire. La Fig. 112 montre en outre les ‘rouleaux’ de la Fig. 107.
Roemer avait sans doute donné de bonnes raisons pour se borner à la considération d'un seul couple de dents et à celle de poids Π et Σ égaux. Voir à ce sujet les Prop. III et IV de l'article de de la Hire. Il est évident qu'il résulte de la constance du rapport des moments exercés par les deux roues l'une sur l'autre dans le cas de l'engrenage d'un seul couple de dents convenablement taillées, que la rotation uniforme d'une des roues correspond à une rotation uniforme de l'autre: cette uniformité subsiste lorsque plusieurs couples de dents s'engrènent simultanément. Voir aussi le cinquième alinéa de la note 2 de la p. 607.
-
voetnoot1)
- Voir ce que nous avons remarqué dans la note 2 de la p. 612 au sujet de la Fig. 110.
-
voetnoot2)
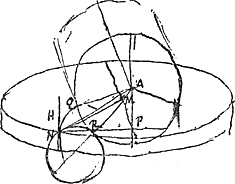
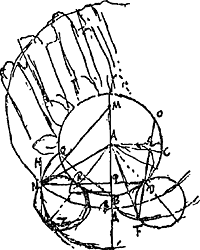
- Le point R est d'après la construction indiquée le point d'intersection du rayon AR et de la circonférence de cercle QBD. Huygens démontre que ce point se trouve sur la droite NP et en occupe le centre.
Il en conclut ensuite que le point de contact N se trouve sur l'épicycloïde QN (faisant en Q un angle de 180o avec AQ) décrite par un point d'une circonférence de rayon ½ AB roulant sur la circonférence de diamètre AB. C'est l'épicycloïde considérée aussi à la p. 399 qui précède. La Fig. 111 fait voir que l'horizontale RN est normale à l'épicycloïde. La forme de la partie courbée de la dent du pignon qu'il s'agissait de déterminer (fin du deuxième alinéa de la note 2 de la p. 612) a donc été trouvée: la surface considérée est un cylindre dont les génératrices sont parallèles à celles du pignon et dont l'épicycloïde est la section droite.
-
voetnoot3)
- En effet, dans le cas de la Fig. 107 (et dans celui de la Fig. 112), le ‘rouleau’, qui produit l'épicycloïde par sa rotation sur une ‘roüe’, a un rayon égal à la moitié de celui de cette ‘roüe’ dans le cas où les deux ‘roües’ ont même diamètre.
-
voetnoot4)
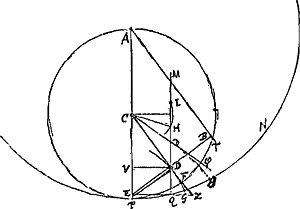
- D'après l'équation de la note 5 (p. 613), on a (en prenant toujours Σ = Π), AP = ⅛ MP, lorsque, ce que Huygens suppose ici [Fig. 111], AB = ⅛ M∆. Il en résulte que dans la Fig. 110 l'arc BR est désormais le tiers de l'arc QB. Il en est de même dans la Fig. 111 et il faut donc, pour que le point N, intersection de PR prolongée avec la circonférence RNZ, vienne s'appliquer au point Q par le roulement de cette circonférence, que le rayon du cercle roulant RNZ soit égal à celui du cercle BRQ.
Lorsque ÀB = 1/n M∆, donc aussi AP = 1/n MP, on aura: arc BR = 1/n arc QB, ou bien: 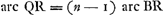 . Le rayon x du cercle roulant doit être tel d'après la Fig. 11 que arc QR:2 arc RB = x: AB, rayon du cylindre. Il en résulte . Le rayon x du cercle roulant doit être tel d'après la Fig. 11 que arc QR:2 arc RB = x: AB, rayon du cylindre. Il en résulte 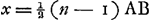 . Par conséquent, comme le dit Huygens, le rayon du cylindre augmenté du double du rayon x, est toujours égal au rayon M∆ de la roue de champ. . Par conséquent, comme le dit Huygens, le rayon du cylindre augmenté du double du rayon x, est toujours égal au rayon M∆ de la roue de champ.
-
voetnoot1)
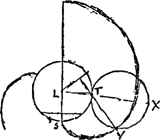
- La roue ‘ST’ à rayon AB (section plane du cylindre des Fig. 109 et 110, menant la roue de champ à rayon n.AB) a des dents dont la surface épicycloïdale est déterminée (note 4, p. 516) par le roulement du cercle à rayon ½ (n - 1) AB sur le cercle à rayon AB. Or, d'après ce que nous avons dit dans la note 1 de la p. 611, la roue plane à rayon AB qui mène une autre roue plane de rayon (n - 1) AB, possède également des dents dont la forme épicycloïdale est déterminée par le roulement du ‘rouleau’ - Fig. 107 et Fig. 112 - à rayon ½ (n - 1) AB sur le cercle à rayon AB.
-
voetnoot2)
- Dans le § 2, contrairement à ce qui a été supposé dans le § 1, ce sont les dents de la roue de champ qui sont courbées de manière à être constamment en contact avec les dents plates du pignon, les mouvements de la roue et du pignon étant l'un et l'autre uniformes. Ainsi que Huygens le dit un peu plus loin, le rayon du cercle PTA est d'abord supposé (comme dans le § 1) égal à la moitié de celui du cercle PGN.
-
voetnoot3)
- Il existe évidemment un cylindre qui ‘termine toutes les dents’ du pignon. Le ‘cercle PTA, qui est celuy du pignon’ est une section droite de ce cylindre, savoir le cercle qui donne avec celui de la roue de champ (d'où s'élève la courbure des dents) l'intersection EQ.
-
voetnoot4)
- Huygens dit donc que le point de contact de la dent considérée avec la surface plane d'une aile du pignon se projette toujours sur le contour du cercle de la roue de champ. En d'autres termes, la dent (supposée apparemment sans épaisseur) est par hypothèse une partie de la surface cylindrique élevée perpendiculairement sur la circonférence du cercle de la roue de champ.
-
voetnoot5)
- ‘La force de la pression’ est évidemment son moment par rapport à l'axe de rotation.
-
voetnoot7)
- C.à.d. qui est le bras de levier de la pression exercée par, ou sur, la dent du pignon.
-
voetnoot9)
- Soit AP, rayon du cercle de la roue de champ = R. La Fig. 114 fait voir
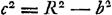 . On a donc . On a donc 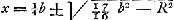 . Par conséquent b est comprise entre les limites R √16/17 et R. Pour b = R √16/17 on a x = R √1/17 et c = R √1/17. On peut trouver des limites analogues dans le cas du ‘pignon double de la roue de champ’, etc. . Par conséquent b est comprise entre les limites R √16/17 et R. Pour b = R √16/17 on a x = R √1/17 et c = R √1/17. On peut trouver des limites analogues dans le cas du ‘pignon double de la roue de champ’, etc.
-
voetnoot1)
- Suivant l'équation le point D le plus bas est obtenu en prenant
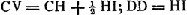 donne ensuite le point supérieur D. donne ensuite le point supérieur D.
-
voetnoot2)
- Dans le cas où le rayon du pignon est double (ou quadruple) de celui de la roue de champ - ou bien égal à ce dernier -, l'égalité des moments exige que l'on ait AB = ½ CD (ou = ¼CD) - ou bien AB = CD.
-
voetnoot2)
- Dans le cas où le rayon du pignon est double (ou quadruple) de celui de la roue de champ - ou bien égal à ce dernier -, l'égalité des moments exige que l'on ait AB = ½ CD (ou = ¼CD) - ou bien AB = CD.
-
voetnoot2)
- Dans le cas où le rayon du pignon est double (ou quadruple) de celui de la roue de champ - ou bien égal à ce dernier -, l'égalité des moments exige que l'on ait AB = ½ CD (ou = ¼CD) - ou bien AB = CD.
-
voetnoot4)
- La phrase que nous avons placée entre crochets, a été biffée par Huygens. En effet, cette construction ne s'accorde pas avec l'équation trouvée qui donne CO ou x et par conséquent la place du point G [Fig. 115] lorsque b (CE) ou c (ED) est donnée.
-
voetnoot5)
- Il faut sans doute lire AB. Comparez la note 4 de la p. 617.
-
voetnoot6)
- Pour trouver un point de la dent AX (la courbe AX se trouve en réalité sur la surface cylindrique dont il vient d'être question), il faut décrire sur cette surface vers le côté gauche à partir du point G - situé au-dessus du point D par rapport au plan du papier - uu arc horizontal égal à l'arc AB. On trouve tous les points AX en tenant compte de tous les points G correspondant à des angles ACB quelconques.
|



 verticalis erit aequale radio AB. Cumque posito tactu in N, sit AP ∞ ½ MP, patet punctum N esse altius puncto tactus dicto quod fit in plano verticali per M∆Ga naar voetnoot1).
verticalis erit aequale radio AB. Cumque posito tactu in N, sit AP ∞ ½ MP, patet punctum N esse altius puncto tactus dicto quod fit in plano verticali per M∆Ga naar voetnoot1).
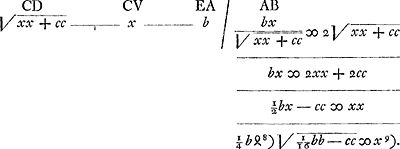
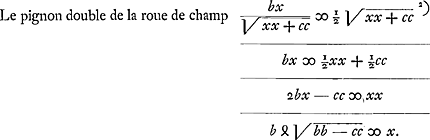
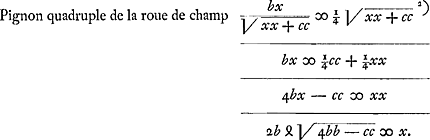
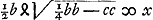 . Et jam hic A et C in unum punctum conveniunt.
. Et jam hic A et C in unum punctum conveniunt.