Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695
(1934)–Christiaan Huygens–
[pagina 27]
| |||||||
Horologium oscillatorium de 1673. | |||||||
[pagina 29]
| |||||||
Avertissement.Nymphes de Schéveningue habitant l'onde pure,
Vous qui de ces pays protégez la structureGa naar voetnoot1),
Délices de tous ceux qui fréquentent vos plages,
Bien aimées de Phébus, esprits gracieux et sages,
Veuillez me secourir et inspirer mes chants.
Qu'en revanche ni Pan ni ses Faunes hideux
Ne se puissent jamais approcher de ces lieux
Et souiller la blancheur de vos flots écumantsGa naar voetnoot2).
Toi que la Gloire élève au-dessus du ciel même,
Daigne prêter l'oreille, Huygens, à ce poème
Ecrit en ton honneur, en l'honneur de ton père,
De tes frères aussi et de ta race entière
| |||||||
[pagina 30]
| |||||||
Dont tu es le fleuron. Tes sublimes penséesGa naar voetnoot1)
Dans un cadre mythique ici seront placées.
Puisse ainsi des anciens la riche fantaisie
Orner de ses splendeurs la noble astronomie.
Qu'on nous pardonne de commencer cet Avertissement par une traduction, nécessairement peu littérale, du début de la ‘Hadriani Vallii Daphnis Ecloga ad Christianum Hugenium Zulichemium, Constantini F.’ que Huygens a fait imprimer conformément à l'intention de ValliusGa naar voetnoot2) dans son ouvrage de 1673Ga naar voetnoot3). Nos ancêtres du dix-septième siècle goûtaient plus que nous les imitations des bucoliques classiquesGa naar voetnoot4). Suivant beaucoup de commentateurs la cinquième églogue de Virgile célèbre Jules César sous le masque du héros Daphnis; pareillement chez Vallius ou van der Wall la figure de Daphnis prend de plus en plus les traits de Huygens. Toutefois ce n'est pas seulement chez Virgile ou d'autres auteurs latins que van der Wall a cherché son inspiration: il mentionne aussi le poète Aratos, imbu de la sagesse d'Eudoxe et de Théophraste, dont les Φαινὀμενα ϰαὶ Διοσημεῖα, fort connus au dix-septième siècle, sont voués en majeure partie à la description des constellationsGa naar voetnoot5). | |||||||
[pagina 31]
| |||||||
Ce qui nous frappe dans le poème considéré - et c'est là la raison pour laquelle nous accordons aux premiers vers ici traduits une place d'honneur -c'est que l'auteur en chantant la louange de Huygens le range du côté de Phébus ApollonGa naar voetnoot6) par opposition à Pan: c'est dire qu'il le glorifie comme un héros intellectuel recherchant en premier lieu la science pure, la science dans le sens le plus élevé du mot. Il convient en effet, puisque l'‘Horologium oscillatorium’ est un des chefs-d'oeuvre de Huygens, de faire ressortir, comme nous l'avons aussi fait brièvement en d'autres occasionsGa naar voetnoot7), que le but le plus élevé qu'il se propose c'est d'abord l'étude rationnelle de la géométrie - appelée fort justement à la p. 77 qui suit ‘pars multò praecipua’ de l'ouvrage de 1673 -, ensuite celui d'approfondir ‘experientia ac ratione’Ga naar voetnoot8) la structure de l'univers. On peut dire qu'au fond ces deux études n'en font qu'une: pour Huygens et ses contemporains la conformité de la géométrie euclidienne avec l'espace réel et les objets qu'il contient est au-dessus de tout soupçonGa naar voetnoot9). Huygens se sent ϰοσμοθέωρος, pour employer le mot forgé par lui vers la fin de sa vie. C'est pour mieux connaître la structure de l'univers qu'il taille des lentilles, qu'il calcule la marche des rayons dans les lunettes, qu'il s'applique à perfectionner les horloges. Les questions pratiques ont leur importance et l'observation est indispensable. Il n'en est pas moins vrai qu'il nous faut aussi, qu'il nous faut même avant toutGa naar voetnoot10), aussi bien pour les découvertes que pour les inventions, les yeux de l'esprit; nous avons cité cette expression shakespearienne dans la note 14 de la p. 343 du T. XVII; nous la rencontrons en 1686 ou 1687 chez Huygens lui-même: à la p. 259 du Manuscrit F il dit en parlant de la forme sphéroïdale aplatie que la terre doit avoir en vertu de sa rotation: ‘Ad haec mentis oculos aegrè et quasi caligantes plerique attollunt haud aliter atque ad lucis radios ii qui è diuturnis tenebris emersere’. Ceci ne rappelle pas seulement Shakespeare, mais surtout la fameuse caverne de PlatonGa naar voetnoot11). | |||||||
[pagina 32]
| |||||||
Dans sa Dédicace à Louis XIV - dont il est déjà question en février 1665Ga naar voetnoot1) - Huygens fait ressortir son amour pour la science pure. En insistant en même temps sur l'utilité générale d'horloges exactesGa naar voetnoot2) il exprime sans doute une pensée propre à faire apprécier son ouvrage par les fondateurs de l'Académie des Sciences, mais pour cela il n'a nul besoin de forcer son naturel: il voyait fort bien la nécessité pratique d'aider les marins à trouver les longitudesGa naar voetnoot3). Rappelons aussi que le travail manuel, la construction d'instruments, lui plaisait depuis son enfanceGa naar voetnoot4). Il n'est pas possible à l'homme de vivre uniquement sur les cimes de l'Olympe. En s'intéressant à la fois aux mathématiques pures, à l'astronomie, à la physique et à la technique et en ne considérant pas ces sciences (ou arts) comme séparées les unes des autres par des cloisons étanches, Huygens devenait un des fondateurs de l'astronomie théorique et de la physique mathématique et pratique en même temps qu'un promoteur du contact souvent étroit qui existe de nos jours entre la science et la technique. Déjà au seizième et dix-septième siècle nous trouvons dans la personne de Jost Burgi un horloger doublé d'un mathématicien. Huygens est, lui, un mathématicien doublé d'un horloger. Ses inventions du pendule régulateur librement suspenduGa naar voetnoot5), des arcs cycloïdauxGa naar voetnoot6), du poids curseurGa naar voetnoot7), dont la première était une heureuse trouvaille tandis que les deux autres avaient un caractère nettement mathématique - quoique l'idée d'un réglage par le déplacement de certains poids fût ancienneGa naar voetnoot8) -, le rapprochèrent des artisans et le forcèrent de s'associer avec eux tout en gardant à bon droit le sentiment de sa prééminence. Il n'est certes pas étonnant que les maîtres reconnus de l'art, capables de construire des horloges tandis que Huygens ne construisait que des modèlesGa naar voetnoot9), et dont plusieurs étaient doués eux aussi d'un esprit inventifGa naar voetnoot10), n'étaient pas toujours disposés à reconnaître cette supériorité. Ce que nous | |||||||
[pagina 33]
| |||||||
avons dit aux p. 8-9 des relations entre Huygens et Thuret fait bien voir combien il était probable que ces deux hommes de mérite ne parviendraient pas toujours à se mettre absolument d'accordGa naar voetnoot11). Huygens s'est appliqué à donner à l'ouvrage de 1673 un caractère monumental. Nous avons déjà parléGa naar voetnoot12) du soin extrême qu'il mit à donner de plusieurs théorèmes des démonstrations fort exactes à la mode d'Archimède. Voir encore sur ce sujet le premier alinéa de la p. 50 qui suit. Ce n'est d'ailleurs pas seulement la forme de ses démonstrations qui est empruntée aux mathématiciens grecs. Nous avons dit à la p. 369 du T. XVI, en parlant de la formule fondamentale des corps oscillants
l = ∑r2/nb ou, si l'on veut, l = I/MbGa naar voetnoot13)
que dans la Pars Quarta de l'‘Hor. osc.’ Huygens lui donne avec raison une place éminente. Rappelons qu'il trouva la première de ces formulesGa naar voetnoot14) peu avant le 10 octobre 1664Ga naar voetnoot15) et que ce fut également en octobreGa naar voetnoot16) qu'il établit ensuite le théorème énoncé à la p. 461 du T. XVI (Prop. XIII de la Pars Quarta de l'‘Hor. osc.’) dont nous avons dit à la p. 373 du T. XVI qu'on en trouve de plus dans l'‘Hor. osc.’ une généralisation (Prop. XVI de la Pars Quarta) qu'il connaissait en 1669Ga naar voetnoot17). Ce | |||||||
[pagina 34]
| |||||||
que nous n'avons pas dit dans les notes 3 de la p. 461 et 3 de la p. 462 du T. XVI c'est que ce qui permettait à Huygens de tirer immédiatement de la formule fondamentale la proposition de la p. 461 c'était sa connaissance d'un théorème de Pappus dont il s'était occupé en 1650; voir à ce sujet la p. 229 du T. XI. Dans l'‘Hor. osc.’ ce théorème forme la Prop. XII de la Pars Quarta, mais Pappus n'y est pas mentionné. Il est intéressant de noter l'influence directe des recherches des géomètres grecs sur l'établissement des Prop. XIII et XVI.
L'‘Horologium oscillatorium’ débute (p. 74-81) par la Dédicace au Roi dont nous venons de parler, où Huygens en le remerciant de sa libéralité (comparez la note 5 de la p. 4 qui précède) lui adresse les compliments d'usageGa naar voetnoot1). En faisant une allusion à sa nationalité en même temps qu'à la guerre de Hollande et en parlant en général de la gloire militaire du règne de Louis XIV, il trouve sans se départir de l'extrême politesse rendue nécessaire par les circonstances, l'occasion de dire qu'à son avis la gloire la plus haute du règne réside ailleursGa naar voetnoot2). C'est la gloire de Louis XIV protecteur des arts et des sciences qu'expriment aussi, avec l'emphase obligatoire, les trois vers insérés par Huygens (comparez la note 3 de la p. 30) dans le poème de ValliusGa naar voetnoot3): Inferior nullis ut item neque Gallia desit;
Gallia magnanimi Regis spendore superba,
Borbonios ignes cui parturit arduus aetherGa naar voetnoot4).
Vallius vient de dire que l'astronomie a été cultivée par les Chaldéens, les Babyloniens, les Grecs, les Egyptiens, les Italiens, les Arabes, les Espagnols et les Allemands - il eût pu mentionner les Polonais (Copernic) et les Danois (Tycho Brahé), mais il | |||||||
[pagina 35]
| |||||||
est évident qu'il n'a pas la prétention d'être complet -; quant aux Allemands: ‘.. canit .. Daphnis .. tandem quos consultos Germania misit Astrorum coelique, suae qui sidera terrae’Ga naar voetnoot5), c.à.d. ‘Daphnis mentionne enfin les astronomes provenant de l'Allemagne, étoiles de leur pays’. Dans ce catalogue la France manquait; c'est pourquoi Huygens, faisant allusion à la création de l'Observatoire de Paris (comparez la p. 78 qui suit) qui n'existait pas encore lorsque le poème fut composé, écrit: [Daphnis ajoute] que la France elle aussi, n'étant inférieure à aucune autre nation, ne fait pas défaut,
La France qui se distingue par la magnificence et l'éclat de son Roi,
Auquel le ciel s'apprête à vouer les astres de Bourbon.
Suivant l'exemple de Galilée qui baptisa ‘étoiles des Medicis’ les satellites de Jupiter, Huygens proposait en effetGa naar voetnoot6) de donner le nom d'‘étoiles des Bourbons’ aux satellites de Saturne dont il avait découvert le premier à la Haye tandis que l'astronome italien Cassini, également appelé à Paris par la libéralité du Roi, ou, si l'on veut, par le grand Colbert, et attaché à l'Observatoire de ParisGa naar voetnoot7) en avait découvert un deuxième vers la fin de 1671 et bientôt après un troisième. Huygens avait d'ailleurs pris part aux observations de CassiniGa naar voetnoot8). Sans le privilège accordé par Louis XIV (p. 7) et sans l'appel de Huygens à Paris, il ne serait fort probablement pas entré en relations personnelles avec I. Thuret. Attendu que la Pars Prima de l'‘Hor. osc.’ contient la description des horloges astronomiques et marines construites à Paris, la Dédicace dit à bon droit qu'une partie de l'honneur de l'ouvrage revient à Louis XIV. Cependant les mots ‘ante omnia’ de la l. 13 de la p. 81 exagèrent évidemment l'importance de la part du Roi dans le développement des sciences en général et dans la genèse de l'oeuvre de Huygens en particulier. Le contenu des Tomes XVI et XVII fait voir que Huygens, en arrivant à Paris, était en possession de tous les matériaux nécessaires pour composer son oeuvre, comme le dit d'ailleurs déjà un article de P. Tannery imprimé en 1924 dans l'‘Histoire Générale du IVe Siècle à nos jours’ publiée sous la direction de E. Lavisse et A. RambaudGa naar voetnoot9). | |||||||
[pagina 36]
| |||||||
Tannery écrit fort justementGa naar voetnoot1): ‘L'ouvrage capital d'Huygens est son Horologium oscillatorium publié seulement en 1673; mais ses découvertes sont bien antérieures’. Le reste de la phrase: ‘et avaient été en grande partie communiquées soit à l'Académie des Sciences, soit à la Royal Society’ doit toutefois être pris cum grano salis: les Pièces des T. XVI et XVII écrites à la Haye avant la création de l'Académie des Sciences sont en majeure partie restées inédites jusqu'à nos jours et Huygens n'avait communiqué à la ‘Royal Society’, ainsi qu'à quelques personnes en France, que quelques résultats sans démonstrationGa naar voetnoot2).
Huygens ne commença probablement que vers septembre 1669 la rédaction de son ouvrage, avant ou après avoir envoyé à la ‘Royal Society’ au commencement de ce mois les anagrammes du T. VIGa naar voetnoot3) qui s'y rapportent en partie. Le programme de la Pars Secunda qui constitue la partie B de notre Appendice II à la Pars Prima date du mois nomméGa naar voetnoot4), et les Pièces qui constituent l'Appendice à la Pars Secunda et les Appendices III-V à la Pars Quarta sont de janvier 1670Ga naar voetnoot5). Il paraît donc avoir repris en 1669 le projet de 1660 (voir les p. 117-118 du T. XVII) qu'il disait en janvier 1665 avoir ‘achevè pour la plus grande partie’Ga naar voetnoot6). Vers la fin de janvier 1670 Huygens tomba malade. Il fut visité par Fr. Vernon qui écrit le 25 févrierGa naar voetnoot7) avoir reçu de lui un paquet cacheté contenant la solution des 12 anagrammes de septembre 1669, c.à.d. des 12Ga naar voetnoot8) propositions sur le mouvement avec leurs démonstrationsGa naar voetnoot9). Lodewijk Huygens qui vint tenir compagnie à son frère mit G. MoutonGa naar voetnoot10) au courant en juin 1670 ou plus tôt du titre du livre et du fait qu'il paraîtrait, suivant l'expression de Mouton, ‘dans l'Esclat & la majesté de ses belles demonstrations’. La rédaction d'une partie des démonstrations de l'‘Hor. osc.’ avait apparemment eu lieu avant la maladie. Il ne peut en effet être question | |||||||
[pagina 37]
| |||||||
dans le cas du paquet cacheté de Pièces publiées dans le T. XVI seulementGa naar voetnoot11) puisque les propositions des anagrammes contiennent quelque chose de plus sur le ‘rectangulum distantiarum’ (T. XVI, p. 373). C'est sans doute à la Haye à la maison paternelle où il séjourna du 9 septembre 1670Ga naar voetnoot12) au 12 juin 1671Ga naar voetnoot13) - et peut-être dans le même cabinet d'étude où il avait rédigé les parties achevées avant 1665 de l'ouvrage tel qu'il se le figurait en 1660, et avant elles les longues démonstrations géométriques de la Dioptrique qu'on trouve dans le T. XIII - que Huygens continua ou termina la rédaction des démonstrations de l'‘Hor. osc.’. Pendant ce travail il a pu avoir la même impression qu'en 1663 où dans une lettre à J. de Witt (T. IV, p. 311) il se dit ‘miratus ... quae momento pene temporis cogitatione complecti ac singula persequi poteram, tot verbis, ut legenti plana fierent, opus habere’. Le 9 mars 1672Ga naar voetnoot14) il est déjà question dans une lettre de lui d'‘achever nostre impression’, quoique le permis d'imprimer (voir la p. 84 qui suit) ne date que du 30 septembre 1672. Ajoutons que Huygens reçut la première feuille imprimée peu avant cette date (T. VII, p. 229) et que l'impression fut terminée avant mai 1673 (T. VII, p. 269). Nous avons dit dans le T. XVIIGa naar voetnoot15) qu'il est possible qu'une démonstration aussi exacte que possible du tautochronisme de la cycloïde ait existé dès 1664.
C'est ici le lieu de remarquer que, quelque peine que Huygens se soit donné pour rendre ses démonstrations rigoureuses, celle du tautochronisme de la cycloïde, ou plutôt une de celles qui se rapportent au mouvement d'un point pesant suivant une courbe matérielle cycloïdale ou autre située dans un plan vertical, fut pourtant jugée insuffisante par Newton: voir les p. 326-327 du T. VII, où Newton critique la phrase: ‘cum flexus ad B nihil obstare motui ponatur’ de la l. 35 de la p. 145 qui suit. La raison pour laquelle cette supposition n'a pas été mentionnée parmi les hypothèses fondamentales de la Pars Secunda c'est sans doute que Huygens ne croyait cette | |||||||
[pagina 38]
| |||||||
supposition pratiquement vraie (c'est là aussi l'opinion que Newton lui attribue) que dans le cas limite où la ligne brisée devient une courbe. Il eût sans doute pu faire mention de cette conviction dans les hypothèses fondamentales; mais dans ce cas n'aurait-il pas été obligé d'y parler aussi de l'hypothèse de la rigidité absolue des courbes matérielles qui ne se déforment pas par le mouvement du mobile, et n'aurait-il pas dû disserter sur la possibilité d'identifier plus ou moins le mouvement réel d'un petit corps avec celui du point pesant sans aucunes dimensions qui constitue le mobile de tous les théorèmes de la Pars Secunda? Des discussions de ce genre l'eussent entraîné assez loin sans contribuer, nous semble-t-il, à la clarté de l'exposition. Toutefois l'observation de Newton mérite certainement notre attention: elle nous fait bien voir qu'une mécanique rationnelle absolument conforme à l'observation est une chimère. Pour pouvoir appliquer nos théories de physique mathématique à ce qui nous paraît être la réalité objective, il est nécessaire d'idéaliser cette dernière; comparez le premier alinéa de la p. 256 du T. XVI ainsi que la p. 241 du T. XVII.
Dans la Pars Quarta on rencontre également une sentence qui donne à réfléchir; Huygens y dit (Hypoth. II) qu'un pendule matériel parcourt des arcs égaux en montant et en descendant et il ajoute: ‘De pendulo simplici hoc demonstratum est prop. 9 de Descensu gravium. Idem vero et de composito tenendum esse declarat experientia’. La proposition repose donc sur certains principes (les hypothèses de la Pars Secunda) pour le pendule simple qui est une fiction, mais pour le pendule composé seul existant elle est indémontrable et relève directement de l'expérience. On pourrait se demander quelle est dans ces circonstances la raison d'être de la démonstration donnée pour le pendule simple. Gardons-nous cependant de critiquer ici l'oeuvre de Huygens. Nous pouvons être assurés qu'en cet endroit il s'est critiqué lui-mêmeGa naar voetnoot1): il eût sans doute été heureux de donner une démonstration, basée sur des hypothèses évidentes, de la réversibilité du mouvement du pendule composé, et il n'a dû invoquer qu'à regret le recours à l'expérience directe. D'ailleurs il n'y a ici, malgré son désir de faire la part de la raison pure aussi grande que possibleGa naar voetnoot2), aucune contradiction réelle: les hypothèses de la Pars Secunda, tout aussi bien que l'hypothèse | |||||||
[pagina 39]
| |||||||
nommée de la Pars Quarta, ont apparemment été tirées de l'expérience ou, si l'on veut, suggérées par elle. Quant à la Pars Tertia, entièrement géométrique, elle n'est précédée d'aucune hypothèse: voir ce que nous avons dit à la p. 31 sur la conformité jugée certaine de la géométrie euclidienne avec l'espace réel et les objets qui s'y trouvent. L'autre hypothèse, la première, de la Pars Quarta, c'est le célèbre principe - évidemment emprunté lui aussi à l'observation - que par le mouvement spontané d'un groupe de corps partant du repos leur centre commun de gravité ne peut pas s'élever à une hauteur supérieure à celle qu'il avait au commencement. Nous nous sommes suffisamment étendus sur ce principe dans les Tomes précédentsGa naar voetnoot3); cependant nous devrons y revenir plus loin dans le présent Tome à l'occasion de la ‘Controversia’ qui s'engagea plus tard (et même déjà avant 1673) sur ce sujet. À propos de cette hypothèse de la Pars Quarta nous devons d'ailleurs remarquer que déjà dans la Prop. VI de la Pars Secunda Huygens admet que le centre de gravité d'un corps ne peut pas s'élever spontanément, mais sans avoir énoncé cette hypothèse au début de la Pars Secunda.
Il nous semble parfaitement inutile de donner ici, après tout ce que nous avons dit dans les T. XIV-XVII, un résumé systématique du Traité de Huygens. Nous nous bornons à attirer l'attention sur quelques questions particulières. | |||||||
Questions de mathématiques pures.A. Quadrature du cercle. Les trois grands problèmes de l'Antiquité, la duplication du cube, la trisection de l'angle et la quadrature du cercle, ont intéressé Huygens depuis sa jeunesseGa naar voetnoot4). Il n'a jamais été convaincu de l'impossibilité de la quadrature du cercle et a toujours espéré qu'on finirait par la trouverGa naar voetnoot5). On rencontre dans l'‘Hor. | |||||||
[pagina 40]
| |||||||
ofc.’ (Prop. IX de la Pars Tertia) quelques théorèmes sur la quadrature des conoïdes et sphéroïdes que Huygens fut amené à établir à la suite de ses recherches sur la quadrature du cercle; voir la lettre de de Sluse de décembre 1657 citée à la p. 211 qui suit et celle de Huygens à de Sluse de février 1658Ga naar voetnoot1). Ajoutons en passant que la démonstration de ces théorèmes n'a été publiée par Huygens ni ici ni ailleurs; comparez le deuxième alinéa de la p. 33 qui précède. Nous avons publié les démonstrations de Huygens dans le T. XIV auquel, ici comme dans d'autres cas analogues, nous renvoyons le lecteur dans les notes. Dans l'‘Hor. osc.’ Huygens n'exprime plus le vague espoir (voir les p. 536-539 du T. XVI) que la recherche des centres d'oscillation pourra conduire à la quadrature du cercle. Comparez la note 2 de la p. 56 qui suit.
B. Développées et développantes semblables. À la p. 104 qui suit Huygens pose la question de savoir s'il existe, outre la cycloïde, d'autres courbes telles qu'en choisissant convenablement la longueur du fil à partir d'un point donné de la première courbe, l'on obtient par le développement une courbe pareille. Vers la fin d'octobre 1678 un certain de Vaumesle qui avait lu l'‘Hor. osc.’ découvritGa naar voetnoot2) ‘que par leuolution de la cycloide circulaire [c.à.d. de la cardioïde, en d'autres termes de l'épicycloïde produite dans le cas où le cercle générateur est égal au cercle immobile] est décrite une autre cycloïde circulaire triple de la premiere’. Ceci donna occasion à Huygens de démontrer avant la fin de la même année que par l'évolution d'une épicycloïde quelconque on peut obtenir une épicycloïde semblable. Voir les §§ 2 et 3 de l'Appendice III à la Pars Tertia; c'est une Pièce lue à l'Académie des Sciences le 3 décembre 1678 qui fait défaut dans les Régistres de l'Académie. Jacques Bernoulli publia en mai 1692Ga naar voetnoot3) la proposition que la spirale logarithmique a la même propriété et peut même engendrer une spirale égale. La question fut reprise quelques dizaines d'années plus tard par Iac. HermannGa naar voetnoot4) et par G.W. Krafft qui démontra dans son | |||||||
[pagina 41]
| |||||||
article de 1727 ‘De Lineis Curvis quae evolutae ipse se generant’Ga naar voetnoot5) que la cycloïde et la spirale logarithmique à angle constant de 45o sont les seules lignes qui engendrent des lignes égales tandis que des lignes semblables ne peuvent provenir par évolution que des autres spirales logarithmiques et des épi- ou hypocycloïdesGa naar voetnoot6). Il dit à tort que ce fut Tschirnhaus qui s'occupa pour la première sois (d'après l'article ‘Inventa nova etc.’ des Acta Erud. de 1682) de ces dernières lignes. Comparez la fin du § 1 de l'Appendice III nommée. Voir sur les relations de Huygens avec Tschirnhaus la p. 381 du T. VII ainsi que les p. 499 et 511 du T. IX.
C. Rayon de Courbure. On a remarqué qu'en établissant la théorie des développées Huygens ne dit rien sur la courbure. Cantor affirme ‘dass Huygens an Krümmungsverhältnisse gar nicht dachte’Ga naar voetnoot7). Il est vrai qu'il n'observe pas - non plus qu'Apollonios dans le cinquième livre de ses ‘Conica’Ga naar voetnoot8) - que le point d'intersection de deux normales infiniment voisines est le centre d'un cercle de courbure, mais | |||||||
[pagina 42]
| |||||||
la notion de courbure ne lui était nullement étrangère. On peut voir aux p. 17-18 du T. XVII qu'avant d'avoir trouvé la vraie forme des arcs du pendule (et c'est de la construction de ces arcs qu'est sortie la théorie des développéesGa naar voetnoot1), il composait en 1657, du moins en théorie, ces arcs ou ‘platines courbes’Ga naar voetnoot2) de portions de circonférences de cercle. D'ailleurs, comme nous l'avons observé dans la note 2 de la p. 288 du T. XVII, déjà en 1654 il considérait, en s'occupant théoriquement de la taille d'une lentille elliptique, le point où les normales infiniment voisines de l'axe de rotation d'un ellipsoïde coupent cet axe comme un véritable centre de courbure, quoique sans se servir de ce termeGa naar voetnoot3). Dans la partie B datant de 1670 de notre Appendice à la Pars Secunda de l'‘Hor. osc.’ Huygens détermine la relation qui existe dans un cas spécial entre deux rayons de courbure, ici aussi sans se servir de ce terme. En juin 1686 Leibniz publia dans les ‘Acta eruditorum’Ga naar voetnoot4) sa ‘Meditatio nova de natura anguli contactus et osculi’: il y parle du cercle osculateur. Comme Kepler (note 3) et Huygens en 1654 - il ne cite d'ailleurs nil'un nil'autre - ils'inspire plus ou moins de la ‘praxis catoptrica et dioptrica’. Leibniz séjourna à Paris de 1672 à 1676 et Huygens eut alors une grande influence sur lui: voir la note 12 de la p. 244 du T. VII, où Leibniz dit e.a. sur le don que Huygens luifit de l'‘Hor. osc’: ‘Id mihi accuratioris Geometriae initium vel occasio fuit’Ga naar voetnoot5). En mars 1691 dans une Pièce envoyée à LeibnizGa naar voetnoot6) | |||||||
[pagina 43]
| |||||||
Huygens se sert de l'expression ‘radius curvitatis’ qu'il n'emprunte, semble-t-il, à aucun autre auteur. La même expression se trouve dans son article sur la chaînette du 5 mai 1691 publié dans la livraison de juin 1691 des ‘Acta eruditorum’. Comme son frère (note 5) Jean Bernoulli en 1691 ou 1692 témoigne en faveur de HuygensGa naar voetnoot7). Dans le traité posthume ‘Methodus fluxionum et serierum infinitarum’, Newton parle du ‘radius curvaturae’ ainsi que du ‘centrum curvaturae’. D'après les lettres de décembre 1671 de J. Collins à G.A. Borelli et à F. VernonGa naar voetnoot8) ce traité fut prêt pour la presse déjà en 1671Ga naar voetnoot9), mais il a dû avoir été remanié plus tard par l'auteur puisque, comme l'observe CantorGa naar voetnoot10), il contient des propositions rappelant si fortement certaines parties de l'‘Hor. osc.’ que l'on doit admettre ‘Newton habe diese Stellen der M. fl. erst geschrieben nachdem er das Hor. osc. gelesen hatte’Ga naar voetnoot11). D'ailleurs, dans les deux lettres nommées, Collins donne beaucoup de détails sur le contenu du traité, mais il ne dit rien sur la courbure ni sur l'évolution des courbes, si ce n'est qu'il a exhorté Newton à publier bientôt son ouvrage puisque ‘D. Hugenius tractatum de Dioptrica et de Curvarum evolutione jam molitur’, ce qu'il avait | |||||||
[pagina 44]
| |||||||
appris probablement de Vernon lui-même (voir la p. 36 qui précède). Dans sa lettre du 24 octobre 1676 à LeibnizGa naar voetnoot1) Newton dit à propos de ce même traité: ‘Ipse autem tractatum meum non penitus absolveram, ubi destiti [il ne dit pas quand] a proposito; neque in hunc diem mens rediit ad aliqua adjicienda’. Il est possible qu'-après l'exhortation de Collins et avant d'avoir reçu l'‘Hor. osc.’ Newton, sachant que Huygens traiterait ‘de Curvarum evolutione’, ait ajouté quelque chose à son traité déjà en 1672, puisque dans sa lettre du 10 décembre 1672 à CollinsGa naar voetnoot2) il dit que sa méthode ne sert pas seulement à mener des tangentes, mais aussi ‘ad resolvendum alia abstrusiora Problematum genera de Curvitatibus [nous soulignons], Areis, Longitudinibus, Centris Gravitatis Curvarum, etc.’ (les trois derniers sujets avaient déjà été mentionnés par Collins dans ses lettres de déc. 1671) et que ‘hanc methodum intertexui alteri isti, qua Aequationum Exegesin instituo, reducendo eas ad Series infinitas’. Nous ignorons donc à quelle époque Newton s'est servi la première fois de l'expression ‘radius curvaturae’.Ga naar voetnoot3). Comme dans notre édition du Traité sur la Force Centrifuge (T. XVI), nous nous abstenons généralement dans celle de l'‘Hor. osc.’ de notes traduisant en formules plus modernes les théorèmes de Huygens. On trouve des notes de ce genre dans la traduction allemande publiée en 1913Ga naar voetnoot4). Toutefois nous avons indiqué dans une note à la Prop. XI de la Pars Tertia que les raisonnements géométriques de Huygens conduisent à la formule générale du rayon de courbure. | |||||||
Questions de mécanique théorique.A. Pesanteur et force centrifuge. Dans l'‘Hor. osc.’ Huygens s'abstient de toute hypothèse sur la cause de la pesanteur dont il avait traité en 1659 et en 1668Ga naar voetnoot5); voir | |||||||
[pagina 45]
| |||||||
sur les considérations de 1659 les p. 244 et 276-277 du T. XVII. Il se contente de parler (Hyp. II de la Pars Secunda) de la ‘gravitatis actio, undecunque illa oriatur’, se plaçant ainsi au point de vue phénoménologique de Galilée. Comparez d'ailleurs la note 4 de la p. 277 du T. XVII et remarquez que le calcul de la viteffe √gr (note 7 et 8 de la même page) d'un mobile décrivant une circonférence concentrique avec un grand cercle de la terre est indépendant de toute hypothèse sur la nature de la pesanteur. Huygens connaissait dès 1659 la grandeur absolue de la force centrifuge. Plusieurs de ses Propositions sur cette force, p.e. la treizième et dernière, par laquelle se termine l'‘Hor. osc.’, font bien voir - et ceci mérite d'être remarqué - que selon luiGa naar voetnoot6) le facteur m de la formule mg est le même que celui de la formule mv2/rGa naar voetnoot7), résultat qui, nous semble-t-il, peut provenir tout simplement de la considération de 1659 du mobile susdit décrivant la circonférence concentriqueGa naar voetnoot8): l'égalité des accélérations centripète g et centrifuge v2/r dans ce cas peut avoir amené Huygens tout naturellement à admettre aussi l'égalité des conatusGa naar voetnoot9) (ou forces) correspondants. Le dernier alinéa de la p. 277 du T. XVII, ainsi que les p. 303 et 304 du T. XVI, | |||||||
[pagina 46]
| |||||||
font voir clairement qu'en étudiant la force centrifuge il a commencé par considérer le cas où la gravité et la force centrifuge se balancent. Dans le début de la Pars Secunda de l'‘Hor. osc.’ ce sont des idées et des théorèmes de Galilée que Huygens précise. Ici comme dans la Pars Quarta et dans les théorèmes V-XIII sur la force centrifuge de la Pars Quinta, c.à.d. dans tout ce qui se rapporte au mouvement des corps sous l'action de la pesanteur, la philosophie corpusculaire de Descartes, en d'autres termes la théorie des tourbillons, ne joue aucun rôle. Voir sur un sujet non traité dans l'‘Hor. osc.’ les p. 247, 285 et 286 du T. XVII.
B. Arcs cycloïdaux et pendule composé. Les arcs cycloïdaux n'assurent l'isochronisme que pour le pendule simple. Quelle doit être en théorie la forme des arcs pour un pendule composé (en supposant toujours le poids du fil négligeable)? C'est une question dont L. Euler s'est occupé en 1750Ga naar voetnoot1). Huygens ne l'a pas abordée. Il se contente de dire (Prop. XXIV de la Pars Quarta) que les arcs cycloïdaux seraient corrects si tous les points du corps suspendu au fil impondérable décrivaient des cycloïdes, ce qui serait le cas si ce corps se déplaçait sans aucune rotation. Voir sur cette question l'Appendice IV à la Pars Quarta.
C. Rectangulum oscillationis ou rectangulum distantiarum. En 1669 Huygens donna le nom de ‘rectangulum distantiarum’ au produit de la distance de l'axe d'oscillation au centre de gravité du corps oscillant considéré, par la distance de ce centre au centre d'oscillation. Comme nous l'avons dit à la p. 373 du T. XVI, Huygens avait établi en 1664 la constance de ce produit pour différents axes d'oscillation parallèles entr'eux dans deux cas: 1. celui où le corps est une surface oscillant perpendiculairement à son plan (T. XVI, p. 508), 2. celui où le corps est une surface symétrique par rapport à un axe vertical qui oscille dans son plan (T. XVI, p. 528). Il ajoutait, mais sans le démontrer, que le produit nommé est constant pour une surface plane quelconque (T. XVI, p. 528, note 2). Il est entendu que le plan qui contient les deux axes parallèles considérés passe toujours par le centre de gravité du corps. Dans l'‘Hor. osc.’ la constance du ‘rectangulum distantiarum’ pour un corps quel- | |||||||
[pagina 47]
| |||||||
conque oscillant suivant un plan déterminé est démontré (Pars Quarta, Prop. XIX) en partant des Prop. VI et XVIII de la même Pars. La Prop. VI établit la formule générale
l = ∑r2/nb
(voir la p. 33 qui précède) et la Prop. XVIII conduit à la formule également applicable à un corps quelconque 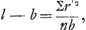
où r est la distance d'un point du corps à l'axe d'oscillation et rʹ celle du même point à un axe parallèle passant par le centre de gravité du corpsGa naar voetnoot2). Comme les deux formules peuvent s'écrire l = I/Mb et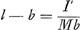 ,
où M est la masse du corps et I et Iʹ désignent les moments d'inertieGa naar voetnoot3) par rapport aux deux axes nommés, la deuxième formule résulte de la première aussitôt qu'on a établi la relation ,
où M est la masse du corps et I et Iʹ désignent les moments d'inertieGa naar voetnoot3) par rapport aux deux axes nommés, la deuxième formule résulte de la première aussitôt qu'on a établi la relation 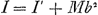 , ce qui est une formule moderne bien connue. Il est évident par là que la démonstration de Huygens consiste en somme à établir cette relation. Et celle de la Prop. XIX consiste à tirer des formules , ce qui est une formule moderne bien connue. Il est évident par là que la démonstration de Huygens consiste en somme à établir cette relation. Et celle de la Prop. XIX consiste à tirer des formules
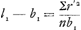 et et 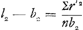 , ,
qui s'appliquent à un même corps oscillant d'abord autour de l'axe 1, ensuite autour de l'axe parallèle 2 situé dans le plan passant par l'axe 1 et le centre de gravité du corps, la formule 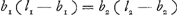 , ,
qui exprime la constance du ‘rectangulum distantiarum’. De cette dernière formule résulte la célèbre Proposition XX qui exprime la réversibilité du pendule, puisque les relations 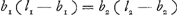 et et 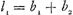
ne peuvent coëxister à moins qu'on n'ait aussi 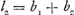 , donc l2 = l1. , donc l2 = l1.
| |||||||
[pagina 48]
| |||||||
Si l'on écrit I = Mρ2 et Iʹ = Mρʹ2, où ρ et ρʹ désignent des rayons d'inertie (nous continuons à nous servir d'accents pour désigner les grandeurs se rapportant à un axe passant par le centre de gravité), l'équation 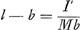
donne 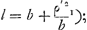
en d'autres termes ρʹ2 ou ∑rʹ2/n est identique avec le ‘rectangulum distantiarum’ que Huygens désigne toutefois dans l'‘Hor. osc.’ par le terme ‘rectangulum oscillationis’ ou ‘spatium applicandum’, c.à.d. espace qui doit être divisé par une longueur (savoir b). Voir p.e. dans le calcul du ‘Centrum oscillationis rectanguli’ de la Prop. XXI de la Pars Quarta l'expression ‘spatium applicandum sive rectangulum oscillationis’. Le calcul pratique de ρʹ2 ou ∑rʹ2/n exige en général la décomposition de ∑rʹ2 suivant des axes rectangulaires, situés dans le ‘planum oscillationis’ et passant l'un et l'autre par le centre de gravité du corps, en ∑yʹ2 + ∑zʹ2 (comme on peut le voir dans les exemples que Huygens propose) et l'application des méthodes pour trouver ces dernières sommes, déjà consignées dans une Pièce de 1664 ou 1665 (p. 545-549 du T. XVI) à laquelle sont empruntées les Prop. IX-XI de la Pars Quarta. Les grandeurs ∑yʹ2/n et ∑zʹ2/n sont simplement appelées rectangula. Dans l'Appendice II à la Pars Quarta nous les appelons respectivement premier et deuxième rectangulum. En comparant p.e. le calcul de l'‘Hor. osc.’ dans le cas du rectangle oscillant dans son plan dont nous venons de parlerGa naar voetnoot2) avec les calculs du T. XVI (p. 456 - | |||||||
[pagina 49]
| |||||||
méthode inconnue dite fort difficile -, p. 463-469 - méthode de réduction, d'après la p. 369, de l'oscillation latérale à l'oscillation perpendiculaire au plan de la figure - et p. 520-523 - méthode générale, d'après la p. 370, pour les surfaces planes symétriques oscillant dans leur plan), on voit combien le procédé de calcul a été successivement simplifié. C'est dans le septième alinéa de la Prop. XXI de la Pars Quarta que Huygens fait connaître la méthode de calcul pour une surface plane quelconque oscillant dans son plan, que l'on peut comparer avec celle du dernier alinéa de la p. 370 du T. XVI.
D. Méthode de la Prop. XV de la Pars Quarta. Nous avons dit à la p. 371 du T. XVI que cette méthode était connue à Huygens en 1665, du moins pour le cas particulier des corps de révolution. Il semble sort possible qu'il l'ait conçue déjà en ce temps pour des corps quelconques possédant les propriétés qu'il mentionne dans la Prop. XV. Remarquons que dans son raisonnement géométrique il y fait usage de la règle dite de Guldin qui est en réalité une règle de Pappus: on la trouve à la fin de la Préface du Livre VII de sa ΣυναγωγήGa naar voetnoot3). Dans la Prop. XXII Huygens cherche le centre d'oscillation de la sphère en se basant sur la Prop. XV; comparez le dernier alinéa de la p. 472 du T. XVI.
E. Recherche du centre d'oscillation dans quelques cas particuliers. Dans l'‘Hor. osc.’ Huygens considère quelques cas particuliers qui ne se trouvent pas dans les Manuscrits B et C ni dans les brouillons de 1664, du moins dans ceux qu'il a conservés. Ce sont 1. le polygone régulier à nombre quelconque de côtés oscillant dans son plan (Prop. XXI)Ga naar voetnoot4), 2. la pyramideGa naar voetnoot5), 3. le côneGa naar voetnoot6), 4. le cylindre, 5. le demi-cône (Prop. XXII de la Pars Quarta). Voir sur la parabole oscillant dans son plan (Prop. XXI) qu'on ne trouvera pas dans le T. XVI, l'Appendice II à la Pars Quarta qui traite aussi de l'oscillation d'une croixGa naar voetnoot7). Dans la Pièce qui constitue le § 3 de notre Appendice III à la même Pars Huygens considère le cas d'un secteur de sphère. | |||||||
[pagina 50]
| |||||||
À la fin des Prop. XXI et XXII il parle de figures scalènes, planes ou solides, isochrones avec les figures droites dont elles proviennent par luxation. Pour prouver cet isochronisme il se contente de remarquer que d'après une proposition antérieure les ‘lineae graves’ dans le premier cas, les surfaces planes graves dans le deuxième, dans lesquelles on peut découper les figures données et les figures scalènes, sont isochrones deux à deux. Ce raisonnement nous paraît un peu trop court pour être convaincant. Ne fallait-il pas plutôt dire que d'après la formule l = ∑r2/nb appliquée aux éléments isochrones deux à deux, l'égalité de l et de b entraîne celle de ∑r2, que par conséquent le ∑r2 pour la figure scalène entière est égal à celui de la figure droite entière, et que, les b, c.à.d. les distances des centres de gravité à l'axe de suspension, étant aussi égales entre elles pour les deux figures entières, il en est de même de leurs l, c.à.d. des longueurs de leurs pendules simples isochronesGa naar voetnoot1)? Et même contre cette preuve-là on pourrait encore faire l'objection qu'elle est trop conforme à l'esprit de Cavalieri. Il est vrai que la même objection pourrait être faite contre les démonstrations des Prop. VII-XI et XIII-XVIII de la Pars Quarta puisque les surfaces ou les corps y sont considérés comme composés de fort petites particules égales parfois représentées par des carrés ou points centraux de carrés (Prop. IX, XIII, etc.), d'autres fois p.e. par de petits prismes ou parallélépipèdes dont il est dit dans la Prop. VII ‘totum cuneum ABD componi’. La rigueur de ces preuves est apparemment inférieure à celle des Prop. II-VI, IX, X et XXIV de la Pars Secunda, III de la Pars Tertia et IV-V de la Pars Quarta, où Huygens applique la méthode antique de la réduction à l'absurde en commençant par supposer que l'égalité qu'il s'agit de démontrer n'existe pas. En revanche, les démonstrations dans lesquelles l'objet mathématique considéré est supposé découpé en un fort grand nombre de parties sont évidemment moins artificiellesGa naar voetnoot2). | |||||||
Expéditions pour déterminer les longitudes et Table de l'Equation.Nous reviendrons plus loin dans ce Tome sur les résultats pratiques des expéditions | |||||||
[pagina 52]
| |||||||
mentionnées par Huygens dans la Pars Prima en parlant en même temps des expéditions ultérieures. Puisqu'une détermination exacte des longitudes à l'aide d'horloges n'exige pas seulement une régularité parfaite de la marche de celles-ci mais aussi l'emploi d'une Table fort juste de l'Équation du Temps, nous nous sommes demandés si la Table des p. 112-113Ga naar voetnoot1) estabsolument correcte. Le doute est d'autant plus permis qu'il eût en tout cas, pour satisfaire à toutes les exigences, fallu calculer des tables pour quatre années consécutives dont une bissextile. On a eu à l'Observatoire de l'Université de Leiden la bonté d'exécuter les calculs nécessaires pour l'année 1670. Dans la figure qui précède on peut voir de combien la courbe correspondant à la Table de Huygens s'écarte de celle calculée à Leiden. | |||||||
Précurseurs et concurrents de Huygens.A. Tangentes aux courbes engendrées par les points d'une figure roulante. Comme Huygens le remarque dans la Pièce qui constitue la partie A de notre Appendice à la Pars Secunda, il s'est inspiré dans la démonstration générale de la Prop. XV de cette Pars d'une proposition de Descartes et du commentaire de van Schooten sur ce sujet. On peut consulter là-dessus la note 1 à l'Appendice nommé.
B. Centre d'oscillation et mesure universelle de la longueur. Aux considérations des p. 349-353 du T. XVI nous devons ajouter quelques mots sur Honoré Fabry, mentionné par Huygens, avec Descartes, dans le début de la Pars Quarta. Nous avons dit à l'endroit nommé qu'avant octobre 1664 Huygens n'avait pas pris la peine de s'enquérir des recherches de Descartes et de Roberval sur le centre d'agitation; comparez la fin de l'alinéa suivant. Le troisième Tome des ‘Lettres de Descartes’ publiées par Clerselier qui contient les lettres de 1646 de Descartes à Mersenne et à CavendishGa naar voetnoot2) sur ce sujet, ainsi que des observations de Roberval, ne parut qu'en 1667. Huygens a appris à le connaître vers ce temps, quoiqu'il n'en fasse mention dans sa correspondance qu'en 1687Ga naar voetnoot3), mais il ne discute la théorie erronée de Descartes ni dans l'‘Hor. osc.’ | |||||||
[pagina 53]
| |||||||
ni ailleurs. Quant au ‘Tractatus Physicus de Motu locali, in quo Effectus omnes, qui ad Impetum, Motum naturalem, violentum, & mixtum pertinent, explicantur & ex principiis Physicis demonstrantur. Auctore Petro Mousnerio Doctore Medico: Cuncta excerpta ex praelectionibus R.P. Honorati Fabry, Societatis Iesu’ de 1646Ga naar voetnoot4), où l'auteur, ou plutôt Fabry, ‘de pendulis isochronis egit .. sed pleraque falsa dedit nec quicquam demonstravit’Ga naar voetnoot5), Huygens dit en 1664 le connaître dans une lettre d'octobre de cette annéeGa naar voetnoot5); il le connaissait dès 1647 comme nous le ferons voir.
Mersenne, assez longtemps, paraît-il, avant 1646 où il proposa la question du centre d'oscillation ou plutôt celle du centre de percussion à Descartes et à Huygens, s'était adressé à Honoré Fabry, alors à Lyon, et les propositions sur ce sujet de ce dernier qu'il appelle ‘un géant en science’ lui étaient déjà connues avant l'apparition du livre de MousnierGa naar voetnoot6). Naturellement il désirait que Chr. Huygens fît connaissance avec ce livre. C'est de lui - et du livre antérieur de Fabry sur la philosophieGa naar voetnoot7) - qu'il parle dans sa lettre à Const. Huygens du 3 janvier 1647 (T. I, p. 48); et non pas des oeuvres de Noel, comme le suppose la note 9 à la page citée. Le volume de Mousnier contient en effet ‘10 Livres’ et ‘un traité particulier des centres de percussion à la fin’; Mersenne dit qu'il ‘brusle d'enuie que Mr. vostre fils le voye ce | |||||||
[pagina 54]
| |||||||
traité et qu'il l'examine, peut estre que l'enuie luy en prendra a luy mesme de le mieux demonstrer, ou du moins il pourra le faire voir a Mr. des Cartes, qui y a desia trauaillé’. Commençons par remarquer que, vu les dates, il semble qu'il faille admettre, et la dernière phrase citée de Mersenne l'indique également, que Fabry s'est occupé de la question indépendamment de Descartes (Mousnier ne fait mention ni de lui ni de Roberval). P. Duhem dit certainement à tortGa naar voetnoot1): ‘Par l'intermédiaire du livre composé par l'abbé de Guastalla [c.à.d. B. Baldi; comparez la note 2 de la p. 350 du T. XVI] certaines idées de LéonardGa naar voetnoot2) seront communiquées à Descartes et à Roberval; elles provoqueront entre ces deux grands géomètres un débat qui ne sera pas exempt d'aigreur; portés par Mersenne, par le P. Fabry, par Pierre Mousnier à la connaissance du jeune Chr. Huygens, les affirmations contradictoires de Roberval et de Descartes suggéreront à ce physicien de génie la théorie du pendule composé; etc.’ Au contraire Huygens semble n'avoir appris avant 1665, ou déc. 1664Ga naar voetnoot3), sur les recherches de Descartes et de Roberval (que nous jugeons quelque peu postérieures à celles de Fabry, quoiqu'indépendantes des siennes) que ce que Mersenne lui en écrivit. Il est vrai qu'il a connu Roberval personnellement en 1655 (T. I, p. 370), et qu'en cette année et la suivante il a été en correspondance avec lui; mais dans ces lettres il n'est pas question du centre d'agitation. D'après le Journal de Voyage il visita Roberval à Paris le 13 décembre 1660; sa lettre à Thévenot du 29 janvier 1665 (T. V, p. 209) fait voir qu'alors aussi il n'a pas fait connaissance avec les recherches de Roberval sur le sujet en question. Quant à Descartes, Huygens ne fait nulle part mention d'aucun entretien avec lui; ce n'est que peu avant le 29 janvier 1665, paraît-ilGa naar voetnoot3), qu'il reçut de Thévenot (lettre citée) des nouvelles sur les recherches de Descartes. Après l'apparition du livre de Mousnier Descartes ne semble plus s'être occupé de ce sujet. Dans sa lettre citée Mersenne annonce qu'il enverra le livre nommé ou en tout | |||||||
[pagina 55]
| |||||||
cas ‘les 2 ou 3 feuillets où sont les centres de percussionGa naar voetnoot4)’. Or, nous avons pu établir qu'il a tenu sa promesse. En effet, comme aucune bibliothèque publique en Néerlande ne possède l'oeuvre de Mousnier, nous avons demandé l'exemplaire de la Bibliothèque de l'Université de Göttingue et il s'est trouvé que celui-ci porte sur la première page l'inscription: ‘Constanter 1647. don. Mar. Mersenni’. L'‘Appendix Prima physicomathematica, De Centro percussionisGa naar voetnoot4)’ a été lu par Chr. Huygens puisqu'on y trouve en marge quelques observations de sa mainGa naar voetnoot5). Ces notes marginales datent sans doute de 1664: on y trouve e.a. (p. 437) la multiplication de b + ⅓zz/b par ¾ que nous avons signalée dans la note 1 de la p. 456 du T. XVI. Il est question chez Mousnier (p. 436-437) de la ‘rationem egregij experimenti, quod saepè Doctus Mersennus proposuit, scilicet longitudinem funependuli isochroni esse ferè quadruplam perpendicularis ductae in basim trianguli Isoscelis, librati circa angulum verticis 150. grad.’; c.à.d. si l'on fait osciller dans son plan un triangle isoscèle suspendu au sommet et dont l'angle au sommet est de 150o, la longueur du pendule simple isochrone sera environ le quadruple de la hauteur du triangle. Après avoir établi par la multiplication susdite la longueur du pendule simple isochrone pour le cas d'un triangle isoscèle de hauteur b et de base 2z, Huygens pose donc  Cette équation conduit pour l'angle au sommet à 148o59′50″, ce qui est en effet à peu près 150o. À l'endroit cité Huygens n'exécute pas le calcul de l'angle. Il tire correctement la racine carrée de 13 et écrit à côté des mots ‘angulum verticis 150. grad.’: ‘[de]bebat esse [...] 0o48′ proximè’. Il n'est pas bien clair ce qu'il a écritGa naar voetnoot5). Dans le calcul de la valeur de l'angle il semble avoir commis une erreur, mais sa formule est correcte. Les autres notes marginales de Huygens sont les suivantes: 1) À la p. 430, où | |||||||
[pagina 56]
| |||||||
Mousnier énonce et croit prouver son ‘Theorema 22. Si voluatur circulus circa punctum circumferentiae in circulo parallelo suo plano, determinari potest centrum percussionis, quod distat ⅔ diametri à centro motus’, Huygens observe: ‘[Im]oGa naar voetnoot1)¾ diametri’. Il s'agit de l'oscillation du cercle dans son plan sur laquelle on peut comparer le premier alinéa de la p. 455 du T. XVI. 2) À la p. 431, où Mousnier dit par inadvertance ‘Theorema 24. Potest determinari centrum percussionis solidi trium facierum ABDE’, Huygens écrit: ‘mirabile solidum, nam tribus pla[nis] solidam figuram constitui nega[nt] geometrae. Sed auctor qua[rtum] planum non ani[mad]vertit, est enim ABDE pyrami[s]’. 3) À la p. 426, où Mousnier cherche (sans pouvoir achever le calcul) le centre de percussion d'un secteur de cercle suspendu au centre du cercle et tournant perpendiculairement à son planGa naar voetnoot2) et parle e.a. d'un ‘solidum AEFDCB, quod scilicet constat ex pyramide AEDCB, & segmento cylindri EFDCB’, Huygens annote: ‘et praeterea ex cuneo super basi EDF quem autor oblitus est’Ga naar voetnoot3).
À la p. 421 Mousnier écrit à propos du centre de percussion: ‘Centrum percussionis est punctum illud corporis impacti in quo si contactus fiat, maximus ictus infligitur’Ga naar voetnoot4), et: ‘Centrum percussionis est in illa linea, quae dirimit utrimque momenta, tùm ratione impetus, tùm ratione distantiae’, ce qui veut dire que, lorsqu'on tire par ce centre une droite parallèle à l'axe de rotation considéréGa naar voetnoot5), les moments des ‘impetus’, c.à.d. la somme (ou intégrale) des moments de tous les ‘impetus’ partiels | |||||||
[pagina 57]
| |||||||
est égale de part et d'autre de cette droiteGa naar voetnoot6). Ici il est apparemment question d'un corps constitué par une surface plane. Ajoutons que Mousnier ne considère que les corps homogènes. Quant à l'‘impetus’ du mouvement, il est proportionnel à la vitesse linéaire (Th. 6 de la p. 423) et à la grandeur de l'élément considéré du corps. C'est, peut-on dire, la quantité de mouvement mv. Pour évaluer l'intégrale des quantités de mouvement de la surface en ‘mouvement solide’ (voir sur ce terme la p. 376 du T. XVI) Mousnier représente les vitesses de tous les points par des normales à la surface. Il obtient ainsi un ‘solidum’ qui n'est autre que le ‘cuneus’ (ou le ‘truncus’) considéré par Huygens dans le cas du mouvement solide. Nous avons dit dans la note 2 de la p. 458 du T. XVI que Huygens (cherchant le centre d'oscillation) passe par le raisonnement considéré en cet endroit de la ‘méthode de la parabole’ à la ‘méthode de l'onglet (ou cuneus)’. Nous pouvons ajouter maintenant que puisque Huygens admettait avec Mersenne et Mousnier l'identité du centre d'oscillation avec le centre de percussion, ce qui ressort des notes marginales que nous venons de citer, il avait l'avantage de savoir que ce serait probablement la subcentrique de l'onglet (ou du tronc, voir la note 5 de la p. 459 du T. XVI) qui lui donnerait la longueur du pendule isochrone avec la surface en mouvement solide. Il a donc certainement profité de la lecture du livre de Fabry. En somme, dans le livre de Fabry, ou de Mousnier, la détermination du centre de percussion est correcte pour les surfaces planes en mouvement solide. C'est ce que Huygens reconnaît en disant dans la Prop. XXI de la Pars Quarta de l'‘Hor. osc.’: ‘Quod unum [savoir: la position du centre d'oscillation dans le cas du mouvement nommé] ab aliis ante animadversum fuit, non tamen demonstratum’. Non pas démontré: en effet, même si le raisonnement de Mousnier, qui conduit à fixer l'endroit du centre de percussion dans ce cas est considéré comme suffisant, celui par lequel il tâche d'établir l'identité des deux centres ne l'est certainement pasGa naar voetnoot7). | |||||||
[pagina 58]
| |||||||
Il convient d'ajouter que dans l'‘Hor. osc.’ Huygens ne parle point du centre de percussion et qu'il n'apparaît pas d'où résulte sa conviction, apparemment déjà générale en 1664, de l'identité des deux centresGa naar voetnoot1). Par sa démonstration même des p. 457-460 du T. XVI l'identité du centre d'oscillation avec le centre de percussion tel que celui-ci avait été défini par Fabry par la considération des moments des ‘impetus’ était prouvée pour les surfaces planes en mouvement solide. Mais sa note marginale à la p. 430 de Mousnier fait voir qu'il admet aussi l'identité des deux centres pour le cas d'une surface oscillant dans son plan. Comme on peut le voir par cette note marginale, les considérations de Mousnier sur le centre de percussion dans le cas des surfaces oscillant dans leur plan - et il en est de même dans le cas des corps - ne conduisent pas à la connaissance de la position du centre d'oscillation dans ces cas.
Nous avons mentionné à la p. 375 du T. XVI le principe de Brouncker pour le cas des surfaces planes en mouvement solide. Ce principe s'accorde parfaitement avec la méthode de construction de Fabry; mais Brouncker (p. 144 du T. V) parle seulement du centre d'oscillation et ne donne aucune preuve. Wallis en 1671Ga naar voetnoot1) parle dans le même cas du centre de percussion qu'il trouve en se servant d'une considération identique avec celle de Fabry sur les moments des quantités de mouvement.
Nous avons parlé de la mesure universelle de la longueur au moyen des pendules aux p. 353-356 du T. XVI et 120-121 du T. XVII. Malgré le texte de la p. 120 nommé, il semble - voir la lettre de 1668 de Huygens à Estienne (T. VI, p. 260) citée dans la note 8 de la p. 121 nommée - que l'idée d'établir à l'aide de pendules une mesure universelle ait été promulguée en Angleterre indépendamment de Huy- | |||||||
[pagina 59]
| |||||||
gens et avant lui. Il est vrai que cette idée ne pouvait sembler absolument pratique que depuis le moment où la formule qui donne la place exacte du centre d'oscillation avait été établie. Toutefois G. Mouton (comparez la p. 36 qui précède), connaissant la marche exacte des horloges de HuygensGa naar voetnoot1), se montre déjà en 1670 un avocat convaincu de cette idée qu'il développe dans la dernière partie (p. 427-448) de son livre. Il y propose un système décimal de longueurs, l'unité étant empruntée à la dimension du globe terrestre: il veut que le ‘Milliare Geometricum in uno gradu circuli terrae maximi sexagies exactè continetur’. La millième partie du ‘milliare’ est nommée ‘virga’ et la dix-millième partie ‘virgula’, la longueur approximative de cette dernière étant donnée par une ligne de 20,2 cm. Il constate qu'un pendule simple de cette longueur exécuterait 3959,2 oscillations simples en une demi-heure, valeur moyenne calculée d'après les nombres observés des oscillations de différents pendules pouvant être considérés comme simples, l'un deux ayant p.e. un globe de plomb et une verge formée d'un fil de fer fort mince, un autre étant formé par un globe de fer suspendu à un cheveu, etc. La longueur de chacun de ces pendules (comparez la p. 355 du T. XVI) est pour Mouton la distance du point de suspension au centre du globe.
C. Horloges à pendule oscillant dans un plan antérieures à celles de Huygens. Le passage bien connu de la Préface (p. 91 qui suit), où Huygens avance qu'il est fort peu croyable que des horloges à pendule aient été achevées et employées avant celles construites à la Haye depuis 1657, nous oblige de revenir brièvement sur ce sujet, sur lequel on peut consulter aussi les p. 36-39 du T. XVII. Nous ne discuterons pas la question de l'horloge à pendule qui aurait existé depuis 1615 ou 1616 à Angoulême chez de BoismorandGa naar voetnoot2), vu que de Carcavy, qui n'avait pas vu cette | |||||||
[pagina 60]
| |||||||
horloge lui-même et que Huygens a connu personnellement à Paris, paraît ne pas être revenu sur ce sujet dont Huygens ne dit rien dans l'‘Hor. osc.’Ga naar voetnoot1). Les croquis de Leonardo da VinciGa naar voetnoot2) que Huygens n'a pas connus font voir, comme nous l'avons dit, qu'il avait été question depuis longtemps de balanciers en forme de pendule, lesquels ne paraissent pas cependant - et c'est là un point d'une importance capitale - avoir dû servir à contrôler la marche de l'horloge par un mouvement oscillatoire plus ou moins indépendant (comparez la note 5 qui suit). Cette remarque s'applique aussi à l'horloge à pendule d'un certain Camerini portant la date 1656 (N.B.) qui est représentée à la p. 139 de ‘The Evolution of Clockwork, etc.’ de Mons. J. Drummond RobertsonGa naar voetnoot3). Un pendule de forme primitive s'y meut devant le cadran. Des horloges de ce genre, dont l'histoire est fort peu connueGa naar voetnoot4), ne pouvaient évidemment être des instruments de précision. On semble être d'accord pour considérer comme trompeur le passage des Saggi de 1667 de l'Accademia del Cimento où l'horloge de 1649 de Vincenzio Galilei est mentionnée dans des termes qui portent le lecteur à croire (quoique cela ne soit pas dit expressis verbis) que cette horloge a marché et a pu, telle qu'elle était, servir de modèle pour la construction d'autres horloges exactesGa naar voetnoot5). Quant à cette horloge de Vincenzio Galilei ou ‘horologe a pendule commencee par Galilei’, pour nous servir des termes de BoulliauGa naar voetnoot6), il est certain qu'elle n'était point achevée, puisque Viviani dans sa lettre du 20 août 1659 au grand-duc Leopoldo | |||||||
[pagina 61]
| |||||||
de MediciGa naar voetnoot7) dit e.a. que Vincenzio était occupé peu avant sa mort à ‘intagliar l'altra ruota dentata’. La figure de la p. 656 du T. XIX de l'Ed. Naz. montre clairement que la moitié de la grande roue seulement est pourvue de dents. Cette figure représente sans aucun doute un instrument réel puisqu'il en existe une deuxième figure où il est vu sous un autre angleGa naar voetnoot6). Mais quoique l'horloge ne fût pas achevée, l'auteur avait apparemment déjà éprouvé, en y attachant un poids moteur, le mécanisme de l'échappement à double virgule qu'on y voit. En effet, Viviani dit: ‘volle il Sig.r Vincenzio che io .. vedessi così per prova e più d'una volta, come pur vedde ancora il suddetto artefice [Dom. Balestri], la congiunta operazione del contrapeso e del pendolo’. J.B. Biot qui en 1858 prend le parti de HuygensGa naar voetnoot8) commet une étrange erreur (entièrement sans conséquence chez lui) en disant (p. 677) que Vincenzio G. a consacré ‘tout au plus deux mois et demi à ce travail’. En effet, il vient de dire, en citant la lettre de Viviani, que Vincenzio commença son travail en avril 1649 et qu'il mourut le 16 mai suivant. A-t-il voulu écrire: un mois et demi? Ce serait encore beaucoup trop, puisque Viviani dit que Vincenzio mourut ‘nel giorno XXII del suo male’. Suivant Viviani, il tomba donc malade le 25 avril. Par conséquent vingt-cinq jours au plus ont été consacrés à la construction de l'horloge si le récit de Viviani, comme nous l'admettons ici, est absolument conforme à la véritéGa naar voetnoot9). Mons. Drummond Robertson - à qui nous avons de grandes obligations; voir les p. 38 et 546 du T. XVII - fait mention sans critique (p. 96) des ‘at the most two and a half months’ de Biot. Il est d'avis qu'en ce temps Vincenzio a pu construire plus d'une horloge. Mais comme tailler les roues était pour lui une ‘insolita fatica’, il paraît peu probable qu'en vingt-cinq jours tout au plus il ait pu construire autre chose que le modèle inachevé dont d'ailleurs il est seul question chez Viviani. Il est vrai que Viviani ajoute: ‘stimava [nous soulignons] di potere in diversa forma e con altre invenzioni adattare il pendolo all' oriuuolo’, et que l'inventaire de sa veuve, morte en 1668, mentionne ‘Un Oriuolo non finito di ferro col Pendolo, prima invenzione del | |||||||
[pagina 62]
| |||||||
Galileo’.Ga naar voetnoot1) La question de savoir si Vincenzio G. a construit un ou plusieurs oriuoli serait importante si l'on voulait soutenir qu'il a trouvé le temps de fabriquer, outre de grossiers modèles, une horloge à pendule exacte et marchant bien, ce que nous ne pouvons nullement admettreGa naar voetnoot2). D'ailleurs, l'‘Oriuolo non finito’ de l'inventaire de la veuve n'est-elle pas précisément le modèle unique dont parle Viviani? Albéri le pensaitGa naar voetnoot1), Biot de même, et cette hypothèse peut paraître au premier abord presque certaine. Elle ne l'est pourtant pas, car, nous l'avons dit à la p. 472 du T. III, ‘dès 1659 un modèle, attribué à Galilei, était en possession du Prince Léopold’ et c'est de ce modèle qu'il envoya la figure à BoulliauGa naar voetnoot3). Or, cette figure s'accorde avec celle du T. XIX de l'Ed. Naz. comme nous l'avons dit à la p. 61. D'autre part la figure du T. XIX s'accorde parfaitement avec la description détaillée qui se trouve dans la lettre de Viviani. Quoiqu'à Florence cette figure n'ait pas été trouvée dans la lettreGa naar voetnoot4) il paraît donc à peu près certain, comme on l'admet généralement, que c'est bien là la figure du modèle dont Viviani parle. S'il en est ainsi, ce modèle-là était donc en 1659 en possession de | |||||||
[pagina 63]
| |||||||
Leopoldo. On peut trouver étrange qu'il l'attribue à Galilée père (T. III, p. 468), mais ceci pourrait s'expliquer par le fait que la lettre à Boulliau où il semble le dire est du 21 août 1659, tandis que la lettre de Viviani adressée à lui est du 20 août (T. III, p. 470); en écrivant à Boulliau il venait donc de recevoir cette dernière dont les premières lignes parlent du ‘maraviglioso misurator del tempo col pendolo di Galileo Galilei’: il a donc pu penser en ce moment que l'instrument en question provenait suivant Viviani de Galilée père. D'ailleurs dans sa lettre d'août il n'en attribue en somme que l'invention à Galilée, et les mots ‘è fabricato il modello del [et non pas: dal] medesimo’ ne disent pas nettement que la construction aurait eu lieu par Galilée lui mêmeGa naar voetnoot5). Il n'y a donc là aucune difficulté. Et il n'est pas déraisonnable de supposer qu'il ait restitué le modèle à la veuve, de qui il doit l'avoir reçu. Quoi qu'il en soit, ce point n'est pas de grande importance: si Vincenzio G. a trouvé le temps en avril 1649 de construire un deuxième modèle imparfait, à plus forte raison n'a-t-il pas eu celui de construire une horloge achevée. Viviani dit ensuite que Philippe Treffler construisit pour le Prince Leopoldo un compteur à roues très légères. La note 53 de la p. 483 du T. III dit que ce mécanicien s'établit à Florence en 1658, mais nous ignorons l'origine de cette date apparemment inexacte: Mons. Drummond Robertson cite à la p. 102 de son livre une pièce qui prouve que Treffler était déjà en 1656 horloger de son Altesse. Ce compteur fut, paraît-il, construit en ou vers 1655, puisque Viviani ajoute qu'en ce temps, savoir 14 ans après le moment où Galilée proposa d'appliquer le pendule aux horloges, Fr. Generini construisit pour le Prince un modèle de fer dans lequel ‘era unito al pendolo il contrappeso’. Il dit enfin ‘che Filippo soprannominato adattò la 'nvenzione ad un oriuuolo da camera per Sua Altezza etc.’; malheureusemment il ne dit pas - ce qui est le point important dans la question de priorité - si cette construction d'horloges à pendule par Treffler - les premières horloges de ce genre construites à Florence qui aient marché - eut lieu avant ou après que le Grand-duc Ferdinando, frère de Leopoldo, eut reçu en 1657 l'horloge de Coster, dont il est | |||||||
[pagina 64]
| |||||||
question dans la première note de la p. 38 du T. XVII et que Viviani semble ne pas avoir connue. D'après Leopoldo écrivant en mai 1659 (T. III, p. 464) ce fut pour Ferdinando que le ‘virtuoso’ [Treffler?] construisit ‘tre anni sono’ un ‘oriuuolo rozzamente fatto’. C'est de cette horloge qu'il est aussi question dans la lettre de Leopoldo de mars 1659 (T. III, p. 462); on y trouve également l'expression ‘tre anni sono’. Si cette expression est littéralement exacte, le ‘virtuoso’ avait construit en 1656 pour Ferdinando une horloge à pendule ‘rozzamente fatto’, mais qui pouvait marcher. On nous permettra d'ajouter que lors même que cette construction n'aurait eu lieu que dans la deuxième moitié de 1657, après que Ferdinando eut reçu l'horloge de Coster, elle aurait cependant été antérieure d'un an à la publication de septembre 1658 de l'‘Horologium’ de Huygens et aurait pu passer pour ceux qui la voyaient fans connaître celle de Coster pour une invention originale faite à Florence. Observons encore qu'il n'y a aucune raison pour admettre que les horloges de Treffler aient été pourvues de l'échappemeut à deux virgules du modèle de Vincenzio, puisque Viviani dit que le modèle de Generini dont Treffler s'inspiraGa naar voetnoot1) était ‘con diversa e molto ingegnosa applicazione’. Leopoldo dit en mai 1659 (T. III, p. 464), après avoir vu la figure de l'‘Horologium’ de 1658 de Huygens, que le ‘virtuoso tre anni sono ne inventò un simile [nous soulignons]Ga naar voetnoot2)’. Il ne faut sans doute pas attacher trop d'importance à ce mot. Mais alors, pourquoi attribuer une valeur absolue à l'expression ‘tre anni sono’? D'ailleurs il n'est pas absolument impossible qu'en disant ‘tre anni sono’ Leopoldo entende parler de 1657, puisque 1657, 1658 et 1659 sont trois années; de même que Huygens dit au début de l'Hor. osc’: ‘Annus agitur sextus decimus...’ quoique l'intervalle entre la publication de l'‘Horologium’ (sept. 1658) et celle de l'‘Hor. osc.’ (avril 1673) ne soit que de quatorze ans et demi. Viviani (voir la p. 441 qui suit) écrit en 1674 que l'‘Hor. osc.’ a paru ‘due anni sono’. Il mérite en outre d'être remarqué que Leopoldo dans la lettre d'août 1659 (T. III, p. 468) dit qu'on a envoyé de Florence au Roi de Pologne, qui ne croyait pas que ‘mio Signore e sratello havesse appresso di se tale invenzione’ une horloge à pendule fabriquée en Hollande, sans doute de Coster ou d'un de ses collaborateursGa naar voetnoot3). | |||||||
[pagina 65]
| |||||||
Somme toute, il semble impossible d'arriver à une conclusion certaineGa naar voetnoot4). D'ailleurs, cette question de priorité n'est pas énormément importante. Ce qui paraît certain, c'est que, si une véritable horloge à pendule a été construite avant juin 1657 par un horloger travaillant pour l'un ou l'autre Grand-duc, Huygens ne le savait point et qu'en Italie même on l'ignorait généralementGa naar voetnoot5); comparez le premier alinéa de la note 5 de la p. 37 du T. XVIIGa naar voetnoot6).
D'autre part, il est absolument possible, comme le dit Viviani, que Galilée, frappé de cécité, ait eu peu avant sa mort l'idée d'adapter le pendule aux horloges; l'affirmation contraire de la note 2 de p. 281 du T. VII ne fait aucune impression sur nous. Ce qui reste évidemment douteux c'est - comme le dit aussi Biot - si l'échappement à double virgule, que nous avons désigné à la p. 39 du T. XVII par l'expression ‘échappement de Galilée’, comme on en a l'habitude, a réellement été conçu par lui. Quant à la remarque pathétique de la note 3 de la p. 281 du T. VII sur la disparition du modèle de Vincenzio ‘qui aurait dû être d'un prix inestimable aux yeux du Prince Léopold’, nous n'y attachons aucune valeur, aussi peu qu'à la conclusion de la même note (p. 282) que ‘Viviani s'est laissé égarer lorsqu'il affirme avoir vu marcher la machine’. Sans doute, le modèle de 1649 ne marchait pas, mais Viviani se contente de dire qu'il l'a vu fonctionner ‘per prova’, un poids moteur y ayant été attaché. On ne peut raisonnablement parler (T. VII, p. 286) de ‘l'impossibilité de la marche de l'instrument’, ce que Huygens lui-même (voir sa lettre de janvier 1660 à la p. 12 du T. III) ne fait pointGa naar voetnoot7).
Nous avons dit à la p. 39 du T. XVII que l'‘échappement de Galilée’ peut être considéré comme le précurseur de l'échappement à ancre, inventé, à ce qu'il paraît, en Angleterre. En effet, l'origine de l'échappement à ancre, comme de beaucoup | |||||||
[pagina 66]
| |||||||
d'autres inventions, ne peut être déterminée avec une certitude absolue. On trouvera plus loin dans le présent Tome une courte Pièce sur ce sujet. On peut encore se demander, principalement en ayant égard à un des croquis mentionnés de L. da Vinci, s'il y a eu, avant Huygens, des horloges publiques à pendule, ce dont il n'existe, paraît-il, aucune preuve. La question se pose même pour les Pays-Bas. On a vu à la p. 79 du T. XVII que nous n'avons pas réussi à démontrer que l'horloge de 1652 de la cathédrale d'Arnhem n'avait pas de pendule. Il semble toutefois extrêmement improbable, que si des horloges publiques de ce genre avaient existé en Néerlande avant 1658, les horlogers qui attaquèrent Huygens en cette année (p. 82-83 du T. XVII) n'en auraient rien dit. Ils paraissent aussi n'avoir connu aucune horloge publique à pendule à l'étranger. L'argumentum ex silentio a ici beaucoup de force.
D. Horloges à pendule conique. On a prétendu que l'horloge publique d'Osnabrück de la fin du seizième siècle a probablement été une horloge à pendule coniqueGa naar voetnoot1). Ceci est incertain, puisque nous n'avons sur cette horloge d'autre renseignement que celui fourni par le texte cité dans la note 1. Les historiens ne mentionnent, croyons-nous, aucune autre horloge conique qui aurait été construite avant les jours de Huygens.
R. Hooke exhiba en 1666 une horloge à pendule conique dans une séance de la ‘Royal Society’ (T. VII, p. 304). Voir encore sur ce sujet la note 13 de la p. 337 du T. VII ainsi que la lettre de Huygens à son père d'août 1674 (T. VII, p. 390). Consultez aussi l'Appendice II à la Pars Quinta qui suit. | |||||||
[pagina 67]
| |||||||
Aucune horloge à pendule conique de ce temps, croyons-nous, n'a été conservée. Apparemment ces horloges n'ont jamais été en vogue.
Nous indiquons en marge les pages de l'édition originale de 1673 de l'‘Hor. osc.’. La Bibliothèque de l'Université de Leiden possède l'exemplaire de Huygens (comparez la note 3 de la p. 92 qui suit), où celui-ci a corrigé plusieurs fautes d'impression et introduit dans le texte quelques autres modifications, 's Gravesande dans son édition de 1724 a tenu compte de ces remarques, dont quelques-unes se rapportent à certaines figures légèrement défectueuses. Nous reproduisons ici les figures de 's Gravesande, qui, sauf ces corrections, s'accordent avec les figures originales; à cela près que celles qui représentent des instruments ou plus généralement des corps ont été ombrées dans les éditions de 1724 et de 1751. |
|