Oeuvres complètes. Tome XVII. L'horloge à pendule 1656-1666
(1932)–Christiaan Huygens–
[pagina 364]
| ||||||||||||||||||||||||||||||||||||||||||||||
Traité des couronnes et des parhélies.§ 1Ga naar voetnoot1). Quoique les causes des couronnes et des parhélies que nous avons entrepris d'établir ne diffèrent pas beaucoup entre elles, je commencerai cependant par traiter celles des couronnes, parce que l'explication en est plus aisée et qu'étant entendue elle facilite aussi la compréhension de celle des parhélies. Les couronnes donc sont des anneaux ronds qu'on voit parfois le jour autour du soleil et la nuit autour de la lune, tantôt blancs, tantôt aussi, lorsqu'ils apparaissent avec plus d'intensité, ornés de couleurs pareilles à celles de l'arc-en-ciel. Généralement les couronnes s'étendent sur un espace d'environ 45oGa naar voetnoot4) mesurées selon le diamètre, mais parfois on en observe de plus grandes possédant un diamètre de 90o ou même davantage. On raconte qu'il en est apparu simultanément trois ou un plus grand nombre ayant toutes le soleil pour centre. J'ai souvent observé les couronnes de 45o, mais la première fois j'ai vu la plus intense, dont j'ai noté, moi aussi, ce qu'elle présentait de remarquable; cette observation date d'un temps où je n'avais encore jamais recherché la cause de pareils phénomènes. Je notai donc que cette couronne était colorée quoique faiblement en comparaison avec un bel arc-en-ciel, et que la couleur rouge se trouvait à l'intérieur, la couleur bleue, fort pâle, à l'extérieur. De plus que tout l'espace entouré par cette couronne (et c'est peut-être la raison pour laquelle on a donné à ces espaces le nom d'‘areae’) semblait plus foncé que le reste de l'air en dehors d'elle, lequel était presqu' entièrement serein et couvert seulement de petits nuages blancs rares et transparents. Quant au diamètre de la couronne je le trouvai de 45o environ. Il est vrai que je me contentai de le mesurer grossièrement à l'aide d'un petit bâton que je portai devant moi en étendant le bras; constatant ainsi quelle partie du bâton correspondait au diamètre de la couronne, je pus en conclure à une valeur approchée de l'angle. Cette observation porte la date du 30 mars 1652Ga naar voetnoot5). Il me souvient | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 365]
| ||||||||||||||||||||||||||||||||||||||||||||||
De coronis et parheliis.§ 1Ga naar voetnoot1). Alhoewel de oorsaecken van de Coronae en van de parelia die wij sullen bijbrengen niet veel van malkander verscheyden en sijn, soo sal ick nochtans eerst van die van de Coronae handelen, om dat die explicatie facilior is, ende verstaen sijnde oock die van de parelia verstaenelycker maecktGa naar voetnoot2). De Coronae dan sijnGa naar voetnoot3) ronde ringen, die bij daegh om de son en bij nacht om de maen somtijts gesien werden, altemet wit, altemet alsse stercker sich vertoonen oock met couleuren verciert als den regenboogh, ende beslaen gemeenlyck ontrent de 45 gr.Ga naar voetnoot4) met haer diameter, doch somtijdts werdender oock grooter geobserveert die den diameter van 90 gr. of noch meer hebben, en daer wert verhaelt van 3 en meer te gelijck die alle de son voor center hadden. Ick heb die van 45 gr. dickmael geobserveert doch de eerste reijs de maxime expressam van welcke oock ick aenteyckende het geen daer ontrent remarquabel was, ende dat al eer ick noch oijt nae de reden getracht hadde van sulcke phaenomena. Ick noteerde dan dat desen ringh gecouleurt was, doch flaeuw in comparatie van een schoone regenboogh en dat de roode kouleur nae de binnen kant stondt, en de blaeuwe nae buijten, de welcke seer wittachtigh was. Voorts dat de heele spatie binnen den ring vervat (en hierom sijn dit misschien areae genaemt geweest) duysterder scheen als de andere lucht daer buijten, die bij nae heel klaer was, en maer met dunne doorschijnige witte wolckjes betrocken. den diameter eyndelyck van den ringh bevond ick ontrent de 45 gr. alhoewel die maer in 't ruwe afmat met een stockjen, streckende dat soo veer uijt als mijn arm kost reycken, en siende wat gedeelte daer van de breete van den ringh begreep, waer uijt daer nae den hoeck naegenoegh konde bereeckenen. diem adscriptum habet haec observatio 30 Martij anno 1652Ga naar voetnoot5). Mij gedenckt dat ick dese observatie gedaen hebbende nae | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 366]
| ||||||||||||||||||||||||||||||||||||||||||||||
qu'après l'avoir faite j'allai lire ce que Descartes écrit sur la cause de pareilles couronnes, savoir qu'elles proviennent de la réfraction des rayons du soleil dans certaines petites étoiles planes de glace, et que je ne fus pas content de cette explication, parce que, comme il le dit lui-même, il s'ensuivrait que l'espace compris dans la couronne devrait être plus clair que l'air extérieurGa naar voetnoot1), ce dont j'avais constaté le contraire.
§ 2. Je pensai donc qu'il fallait chercher une autre raison de ce météore, quoique le même auteur dise que nous ne pouvons trouver dans les nues aucune autre cause qui puisse produire un effet de ce genreGa naar voetnoot2). J'examinai toutes les réflexions et réfractions que les rayons du soleil peuvent subir dans des gouttelettes d'eau, sans trouver toutefois qu'une couronne ayant environ la grandeur requise pût être engendrée de cette manière. Je pris aussi la liberté d'imaginer arbitrairement quelques autres formes de grêlons, mais le tout en vain, tant il est difficile de se former une image adéquate d'une chose qu'on n'a jamais vue. Mais lorsque six ans plus tard je repris les mêmes pensées à l'occasion d'un phénomène de 5 soleils vus à Varsovie en 1658Ga naar voetnoot3), en considérant attentivement la forme de la dite couronne la véritable cause s'est enfin présentée à mon esprit, et bientôt après aussi celle des parhélies dont j'avais commencé à recueillir de partout des observations. En effet, je n'hésite pas à appeler vraies les causes qui correspondent si bien aux observations que je perdrais, me semble-t-il, ma peine en en recherchant d'autres. Comprenant donc que certains corpuscules voltigeant dans les nuages devaient fournir la matière de ces météores - ceci en effet semblait résulter nettement du fait que, tandis que les nuages passaient, la couronne était néanmoins restée en place; d'autre part l'obscurité du cercle intérieur à la couronne suggérait que les particules se trouvant en cet endroit ne laissaient pas passer les rayons solaires aussi bien que lorsqu'elles en avaient franchi le contour - j'aperçus soudainement qu'il en devait être ainsi si chacune de ces particules était vers l'extérieur une sphère de glace pure ou bien d'eau laquelle entourait une petite sphère moins transparente; car lorsqu'un grand nombre de particules de ce genre, toutes pareilles, voltigent entre notre oeil et le soleil, je compris aisément que celles d'entre elles qui se trouvent à l'intérieur d'un certain angle à partir du soleil ne laissent passer vers notre oeil aucun de ses rayons, tandis qu'au contraire celles situées à l'extérieur de cet angle en laissent passer, comme cela sera démontré un peu plus loin [Fig. 1]. Or, | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 367]
| ||||||||||||||||||||||||||||||||||||||||||||||
gingh sien het geen des Cartes van de oorsaeck van diergelycke Coronae schrijft, te weten dat die voort komen van de sonnenstralen gerefringeert in seeckere platachtige sterreties van ijs, en dat daer van niet voldaen was, om dat daer uyt volgen moste, gelijck hij oock selfs seght dat de spatie van de ring besloten soude moeten klaerder sijn als de lucht daer buijtenGa naar voetnoot1), 't welck ick contrarie bevonden had.
§ 2. Ick dachte dan dat men een andere reden van dit meteorum most soecken, niet tegenstaende den selfden auteur seght dat wij geen andere oorsaeck in de wolcken konnen vinden die soo iets soude voortbrengenGa naar voetnoot2). Ick examineerde alle reflexien en refractien die de ☉ radij in water droppelties konnen lijden, doch vont niet dat daer enighsins een ring van dese maet uyt kon ontstaen. ick nam oock de vrijheijt van eenighe andere figuren van ijsdroppels te fingeren nae beliefte, maar al te vergeefs, soo moeijelyck is 't imaginem sibi fingere rei nunquam visae. Maer als ick nae 6 jaeren verloop wederom de selve gedachten begon te hervatten bij occasie van een phaenomenon van 5 sonnen te Warsau gesien ao 1658Ga naar voetnoot3) ende wel te letten op de gedaente van de Corona voors. is mij eijntelyck de waere oorsaeck in gevallen ende korts daer aen oock die van de parelia, waer van ick undique observatien had beginnen te vergaren. Non enim vereor veras eas [causas] dicere quae ita cum observatis conveniuntGa naar voetnoot4) ut operam mihi perditurus videar si quas alias requisivero. als ick dan bedacht dat eenighe kleijne deelties in de wolcken vliegende, materie mosten suppediteren aen dese meteora, want dat bleeck genoegh om dat de wolcken vervliegende den ring nochtans op de selve plaets was blijven staen, en datGa naar voetnoot5) de duysterheyt van het rond in den ring begrepen argumento esset dat die deelties aldaer zijnde de sons straelen niet soo wel en laeten passeren dan alsse buyten dien hoeck vervlogen sijn, soo quam mij schielyck te voorenGa naar voetnoot6) dat dit kon gebeuren indien ieder deser deelties een ronde kerrel waer van klaer ijs of wel water buyten om en met een min transparent kerreltie van binnen in, want groote menichte van sulcke deelties alle eveleens gemaeckt tusschen ons oogh en de son vliegende soo verstond ick lichtelijck dat die van haer die binnen een seeckeren hoeck van de ☉ afstonden geen van sijn straelen nae ons oogh lieten komen, maer wel de andere buyten den selven hoeck gelegen, gelijck terstond bewesen sal werden [Fig. 1]. datter nu sulcke hageldroppelen reipsa in de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 368]
| ||||||||||||||||||||||||||||||||||||||||||||||
l'existence de pareils grêlons dans les nuages n'est pas seulement probable mais absolument certaine, attendu qu'il en tombe quelquefois sur la terre comme Descartes le témoigne dans ses Météores, car là, parlant de leur génération, il dit: ‘..... D'où vient que le dehors de chasque grain de cette gresle, estant ordinairement composé d'une glace continuë & transparente, il y a dans le milieu un peu de neige, ainsi que vous pourrés voir en les cassant’Ga naar voetnoot1). Et personne ne doit trouver étrange que les petites sphères de neige se maintiennent au centre de l'eau, car on doit considérer que l'eau, attendu que les gouttes entières sont soutenues par les vapeurs montantes, n'a point d'inclinaison à quitter en tombant les noyaux centraux, lesquels, étant de même densité que l'eau, ne sont eux aussi nullement portés à quitter le centre des gouttes en s'y élevant ou en y descendant. D'ailleurs les grêlons tombés sur terre, dont nous avons parlé, montrent clairement qu'il en est ainsi. Mais il faut à mon avis, que les gouttes entières soient fort petites, de la grandeur des graines de navette peut-être ou encore moindres, pour pouvoir être soutenues par les vapeurs. Laquelle petitesse n'empêche pas toutefois la perfection de la forme, ni celle de la proportion, dont je traiterai, de l'épaisseur des gouttes entières à celle du noyau central. Ayant donc constaté que de pareilles particules ou corpuscules mixtes sont engendrés dans l'air, je veux faire voir comment ils produisent le phénomène de la couronne.
§ 3. À cet effet, nous représenterons une de ces gouttes à grande échelle afin d'y pouvoir indiquer la réfraction des rayons solaires. Soit donc ABCD [Fig. 2] cette goutte avec un noyau de neige EF au milieu. Supposant alors que les rayons solaires tombent sur la goutte du côté GH, nous savons qu'ils sont d'abord réfractés par la surface AD et pénètrent dans l'intérieur en suivant à partir de la surface une direction plus voisine de la normale, d'où résulte nécessairement qu'une grande partie des rayons est arrêtée par le noyau de neige EF. Puissent les rayons GA et HD, réfractés en AB et DC, friser le noyau EF susdit. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 369]
| ||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 1.]
wolcken gevonden werden is niet alleen waarschijnelijck maer plane certum dewijl die somwijlen op d'aerde nedervallen gelijck Des Cartes getuijght in Meteoris namque ibi de generatione eorum locutus. Hinc fit inquit ut cum exterior superficies cujuslibet grani ex glacie continua et pellucida constare consueverit in ejus tamen centro nonnihil nivis saepe reperiatur, quod haec grana frangentibus sese offertGa naar voetnoot1). nec mirum cuiquam videri queat hoe de sneeubolleties midden in 't water blijven sitten, want ze moeten dencken, dewijl de heele droppelen, van de vapeuren van beneden komende, opgehouden werden, dat het water geen conatus en 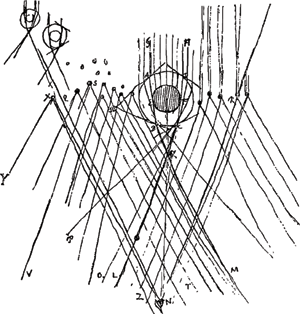 [Fig. 2.]
heeft om af te vallen en de middelste kernen te verlaeten, dewelcke oock evenwichtigh met water sijnde geen reden hebben om van het center der droppelen opwaerts of neerwaerts te sacken. atque haec saltem ita se habere grana illa glaciata in terram delata clare demonstrant. doch de gansche droppelen moeten mijns oordeels seer kleijn sijn gelijck als raepsaedt misschien of noch minder om van de vapeuren om hoogh gehouden te konnen werden. Welcke kleynicheijt nochtans niet en beletGa naar voetnoot2) de perfectheijt van de figuer noch van de proportie tusschen de dickte van de heele droppels tot die van de middelste kern. van welcke proportie mede ick sal disquire[re]. gesien hebbende dan datter sulcke corpuscula mixta in de lucht gegenereert werden soo wil ick thoonen hoe dat dese de apparentia van de corona veroorsaecken.
§ 3. In quem finem soo sullen wij een van dese droppelen in 't groot verthonen om der sonnen stralen refractie daer in te konnen aenwijsen. dese droppel sij dan ABCD [Fig. 2], met een kerrel van sneeuw in midden EF. Stellende dan dat de stralen der sonne vallen van de sijde GH, soo weten wij dat die eerst op de superficies AD gerefrangeert werden, ende van daer binnenwaerts gebogen, waer door nootsaeckelyck moet geschieden dat een groot deel derselve komt te steuyten tegens de sneeuwkerrel EF. doch laet het de stralen GA′ en HD sijn | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 370]
| ||||||||||||||||||||||||||||||||||||||||||||||
Ces rayons sont réfractés de nouveau aux points B et C, après quoi ils convergent, se coupant en K, point situé à une distance de moins d'un demi-diamètre de la goutte ABCD, comme cela a été démontré dans la Prop. XIII de la DioptriqueGa naar voetnoot1). Les droites BK et CK étant prolongées jusqu'en M et L il s'ensuit qu'en quelque lieu à l'intérieur de l'angle ou, pour mieux dire, du cône LKM, que l'oeil soit placé, il ne peut percevoir aucune clarté venant du soleil à travers la sphère ABCD, puisque tous les rayons qui passent à côté du noyau EF se coupent sous un plus grand angle et plus près de la sphère ABCD, de sorte qu'ils tombent en dehors du cône LKM, comme cela est également démontré dans la Dioptrique. Mais lorsque l'oeil du spectateur qui se trouve au-dessous de la goutte est placé en dehors de ce cône, p.e. en O ou en P ou ailleurs, des rayons de soleil l'atteignent et lui font apercevoir son image dans la goutte. Or, comme cela a lieu dans cette goutte, ainsi en arrive-t-il à toutes ses pareilles: chacune d'elles a derrière soi un cône d'ombre tel que, lorsqu'on s'y trouve, on ne peut percevoir de rayons solaires (je veux dire de rayons solaires ayant passé par cette goutte), mais qu'on en reçoit dans l'oeil du moment qu'on se trouve tant soit peu en dehors du cône. Supposons maintenant que l'oeil soit en N et considérons un cône dont le sommet soit également en N et qui ait ses génératrices NR et NQ parallèles à KL et KM, génératrices du cône LKM: il est certain qu'aucune goutte à noyau, telle que ABCD, se trouvant à l'intérieur du cône QNR ne peut diriger les rayons du soleil vers l'oeil N. En effet, lorsqu'on tire de quelqu'une de ces gouttes, telle que S, deux droites parallèles à KL et KM, telles que SV et ST, lesquelles représentent dans ce plan les génératrices du cône d'ombre qui se trouve derrière la goutte S, il apparaît que l'oeil N qui constitue le sommet du cône QNR tombe à l'intérieur du cône susdit VST et ne reçoit donc point de rayons du soleil ayant traversé la goutte S. Et il en est de même de toutes les gouttes à l'intérieur du cône QNR, car l'oeil N se trouve à l'intérieur des cônes correspondant à chacune d'elles, comme cela ressort clairement de cette figure.
§ 4. Mais si l'on considère une goutte quelconque extérieure au cône QNR telle que X, et son cône YXZ, il est manifeste que l'oeil N tombe en dehors de lui; c'est pourquoi des rayons du soleil ayant passé par la goutte X frapperont l'oeil, de sorte | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 371]
| ||||||||||||||||||||||||||||||||||||||||||||||
welcker refractien AB, en DC even passeren voorbij de voorn. kerrel EF. dese dan werden in B en C noch eens gebroocken, en loopen dan tot malkander, kruyssende sich in K welck punct wat min als een halve diameter lenghde van den drop ABCD af staet, gelijck Dioptricae, P. 13 gedemonstreert isGa naar voetnoot1). sijnde dan BK en CK verlenght naer M en L soo volght dat op wat plaets binnen den hoeck, ofte om recht te seggen, binnen de Conus LKM het oogh gestelt werdt, het selve geen klaerheijt van de son door sphaera ABCD kan vernemen, dewijl alle radij die nevens de kerrel EF passeren, sich in grooter hoeck kruijssen en dichter aen de sphera ABCD, soodat se buyten de conus LKM vallen, gelijck mede in DioptricisGa naar voetnoot2) geprobeert wert. Maar buijten dese conus als in O of P of waer 't soude mogen sijn, beneden den drop het oogh gestelt sijnde, soo komen daer stralen van de son en maecken dat men sijn schijnsel in den drop gewaer wert. Gelijck nu in dese droppel geschiet van gelijcken is het met alle die van 't selfde maecksel sijn, te weten dat ieder een van haer soo een umbrosum conum achter sich heeft daer men binnen sijnde geen straelen van de son en kan sien, (ick segh van die door de druppel heen passeren) maer even daer buijten altijdt soodanighe stralen in 't oogh krijght. Genomen nu dat het oogh sij in N en dat men een Conus imaginere wiens top sij N ende sijn sijden NR, NQ parallel met KL KM de sijden der conus LKM, het is seecker dat geene droppels met kerrels, gelijck ABCD, die binnen den geheelen Conus QNR gevonden werden de radios solis na het oogh N dirigeren konnen. Want als men uijt eenighe deser droppels als S twee linien treckt evenwijdigh met KL, KM, als SV, ST, dewelcke in dit vlack representeren de syden van de conus umbrosus achter den drop S, soo blijck dat het oogh N ofte den top van de conus QNR valt binnen de voorseijde conus VST, en dienvolgens geen straelen van de son ontfanght dergener die door den drop S passeren. En van gelycken is het met al de droppels binnen de conus QNR, want het oogh N staet binnen ieder van haer coni, gelijck uyt dese figuer manifest is.
§ 4. Maer indien men eenige droppel considereert die buijten de conus QNR sij als X, ende sijn conus YXZ, het is klaer perspicuum dat het oogh N daer buyten gevalt, en daerom sullender radij van de son door den drop X komende daer op strae- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 372]
| ||||||||||||||||||||||||||||||||||||||||||||||
que cette goutte paraîtra éclairée et toutes les autres en dehors du cône QNR de même, tandis que celles situées dans le cône seront bien plus obscures puisqu'elles ne présenteront pas d'image du soleil. Il est évident d'après ces considérations qu'il doit apparaître une aire ronde obscure autour du soleil, tandis que ce qui est situé en dehors du contour de cette aire sera plus lumineux, surtout les parties avoisinantes, parce que les gouttes très voisines du cône QNR donnent la plus grande image du soleil, comme on pourrait aisément le démontrer. Il apparaît en outre que pour chaque hauteur du soleil une couronne peut être produite de la même manière, savoir par la forme sphérique tant des gouttes entières que de leurs noyaux centraux. Que si quelqu'un désire se représenter ce phénomène aussi par expérience, qu'il prenne un bocal en verre mince et qu'il le remplisse d'eau après avoir placé en son centre une boule opaque, ce qu'il trouvera bien moyen de faire. Tournant cette sphère vers le soleil on constatera qu'on n'y voit aucune lumière solaire à moins que de l'écarter à une certaine distance de la droite qui va de l'oeil au soleil; on remarquera de plus en exécutant ce mouvement qu'à l'endroit même où l'on voit apparaître le soleil, son image est la plus lumineuse, et dans cette expérience aussi on apercevra la couleur rouge, laquelle doit être vue ici pour la même raison que dans le cas d'un prisme de cristal ou plutôt d'eau, si l'on pouvait en faire un de ce dernier genre, quisque le rayon GA par exemple souffre la même réfraction en entrant dans la goutte en A et en en sortant en B que s'il passait par le prisme A ☊ B dont les côtés A ☊ et B ☊ touchent la goutte en A et B. Et le noyau EF qui limite la lumière d'un côté contribue aussi à colorer les rayons tels que AB qui le frisent. Mais quant à examiner plus à fond l'origine de ces couleurs et établir pourquoi elles sont engendrées dans un prisme, c'est ce que je ne veux nullement entreprendre; j'avoue au contraire en ignorer absolument la cause et je pense que personne ne comprendra aisément leur nature tant qu'une plus grande lumière n'aura pas éclairé la science des choses naturelles. Je désire seulement faire remarquer que la couleur rouge qui apparaît dans cette sphère doit aussi être vue dans les gouttes susdites situées tout juste en dehors du cône QNR et qu'en diminuant d'intensité dans les gouttes situées à plus grande distance elle produit aussi les autres couleurs comme cela arrive de la même manière dans le cas de l'arc-en-ciel. Aussi loin que ces couleurs s'étendent (il s'agit de la région où se trouvent les gouttes les plus éclairées) aussi large cet anneau ou couronne est censé être; en réalité toutefois il n'est terminé qu'à l'intérieur, c.à.d. du côté du soleil, et non pas extérieurement. C'est ce qui a lieu aussi chez l'arc-en-ciel: il apparaît par l'explication de Descartes que cet arc n'est également terminé que du côté de la couleur rouge. Souvent aussi ces couronnes sont vues autour de la lune pour la même raison que | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 373]
| ||||||||||||||||||||||||||||||||||||||||||||||
len, soo dat dien droppel verlicht sal schijnen, en van gelycken al d'andere buyten de conus QNR, daer die daer binnen sijn veel duysterder sullen sijn als geen imaginem solis hebbende. Patet itaque ex his rotundam apparere debere aream circa solem obscuram, quae vero extra areae ambitum sunt luminosiora, et maximè quidem quae proxime eam ambiunt, om dat de droppels die naest buyten aen de conus QNR leggen, de grooste imaginem solis exhiberen, als licht waer te bewijsen. Patet etiam in qualibet altitudine solis eodem modo coronam produci posse ob sphaericam nimirum cum guttarum totarum tum nucleorum intus positorum figuram. Quod si veroGa naar voetnoot1) et experimento sibi phaenomenon hoc repraesentare voluerit, die neme een bol van dun glas en die met water vullende en stellende daer in midden een bol die niet transparent is, waer toe wel middel is te vinden, men sal bevinden als men die nae de son toe keert dat men geen schijnsel van de son daer in sal sien dan als mense een stuck weeghs buijten de linie die van het oogh nae de son streckt amoverit, ende gekomen sijnde even daer men de son daer door kan sien dat sijn imago daer alder klaerst is, en men sal oock hier de roode couleur gewaer werden, dewelcke hier door de selve reden moet gesien werden als in een prisma crystallinum, of liever aqueum indien men soo een konde maecken, want den radius GA bij exempel lijdt even de selve refractie in 't inkomen van den drop in A en in 't uytkomen in B, als hij soude doen passerende door het prisma A ☊ B, wiens sijden A ☊ en B ☊ den drop raecken in A en B. Ende de kerrel EF die het licht aen d'eene sijde termineert, contribueert mede tot het coloreren van de radij als AB die daer naest by heen passeren. Doch de reden van dese couleuren verder te ondersoecken, te weten waerom die in een prisma gegenereert worden, wil ick geensins ondernemen, imo fateor rationem eorum me prorsus ignorare, neque facile quemquam ipsas perspecturum arbitror quandiu naturalium rerum scientiae major aliqua lux non affulserit. Alleenlick wil ick dat men aenmercke dat de rode couleur die in dese sphaera gesien wert oock in de voors. droppels die even buyten de conus QNR liggen moet gesien werden, de welcke in de verder afgelegen droppels verminderende oock de andere voortbrenght gelijck oock in den regenboogh geschiet. Ende soo veer als dese couleuren strecken, dewijl te gelyck oock hier de meest verlichte droppels sijn, soo breedt werdt den ringh ofte corona geoordeelt te wesen, dewelcke alioqui in der daet alleen aen de binnen kant nae de son toe getermineert is, en niet aen d'andere buijtenste. het welck mede van gelycken in den regenboogh geschiet, want die mede als uyt Descartes explicatie blyckt alleen aen de syde van de roode couleur getermineert is. Dese coronae worden oock om de maen dicmaels gesien, even door de selfde retenGa naar voetnoot2) als om de son, doch veeltijts sijn die soo | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 374]
| ||||||||||||||||||||||||||||||||||||||||||||||
dans le cas du soleil, mais généralement les couronnes lunaires sont si peu colorées qu'elles ne paraissent que blanches. C'est ce que j'ai aussi plusieurs fois remarqué chez les couronnes solaires et dans ce cas on distingue à peine la teinte de l'aire intérieure, tant soit peu plus obscure, de celle du ciel extérieur plus clairGa naar voetnoot1). Ceci s'explique par la petite quantité des grêlons en question, car plus il y en a plus les couronnes paraissent belles, comme on peut le constater par l'observation de Golius mentionnée ci-après ainsi que par celle de Lesna: on y voit clairement que là où l'aire intérieure à la couronne est la plus obscure, c.à.d. où l'essaim des grêlons est le plus dense, là aussi la couronne qui borde cet espace présente les plus belles couleurs. Mais c'est pour une autre raison encore que les couleurs les plus belles et les plus vives sont vues dans ces couronnes-là qui apparaissent simultanément avec les parhélies ou parasélènes; je ferai connaître cette raison lorsque je traiterai de ces derniers phénomènes.
§ 5. Considérons maintenant la grandeur du diamètre de la couronne dont nous disions qu'il est généralement de 45oGa naar voetnoot2). Il apparaît que ce diamètre dépend de la grandeur du noyau opaque EF. Car plus celui-ci est grand en comparaison avec la goutte entière AC, plus aussi sera grand l'angle BKC [Fig. 2, Fig. 3] auquel est égal l'angle du cône QNR [Fig. 2] lequel détermine le diamètre de la couronne comme cela a été suffisamment démontré. Je dis donc que le diamètre du noyau opaque etc. Tirons en effet (outre les rayons HDCK et GABK qui passent par la goutte et touchent le noyau en E et en F) à partir du centre M la droite MKO passant par leur intersection K et rencontrant en O le prolongement de la droite DG. Puissent HD et KC prolongées à l'intérieur de la goutte se couper en L. Alors les angles D et C du triangle DLC sont égaux parce que le rayon HD est également réfracté en entrant la goutte en D qu'en en sortant en C; or, l'angle DOK est égal à l'angle D puisque HL et MO sont parallèles. Par conséquent les angles O et C seront aussi égaux entre eux dans le triangle CKO. Mais l'angle CKM, moitié de l'angle CKB, est égal à la somme des angles O et C. Comme l'angle BKC doit être de 45o, sa moitié MKC sera de 22½o et la moitié de ce dernier, l'angle O, de 11o15′. Dans le triangle OMF, ayant un angle droit en F, le rapport des côtés est donc donné, et si l'on attribue 100000 parties au rayon OM, MF, sinus de 11o15′, en aura 19509, et OF 98078. D'autre part le rapport OM: OD est donné: c'est celui qui mesure les réfractions de l'eau comme cela a été démontré dans la Prop. 8 de la DioptriqueGa naar voetnoot3), savoir 187 : 250. Puisque OM a par hypothèse 100000 parties, OD en aura 133690 et en en retranchant les 98078 parties de OF il reste FD = 35612. Mais MF était | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 375]
| ||||||||||||||||||||||||||||||||||||||||||||||
weynigh gecouleurt dat alleen wit schijnen. gelyck ick mede dickwils in die om de son geobserveert heb quando etiam vix obscurior intra circulum area ab reliquo clariore discerniturGa naar voetnoot1). Dit gebeurt door de weynigh materie van sulcke grana, want hoe deser meer is hoe de coronae schoonder gelijckenen, gelijck te sien is uit de observatie van Golius, hier achter, en die van Lesna, want men daer klaerlyck siet dat daer de area intra coronam donckerste is hoc est ubi maxime conferta granorum multitudo dat daer neffens de corona oock schoonst gecouleurt is. Doch noch om een andere oorsaeck werden de schoonste couleuren autem ende levendighste in de coronae gesien die te gelyck met parelia of paraselene apparent, waer van ick de reden sal seggen ubi ad illas ventum erit. § 5. De diametro vero coronae porro nunc videamus, quam frequentissime 45o esse dicebamusGa naar voetnoot2). Hanc autem manifestum est pendere ex magnitudine grani opaci 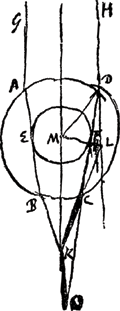 [Fig. 3.]
EF. Want hoe grooter dat het is tegens de heelen droppel AC te reeckenen soo veel te grooter sal oock sijn den hoeck BKC [Fig. 2, Fig. 3] aen wien gelyck is den angulus coni QNR die den diameter determineert van de Corona als genoegh is bewesen. Ick segge dan dat den diameter van het granum opacum &c. Want laet behalven de radij HDCK, GABK die door den droppel ABCD passeren en de kerrel aenraecken in E en F, getrocken werden uijt het center M de rechte linie MKO passerende door haer intersectie K, en concurrerende met de verlenghde rechte DC in O. laet oock HD en KC binnen den droppel verlenght sich ontmoeten in L. In den triangel DLC dan sijn de hoecken D en C gelyck door dien den radius HD in 't inkomen van den droppel in D even soo veel gerefringeert wert als in 't uytgaen in C. angulo autem D aequalis est angulus DOK, quia HL, MO sunt parallelae. Ergo in ∆CKO aequales quoque erunt anguli O et C, hisce vero duobus aequatur ang. CKM, dimidius anguli CKB. dewijl dan den hoeck BKC van 45o moet sijn, soo sal sijn helft MKC sijn van 22½ gr. en dese sijn helft den hoeck O van 11o15′. In ∆o igitur OMF rectum angulum F habente data est ratio laterum, sumptaque OM pro radio partium 100000, erit MF sinus 11o15′, partium 19509, et OF 98078. Datur autem et ratio OM ad OD quae est ea quae refractiones aquae metitur ut ostensum prop. 8. dioptricorumGa naar voetnoot3), nimirum 187 ad 250. cum ponatur ergo OM 100000, erit OD 133690 a qua si auferatur OF 98078 relin- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 376]
| ||||||||||||||||||||||||||||||||||||||||||||||
de 19509 parties. Par conséquent, le rapport des côtés nommés du triangle rectangle MFD étant connu, celui de chacun d'eux au côté MD le sera aussi et ce dernier sera trouvé être de 40605 parties. Le rayon MD de la goutte doit donc être au rayon MF du noyau de neige dans le rapport 40605 : 19509 ou approximativement 1000 : 480 pour que le diamètre de la couronne devienne égale à 45o. On trouvera de la même manière que pour faire en sorte que le diamètre de la couronne soit de 90o, le rapport MD : MF doit avoir la valeur 1000 : 680Ga naar voetnoot1).
§ 6. Au sujet de la genèse des grêlons semiaqueux il faut admettre que ce soient primitivement de petits globules de neige fine, lesquels s'arrondissent en voltigeant dans l'air. Ces globules se liquésient extérieurement jusqu'à une certaine profondeur par la chaleur du soleil. Il faut prendre en considération que l'air, pour que les couronnes apparaissent, doit se trouver dans un certain état tempéré entre le froid et le chaud, de sorte que les grêlons ne viennent à dégeler qu'à peine et lentement. Et dès qu'ils sont exposés à un froid tant soit peu plus intense ils ne se liquéfient pas davantage. Mais lorsqu'ils ont été liquéfiés jusqu'à la moitié de leur épaisseur ou un peu plus, le cône des rayons réfractés à l'intérieur de la goutte empêche leur regel par sa chaleur, même lorsque la goutte traverse une région plus froide. Par cette chaleur qui est la plus intense vers le sommet du dit cône le noyau de neige non transformée est également arrondi parce que la goutte tourne tantôt un côté tantôt l'autre vers le soleil ou bien parce que la chaleur du cône [Fig. 4] se répand dans toute la goutteGa naar voetnoot2). Cette forme sphérique est nécessaire pour que la couronne apparaisse. Or, il est sans doute évident que beaucoup de gouttes se liquésient davantage ou au contraire moins, mais puisque leurs noyaux centraux ne sont pas arrondis elles ne peuvent produire aucun effet collectif. Et peut-être, par l'effet de cette même chaleur, le froid est-il concentré dans une plus grande mesure au milieu de la goutte (en hiver on voit arriver la même chose en diverses façons) de sorte que le noyau est empêché de se liquéfier davantageGa naar voetnoot3). Car il faut savoir que le moindre empêchement d'un côté ou de l'autre suffit, dans l'état tempéré de l'air dont nous avons parlé, pour maintenir ces grêlons dans leur état de liquidité partielle. Je suppose ici que la partie extérieure des petites sphères soit formée par de l'eau, parce que cela est quelque peu plus probable; en effet, de cette façon la surface devient plus unie et plus capable, semble-t-il, que lorsqu'elle est de glace de produire certaines réfractions. Toutefois il peut également arriver parfois que les grêlons formés comme il a été dit viennent à congeler et peut-être cette eau gelée est-elle néanmoins encore assez limpide et assez parfaitement sphérique pour produire la couronne. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 377]
| ||||||||||||||||||||||||||||||||||||||||||||||
quitur FD 35612. Sed MF erat 19509. Itaque cognita horum laterum proportione in triang. rectango MFD, dabitur etiam utriusvis ratio ad latus MD idque invenietur partium 40605. debet itaque semidiameter guttae MD ad MF semidiam. nuclei nivalis se habere ut 40605 ad 19509, seu proxime ut 1000 ad 480 ut fiat coronae diameter gr. 45. Op de selfde manier sal men vinden dat om den diameter van de Corona van 90 gr. te maecken de reden van MD tot MF moet sijn als 1000 tot 680Ga naar voetnoot1). § 6. Circa generationem grandinis semiaqueae considerandum dat het eerst bolleties van fijne sneeuw sijn, die door het vliegen door de lucht rondachtigh werden. Dese werden door de warmte der son van buijten een stuckweeghs gesmolten. Dat de lucht een seeckere getempertheijt tusschen koude en warmte moet hebben als de coronae gesien werden, soo dat de grana maer even en langhsaem komen te smelten. En alsser wederom maer een weynigh meer koude overkomt, soo smeltense niet verder. Doch gesmolten sijnde tot op de helft van haer dickte of een weijnigh verder soo belet de Conus van de gereflecteerde radij binnen den droppel door sijn warmte dat se niet weer verder bevriesen en kan, alhoewel in meerder koude komt. door welcke warmte die de grootste is ontrent de punt van de voors. conus oock de resterende kern van sneeuw rond gemaeckt werdt dewijl den droppel nu d'een nu d'ander sijde na de son toe keert of wel dat de warmte van die conus [Fig. 4] sich rontom  [Fig. 4.]
den drop verspreijtGa naar voetnoot2). welcke rontheijt tot het verschijnen van de Corona gerequireert is. want apparent oock wel veel droppen verder of minder smelten, maer der selver binnen kernen niet gerondt werdende soo en connense te saemen geen effect doen. En misschien soo wert door dese selfde warmte de koude te meer int midden van den droppel geconcentreert (gelijck men het selfde in verscheijde manieren des winters siet gebeuren) en daer door belet dat de kern oock niet licht verder en dooijtGa naar voetnoot3). Want men moet weten dat de minste tegenstant van d'een en d'andere sijde in de voors. getempertheijt des luchts, genoegh is om dese droppels aldus half ontdooijt te onderhouden. Ick stelle dat het buytenste deel der bolleties water sij, om dat eenighsins waerschijnelijcker is, want daer door de superficie effenderGa naar voetnoot4) werdt en bequaemer om seeckere refractien te maecken, dan als se van ijs sijnde schijnt te konnen. Doch evenwel soo kan oock wel somtijdts gebeuren dat de grana als voren geformeert sijnde komen te bevriesen, en misschien is dat bevroren water daer om noch klaer genoegh en perfect van figuer om de corona te maecken. Den droppel | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 378]
| ||||||||||||||||||||||||||||||||||||||||||||||
Outre la concentration des rayons qui fait fondre les gouttes jusqu'à la profondeur nommée, une autre concentration encore se produit, comme on peut le voir dans la goutte susdite de ....Ga naar voetnoot2), par l'effet de laquelle les noyaux de neige peuvent être arrondis et conservés dans un état de grandeur supérieur, par rapport à la goutte totale, à celui considéré précédemment; ces gouttes-là font apparaître une deuxième couronne, ayant un diamètre double environ de celui de la première: on verra ci-après qu'elle a été parfois observée. Cette concentration des rayons semble être la cause pour laquelle le plus souvent les couronnes sont aperçues avec de tels diamètres. Toutefois des couronnes de toutes sortes d'autres diamètres peuvent également apparaître, parce que, à ce qu'on peut se figurer, les gouttes continuent à fondre très lentement dans ce froid modéré et qu'une partie plus ou moins grande de chaque goutte étant liquéfiée, elles gardent assez longtemps à peu près la même proportion pour faire paraître durant quelques heures une couronne de diamètre sensiblement invariable. Et ainsi il peut arriver qu'un groupe de gouttes étant liquéfiées jusqu'à une certaine profondeur et un autre, voltigeant plus haut ou plus bas, jusqu'à une autre, et d'autres groupes encore dans une proportion différente, beaucoup de couronnes diverses viennent à se montrer, comme quelques auteurs racontent en avoir vu six en même temps ayant le soleil au centre. Snellius dans son livre de la Comète de 1618Ga naar voetnoot3).
§ 7. Après avoir examiné jusqu'ici les couronnes, nous devons maintenant traiter des parhélies et des parasélènes. Dans ceux-ci il y a à remarquer des choses bien plus nombreuses et plus étranges, comme on peut s'en faire une idée rien qu'en contemplant les figures qui suiventGa naar voetnoot5). Car outre de fort étranges circonférences de cercle on n'y trouve pas seulement les deux parhélies de part et d'autre du soleil auxquels seuls on a fait attention dans les siècles passés, mais au surplus encore 2 ou 3 ou même parfois 4 autres, comme dans le phénomène observé par Hevelius en 1661Ga naar voetnoot6). On peut se demander avec étonnement comment il se fait qu' AristoteGa naar voetnoot7), et Cardan encore | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 379]
| ||||||||||||||||||||||||||||||||||||||||||||||
met de radij verthoontGa naar voetnoot1) behalven nu de vergaringh van straelen die de droppels tot soo veer als geseght is doet smelten, wordt noch een andere vergaring gevonden als in den voors. droppel te sien is in ....Ga naar voetnoot2) door de welcke de kernen van sneeuw grooter als de voorgaende, nae proportie van den heelen droppel, geconserveert konnen werden en rond gemaeckt, door welcke droppels een tweede corona komt te verschijnen hebbende den diameter ontrent 2 mael soo groot als de eerste, welcke oock somtijdts geobserveert is als hier naer sal gesien werden. Dat dese vergaringh van radij de reden schijnt te sijn waerom dat de meesten tijdt de Coronae op sulcke diameters gesien werden, maer dat oock wel Coronae van andere allerhande diameters konnen gesien werden dewijl men mach concipieren dat de droppels in die matighe koude seer langhsaem voortsmelten, ende, een meerder of minder deel daer van gesmolten sijnde, langh genoegh ontrent de selfde proportie blijven, om een Corona sonder sensible verandering van diameter voor eenige uren te doen verschijnen. En hier door kan het gebeuren dat een partij droppels tot een seeckere diepte gesmolten sijnde ende een andere die wat hooger of laeger vliegen weer op een andere diepte, en noch andere partijen op andere proportie, veel verscheyde coronae sich komen te verthoonen gelijck bij sommighe verhaelt wert van 6 te gelijck gesien te hebben die de son tot center hadden. Snellius in libro de Cometa. Ai 1618Ga naar voetnoot3).
§ 7. Dus verre van de Coronae ondersocht hebbende soo sullen wijGa naar voetnoot4) deinceps de Parelijs ac paraselenis agendum est. Waer in veel meer en wonderlycker dingen sijn aen te mercken, gelijck men kan oordelen als men alleen de figuren hier achter geinsereert nae sietGa naar voetnoot5). want behalven de circels die seer vreemt sich verthoonen soo vindt men daer niet alleen de 2 parelia aen weder sijden vande son, die in vorige saecula alleen zijn aengemerckt maer daer en boven noch 2 of 3 of somtijdts noch 4 andere gelijck in dat van Hevelius ao 1661Ga naar voetnoot6). Mirum autem videri potest hoe het komt, dat | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 380]
| ||||||||||||||||||||||||||||||||||||||||||||||
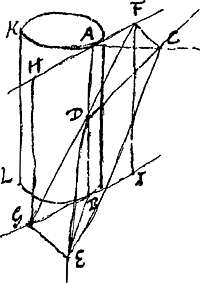
plusieurs siècles après luiGa naar voetnoot2), écrivent que jamais plus de deux parhélies n'ont été vus simultanément, car il est incroyable que ce qui maintenant est arrivé plusieurs fois en peu d'années, savoir que 5, 6 ou 7 parhélies ont été vus simultanément, n'aurait pas eu lieu auparavant en tant de fois cent ans. La raison en est peut-être celle-ci que les deux parhélies à côté du soleil qui sont toujours les plus resplendissants, ont été seuls pris en considération par les observateurs ignorants et comptés pour soleils adjoints; en effet les autres paraissent le plus souvent faibles. Mais aujourd'hui tous les ‘soleils’ qui occupent une place bien déterminée sont appelés parhélies par les observateurs consciencieux, même s'ils ont si peu d'éclat que les ignorants pourraient les considérer comme de petits nuages. Or, quoiqu'il se trouve une grande diversité dans ces phénomènes, il y a pourtant aussi quelques côtés par où ils se ressemblent tous; c'est pourquoi il me semble le mieux de traiter d'abord d'un des principaux phénomènes qui est tel qu'en découvrant et expliquant ses causes je pourrai parler en même temps des autres pour autant qu'ils ont quelque chose de commun avec lui. Nous considérerons ensuite l'un après l'autre ce qui se remarquera de nouveau dans chacun des autres phénomènes. Proposons-nous donc l'examen du phénomène de Rome observé le 20 mars de l'année 1629 par Chr. Scheiner et traité un peu plus tard par Descartes et GassendGa naar voetnoot5); je place ici la figure [Fig. 5] ainsi que la description tirées de leurs livresGa naar voetnoot6).
§ 8. A est l'observateur de Rome, B son zénith, C le vrai soleil aperçu par lui. AB est le plan vertical dans lequel se trouvent l'oeil de l'observateur et le soleil, ainsi que le zénith. Tout ceci est donc représenté par la droite verticale AB; c'est suivant cette droite que le plan vertical se projette sur le plan du papier. Autour du soleil C apparurent deux iris incomplètes ayant l'une et l'autre le même centre que le soleil et présentant diverses couleurs. La plus petite, ou l'intérieure, DEF était plus vive et plus parfaite, quoiqu'elle fût ébrèchée ou ouverte de D à F tout en cherchant continuellement à se fermer; elle se fermait même parfois, mais s'ouvrait bientôt de nouveau. L'autre, GHIGa naar voetnoot7), extérieure et secondaire, était toujours faible et à peine visible; | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 381]
| ||||||||||||||||||||||||||||||||||||||||||||||
AristotelesGa naar voetnoot1) en noch soo veel eeuwen naer hem CardanusGa naar voetnoot2) schrijven dat noijt meer als 2 parelia 't seffens gesien sijn, want hetgeen nu in korte jaren meermaels gebeurt is, te weten datter 5 6 of 7 parelia gesien sijn op een tydt, het is niet te gelooven dat het te vooren in soo veel hondert jaeren niet soude gebeurt sijn. doch de reden mach sijn dat de 2 parelia neffens de son, die altijdt de sterckste schijn hebben alleen sijn aengemerckt geweest door de onkundige observ. en voor bysonnen gerekent want de andere meesten deel flaeuw schijnen, doch door de neerstige waernemers worden het nu al parelia geheten, die maer een seeckere plaets hebben, al hebben se soo weijnigh glans dat de onwetende die maer voor wolckjes souden rekenen. Alhoewel nu vele verscheijdenheijt in deselve gevonden werdt, soo sijn nochtans oock eenighe dingen waer in d'eene d'andere gelycken daerom dunckt my best dat ick eerst onderneme van een der principaelste phaenomena te verhandelen, wiens oorsaecken terwijl ick ontdecke en uytlegge, oock tegelijck van d'andere sal spreecken voor soo veel als sij met dit phaenomenon iets gemeens hebben. quae autem praeterea nova in caeteris offerentur, ea sigillatim postea excutiemusGa naar voetnoot3). Proponatur itaque Phaenomenon Romanum Ao. 1629. die 20 Martij a .....Ga naar voetnoot4) Scheinero observatum de quo circa id tempus Cartesius GassendusqueGa naar voetnoot5) egerunt, è quorum libris petitam cum descriptione figuram [Fig. 5] oculis hic subjicioGa naar voetnoot6).
[§ 8.] ‘A observator Romanus. B vertex loco obseruatoris incumbens. C sol verus obseruatus. AB planum verticale, in quo & oculus obseruatoris, & sol obseruatus existunt, in quo & vertex loci B iacet. ideoque omnia per lineam verticalem AB repraesentantur: in hanc enim totum planum verticale procumbit. Circa Solem C apparuere duae incompletae Irides eidem homocentricae, diuersicolores, quarum minor siue interior DEF plenior & perfectior fuit, curta tamen siue aperta à D ad F, & in perpetuo conatu sese claudendi stabat, & quandoque claudebat, sed mox denuo aperiebat. Altera, sed debilis semper & vix conspicabilis, fuit GHIGa naar voetnoot7), exterior & secundaria, | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 382]
| ||||||||||||||||||||||||||||||||||||||||||||||
cependant celle-ci aussi était diversement colorée, quelqu'instable qu'elle fût. Il existait une troisième iris fort grande et unicolore, KLMN, toute blanche, comme on en voit souvent autour de la lune dans le cas de parasélènes: c'était un anneau complet dès le commencement, n'ayant pas le soleil pour centre mais passant par lui; toutefois sa partie extrême, de M à N, était pâle et pleine de lacunes, même à peu près nulle. De plus aux points d'intersection de cet anneau avec l'iris extérieure GHI, apparaissaient deux parhélies plus ou moins imparfaits, N et K, dont le dernier brillait plus faiblement, mais le premier avec un éclat plus fort et plus vif: leur éclat moyen rivalisait avec celui du soleil. Cependant leurs bords présentaient des couleurs d'arc-enciel, et leurs contours n'étaient pas ronds et nets, mais inégaux et pleins de lacunes. N, spectre inconstant, jetait, non sans balancements, une large queue plus ou moins lumineuse NOP. De l'autre côté du zénith B se trouvaient L et M, moins brillants que les premiers, mais plus ronds; ils étaient blancs comme l'anneau sur lequel ils se trouvaient, d'une teinte de lait ou d'argent pur. Toutefois au milieu de la troisième heure M avait déjà à peu près disparu et ne montrait par après que de légères traces de son existence; d'ailleurs l'anneau lui aussi s'était évanoui en cet endroit. Le soleil N perdit sa force avant le soleil K, et tandis qu'il se dissipait, K se fortifiait. Ce sut donc K qui disparut le dernier de tous. Etc.
§ 9. Pour bien comprendre comment ce phénomène est apparu, il faut se représenter que la grande et blanche iris KLMN [Fig. 5] passant à travers le soleil véritable était un cercle parallèle à l'horizon dont le pôle B se trouvait par conséquent au zénith. Il est vrai que la figure semble indiquer que le spectateur était un peu plus proche du côté LM que du côté KN, mais il faut croire que ceci à été indiqué ainsi par erreur, puisque dans toutes les observations suivantes où un anneau blanc de cette espèce se présente et que sa position est marquée dans la figure, cet anneau est parallèle à l'horizon, quoiqu'il ne soit pas impossible qu'il ait une position légèrement oblique comme nous le démontrerons plus loinGa naar voetnoot1). Il faut donc se représenter le spectateur A debout au pied de la verticale du point B de telle manière qu'il regarde les soleils EGa naar voetnoot2), K, N et qu'il ait les deux autres L et M derrière lui.
§ 10. Il faut savoir en outre que les couleurs attribuées aux circonférences de cercle DEF et GKNI présentaient le même ordre que celles des couronnes susdites, c.à.d. que la couleur rouge se trouvait du côté du soleil; c'est ce qui paraît par la description de Scheiner du phénomène de 1630 sur lequel on peut consulter la suiteGa naar voetnoot3). | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 383]
| ||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 5.]
variegata tamen & ipsa suis coloribus, sed admodum instabilis. Tertia, & vnicolor, eaque valde magna Iris, fuit KLMN, tota alba, quales saepe visuntur in paraselenis circa lunam: haec fuit arcus excentricus, integer ab initio, solis per medium incedens, circa finem tamen ab M versus N debilis & lacer, imo quasi nullus. Caeterùm, in communibus circuli huius intersectionibus cum Iride exteriore GHI, emerserunt duo parhelia non vsque adeo perfecta, N & K, quorum hoc debilius, illud autem fortius & luculentius splendescebat; amborum medius nitor aemulabatur solarem, sed latera coloribus Iridis pingebantur; neque rotundi ac praecisi, sed inaequales & lacunosi, ipsorum ambitus cernebantur. N, inquietum spectrum, eiaculabatur caudam spissam subigneam NOP, cum iugi reciprocatione. L & M fuere trans Zenith B, prioribus minus viuaces, sed rotundiores & albi, instar circuli sui cui inhaerebant, lac seu argentum purum exprimentes, quanquam M mediâ tertiâ iam prope disparuerat; nec nisi exigua sui vestigia subinde praebuit, quippe & circulus ex illâ parte defecerat. Sol N defecit ante solem K, illoque deficiente roborabatur K, qui omnium vltimus disparuit’, &c.
§ 9. Om wel te begrijpen hoe dit phaenomenon sich vertoont heeft cogitandum est magnam eamque albam iridem KLMN [Fig. 5] per solem verum transeuntem fuisse circulum horizonti parallelum cujus polus fuerit punctum B vertici spectatoris superimminens. Want dat de figuer schijnt uyt te drucken dat de spectator wat naeder aen de kant LM als KN gestaen heeft, het is te gelooven dat dit bij abus alsoo geteyckent is geweest, dewijl in al de volgende observatien daer een diergelycke witten ringh komt ende sijn positus aengemerckt wert, den selven met den horizont parallel staet. Doch evenwel en is het niet onmogelijck dat hij een weynigh scheef leght gelyck wij hier naer sullen thoonenGa naar voetnoot1). Locus igitur van den spectator A moet bedacht werden te staen recht onder 't punt B, soo dat als hij sich keerde nae de sonnen EGa naar voetnoot2), K, N, dan de twee andere L en M achter hem hadde.
§. 10. Voorts soo is te weten dat de couleuren die de circels DEF en GKNI werden geseght gehadt te hebben, op gelycke ordre als die van de Coronae hier tevoren gemelt stonden, te weten de roode naest naer de son, als blijckt uijt de beschrijving van Scheijnerus van het phaenomenon des jaers 1630 (en hier naer te lesenGa naar voetnoot3)). Waer | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 384]
| ||||||||||||||||||||||||||||||||||||||||||||||
D'où il appert aussi que le diamètre de la circonférence intérieure a été de 45o environ ce qui est la dimension ordinaire des couronnesGa naar voetnoot1). Je crois cependant que dans le phénomène de 1629 le diamètre de la circonférence extérieure a été plus petit que celui de la circonférence extérieure dans le phénomène de 1630, comme il résulte de la figure et peut être démontré à son aide. A propos de cette figure nous devons encore remarquer que la queue du parhélie N s'étend le plus souvent le long de la circonférence KLMN comme Hevelius l'a mieux constaté dans son observation de 1661 insérée plus loinGa naar voetnoot2). Mais ici Scheiner l'a indiqué autrement dans la figure pour exprimer que la queue avait une direction opposée à celle vers le soleil. De plus les soleils et parhélies sont figurés beaucoup trop grands par rapport aux circonférences, et les lignes des circonférences sont beaucoup trop larges par rapport à leurs diamètres. Car pour représenter les choses fidèlement le diamètre du soleil ne devrait être que de 1/90 environ de celui de la couronne DEF vu que ce dernier était de 45o, et la largeur de la ligne de la circonférence KLMN aurait dû être environ égale au diamètre du soleil. En effet, de l'explication du phénomène de 1630 il ressort que la largeur nommée était même inférieure à ce diamètre.
§ 11. Examinous maintenant après nos remarques préalables sur la figure, les causes de ces étonnants spectacles. Je pus facilement comprendre que les gouttes sphériques soit d'eau, soit moitié d'eau moitié de neige, ne peuvent servir à les expliquer; toutefois comme dans tous les cas où des parhélies furent observés il y avait aussi des couronnes, je ne doutai pas qu'il n'y eût une grande similitude entre les causes des uns et des autresGa naar voetnoot3). Songeant doncGa naar voetnoot4) quelle est la forme la plus simple après la forme sphérique qui | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 385]
| ||||||||||||||||||||||||||||||||||||||||||||||
uijt dan oock consteert dat den diameter van den binnensten circel ontrent 45 gr. geweest is, zijnde de gemeene grootte van de CoronaeGa naar voetnoot1). alhoewel de buytenste circels diameter in dit van 1629 soo ick geloof kleinder geweest is als die van de buytenste circel int phaenomenon van 1630, gelijck uijt de figuer blyck en daer uijt bewesen kan werden. Daer is noch ontrent dese figuer aen te mercken dat de steert van het parelium N meest langhs den grooten circel KLMN strecken gelijck bij Hevelius beter is waer genomen in sijn Observatie 1661. hier naer geinsereertGa naar voetnoot2). Maer hier is het van Scheijnerus anders geteyckent om te exprimeren dat de steert recht van de son af stont. De sonnen en bijsonnen sijn oock veel te groot gerepresenteert nae proportie vande circels, en de circels selfs oock veel te dick naer proportie van haer eigen diameters. Want in der daer moest de sons diameter maer 1/90 ontrent wesen van den diameter der coronae DEF als synde van 45 gr. en de breedte des circels KLMN ontrent mede soo veel. want uijt de explicatio van dat van 1630 blyckt dat de voors. breedte noch niet soo groot en was als des sons diameter.
§ 11. Dit van de figuere gepraemitteert sijnde, so laet ons verder nu van de causis van dese wonderlijcke verthooningen ondersoecken. Ick hebbe lichtelijck konnen verstaen dat de ronde droppels 't zij van water of half water en sneeuw hier toe niet konden te pas komen, doch dewijl in al de observatien van parelia oock Coronae waren soo twijffelden ick niet of de oorsaecken van beijde mosten niet veel van malkander onderscheijden sijnGa naar voetnoot3). Denckende danGa naar voetnoot4) wat figuer nae de spherische de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 386]
| ||||||||||||||||||||||||||||||||||||||||||||||
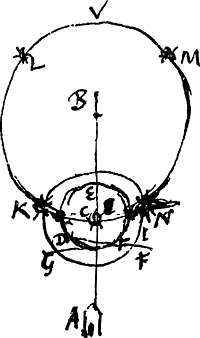
puisse être attribuée aux grêlons dans l'air, je n'en trouvai point d'autre que celle du cylindre; et en effet j'avais souvent remarqué que parmi la neige étaient mêlés une foule de petits bâtons, fort minces en vérité. Or, tandis que les petites gouttes sphériques suffisaient pour faire apparaître les couronnes, je me figurai que de nombreux petits cylindres suspendus drus dans l'air pourraient également produire un certain effet. Je trouvai aussi que certaines petites colonnes ou cylindres de glace [Fig. 7] tombant de l'air avaient été observés par Descartes lesquels portaient aux extrémités supérieure et inférieure une petite étoile hexagonaleGa naar voetnoot1). Commençant donc par examiner la forme et la situation des petits cylindres et songeant qu'ils ne pouvaient guère être engendrés que dans la position verticale [Fig. 8], et en outre qu'il devait leur arriver parfois la même chose que nous avons dit arriver aux grêlons sphériques, savoir qu'ils devaient dégeler partiellement par la chaleur du soleil ou de l'air, je trouvai bientôt que tout ce qui a été remarqué dans le phénomène de Rome de 1629 pouvait provenir de ces petits cylindres exclusivement. C'est ce que je compris fort clairement après avoir rempli d'eau un cylindre de verre assez ample où j'avais suspendu à l'intérieur un cylindre en bois moins épais. Car en donnant à ce bocal cylindrique diverses positions par rapport au soleil et à mon oeil, je constatai d'abord que le grand anneau blanc provient uniquement de la réflexion due aux cylindres, ensuite que les deux parhélies latéraux par rapport au soleil doivent leur origine à une réfractions double, enfin que les parhélies opposés au soleil proviennent de deux réfractions et d'une réflexion le tout de la manière que nous expliquerons plus loin.
12. Nous devons débuter par quelques remarques sur la genèse de ces cylindres et sur leur position, leur forme et leur grandeur. Comme j'ai dit que les grêlons sphériques qui causent les couronnes doivent être fort petits, tels environ que des graines de navette, pour pouvoir être soutenus par les vapeurs ascendantes, je suppose pareillement les cylindres susdits fort petits et minces pour la même raison, laquelle petitesse toutefois ne nuit pas à la perfection de leur forme, mais au contraire y contribue plutôt. La matière qui les compose primitivement doit, comme celle des particules | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 387]
| ||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 7.]
simpelste moste sijn die den hagel soude konnen in de lucht gegeven werden, soo en vondt ick geen als de cylindrische, en inder daet had ick wel dickmaels gemerckt dat inde sneeuw menichte van langwerpige stuckjes gemenght waeren alhoewel seer dun, doch dewijl de kleine ronde droppelties genoegh waren om de coronae te verthoonen, soo dacht ick dat oock kleijne cylinderties doch dicht en menichvuldigh inde lucht hangende, mede iets konden effecteeren. Ick vondt oock dat bij Des Cartes seeckere columnulae of cylinderties van ijs [Fig. 7] geobserveert waeren die uijt de lucht vielen, hebbende onder en boven een seshoeckigh sterretieGa naar voetnoot1). Beginnende dan de figuer en positie van cylinderties te examineren, en denckende datse niet wel gegenereert  [Fig. 8.]
konden werden als recht over endt staende [Fig. 8], ende voorts dat haer mede somtijdts gebeuren most, als hier voor vande ronde grana gesecht is, te weten datse ten deelen van de warmte der son of lucht ontdoijden, soo vondt ick wel haest dat al 't geen in het phaenomenon Romanum van 1629 gesien is alleen door middel van dese cylinderties konde voortkomen. Et clarissime quidem posteaquam vitreum cylindrum satis capacem aqua implevissem, solido cylindro ligneo minus crasso intus suspenso. eum enim varie soli oculoque meo objiciens, tum circulum magnum album ex reflexione sola cylindrorum, tum parelia ad latus solis ex geminata refractione, quae vero in parte opposita ex refractionibus duabus et reflexione ortum ducere deprehendi, ea nimirum ratione quam deinceps exponemus.
§ 12. Pauca autem de generatione illorum deque positu figura ac magnitudine praemittenda sunt. Gelijck ick gesecht heb dat de ronde grana die de oorsaeck vande Coronae sijn, seer kleijn als raepsaedt of daerontrent moeten wesen, op datse door de opstygende dampen opgehouden konnen werden, soo stel ick mede dese cylinderties, om deselve reden, seer kleijn en dun, welcke kleinigheijt nochtans de perfectheijt harer figuer niet wegh en neemt maer eerder daer toe kontribueert. De materie daerse eerst van gecomposeert werden moet gelijck die van de deelties der coronae van | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 388]
| ||||||||||||||||||||||||||||||||||||||||||||||
causant les couronnes, être de la neige très fine, c.à.d. un amas de particules de brouillard gelé extrêmement petites et presqu'invisibles (la neige en effet n'est autre chose que de la glace fort déliée); un certain nombre de ces particules de brouillard s'étant assemblées d'abord en un petit globule il est facile de comprendre comment d'autres particules s'y joignent à l'extrémité inférieure et non pas latéralement. En effet, puisque les particules du brouillard moment rapidement avec l'air ascendant, tandis qu'au contraire les petits globules nommés s'opposent à ce mouvement par leur pesanteur ou du moins sont entraînés en haut plus lentement, il n'est pas étonnant que les particules du brouillard pressées contre l'extrémité inférieure d'un globule y adhèrent et s'y attachent [Fig. 9], prolongeant ainsi peu à peu le globule de manière à le changer en un cylindre, tandis que d'autres particules du brouillard, étant entraînés le long de ce petit corps, peuvent facilement glisser sur lui. Attendu que ces petits cylindres sont ainsi produits en grande quantité et à peu de distance l'un de l'autre et que l'air qui les soutient passe entre eux, il est avéré que par là ils sont maintenus debout, c.à.d. dans la position verticale dans laquelle ils ont été engendrés. Toutefois, lorsqu'ils sont dispersés par quelque vent ou autrement, il faut savoir qu'ils ne restent pas précisément debout, mais peuvent tournoyer de maniäre à prendre toutes sortes de positions. Or, la chaleur du soleil ou de l'air venant à fondre a l'extérieur ces petits cylindres jusqu'à une certaine profondeur, il reste au centre un petit cylindre mince de neige fine entouré d'eau de tous les côtés comme nous l'avons vu dans le cas des grêlons causant les couronnes, et la même raison que nous avons alléguée là doit avoir ici aussi pour effet que lorsqu'ils ont été liquéfiés dans une certaine mesure le noyau central s'arrondit parfaitement et que la partie liquéfiée ne se regèle pas aisement. Mais même si elle venait à se regeler, la glace ainsi formée serait peut-être assez claire et lisse pour pouvoir servir aux réfractions et réflexions dont nous allons traiter.
§ 13. Pour en venir maintenant au phénomène de Rome [de 1629]: je dis d'abord que le grand anneau blanc vu en cette occasion a été produit par la réflexion des rayons solaires sur la surface extérieure des petits cylindres verticaux, d'autre part que, lorsque de tels cylindres suspendus se trouvent en foule dans l'air et que le soleil les éclaire, il est nécessaire qu'on aperçoive une grande circonférence de cercle, laquelle est blanche, passe par le soleil, est parallèle à l'horizon c.à.d. partout à la même hauteur au-dessus de lui, et d'une largeur égale au diamétre du soleil. Pour le démontrer considérons d'abord un cylindre plus grand qui figure un de ces tout petits cylindres et voyons quelle est la règle suivie par les rayons du soleil réfléchis sur sa surfaceGa naar voetnoot1). Soit AKLB le cylindre à axe vertical [Fig. 10]. Puisse le rayon CD venant du centre du soleil tomber sur lui et puisse celui-ci, rencontrant le cylindre | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 389]
| ||||||||||||||||||||||||||||||||||||||||||||||
seer sijne sneeuw sijn dat is van de alderkleijnste en bynae onsichbare deelties van bevrosen nevel (want sneeuw niet anders als deelties van ijs is) van welckers nevels deelties eerst een klein bolletie vergaert sijnde so is licht te verstaen hoe onder aen dat bolletie sich noch meer deelties aansetten, en niet aen de kanten; want de kleijne deelties der nevel met de opwaerts gaende lucht ras opklimmende daer integendeel dese bolleties alreets door haer swaerte daer tegens obniteren ende ten minsten langhsamer nae om hoogh gevoert werden, soo is niet vreemt dat de deelties der nevel die onder tegen een bolletie aengedreven werden daer tegen steuyten en daer aen vast
 [Fig. 9].
blijven [Fig. 9], verlenghende soo allenghs het bolletie tot een cylinder, daer de andere deelties der nevel verbij de sijden gedreven werden licht verbij schuijven. Dewijl nu dese cylinderties alsoo denso agmine en niet ver van malkander geproduceert werden en de lucht die se ophoudt tusschen haer door passeert, soo is het consentaneum dat die daer door recht over ende dat is inde selve positie daer inse gegenereert sijn werden staende gehouden. Maer alsse door eenige wint of anders verder van een geraecken, soo moet men weten datse niet juyst over endt en blijven, maer oock wel op aller hande posturen rondtom tuijmelen. De warmte nu vande son ofte vande lucht, even gelijck wij inde greinen der Coronae gesien hebben, oock dese cylinderties van buyten een stuckweeghs komende te smelten soo blijft in midden een dun cylindertie van fijne sneeuw over, rondtom met water omvangen. en de selve reden die wij daer bygebracht hebben moet oock hier maecken, datse tot op seeckere maet gesmolten wesende de binnenste kern perfect gerondt werdt, en het gesmolten deel oock niet licht weer komt te bevriesen. Doch of het al quam daer nae te bevriesen soo is misschien dat ijs klaer genoegh en glad van superficie om tot de refractien en reflexien te dienen daer wij van handelen sullen.
§ 13. Om dan tot het phenomenon van Romen te komen soo segh ick voor eerst dat den grooten witten ringh die daer is gesien ontstaet uijt de reflectie der sonne buyten tegen de superficie der rechtoverendstaende cylinderties, ende dat het nootsaeckelijck is, als er sodaenighe cylinderties met meenichte inde lucht hangen en de son daer op schijnt dat men dan soo een grooten circel gewaer sal werden, die wit is, die door de son passeert, die parallel met den horizont is of, over al even hoogh daer boven verheven staet, en die van de breedte der sons diameter zij. En om dit te doen blijcken soo laet ons eerst een grooter cylinder considereren die een deser minimorum cylindrulorum representeere ende sien wat regel de daer op gereflecteerde sonsstraelen volgenGa naar voetnoot1). Laet de cylinder sijn AKLB [Fig. 10], axe ad perpendiculum erecto. Radius autem ex solis centro in eum incidat CD, qui ad D | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 390]
| ||||||||||||||||||||||||||||||||||||||||||||||
au point D, être réfléchi selon DE. Traçons sur la surface du cylindre la droite AB parallèle à l'axe et passant par le point D; prenant ensuite DC et DE égales l'une à àl'autre, menons à la droite AB les perpendiculaires CA et EB. Manifestement l'angle DCA est donc la hauteur du soleil au-dessus de l'horizon. Je dis que l'angle BDE qui représente l'inclinaison du rayon réfléchi DE par rapport au même plan de l'horizon, lui est égal. En effet, figurons-nous que le plan FHGI touche le cylindre suivant sa génératrice AB. Considérons de même un deuxième plan GECF passant par le triangle CDE et coupant le plan FHGI suivant la droite FDG. Or, comme la réflexion du rayon CD sur le cylindre KABL a lieu suivant la même droite que sur le plan HFIG touchant sa surface en D, DE sera aussi la réflexion du rayon CD sur le plan HFIG. Par conséquent, comme cela est établi dans la catoptrique, il est nécessaire que le plan GECF qui contient à la fois le rayon incident CD et le rayon DE réfléchi soit perpendiculaire au plan HFIG sur lequel se fait la réflexion et que les angles d'incidence et de réflexion, CDF et EDG, soient égaux. Menons maintenant CF et EG, l'une et l'autre perpendiculaire à FG et se trouvant évidemment dans le plan GECF. Traçons aussi les droites AF et BG. Attendu qu'alors dans les triangles EDG et CDF, rectangles en G et F, les angles EDG et CDF sont aussi égaux entre eux et que les hypoténuses ED et DC sont égales par construction, les côtés DG et DF seront pareillement égaux et les côtés EG et CF de même. De plus comme CF et EG se trouvent dans le plan GECF perpendiculaire au plan HFIG, et sont en même temps perpendiculaires à la droite FG située dans ce plan, les dites droites CF et EG seront perpendiculaires au plan HFIG, et comme ce dernier est perpendiculaire à l'horizon, il apparaît que les droites CF et EG sont horizontales. Or, CA et EB sont également horizontales vu qu'elles sont perpendiculaires à AB; deux côtés de chacun des triangles CAF et EBG étant donc horizontaux, il en sera de même de leurs troisièmes côtés AF et BG. Ces derniers seront donc aussi perpendiculaires à AB. Comme les triangles FDA et GDB ont donc des angles droits en A et en B et de plus des angles égaux en D et des hypoténuses égales DF et DG, les autres côtés y seront aussi égaux deux à deux. Partant AD est égale à DB. D'autre part, vu que dans les triangles DAC et DBE il y a des angles droits en A et en B et des côtés égaux AD et DB, et que les hypoténuses CD et DE sont égales par construction, il apparaît que les côtés qui restent, savoir AC et BE, sont aussi égaux. Par conséquent les angles opposés à ces côtés ADC et BDE seront pareillement égaux entre eux, ainsi que les angles ACD et BED, ce que nous voulions démontrer.
§ 14. Il résulte de cette démonstration que lorsque l'air est rempli de petits cylin- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 391]
| ||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 10.]
punctum cylindro occurrens reflectatur secundum DE. Ducta autem in cylindri superficie recta axi parallelâ AB quae transeat per punctum D sumtisque aequalibus inter se DC, DE, ducantur ad rectam AB perpendiculares CA, EB. Manifestum itaque angulum DCA esse eum quo sol super horizontis planum attollitur. Huic autem aequalem esse dico angulum BDE, quo radius reflexus DE ad idem horizontis planum inclinatur. Intelligatur enim planum FHGI quod cylindrum contingat secundum rectam in ejus superficie AB. itemque alterum planum intelligatur GECF, ductum per ∆lum CDE, cujus intersectio communis cum plano FHGI sit recta FDG. Quia autem secundum eandem lineam fit reflexio radij CD à cylindro KABL, atque a plano HFIG cylindri superficiem in D contingente, erit proinde DE etiam reflexio radij CD a plano HFIG. Quamobrem, ut constat et catoptr. necesse est planum GECF in quo radij uterqueGa naar voetnoot1) CD incidens, et DE reflexus, insistere plano HFIG, in quo fit reflexio, adangulos rectos. Atque etiam angulos incidentiae et reflexionis inter se aequales esse, nempe CDF, EDG. Ducantur jam CF, EG utraque perpendicularis ad FG, quas patet esse in plano GECF, et jungantur AF, BG. Quia igitur in triangulis EDG, CDF rectos angulos ad G et F habentibus, etiam aequales sunt inter se anguli EDG, CDF, et hypotenusae item aequales ED, DC ex contr. erunt et latera DG, DF, itemque EG, CF aequalia. Porro quia CF, EG sunt in plano GECF recto ad planum HFIG, simulque rectae GF in hoc plano sitae perpendiculares, necessario erunt ipsae CF, EG plano HFIG ad angulos rectos, quod cum ad horizontem erectum sit, patet rectas CF, EG debere esse horizonti parallelas. Sed et CA, EGBGa naar voetnoot2) horizonti parallelae sunt, quippe ipsi AB ad angulos rectos insistentes itaque tum ∆li CAF tum ∆li EBG duobus lateribus horizontis plano parallelis existentibus, erunt et reliqua eorum latera AF, BG eidem plano horizontis parallela, ac proinde ipsi quoque AB ad angulos rectos. Cum itaque ∆la FDA, GDB angulos ad A et B rectos habeant et aequales quoque angulos ad D, praetereaque hypotenusas aequales DF, DG, etiam reliqua latera aequalia habebunt. Quare AD aequalis DB. Rursus itaque cum in ∆lis DAC, DBE, anguli recti sint ad A et B; lateraque aequalia AD, DB; atque item aequales hypotenusae CD, DE ex constructione: patet et reliqua latera nempe AC, BE aequalia esse. Hinc itaque et anguli lateribus hisce oppositi aequales erunt ADC, BDE, adeoque et ACD, BED, quod demonstrare voluimus.
§ 14. Hier uyt blijckt dan, als de lucht vol van rechtoverend staende cylinderties | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 392]
| ||||||||||||||||||||||||||||||||||||||||||||||
dres verticaux s'y trouvant suspendus, tous les rayons émanant du centre du soleil ou de quelqu'autre point de son disque et tombant sur ces cylindres, se dirigent après réflexion vers la terre sous un angle égal à la hauteur du point mentionné au-dessus de l'horizon, attendu qu'a cause de la grande distance du soleil l'angle d'incidence FEO est le même pour chaque cylindre voltigeant haut ou bas. Une personne placée sur la terre ne peut donc voir la réflexion du soleil que dans les petits cylindres planant en un endroit tel que la droite qui va du cylindre à l'oeil de l'observateur fait avec le plan horizontal un angle égal à la hauteur du soleil. Or, si l'on se figure des droites allant de l'oeil du spectateur vers tous les côtés et faisant tous avec le plan horizontal des angles égaux entre eux et à la hauteur du soleil, il est certain qu'ils aboutissent tous au firmament en une circonférence de cercle parallèle à l'horizon. Il est donc manifeste que l'observateur verra un anneau blanc lumineux parallèle à l'horizon et passant par le vrai soleil. On comprend de plus aisément que sa largeur doit être égale à celle du diamètre du soleil car comme nous l'avons dit à propos du centre du soleil, ainsi et pour la même raison chaque point du soleil doit éclairer un groupe de petits cylindres se trouvant de tous les côtés autour du spectateur de sorte qu'un anneau apparaît à la même hauteur que ce point. D'où il résulte que les bords supérieur et inférieur de l'anneau blanc doivent être à la même distance l'un de l'autre que les parties extrêmes supérieure et inférieure du soleil. Et il mérite d'être remarqué que lorsque le soleil s'élève ou baisse, cet anneau monte ou descend en même temps en devenant par conséquent plus petit ou plus grand; et que de différents spectateurs, qui peuvent être fort éloignés l'un de l'autre, chacun voit son anneau à lui (passant par le soleil), comme il en est aussi dans le cas de l'arc-en-ciel. Ce qui ne peut nullement avoir lieu dans le cas du cercle qui produirait ce phénomène selon Descartes; il suppose en effet un grand anneau solide de glace suspendu dans l'airGa naar voetnoot2), lequel ne pourrait se trouver simultanément dans une position horizontale au-dessus de différents observateurs. Il n'y a de plus aucune raison dans cette hypothèse pour laquelle l'anneau passerait par le soleil, et cela parfois durant deux ou trois heures, comme on peut le lire dans les observations qui suivent. Il faut savoir en outre que lorsque ces anneaux apparaissent, il n'y a jamais d'épais nuages au firmament, mais seulement de si légers qu'on ne peut guère, ou à peine, les apercevoir, car on verra que dans les rapports de diverses observations il est dit que le temps était clair. Ce qui n'est pas étonnant d'après notre hypothèse à nous, lorsqu'on considère que ces petits cylindres ne produisent qu'un nuage rare et homogène è travers lequel les rayons du soleil et une grande partie du ciel bleu sont parfaitement visibles. Le fait que parfois quelques parties de cet anneau ne sont aperçues que faiblement ou point du tout s'explique par le manque de matière, c.à.d. l'absence des petits cylindres susdits, excepté lorsqu'il | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 393]
| ||||||||||||||||||||||||||||||||||||||||||||||
hanght, dat al de radij uyt het center der sonne, of eenigh ander punt sijns disci, tegen dese cylinderties schynende, haere reflexien nae de eerde strecken even met den selven hoeck, als die van des selven punts hooghte boven den horizont, aengesienGa naar voetnoot1) dat, om de groote veerheijt der son, den angulus incidentiae FEO, op ieder cylinder, 't zij hoogh of leegh vliegende, den selfden is. Iemand dan op de aerde staende kan de sons reflexie alleen in die cylinderties sien die op sodanigen plaets hangen, dat de linie die van haer tot het oogh des spectateurs streckt, een hoeck maeckt op het planum horizontis gelijck aen die van de hooghte der son. Als men nu rondtom nae alle kanten uyt des spectateurs oogh linien bedenckt te gaen maeckende alle gelijcke hoecken boven den horizont, en weer gelijck aen de sons hooghte, het is seecker dat die alle in een hemelsche circel belenden die parallel met den horizon is. Het is dan manifestum dat den spectator een witten verlichten ringh sal sien die parallel met den horizont is, en in welcken oock de rechte son komt te staen. Het is oock licht te begrijpen dat sijn breedte gelijck moet sijn aen de breedte der sons diametri, want gelijck wij van des sons center geseght hebben, alsoo moet door deselfde reden ieder punct van de son een ringh van cylinderties verlichten die op de selfde hooghte van dat punct gesien werdt. Waer door dan de opperste en onderste kant van den geheelen witten ringh even soo veer van malkander moeten sijn als het bovenste en onderste deel der son. Ende het is aenmerckens waerdigh dat de son rijsende of dalende, desen ringh te gelijck oock mede rijft of daelt werdende alsoo kleinder of grooter. ende dat verscheyden spectateurs alhoewel veer van malkander staende elck evenwel sijn circel siet die door de son passeert gelijck mede in den regenboogh ges[chiet]. het welck geensins en gebeuren kan in die circel die de Cartes woude hebben dat dit phaenomenon produceren soude, want hij stelt dat het een grooten solidum ring van ijs is die in de lucht hangen soudeGa naar voetnoot2). denwelcke sich niet te gelyck recht boven verscheyde spectateu[ren] kan rencontreren. Behalven dat oock geen reden en is waerom hij door de son soude passeren. en dat altemet 2 of 3 uren langh, gelijck inde volgende observatien te lesen is. Daerenboven is oock te weten dat als dese ringen sich verthonen, geen dicke wolcken noyt aen de lucht sijn maer soo dunne alleen dat men die niet of quaelyck sien kan, want in verscheyden der observatien salmen sien dat geseght wert klaere lucht geweest te sijn. het welck volgens onse hypothesis niet wonder is, als men considereert dat dese cylinderties maer een raram nubem produceren ende die aequaliter extensam daer de son licht en oock veel van de blaeuwe lucht door heen schijnt. Dat nu altemet eenighe delen deses circels flaeuw of heel niet gesien werden en is niet anders als door defect van materie dat is van de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 394]
| ||||||||||||||||||||||||||||||||||||||||||||||
s'agit de la partie de cet anneau qui se trouve dans la couronne, car quoiqu'il puisse y avoir là assez de matière cette partie est moins visible, et n'est par conséquent pas indiquée dans le cas de certaines observations, d'abord à cause de la vicinité du soleil resplendissant, ensuite et surtout parce qu'à l'exterieur de la couronne et près d'elle l'anneau blanc est beaucoup plus intensif qu'ailleurs. La raison de ce dernier sait sera comprise lorsque nous aurons donné celle des deux parhélies N et K qui se trouvaient à côté du soleil.
§ 15. Pour en venir là, je dis donc que les mêmes petits cylindres verticaux qui font voir l'anneau blanc, causent aussi ces deux parhélies en réfractant deux fois les rayons du soleil [Fig. 11]Ga naar voetnoot2), de la même manière dont à ce que nous avons vu plus haut, les gouttelettes sphériques avec leurs noyaux centraux de neige produisent la couronne. Car puisque ces petits cylindres sont partiellement fondus à l'extérieur et renferment des noyaux cylindriques de neige, le soleil, à cause de ces noyaux, ne peut être vu au travers des cylindres qui causent la partie KN de l'anneau blanc [Fig. 5], mais seulement à travers ceux qui se trouvent en dehors; d'où il résulte que la distance de ces deux parhélies est d'autant plus grande que le noyau de neige occupe une plus grande partie des cylindres. Or, le soleil est vu avec le plus d'éclat à travers les petits cylindres que se trouvent très peu en dehors de la partie KN, avec un moindre éclat de plus en plus faible jusqu'à une certaine limite au travers de ceux qui en sont de plus en plus éloignés, et ceci fait que ces parhélies sont vus munis de queues. Cependant, attendu que les couleurs vives de l'arc-en-ciel se produisent dans les petits cylindres situés tout juste en dehors de KN, par la même cause par laquelle nous avons dit que se produisent celles de la couronne, ceci permet de distinguer les parhélies de leurs queues plus pâles et peu colorées, de même qu'on n'attribue qu'une faible épaisseur à la couronne et à l'arc-en-ciel quoique ceux-ci aussi soient illimités d'un côté. Ces queues, comme les parhélies auxquels elles appartiennent, s'étendent toujours, comme il paraîtra par ce qui suit, le long de l'anneau blanc, en le rendant beaucoup plus brillant jusqu'aux points où elles s'évanouissent. Car en figurant la queue du parhélie | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 395]
| ||||||||||||||||||||||||||||||||||||||||||||||
bovens. cylinderties. behalvenGa naar voetnoot1) alleen dat sijn deel dat binnen de Corona is alhoewel daer materie suppediteert te minder gesien werdt en daerom oock in sommige observatien niet gemerckt staet om de vicina claritas solis en praecipuè om dat even buyten de corona den witten ringh veel stercker is als op andere plaetsen. Daer van de reden sal verstaen werden als wij die vande 2 parelia N en K die nevens de son stonden geseght sullen hebben. § 15. Om dan hier toe te komen, soo segghe ick dat de selfde rechtoverendt staende cylinderties die den witten ringh doen sien, oock dese 2 parelia veroorsaecken door 2 mael de sons stralen te refringeren [Fig. 11]Ga naar voetnoot2) even op de manier als wij boven gesien hebben dat de ronde dropjes met sneeuw kerrels in midden de corona produceren. Want dese cylinderties oock ten deelen van buijten gesmolten sijnde ende langwerpige cylindrische sneeuwkerrels van binnen hebbende, soo kan om de selve kerrels wil de son niet gesien werden door de cylinders die het deel des witten  [Fig. 11.]
ringhs KN [Fig. 5] maecken, maer door die daer buyten komen, waer door dan de distantie deser 2 pareliums oock te grooter valt hoe de kerrel van sneeuw grooter deel der cylinders beslaet. De son nu werdt aldersterckst gesien door de cylinderties die effen buyten het deel KN komen en dan door die noch verder en verder afstaen doch hoe langhs hoe flaeuwer tot een seeckeren terminus toe, ende dit maeckt dat dese parelia met steerten gesien werden, doch evenwel, doordien de vierige couleuren van den regenboog in de cylinderties die effen buyten KN komen sich verthoonen, even door de selfde reden als daer wij de couleuren van de corona uyt geseght hebben te ontstaen, soo doet dit de parelia distingueren van de rest harer steerte die min licht en weynigh gecouleurt is, even gelijck de corona en Iris oock maer weynigh breedte toegeschreven werdt alhoewel die aen d'een syde ongetermineert sijn. Dese steerten nu gelijck oock de parelia daerse aen staen, als uyt het volgende blycken sal, strecken altijdt langhs den witten ringh en maecken die soo veer sij gaen veel illustriorem. Want | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 396]
| ||||||||||||||||||||||||||||||||||||||||||||||
N [Fig. 5] en dehors de cet anneau, on a commis une erreur (à moins que l'observateur n'ait voulu indiquer que la queue avait une direction opposée à celle allant vers le soleil). Mais chez Hevelius dans son phénomène de 1661 on voit que ceci a été mieux observé. On peut conclure, quoiqu'il ne soit pas dit en cette occasion que le parhélie K fût pourvu lui aussi d'une queue, que néanmoins il en avait une coïncidant avec une partie de l'anneau blanc; toutefois, comme il est dit que ce parhélie était plus faible que l'autre, cette queue a aussi eu fort peu d'éclat. En effet, le fait que les parhélies se trouvant à côté du soleil sont généralement munis de queues, ainsi que les parasélènes à côté de la lune, peut être déduit des observations d'Hevelius où ils en ont tous, ainsi que de mon observation du .....Ga naar voetnoot1). Enfin la raison de la grande clarté des parhélies (on affirme en effet dans cette occasion que l'éclat moyen des deux rivalisait avec celui du soleil) est facile à comprendre si l'on songe que chaque petit cylindre resplendit suivant toute sa longueur, tandis que les gouttes sphériques de la couronne ou du vulgaire arc-en-ciel ne projettent qu'une lumière pour ainsi dire punctiforme, de sorte qu'un seul petit cylindre donne peut-être plus de clarté que dix gouttelettes sphériques. Lorsqu'une grande quantité de petits cylindres sont suspendus dans l'air il n'est donc pas étonnant qu'il en résulte de brillantes images du soleil. Démontrons maintenant ce que nous avons dit en examinant exactement les réfractions subies, en traversant ces cylindres, par les rayons solaires. Nous prouverons d'abord que les parhélies considérés et leurs queues doivent se trouver précisément dans le grand anneau blanc.
§ 16. Soit ABCD [Fig. 12] un des cylindres nommés suspendus verticalement dans l'air et puisse un rayon de soleil EF tomber sur la surface extérieure de son enveloppe aqueuse. Réfracté en F ce rayon se dirigera suivant FG à l'intérieur du cylindre; brisé une deuxième fois en G, où il rencontre de nouveau la surface de l'eau, ce rayon quittera le cylindre p.e. suivant GH. Je dis que ce rayon GH sera nécessairement le même angle avec le plan horizontal que le rayon de soleil EF, savoir un angle égal à la hauteur du soleil. En effet, si nous menons un plan ADBC parallèle à l'axe du cylindre et passant par les points F et G, il apparait que ce plan coupe de part et d'autre la surface cylindrique sous le même angle suivant les droites parallèles AB et DC. Attendu que le rayon FG, compris entre les dites parallèles | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 397]
| ||||||||||||||||||||||||||||||||||||||||||||||
dat dese steert van het parelium N [Fig. 5] buyten dien ringh geteyckent is, is bij abus alsoo geschiet, ofte wel om dat den observator heeft willen thoonen dat hij recht van de son afstond. Maer bij Hevelius in sijn phenomenon van 1661 siet men dat het beter waergenomen is. Ende daerom oock al werdt hier niet geseght dat het parelium K mede een steert gehadt heeft, soo is nochtans een deel van den witten ringh sijn steert geweest, maer om dat dit parelion flaeuwer wordt geseght gewees te sijn als het ander soo heeft die steert oock seer weynigh glans gehadt. Quod enim de steerten ordinaris zijn aende pareliums neffens de son, of paraselene neffens de maen, is mede uyt Hevelius observatien af te nemen, daerse altemael met steerten te sien sijn, ende uyt mijn observatie mede van den .....Ga naar voetnoot1). Eyndelyck de reden der groote klaerheijt der parelia (gelijck hier geseght werdt dat amborum medius nitor aemulabatur solarem) is licht te verstaen als men bedenckt dat ieder cylindertie secundum totam longitudinem suam splendescit, daer de ronde droppen van de corona of van de gemeene Iris alleen een rond lichtie van haer werpen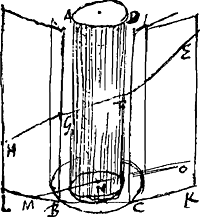 [Fig. 12.]
soo dat een cylindertie sorte meer klaerheyt als 10 ronde droppies geeft. Quod si igitur magna cylindrulorum copia in aere suspensa sit nihil mirum est luculentas solis imagines existere. Sed jam haec que dicta sunt demonstremus refractionibus quasin transituGa naar voetnoot2) cylindrorum istorum patiuntur radij solares accurate expensis ac primo quidem often dermis, dat dese parelia en haere steerten juijst in den grooten witten ring moeten staen.
§ 16. Laet ABCD [Fig. 12] een der voors. cylinders hangende recht overeindt inde lucht beteyckenen, op de welckens waterige superficies een strael der sonne valle EF, dewelcke wesende in F gerefringeert sal binnen den cylinder tenderen als in FG; ende in G, daer hij de superficies aquea weder occurreert, ten 2den gerefringeert, salGa naar voetnoot3) uyt de cylinder egredietur, puta secundum GH. Ick segge nu dat noodsaeckelyck desen radius GH even den selven hoeck sal maecken op het planum horizontis als de sons strael EF op het selve planum horizontis maeckt, dat is even aen den hoeck der sons hooghte. ducto enim plano axi cylindri parallelo ADBC, quod transeat per puncta F, G: patet hoc planum aequalibus utrinque angulis occurrere superficiei cylindricae, secundum lineas AB, DC sibi mutuo parallelas. Cum ergo in hoc plano sit radius FG, inter dictas parallelas AB, DC contentus, necesse est et hunc in punctis F et G cylindricae | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 398]
| ||||||||||||||||||||||||||||||||||||||||||||||
AB et DC, se trouve dans ce plan, ce rayon coupera nécessairement lui aussi la surface cylindrique, aux points F et G, sous le même angle et fera avec les parallèles nommées des angles égaux GFC et FGA. Il est par conséquent trop manifeste pour qu'il soit nécessaire de le démontrer que GH, provenant par réfraction du rayon GF, doit se diriger vers la terre sous un angle égal à celui sous lequel s'élève le rayon réfracté FE provenant de GF, en d'autres termes que les angles que les deux rayons réfractés [GH et FE] font avec les génératrices du cylindre sont égaux. C'est suivant une propriété connue des rayons réfractés que le rayon GF se réfracte en FE, FG étant par hypothèse le rayon réfracté provenant de EF. Les angles EFD et BGH seront done égaux. Que si l'on suppose en outre des plans menés l'un par la droite DC et le rayon EF, l'autre par la droite AB et le rayon GH, il est évident que ces plans aussi seront l'un et l'autre inclinés par rapport au plan ABCD contenant le rayon GF sous des angles égaux, dont la mesure est donnée par les angles KCB et LBC formés par les intersections des dits plans avec le plan de base du cylindre. Par conséquent les angles nommés KCB et LBC seront aussi égaux entre eux. Or, comme il s'est montré que les angles EFD et BGH sont égaux, il appert par là que le rayon EF venant du soleil d'une part et le rayon GH quittant le cylindre après deux réfractions d'autre part sont inclinés d'un même angle par rapport au plan de l'horizon. C'est pourquoi la lumière du soleil ainsi transmise au travers des cylindres diaphanes ne pourra atteindre l'oeil du spectateur qu'en provenant de cylindres tels que la droite tirée de ces cylindres vers l'oeil fasse avec le plan de l'horizon un angle égal à celui qui donne la hauteur du soleil. En d'autres termes, ces rayons proviennent précisément des cylindres qui engendrent aussi l'anneau blanc. Par conséquent les deux parhélies produits par une réfraction de ce genre ne peuvent être aperçus que dans le grand cercle nommé.
§ 17. Pour examiner maintenant en quel endroit et à quelle distance du soleil les parhélies doivent être aperçus, il faut considérer le rayon solaire qui, en traversant le cylindre comme il a été dit, frise le cylindre de neige placé au centre du cylindre d'eau. Posons donc que dans la figure précédente ce soit le rayon FG qui touche le cylindre central susdit, d'où résulte qu'il en sera de même pour la droite CB, projection de FG sur le plan de la base. Si l'on tire alors dans le même plan par le centre N de la base du cylindre la droite ONM parallèle à KC, projection du rayon EF venant du soleil, laquelle droite ONM coupe en M la droite BL, projection du rayon GH, BMN sera l'angle que font entre eux deux plans verticaux dont l'un passe par hypothèse par le soleil, l'autre par un parhélie, l'un et l'autre par l'oeil du spectateur. C'est pourquoi la partie CN de l'anneau blanc située entre le soleil et un des parhélies latéraux comprend autant de degrés de cet anneau qu'en a l'angle susdit BMN. Or, cet angle ou distance du parhélie latérial au soleil est d'autant plus grand que le cylindre de neige est plus gros par rapport au cylindre d'eau. D'autre part, lorsqu'on adopte un rapport déterminé entre les grosseurs des deux cylindres, la distance nom- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 399]
| ||||||||||||||||||||||||||||||||||||||||||||||
superficiei aequali inclinatione occurrere, ac facere, ad dictas parallelas, angulos aequales GFC, FGA. Unde porro manifestius est, quam ut demonstrationem exigat, radij GF refractionem GH, eodem angulo deorsum ferri debere, quo ejusdem refractio FE sursum fertur, hoc est angulos aequales fore quos dictae refractiones efficiunt cum cylindri lateribus. Est autem radij GF refractio secundum FE, cum ipsius EF refractio ponatur esse FG, ex nota refractionum proprietate. Aequales itaque erunt anguli EFD, BGH. Quod si vero et plana intelligantur duci alterum per rectam DC et radium EF, alterum per AB et radium GH, perspicuum est et haec utraque aequalibus angulis inclinata fore ad planum ABCD in quo radius GF. quorum quidem angulorum mensura sunt anguli KCB, LBC, quos nimirum efficiunt intersectiones dictorum planorum cum plano basis cylindri. Unde itaque et dicti anguli KCB, LBC aequales erunt. Quandoquidem autem angulos EFD, BGH aequales esse apparuit, liquet hinc etiam aequalibus angulis ad planum horizontis inclinatos esse radium EF a sole venientem et GH, qui post geminas refractiones e cylindro egreditur. Quare lux solis per diaphanos cylindros ita transmissa non poterit ad spectatoris oculum pervenire, nisi ab ijs cylindris a quibus recta ad oculum ducta, angulum cum horizontis plano efficit, aequalem illi qui est altitudinis solis, hoc est nisi ab ijsdem qui etiam circulo albo materiam praebent. adeoque parelia bina ex tali refractione generata non possunt nisi in dicto circulo magno conspici.
§ 17. Om nu te examineren quo loco quâque a sole distantiâ conspici debeant soo moet men considereren den radius der sonne die door de cylinder als geseght is passerende, even aenraeckt int voorbij gaen den cylindrus niveus die in midden aquei staet. Want genomen dat in de voorgaende figuer den radius FG den voors. middelsten cylinder aenraeckt en daerom oock de rechte CB quae in plano basis subjacet ipsi FG; als men dan treckt in het selfde planum basis de rechte ONM door 't centrum baseos cylindri N en parallel met KC quae subjacet radio a sole venienti EF; welcke ONM occurrat in M rectae BL quae subjacet radio GH: soo is BMN den hoeck quem faciunt plana duo verticalia quorum alterum per solem, alterum per parelium utraque vero per oculum spectatoris transire intelliguntur. Waer om dan oock het deel des witten ringhs CN, tusschen de son en een der laterale parelia even van soo veel graden van den selven ringh begrijpt als er heeft den voors. hoeck BMN. Desen hoeck nu ofte de distantia parelij lateralis a sole eo major quo crassior est cylindrus niveus pro ratione aquei. Rursusque posita certa proportione illius ad hunc | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 400]
| ||||||||||||||||||||||||||||||||||||||||||||||
mée devient d'autant plus grande que le soleil s'élève davantage au-dessus de l'horizon, comme il apparaît par les deux tables suivantes. Nous dirons à la fin de ce traité comment ces tables ont été construites pour ne pas nous attarder en ce moment à exposer cette démonstration assez prolixeGa naar voetnoot1).
§ 18. Il ressort de ces tableaux que, lorsque différents groupes de cylindres sont suspendus les uns au-dessus des autres, dont les uns sont liquéfiés à un moindre degré que les autres, deux ou plusieurs autres parhélies plus éloignés peuvent être vus outre les deux qui se trouvent à côté du soleil, tous également placés dans le grand anneau | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 401]
| ||||||||||||||||||||||||||||||||||||||||||||||
major fit eadem distantia quo magis altè sol supra horizontem scandit; als uyt de 2 volgende tabellen te sien is: quae quo pacto constructae sint ad finem horum dicetur ne nimis prolixae demonstrationi nunc immoremurGa naar voetnoot1).
§ 18. Het blyckt uyt dese tafels dat als er verscheijde partijen van cylinders boven malkander hangen daer van d'eene minder als d'andere gesmolten sijn, dat dan oock behalven de 2 parelia naest de son wel 2 of meer andere verder af maer evenwel mede in den grooten witten circel konnen gesien werden, gelijck sulx oock uytwijsen d'ob- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 402]
| ||||||||||||||||||||||||||||||||||||||||||||||
blanc, comme le font bien voir les observations d'Hevelius du 20 février de l'année 1661Ga naar voetnoot1) et de Scheiner de 1630Ga naar voetnoot2); ce dont nous traiterons plus amplement tout à l'heureGa naar voetnoot3). Il résulte e.a. de nos tableaux que lorsque les cylindres demeurent dans le même état, il doit y avoir augmentation de la distance de chaque parhélie au soleil et des parhélies entre eux lorsque le soleil s'élève et diminution lorsque le soleil descend, ce que j'ai en effet une fois observé, comme je le dirai en racontant cette observationGa naar voetnoot5). Mais un plus grand changement de cette distance des parhélies peut avoir lieu par une plus ample fusion des cylindres, ce dont un exemple remarquable a été observé dans les temps anciens. En effet, Julius Obsequens rapporte qu'au temps de l'empereur Auguste sous le consulat de Marc Lepidus et de Munatius Plancus trois soleils furent vus qui se contractèrent bientôt en un disque unique, ce que je n'ai point lu avoir jamais été observé ailleursGa naar voetnoot6). Or, nous comprendrons aisément comment ce phénomène s'est produit puisqu'il n'y faut autre chose qu'une chaleur capable d'élever la température de l'air au point de liquéfier entièrement les noyaux des cylindres, ce qu'elle peut faire en peu de temps, et de rapprocher par conséquent les deux parhélies de plus en plus du soleil jusqu'à ce qu'enfin, lorsque la fusion des petits cylindres est complète et qu'ils se sont transformés en gouttelettes rondes, il ne reste d'autre soleil que le soleil véritable. Et puisque cette explication découled'une façon si naturelle de notre hypothèse, je pense que personne ne révoquera en doute notre interprétation des paroles d'Obsequens, quoique Gassend ait tâché de leur donner un autre sens, suivant lequel une couronne circulaire se serait formée passant par les parhélies apparus d'abord. En effet, si c'était là le véritable sens, l'auteur n'aurait pas pu dire correctement que les trois cercles ou disques s'étaient contractés en un seul, tandis qu'il pouvait le dire de deux d'entre eux; d'ailleurs suivant cette interprétation du texte ce spectacle n'aurait pas été aussi insolite. Il faut en outre remarquer qu'on voulut voir dans ce prodige une image du triumvirat, comme il résulte d'une comparaison du passage suivant de Dio CassiusGa naar voetnoot7) avec celui d'Obsequens. Dio donc dit au 45ième livre que la lumière du soleil diminuait et s'évanouissait de temps en temps, mais qu'à d'autres instants il apparaissait brillant et triple (car c'est ainsi qu'il faut entendre son expression τοτἐ δὲ ἐν τρισὶ ϰύϰλοις φαντάζεσθαι) tandis qu'une couronne ardente d'épis entourait l'un des trois; ce qui était censé contenir une profétie d'événements futursGa naar voetnoot8). Nous pourrions encore déterminer exactement la plus grande longueur des queues attachées latéralement à ces parhélies, mais comme leur éclat diminue d'autant plus qu'elles s'éloignent davantage du parhélie et que leur extrémité véritable n'est donc pas facilement aperçue, qu'il suffise de savoir qu'elles s'étendent jusqu'à la longueur d'un | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 403]
| ||||||||||||||||||||||||||||||||||||||||||||||
servatien van Hevelius in t jaer 1661 20 feb.Ga naar voetnoot1) en van Scheijnerus 1630Ga naar voetnoot2). waer van terstond noch breederGa naar voetnoot3). Het blyckt oockGa naar voetnoot4) uyt deselve tafels dat de cylinders blijvende alsse sijn, en de son hooger klimmende, dat de distantie der 2 parelia daer uyt ontstaen van de son en van malkander moet grooter werden; of kleynder als de son daelt, het welck ick oock in der daet eens geobserveert hebbe, als ick sal seggen in 't verhalen van die observatieGa naar voetnoot5). Maer daer kan in dese distantie der parelia noch grooter verandering gebeuren door het verder smelten van de cylinders, gelyck hier ontrent iets seer notabels priscis temporibus geobserveert is, Refert enim Jul. Obsequens Augusti caesaris aetate M. Lepido Munatio Planco coss., tres soles visos eosque fuisse mox in unum orbem contractos, quod quidem nunquam alias observatum legiGa naar voetnoot6). sed quomodo evenerit facile intelligemus cum nihil aliud ad hoc requiratur quam calor qui priorem aeris temperiem vincens cylindrorum nucleos totos liquefaciat hoc enim brevi tempore perficere potest, eoque parelia utraque magis magisque in solis viciniam attrahere, donec tandem totis cylindrulis resolutis atque in rotundas aquae guttulas abeuntibus nullus praeter verum solem supersit. Atque hoc cum tam apte per hypothesin nostram explicetur, non puto quenquam in dubium vocaturum quin verborum Obsequentis is verus sensus sit quem secuti sumus, licet in alium quoque vertere ea tèntarit P. Gassendus, quasi existentibus prius parelijs circulus deinde extiterit cujus ambitu illi tenerentur. neque enim recte sic dicti fuissent tres in orbem unum contracti sed duo potius, neque etiam insolitum adeo spectaculum illud fuisset. Accedit quod et triumviratus imaginem tali prodigio significari voluere, sicut patet ex sequenti Dionis Cassij loco, cum altero Obsequentis collato, sic enim DionGa naar voetnoot7) lib. 45. Solis lumen aliquando diminui extinguique, aliquando rursus triplici orbe effulgere visum (ita enim intelligendum quod ait τὁτε δὲ ἐν τρισὶ ϰύϰλοις φανταζεσθαι) quorum unum corona spicea ignita circumdabat. Quo quae eventura erant praenunciabanturGa naar voetnoot8). Caudarum longitudinem summam quae parelijs hisce lateralibus adhaerent accurate etiam definire possemus sed cum quo longius a parelio recedunt eo magis extenuetur earum fulgor, neque verus terminus proinde observatione facile comprehendatur, sufficiat scire eas usque ad quadrantem circiter | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 404]
| ||||||||||||||||||||||||||||||||||||||||||||||
quart environ de l'anneau blanc, ce quadrant étant compté à partir du vrai soleil, et même un peu plus loin selon que la hauteur du soleil est plus grande; mais que leur éclat est généralement si faible que les observateurs ne les considèrent que comme une partie de l'anneau blanc lui-même.
§ 19. Nous devons nous occuper maintenant des couronnes qui apparaissent presque toujours simultanément avec ces parhélies latéraux. Il est vrai que quelques couronnes n'ont pas de parhélies mais les parhélies ont toujours une couronne passant par eux, à moins qu'elle ne soit dans quelques cas si pâle qu'on ne peut l'apercevoir. Ce phénomène n'étant donc pas accidentel doit avoir une cause bien déterminée. Il est sans doute probable que lorsque de petits cylindres sont engendrés dans l'air il s'y trouve simultanément de ces gouttelettes rondes à demi gelées qui donnent lieu à l'apparition des couronnes, mais il est malaisé de trouver une raison pour laquelle celles-ci seraient fondues précisément jusqu'à une profondeur telle qu'elles produiraient une couronne passant exactement par les deux parhélies. En effet, lorsqu'on suppose les grêlons sphériques et cylindriques fondus suivant une même proportion par rapport au diamètre, les parhélies tombent en dehors des couronnes comme on peut le voir par les tables qui précèdent: le rapport du diamètre total du cylindre étant à celui du noyau central comme 1000 est à 473Ga naar voetnoot1), la distance des parhélies se calcule, pour diverses hauteurs du soleil, comme étant de 22, 28, 36, 51Ga naar voetnoot2) ou un plus grand nombre de degrés de l'anneau blanc, tandis que la couronne demeure invariablement de 44oGa naar voetnoot3), les gouttes rondes étant par hypothèse liquéfiées suivant le rapport susdit. Il faut en outre tenir compte du fait que pendant les 3 ou 4 heures que les parhélies subsistent parfois, ils s'éloignent ou se rapprochent l'un de l'autre à mesure que le soleil s'élève ou descend, comme nous l'avons déjà remarqué un peu plus haut, ce qui a pour conséquence que la couronne devrait en même temps s'élargir ou se rétrécir de concert, puisqu'elle continue à passer par eux; ce dont on ne peut toutefois trouver de raison en attribuant le phénomène à des grêlons sphériques.
§ 20. Mais il est certain qu'outre les grêlons sphériques les cylindres dont j'ai dit plus haut qu'ils voltigent dans l'air en prenant des positions quelconques sont également capables de produire des couronnes. Car en tournoyant entre l'oeil et le soleil ils empêchent eux aussi par leurs noyaux centraux de neige les rayons du soleil de parvenir jusqu'à nous à moins que de se trouver éloignés du soleil de plus d'un certain angle, lequel est déterminé par ceux d'entre ces cylindres sur les génératrices | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 405]
| ||||||||||||||||||||||||||||||||||||||||||||||
circuli albi, initium a vero sole sumendo revera excurrere, et paulo quoque ulterius prout major solis fuerit altitudo. Cum tamen adeo debilis saepe earum lux esse soleat ut tantum pro parte dicti circuli ab observatoribus accipiantur. § 19. De coronis autem quae una cum parelijs hisce lateralibus semper fere apparent hoc loco nunc videndum. Want sommige coronae hebben wel geen parelia, maer de parelia hebben altijdt een corona die door haer passeert ten zij die altemets soo flaeuw zij dat niet en is te mercken. het welck itaque geensins casueel zijnde moet een seeckere reden hebben. Het is wel waerschynelijck dat als er van de cylinderties inde lucht gegenereert werden, oock te gelyck van die ronde sphaerulae semigelatae gevonden werden die de coronarum materies sijn, maer het is quaelijck te bedencken hoe die juyst op sulcke proportie souden gesmolten sijn dat se de corona effen door de 2 parelia extenderen souden. want voor eerst, als men stelt dat de ronde grana en de langwerpige op de selve proportie secundum diametrum gesmolten sijn soo vallen evenwel de parelia noch buyten de corona als uyt de voorgaende abaci te sien is, want  [Fig. 13.]
de proportie des heelen cylinders diametri tot die van de binnen kerrel sijnde als 1000 tot....Ga naar voetnoot1) soo komt de distantie der parelia, op verscheyde hoogden der son, van ......Ga naar voetnoot2) en meerder graden des witten circels, daer de corona altijdt van 45Ga naar voetnoot3) gr. blijft, als de ronde droppen op de voorseyde proportie gesmolten sijn. Deinde et hoc reputandum dat in 3 of 4 uren dat altemet de parelia duren, de selve met het klimmen of dalen van de son verder van malkander gaen of naeder bij een komen, als weynigh te voren oock is aengemerckt, waer om de corona mede grooter en kleinder hier nae soude moeten werden, dewijl sij continueel blijft door de parelia heen strecken. Waer nochtans in de ronde grana geen reden en is te vinden.
§ 20. At vero praeter rotunda grana, etiam cylindros illos quos incerto positu per aerem fluitare superius dixi coronis producendis aptos esse certum est. Want dese tusschen het oogh en de son op allerhande positien tuijmelende, soo en laeten sij mede van wegen haer sneeuwkerrels de radij der sonne niet tot ons komen, ten zy se buyten een seeckeren hoeck van de son afstaen, welcken hoeck gedetermineert wert door de gene der cylinders daer de sons straelen perpendiculaer op de sijde vallen, want de andere | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 406]
| ||||||||||||||||||||||||||||||||||||||||||||||
desquels les rayons du soleil tombent perpendiculairement. En effet, les autres sur les génératrices desquels les rayons du soleil tombent obliquement. [Fig. 13] doivent être encore plus éloignés du soleil pour pouvoir transmettre ses rayons à notre oeil, comme on peut le conclure des tables placées plus haut [§ 17] en prenant ce qui y est appelé ‘hauteur du soleil’ pour la hauteur du soleil au-dessus du plan de base des cylindres. De sorte que ces petits cylindres doivent former, comme les grêlons sphériques, une couronne limitée du côté du soleil et colorée en rouge de ce côté. Et l'on pourrait croire que les couronnes apparaissant simultanément avec les parhélies proviennent de cette cause, d'une part parce que de cette manière on n'a pas besoin de supposer la formation d'autres corpuscules que les petits cylindres, de l'autre parce que souvent des couronnes plus vivement colorées apparaissent avec les parhélies que sans eux; or, ces couleurs plus intenses peuvent mieux provenir des cylindres, lesquels resplendissent bien davantage, vu qu'ils transmettent l'image du soleil par toute leur longueur, que les gouttes sphériques lesquelles ne reproduisent le soleil pour ainsi dire qu'en un point unique. Toutefois, pour revenir à notre sujet, il n'y a pas plus de raison pour laquelle cette couronne produite par de petits cylindres devrait, mieux que celle produite par les grêlons sphériques, passer par les parhélies, et la difficulté provenant du changement des distances des parhélies est par conséquent ici la même que là. C'est pourquoi on ne pourrait admettre comme bien fondée l'assertion que la couronne produite par ces cylindres de positions quelconques serait celle qui passe par les parhélies. Et quant à notre phénomène de Rome [de 1629], je suis persuadé que c'est la couronne intérieure DEF [Fig. 5] qui seule fut produite par ces cylindres de positions diverses; de sorte que cette partie du phénomène semble renfermer une difficulté sérieuse.
§ 21. Il apparaîtra toutefois que cette difficulté aussi peut être aisément surmontée si nous considérons plus à fond la forme des cylindres. Jusqu'ici nous n'avons pris en considération que leurs côtés, voyons maintenant la forme de leurs extrémités. Car si nous les estimons limités par des bases planes, cette supposition ne sera nullement conforme à la nature des choses. Mais puisqu'au contraire ils doivent nécessairement être liquéfiés aux extrémités supérieure et inférieure, et cela jusqu'à la même profondeur, l'eau prendra certainement à ces extrémités aussi autant que possible la forme ronde, d'où il résulte que le noyau est également arrondi de part et d'autre et terminé par une surface telle qu'une demi-sphère ou demi-ellipsoïde, de sorte que la forme entière du cylindre avec son noyau doit être environ celle que nous montrons ici à-côté en grand [Fig. 14]. Par conséquent ce ne sont pas seulement les cylindres | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 407]
| ||||||||||||||||||||||||||||||||||||||||||||||
daer de sons stralen schuynsGa naar voetnoot1) op de zijden vallen [Fig. 13] moeten noch verder als die van de son afstaen om sijn radij tot ons oogh te transmitteren, gelijck uijt de voor gestelde tafeltiens te verstaen is als men, het geen daer de ☉ hooghte is, neemt voor desselfs hooghte boven het planum baseos horum cylindrorum. Soo dat dese cylinderties mede even als de ronde grana een corona formeren moeten die aen de sijde na de son getermineert is en de roode couleur heeft. Ende het is te geloven dat de coronae die te samen met de pareliaGa naar voetnoot2) verschijnen uyt dese oorsaeck ontstaen, eerstelyck om dat men dan geen generatie dan alleen van cylinderties behoeft te stellenGa naar voetnoot3), ten anderen om dat veeltijdts met de parelia schoonder gecouleurde coronae appareren als sonder die. welcke stercke couleuren uijt de cylinders beter konnen voortkomen, die longe majori luce splendent per totam longitudinem transmissa solis imagine, als de ronde droppies die maer als op een punct de selve representeren. Doch om weder tot het propositum te komen soo vindmen geen meer reden waerom dese corona van cylinderties gecauseertGa naar voetnoot4) meer soude moeten door de parelia passeren als die voorgaende der ronde grana en de difficulteyt door het veranderen der distantiae pareliorum is hier mede de selfde als daer. Daerom en machmen oock met geen fundament stellen dat de corona in dese confuselyck gesitueerde cylinders gegenereert die soude sijn die door de parelia heengaet. En wat ons phaenomenon Romanum aengaet, ick houde voor vast dat het de interior corona DEF [Fig. 5] was die door alsulcke cylinders geproduceert wierdt. Soo dat haec phaenomeni pars difficultatem haud levem continere videatur.
§ 21. Veruntamen et hanc facile superari apparebit si penitius figuram cylindrorum istorum inspiciamus. latera eorum hactenus tantum consideravimus, nunc vero et extremas utrinque partes quales sint videamus. Nam si planis basibus terminari credamus id quidem haudquaquam naturae consentaneum fuerit, maer dewijlse soo wel van boven en onder als om de kanten nootsaeckelyck moeten gesmolten sijn, en even diep, soo sal voorseecker het water aen die beyde kanten mede sich soo veel tot een ronde figuer schicken als mogelijck is, waerdoor dan oock de kern van binnen aen weder sijden als in een hemispherium of hemiellipsis geformeert en gerond werdt. soo dat de figuer des gantschen cylindri met sijn kern moet ontrent sijn als hier nevens [Fig. 14.] int groot verthoont wertGa naar voetnoot5). Waer door dan niet alleen de cylinders die | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 408]
| ||||||||||||||||||||||||||||||||||||||||||||||
proches du soleil et causant les parhélies qui dirigent les rayons vers notre oeil, mais encore ceux parmi les cylindres verticaux qui sont aperçus en dehors d'un certain angle déterminé, soit au-dessus soit au-dessous ou à côté du soleil, de sorte que par cette cause aussi une couronne doit apparaître autour de lui. Pour préciser cet angle déterminé, il faut considérer, pour les cylindres les plus proches paraissant au-dessus du soleil, un rayon tel que le rayon DCBA de la figure frisant le noyau en H et de la même manière pour les cylindres les plus proches paraissant au-dessous de lui, le rayon EFGA frisant le noyau au point K. Toutefois, comme la forme de la convexité en BCL et MGF n'est pas connue avec certitude, nous ne pouvons définir précisément les rayons réfractés provenant des rayons nommés, et moins bien encore calculer la marche des rayons réfractés provenant de ceux qui tombent latéralement sur ces parties convexes. Cependant, ayant fait construire un cylindre en verre représentant la partie moyenne du corps ici figuré (ce qui suffit), et ayant suspendu à l'intérieur dans l'eau un cylindre figurant la partie moyenne du cylindre opaque HK, de telle manière que la distance entre le noyau et la surface du verre était la même de tous les côtés, j'ai constaté par expérience, en tenant ce cylindre artificiel du côté du soleil dans une position verticale et en le mouvant à l'entour, qu'il transmet les rayons du soleil de telle manière qu'il y a égalité approximative entre les angles BAN et GAN ainsi que tous les autres formés par les rayons transmis frisant le cylindre opaque avec l'axe AN allant de l'oeil au soleil.
§ 22. Ceci doit donc se passer de la même manière dans les petits cylindres et engendrer dans ce cas aussi une couronne circulaire. De sorte qu'alors les mêmes petits cylindres verticaux qui donnent lieu à l'apparition du grand anneau blanc et des parhélies latéraux produisent également les couronnes qu'on voit passer par ces derniers. Et si l'on considère bien que la forme des petits cylindres doit nécessairement être telle que nous l'avons décrite et que par conséquent les rayons qui traversent leurs deux extrémités doivent produire quelques arcs colorés, l'on ne peut douter que ces arcs ne soient les couronnes mentionnées elles-mêmes, car sinon il en devrait provenir des arcs de forme bizarre et non pas circulaire. Or, bien que l'oeil ne puisse aisément percevoir le défaut de rondeur, il peut arriver parfois que la largeur de ces couronnes surpasse légèrement leur hauteur ou inversement, comme cela a été remarqué en effet dans une des observations qui suivent. Car, lorsqu'il est dit qu'en | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 409]
| ||||||||||||||||||||||||||||||||||||||||||||||
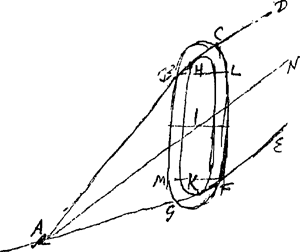 [Fig. 14.]
neffens de son staen en de parelia veroorsaecken, de radij nae ons oogh senden, maer oock dese der rechtoverendt staende die buyten een seeckeren hoeck boven en order en ter syden rondom de son gesien worden soo dat hier door oock een corona rondom de son moet verschijnen. Te weten door d' eerste der bovensteGa naar voetnoot1) passeert de radius als hier DCBA, die de kerrel raeckt in H, en door de naeste der onderste van gelijcken de radius EFGA die de kerrel raeckt in K. Quia vero de figuer der convexiteijt in BCL en MGF niet seecker bekent is, soo konnen wij de refractien van dese radij nietGa naar voetnoot2) precis definieren, en noch minder van de geene die van ter sijden op deselve convexa vallen, attamen cum vitreum cylindrum ad hanc formam confici curassem, qui nempe medietatem ejus qui hic depitus est referret quod sufficit, atque intus cylindri opaci HK medietatem intra aquam suspendissem qui undique aequaliter a vitri superficie distaret, reipsa cognovi ad solis radios factitium hunc cylindrum erectum opponendo, atque in omnem partem circumducendo ea lege eum solis radios transmittere ut aequales fere sint anguli BAN, GAN omnesque alij quibus radij transmissi, opacumque cylindrum stringentes, inclinantur ad axem AN, qui ab oculo ad solem extenditur.
§ 22. Het welck dan oock eveleens in de kleyne cylinderties geschiedende, ten naesten bij oock een ronde corona moet veroorsaecken. Soo dat dan de selfde rechtstaende cylinderties die den grooten witten ring en de parelia a latere materiam praebent oock de coronae voortbrengen die men door die parelia siet passeren. En als men wel considereert dat de figuer der cylinderties nootsaeckelijck als de voorseyde moet wesen, en dat dan oock de stralen die door de 2 eynden der selve passeren eenighe gecouleurde circuitus moeten maecken, soo en kan men niet twijffelen of dat sijn die coronae selfs, want anders eenighe ongeschicte en niet ronde daer uyt moest voortkomen. Alhoewel nu het oogh de defect der volkome rondheijdt niet licht mercken en kan soo kan nochtans wel somtijdts gebeuren dat dese coronae wat breeder als hoogh sijn of in tegendeel gelyck oock sulx in eene der volgende observatien | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 410]
| ||||||||||||||||||||||||||||||||||||||||||||||
1630 à RomeGa naar voetnoot1) les deux circonférences de cercle les plus proches du soleil se coupaient en haut et en bas et que les parhélies se trouvaient sur leurs arcs extérieurs, il est absolument vraisemblable qu'au lieu de deux circonférences de cercle qui se coupaient il faut entendre d'abord une circonférence un peu oblongue, causée par les petits cylindres verticaux, et dans laquelle étaient situés les deux parhélies, ensuite une autre plus circulaire touchant l'oblongue en bas en en haut [Fig. 16], peut-être produite par des cylindres occupant des positions quelconques ou bien par des grêlons sphériques. En effet, la figure formée par ces deux dernières circonférences ressemble tant à celle formée par deux circonférences de cercle qui se coupent qu'elle n'en peut guère être distinguée, et il est raisonnable d'admettre que les deux parhélies se soient trouvés sur une même circonférence.
§ 23. Cette circonférence passant par les parhélies fut souvent vue pâle et presqu'-évanouie aux parties supérieure et inférieure, mais vive auprès des parhélies, comme cela a été consciencieusement marqué dans beaucoup d'observations d'HeveliusGa naar voetnoot2). La raison de cette différence apparaît aussi par la considération du cylindre de verre nommé, car les rayons qui traversent les parties convexes situées aux extrémités supérieure ou inférieure de ce bocal ne donnent qu'une petite image ronde du soleil comme le font aussi des grêlons sphériques, tandis qu'au contraire ceux qui traversent le cylindre là où la surface cylindrique commence peu à peu à se courber vers la partie convexe jettent, comme ceux qui causent les parhélies, une lumière oblongue et par conséquent plus forte. Ce qui doit fortisier et colorer vers le haut et vers le bas une partie de la couronne à partir du parhélie.
§ 24. Ayant donc exposé de cette façon la raison des deux couronnes dans le phénomène de Rome [de 1629], nous procéderons maintenant à l'explication des deux derniers parhélies qui furent aperçus dans la partie de l'anneau blanc opposée an soleil. Je dis que ceux-ci furent également causés par les cylindres verticaux et cela par des réfractions des rayons solaires analogues à celles dont provient l'arc-en-ciel ordinaire; et il faut savoir que le cylindre opaque central ne joue aucun rôle dans la genèse de ces parhélies, mais peut au contraire les empêcher parfois d'être vus, comme it sera démontré plus tard. Néanmoins on comprend que le noyau de | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 411]
| ||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 16.]
gevonden werdt gebeurt te sijn. Want als in die van t jaer 1630 tot RomenGa naar voetnoot1) de 2 circels die naest om de son sijn malkander geseght werden boven en onder geinterseceert te hebben, en de parelia in beijde buytenste bogen deser circels gestaen te hebben, in hoc inquam omnino verisimile est dat in plaets van 2 circels die malkander sneden moeten verstaen werden eerst een wat langwerpige daer de 2 parelia in stonden, veroorsaeckt te weten uyt de recht over endt staend cylinderties, en dan noch een andere ronder die dese langwerpige onder en boven raeckte [Fig. 16], en uijt confuse jacentibus cylindris of uit ronde grana mocht voorkomen. Want de figuer die dese twee circels maecken is soo gelyck datse niet wel kan gedistingueert werden van die 2 doorsnydende maecken souden, en het is seer consentaneum dat de 2 parelia in een selven ambitus gecontineert geweest sijn. § 23. Dese circel nu die door de parelia gaet werdt dickmael flaeuw en evanidus gesien aen sijn bovenste en onderste deelen, maer sterckst daer hij naest aen de parelia komt als in vele van Hevelius observatienGa naar voetnoot2) naeuw is waergenomen waer van de reden in den voorverhaelde cylindrus vitreus mede te sien is, want de radij door het superius of inferius convexum desselven doorgaende, geven maer een kleyne ronde imago solis gelyck ronde grana; maer die door gaen daer de cylindrica superficies begint allengs na de convexitas te buygen dese soo wel als die de parelia maecken 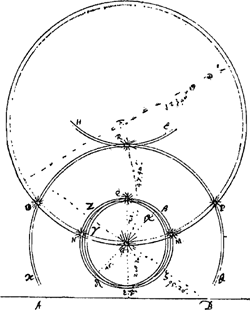 [Fig. 15.]
werpen een veel langwerpiger en stercker licht. Het welck dan van het parelie af een stuckweegh nae boven en nae order de coronae levendiger licht in couleuren moet bijbrengen.
§ 24. Hebbende dan per haec de reden der 2 coronae in het phaenomenon Romanum geexpliceert, soo sullen wij nu verder gaen tot die van de 2 overige parelia die in parte circuli albi postica wierden gesien. Welcke ick segge mede door de perpendiculare cylinders te werden veroorsaeckt en door even diergelycke refractien radiorum solarium als de ordinaries regenboogh en is te weten, dat de interior cylindrus opacus tot dese parelia niet en contribueert, maer ter contrarie altemet deselve wel kan beletten gesien te werden, gelyck hier naer sal gethoont | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 412]
| ||||||||||||||||||||||||||||||||||||||||||||||
neige doit nécessairement exister à l'interieur, soit qu'on dise que les cylindres consistent en eau à l'extérieur, soit qu'on admette que la partie extérieure est formée de glace transparente. En effet, des cylindres d'eau toute seule ne peuvent exister: ils seraient changés incontinent en gouttes sphériques; et si l'on admet qu'ils consistent uniquement en glace transparente, il est difficile de se figurer comment ils pourraient être devenus si transparents sans avoir été entièrement liquides.
§ 25. Mais avant de traiter la réfraction des cylindres, il sera utile d'entendre d'abord cette réfraction dans les gouttes sphériques, ainsi que la cause de l'arc-en-ciel que Descartes a trouvée le premier. Soit donc ABC [Fig. 17] une goutte de pluie et DA un rayon de soleil tombant sur lui, lequel est réfracté de A en B et réfléchi de B en C, les droites AB et BC étant nécessairement égales; puisse ce rayon, réfracté de nouveau en C, se diriger à partir de là vers l'oeil E. Menons CH et EF parallèlement au rayon de soleil DA, et prenons l'angle FEG égal à l'angle CEF. Or, les angles HCE sont de différentes grandeurs, selon qu'on laisse tomber les rayons DA en divers endroits de la goutte ABC; mais cet angle ne peut jamais être supérieur à 41o 30′, comme on peut le voir par les tables de Descartes. Il en résulte que l'angle CEF et l'angle FEG ne peuvent être plus grands que 41o 30′. Par conséquent aucune des gouttes qui se trouvent à l'extérieur du cône CEG ne peut diriger ces rayons de soleil réfractés vers l'oeil E; seules celles qui se trouvent à l'intérieur peuvent le faire. Parmi elles celles qui se trouvent le plus près de la surface conique CEG en envoyent le plus. C'est pourquoi l'opposition entre ces gouttes lucides et les gouttes obscures à l'extérieur du cône est d'autant plus frappante: il en résulte l'apparition en ce lieu d'un arc rond qui aurait la forme d'une circonférence de cercle entière si la surface de la terre n'y faisait obstacle. Actuellement l'arc peut tout au plus être une demi-circonférence, ce qui a lieu lorsque le soleil est tout juste au-dessus de l'horizon. Voilà la véritable cause de l'arc-en-ciel; chacun peut constater que cette théorie est d'accord avec l'expérience en remplissant d'eau de pluie un bocal sphérique et en l'exposant au soleil dans une position telle par rapport à l'oeil qu'est celle de la sphère ABC dans notre figure. Or, si l'on admet maintenant que cette circonférence ABC représente la section horizontale d'un cylindre vertical, dont on doit s'en figurer une foule près de l'horizon et que le rayon provenant du soleil que je supposerai d'abord très près de l'horizon, traverse un de ces cylindres en subissant les mêmes réfractions que le rayon DABCE passant par la goutte sphérique de telle manière qu'il fait de nouveau un angle HCE ou CEF de 41o 30′ au maximum, il s'ensuit pareillement qu'aucun cylindre extérieur à l'angle CEG ne peut envoyer de rayon réfracté vers l'oeil E, et que ceux qui se trouvent tout juste à l'intérieur de cet angle dirigent vers l'oeil le plus grand nombre de rayons; ce qui a pour effet de faire apparaître dans les cylindres en C et de même en G, un petit arc analogue à une partie de l'arc-en-ciel, | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 413]
| ||||||||||||||||||||||||||||||||||||||||||||||
werden. Doch moet men nochtans weten dat de cylinder van sneeuw daer binnenin nootsaeckelyck moet wesen utrumcunque dicitur datse buyten klaer water of klaer ijs sijn, want geen cylinders van water alleen konnen sijn want se dan terstont tot een ronden drop werden souden. En soose t'eenemael van klaer ijs sijn soo is het evenwel quaelyck te bedencken hoe se heel klaer souden konnen werden sonder heel gesmolten geweest te zijn. § 25. Priusquam vero de cylindrorum refractione agamus utile erit deselve eerst 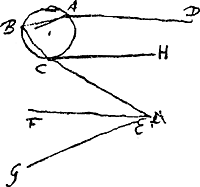 [Fig. 17.]
in de ronde droppen te verstaen en de oorsaeck des regenbooghs welke de Cartes eerst gevonden heeft. Laet dan ABC [Fig. 17] een regen droppel beteeckenen, en DA een strael der son daer op schynende, dewelcke van A na B gerefringeert werdt, en van B gereflecteert nae C; sijnde AB en BC nootsaeckelyck gelyck; en in C wederom gerefringeert tendere van daer nae t'oogh E en zij getrocken CH en EF parallel met de sons strael DA, en den hoeck FEG ∞ CEF. Den hoeck nu HCE kan van verscheyden groote wesen, naer men den radius DA op verscheyde plaetsen des drops ABC doet vallen, maer kan noijt grooter wesen als van 41.30′ als uyt de Cartes tafelen te sien is; soo dat dan oock den hoeck CEF en FEG niet grooter kan wesen als van 41.30′, waer door gebeurt dat geen van de droppels die buyten de Conus CEG gevonden werden, dese gerefringeerde sons stralen naer het oogh E konnen senden, maer alleen die daer binnen sijn, doch die senden de meeste dewelcke die naest de superficies conica CEG komen, en daerom is de afscheydingh van dese lichte en de duystere buyten de conus soo veel te merckelycker en maeckt alsoo dat hier een ronden ring appareert die integer appareren soude indien de superficies terrae niet in de wegh was, want nu kan het ten uytterste maer een halven circel werden als de son maer even boven den horizont staet. Dit is de ware oorsaeck des regenbooghs, die oock ieder kan sien met de experientie over een te komen als hij een glasen bol met regenwater gevult op soodanige positie ad oculum solemque exponat als hier is den bol ABC. Quod si jam het rondt ABC bedenckt te sijn de snee sectio horizonti parallela van een erectus cylindrus waer van men een groote menichte dicht bij den horizont moet imagineren, en dat de strael der sonne, welck ick eerst sal nemen maer even aen den horizont te sijn daer mede met de selve refractien door passeert als de radius DABCE door den ronden drop, maeckende mede den hoeck HCE of CEF ten grootsten van 41.30′, soo volght van gelycken dat geen cylinders buyten den hoeck CEG staende, konnen de radium refractum nae 't oogh E senden, en dat die even daer binnen staen de meeste radij daer nae toe werpen, waer door als een stuckje van een regenboogh in de cylinders nae C en van | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 414]
| ||||||||||||||||||||||||||||||||||||||||||||||
l'arc de l'horizon pui sépare les deux étant d'un nombre de degrés égal à celui de l'angle CEG, savoir 83o. Or, ces petits axes constituent deux parhélies plus lumineux que des parties de l'arc-en-ciel en tant que provenant de cylindres, lesquels produisent des phénomènes plus brillants que les gouttes sphériques comme nous l'avons dit plusieurs fois dans ce qui précède. Voilà ce qui arrive lorsque le soleil se trouve précisément à l'horizon. § 26. Mais lorsque le soleil est élevé au-dessus de l'horizon, je dis que ces deux parhélies doivent être situés dans le même anneau blanc où nous avons démontré 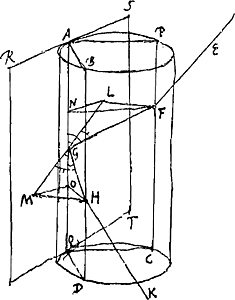 [Fig. 18].
que les autres se trouvent. Pour que ceci apparaisse, soit le cylindre ABDC [Fig. 18] suspendu verticalement dans l'air et puisse le rayon de soleil EF tomber sur lui, lequel, étant réfracté en F, rencontre à l'intérieur en G la surface cylindrique, ensuite (après réflexion en cet endroit) de nouveau la même surface en H; posons que, réfracté de nouveau en ce point, il suive en dehors du cylindre la direction HK. Je dis que les rayons EF et HK forment des angles égaux avec le plan de l'horizonGa naar voetnoot1).
§ 27. Il faut donc savoir en premier lieu que le rayon FG [Fig. 19], réfléchi à angles égaux sur la surface intérieure du cylindre, prend une direction GH telle que lorsqu'on mène par FG et GH des plans parallèles à l'axe du cylindre, leurs intersections avec la surface du cylindre déterminent des rectangles égaux en hauteur et en largeur PAQC et ABDQ et que les rayons FG et GH font avec les côtés de ces rectangles des angles égaux de part et d'autre. Ceci pourrait facilement être démontré, mais pour quelqu'un qui considère attentivement la figure la chose est évidente d'elle-même. Attendu donc que les rayons GH et GF rencontrent la surface cylindrique à l'intérieur absolument de la même manière et sous le même angle, à cette exception près que l'un se dirige vers le haut et l'autre vers le bas, il est manifeste que les rayons FE et HK doivent aussi avoir des directions telles qu'ils font des angles égaux avec les génératrices PC et BD du cylindre. Or, le rayon GF se réfracte en FE, puisque FG est par hypothèse le rayon réfracté provenant de EF, d'après une propriété des rayons réfractés démontrée dans la dioptrique. Les angles PFE et DHK devront donc être égaux. Et si l'on suppose en outre que sur le plan | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 415]
| ||||||||||||||||||||||||||||||||||||||||||||||
gelycken nae G toe moet gesien werden, sijnde den arcus horizontis tusschen haer beyde van soo veel graden als den hoeck CEG, te weten 83o. En dit sijn 2 parelia,
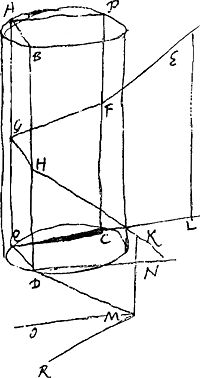 [Fig. 19.]
sijnde veel lichter als stucken van regenboogh de wijl door cylinders voortkomen, welcke veel stercker schynsel geven als de ronde droppen, gelyck meermaels te vooren is geseght. Et haec quidem sole in ipso horizonte existente.
§ 26. Maer als die nu daer boven verheven is, soo segh ick dat dese 2 parelia in den selven witten ring moeten staen, daer wy d'andere in betoont hebben. Quod ut fiat manifestum, sit cylindrus ABDC [Fig. 18] perpendiculari situ in aere sublimis suspensus, inque eum cadat radius solis EF qui ad F refractus occurrat intrinsecus superficiei cylindricae in G, unde reflexus eidem superficiei occurrat in H, atque hîc iterum refractus tendat extra cylindrum secundum rectam HK. dico radios EF, HK aequalibus angulis ad planum horizontis inclinatos esseGa naar voetnoot1).
§ 27. Sciendum enim primo est radium FG [Fig. 19] reflexum in GH ita ferri propter leges reflexionis ad angulos aequales quae sit intus in superficie cylindri, ut ductis per FG, GH planis axi cylindri parallelis, eorum intersectiones cum superficie cylindri faciant rectangula aequali altitudine latitudineque PAQC, ABDQ; utque radij FG, GH lateribus horum rectangulorum occurrant aequali angulorum inclinatione. Haec enim facile demonstrari possent, sed attente consideranti per se satis clara sunt. Cum itaque plane eodem modo, eademque inclinatione superficiei cylindricae intrinsecus occurrant radij GH, GF, nisi quod hic sursum ille deorsum feratur, manifestum est et refractos in FE HK ita tendere debere, ut pares angulos cum cylindri lateribus PC, BD constituant. Est autem radij GF refractio secundum FE, siquidem ipsius EF refractio ponitur esse FG; ex proprietate nempe refractionum in dioptricis ostensa. Aequales igitur esse debebunt anguli PFE, DHK. Jam vero praeterea si in plano baseos cylindri DQC qui ad horizontis | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 416]
| ||||||||||||||||||||||||||||||||||||||||||||||
de base du cylindre DQC, prolongé horizontalement, la droite CL soit la projection du rayon FE et DM de même celle du rayon HK, il est avéré que les angles QCL et QDM seront aussi égaux entre eux. Or, de l'égalité des angles PFE et DHK on tire facilement la conclusion que les rayons EF et HK auront aussi la même inclinaison par rapport au plan de l'horizon. C'est pourquoi la lumière solaire transmise en se brisant comme il a été dit par les cylindres aqueux suspendus en l'air ne pourra parvenir à l'oeil du spectateur que de ces cylindres-là à partir desquels une droite peut être menée à l'oeil faisant avec le plan de l'horizon un angle égal à la hauteur du soleil; en d'autres termes, de ces cylindres-là seulement qui engendrent aussi l'anneau blanc dont il a été parlé plus haut. Et il appert de cette façon que les deux parhélies ainsi produits ne peuvent être aperçus que situés sur le dit anneau.
§ 28. Or, la raison pour laquelle ces parhélies sont aperçus en des endroits déterminés de l'anneau blanc est absolument semblable à celle dont nous avons parlé un peu plus haut en traitant de l'arc-en-ciel. En effet, si l'on tire dans la figure précédente dans le plan de base du cylindre la droite DN et de même MO parallèles à LC, dont nous avons dit que c'est la projection du rayon EF, on constate que l'angle MDN, c.à.d. DMO, ne peut croître au-delà d'une certaine valeur différente d'après les différentes hauteurs du soleil; par exemple, lorsque la hauteur du soleil est de 25o, cet angle maximum est de 33o 18′. Et comme le nombre des rayons tombant sur le cylindre qui font environ cet angle maximum est beaucoup plus grand que celui de ceux qui font des angles plus petits, comme cela a été dit pour la goutte d'eau dans le cas de l'arc-en-ciel, cette multitude de rayons a pour effet de faire voir les parhélies sous cet angle de part et d'autre de la ligne MO. Si l'on prend donc l'angle OMR égal à l'angle OMD dans le plan de base du cylindre, la distance qui sépare les parhélies l'un de l'autre est représentée par l'angle entier DMR, vu que les plans verticaux érigés sur les droites MD et MR passent chacun par un des deux parhélies. De sorte que l'arc du cercle de l'horizon, et aussi l'arc de l'anneau blanc parallèle à l'horizon, qui est intercepté par ces plans, est d'autant de degrés que l'angle DMR. Or, la moitié de cet angle, c.à.d. la demi-distance des deux parhélies qu'il faut compter le long de l'anneau blanc d'après les diverses hauteurs du soleil est comprise dans le tableau suivant dont la méthode de construction est réléguée à cause de sa prolixité à la fin de ce traité, de même que nous l'avons fait pour quelques tables antérieuresGa naar voetnoot1). | ||||||||||||||||||||||||||||||||||||||||||||||
Table.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 417]
| ||||||||||||||||||||||||||||||||||||||||||||||
planum usque extensus sit intelligatur recta CL subjacere directè radio FE, atque itidem DM radio HK, constat et angulos QCL, QDM aequales fore. Ex aequalitate autem angulorum PFE, DHK, intelligitur etiam ad horizontis planum aequaliter inclinatos fore radios EF, HK. Quamobrem lux solis istis flexibus per cylindros aqueos in aere pendentes transmissa non poterit ad oculum spectatoris pervenire, nisi ab illis cylindris unde recta ad oculum ducta angulum super horizontis plano fecerit altitudini solis aequalem: hoc est, nisi ab illis qui et circulo albo de quo supra materiam praebent. Atque ita liquet parelia bina hoc modo genita non nisi dicto circulo inserta spectari posse.
§ 28. De reden nu waerom dese parelia op seeckere plaetsen des witten circels gesien werden is similis plane aen de gene die wij weynigh te voren vanden regenboogh geseght hebben. want in praecedente schemate, als men treckt in plano basis cylindri rectam DN atque item MO parallel met LC die onder de radius EF geseght is gelegen te sijn, soo wordt bevonden dat den hoeck MDN dat is DMO niet grooter als een seeckere kan werden, welcke grootsten hoeck verscheyden is volgens de verscheijde gestelde sons hooghtens, als bij exempel, als de son 25 gr. hoogh is, soo is desen hoeck ten grootsten van 33.18′. en dewijl veel meer radij op de cylinder vallende desen maximus angulus ontrent maecken als de mindere hoecken, even als in den droppel van de regenboog geseght is, soo maeckt die menighte van radij, dat de parelia op dien hoeck aen wedersijden der linie MO gesien werden. Nemende dan den hoeck OMR ∞ OMD in eodem plano baseos cylindri, soo werdt de distantie tusschen beyde dese parelia aengewesen door den ganschen hoec DMR, want de plana verticalia super rectis MD, MR erecta door beijde der parelia heen passeren. Soo dat den boog des horizontis circuli, atque etiam arcus circuli albi horizonti parelleli ijs planis intercepti even van soo veel graden is als den hoeck DMR begrijpt. De helften dan deses hoecks dat is de halve distantie deser 2 parelia, inde witten ringh te rekenen secundum varias solis altitudines, werdt in de navolgende tafel vervat welckers construendi ratio quia prolixior est ad finem hujus, uti et superius traditarum, relegaturGa naar voetnoot1). | ||||||||||||||||||||||||||||||||||||||||||||||
Tabella
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 418]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 29. En examinant suivant cette table la distance des deux parhélies postérieurs dans le phénomène de Rome [de 1629] que nous nous sommes proposé, je vois qu'elle a dû être de 60o environ; en effet, la hauteur du pôle étant à Rome de 42o 2′, le 20 mars vers 3 heures de l'après-midi la hauteur du soleil était de 30o environ; or, on voit dans notre table que cette hauteur correspond à une demi-distance des parhélies de 29o 36′. Il est vrai que suivant la figure de Scheiner, telle qu'elle est représentée dans le livre de GassendGa naar voetnoot2), la distance des parhélies aurait été de plus de 90o. Cependant on n'a apparemment pas mesuré cette grandeur puisqu'elle n'est pas indiquée dans le livre; c'est pourquoi j'ose soutenir que la distance est figurée beaucoup plus grande qu'elle n'était en réalité, d'autant plus qu'il y a une autre raison pour le croire, savoir que toujours la distance de deux points du firmament semble être d'autant plus grande que ces points sont plus proches de l'horizon: on peut souvent observer que les étoiles du Grand Ours lorsqu'elles sont proches de l'horizon semblent être à des distances l'une de l'autre environ deux fois plus grandes que lorsqu'elles sont près du zénith. Pareillement dans cette occasion la distance des deux parhélies a semblé à celui qui les regardait avoir à l'arc partant du zénith lequel constituait le rayon sphérique de l'anneau blanc, un rapport plus grand qu'il n'était en réalité. Et la raison pour laquelle la même erreur n'a pas été commise dans l'évaluation de la distance des parhélies N et K, c'est que la circonférence DE avait déjà une mesure connue, savoir de 45o environ. Dans quelques-unes des observations suivantes nous remarquerons de nouveau cette fallace de la vision, tant dans la distance de deux parhélies semblables qu'ailleurs. C'est elle aussi qui fait que le soleil semble presque deux fois aussi grand près de l'horizon qu'au haut du firmament, et de même qu'on a l'impression que l'arc-en-ciel fait partie du contour d'un grand cercle à peu près, tandis qu'en réalité il est plus de deux fois moins largeGa naar voetnoot3).
§ 30. Indiquons en passant en peu de mots la cause de cette erreur. Il faut savoir qu'elle provient du fait que lorsque le soleil ou quelqu'autre objet apparaissant au firmament se trouve près de l'horizon, il est jugé par notre vision être beaucoup plus éloigné que lorsqu'il est près du zénith, et cela pour cette raison que nous nous figurons la distance d'objets élevés dans l'air qui sont à grande distance de l'horizon deGa naar voetnoot1) | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 419]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 29. Als ick volgens dese tafel de distantie der 2 parelia postica in het Phaenomenon Romanum nobis propositum examineer soo soude die ontrent de 60 gr. geweest sijn, want de polus hooghte te Romen sijnde van 42o2′, soo was op den 20 Martij ontrent 3 uren nae middaghs de sons hooghte ontrent 30 gr. welcke hooghte men siet in dese tafel dat de halve distantie der parelia geeft 29.36′. Maer volgens het schema Scheijneri soo het in Gassendus boeck staetGa naar voetnoot2) soude de distantie der parelia meer als 90 gr. geweest sijn, doch de mensura daer van en is niet geobserveert geweest noch daer aengeteyckent, en daerom derf ick wel seggen dat veel grooter distantie geteyckent is alsse in der daet was, want daer oock een reden is om sulx te dencken, te weten dat altydt de distantie van 2 puncten in den hemel apparerende soo veel te grooter schynt te sijn als die puncten nader den horizont sijn, gelyck men dickwils sien sal de stellae plaustri borei als se naest den horizont komen wel 2 mael soo wijdt schynen van een te staen dan als de selve ontrent het punctum verticale naederen. soo heeft dan hier oock aen degene die sijn aensight nae dese 2 parelia keerde haer distantie grooter proportie schynen te hebben tot den boogh die door de vertex passerende de wydte van den witten circel LMNK referebat alsse in der daet hadden. Waerom nu het selve oock niet gebeurt is in de distantie der parelia N en K is de reden om dat den circel DE alreets een bekende maet had van ontrent 45 gr. Wij sullen in sommige der volgende observatien dese fallacia visus noch meerder bemercken in de distantie van diergelycke 2 parelia en elders. en het is oock deselfde die maeckt dat de son bijnae 2 mael soo groot ontrent den horizont als boven in den hemel schynt, als mede dat
men den regenboogh bijnae oordeelt een stuck van een
 [Fig. 20.]
maximus circulus te sijn daer hij nochtans niet half soo wijt isGa naar voetnoot3).
§ 30. Ut vero et causam ejus erroris paucis indicemus, hinc eam manare sciendum est, dat wijGa naar voetnoot4) de son of iets anders in den hemel ontrent den horizont wesende veel verder bij ons gesight werdt geoordeelt dan als het ontrent de vertex is, en dat uyt oorsaeck dat wij van de distantie rerum sublimium in aere quae multum ab horizonte absunt geen grooter idea hebben als van die van de welcken die ontrent onsen vertex drijven, maer tusschen ons en die ontrent den horizont syn, sijn wij gewent een groote terrae spacium te sien intercederen ten eynde van welck het caeli convexum schijnt | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 420]
| ||||||||||||||||||||||||||||||||||||||||||||||
l'ordre de grandeur de celle d'objets planant près du zénith, tandis qu'entre nousmêmes et les objets visibles à l'horizon nous savons par expérience qu'il y a un grand intervalle, au bout duquel le ciel convexe semble prendre naissance, lequel, avec tout ce qui y apparaît, nous avons donc l'habitude de juger plus distant là où il est près de l'horizon. Or, lorsque la vue comprend deux grandeurs sous le même angle, ce que nous jugeons être à plus grande distance est toujours estimé être lui aussi plus grand; voilà donc la cause de la déception en question. Mais retournons aux parhélies.
§ 31. L'on doit remarquer, outre ce qui a été traité auparavant, que dans cette observation [de Rome de 1629] les parhélies en question sont dits avoir été blancs, tandis qu'ils auraient dû être colorés, puisqu'ils sont produits par la même cause et la même réfraction que l'arc-en-ciel, et que de plus ils apparaissent colorés dans notre cylindre de verre rempli d'eau. Il faut croire que cela a eu lieu pour la même raison pour laquelle les couronnes se montrent parfois blanches lorsqu'elles sont pâles, ce qui arrive même aussi dans le cas des parhélies paraissant de part et d'autre du soleil, comme on peut le voir ci-dessous dans l'observation exacte de Sam. KecheliusGa naar voetnoot2), où le parhélie C le moins lucide des deux est dit avoir été jaune-blanc, laquelle couleur semble correspondre à la couleur argentée qui se présenta dans le cas de notre observation des parhélies latéraux. Voici cette raison: la couleur jaune et blanchâtre que les cylindres dirigent vers notre oeil dans les réfractions susdites possédant beaucoup plus d'éclat que la couleur rouge, il en résulte nécessairement que lorsqu'il y a peu de corpuscules produisant les parhélies, cette dernière couleur devient invisible avant l'autre et qu'ainsi il subsiste dans les parhélies de la lumière sans couleurs. Il est cependant prouvé que ces parhélies postérieurs sont aussi quelquefois vus colorés: c'est ce que démontre l'observation anglaise tirée de l'histoire de Matthée ParisGa naar voetnoot3) qu'on peut voir plus loin avec les autres, où il est raconté qu'outre le vrai soleil apparurent dans le grand cercle de couleur crystalline quatre faux soleils de couleur rougeâtre, dont la figure, quoique sous d'autres rapports elle ne soit peut-être pas exempte de fautes, fait clairement voir qu'il y en avait deux de postérieurs.
§ 32. C'est peut-être aussi dans la rareté des corpuscules cylindriques qu'il faut chercher la raison pour laquelle dans plusieurs observations ces parhélies n'ont pas du tout été remarqués tandis que l'anneau blanc, lui, fut visible, comme cela a été le cas dans le phénomène de Rome de l'année 1630, dans celui d'Hevelius du 20 février 1661 et dans quelques autres: les parhélies peuvent avoir été si pâles qu'ils étaient inapercevables. Il peut toutefois y avoir eu encore une autre raison, savoir | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 421]
| ||||||||||||||||||||||||||||||||||||||||||||||
te beginnen. het welck dan daer ontrent, met het geen daer in gesien werdt, wij verder gewent sijn te imagineren. Jam vero als men twee grootheden eodem visionis angulo comprehendeert, soo werdt altijdt het geen wij verder meenen te sijn des te grooter oock geoordeelt en dit is de reden ejus quam diximus deceptionis. Ad parelia vero ut revertamurGa naar voetnoot1).
§ 31. Voorts is hier aen te mercken dat dese parelia in dese observatie geseght werden wit geweest te sijn, daerse nochtans gecouleurt moesten wesen, dewylse door de selfde reden en refractie als den regenboog geproduceert werden, en datse oock in onsen glasen cylinder met water gevult gecouleurt schijnen. Illud autem eadem ratione evenisse credendum qua et de coronae altemets wel wit schijnen te wesen alsse flaeuw van licht sijn en selfs oock de parelia quae a latere solis fulgent gelijck te sien is hier onder in de accurata observatio van Sam. KecheliusGa naar voetnoot2) daer het parelium C dat min licht was als t ander geseght wert e flavo candidum geweest te sijn qui color convenit cum argenteo qui in nostris hisce parelijs observatus fuit. Nempe flavus atque albicans color quem cylindri supradictis refractionibus ejaculantur, cum rubro longe sit splendidior, fieri necesse est cum rarior parelijs materia suppetit, ut prius hic quam ille videri desinat atque ita lux sine colorum tinctura in parelijs supersit. Quod autem et colorati aliquando hi postici parelij conspiciuntur comprobat observatio Anglica petita ex historia Matthei ParisGa naar voetnoot3) cum caeteris inferius cernenda, ubi narrantur praeter solem verum apparuisse in circulo magno crystallini coloris quatuor soles adulterinos, rubei coloris, ex quibus duos fuisse posticos figura manifestum facit, etsi forte vitio alioqui non carens.
§ 32. Men moet oock misschienGa naar voetnoot4) tot de raritas van materie der cylinders de causam refereren waerom dat in verscheyde observatien dese bysonnen geheel niet en sijn geremarqueert daer nochtans den witten ringh gesien is geweest. gelyck in het phaenomenon Romanum Ai. 1630, en in dat van Hevelius 1661. 20 febr. en noch andere want dese bijsonnén daer konnen soo flaeuw geweest sijn dat se niet merckelyck sijn geweest. Doch daer kan oock een andere reden geweest sijn te weten dat in | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 422]
| ||||||||||||||||||||||||||||||||||||||||||||||
que dans cette partie de l'anneau blanc les cylindres opaques situés au milieu de l'eau ont été peut-être trop épais par rapport aux corpuscules entiers pour pouvoir livrer passage aux rayons causant ces parhélies. Je trouve en effet, pour une hauteur du soleil de 25o, que si le diamètre du cylindre opaque a été à celui du cylindre aqueux dans un rapport supérieur à 590 : 1000, pas de parhélies postérieurs n'ont pu apparaître, comme cela sera démontré dans ce qui suit. C'est pourquoi dans le phénomène de Rome [de 1630], où le soleil était encore plus élevé, savoir à une hauteur de 28o, si (comme nous pouvons le supposer) les cylindres qui produisaient les parhélies O et P existaient seuls dans les parages où se montrent les parties postérieures de l'anneau blanc, tandis que les cylindres autrement bâtis qui engendrent les parhélies M et N voisins du soleil ne s'étendaient pas jusque là, il ne peut y avoir eu de parhélies dans cette partie postérieure de l'anneau blanc; en effet, dans ces cylindres-là la dimension du noyau est à celle du cylindre entier environ dans le rapport 624 : 1000 [Fig. 21]. Et il en est de même dans le phénomène d'Hevelius où il y avait 6 parhélies et où la hauteur du soleil était de 25o: si les cylindres produisant les parhélies E et D existaient seuls du côté où étaient situées les parties postérieures de l'anneau, ceux qui engendraient les parhélies latéraux D et C ne s'y trouvant point, il ne pouvait à beaucoup près se former de parhélies postérieurs, car dans ces cylindres-là le diamètre du noyau était environ de 714 parties, le diamètre du cylindre aqueux qui l'entourait en ayant par hypothèse 1000.
§ 33. Nous avons donc expliqué toutes les parties du premier phénomène qui fut observé à Rome [en 1629], en attribuant à des cylindres demi-gelés les causes de tous les parhélies et aussi de toutes les circonférences de cercle qui y furent remarquées, cylindres dont une partie étaient suspendus verticalement dans l'air et dont une autre partie voltigeaient sans aucun ordre. Ces causes, si exactement conformes aux phénomènes et si bien reliées entre elles, se corroborent fortement, de sorte qu'on ne peut guère, nous semble-t-il, les révoquer en doute.
§ 34. Nous avons donc montré que la cause de toutes les circonférences de cercle et de tous les parhélies qui apparurent dans le phénomène de Rome de 1629 réside dans les cylindres verticaux ou voltigeant pêle-mêle; de plus il n'y a rien dans les circonstances particulières de cette observation qui ne soit en bon accord avec cette hypothèse. Car la forme plus ronde des parhélies postérieurs en comparaison avec celle des deux autres s'explique par le fait que, bien que quelques-uns des cylindres de l'arc LM de l'anneau blanc, savoir ceux situés près de L et de M, dirigent eux aussi des rayons réfractés vers l'oeil, la quantité de ces rayons est toutefois bien plus | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 423]
| ||||||||||||||||||||||||||||||||||||||||||||||
ea parte circuli albi de cylindri opaci in medio aqueorum te dick sijn geweest nae proportie, niet toelaetende daerom dat de radij die dese parelia maecken door de cylinders passeren. Want ick vind op de sons hooghte van 25 gr. dat indien de diameter van de opacus cylindrus groter reden tot die van de aqueus heeft gehadt als 590 tot 1000, dat dan geen parelia postica konden gesien werden, ut in sequentibus demonstrabitur. Daerom in het phaenomenon romanum daer de son noch hoger was te weten 28 gr. soo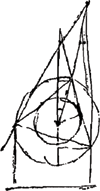 [Fig. 21.]
alleen de cylindri die de parelia O en P maeckten ontrent de achterste delen van den witten ring gevonden wierden, de andere cylinders van de parelia naest de son M en N soo veer niet streckende, soo konnen daer geensins bijsonnen in dat achterste deel des witten rings geweest sijn. want in die cylinders heeft de kern tot de heele cylinder de proportie van ontrent 624 tot 1000 [Fig. 21]. En van gelycken in dat van Hevelius ubi 6 parelia, solis autem altitudo 25o, indien de cylinders die de parelia E en D maeckten alleen ontrent de achterste delen des ringhs gevonden wierden en niet die tot de parelia B en C naest de son stof gaven, soo konden op veer nae geen achterste parelia verschijnen, want de diameter der kernen in illis cylindris fuereGa naar voetnoot1) circiter partium 714 qualium diameter cylindri aquei circumambientis 1000.
§ 33Ga naar voetnoot2). Jam igitur partes omnes phaenomeni prioris quod Romae observatum fuit explicuimus, omnium in eo pareliorum nec non et circulorum causis ad cylindros semigelatos relatis, partim quidem erecto situ pendentes partim vero inordinate volitantes quae causae exacte adeo phaenomenis consentientes, sibique invicem connexae, non parum utique sese mutuo confirmant, adeo ut veras esse haudquaquam ambigi posse videatur.
§ 34. Wij hebben dan al de circels en bysonnen die int phaenomenon Romanum van 1629 gesien sijn haer oorsaeck in de rechtstaende of inordinate volantibus cylindris aengewesen, en daer is voorts niets in eenige circumstantien van die observatie het welck niet en quadreert op de selve hypothesis. Want dat dese achterste parelia ronder als d'andere 2 waeren is om dat alhoewel eenige der cylinders van den boogh LM des witten rings, teweten die niet ver van L en M, oock wel gerefringeerde radij na 't oogh werpen soo is het evenwel longe minor estGa naar voetnoot3) quam quod ab his qui | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 424]
| ||||||||||||||||||||||||||||||||||||||||||||||
petite que celle des rayons provenant de L et de M; pour cette raison les parhélies postérieurs ne s'étendent pas en longueur, en d'autres termes ne possèdent pas de queues lumineuses comme ceux qui sont situés près du soleil. D'autre part les réfractions qui se font dans ces cylindres postérieurs sont plus uniformes parce que la marche des rayons [qui causent les parhélies postérieurs] n'est pas limitée par le cylindre opaque mais uniquement déterminée par la surface fort régulière du cylindre aqueux; en effet, les noyaux opaques ne sont pas exactement semblables entre eux dans tous les cylindres formant un groupe, ce qui explique les contours défectueux et peu permanents des parhélies latéraux. Les alternances de la queue du parhélie N ont été produites elles aussi par le fait que tantôt un plus petit, tantôt un plus grand nombre de cylindres se trouvaient amenés au bon endroit. Une même considération fait comprendre pourquoi la couronne DEF était tantôt fermée en bas et tantôt ouverte, et pourquoi l'intensité du parhélie K augmenta tandis que le parhélie N commençait déjà à s'évanouir.
§ 35. Considérons maintenant l'observation d'Hevelius du 20 février 1661Ga naar voetnoot2), dans laquelle se remarquent plusieurs soleils et plusieurs arcs de cercle, dont quelquesuns, parmi l'un et l'autre groupe, étaient autrement situés que dans les cas précédents. Comme leur cause ne peut être trouvée dans les cylindres verticaux ou voltigeant pêle-mêle (car notre cylindre de verre, transporté çà et là, ne montre rien que ce qui s'est manifesté dans le phénomène de Rome susdit [de 1629]), il faut qu'il y ait eu, outre les cylindres tels que nous les avons décrits, encore autre chose dans l'air. Je montrerai toutefois que cette nouveauté n'a été rien d'autre qu'une position diverse des dits cylindres non considérée jusqu'ici. Mais représentons d'abord le phénomène d'Hevelius avec ses propres paroles et une figure semblable à la sienne. | ||||||||||||||||||||||||||||||||||||||||||||||
Parhélies d'hevelius du 20 février 1661.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 425]
| ||||||||||||||||||||||||||||||||||||||||||||||
in L et M progreditur waer om dan dese parelia door geen vurige steerten in de lenghde geextendeert werden als de andere nevens de son. en ten anderen soo observeren de refractien die in dese achterste cylindri geschieden meerder eenparigheijt dewijl de radiorum cursus non terminatur cylindri opaci objectu. maer alleen sich reguleertGa naar voetnoot1) a superficie politissima cylindri aquei. Want de cylindri opaci juyst soo heel gelyck niet en sijn in al de cylinders die bij malkander hangen, het welck de ambitus lacunosi nec permanentes van de parelia lateralia causeeren moet. En voorts de reciprocatio vande cauda parelij N is geweest door dat altemet minder altemet meerder cylinders op die plaets quaemen gedreven. En soo is mede te verstaen waerom de corona DEF nunc integra a parte inferiori nunc aperta fuerit. En waerom het parelium K stercker wierdt doen N begost te deficieren.
§ 35. Inspiciamus jam porro Hevelianam observationem van de 20 febr. 1661Ga naar voetnoot2) in de welcke plures soles pluresque circuli, et in utrisque aliqui diverso a precedentibus situ notantur. Welcker oorsaeck dewijl niet kan gevonden werden in de recht staende of confuse vliegende cylinders (want onse glase cylinder undique circumlatus nihil praeterquam quod in supradicto Romano Phaenomeno extiterit prodit), soo moet daer behalven noch iets anders in de lucht gebeurt sijn. Het welck ick nochtans sal bethoonen niet als een andere positie der voorseyde cylinders quam nondum consideravimus geweest te sijn. Maer laet ons eerst het phaenomenon ipsius Hevelij verbis similique figura representeren. | ||||||||||||||||||||||||||||||||||||||||||||||
Parelia hevelij 20 febr. 1661.
| ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 426]
| ||||||||||||||||||||||||||||||||||||||||||||||
pâles et se terminant en pointes. 3. Une autre couronne YXHVZ beaucoup plus grande, ayant un diamètre de près de 90o et coupant l'horizon, entourait le soleil et la couronne plus petite GBIC déjà mentionnée. En haut elle étalait des couleurs fort brillantes, tandis qu'aux côtés elle était un peu plus terne et plus mince. 4. À la partie supérieure de chacune des deux couronnes nommées on voyait un arc inverse, montrant pareillement des couleurs diverses, fort beau et fort lumineux; ces arcs avaient le zénith pour centre et touchaient les couronnes en G et H, le diamètre de l'arc inférieur QGR étant de 90o et celui de l'arc supérieur plus petit THS de 45o. Au milieu de l'arc inférieur, au point G où il touchait le cercle BGC, un autre parhélie brillait, mais avec des couleurs plus pâles et une moindre clarté. 5. Il y avait en outre un très grand cercle BEFDC, beaucoup plus ample que les couronnes mentionnées, d'une seule couleur, c.à.d. blanchâtre, parallèle à l'horizon, en d'autres termes partout distant de lui d'un même nombre de degrés (25 à peu près); son diamètre était de 130o et il provenait précisément, pour ainsi dire, des parhélies latéraux B et C. Dans ce cercle brillaient encore trois autres parhélies, d'une couleur absolument argentée ou blanchâtre: le premier se trouvait en D vers l'orient à une distance d'environ 90o du vrai soleil, un deuxième en E vers l'occident et le troisième F au nord. Ce dernier était diamétralement opposé au vrai soleil. Ils étaient tous de la même couleur et de la même clarté. Nous avons vu en outre les parhélies D et E, situés vers l'orient et l'occident, traversés par d'autres arcs de cercle, savoir des arcs d'un certain grand cercle passant par le pôle K de l'écliptique et coupant l'horizon obliquement en P et NGa naar voetnoot2); le même cercle coupait l'écliptique à angles droits et il y avait là des croix pâles parfaitement distinctes. Sept soleils furent donc simultanément et nettement observés; et si j'avais remarqué plus tôt ce phénomène et que je l'avais contemplé d'un lieu élevé, je ne doute guère que j'aurais découvert encore deux autres parhélies en H et I, done neuf et tout; en effet, il y avait là des vestiges tels qu'on pouvait fort bien en tirer cette conclusion. Or, ce phénomène merveilleux et fort agréable à voir dura environ de 10½ heures à 11 h. 51′. Toutefois durant ce temps il ne présentait pas continuellement le même aspect: peu à peu il changeait de forme. Au commencement, vers onze heures, on l'apercevait tel que nous l'avons décrit; après cette heure il dégénéra lentement. D'abord le parhélie septentrional F s'évanouit avec une partie de sa couronne. Les autres parhélies avec leurs couronnes subsistèrent en entier jusqu'à 11 h. 10′. Ensuite le parhélie oriental, et le parhélie occidental après lui, disparurent et les deux croix de même. Peu de temps après les deux parhélies latéraux D et C changèrent de forme; tantôt l'un deux était plus brillant et plus coloré que l'autre, tantôt au contraire il était plus pâle et terne. À 11 h. 18′ par exemple le parhélie occidental B était fort bien visible, tandis qu'au contraire le parhélie C s'évanouissait. Mais à 11 h. 24′ le parhélie oriental était redevenu fort brillant, de sorte qu'à 11 h. 40′ on l'apercevait | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 427]
| ||||||||||||||||||||||||||||||||||||||||||||||
Soles variegati, inprimis Solem versùs, longissimis spissisque caudis, sed albicantibus, & in mucronem terminantibus, videbantur. 3. Alius circulus YXHVZ longè major, 90 gr. propemodùm quoad diametrum, Solem & priorem circulum minorem GBIC ambiebat, ad ipsum horizontem sese exporrigens. A superiore parte, coloribus admodum erat conspicuus, ad latera verò aliquantò tristior, & tenuior. 4. In summitate utriusque dicti circuli duo arcus inversi, itidem diversicolores elegantissimi & lucidissimi, ex puncto Zenith tanquam centro, ad G & H descripti conspiciebantur: illius inferioris arcus QGR, diameter 90. gr. erat; alterius verò superioris & minoris THS 45. gr. In medio inferioris arcus ad G, ubi cum circulo BGC concurrebat, alius pseudo-Sol emicuit, sed colore, & lumine obtusiori, ac debiliori. 5. Ingens circulus prioribus multo amplior, unicolor, albicans, horizonti parallelus, sive à finitore undique 25. gr. ferè aequidistans BEFDC, magnitudine 130. gr. quoad diametrum, ex ipsis pseudo-Solibus collateralibus B, C ortum quasi trahens, deprehensus est. In quo insuper tres parelii, colore omninò argenteo, seu albescente affulgebant: in D ad Orientem gr. 90 propemodum à Sole genuino remotus, eorum unus, in occidente ad E alter, tertius verò F in septentrione, planè in veri Solis oppositione extabat; omnes similis coloris & splendoris. Per pseudo-Soles autem D & E, orientalem & occidentalem, aliaeGa naar voetnoot1) sectiones cujusdam circuli maximi, per Polum Eclipticae K, ad ipsum horizontem usque P & NGa naar voetnoot2), atque per circulum horizonti parallelum ad angulos obliquos, per Eclipticam verò ad angulos rectos incidentes, crucesque albicantes ibidem distinctè referentes, conspeximus. Adeò ut septem Soles simul clarè admodùm observarentur; imo, si citiùs hocce phaenomenum ex edito loco advertissem, non dubito quin duos praeterea Parhelios ad H & I, atque sic numero novem deprehendissem: aderant enim ibidem ejusmodi vestigia, unde id haud malè colligi poterat. Duravit autem insigne & jucundissimum hocce phaenomenum ab hor. fere 10.30′ ad hor. 11.51′. Verùm non eadem facie toto durationis tempore continenter affulgebat, sed paullatim aliam atque aliam induebat formam. Initiò, circa undecimam, dictâ quidem specie notabatur, postmodum autem pedetentim degenerabat. Primo pseudo-Sol F Septentrionalis, cum portione sui circuli evanuit; reliqui Parhelii cum suis arcubus integri ad hor. 11.10′ perseverabant, Deinde, Pseudo-Sol orientalis, postea occidentalis, cum utrâque cruce extinguebantur. Rursùs, paullò post bini Parhelii collaterales D & C immutabantur, modò alter altero erat lumine clarior, & colore distinctior, modò obtusior & obscurior. Hor. namque 11.18′. Parhelius occidentalis B valde erat conspicuus, evanescente contrà orientali C. Rursùs hor. 11.24′ Orientalis perquam clarus extitit; sic ut hor. 11.40′ distinctè adhuc cerneretur, occidentali | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 428]
| ||||||||||||||||||||||||||||||||||||||||||||||
encore nettement, tandis que le parhélie occidental disparaissait complètement. Remarquons encore que ce dernier avait presque toujours été flanqué d'une queue plus longue que le parhélie oriental. En effet, il étendait souvent la pointe de sa queue de 30o, parfois même de 90o, par conséquent jusqu'au parhélie E, tandis que le parhélie oriental C étendait rarement sa queue plus loin que de 20o. A 11½ h. la grande couronne verticale YXHVZ était évanouie. Mais les arcs inverses H et G, avec les deux parhélies nommés B et C, subsistèrent jusqu'à la fin. Quant à la figure, pour qu'on l'entende mieux, nous l'avons présentée comme on pourrait le faire pour les étoiles fixes indiquées sur un globe artificiel en nous supposant placés en dehors de ce globe: en effet de cette manière tout peut être représenté beaucoup plus distinctement et intelligiblement. Mais le véritable endroit d'où le phénomène fut observé se trouvait à peu près sous le zénith, à l'intérieur du cercle horizontal; par conséquent le vrai soleil fut aperçu par nous au sud, l'un des parhélies, savoir F, au nord, et les autres E et D aux côtés (est et ouest). Que si vous désirez vous mettre sous les yeux ce phénomène rarissime un peu plus distinctement, décrivez du soleil A (toujours sur le globe artificiel) placé au 2ième degré des Poissons et en adoptant une hauteur du pôle telle que nous l'avons ici à Danzig, d'abord le cercle GBIC d'un rayon de 22½o; ensuite le cercle YXHVZ d'un rayon de 45o; 3. le cercle NEKDP d'un rayon de 90o passant par les deux parhélies pâles distants de 90o du soleil; 4. du zénith avec un rayon de 22½ l'arc THS; 5 du même centre avec un rayon de 90o l'arc QGR. Enfin, avec un rayon de 65o, le cercle BEFDC parallèle à l'horizon. Lorsque vous aurez accompli ce travail, la fort belle harmonie et symétrie de tous ces cercles vous sautera aux yeux; de cette manière vous aurez aussi l'occasion de concevoir d'autant plus aisément avec l'aide de Dieu les causes naturelles de tous les parhélies et de toutes les parasélènes.
§ 36. Dans ce phénomène [Fig. 22] on rencontre, comme dans celui expliqué plus hautGa naar voetnoot1), le grand anneau blanc, les parhélies latéraux B et C, et la couronne BGCI, tirant tous leur origine des cylindres verticaux comme nous l'avons fait voir précédemment. On y rencontre aussi les parhélies E et D avec les arcs HE, PD passant par eux pour la raison donnée dans les §§ 21 et 22. Il apparaît que ces arcs sont des parties d'une circonférence de cercle ayant le soleil pour centre comme les deux autres circonférences. Or, il est évident par ce qui a été dit aux §§ 23, 25 et 31 pourquoi ce cercle paraissait interrompu vers le haut. Nous avons expliqué en outre au § 32 pourquoi les parhélies postérieurs ne sont pas apparus.
La distance du soleil A aux deux parhélies E et D doit avoir été inférieure à 88o 48′, car à cette hauteur de 25o du soleil les parhélies latéraux ne peuvent être | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 429]
| ||||||||||||||||||||||||||||||||||||||||||||||
interim penitùs disparente; ut ut hic perpetuo orientali longiorem ferè caudam prae se tulisset. Saepiùs enim mucronem 30. gr. non nunquam 90. gr. ad ipsum pseudo-Solem E exporrigebat, at orientalis C caudam suam vix supra 20. gr. extendebat. Hor. 11.30′. circulus maximus verticalis YXHVZ dissipatus est. Inversi verò arcus H & G, simul cum duobus illis Parheliis B & C ad finem usque subsistebant. Ipsam delineationem quod attinet, melioris intellectûs gratiâ, ita spectandam exhibuimus, adinstar Fixarum in globo artificiali extantium; acsi extra sphaeram consisteremus: eâ enim ratione longè distinctiùs, & clariùs adumbrantur omnia. Interea tamen locus observationis fuit sub puncto Zenith circiter, intra circulum horiz. parallelum: hincque genuinus Sol nobis in Meridie, alter Pseudo-Sol F in Septentrione, & reliqui E & D ad latera conspiciebantur. Quod si autem aliquantò clariùs hocce rarissimum phaenomenum Tibi ob oculos poni desideras; describe ex Sole A (in globo nempe artificiali) in 2. gr. Piscium tunc constituto, & quidem ad nostram Elevationem Poli Dantiscanam, radio 22½ gr. primùm circulum GBIC; deinde, radio 45. gr. circulum YXHVZ; 3. Circulum NEKDP, per duos albescentes pseudo-Soles, à Sole 90. gr. distantes, transientem radio 90. gr. 4. Ex puncto Zenith radio 22½ gr. rursùs arcum THS. 5. Ex eodem Centro radio 90. gr. arcum QGR. Denique Circulum BEFDC horizonti parallelum radio 65. gr. Re sic peractâ, luculentissimè patebit, omnium circulorum pulcherrima harmonia atque Symmetria; sic ut inde eò faciliùs caussas naturales omnium Parheliorum, & Paraselenarum penetrandi, annuente Deo, dabitur occasio.
§ 36. In dit phaenomenon [Fig. 22] sijn even als in 't voor geexpliceerdeGa naar voetnoot1) de witten grooten ring de parelia lateralia B en C, en de corona BGCI, hebbende alle haer oorsprong uyt de rect over end staende cylinders gelyck aldaer aengewesen is. En van gelycken oock de parelia E en D met de bogen HE, PD daer door gaende om de reden § 21, 22Ga naar voetnoot2) welcke bogen blyckt dat stucken sijn van een circulus ex sole A quo et reliqui duo descriptus. En uyt het geen § 23, 25, 31Ga naar voetnoot2) is geseght is manifest waerom desen circel boven interruptus apparuerit. Qui autem fieri potuerit ut parelia postica non apparerent explicuimus § 32. De distantie porro tusschen de son A en beyde de parelia E en D moet | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 430]
| ||||||||||||||||||||||||||||||||||||||||||||||
vus à une plus grande distance comme cela sera démontré plus loinGa naar voetnoot1); et lorsqu'ils atteignent cette position extrême ils ne peuvent être que fort pâles en comparaison des deux autres B et C; c'est pourquoi dans cette occasion ils ont paru blancs et les arcs EH, DP de même, suivant ce qui a été dit au § 31. La circonférence ZHY a été produite soit par des grêlons sphériques soit par des cylindres voltigeant sans aucun ordre, ce dont nous avons traité plus haut au § 20. Soit encore par une autre cause dont nous parlerons ci-après au § 41.
§ 37. Mais ce qu'il s'agit de rechercher ici en premier lieu c'est la cause des arcs THS et QGR et celle des parhélies G et H qui s'y trouvent. Quant au parhélie F, diamétralement opposé au vrai soleil, nous ne tâcherons pas encore ici de l'expliquer: nous le ferons tout à la finGa naar voetnoot3). Nous avons dit plus haut qu'une vapeur montante, comparable à un vent, maintient les cylindres en l'air, et que ce ‘vent’ est aussi en partie la cause qui sorme les cylindres et assure souvent leur verticalité. Toutefois outre cette position-là des cylindres j'en trouve encore une autre que beaucoup d'entre eux doivent prendre, savoir la position horizontaleGa naar voetnoot4). Certaines expériences font voir qu'il en est vraiment ainsi: lorsqu'on forme de petits cylindres tels que dans l'eau, ou bien dans l'air, ils descendent lentement, on verra qu'ils le font presque toujours en prenant la position horizontale, bien entendu depuis le moment où leur vitesse n'augmente plus. Or, si l'eau ou l'air dans lequel les cylindres tombent montait avec une vitesse égale à celle avec laquelle les cylindres descendent, ils figureraient exactement les cylindres demi-gelés maintenus en haut par l'air, de sorte qu'il est indubitable que beaucoup d'entre ces derniers doivent prendre la position nommée. Même on dirait, en considérant les expériences susdites, qu'ils devraient presque tous devenir horizontaux et qu'il ne pourrait en subsister de verticaux. Mais ici il faut prendre en considération que nous ne pouvons imiter parfaitement ce que la nature opère dans la région éthérée, car la position verticale des cylindres est abondamment prouvée par le fait que tant de phénomènes, comme nous l'avons vu, s'expliquent par lui. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 431]
| ||||||||||||||||||||||||||||||||||||||||||||||
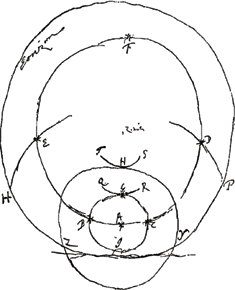 [Fig. 22.]
binnen de 88 gr. 48′Ga naar voetnoot1) geweest sijn, want op dese hooghte der son van 25 gr. konnen de lateralia parelia niet verder gesien werden als hier nae sal bewesen werden, en ontrent dese uytterste veerheijt komende konnen oock niet als seer flaeuw in comparatie van de 2 B en C wesen, daerom hier oock maer wit geschenen hebben als mede de bogen EH, DP, volgens t gene geseght is § 31Ga naar voetnoot2). Den circel ZHY is of uyt ronde kernen, of uijt confuse volitantibus cylindris gemaect geweest waer van hier boven § 20Ga naar voetnoot2). of uyt noch een andere oorsaeck daer van hier naer § 41Ga naar voetnoot2).
§ 37. Maer dat hier praecipue te inquireren is, is de oorsaeck der bogen THS QGR, en daerin des parelij G en H nam de parelio F soli vero è diametro, nondum hoc loco inquiremus, sed postremo omniumGa naar voetnoot3). Wij hebben te voren geseght dat een opwaerts treckende damp venti instar de cylinders in de lucht om hoogh houdt, den selven ventus synde oock ten deelen de oorsaeck die de cylinders formeert, ende waerom die veeltijdts recht over endt blyven staen. Jam vero soo vindt ick behalven dese positie der cylinders noch een andere die veele der selver moeten aen nemen, te weten dat se met haer zijde parallel met het plat der eerde gaen leggenGa naar voetnoot4). Om van t welck verseeckert te sijnGa naar voetnoot5) experimenta quaedam edocent. Want als men cylinderties formeert die of per aquam vel per aerem lentioreGa naar voetnoot6) motu deorsum ferantur, men sal sien dat sy altydt bynae meest transverso situ neerdalen te weten als se soo ver gekomen sijn dat haer celeritas niet meer en vermeerdert. Indien nu het water of de lucht daer se in neerdalen met die selve rasheijt naer boven steegh, als die daer de cylinders mede neerdalen soo soudense juijst de cylinders van halfijs representeren die door de lucht om hoog werden gehouden, soo dat dan niet te twijffelen is of vele deser moeten oock tot dusdanigen positie sich voegen. Jae men soude moeten seggen als men de voors. experimenta considereert dat se bijnae aile aldus transverse souden moeten gaen leggen, en datter geen rechtoverendt souden konnen blijven. Maer hier moet men dencken dat wij niet t'eenemael perfect konnen imiteren 't geen de natuerGa naar voetnoot7) in regione aetherea perficit, want van de perpendiculaire standt der cylinders abunde testantur al 't gene wij hier te voren gesien hebben daer door soo klaerlyck door gecauseert te werden. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 432]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 38. Je dis donc que c'est dans les cylindres horizontaux mentionnés, en d'autres termes dans ceux dont les axes sont tous parallèles au plan de la terre, quoique nullement entre eux, que doivent être vus les arcs colorés inverses tels que le sont ici QGR et THS. Pour le comprendre il faut considérer que, bien que les cylindres gisent pêle-mêle, il y en a un grand nombre dont les axes sont dirigés vers chaque point déterminé de l'horizon, p.e. vers l'est, le sud-sud-est, le sud-ouest, ainsi que vers tout point quelconque intermédiaire. Il faut savoir en outre que les rayons du soleil, pour produire [Fig. 23.]
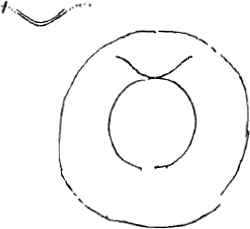 [Fig. 24.]
ces arcs, pénètrent dans les cylindres en se réfractant deux fois comme ils le font en produisant les parhélies latéraux. Lorsque le soleil se trouve p.e. au sud, la partie de l'arc la plus proche du soleil, telle que G et H dans notre figure, se forme dans les cylindres dont les axes sont couchés dans la direction est-ouest, ceux par conséquent sur les côtés desquels les rayons solaires tombent à angles droits. On sait, d'après ce qui précède, que parmi les cylindres dont les axes ont cette direction, il n'y en a pas de plus proches du soleil qui puissent transmettre les rayons solaires à l'oeil. Quant aux autres dont les axes sont couchés dans d'autres directions, ils ne peuvent pas encore laisser passer les rayons lorsqu'ils se trouvent à la même proximité du soleil que les précédents (puisque le soleil a une certaine élévation au-dessus de leur plan de base), comme cela paraît par la table du § 17. Plus précisément, il doit arriver ceci dans les cylindres de chaque position différente: plus ces positions s'écartent de la direction est-ouest, plus éloignées du point milieu seront les parties des arcs que ces cylindres produiront. Et en investigant avec soin la vraie forme de ces arcs, je trouve la diversité suivante: lorsque le soleil est près de l'horizon, les arcs inverses touchant l'un la circonférence à diamètre de 45oGa naar voetnoot2), l'autre celle à diametre de 90o, ont les formes que voici [Fig. 23]: l'arc qui touche la plus petite circonférence | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 433]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 38. Ick segge dan dat in de voors. leggende cylinders te weten wiens axes altemael parallel sijn met het plat der aerde, alhoewel niet inter se, de inversi gecouleurde bogen als hier QGR en THS moeten gesien werden. Om het welk te verstaen, soo moet men concipieren dat een groot getal van dese cylinders, alhoewel onder een gemenght, met haer assen naer elcken oort des horizonts gestreckt leght als nae oost, zuydt zuyd oost, zuyd west, en nae alle bedenckelycke puncten daer tusschen. voorts is te weten dat de radij solis om dese bogen te maecken met 2 refractien even als in 't maecken der parelia lateralia door de cylinders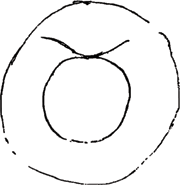 [Fig. 25.]
 [Fig. 26.]Ga naar voetnoot1)
penetreren. Sijnde dan de son bij exempel in 't zuijden soo wert het deel des booghs naest aen de son als hier G en H geformeert in de cylinders die met haer as oost en west leggen, te weten op welcker sijden de sons stralen rechthoekigh schijnen; notum quippe ex praecedentibus dat van de cylinders diens assen soo leggen, nullos propiores soli solares radios ad oculum transmittere posse, d'andere nu diens assen anders gestreckt leggen en konnen noch soo nae niet aen de son, als de voorgaende, de stralen door laten passeren, dewijl de son boven het plat harer basis verheven is, als blijckt bij het tafeltien supra § 17. atque ita porro in singularum positionum cylindris fieri necesse est dat hoe verder dat se van de positie van Oost en West verscheyden sijn hoe veerder delen der bogen (van 't midden af te rekenen) bij haer veroorsaeckt werden. Ende als ick de rechte figuer deser bogen curiose investigo soo vind ick dese naevolgende differentie, te weten als de son aen den horizont is, soo komt de inversus bogenGa naar voetnoot2) aen de circels d'een van diameter 45 gr.Ga naar voetnoot3) en d'ander van 90 gr. op dese manier [Fig. 23], sijnde die van de kleynste als 2 hoornen. Ende | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 434]
| ||||||||||||||||||||||||||||||||||||||||||||||
a, comme on voit, l'apparence de deux cornes. C'est toujours la couleur rouge qui se trouve du côté du soleilGa naar voetnoot1). Lorsque le soleil a une hauteur de 10o, je trouve des arcs tels que les suivants [Fig. 24]. Lorsque le soleil a une hauteur de 20o, des arcs tels que ceux-ci [Fig. 25]. On voit par ces figures qu'au milieu ces arcs peuvent en vérité être assimilés à des circonférences de cercle, mais que vers les extrémités il ont une courbure inverse. Mais puisque les cylindres qui produisent la partie centrale sont, comme il a été dit, éclairés plus perpendiculairement par le soleil, et les autres d'autant plus obliquement que la partie de l'arc qu'ils produisent est plus éloignée du point milieu, il n'est pas étonnant que généralement la partie centrale de ces arcs paraisse seule assez fortement lumineuse.
§ 39. Or, les parhélies qui apparaissent quelquefois précisément au milieu de ces arcs, comme ici au point G, ne sont pas autre chose que la partie des arcs la plus lucide de toutes. C'est pourquoi ces parhélies ne peuvent jamais paraître nettement limités ou luisants à eux seuls parmi les parties voisines des arcs. C'est aussi ce que remarque Hevelius dans toutes les images de ce genre du soleil ou de la lune aperçues par lui (savoir deux parhélies et une parasélène), disant qu'elles étaient plutôt obscures, mal visibles et faibles; il ajoute que le parhélie en H était également douteux. Ce que explique peut-être pourquoi cette partie centrale de l'arc inverse est plus ou moins séparée du reste de l'arc, c'est qu'une grande partie des cylindres horizontaux étant plutôt courts peuvent ne pas posséder précisément une surface cylindrique, mais présenter plutôt l'aspect d'ellipsoïdes oblongs. On voit du reste qu'il y a un accord parfait entre nos figures et l'observation d'Hevelius en ce que l'arc inverse est d'autant moins courbé que le soleil ou la lune, ainsi que la couronne, sont plus élevés au-dessus de l'horizon. En effet, dans son observation des parasélènes, où la lune était quelque 26o ou 27o au-dessus de l'horizon, l'arc qui touchait la première couronne était une partie d'une très grande circonférence. Il en fut de même dans le phénomène des 7 soleils. Mais dans ceux du 6 avril et du 17 décembre 1660, où le soleil ou la lune n'avait qu'une hauteur de 14o à 15o on voit que ces arcs sont des parties de circonférences de cercle bien plus petites. Il est vrai que dans l'observation d'Hevelius ici considérée l'arc inverse supérieur semble montrer une plus forte courbure qu'il n'en devrait avoir suivant notre calcul: la raison en est que ces arcs, étant si élevés au-dessus de l'horizon, trompent nécessairement l'oeil, de sorte qu'ils paraissent appartenir à des circonférences bien plus petites que celles dont ils font partie en réalité. Car d'après ce que nous avons dit au § 29 la grandeur d'une circonférence située près du zénith n'est estimée qu'à la moitié de la valeur qu'on lui atttibue lorsqu'elle se trouve dans une position basse, c.à.d. près de l'horizon; ce qui doit avoir lieu également lorsqu'il ne s'agit que d'une partie d'une circonférence. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 435]
| ||||||||||||||||||||||||||||||||||||||||||||||
altijdt de roodt gecouleurde sijde nae de son toeGa naar voetnoot1). als de son 10 gr. hoogh is vind ick de bogen aldus [Fig. 24]. De son 20 gr. hoogh sijnde, aldus [Fig. 25]. Men siet ex his dat dese bogen in midden wel aen stucken van circels gelyck schijnen, maer nae de eynden weder met contrarie bochten om gekromt werden. Doch dewijl de cylinders die het middelste deel maecken, als geseght is, rechter van de son beschenen werden, en d'andere hoe veerder daer van daen hoe obliquius soo is 't niet wonder dat gemeynlyck alleen het middelste stuck deser bogen als stercker licht hebbende gesien wert.
§ 39. Ende de parelia die recht in midden deser bogen somtijdts verschijnen als hier in G en sijn anders niet quam in praedictis arcubus pars luciddimaGa naar voetnoot2) omnium. Daerom oock dese parelia noijt seer afgescheijden of boven de partes arcuum vicinas verlicht konnen schijnen; gelyck oock Hevelius in alle dergelycke imagines bij hem geobserveert sijnde 2 parelien een paraselene annoteert dat se obscuriores, obtusiores en luce debiliori waren sijnde alhier oock in H een dubium parelium. Of misschien mach dit oock de reden wesen waerom dit middelste deel eenighsins van de rest des booghs afgescheyden schijnt, te weten dat een menichte der leggende cylinders kortachtiger sijn, en daer door weynigh of niet van een cylindrische superficies hebben maer als een langwerpigh sphaeroides geformeert sijn. Voorts soo siet men dat hier t'eenemael met de observatien van Hevelius over een komt, dat hoe hoger de son of maen en de corona boven den horizont staen, hoe vlacker de inversus arcus komt te sijn. Want in sijn observatie paraselenarum daer wel 26 of 27 gr. boven den horizont geweest is den boog aen d'eerste Corona een stuck van een seer groot ront als oock int phaenomenon van 7 sonnen, maer in die van den 6 Apr., en van den 17 Dec. 1660 daer de son of maen maer ontrent 14 of 15 gr. hoogh was, siet men dese bogen vrij van kleynder circels stucken te sijn. Het is waer dat de bovenste deser bogen in Hevelius observatie kleynder ronds stucken werden verthoont als volgens onse rekening mosten wesen, maer de reden is dat dese bogen soo hoog boven den horizont staende daer door nootsaeckelijck het oogh bedriegen, soo datse stucken van veel kleynder rondt schynen als se sijn. Want volgens het geene wij § 29Ga naar voetnoot3) gesecht hebben, soo werdt een selfde rondt ontrent den zenith staende maer half soo groot geestimeert dan als het om leegh ontrent den horizont staet, het welck dan even mede van gelycken in de stucken der ronden moet plaets hebben. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 436]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 40. Les arcs qui doivent selon nous toucher la couronne intérieure en bas auraient pu être visibles dans deux observations d'Hevelius, savoir celle du 30 mars 1660 et celle des 7 soleils; dans ce dernier cas on en a remarqué du moins quelque chose: il dit qu'on voyait en I le vestige d'un parhélie. Mais faute de matière, laquelle s'étend rarement au loin, ceci n'a été qu'une pâle lueur.
§ 41. Or, la méthode pour trouver les formes susdites des arcs est la suivante. Décrivons sur une sphère ABC [Fig. 27] un grand cercle ADC ayant le point B pour pôle et représentant l'horizon. Ensuite un cercle vertical BD passant par le soleil qui se trouve par hypothèse en E, de telle manière que l'arc DE soit d'autant de degrés qu'en avait la hauteur du soleil dans l'observation considérée. Si nous voulons donc trouver l'arc inverse qui touche la plus petite couronne, prenez les arcs EF et EG du cercle vertical BED chacun de 22½oGa naar voetnoot2). F et G sont alors le point le plus élevé et le point le plus bas de la couronne et en même temps les points milieux des arcs inverses que nous cherchons. Pour en trouver d'autres points, lesquels doivent provenir des cylindres couchés dans diverses positions, considérons une multitude de cylindres horizontaux dont le plan de base soit parallèle à un certain cercle vertical MB, et menons par le soleil un plan HEK parallèle à ce dernier. Si alors, songeant à ce que nous avons démontré plus haut à propos des cylindres verticaux, l'on se figure que le cercle MB représente l'horizon, au centre duquel N se trouve le spectateur, et que la circonférence parallèle HEK soit l'anneau blanc passant par le soleil, l'arc HM sera la hauteur du soleil au-dessus de cet ‘horizon’ MB et par conséquent aussi la hauteur du soleil au-dessus du plan de base des cylindres considérés, car nous avons posé que leurs bases sont parallèles au cercle MB. Cela étant ainsi, il est évident qu'il suffit de prendre dans le cercle HEK les endroits L et K où les parhélies latéraux devraient être aperçus dans ces cylindres ce qui est aisé en faisant usage de la table du § 17. Car lorsque p.e. l'arc HD, lequel représente ici par hypothèse la hauteur du soleil au-dessus des bases du cylindre, est de 30o, la table fait voir que les arcs EK et EL doivent être chacun de 28o 48′ de leur circonférence. De cette manière les endroits K et L sont connus: ce sont deux des points cherchés dont l'un appartient à l'arc inverse inférieur et l'autre à l'arc inverse supérieur. Pareillement on peut trouver d'autres points en nombre suffisant pour rendre manifeste la courbure de l'arc. Et l'on peut suivre la même méthode pour trouver l'arc inverse qui touche la plus grande circonférence. Avant d'abandonner la considération de ce phénomène observons que la circon- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 437]
| ||||||||||||||||||||||||||||||||||||||||||||||
§ 40. De bogen die volgens ons onder aen de binnenste corona moeten komen, souden in 2 observatien van Hevelius te weten die van de 30 Mart. 1660 en in die van de 7 sonnen konnen gesien geweest hebben en sijn oock eenighsins altydt in dit laetste gesien, want hij seght dat in I een vestigium van een parelium wierdt gesien. Doch door defect van materie, dewelcke raro soo veer sich extendeert heeft dit maer een flaeuwe schijn geweest. 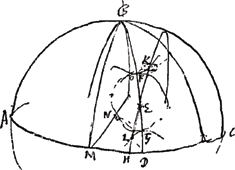 [Fig. 27.]Ga naar voetnoot1)
§ 41. Porro siguras arcuum praedictas inveniendi ratio est hujusmodi. In sphaera aliqua ABC [Fig. 27] describatur polo B circulus maximus ADC qui horizontem referat. deinde verticalis per solem transiens BD, posito nempe solem esse in E, ita ut arcus DE sit tot partium quot erat in observatione altitudo solis. Si igitur arcum inversum qui minorem coronam tangit invenire velimus, soo neemt de bogen EF, EG in de verticalis BED ieder van 22½ gr.Ga naar voetnoot2) soo zijn de puncten F en G het opperste en onderste deel der corona, ende te gelyck de middelste puncten der inverse bogen die wij soecken. On nu d'andere puncten daer van te vinden die in de cylinders van verscheyde positien moeten gesocht werden, soo laet geconsidereert werden een menighte der plat leggende cylinders quorum planum basesGa naar voetnoot3) parallelum sit alicui verticali circulo MB, aen welcken een circulus parallelus per solem ducatur HEK. Als men nu gedenckt t geen wij boven bewesen hebben van de recht over endt staende cylinders, en dat men sich den circel MB als horizont inbeelt in wiens center N den spectator gestelt zij en de parallel HEK als sijnde den witten ring door de son gaende, soo is dan den boogh HM de sons hooghte boven dien horizont MB, zijnde mede alhier de hooghte des sons boven het planum baseos cylindrorum de quibus nunc agitur, want wij hebben gestelt haer bases parallel te sijn aen den circel MB. quibus ita se habentibus soo consteert dat men alleen nemen moet in den circel HEK de plaetsen L en K daer de parelia lateralia soude moeten in die cylinders gesien werden, het welck door de tafel [van § 17] licht is. want sijnde bij ex. den boogh HD, die hier fingitur esse solis altitudo supra bases cylindrorum, van 30 gr. soo wyst de tafel dat de bogen EK, EL ieder gr. 28.48 van haer circel moeten wesen. Waer door dan de plaetsen K en L bekent syn synde 2 der gesochte puncten 't een in d'onderste arcus inversus en t' ander inde bovenste. En op de selve manier maghmen soo veel der selve puncten vinden dat de flexus van de arcus daer door manifestus werdt. En de selfde manier is te observeren in 't vinden der arcus inversi die de groter circel aen raeckt. Priusquam autem ab hujus phaenomeni consideratione digredia- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 438]
| ||||||||||||||||||||||||||||||||||||||||||||||
férence de cercle ZHY a pu également provenir de ces cylindres horizontaux, phénomène dont auparavant nous cherchions la cause dans de petits cylindres voltigeant sans ordre ou dans des grêlons sphériques à moitié fondus. En effet, comme, d'après notre démonstration du § 21, les cylindres verticaux peuvent engendrer une couronne, de même ces cylindres couchés horizontalement sont capables de produire le même effet, vu la rondeur de leurs extrémités se terminant par exemple en demisphères ou demi-ellipsoïdes. Il est même probable que ce soit là dans le cas considéré l'origine du phénomène, puisqu'on voit que de part et d'autre cet anneau ZHY provient précisément du parhélie H, et qu'on puisse observer la même chose chez d'autres parhélies de ce genre. En effet le fait que l'anneau provient des parhélies semble indiquer que les mêmes cylindres horizontaux causent et ces anneaux et les arcs inverses.
§ 42. Ayant compris ceci, nous ne trouverons rien qui nous cause quelque difficulté dans la deuxième observation de Scheiner de l'année 1630 dans laquelle brillèrent 6 soleils et que nous représentons plus bas avec les autresGa naar voetnoot2). Il faut seulement remarquer que les parhélies O et P sont apparus dans les intersections de la plus grande couronne et de l'anneau blanc pour cette raison que des cylindres verticaux furent la matière servant à produire cette couronne d'après ce qui a été démontré plus haut au § 21. Toutefois comme le parhélie supérieur H est également indiqué comme situé cur cette couronne, la partie supérieure de la couronne a pu être engendrée elle aussi par des cylindres horizontaux comme nous venous de le dire. Or, la cause pour laquelle l'arc inverse passant par le parhélie Q n'a pas été noté peut avoir été qu'il s'étendait peu de part et d'autre en que par conséquent on ne l'a pas vu s'écarter suffisamment de la couronne ZQB; en effet pour cette hauteur de 28½o du soleil cet arc n'a qu'une très légère courbure vers le haut: nous avons déjà vu que pour une hauteur du soleil de 27o l'arc devient parfaitement horizontal. Enfin, quant à la double couronne intérieure qui est aperçue dans ce cas, nous en avons donné la cause plus haut au § 22.
§ 43. Les trois autres phénomènes d'HeveliusGa naar voetnoot3), savoir ceux qu'il observa le 30 mars, le 6 avril et le 17 décembre, ont des causes évidentes d'après ce qui a été dit plus haut. A cette exception près que dans la dernière de ces observations une croix blanchâtre a été vue composée de deux bras, l'un horizontal l'autre vertical, se coupant dans le disque même de la lune. Or, la cause de cette croix s'offre d'ellemême: elle doit être provenue des cylindres verticaux et horizontaux suspendus dans l'air et capables de produire les parasélènes et les diverses circonférences. En effet, d'abord le bras horizontal n'était rien d'autre qu'une partie du grand anneau blanc lequel, d'après le § 13, passe aussi par le soleil dans tous les cas analogues. Le fait que cet anneau n'apparaît pas toujours accompagné de parhélies ou de parasélènes latéraux s'explique ou par la rareté de la matière, c.à.d. le petit nombre des cylindres | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 439]
| ||||||||||||||||||||||||||||||||||||||||||||||
mur notetur causam circuli ZHY etiam ab his jacentibus cylindris esse potuisse, quam supra ad cylindrulos confuse volitantes vel grana rotunda semiliquata retulimus; te weten, gelyck wij ad § 21Ga naar voetnoot1) gethoont hebben hoe de rechstaende cylinders een corona konnen veroorsaecken, even soo konnen oock dese leggende cylinders het selfde te weegh brengen, aengesien de rondheijt haerer eynden quae in semisphaeras vel semiellipses veluti desinunt. Ende het is waerschynelijck alhier soo te geschieden, dewijl men siet dat desen ring ZHY juijst ten weder sijden uijt het parelium H vloeijt, en dat van gelijcken in andere diergelycke parelia accidere animadversuri simus, want dit significare videtur dat de selfde leggende cylinders dese ringen en de arcus inversi causeren.
[§ 42]. Et his quidem intellectis nihil admodum quod remorari nos possit in Scheineri altera observatione anni 1630 reperiemus, in quo 6 soles effulsere quodque cum caeteris infra exhibemusGa naar voetnoot2). Animadvertendum tantum parelia O et P in intersectionibus coronae majoris et circuli albi apparuisse eo quod erecti cylindri materia hujus coronae fuerint, secundum superius ostensa § 21Ga naar voetnoot1). Veruntamen cum et parelius superior H in eadem corona notetur, potuit superior coronae pars ex jacentibus quoque cylindris constitui ut modo dictum. Trans parelium Q vero arcum inversum non esse notatum causa fortasse fuerit quod parum utrinque extensus fuerit ideoque à corona ZQB non satis recedere visus, nam in ista solis altitudine gr. 28½, valde parum sursum curvatur arcus hic, quippe quem jam in altitudine solis 27 gr. admodum planum fieri vidimus. De duplici denique circulo interiori, qui hic cernitur, causam attulimus supra § 22Ga naar voetnoot1).
[§ 43]. Porro autem et alia tria phaenomena HevelianaGa naar voetnoot3) nempe quae 30 Mart. et 6 Apr. et 17 Dec. observavit causas manifestas habent ex antedictis. nisi quod in postremo horum crux albicans visa est e trabibus binis transversa rectaque in ipso lunae disco sese intersecantibus. Hujus vero causa in ipsis illis cylindris erectis transversisque qui ad paraselenas circulosque efficiendos in aere pependere ultroGa naar voetnoot4) sese offert. Primo namque trabs transversa nihil aliud fuit quam pars circuli magni albi qui et per solem transire solet de quo § 13Ga naar voetnoot1). qui quo minus semper una cum parelijs aut paraselenis lateralibus appareat, vel raritate materiae sit hoc est cylindrulorum erectorum, vel | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 440]
| ||||||||||||||||||||||||||||||||||||||||||||||
verticaux, ou bien par le trop grand éclat du soleil ou de la lune, comme je l'ai déjà remarqué ci-devant au § 14.
§ 44. Quant à l'autre bras, perpendiculaire à l'horizon, il doit son origine à la réflexion des rayons lunaires contre les petits cylindres horizontaux qui produisaient également les arcs inverses d'après ce qui a été dit plus haut. Ces petits cylindres ayant leurs génératrices et leurs axes parallèles au plan de la terre, quoique nullement entre eux, il s'ensuit nécessairement, lorsque le soleil est si près de l'horizon qu'il le fut ici (car sa hauteur n'était que de 12o) qu'un très grand nombre de ceux qui apparaissent depuis l'horizon jusqu'à une certaine hauteur au-dessus du soleil, doivent avoir leur point brillant dans ce bras vertical [Fig. 28], lequel, près du soleil et de part et d'autre de lui, doit être le plus étroit et le plus nettement limité; c'est la partie inférieure entre le soleil et l'horizon qui doit être la plus parfaite; au-dessus de lui le bras doit peu à peu s'élargir et disparaître. Tout cela paraît avoir été ainsi dans le cas considéré, comme la figure l'indique. Toutefois ce bras vertical, provenant de la réflexion sur les cylindres dont nous avons parlé, n'a pu avoir des contours tout-à-fait aussi nets que la figure semble nous les représenter, attendu que dans les cas de ce genre les points brillants d'une partie des cylindres horizontaux doivent être aperçus en dehors de ce bras, quoiqu'en bien moins grande quantité que ceux qui apparaissent dans lui. Or, la démonstration du fait que ce bras doit avoir tant d'éclat peut être donnée à l'aide d'une figure [Fig. 29] telle que l'avant-dernière. De même qu'il a été dit là, soit ADC l'horizon, E le soleil, ED sa hauteur, c.à.d. l'arc d'un cercle vertical (mesurant 12o dans le cas ici considéré), BM le cercle vertical supposé parallèle aux bases d'une multitude de cylindres horizontaux, HEK la circonférence parallèle à BM: cette circonférence HEK est alors la seule dans laquelle le spectateur N peut apercevoir les points brillants du groupe de cylindres dont nous venons de parler. De la même manière tout autre groupe ou autre direction des cylindres correspond à une circonférence lucide traversant le soleil et allant de là à l'horizon. Or, ainsi que dans notre figure la circonfé- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 441]
| ||||||||||||||||||||||||||||||||||||||||||||||
ipsorum luminum solis aut lunae fulgore vehementiore sicut jam supra monui § 14Ga naar voetnoot1). [§ 44]. De andere trabs autem die uyt den horizont perpendiculaer op stondt is voortgekomen uijt de reflexie radiorum lunarium tegen de leggende cylinderties welcke oock de arcus inversus hier gecauseert hebben volgens het gene hier te voren is geseght. Dese cylinderties dan met haer sijden en assen leggende parallel met het planum terrae, alhoewel niet met malkander parallel, soo volght nootsaeckelyck als de son soo leeg is als hier, fuit enim tantum 12 gr., dat een seer groote menichte der gener die van onder den horizont af tot een stuckweeghs boven de son gesien werden,  [Fig. 28.]
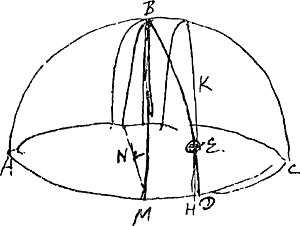 [Fig. 29.]
moeten haer blinck punt hebben in dese rechtstaende trabs [Fig. 28]. dewelcke dicht aen weder sijden der son op sijn smalste moet sijn en perfectst getermineert, en sijn onderste deel tusschen de son en den horizont perfecter als een stuckweeghs boven dese, waer van daen sich verspreiden moet en evanesceren. alle twelck in dese oock alsoo geweest te sijn schijnt de figuer te demonstreren. Alleenlijck en heeft ex dicta cylindrorum reflexione dese trabs erecta niet soo net getermineert konnen wesen als de figuer schijnt mede te brengen, om dat oock een deel der platleggende cylinders haer blinck punct buyten dese trabs gesien moet werden, maer op veer nae niet soo vele alser daer in komen. De demonstratie autem waerom dese trabs soo illustris moet wesen kan door een figuer [Fig. 29] de naest voorgaende gelyck geexpliceert werden. Want gelyck daer geseght is, ADC den horizont zijnde, E de son, zijnde hier haer hooghte, dat is den boogh circuli verticalis ED, 12 gr. en deGa naar voetnoot2) verticale circel BM parallel gesupponeert met de bases van een menighteGa naar voetnoot3) der plat leggende cylinders, den circulus HEK parallel met BM, soo is desen circel HEK den genen in welcken den spectator N den blinck van de geseijde portio cylindrorum alleen kan vernemen en op gelycke wijse heeft ieder portio of directio cylindrorum sijn circulum lucidum die door de son E tot op den horizont komt. | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 442]
| ||||||||||||||||||||||||||||||||||||||||||||||
rence KEH (ou du moins ses parties situées près du soleil) est proche du vertical passant par le soleil, ainsi en est-il aussi d'un grand nombre d'autres circonférences pareilles, et ceci a pour effet de faire apparaître, pour ainsi dire, une colonne lumineuse le long de la ligne verticale BD dans lequel le soleil est vu. Or, plus le soleil est bas, plus cette colonne doit apparemment être forte et nette, puisque dans ce cas un nombre de plus en plus considérable des dites circonférences lumineuses sont serrées dans un espace fort étroit, et puisqu'en même temps une plus grande quantité de cylindres planent entre nous et le soleil que lorsque celui-ci se trouve à une grande hauteur au-dessus de l'horizon.
§ 45. On pourrait attribuer à la même cause un genre de météore observé par Christophe Rothmann à Cassel le 2 janvier 1586 qu'il décrit comme suit. Consultez sa description de la comète de l'année 1585Ga naar voetnoot2). Dans l'aurore, avant le lever du soleil - or, le ciel était serein auprès de l'horizon - apparut une colonne droite située exactement dans un cercle vertical, d'une largeur égale environ au diamètre apparent du soleil. Si vous l'aviez vue, vous auriez cru contempler l'incendie d'un village au-delà des montagnes. La colonne était en effet couleur de feu et absolument pareille à une flamme si ce n'est qu'elle était partout également large. Peu après se leva dans cette colonne une image du soleil tout-à-fait comme si c'eût été le vrai soleil. A peine un doigt de cette image était-il encore caché par l'horizon lorsque le vrai soleil se leva dans la même colonne, lequel fut suivi de la même manière par une deuxième image. Cette colonne continua à être visible avec la série de ses trois soleils qui se touchaient. Elle se tenait pour ainsi dire toujours toute droite dans le cercle vertical, comme le montrait le quadrant, et ces soleils étaient tous de la même forme si ce n'est que le soleil du milieu, le vrai, surpassait les autres par son éclat. Ils subsistèrent avec cette colonne durant un quart d'heure environ jusqu'à ce qu'un nuage noir venant d'en haut les cacha. Ceci, dis-je, est arrivé par la réflexion due aux cylindres horizontaux. Ou peut-être (et l'on pourrait préférer cette hypothèse à cause des images du soleil) y-a-t-il eu une multitude de petits cylindres verticaux avec de petites étoiles plates aux extrémités inférieures et supérieures telles que Descartes en a vu tomber. Car ceux-ci, quoique voltigeant séparément dans l'air (c'est ainsi que je me les représente), étant soutenus par le courant ascendant, doivent en général garder la position verticale qu'ils avaient en se formant (nous parlerons de leur génération dans la suite), sans toutefois se tenir debout si exactement qu'ils ne pourraient s'écarter tant soit peu de la verticalité. Ces lamelles stelliformes constituent donc autant de petits miroirs plans dans lesquels les rayons de soleil sont réfléchis à angles égaux, de sorte que la partie supérieure de la colonne avec le parhélie qu'elle contenait a été vue par réflexion sur les bases inférieures de ces cylindres et le parhélie inférieur ainsi que la partie cor- | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 443]
| ||||||||||||||||||||||||||||||||||||||||||||||
Sicut autem hîc de circulus KEH partibus suis soli E vicinis dicht aen de verticalis solis komt, soo doet oock een groote menichte der andere, en dit maeckt alsoo dat als een lucida columna langhs de verticalis BD daer de son in is gesien werdt. Quanto autem humilior sol erit soo veel te stercker en afgescheydender blyckt dat dese columna moet wesen om dat dan intra angustius spatium plures ex dictis lucidis circulis cogantur. en om dat dan te gelyck oock major multitudo cylindrorum inter nos ac solem interjicitur dan als de son hoogh boven den horizont sublatus is.
[§ 45]. Ad eandem causam referri posset meteori genusGa naar voetnoot1) a Christoph. Rothmanno observatum Cassellis 2 Jan. 1586 quod ita describit. Vide descriptionem ejus de cometa anni 1585Ga naar voetnoot2). Apparebat primo antequam sol oriretur in aurora, (erat enim caelum circa horizontem clarum) columna erecta ad amussim in circulo verticali, latitudine ubique tanta quanta apparebat diameter solis. Incendium alicujus pagi ultra montes dixisses si vidisses. Erat enim prorsus specie ignea tanquam flamma, nisi quod ubique ejusdem esset spissitudinis. Paulo post oriebatur in ea columna idolum solis, non aliter atque si esset sol verus. Vix digitus de hoc idolo adhuc sub horizonte latebat, cum in eadem columna oriretur sol verus, quem eodem modo subsequebatur aliud idolum, permanebatque columna haec cum tribus suis continuè se contingentibus solibus, ut ita dicam semper erecta in circulo verticali, ut quadrans ostendebat; erantque soles hi ejusdem formae, nisi quod intermedius et verus reliquos fulgore antecelleret, durabantque cum ea columna ad quadrantem fere horae, donec nubes nigra a vertice superveniens eos obtegeret. Dit segh ick is door reflexie der leggende cylinders geschiet of om de imagines solis soudemen misschien seggen dat ter een menichte van rechtoverend staende cylinderties geweest zij met sodanige platte sterreties onder en boven aen als die bij de Cartes gesien sijn nedervallende. Want dese alhoewel seorsim door de lucht vliegende (want soo stel ick se) ab aura sursum tendente suspensae, ut plurimum erectam positionem servare debent, qua et genitae sunt (dicemus autem de generatione earum in sequ.) nec tamen adeo accuratè quin saepe pauxillo ab ea declinent. Dese lamellae stellatae sijn dan totidem parva specula plana in quibus radij solares ad angulos aequales reflectuntur, soo dat de pars columnae superior met het parelium daer in door reflexie der onderste bases van die cylindri is gesien, en het onderste parelium en stuck vande | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 444]
| ||||||||||||||||||||||||||||||||||||||||||||||
respondante de la colonne par réflexion sur les bases supérieures. J'ai dit que ces cylindres ne demeurent pas si exactement verticaux que quelques-uns d'entre eux ne s'inclinent légèrement, d'un ou deux degrés p.e., parce que, s'ils se tenaient parfaitement droit, de sorte que leurs bases supposées planes étaient exactement horizontales, il ne pourrait y avoir de réflexion des rayons solaires dans ces bases vers notre oeilGa naar voetnoot1). | ||||||||||||||||||||||||||||||||||||||||||||||
[pagina 445]
| ||||||||||||||||||||||||||||||||||||||||||||||
columna door reflexie der bovenste bases. Ick hebb geseght dat se soo juijst niet perpendiculaer en blyven dat niet een weynighje, puta gr. uno aut altero sommige inclineren, om dat indiense heel recht stonden en haer bases juijst plat en parallel met den horizont waren, dan soude geen reflexie der radij der son in de bases konnen geschieden nae ons oogh toeGa naar voetnoot1). |
| |||||||||||||||||||||||||||||||||||||||||||||


