Oeuvres complètes. Tome XVII. L'horloge à pendule 1656-1666
(1932)–Christiaan Huygens–
[pagina 273]
| ||||||||||||||||
II.
| ||||||||||||||||
[pagina 274]
| ||||||||||||||||
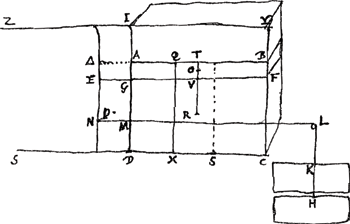
laet het vat sijn IDCY [Fig. 3], het waters oppervlack AB. En laet ons nemen de
 [Fig. 3.]
sijde die overkants gesien wort en verthoont door de lini ID. en zij gestelt AQ gelijck aen de helft van AD des waters hoogde en getrocken QX met AD evenwijdigh so dat &c. Ick segh dat het gewight rustende tegen de sijde AD even is aen het gewight des waters van de pylaer AQXD, dewelcke beteyckent een pylaer wiens grond is het plat AD en de hooghde AQ, even aen de helft van AD des waters hooghde. Ofte om alles klaerder voor te stellen: genomen dat den bodem ID beweeghelijck waer, zijnde de buijten sijde van 't lichaem ZIDS, het welck ick neem dat sonder swaerte sij, en voorwaerts en achterwaert kan schuijven tusschen de vlacken SC en ZY; en dat daeraen in M vast gemaeckt waer de lijn MLH, gaende tot het katrol L toe evenwijdigh met de grond DC, en dat daer aen hingh het gewight H, van de selve swaerte sijnde als de gesegde pylaer waters AQXD. Ick segh dat dit aldus gestelt sijnde het gewicht H even machtich is &c., het lichaem ZIDS in die stant sal gehouden werden, niet voorwaerts noch achterwaerts schuijvende. Want indien 't sijn kan, laet ons nemen voor eerst dat het gewight H te licht zijnde, het gewelt des waters ADCB de sijde ID achterwaerts persse tot in EN en het gewicht dienvolgens oplichte tot in K; soo sal dan het oppervlack des waters, het welck sij EF nu leger sijn als AB; oock blijckt dat het water vervat in de plaets ED even is aen dat te voren was in AF en dat de plaets GFCD vol blijft. Laet het punt P midden sijn van de plaets ED en O van AF. soo sal P swaerheyts middelpunt sijn des waters ED, en O des selfden waters middelpunt doe het was in AF. Vorders laet door O getrocken werden TVR evenwijdigh met AD, dat VR gelijck sij aen de helft van GD: en verlenght BA tot in ∆. Om dat dan den rechthoeck ED even is aen den rechthoeck AF, soo is DG tot GA als FG tot GE. Maer DA heeft tot AG grooter reden als DG tot dezelve GAGa naar voetnoot1); | ||||||||||||||||
[pagina 275]
| ||||||||||||||||
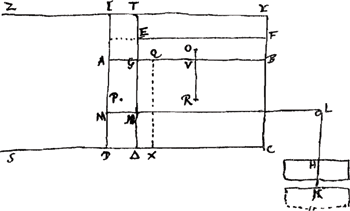
soo heeft oock DA tot AG grooter reden als FG tot GE. Gelijck nu DA tot AG alsoo is den rechthoeck DQ tot GQ: en gelijck FG tot GE alsoo is den rechthoeck AF tot G∆. Soo heeft dan den rechthoeck DQ tot GQ grooter reden als den rechthoeck AF tot G∆; en wisselende oock den rechthoeck DQ tot AF grooter reden als den rechthoeck GQ tot G∆. dat is, als AQ tot A∆ ofte als RO tot MN, want MN is gelijck A∆ en RO gelijck aen AQ, dat's aen de helft van AD, om dat RV is gestelt gelijck de helft van DG, en VO gelijck half GA. Maer gelijck den ▭ DQ tot
 [Fig. 3 bis]
AF alsoo is de swaerte van 't water des pylaers DQ, dat is de swaerte H tot de swaerte van 't water in AF te vooren begrepen. Soo heeft dan de swaerte H tot de swaerte des waters AF grooter reden als de lini RO tot NM dat is KH, want NM en KH sijn nootsaeckelyk gelijck. dewijl nu het punt R even hoogh is als P, het is openbaer dat OR de lenghde is van het daelen des waters het welck uijt AF nedergekomen is in ED. Soo heeft dan de swaerte van H tot de swaerte des lichaems AF grooter reden als het nederdalen van 't selve lichaem AF tot het rijsen van't lichaem H. Waerom oock het swaerheijts middelpunt tusschen de twee lichaemen ED en K sal hoogher wesen, als dat tusschen AF en H. Het welck niet sijn en kan, naedemael de lichamen van selfs geseijt werden beweeght te sijnGa naar voetnoot2). ZijGa naar voetnoot3) nu daerentegens genomen soo 't mogh. is dat het gewicht H [Fig. 3 bis] te swaer zijnde den bodem DI, tot aen T toe voorttrecke, en dienvolghens nedersacke tot in K. Des waters oppervlack sal dan verhooght werden, ick neem dat het kome | ||||||||||||||||
[pagina 276]
| ||||||||||||||||
te sijn EF; en het is seecker dat het water van EB even groot is als het gheene de plaets GD van te vooren vervulde: blijvende de plaets G∆CB even vol. Laet nu het punt P midden sijn van de plaets A∆ en O van EB. en treckt OVR evenwijdigh met AD, dat VR gelijck sij aen de helft van AD of van G∆. Soo is dan het punt R even hoogh als P, en RO de lenghde van het oprijsen des deels water uijt de plaets A∆ tot in EB. Om dat nu VR aen de helft van AD gelijck is, dat is aen AQ, soo sal RO grooter sijn als AQ soo heeft dan RO tot AG dat is tot HK grooter reden als QA tot deselve AG. Maer gelijck QA tot AG, alsoo is den rechthoeck QD tot den rechthoeck GD en de selfde proportie heeft de swaerte des waters van de pylaer QD, dat is de swaerte H tot de swaerte des waters GD. Soo heeft dan RO dat is het opklimmen des waters GD, grooter reden tot HK het nederdaelen van H, als de swaerte van H tot de swaerte des waters GD, daerom dan oock het middelpunt der swaerheijt die bestaet uijt het gewicht K en het deel waters dat in EB opgeklommen is, hoogher sal wesen als te voren het middelpunt der swaerheyt bestaende uijt H en het selfde deel waters synde in GD. Het welck onmoghelijck is, om dat de beweghing van selfs wert geseght geschiet te sijnGa naar voetnoot1). | ||||||||||||||||
II. B. Explication théorique de la gravitation terrestreGa naar voetnoot2) (1659)Ga naar voetnoot3).Hoc idem est gravitas corporis quod conatus materiae ipsi aequalis ac celerrimè motae a centro recedendi. Qui sustinet suspensum is detinet materiam istam ne recedat, qui vero sinit cadere, eo ipso facultatem praebet eidem materiae recedendi a | ||||||||||||||||
[pagina 277]
| ||||||||||||||||
centro secundum radium, cum autem a principio recedat à centro secundum numeros impares ab unitate, id facere non potest quin corpus grave cogat similiter accelerato motuGa naar voetnoot4) versus centrum accedere. adeo ut haec initio motusGa naar voetnoot5) necessario aequalia sint, recessio materiae a centro, et corporis cadentis accessus versus centrum. Unde et comperto descensu hujus qui certo tempore contingit, velut si 1‴ decidit per spatium ⅗ lineae, cognoscemus quoque ascensum materiae istius a centro, qui nempe 1‴ tempore etiam erit ⅗ lineaeGa naar voetnoot6). Hinc jam celeritas materiaeGa naar voetnoot7) data terrae semidiametro. Hinc porro vis centrifuga in minoribus circulis. Videndum enim qua in re consistat et quid determinet magnitudinem istius conatus. Nempe quantitas recessus certo tempore. haec vero et a celeritate gyrationis et a magnitudine circuitus pendetGa naar voetnoot8). | ||||||||||||||||
[pagina 278]
| ||||||||||||||||
II C. Question de la diminution de la pesanteur par l'éloignement du centre de la terre (1666).an ad radicem et in vertice montis 3000 pedum aliqua differentia esset in horologio? non est notabilisGa naar voetnoot1). | ||||||||||||||||
II D. Mesure de la distance verticale parcourue en un temps donné par un corps qui tombe librement et preuve expérimentale du fait que ce corps commence sa chute avec une vitesse nulle.II D. § 1Ga naar voetnoot2). Expertus 21 Oct. 1659. Semisecundo minuto cadit plumbum [Fig. 4]Ga naar voetnoot3) ex altitudine 3 pedum et dimidij vel 7 pollicum circiter. Ergo unius secundi spatio ex 14 pedum altitudineGa naar voetnoot4).
II D. § 2Ga naar voetnoot2). Expertus denuo 23 Oct. 1659. pendulum adhibui [Fig. 4]Ga naar voetnoot3) cujus singulae vibrationes 3/2 secundi unius. unde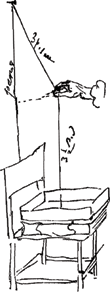 [Fig. 4.]Ga naar voetnoot3)
semivibratio qua usus sum erat ¾″. Erat penduli longitudo circiter 6 p. 11 unc. Sed vibrationes non ex hac longitudine sed conferendo eas cum pendulo horologij colligebam. Illius itaque semivibratione cadebat aliudGa naar voetnoot5) plumbum simul e digitis demissum ex altitudine 7 pedum 8 unc. Ergo colligitur hinc uno secundo casurum ex altitudine 13 ped. 7½ unc. ferèGa naar voetnoot6). Ergo in priori experimentoGa naar voetnoot7) debuissent fuisse non toti 3 ped. 5 poll. Sumam autem uno secundo descendere plumbum pedibus 13. unc. 8Ga naar voetnoot8). Mersenne 12 ped. paris. uno secundo confici scribitGa naar voetnoot9). 12 ped. Paris. conficiunt circiter 12 ped. 8 unc. RhijnlandGa naar voetnoot10). Ergo Mersenni spatium justo brevius est uno pede Rhijnl.
II D. § 3Ga naar voetnoot11) (1659). Et in his quidem eam obtinere cum experimenta alia tum parabolicae lineae demonstrant quas in speculi plani superficie inclinata quocunque angulo sphaerula perfecte rotunda designat, quibus nullae describi possunt accuratiores. Ex quibus etiam probatur certissimè grave cadens per omnes tarditatis gradus transire nam si ita non esset, lineae istae non tantum non possent esse parabolae, sed ne curvae quidem in vertice deprehenderentur sed angulo quodam inflexae. Si enim verbi gratia | ||||||||||||||||
[pagina 279]
| ||||||||||||||||
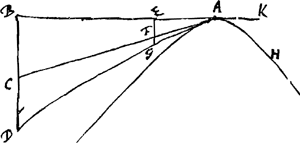
quam primum grave ex A [Fig. 5] descendere rursum incipit celeritatem aliquam habere dicaturGa naar voetnoot12), sit ea ejusmodi qua possit unius secundi tempore conficere aequabili | ||||||||||||||||
[pagina 280]
| ||||||||||||||||
 [Fig. 5.]
motu spatium BC. motu autem horizontali ponatur secundi tempore conficere spatium AB. ubi igitur ad perpendicularem BC pervenerit erit grave inferius puncto C puta in D, nam quia initio descensus ex A habebat celeritatem qua transiret aequabili motu lineam BC; ea autem celeritas secundi spatio aucta est continuè, necesse est proinde uno secundo descendisse per lineam majorem ipsa BC quae igitur esto ut dixi BD. Similiter si AE ponatur ⅓ AB; ergo triente secundi quo pervenit ex A ad perpendm. EG, amplius descendisse grave necesse est quam per EF, quae est ⅓ BC; adeo ut verbi gr. hic descenderit usque in G. Atque ita continuè lineam quandam descripsisse necesse est quae tota cadit infra rectam AC. Sed cum tali linea certum est nullam aliam, ut HA, in puncto A convenire posse quin angulum aliquem cum ipsa constituat non minorem angulo CAK, nempe si HA ut hîc tota sit infra lineam AK. Ergo linea à mobili descripta, ad A angulo esset inflexa, quod non accidit. Ergo nullam celeritatem habet mobile ipso initio descensus ex A. 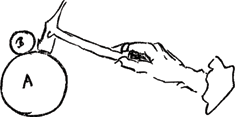 [Fig. 6.]
 [Fig. 7.]
Alio experimento idem confirmatur hujusmodi. Globum A [Fig. 6] e dura materia manu sustine, alterumque minorem superimpone B durum itidem, quem inter digitos tantum leniter contine ne decidere possit. Inferiorem desuper percute malleo C, quamlibet leviter. Videbis, si inter lumen et oculum tuum globi exponantur, etiam minimo ictu parumperalterum ab altero separari. Cum autem minima velocitas motus ex ejusmodi percussione adveniat globo A, qui tamen ab altero disjungitur, apparet non continuo atque A globus | ||||||||||||||||
[pagina 281]
| ||||||||||||||||
recessit inesse globo B celeritatem qua ipsum consequi possit. At in globo A qualibet celeritate minor celeritas leviculo ictu generari potest. ergo globo B cadere incipienti, etiam qualibet minor hoc est nulla celeritas inestGa naar voetnoot1).
II D. § 4Ga naar voetnoot2). 15 Nov. 1659. Pendulum AB [Fig. 7] semivibrationi impendebat 3/4 unius secundiGa naar voetnoot3); filum idem BDC plumbum B et glandem C retinebat, deinde forficibus filum incidebaturGa naar voetnoot4), unde necessario eodem temporis articulo globulus C et pendulum moveri incipiebant. plumbum B in F palimpsestoGa naar voetnoot5) impingebatur, ut clarum sonum excitaret. globulus in sundum capsae GH decidebat. simul autem sonabant, cum CE altitudo erat 8 pedum et 9½ unciarum circiter. Sed etsi 3 quatuorve uncijs augeretur vel diminueretur altitudo CE nihilo minus simul sonare videbantur. adeo ut exacta mensura hoc pacto obtineri nequeat. At ex motu conico penduli debebant esse ipsi 8 pedes et 9½ unciae. unde uno secundo debebunt peragi a plumbo cadente pedes 15. unc. 7½ proximeGa naar voetnoot6). Sufficit quod experientia huic mensurae non repugnet, sed quatenus potest eam comprobet. Si plumbum B et globulum C inter digitos simul contineas ijsque apertis simul dimittere coneris, nequaquam hoc assequeris, ideoque tali experimento ne credasGa naar voetnoot7). Mihi semper hac ratione minus inveniebatur spatium CE, adeo ut totius interdum pedis differentia esset. At cum filum secatur nullus potest error esse, dummodo forfices ante sectionem immotae teneantur. Penduli AB oscillationes ante exploraveram quanti temporis essent ope horologij nostri. Experimentum crebro repetebam. Ricciolus Almag. l. 9 secundo scrupulo 15 pedes transire gravia statuit ex suis experimentis. Romanos nimirum antiquos quos a Rhenolandicis non differre Snellius probatGa naar voetnoot8). | ||||||||||||||||
[pagina 282]
| ||||||||||||||||
 [Fig. 8.]
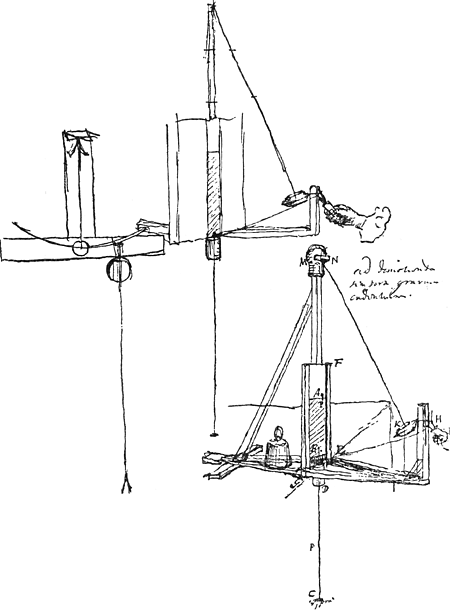
II D. § 5 (1664)Ga naar voetnoot1). Ad dimetienda tempora gravium cadentium. Caput M [Fig. 8] mobile, in que eo mobilis item paxillus N, hoc est ut extrahi amplius vel introrsum trudi possit; haec eo fine ut caput fili NK exacte suo loco constitui possit, hoc est, ut pendente immoto pondere K, tangatur charta AB. Locus autem hujus contactus signo notetur. | ||||||||||||||||
[pagina 283]
| ||||||||||||||||
 [Fig. 9.]Ga naar voetnoot3)
Ut accurate noscatur momentum quo plumbum D casum peregit, prius exiguum | ||||||||||||||||
[pagina 284]
| ||||||||||||||||
pondus C funiculo suspenditur qui superne cohaeret chartae oblongae BA, quae mobilis est sursum ac deorsum super asserculo FG, sed leni pressu retinetur in P. funiculus autem CB per medium transit plumbi D perforati, sed liberrimè. Simul autem descendere incipiunt plumbum D et pendulus discus K, dissectoGa naar voetnoot1) funiculo LHK utrumque retinente, in H. Cum vero pondus D ad C pervenit, simul ipsum ac chartam AB deorsum pellit et discus K facta dimidia oscillatione notam imprimit chartae AB, unde apparebit quantum spatij praeter DC, plumbum cadens peregerit dictae semioscillationis tempore.
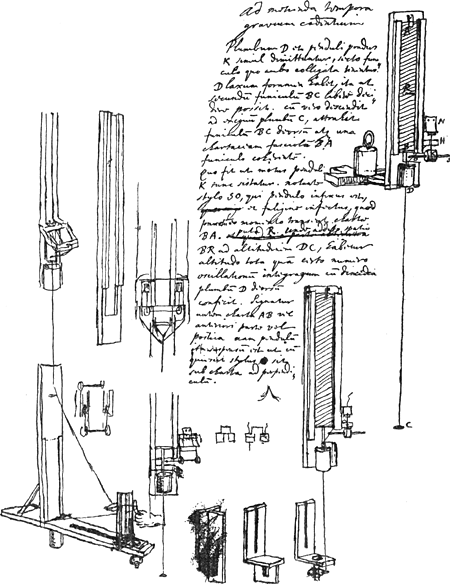
II D. § 6 [1664]Ga naar voetnoot2). Ad metienda tempora gravium cadentium. Plumbum D [Fig. 9] et penduli pondus K simul dimittuntur, secto funiculo quo ambo colligata tenentur. D laxum foramen habet, ita ut secundum funiculum BC libere decidere possit. cum vero descendit ad exiguum plumbum C, attrahit funiculum BC deorsum atque una chartaceam fasciolam BA funiculo cohaerentem. Quo fit ut motus penduli K tunc sistatur. notante stylo SO, qui pendulo infixus est, et fuligine infectus, quod punctum eo momento transeat chartae BA. puta R. unde addito spatio BR ad altitudinem DC, habetur altitudo tota quam certo numero oscillationum integrarum cum dimidia plumbum D deorsum confecit. Signatur autem charta AB vel anteriori parte vel postica. nam pendulum ita suspensum est ut cum quiescit stylus O sit sub charta ad perpendiculumGa naar voetnoot4). | ||||||||||||||||
[pagina 285]
| ||||||||||||||||
II E. Calcul de 1666 de la période d'une oscillation (cycloïdale) en un endroit déterminé de la terre en tenant compte de la force centrifuge due à la rotation du globe terrestreGa naar voetnoot5).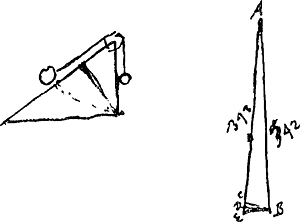 [Fig. 10.]
AD, AC, hoc est ad 341½ prox. Ergo tempus per AB vel per AC ad tempus per AD ut 341 ad 341½ sive ut 682 ad 683Ga naar voetnoot7). 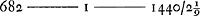 sive 2′7″, quibus horologium pendulum sub 45 gr. latitudinis lentius incederet una die quam idem sub poloGa naar voetnoot8). 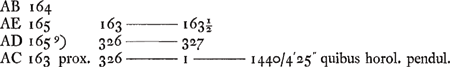 | ||||||||||||||||
[pagina 286]
| ||||||||||||||||
sub aequinoctiali lentius esset una die quam idem sub polo. 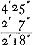 quibus horolog. lentius esset sub aequin. in una die quam idem sub latit. 45 gr.Ga naar voetnoot8) (voir la note 8 de la p. 285). quibus horolog. lentius esset sub aequin. in una die quam idem sub latit. 45 gr.Ga naar voetnoot8) (voir la note 8 de la p. 285).
| ||||||||||||||||
II FGa naar voetnoot1). Remarque générale sur le calcul de la grandeur d'une ligne, d'une surface ou d'un volume en partant p.e. de la considération de la pesanteur (méthode d'Archimède).Quicquid supposueris non impossibile sive de gravitate sive de motu aliave re, si inde probes aliquid de magnitudine lineae superficiei vel corporis hoc verum eritGa naar voetnoot2). velut Archimedes quadraturam parabolae, posito nisu gravium per parallelas. |
| |||||||||||||||