Oeuvres complètes. Tome XVII. L'horloge à pendule 1656-1666

[p. 149]

IV.
Pièces correspondant à quelques parties de la pars quarta de l'‘Horologium oscillatorium’ de 1673, intitulée: ‘De centro oscillationis’¹⁾.
[?]²⁾

§ 1²⁾. Invenire perpendiculum simplex habens vibrationes aequales vibrationibus perpendiculi compositi³⁾.

AED [Fig. 56] est perpendiculum compositum, cujus virga AD inflexibilis et sine pondere intelligitur. Dantur autem longitudines AD ∞ a, AE ∞ b. Pondus D ∞ d. Pondus E ∞ e.

Quaeritur HK ∞ x, longitude perpendiculi simplicis, composito ἰσοχρόνου,

1) La Pars Quarta contient de plus quelques considérations sur la mesure universelle et sur la valeur numérique de l'espace parcouru en une seconde par les corps tombants. Dans les notes 7-9 de la p. 119 et 8 de la p. 121 nous avons déjà fait entendre que la plupart des morceaux qui se rapportent à la fois au Sommaire et à la Pars Quarta ont été publiés ailleurs.
On trouve en outre aux p. 414-555 du T. XVI des Pièces se rapportant à la Pars Quarta datant d'une ou de plusieurs années après 1660; parmi ces pages quelques-unes (p. 424-433) contiennent des considérations au sujet du poids curseur destiné à régler la marche des horloges à pendule, sur lequel on peut consulter aussi les p. 105-111 qui précèdent. Voir pour la mesure de ce que nous appelons la constante g de la gravitation, sujet également traité dans la Pars Quarta, la note 1 de la p. 100 ainsi que la Pièce ultérieure du présent Tome consacrée à ce sujet.

2) Les §§ 1-6 (la division en §§ est de nous) sont empruntés aux p. 46-50 du Manuscrit 13 (voir la note 2 de la p. 139). Nous avons admis ailleurs, tout en reconnaissant l'incertitude des dates, que plusieurs Pièces de ce Manuscrit, quoique se rapportant à des découvertes antérieures, y ont été inscrites en 1667 ou 1668 (voir les p. 458 du T. XIV et 375 du T. XV). Eu égard à l'impossibilité de dater exactement les Pièces en question, nous croyons néanmoins pouvoir les insérer ici: ces pages ne contiennent rien qui fût inconnu à Huygens en 1665. Par contre nous préférons publier plus tard comme Appendice à l'‘Horologium oscillatorium’ les p. 35-37 et 39-40 du même Manuscrit, qui se rapportent aux développées, à la rectification des courbes et à la quadrature des surfaces, quoique la même remarque sur la date y soit applicable.

2) Les §§ 1-6 (la division en §§ est de nous) sont empruntés aux p. 46-50 du Manuscrit 13 (voir la note 2 de la p. 139). Nous avons admis ailleurs, tout en reconnaissant l'incertitude des dates, que plusieurs Pièces de ce Manuscrit, quoique se rapportant à des découvertes antérieures, y ont été inscrites en 1667 ou 1668 (voir les p. 458 du T. XIV et 375 du T. XV). Eu égard à l'impossibilité de dater exactement les Pièces en question, nous croyons néanmoins pouvoir les insérer ici: ces pages ne contiennent rien qui fût inconnu à Huygens en 1665. Par contre nous préférons publier plus tard comme Appendice à l'‘Horologium oscillatorium’ les p. 35-37 et 39-40 du même Manuscrit, qui se rapportent aux développées, à la rectification des courbes et à la quadrature des surfaces, quoique la même remarque sur la date y soit applicable.

3) Comparez sur les formules qui suivent la p. 419 du T. XVI.

[p. 150]

[Fig. 56.]

fit x ∞ daa + bbe/da + be

Quod si vero data longitudine perpendiculi AD et pondere D itemque pondere E, oporteat invenire longitudinem AE, ut fiant oscillationes perpendiculi compositi aequales oscillationibus dati perpendiculi HK, fit ex aequatione praecedenti haec alia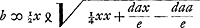



in qua aequatione daa/e major est quam dax/e, quia a major quam x, ac proinde duas veras radices¹⁾ habet aequatio.

§ 2²⁾. Data longitudine et pondere virgae, itemque gravitate ponderis in ima virga affixi, invenire perpendiculum simplex aequipollens.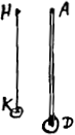

[Fig. 57.]

§ 3³⁾. Data longitudine et pondere virgae, itemque gravitate in ima virga affixa, necnon illa insuper quae certo loco virgae inhaereat invenire perpendiculum simplex aequipollens.

Sit longitudo virgae AD ∞ a [Fig. 56].

gravitas virgae AD ∞ v

gravitas D ∞ d

gravitas E ∞ e

longitudo AE ∞ c

longitudo quaesita HK ∞ x

1) C.à.d. deux racines positives (T. XVI, p. 419, note 2).

2) Comparez sur les formules qui suivent la p. 425 du T. XVI.

3) Comparez sur les formules qui suivent la p. 427 du T. XVI.

[p. 151]

fit x ∞ ⅓ aav + aad + cce/½ av + ad + ce

Ex eadem aequatione patet, datis x et reliquis praeter c, inveniri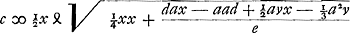

Haec ad corrigendum horologij cursum sic adhibetur. Perpendiculum simplex quod singulis vibrationibus secundum scrupulum (exempli gratia) impendit, est 38 unciarum pedis Rhenolandici. Dato autem pondere in imo virgae, et ipsius virgae gravitate quae gravitates sunt exempli gratia ut 28 ad 1, invenio primum quanta debeat esse virgae longitudo, ut fiat perpendiculum aequipollens simplici unciarum 38, idque per aequationem praecedentem

Deinde, dato etiam pondere exiguo ε, si inveniendum sit quibus locis virgae ponendum illud sit, ut spatio 24 horarum horologium acceleret cursum suum 1′, 2′, 3′ &c. minutis; quaero primo longitudinem perpendiculi simplicis, quod superet perpendiculum simplex 38 unciarum uno minuto in 24 horis quod facile est. Denique vocando inventam longitudinem x, invenitur longitudo AE sive c secundum aequationem antecedentem



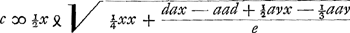atque ita repertus erit locus ubi ponendum pondus ε ut uno minuto citius horologium incedat in 24 horis. Similiter vero et alij loci reperientur, atque in virga signabuntur, ut ea ratione quam accuratissime horologij cursus emendari possit.

Quando perpendiculum singulis vibrationibus secunda scrupula notat, estque ponderis in ima virga ad ipsius virgae gravitatem ratio ea quae 28 ad 1; ipsi autem virgae aequiponderans sumitur gravitas plumbi E. fiunt virgae divisiones ejusmodi quales pagina sequenti [Fig. 58] exhibentur. Numeri centesimas unciarum pedis Rhenolandici significant. Virgae portio divisa, quia integra poni non potuit, in tres partes secta est⁴⁾.

4) On lit au bas de la Fig. 58 les mots: ‘centrum oscillationis’ et ‘centrum gravitatis ponderis’. Plus tard Huygens écrivit au crayon sur la p. 48 du Manuscrit 13: ‘5 May. 1673. J'ay trouvé que le petit poids coulant estoit de 6¾ de gros. et le grand poids de 174 gros. De sorte qu'il seroit un peu plus qu' 1/26 de cettuicy. Et le poids de la verge n'estoit que de 4¼ gros’. Le gros, subdivision de la livre de 16 onces, était égal à la huitième partie d'une once ou à peu près à 4 grammes.

[p. 152]

[Fig. 58.]

[Fig. 59.]

[Fig. 60.]

§ 4¹⁾. AB, DC [Fig. 59] sunt virgae sine pondere connexae ita ut anguli DCB, DCA sint recti, et AC aequalis CB. A et B sunt pondera aequalia. Punctum suspensionis D. Si fiat duabus DC, CA tertia proportionalis CE. Erit DE longitudo perpendiculi aequales oscillationes habentis ponderibus A, B, ita suspensis.

Hinc facile intelligitur, circuli circumferentiam ut DAEB [Fig. 60], suspensam ex puncto sui aliquo, ut D, atque in plano circuli sui motam, facere oscillationes aequales perpendiculi oscillationibus cujus longitudo aequalis sit diametro DE.

Atque item arcum circumferentiae quemlibet, ut ADB, ex puncto sui medio D suspensum, oscillationes toti circumferentiae ita suspensae vel perpendiculo diametri aequales habere, quod notatu dignum.

1) Comparez sur les propositions qui suivent les p. 447 et 455 du T. XVI, en particulier la note 3 de la p. 455.