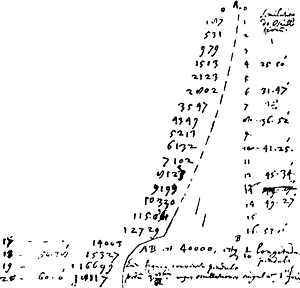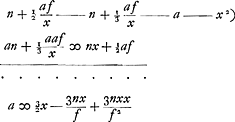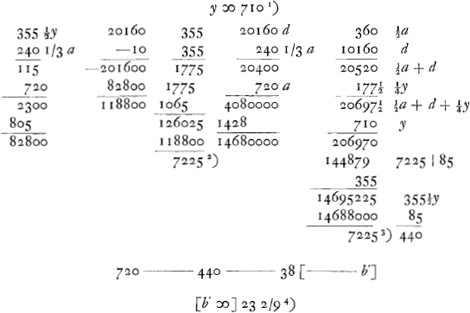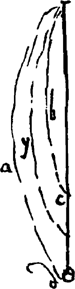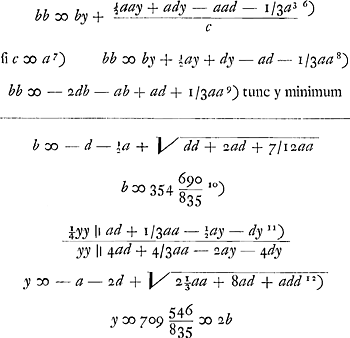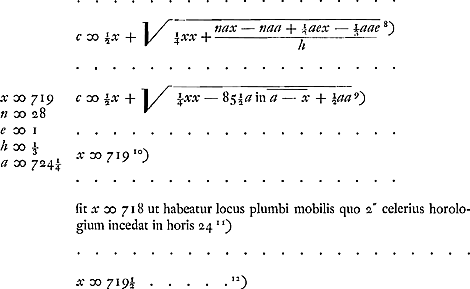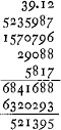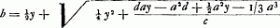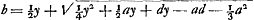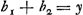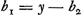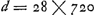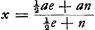[Fig. 26.]
AB ∞ x
gravitas virgae AB ∞ f
gravitas C ∞ n. x - f - a/af/x gravitas AC.
AC ∞ a quaeriturGa naar voetnoot1)
secundum regulam superius inventam
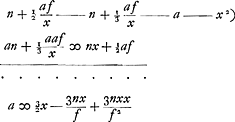
Ga naar voetnoot2)
gravitas AC ∞ 3/2 f - 3n + 3nx/aGa naar voetnoot3)
21 Oct. [1661] met de ☉ ten 12 ur. horologes met malkander eodem die 12.10.
den 22 Oct. hor. 12 het mijne met de ☉ geset.
den 23 Oct. 't mijne 5 achter de ☉.
29o. mijn 25″ achter de ☉.
15 Nov. 't mijne 1′16″ voor de ☉Ga naar voetnoot4).
|
-
voetnoot1)
- Les figures 18 et 19 sont empruntées à la p. 75 verso des ‘Chartae mechanicae’, où l'on trouve aussi la figure [Fig. 18] que nous avons reproduite à la p. 404 du T. XIV. La Fig. 18 représente sans doute un projet d'horloge marine, la lourde cloche devant servir à maintenir l'appareil dans une situation plus ou moins verticale: comparez l'avant-dernier alinéa de la p. 68 du T. IV. La Fig. 19 représente le pendule seul, avec les arcs et la fourchette.
-
voetnoot1)
- Les figures 18 et 19 sont empruntées à la p. 75 verso des ‘Chartae mechanicae’, où l'on trouve aussi la figure [Fig. 18] que nous avons reproduite à la p. 404 du T. XIV. La Fig. 18 représente sans doute un projet d'horloge marine, la lourde cloche devant servir à maintenir l'appareil dans une situation plus ou moins verticale: comparez l'avant-dernier alinéa de la p. 68 du T. IV. La Fig. 19 représente le pendule seul, avec les arcs et la fourchette.
-
voetnoot1)
- Les Fig. 20, 21 et 22 et les calculs qui se rapportent aux deux premières ont été empruntés aux p. 250 et 252 du Manuscrit A.
-
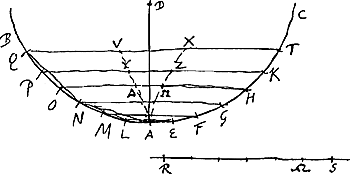
voetnoot2)
- La ligne FD [Fig. 20] est la cycloïde correspondant au cercle CB roulant sur FC. Comme on voit, la ligne AC est divisée en 16 parties égales. DE et chacune des autres petites lignes horizontales comprises entre la cycloïde et la verticale FE sont calculées en prenant les différences des arcs, tels que BC, et des demi-cordes, telles que BA, qui leur correspondent. 53.8′ est l'arc BC exprimé en degrés et minutes. À la p. 253 du Manuscrit on trouve des calculs numériques faisant voir que la longueur des arcs a été trouvée, peut-être d'après une table construite d'avance, en ajoutant 3, 4 ou 5 longueurs. Pour la partie No 9 p.e. le calcul est le suivant:
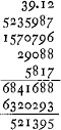
-
voetnoot3)
- La Fig. 21 représente en grand et en position inverse l'arc cycloïdal FD de la Fig. 20; le point A de la Fig. 21 correspond donc au point F de la Fig. 20. Les nombres 187, 531 etc. sont les mêmes, sauf quelques corrections, que ceux de la Fig. 20; on y trouve de plus les No 17 (14003), 18(56.38′.15327), 19(16699) et 20(60.0′.18117). En haut de la colonne 25.50′, 31.47′ etc. on lit les mots ‘Semilatitudo Oscillationum’; toutefois ces chiffres (qui correspondent à ceux de la troisième colonne appartenant à la Fig. 20, colonne indiquée par le seul chiffre 53.8′) donnent le double de l'angle qui fait avec la verticale la tangente au point considéré de la cycloïde, c.à.d. l'amplitude de l'oscillation entière correspondant à ce point. On trouve un autre calcul moins complet de ce genre à la p. 182 du Manuscrit A. Comparez avec la Fig. 21, celle de la p. 65 du T. IV représentant ‘une platte limée exactement de la forme qui se doit ajuster entre les deux platines courbes’.
Les horlogers ne construisirent pas toujours les arcs avec le soin requis; voir la fin de la p. 27 du T. IV. C'est ce qu'on constate aussi en considérant les horloges de P. Visbach (voir sur lui la note 2 de la p. 12) du ‘Rijksmuseum’ d'Amsterdam.
-
voetnoot4)
- Ailleurs (voir les p. 63 et 75 qui précèdent) Huygens évalue la longueur du pendule à secondes à 3 pieds 4 pouces et 3 pieds 2 pouces respectivement. Ici il prend une longueur de 3 pieds 2/3 pouce. La longueur du pendule à secondes, mesurée jusqu' à l'extrémité du pendule, dépend évidemment de sa forme (comparez l'avant-dernier alinéa de la note 5 de la p. 14).
-
voetnoot1)
- Les Fig. 20, 21 et 22 et les calculs qui se rapportent aux deux premières ont été empruntés aux p. 250 et 252 du Manuscrit A.
-
voetnoot1)
- Comme le paragraphe précédent, celui-ci - emprunté à la p. 211 du Manuscrit A et datant environ du 1 janvier 1660, vu que la p. 202 est datée: 25 décembre 1659 et qu'on trouve à la p. 212 une série d'observations (T. XV, p. 534), dont la première est du 1 janvier 1660 - est destiné aux artisans chargés de construire les horloges. Il enseigne à trouver la longueur du pendule (comparez toutefois la note précédente) d'après la loi, déjà trouvée empiriquement par Galilée, suivant laquelle le produit de la longueur du pendule par le carré du nombre des oscillations en un temps donné est constant. Il est possible (voir la note 5 de la p. 18) que cette loi fut déjà établie théoriquement par Huygens quelques années avant 1660, évidemment pour le cas du pendule simple. Dans le cas des oscillations cycloïdales elle est, toujours pour le pendule simple, une conséquence de la règle trouvée par Huygens en décembre 1659 (comparez l'avant-dernier alinéa de la note 5 de la p. 14). D'après cette règle l'accélération de la pesanteur en une seconde est donnée par la formule
g = 4π2n2l/36002,
où l est la longueur du pendule et n le nombre d'oscillations doubles par heure. Huygens prend donc ici en pieds rhénans et en secondes
g = 4π2 .123120000/12.36002 (puisqu'il dit que 123120000,00/n2 = l en pouces rhénans),
ce qui donne précisément
g = 31,25 pied rhénan/sec2.
C'est là la vraie valeur (voir la note 4 de la p. 91 qui précède, ainsi que la note 1 de la p. 280 du T. XVI), que Huygens paraît donc avoir connue vers la fin de 1659. Cette valeur de g a été trouvée par lui à l'aide d'expériences avec un pendule tel que celui représenté dans la Fig. 19 de la p. 97: voir la note 1 de la p. 278 du T. XVI. On lit d'ailleurs sur la p. 211 ici considérée du Manuscrit A: ‘950/100 van een duym lengde geeft 3600 dobbele slagen in een uur’ (une longueur de 9,5 pouces donne 3600 oscillations doubles par heure) ce qui sert à calculer le nombre 12312000000. Comparez la note 13 de la p. 440 du T. III. Il est vrai que dans un morceau de 1666 (voir la note 4 de la p. 323 du T. XVI) Huygens se sert encore d'une valeur de g beaucoup plus petite; mais d'autres erreurs numériques font voir qu'il s'agit là d'un calcul hâtif.
-
voetnoot2)
- P. 260 et suiv. du Manuscrit A. Ces observations, servant apparemment à constater ce qui manquait encore à la régularité de la marche d'une des horloges de Huygens, ont toutes été faites en 1660, comme cela résulte aussi d'autres dates qu'on trouve à la p. 260 (comparez la note 6 de la p. 67 du T. XV). Il s'agit donc probablement d'une horloge munie d'arcs cycloïdaux. Nous ne reproduisons pas en entier ces observations, dont la première est du 13 janvier et la dernière du 9 septembre.
Le 30 décembre 1661 (T. III, p. 438) Huygens écrit à Moray que les arcs cycloïdaux, mêmé sur la terre ferme, n'assurent pas un isochronisme parfait, ce qu'il attribue au ‘medium de l'air, qui n'est pas considerè dans la théorie’, ainsi qu'au ‘defaut du fil du pendule, qui s'estend plus au moment que le plomb est au bas de l'arc qu'il descrit qu'ailleurs’. Le fil fut quelquefois remplacé par une chaîne (‘Horologium oscillatorium’ de 1673, dernier alinéa de la partie de la ‘Pars Quinta’ qui précède les théorèmes sur la force centrifuge), mais sans succès: le frottement interne de la chaîne ‘non parum impedit liberam penduli oscillationem’. Plus tard, lorsqu'il eut trouvé la règle qui détermine la position du centre d'oscillation, Huygens comprit (voir la Prop. XXIV de la ‘Pars Quarta’ de l'Horologium oscillatorium’ intitulée; ‘Centri oscillationis rationem haberi non posse, in pendulis inter Cycloïdes suspensis, etc.’) que théoriquement les arcs cycloïdaux ne rendent les oscillations isochrones que dans le cas du pendule simple. La dilatation du pendule par la chaleur (voir la note 2 de la p. 66) a surtout dû nuire à la marche régulière de l'instrument: voir la fin de la note 2 de la p. suiv.
-
voetnoot3)
- Une tache d'encre a rendu quelques mots illisibles.
Voir pour la note 4 la p. 102.
-
voetnoot3)
- Une tache d'encre a rendu quelques mots illisibles.
Voir pour la note 4 la p. 102.
-
voetnoot4)
- Traduction: ‘à travers le 4ième carreau d'en-dessous. À savoir le centre du soleil...... côté de la fenêtre vis-à-vis de la statue qui se trouve sur la maison de Mathanes. En ce moment j'ai fait marquer midi à mon horloge’.
Il s'agit d'une maison située dans la Spuistraat, au sud de la maison du Plein de Constantijn Huygens père, habitée aussi par Christiaan. C'était une des plus belles maisons de la Haye. Elle fut appelée successivement maison de Brederode, d'Oostervant et de Mathenesse ou Mathenes. Le grand-pensionaire Johan van Oldenbarnevelt l'habita de 1601 à 1612. D'après J. de Riemer (‘Beschrijving van 's Gravenhage etc. Eerste Deel. Tweede Stuk, Delft, R. Boitet, 1730; p. 753) la maison était surmontée d'une tourelle carrée; nous ignorons si celle-ci portait la statue ou statuette dont Huygens fait mention.
-
voetnoot1)
- D'après la table de l'équation du temps (T. XV, p. 543) la différence entre le temps vrai et le temps moyen augmente de 1′32″ du 5 au 10 avril; ceci s'accorde parfaitement avec une augmentation de 1′16″ du 4 au 8 avril, laquelle correspond d'ailleurs aux données de la Table de la p. 207 du présent Tome.
-
voetnoot2)
- Traduction: ‘Jeudi le 9 septembre j'ai fait avancer mon horloge de 25 minutes, 18 secondes, dont elle retardait [depuis le 4 août]’. Ici Huygens ne tient pas compte de l'équation du temps (comparez la note 1). Tandis que l'horloge était en retard de 25 min. et 18 sec. par rapport au soleil, dont Huygens observait le passage au méridien (note 4), elle était en retard de 16½ min. environ par rapport au temps moyen, ce qui fait un retard de près de 28″ par jour. Du 4au 8 avril le retard journalier était de 4″, et du 27 avril au 7 mai de 7,7″.
-
voetnoot3)
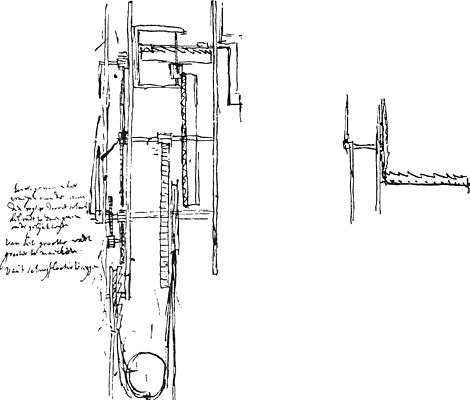
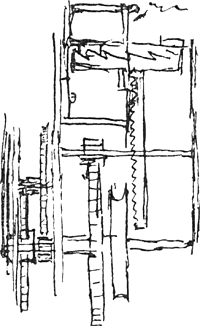
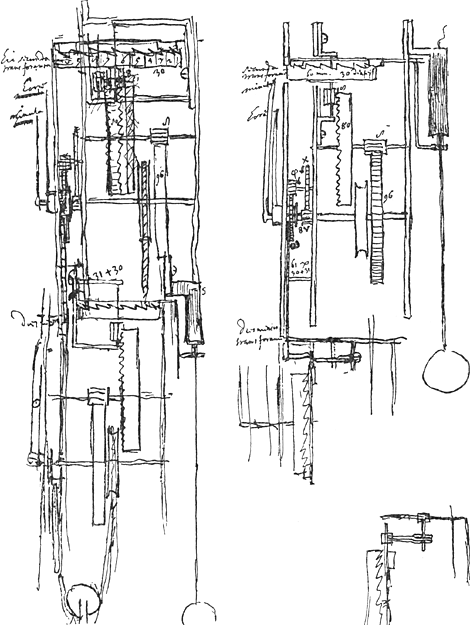
- Les figures 23 et 24 occupent la p. 21 du Manuscrit B. La p. 18 est datée: aoùt 1661 et la p. 23, où il est question du petit poids curseur, déjà mentionné aux p. 353-354 et 428-433 du T. XVI, date également de 1661 (voir la note 4 de la p. 96). On lit à côté de la première figure 24 les mots ‘hic secunda trans foramen... horae... minuta’, ce qui montre que dans ce modèle l'aiguille des heures et l'aiguille des minutes se meuvent sur le même cadran, comme dans l'horloge de 1657 (p. 14) - mais non pas comme dans l'horloge de 1658, comparez la p. 30 - tandis que les secondes sont indiquées par des chiffres paraissant devant une ouverture. Plus bas on lit les mots ‘dies’ et (mal lisible) ‘mensis’. À côté de la deuxième fig. 24 on lit également: ‘secunda trans foramen... minuta... horae’ et en outre ‘dies mensis trans foramen’: ici les jours du mois sont donc indiqués par des chiffres tout aussi bien que les secondes. On voit dans les figures plusieurs chiffres donnant les nombres des dents de différentes roues. Dans la deuxième figure 24 la roue de rencontre porte les mots: ‘60 min. 30 dentes’; ici les ‘min.’ sont évidemment des ‘minuta secunda’ où secondes. La verge à palettes qui est horizontale (comparez le premier alinéa de la p. 96) laisse donc passer une dent en 2 sec., ce qui indique que le pendule fait 1800 oscillations doubles en une heure (comparez la note 5 de la p. 18, le quatrième alinéa de la p. 28 et la note 2 de la p. 76). La troisième Fig. 24, où l'on peut se figurer un pendule à droite, semble, lorsqu'on la considère en elle-même, représenter un mécanisme
servant à transmettre le mouvement alternatif du pendule à une verge à palettes verticale engrenant dans une roue de rencontre également verticale. Ce mécanisme ainsi compris ressemble beaucoup à celui qu'on trouve à la p. 178 dans la Fig. 73 qui représente le remontoir de 1663-1664 (voir le deuxième alinéa de la note 2 de la p. 179).
La deuxième Fig. 24 porte vers le bas un mécanisme du même genre dont la troisième Fig. 24 paraît être une représentation plus correcte. Le sens de ce mécanisme, consideré comme une partie de la deuxième Fig. 24, nous échappe.
Quoique Huygens fût constamment en relation avec quelques horlogers de la Haye, il ne mentionne aucun nom d'horloger en 1660 et 1661. Il est possible (voir le troisième alinéa de la note 2 de la p. 12, ainsi que les p. 84 et 98 du T. III) que P. Visbach, successeur de S. Coster, ait travaillé pour lui, quoiqu'il paraisse bien plus probable (car Visbach n'habitait pas encore la Haye au moment de la mort de Coster) qu'il ait fait construire déjà en 1660 et 1661 ses horloges chez Claude Pascal. Le 18 janvier 1662 (voir la p. 12 du T. IV) il nomme Pascal pour la première fois, et le 6 avril 1663 (T. IV, p. 323) Severijn Oosterwijck. Voir sur ces horlogers la note 5 de la p. 158 qui suit; suivant cette note il avait commandé une horloge chez S. Oosterwijck déjà avant le 1 décembre 1662. Après la mort de Coster Huygens ne laissa pas de s'occuper de l'expédition d'horloges commandées à la Haye par des étrangers; voir pour les années 1660 et 1661, les p. 16, 23, 25, 84, 98 et 284 du T. III. Le 26 novembre 1660 (T. III, p. 193) il écrivit de Paris, où il se trouvait pour quelques mois, que là aussi trois ou quatre horlogers fabriquaient des horloges à pendule et sans doute à arcs cycloïdaux. De retour à la Haye il apprit, en novembre 1661, de son frère Lodewijk qui alors séjournait à Paris avec son père, que le Roi Louis XIV avait acquis une horloge de ce genre, peut-être sur le conseil du père Constantijn qui ‘prosne par tout.... ce pendule’ (T. III, p. 389, 408; comparez la p. 168 du T. IV). D'ailleurs le frère Lodewijk s'y intéressait également (T. III, p. 210).
-
voetnoot1)
- Ces figures sont empruntées à la p. 23 du Manuscrit B.
-
voetnoot2)
- Voir le troisième alinéa de la note 1 de la p. 103.
-
voetnoot3)
- Traduction: ‘Demander à l'horloger de faire mouvoir l'aiguille des secondes par la roue de rencontre, à cause de l'égalité [des périodes]. D'agrandir la grande roue. [Lui] parler du petit poids curseur’.
Comparez sur le poids curseur la note 2 de la p. 28. Quoique Huygens ne considère qu'un poids mobile placé sur la verge elle-même et non pas un poids auxiliaire placé sur le prolongement de cette verge vers le haut (voir la note 1 de la p. 428 du T. XVI), il est possible que la construction de S. Douw (voir la note 4 de la p. 82) ait eu, elle aussi, une certaine influence sur la genèse de cette invention.
-
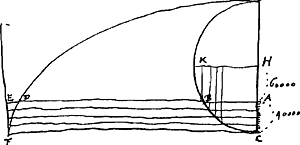
voetnoot1)
- La Fig. 26 est empruntée à la p. 43 du Manuscrit B. Les pages 22 et 26-44 du Manuscrit (dont les p. 33-39 ont été publiées dans le T. XVI, où elles occupent les p. 414-423; voir sur la p. 44 la note 3 de la p. 429 du T. XVI) se rapportent en majeure partie au même pendule, avec ou sans poids curseur. Sans curseur ce pendule était un pendule à secondes (T. XVI, p. 429).
La Fig. 26 fait voir que le poids du pendule en 1661 n'avait plus la forme sphérique: comparez la fin de la note 5 de la p. 15 qui précède. Le 16 mars 1662 (T. IV, p. 93) Moray écrit à Huygens: ‘Je crois aisement que le changement de l'air ne fait rien du tout sur le mouvement de vostre Horologe, la figure du grand plomb estant telle, qu'elle le perce facilement’.
-
voetnoot2)
- P. 22 du Manuscrit B. Le poids de la verge du pendule considéré était donc 1/28 de celui du plomb qui y était suspendu (comparez les p. 428-431 du T. XVI). Nous voyons ici que le poids de 17½ onces était composé de deux parties.
-
voetnoot3)
- Plus loin (voir les p. 429 et 430 du T. XVI) Huygens appelle 720 la longueur du pendule simple de 38 pouces rhéenans isochrone avec le pendule considéré et calcule la longueur que le pendule matériel, à verge pondérable, aurait si son poids était concentré en un point unique; il trouve 724 4/17. Ici au contraire il prend 720 pour la longueur de ce pendule lui-même, en considérant également le poids comme puctiforme. L'équation a = c = 720 exprime que le nombre 720 représente à la fois le poids a de la verge du pendule et le poids c du curseur. La longueur de la verge est également représentée par a.
-
voetnoot4)
-
d représente le poids du ‘plumbum penduli’, l'unité de poids étant
17½/20160 ou 5/8/720 once. 20160 = 28 × 720 (comparez la note 2).
-
voetnoot5)
- Par y Huygens désigne la longueur que le pendule isochrone avec le pendule considéré doit avoir, lorsqu'un poids curseur déterminé y est placé en un endroit qu'il s'agit de calculer. Le nombre 712 est pris arbitrairement. Comme il est inférieur à la longueur 715,8 (comparez la note 4 de la p. 109) du pendule isochrone avec le pendule considéré dépourvu du poids curseur, c'est bien sur la verge elle-même et non pas sur son prolongement vers le bas que le poids curseur (auquel Huygens donne ici - comparez la note 3 - un poids égal à celui de la verge) doit se trouver.
-
voetnoot6)
- L'ensemble de ces calculs (où le nombre 221,3 représente la racine carrée de 48976) est équivalent à l'application de la formule
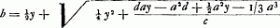
où a/c = 1,
qui correspond à la formule

(où l'on peut prendre e, poids de la verge, = 1, en prenant n = 28 et en exprimant h dans la même unité que e; a est ici aussi la longueur de la verge) de la p. 426 du T. XVI (p. 38 du Manuscrit).
Il résulte du calcul du texte (p. 22 du Manuscrit) que dans le cas considéré le poids curseur doit se trouver à une distance b = 577,3 unités du point de suspension.
-
voetnoot8)
- Comparez la p. 433 du T. XVI. Les 577,3 unités trouvées correspondent à 30 7/15 pouces rhénans, vu que les 720 unités correspondent à 38 pouces. Nous désignons par b′ la distance b (note 6) exprimée en pouces.
-
voetnoot1)
- Autre exemple; a et d gardent les mêmes valeurs.
-
voetnoot2)
- Huygens calcule ¼y2 - [d (a - y) - a (½y - 1/3a), c.à.d.
¼y2 + dy - ad + ½ay - 1/3a2; comparez la note 6 de la p. 107.
-
voetnoot3)
- Huygens calcule la même expression d'une autre façon; il prend y (½a+d+¼y) - a(d + 1/3a).
-
voetnoot4)
- Après avoir tiré la racine carrée du nombre 7225, Huygens y ajoute ½y. Il trouve ainsi 440 unités ou 23 2/9 pouces rhénans (note 8 de la p. 107) pour la distance du poids curseur au point de suspension. Comme dans le cas précédent, le poids du curseur est par hypothèse égal à celui de la verge du pendule; dans la position calculée il réduit la longueur du pendule isochrone (qui sans lui est de 715,8 comme nous l'avons déjà dit à la note 5 de la p. 107 et comme Huygens le dira plus loin - voir la p. 110) à 710 unités.
Aux p. 26 et 27 du Manuscrit B on trouve encore des calculs numériques pour y = 709 2/3, y = 714½, y = 711 et y = 714¾, le poids du curseur étant toujours supposé égal à celui de la verge.
-
voetnoot5)
- La Fig. 27 est empruntée à la p. 29 du Manuscrit B.
-
voetnoot6)
- Dans cette équation, qui correspond à l'équation
c2 = cx + nax - a2n + ½ aex - 1/3 a2e/h
de la p. 426 du T. XVI, b est la distance du poids curseur au point de suspension, y la longueur du pendule simple isochrone avec le pendule donné, consistant dans une verge pondérable, portant à son extrémité inférieure un poids punctiforme et en un autre endroit le curseur également punctiforme, a le poids de la verge, d le poids à l'extrémité inférieure, et c le poids du curseur.
-
voetnoot7)
- D'après cette équation, le poids du curseur est égal à celui de la verge; comparez la note 4, ainsi que les notes 3 et 5 de la p. 107.
-
voetnoot8)
- De cette équation on tire l'équation
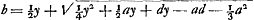 de la note 6 de la p. 107. Aux p. 29-32 du Manuscrit B on trouve plusieurs applications numériques de l'équation considérée qu'il nous semble inutile de reproduire. Comparez le deuxième alinéa de la note 4. de la note 6 de la p. 107. Aux p. 29-32 du Manuscrit B on trouve plusieurs applications numériques de l'équation considérée qu'il nous semble inutile de reproduire. Comparez le deuxième alinéa de la note 4.
-
voetnoot9)
- L'équation de la note précédente fait voir que y atteint un minimum pour b = ½y, ce qui est d'ailleurs vrai pour un curseur de poids quelconque. En substituant cette valeur de y dans l'équation bb ∞ by + etc. qui précède, on obtient l'équation considérée.
Huygens remarque dans sa lettre à Moray du 17 février 1662 (T. IV, p. 60) que ‘le petit plomb estant appliquè en distances egales du point d'en-bas, c'est a dire du centrum oscillationis ou du point de suspension du pendule en haut, le fait aller d'egale vistesse’. Ceci est rigoureusement vrai, lorsque le pendule est linéaire et les poids punctiformes, pourvu qu'on n'entende pas par ‘centrum oscillationis’ le centre d'oscillation fixe du pendule dépourvu de curseur, mais le centre d'oscillation tel qu'il est lorsque le curseur se trouve en un endroit déterminé (le poids du curseur étant arbitraire). En effet il y a toujours (excepté pour b = ½y) deux valeurs b1 et b2 qui donnent la même valeur de y; ces deux valeurs satisfont à l'équation 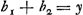 , de sorte que , de sorte que 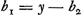 . Comparez à la p. 148 de l'édition originale, le sixième alinéa de la Prop. XXIII de la Pars Quarta de l'‘Horologium oscillatorium’ de 1673, proposition intitulée: ‘Horologiorum motum temperare, addito pondere exiguo secundario, quod super virga penduli, certa ratione divisa, sursum deorsumque moveri possit’. . Comparez à la p. 148 de l'édition originale, le sixième alinéa de la Prop. XXIII de la Pars Quarta de l'‘Horologium oscillatorium’ de 1673, proposition intitulée: ‘Horologiorum motum temperare, addito pondere exiguo secundario, quod super virga penduli, certa ratione divisa, sursum deorsumque moveri possit’.
Dans sa lettre Huygens parle toutefois du centre d'oscillation fixe du pendule dépourvu de curseur, et il considère y comme un minimum lorsque le curseur est placé ‘a la moitiè de la verge’. Ceci est sans doute pratiquement correct: pour les valeurs adoptées pour les poids c, a et d, b (voir le texte) a, pour y minimum, une valeur qui diffère peu de la moitié de 720, longueur de la verge.
Voir pour les la notes 10, 11 et 12 la p. 110 qui suit.
-
voetnoot10)
- C'est la valeur de b pour y minimum lorsqu'on prend, comme précédemment, a = 720 et
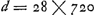 . .
-
voetnoot11)
- Comparez sur le signe ‖ la note 4 de la p. 427 du T. XVI. D'après l'équation de la note 8 de la p. 109 y2 est toujours supérieur au deuxième membre de l'équation considérée (à moins de lui être égal).
-
voetnoot12)
- En remplaçant le signe ‖ par le signe d'égalité, on trouve la valeur minimum de y qui d'après la note 9 de la p. 109 est égale au double de la valeur correspondante de b.
-
voetnoot1)
- Le centre d'oscillation du pendule (verge pondérable, poids punctiforme) dépourvu du poids curseur est à une distance de 715⅘ unités (dans la table qui suit de 715 unités) du point de suspension. Huygens calcule le nombre 715⅘ d'après la formule x = etc. de la p. 424 du T. XVI (p. 36 du Manuscrit B). Voir sur x la note 8.
-
voetnoot3)
- C.à.d. lorsque le petit poids curseur est placé de telle manière que la distance du point de suspension au centre d'oscillation du pendule portant le curseur est de 714 4/5 unités (ou de 714 unités suivant la table), l'horloge dont le mouvement est réglé par ce pendule avancera d'une minute environ en 24 heures par rapport à l'horloge dépourvue de curseur ou dont le curseur se trouve précisément à une distance de 715 4/5 unités (ou de 715 unités) du point de suspension. Etc. Comparez la p. 429 du T. XVI (ou la p. 38 du Manuscrit B).
-
voetnoot5)
- La table qui suit (où la deuxième colonne représente les distances en pouces du poids curseur au point de suspension, et la première colonne les longueurs des pendules isochrones avec le pendule donné portant le poids curseur) s'applique au cas où 1e poids du curseur est égal à celui de la verge, c.à.d. à 1/28 du grand plomb du pendule; voir la note 7 de la p. 109. C'est une table de ce genre que Huygens envoya à Moray le 17 février 1662 (T. IV, p. 60); comparez la note 3 de la p. 429 du T. XVI.
-
voetnoot1)
- Le centre d'oscillation du pendule (verge pondérable, poids punctiforme) dépourvu du poids curseur est à une distance de 715⅘ unités (dans la table qui suit de 715 unités) du point de suspension. Huygens calcule le nombre 715⅘ d'après la formule x = etc. de la p. 424 du T. XVI (p. 36 du Manuscrit B). Voir sur x la note 8.
-
voetnoot7)
- D'après cette remarque (puisqu'on a à peu près 37¾: 38 = 38:38¼) la longueur du pendule matériel doit plutôt être considérée comme étant de 38¼ et non pas de 38 pouces ou bien de 724 unités et une fraction au lieu de 720 unités. Comparez la note 3 de la p. 107 et la p. 430 du T. XVI. Il semble probable qu'ici déjà Huygens songe à attribuer la longueur de 720 unités au pendule simple isochrone avec le pendule réel plutôt qu'à ce dernier lui-même.
-
voetnoot3)
- C.à.d. lorsque le petit poids curseur est placé de telle manière que la distance du point de suspension au centre d'oscillation du pendule portant le curseur est de 714 4/5 unités (ou de 714 unités suivant la table), l'horloge dont le mouvement est réglé par ce pendule avancera d'une minute environ en 24 heures par rapport à l'horloge dépourvue de curseur ou dont le curseur se trouve précisément à une distance de 715 4/5 unités (ou de 715 unités) du point de suspension. Etc. Comparez la p. 429 du T. XVI (ou la p. 38 du Manuscrit B).
-
voetnoot8)
- Après la table qui précède on trouve dans le Manuscrit la Pièce que nous avons reproduite dans le T. XVI (p. 414-433); on y trouve vers la fin la présente équation (comparez la note 6 de la p. 107 qui précède). Les grandeurs c, x et h de cette équation correspondent aux grandeurs qui plus haut etaient désignées par b, y et c.
-
voetnoot9)
- Cette équation (qu'on trouve également dans le T. XVI à la p. 433) s'obtient en substituant dans l'équation précédente les valeurs x = 719, n = 28, etc. Vu que e = 1 et h = ⅓, le poids du curseur ici considéré est le tiers de celui de la verge du pendule.
-
voetnoot10)
- Suit le calcul dont nous avons déjà dit (T. XVI, p. 432, note 1) que nous le supprimons.
-
voetnoot12)
- Après avoir calculé c (c.à.d. la distance du curseur au point de suspension; comparez la note 8) pour x (c.à.d. la distance du point de suspension au centre d'oscillation du pendule muni du curseur) = 719, 718 et 719½, Huygens exécute encore le même calcul pour x = 718½, 719¾, 719¼, 718¾, 718¼, 717 11/12, 717⅚ et 717¾.
-
voetnoot1)
- P. 43 du Manuscrit. AB désigne la longueur du pendule simple isochrone. Le poids du pendule est considéré comme punctiforme et AC désigne la longueur totale de la barre. Le poids total de la barre af/x s'obtient donc par une simple proportion.
-
voetnoot2)
- C'est la règle
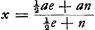 de la p. 424 du T. XVI, où e = af/x. de la p. 424 du T. XVI, où e = af/x.
-
voetnoot3)
- Huygens trouve donc le poids de la barre AC lorsque sa longueur a, ainsi que le poids n et la longueur et le poids de AB sont donnés. Il en tire encore la formula x + ½ af/n ‖ n (voir sur le signe ‖ la note 11 de la p. 110).
On trouve à la p. 44 du Manuscrit la table déjà imprimée à la p. 67 du T. IV.
Huygens ne reprit qu'en 1664 (voir les p. 434 et suiv. du T. XVI) les recherches théoriques sur le centre d'oscillation qu'il avait commencées en 1659 (T. XVI, p. 385).
-
voetnoot4)
- Ces lignes (que nous ne reproduisons pas en entier) sont empruntées à la p. 31 du Manuscrit B. Elles font voir que Huygens fit depuis octobre 1661 des observations avec une horloge réglée par un poids curseur. Il se servit apparemment de deux ou plusieurs horloges dont il appelle l'une ‘la mienne’. Probablement c'était l'horloge à pendule de 38 pouces (99,4 cm.) mentionnée dans le texte.
La p. 46 du Manuscrit est occupée par une table intitulée: ‘Observatio τῶν νυχθημέρων’ qui débute par les mêmes observations du 22 et du 23 octobre, etc. Les observations (avec une seule horloge) y sont continuées jusqu'au 19 mars 1662. On y trouve une colonne ‘aequatio in tabella’ et une colonne ‘differentia’. D'après cette table l'horloge qui était en retard de 5″ sur le soleil le 23 octobre aurait dû être en retard de 7″ donc: differentia 2″. Le 15 novembre elle avançait de 1′16″, tandis qu'elle aurait dû avancer de 45″; donc: differentia 31″. Etc. Nous observons en passant que le nombre 45″ de 1661 ne s'accorde pas parfaitement avec la table da 1660 (T. XV, p. 543). Ces observations, de même que celles du commencement de 1660, servaient en même temps à contrôler la marche de l'horloge et à verifier plus ou moins les résultats du calcul de l'équation du temps: en réponse à une lettre de Huygens de janvier 1660 J. Chapelain (T. III, p. 36) parle de l'‘inégalité des jours τῶν νυχθημέρων que vous avez observée dans l'ajustement de votre machine’. Après le 19 mars 1662 Huygens fit encore des observations du même genre: voir la note 13 de la p. 119 qui suit.
|