Oeuvres complètes. Tome XVII. L'horloge à pendule 1656-1666

[p. 52]

L'horloge par Christian Huygens de Zuylichem, fils de Constantyn¹⁾.

Quoiqu'il fût hors de doute que le nouveau moyen de mesurer le temps, que nous avons imaginé à la fin de l'année 1656²⁾, et que nous avons commencé à divulguer dans notre patrie quelques mois plus tard, serait bientôt connu au loin à cause de sa remarquable utilité - en effet, plusieurs exemplaires du nouvel ouvrage ont déjà été vendus et expédiés de divers côtés³⁾, - nous cédons cependant très volontiers aux conseils de ceux qui nous exhortent à en publier une description, tant afin de rendre service à ceux à qui ce nouveau moyen ne parviendrait peut-être qu'assez tard à cause du grand éloignement, que pour barrer la route à l'audace de certaine espèce de fainéants⁴⁾, les empêchant de s'emparer, suivant leur habitude, de ce qui a été trouvé par un autre et, suprême injustice, de l'offrir au public comme leur propre invention.

1) Une traduction hollandaise anonyme de l'‘Horologium’ a été imprimée dans le ‘Tijdschrift voor Horlogemakers, onder redactie van H.C. Faddegon, uitg. gebr. Faddegon, Amsterdam’ de 1903 (p. 49 et suiv.). On trouve une traduction française plus libre de l'‘Horologium’ (la traduction hollandaise elle aussi n'est d'ailleurs pas exempte d'erreurs) par L. Reverchon dans ‘l'Horloger, Revue Générale, réd. et adm. 19 rue de Turbigo, Paris’, de nov. 1922. En comparant cette traduction française avec la nôtre, on verra que, tout en nous tenant plus fidèlement au texte latin, nous y avons fait de nombreux emprunts.

2) Le 26 décembre 1657 Huygens écrit à I. Boulliau (T. II. p. 109): ‘Il y eust hier un an justement que je fis le premier modelle de cette sorte d'horologes’. Dans la Pièce No. 400 (T. II, p. 46) qui semble plutôt qu'un fragment de lettre être le brouillon d'une Préface de l'‘Horologium’, Huygens dit avoir fait son invention ‘ineunte hoc anno 1657’. Comparez la lettre de Huygens à Fr. van Schooten du 12 Janvier 1657 (T. II, p. 5).

3) Il résulte de la lettre de Huygens à P. Petit du 1 nov. 1658 (T. II, p. 273) qu'une grande quantité d'horloges à pendules avaient été fabriquées déjà avant que Huygens eût introduit la roue P et le pignon O (Fig. 8). D'après la lettre de du Gast (voir sur lui la note 1 de la p. 514 du T. II) à Huygens du 16 janvier 1659 (T. II, p. 317) ce fut le Duc de Luynes qui, sans être connu à Huygens, reçut ‘le premier horologe qui soit venu à Paris de cette sorte’. C'était là sans doute une des horloges de 1657 à verge à palettes horizontale comme celle d'Amsterdam représentée par les fig. 1-6 (p. 14-15). Par contre les horloges dont Huygens mentionne les prix à la p. 313 du T. II (le 16 janvier 1659) - comparez aussi les p. 273 et 281 du T. II, où l'on trouve mentionnées des horloges à roue P et pignon O du prix de 120 francs - peuvent avoir été, du moins en partie, des horloges à palettes verticales. Coster fabriquait encore en 1659 des horloges du type de celles de 1657; voir le dernier alinéa de la p. 403 du T. II. Nous voyons même en cet endroit que Boulliau considérait les prix nommés par Coster et Huygens à l'endroit nommé comme se rapportant à des horloges de ce genre; et en effet, tandis qu'il paya 120 francs pour une horloge à ‘balancier’ - comparez la note 6 de la page 9 - horizontal, Petit dut payer en 1659 130 francs (‘une pistole de plus’) - voir les pages 372 et 420 du T. II - pour une horloge à palettes verticales, que Huygens semble désigner encore le 13 mars 1659 (p. 372), pour cette raison seulement, par l'expression ‘ouvrage.... d'une façon nouvelle’. Quoiqu'il en soit, d'après les passages cités Coster fabriquait en 1658 et 1659 des horloges des deux genres. On ne voit pas que l'horloge de 1658 ait surpassé dans la pratique celle de 1657 (voir encore le deuxième alinéa de la p. 420 du T. II). Dans l'‘Horologium oscillatorium’ de 1673 on ne trouve plus que le type de 1657 à ‘balancier’ horizontal.
Les horloges à verge horizontale de 1657 avaient des arcs ou ‘platines’ comme on peut aussi le voir dans la figure de la p. 271 du T. II, mais les horloges à verge à palettes verticale n'en avaient point. Les arcs ne furent réintroduits que lorsque Huygens eut fait en décembre 1659 la découverte de l'‘isochronisme’ des vibrations cycloïdales (voir les p. 344-349 et 392-413 du T. XVI). Observons que dans la troisième ligne d'en bas de la p. 205 du T. XIV il faut lire 1657 au lieu de 1658.

4) ‘male feriati’, expression d'Horace (Carmina IV, 6, vs. 14).

[p. 53]

Christiani Hvgenii⁺ à Zulichem, Const. f. Horologivm¹⁾.

TEMPORIS dimetiendi rationem novam, quam exeunte Anno 1656, excogitavimus²⁾, paucisque deinde mensibus in patria divulgare instituimus, etsi dubitandum non erat, propter egregiam utilitatem, brevi longé latéque manaturam, quippe pluribus jam distractis, ac dimissis quaquaversum novi operis exemplaribus³⁾; nos tamen haud inviti consiliis eorum obtemperamus, qui ut scripto comprehensam in lucem ederemus, autores fuere. cum ut illos demereamur, ad quos, ob locorum intervalla, tardius fortasse perventura erat: tum ut malè feriatorum⁴⁾ hominum audaciae obviam eamus, ne, quod solenne ipsis est, alienis insidientur inventis,

+ (p. 3).

1) Une traduction hollandaise anonyme de l'‘Horologium’ a été imprimée dans le ‘Tijdschrift voor Horlogemakers, onder redactie van H.C. Faddegon, uitg. gebr. Faddegon, Amsterdam’ de 1903 (p. 49 et suiv.). On trouve une traduction française plus libre de l'‘Horologium’ (la traduction hollandaise elle aussi n'est d'ailleurs pas exempte d'erreurs) par L. Reverchon dans ‘l'Horloger, Revue Générale, réd. et adm. 19 rue de Turbigo, Paris’, de nov. 1922. En comparant cette traduction française avec la nôtre, on verra que, tout en nous tenant plus fidèlement au texte latin, nous y avons fait de nombreux emprunts.

2) Le 26 décembre 1657 Huygens écrit à I. Boulliau (T. II. p. 109): ‘Il y eust hier un an justement que je fis le premier modelle de cette sorte d'horologes’. Dans la Pièce No. 400 (T. II, p. 46) qui semble plutôt qu'un fragment de lettre être le brouillon d'une Préface de l'‘Horologium’, Huygens dit avoir fait son invention ‘ineunte hoc anno 1657’. Comparez la lettre de Huygens à Fr. van Schooten du 12 Janvier 1657 (T. II, p. 5).

3) Il résulte de la lettre de Huygens à P. Petit du 1 nov. 1658 (T. II, p. 273) qu'une grande quantité d'horloges à pendules avaient été fabriquées déjà avant que Huygens eût introduit la roue P et le pignon O (Fig. 8). D'après la lettre de du Gast (voir sur lui la note 1 de la p. 514 du T. II) à Huygens du 16 janvier 1659 (T. II, p. 317) ce fut le Duc de Luynes qui, sans être connu à Huygens, reçut ‘le premier horologe qui soit venu à Paris de cette sorte’. C'était là sans doute une des horloges de 1657 à verge à palettes horizontale comme celle d'Amsterdam représentée par les fig. 1-6 (p. 14-15). Par contre les horloges dont Huygens mentionne les prix à la p. 313 du T. II (le 16 janvier 1659) - comparez aussi les p. 273 et 281 du T. II, où l'on trouve mentionnées des horloges à roue P et pignon O du prix de 120 francs - peuvent avoir été, du moins en partie, des horloges à palettes verticales. Coster fabriquait encore en 1659 des horloges du type de celles de 1657; voir le dernier alinéa de la p. 403 du T. II. Nous voyons même en cet endroit que Boulliau considérait les prix nommés par Coster et Huygens à l'endroit nommé comme se rapportant à des horloges de ce genre; et en effet, tandis qu'il paya 120 francs pour une horloge à ‘balancier’ - comparez la note 6 de la page 9 - horizontal, Petit dut payer en 1659 130 francs (‘une pistole de plus’) - voir les pages 372 et 420 du T. II - pour une horloge à palettes verticales, que Huygens semble désigner encore le 13 mars 1659 (p. 372), pour cette raison seulement, par l'expression ‘ouvrage.... d'une façon nouvelle’. Quoiqu'il en soit, d'après les passages cités Coster fabriquait en 1658 et 1659 des horloges des deux genres. On ne voit pas que l'horloge de 1658 ait surpassé dans la pratique celle de 1657 (voir encore le deuxième alinéa de la p. 420 du T. II). Dans l'‘Horologium oscillatorium’ de 1673 on ne trouve plus que le type de 1657 à ‘balancier’ horizontal.
Les horloges à verge horizontale de 1657 avaient des arcs ou ‘platines’ comme on peut aussi le voir dans la figure de la p. 271 du T. II, mais les horloges à verge à palettes verticale n'en avaient point. Les arcs ne furent réintroduits que lorsque Huygens eut fait en décembre 1659 la découverte de l'‘isochronisme’ des vibrations cycloïdales (voir les p. 344-349 et 392-413 du T. XVI). Observons que dans la troisième ligne d'en bas de la p. 205 du T. XIV il faut lire 1657 au lieu de 1658.

4) ‘male feriati’, expression d'Horace (Carmina IV, 6, vs. 14).

[p. 54]

Toutefois, ces derniers, si besoin était, pourraient être confondus et par la date du privilège accordé par les Etats-Généraux des Provinces Unies, le 16 juin 1657¹⁾, et par les nombreux témoins²⁾ à qui nous avons fait part de notre nouvelle invention aussitôt que l'idée s'en était présentée à nous. Quiconque sait que depuis déjà plusieurs années, les astronomes ont commencé à utiliser les pendules, s'imaginera facilement que ces pendules d'astronomes ont fourni l'occasion de notre invention. En effet, devant l'impuissance des clepsydres et des divers instruments automatiques³⁾ jusqu'alors employés dans leurs observations, ils finirent par adopter la méthode - dont Galileo Galilei, cet homme de génie, fut l'initiateur⁴⁾ - qui consiste à mettre en mouvement à la main un poids suspendu à une chaîne légère, dont les oscillations comptées correspondent à un même nombre d'intervalles de temps égaux⁵⁾. À l'aide de cette méthode ils firent des observations d'éclipses avec plus d'exactitude qu'auparavant et mesurèrent aussi avec succès le diamètre du soleil et quelques distances d'étoiles. Mais, outre que le mouvement venait nécessairement à manquer aux pendules s'il n'était pas entretenu par un assistant, c'était une occupation fastidieuse que de compter toutes les allées et les venues, travail auquel quelques-uns se consacrèrent avec une admirable patience durant des nuits entières, comme ils le disent dans leurs ouvrages⁶⁾. Pour nous, voyant la très grande égalité de ce genre de mouvement, et le considérant comme uniquement apte, parmi les mouvements que la nature nous présente, à passer dans la construction mécanique, nous cherchâmes le moyen de réaliser cette construction le plus commodément possible, et de remédier de cette façon au double inconvénient signalé ci-dessus. Après avoir examiné beaucoup de projets⁷⁾, nous nous sommes arrêtés à celui que nous allons décrire, comme le plus simple et le plus facile. Ce type une fois conçu ayant passé dans les usages public et privé, comme cela commence à

1) Voir la p. 237 du T. II. Le privilège fut accordé à l'horloger Salomon Coster, déjà nommé à la p. 12 (note 2).

2) Entre autres Fr. van Schooten (comparez la note 2 de la p. 52; voir aussi le troisième alinéa de la p. 38 du T. II).

3) Voir p.e. le Chap. IX du Liv. IX de Vitruve dans la traduction de Claude Perrault (‘Les dix livres d'Architecture de Vitruve, corrigez et tradvits nouvellement en François, avec des Notes et des Figures, A Paris, chez J.B. Coignard, MDCLXXIII’), ou dans quelqu'autre édition plus ancienne. Remarquons que Constantijn Huygens père s'intéressait beaucoup à Vitruve et à ses commentateurs; voir p.e. dans l'édition des lettres de C.H. par J.A. Worp la lettre de C.H. du 7 mars 1635 à Heinsius (II, p. 53) et celle du 11 août 1636 à J.A. Bannius (II, p. 182); dans cette dernière il demande à Bannius de lui envoyer l'édition de Barbarus (‘De Architectura II. X cum commentariis Dan. Barbari, multis aedificiorum, horologiorum et machinarum descriptionibus et figuris una cum indicibus copiosis, auctis et illustratis, Venetiae, 1567’). Comparez la p. 36 de l'Avertissement.

4) À sa demande (T. I, p. 322, 323) Huygens reçut en mars 1655 de la part d'Andreas Kolff ou Colvius (T. I, p. 318, note 1) un ‘Galilaei tractatus’ et un ‘aliud manuscriptum ejusdem Galilaei’ dont le premier du moins se rapportait à la ‘longitudinum scientiam’ (l'autre était le traité ‘del flusso e riflusso del mare’ d'après la biographie de Colvius par C. de Waard dans le ‘Nieuw Nederl. Biogr. Woordenboek onder redactie van Dr. P.C. Molhuysen en Prof. Dr. P.J. Blok, A.W. Sijthoff, Leiden 1911’). La Pièce N^o 214 (T. I, p. 318) fait voir qu'avant d'écrire à Colvius Huygens avait commencé à s'intéresser à la question des longitudes, dont son père s'était aussi mêlé activement lors des négotiations des États-Généraux avec Galilée de 1636 à 1640 (comparez la note 2 de la p. 322 du T. I). Le cours d'Hérigone qu'il nomme à ce propos (T. I, p. 324) lui était déjà connu en 1652 (T. I. p. 202, notes 3 et 4).

5) Voir la p. 4 qui précède.

6) Dans son ‘Almagestum Novum’ (ouvrage nommé à la p. 402 du T. I) Riccioli raconte (Pars Prior Tomi Primi, p. 86) dans la Prop. XI et Probl. III du Livre second, proposition intitulée: ‘Inuenire tempus Primi Mobilis, aut Diei Solaris conueniens non solum toti motui perpendiculi dati, sed etiam singulis ipsius vibrationibus simplicibus, & compositis; atque inde porrò per vibrationes illius exactè numerare tempora’, que p.e. ‘Anno 1642, à Meridie diei 2 Aprilis ad Meridiem 3 Aprilis sustinuimus numerationem vibrationum simplicium’.

7) Comparez ce qui a été dit dans la note 3 de la p. 52 sur les horloges de 1657. Voir aussi les Appendices I et II qui suivent.

[p. 55]

ac per summam injuriam pro suis venditent. Quanquam hos, si fuerit opus, & dati Privilegii tempus refellere possit, quod à Celsissimis Foederatarum Provinciarum Ordinibus die 16. Iunij Anno 1657. impetratum est¹⁾; & testes praeterea non pauci²⁾, quos de oblato nobis recens invento subinde certiores fecimus. Occasionem ei praebuisse Astronomorum pendula, facile quivis conjiciet, qui non nescierit aliquot jam retro annis haec | usurpari illis coepta. Nimirum fallentibus clepsydris automatisque⁺ quibuslibet³⁾, quae inter observandum adhibere consueverant, tandem, docente primum Viro sagacissimo Galileo Galilei⁴⁾, hunc modum inierunt, ut è catenula tenui pondus appensum manu impellerent, cujus vibrationibus singulis dinumeratis, totidem colligerentur aequalia temporis momenta⁵⁾. Hac methodo Observationes Eclipsium scrupulosius quam antea peregere, Solisque item diametrum, & Stellarum distantias dimensi sunt non infeliciter. Sed praeterquam quod deficiebat necessario pendulorum motus, nisi adstantis opera identidem juvaretur, taediosus insuper labor evadebat, omnes eorum itus reditusque numerantibus; cui sanè integris noctibus mirabili patientia nonnullos invigilasse, ipsis prodentibus, constat⁶⁾. Nos autem aequabilissimum hocce genus motus cernentes, ac veluti unicum in rerum natura datum, quod ad Mechanicam constructionem posset traduci, quaesivimus quo pacto hoc ipsum brevissime assequi liceret, atque ita remedium invenire gemino quod retulimus incommodo. Ac multa fabricae varietate animo perpensa⁷⁾, hanc denique, quam deinceps tradituri sumus, ut caeteris planiorem facilioremque selegimus. Qua percepta & in publicum

1) Voir la p. 237 du T. II. Le privilège fut accordé à l'horloger Salomon Coster, déjà nommé à la p. 12 (note 2).

2) Entre autres Fr. van Schooten (comparez la note 2 de la p. 52; voir aussi le troisième alinéa de la p. 38 du T. II).

+ (p. 4).

3) Voir p.e. le Chap. IX du Liv. IX de Vitruve dans la traduction de Claude Perrault (‘Les dix livres d'Architecture de Vitruve, corrigez et tradvits nouvellement en François, avec des Notes et des Figures, A Paris, chez J.B. Coignard, MDCLXXIII’), ou dans quelqu'autre édition plus ancienne. Remarquons que Constantijn Huygens père s'intéressait beaucoup à Vitruve et à ses commentateurs; voir p.e. dans l'édition des lettres de C.H. par J.A. Worp la lettre de C.H. du 7 mars 1635 à Heinsius (II, p. 53) et celle du 11 août 1636 à J.A. Bannius (II, p. 182); dans cette dernière il demande à Bannius de lui envoyer l'édition de Barbarus (‘De Architectura II. X cum commentariis Dan. Barbari, multis aedificiorum, horologiorum et machinarum descriptionibus et figuris una cum indicibus copiosis, auctis et illustratis, Venetiae, 1567’). Comparez la p. 36 de l'Avertissement.

4) À sa demande (T. I, p. 322, 323) Huygens reçut en mars 1655 de la part d'Andreas Kolff ou Colvius (T. I, p. 318, note 1) un ‘Galilaei tractatus’ et un ‘aliud manuscriptum ejusdem Galilaei’ dont le premier du moins se rapportait à la ‘longitudinum scientiam’ (l'autre était le traité ‘del flusso e riflusso del mare’ d'après la biographie de Colvius par C. de Waard dans le ‘Nieuw Nederl. Biogr. Woordenboek onder redactie van Dr. P.C. Molhuysen en Prof. Dr. P.J. Blok, A.W. Sijthoff, Leiden 1911’). La Pièce N^o 214 (T. I, p. 318) fait voir qu'avant d'écrire à Colvius Huygens avait commencé à s'intéresser à la question des longitudes, dont son père s'était aussi mêlé activement lors des négotiations des États-Généraux avec Galilée de 1636 à 1640 (comparez la note 2 de la p. 322 du T. I). Le cours d'Hérigone qu'il nomme à ce propos (T. I, p. 324) lui était déjà connu en 1652 (T. I. p. 202, notes 3 et 4).

5) Voir la p. 4 qui précède.

6) Dans son ‘Almagestum Novum’ (ouvrage nommé à la p. 402 du T. I) Riccioli raconte (Pars Prior Tomi Primi, p. 86) dans la Prop. XI et Probl. III du Livre second, proposition intitulée: ‘Inuenire tempus Primi Mobilis, aut Diei Solaris conueniens non solum toti motui perpendiculi dati, sed etiam singulis ipsius vibrationibus simplicibus, & compositis; atque inde porrò per vibrationes illius exactè numerare tempora’, que p.e. ‘Anno 1642, à Meridie diei 2 Aprilis ad Meridiem 3 Aprilis sustinuimus numerationem vibrationum simplicium’.

7) Comparez ce qui a été dit dans la note 3 de la p. 52 sur les horloges de 1657. Voir aussi les Appendices I et II qui suivent.

[p. 56]

avoir lieu, tous en tireront cet avantage, qu'on constatera un accord des horloges, tant entre elles, qu'avec le soleil lui-même, meilleur que jamais auparavant, si parfait même qu'on eût à peine pu l'espérer. Les astronomes obtiendront ce résultat que, débarrassés du souci d'entretenir le mouvement des pendules et de la peine d'en compter les vibrations, ils pourront, outre les recherches dont nous avons fait mention un peu plus haut, en entreprendre avec succès d'autres encore plus subtiles. Ils examineront par exemple l'inégalité des jours de midi à midi¹⁾; jusqu'à présent on pouvait opposer à ceux qui osent nier cette inégalité²⁾ plutôt la force du raisonnement que celle de l'expérience. Je ne parlerai pas en ce moment de ce qu'on appelle la science des longitudes³⁾; beaucoup de gens estiment avec nous que si jamais cette science se fera jour et prêtera son concours si désiré à la navigation, ce but ne pourra être atteint que par le transport sur mer d'horloges très parfaites et sans cause d'erreur possible. Mais de cette question moi-même ou d'autres nous occuperons dans l'avenir; pour le moment je vous mettrai d'abord notre automate sous les yeux au moyen d'une figure et je donnerai de plus l'explication de cette figure aussi clairement que je pourrrai.

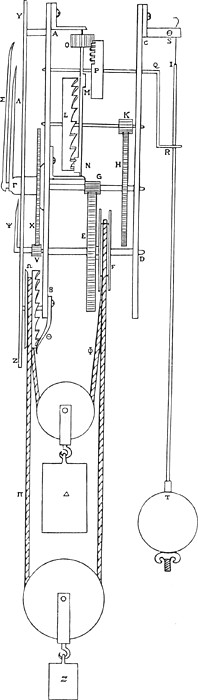
Deux platines oblongues égales entre elles AB, CD [Fig. 8] contiennent la principale partie de l'ouvrage; dans celles-ci sont plantés les axes des roues, de part et d'autre. Ces platines sont seulement représentées de champ. Je me suis expressément abstenu de figurer les quatre pilliers qui les relient vers les angles, pour qu'ils n'offusquassent pas le reste. La première roue ou ‘tympan’⁴⁾ denté est E, à l'axe duquel est aussi fixée la poulie F. Autour de cette poulie passe une corde avec un poids ∆ suspendu de la manière que nous dirons plus loin. La roue E tourne donc par la force de ce poids. Elle met en mouvement la roue voisine H, et celle-ci la roue L dont les dents sont taillées comme celle d'une scie. Près de l'axe de cette dernière roue se dresse verticalement l'axe MN avec ses deux palettes ou oreilles⁵⁾, dont les dents supérieures de la roue L viennent frapper l'une, et les dents inférieures de la même roue l'autre, cela alternativement et indéfiniment, de telle façon que cet axe ne tourne

1) Voir les p. 527 et suiv. du T. XV.

2) Huygens fait sans doute allusion à G. Wendelin (voir sur lui la note 23 de la p. 304 du T. II) nommé plus loin (voir la note 1 de la p. 70). À la deuxième page de son ouvrage ‘Gotifredi Vendelini Luminarcani Arcanorum Coelestium Lampas ΤΕΤΡΑΔϒΧΝΟΣ, Quatuor Hexametris comprehensa. Bruxellae, typis Ioan. Mimartij 1643’ (nous citons cet ouvrage d'après le texte manuscrit qui se trouve dans l'exemplaire de la Bibliothèque de l'Université de Leiden du livre ‘Eclipses Lunares’, nommé plus loin dans la présente note) Wendelin établit la proposition suivante: ‘Lumen primum. In Coelis par est hodiernae crastina summae, hoc est, Omnes dies Νυχθήμεροι sunt inter se aequales’. À la p. 4 de la dédicace de son ouvrage sur les éclipses lunaires (‘Gotifredi Wendelini Eclipses lunares ab anno MDLXXIII ad MDCXLIII observatae, etc.’ Antverpiae, ap. Hier. Verdvssivm MDCXLIV) on trouve de nouveau la proposition: ‘Dies naturales omnes inter se aequales’ (voir aussi la p. 1 du même ouvrage). L'auteur appelle cette égalité un prodige de la nature ‘nemini mortalium ante me vel per somnium [illapsum] in mentem’. D'après le début de son ‘Lampas’ cette idée lui était venue déjà trente ans avant 1643; il avait d'abord ‘timide’ mais depuis 1628 ‘satis fidenter’ combattu la ‘dierum inaequalitatem’. Comparez la p. 343 du T. III.

3) Comparez la note 4 de la p. 55. Voir aussi les p. 7-9 et l'Avertissement qui commence à la p. 193 de ce Tome.

4) ‘Tympan’ (en latin ‘tympanum’) est un mot qu'on trouve e.a. chez Vitruve (comparez la note 3 de la p. 54). Cl. Perrault dans sa traduction écrit (p. 301, note 3) à propos de l'hodomètre (voir sur cet instrument la p. 36 de l'Avertissement qui précède) ‘Bien que Tympanum ainsi qu'il doit estre entendu icy s'apelle en François une roüe, j'ai cru que je ne devois pas luy donner ce nom à cause de l'Equivoque qu'il y auroit eu entre les roües du carrosse & les roues dentelées de la machine’. Plus loin nous traduirons ‘tympanum’ par ‘roue’ ou ‘pignon’, selon le cas. Comparez p.e. la lettre de Huygens à P. Petit du 1 nov. 1658 (T. II, p. 273) où il parle lui-même de la ‘roue’ P et du ‘pignon’ O.

5) Huygens se sert en français du mot ‘palettes’. Voir la l. 6 de la p. 273 du T. II.

[p. 57]

porro privatumque usum, sicut jam fieri coepit, conversa, ad universos quidem hic fructus redundabit, quod horologiorum, cum inter se, tum cum Sole ipso, quantus nunquam antehac, imo quantus penè op|tari posset, consensus animadvertetur. Astronomi⁺ verò id consequentur, ut nulla posthac agitandorum perpendiculorum molestia, numerandive solicitudine, & illa omnia exequantur, quorum paulo ante meminimus, & alia illis subtiliora, ipsam puta dierum de meridie in meridiem inaequalitatem¹⁾, scrutentur; quam qui negare audent²⁾, ratione hactenus magis quam certa experientia refutati sunt. Ut jam de Longitudinum, quam vocant, scientia dicere omittam³⁾: quae si unquam extitura est, desideratumque tantopere usum cursui navigantium praebitura, non aliter, quam vectis per mare exquisitissimis atque omni errore vacuis horologijs, id obtineri posse, multi nobiscum existimant. Verum haec res vel ipsi mihi, vel alijs quandoque curae erit. Nunc automaton nostrum & figura oculis subjiciam, & figuram verbis quam potero dilucidè explicabo.

Praecipuam operis partem binae laminae continent oblongae atque inter se aequales, AB, CD [Fig. 8]; quibus rotarum axes utrinque inserti sunt. Eae laminae lateribus tantum hic sunt conspicuae: columellas autem quatuor, quibus versus angulos connexae sunt, de industria exprimere neglexi, ut ne reliquis officerent. Prima rota seu tympanum⁴⁾ dentatum est E, cujus axi orbiculus quoque F affixus est. Huic circumjectus funis cum appenso pondere ∆, eo quem postea dicemus modo. Ponderis itaque vi tympanum E vertitur. Hoc movet proximum tympanum H. hoc rotam L, cujus dentes ad instar serrae dentium formati sunt. Hujus prope axem erec|tus stat axis MN, cum⁺ affixis lamellis sive auriculis binis⁵⁾, quarum alteri occurrunt superiores rotae L dentes, alteri inferiores, idque perpetua vicissitudine, ita ut non in gyrum axis hic circumagatur, sed reciproco motu, nunc in hanc, nunc in illam partem libretur, dum interim

+ (p. 5).

1) Voir les p. 527 et suiv. du T. XV.

2) Huygens fait sans doute allusion à G. Wendelin (voir sur lui la note 23 de la p. 304 du T. II) nommé plus loin (voir la note 1 de la p. 70). À la deuxième page de son ouvrage ‘Gotifredi Vendelini Luminarcani Arcanorum Coelestium Lampas ΤΕΤΡΑΔϒΧΝΟΣ, Quatuor Hexametris comprehensa. Bruxellae, typis Ioan. Mimartij 1643’ (nous citons cet ouvrage d'après le texte manuscrit qui se trouve dans l'exemplaire de la Bibliothèque de l'Université de Leiden du livre ‘Eclipses Lunares’, nommé plus loin dans la présente note) Wendelin établit la proposition suivante: ‘Lumen primum. In Coelis par est hodiernae crastina summae, hoc est, Omnes dies Νυχθήμεροι sunt inter se aequales’. À la p. 4 de la dédicace de son ouvrage sur les éclipses lunaires (‘Gotifredi Wendelini Eclipses lunares ab anno MDLXXIII ad MDCXLIII observatae, etc.’ Antverpiae, ap. Hier. Verdvssivm MDCXLIV) on trouve de nouveau la proposition: ‘Dies naturales omnes inter se aequales’ (voir aussi la p. 1 du même ouvrage). L'auteur appelle cette égalité un prodige de la nature ‘nemini mortalium ante me vel per somnium [illapsum] in mentem’. D'après le début de son ‘Lampas’ cette idée lui était venue déjà trente ans avant 1643; il avait d'abord ‘timide’ mais depuis 1628 ‘satis fidenter’ combattu la ‘dierum inaequalitatem’. Comparez la p. 343 du T. III.

3) Comparez la note 4 de la p. 55. Voir aussi les p. 7-9 et l'Avertissement qui commence à la p. 193 de ce Tome.

4) ‘Tympan’ (en latin ‘tympanum’) est un mot qu'on trouve e.a. chez Vitruve (comparez la note 3 de la p. 54). Cl. Perrault dans sa traduction écrit (p. 301, note 3) à propos de l'hodomètre (voir sur cet instrument la p. 36 de l'Avertissement qui précède) ‘Bien que Tympanum ainsi qu'il doit estre entendu icy s'apelle en François une roüe, j'ai cru que je ne devois pas luy donner ce nom à cause de l'Equivoque qu'il y auroit eu entre les roües du carrosse & les roues dentelées de la machine’. Plus loin nous traduirons ‘tympanum’ par ‘roue’ ou ‘pignon’, selon le cas. Comparez p.e. la lettre de Huygens à P. Petit du 1 nov. 1658 (T. II, p. 273) où il parle lui-même de la ‘roue’ P et du ‘pignon’ O.

+ (p. 6).

5) Huygens se sert en français du mot ‘palettes’. Voir la l. 6 de la p. 273 du T. II.

[p. 58]

pas, mais oscille d'un mouvement alternant tantôt d'un côte et tantôt de l'autre, tandis qu'en même temps la roue L tourne circulairement. Je n'en dirai pas plus long sur ce mouvement parce qu'on le trouve généralement dans les horloges ordinaires. Jusqu'ici, en vérité, notre horloge ne diffère point de celles-ci¹⁾; mais elle en diffère beaucoup dans ce qui suit. En effet, sur l'axe NM est fixé un pignon O, dans les dents duquel engrènent celles de la roue P [roue de champ]; cette dernière est du type appelé par nos artisans ‘roue à couronne’²⁾. Il n'est pas nécessaire que cette roue soit complètement dentée; il suffit qu'elle le soit à sa partie supérieure³⁾, parce que la roue O, comme l'axe NM, auquel elle est attachée, est animée d'un mouvement alternatif, qu'elle communique donc aussi à la roue P. Le diamètre de cette dernière étant plus grand que celui de la roue O, il s'ensuit que le mouvement se fait sur une fraction de sa circonférence encore moindre que sur celle de la roue nommée [O]. Nous indiquerons ailleurs dans quel but. L'axe de la même roue P traverse la platine CD, la dépasse un peu et se continue avec la manivelle⁴⁾ [fourchette] QR, de nouveau recourbée en bas, et percée en R, de telle manière que la verge de cuivre IT passe librement par ce trou assez large. Or, cette verge est suspendue en haut en S par le fil SI, et supporte en bas le poids T qui peut être, suivant le besoin, haussé ou baissé en tournant l'écrou placé au-dessous.

Ceci ayant été exposé, pour qu'on saisiffe la marche du mécanisme et par conséquent le principe de l'invention entière (car nous expliquerons plus loin ce qui est représenté de plus dans la figure), il faut remarquer d'abord que si la verge SIT ne traversait pas le trou R ou qu'elle faisait défaut, la manivelle QR serait lancée à droite et à gauche, d'un mouvement précipité, par la force du poids ∆ mettant en mouvement

1) Les grandes horloges publiques (voir la p. 62 qui suit) avaient, comme la plupart des horloges de chambre dont Huygens parle ici, la verge à palettes verticale, comme on peut le voir par l'observation de Huygens dans sa lettre à P. Petit du 1 nov. 1658 (T. II, l. 12 de la p. 273). Les horloges publiques pouvaient donc assez facilement être ‘racommodées’ par l'introduction du pendule d'après le schéma de la Fig. 8; consultez les p. 31-36 qui précèdent. Voir sur les horloges à verge horizontale la note 7 de la p. 9 et la note 3 de la p. 52.

2) Huygens donne par conséquent à la roue P le nom de ‘croonrad’ (voir l'Appendice II qui suit). Au lieu de ‘croonrad’ Huygens écrit aussi ‘kamrad’ (comparez la note 2 de la p. 75).

3) Comme on peut le voir dans la Fig. 8. La Fig. 10 que nous reproduisons dans l'Appendice II d'après le Manuscrit A (p. 21) diffère quelque peu de la Fig. 8. La roue qui correspond à la roue P de la Fig. 8 y est complètement dentée, ce qui indique peut-être que la Fig. 10 est plus ancienne que la Fig. 8.

4) La partie QR de l'automate, qu'on désigne aujourd'hui par le nom de ‘fourchette’, est appelée ‘verge’ par Huygens dans sa lettre à J. Chapelain du 28 mars 1658 (T. II, l. 7 de la p. 161); l'extrémité recourbée et percée en R y porte le nom de ‘platine’. Tandis que cette extrémité est fermée chez Huygens (comme on le voit fort bien dans les figures de la p. 160 du T. II) elle est à présent ouverte ce qui donne à cette partie la forme d'une fourchette. Ailleurs cependant Huygens semble désigner lui-même cette extrémité recourbée, seule, par le mot ‘four chette’ quoiqu'elle ne soit pas ouverte, tandis qu'il donne à la partie QR entière le nom de ‘manivelle’: le 25 février 1668 il écrit (Manuscrit C, p. 231 ou T. VI, p. 190): ‘en mettant de l'huile au pivot du pendule et à la fourchette qui sert à mener la manivelle....’ Comparez la l. 5 de la p. 328 du T. II. Les horlogers hollandais de ce temps désignent la fourchette par le mot ‘mick(e)’ ou ‘jucke’ (voir la note 4 de la p. 82 qui suit).

[p. 59]

[Fig. 8.]

rota L in orbem vertitur. Quem motum pluribus exponere supersedeo, quod in vulgaribus passim horologijs reperiatur. à quibus equidem hucusque nostrum hoc non discrepat¹⁾; at plurimum in his quae sequuntur. Axi enim NM infigitur O tympanum, cujus dentibus aptantur dentes rotae P, ejus generis quas coronarias vocant artifices nostri²⁾. Nec vero toto ambitu dentata ut sit necesse est, sed parte superiori duntaxat³⁾. quippe tympanum O, haud aliter atque axis NM cui cohaeret, reciprocam librationem habet, unde & rotam P simili motu agitat. Cumque major sit hujus diameter quam tympani O, sequitur ut minori etiam circuitus parte rota quam tympanum dictum gyretur. quod quo pertineat alibi indicabimus. Porro ejusdem rotae P axis trans laminam CD aliquantum extenditur, habetque conjunctam clavulam⁴⁾ QR, inferius itidem inflexam et terebratam ad R, ita ut per foramen hoc laxiusculum virgula aenea IT liberè transmeet. Haec verò virgula superius ad S suspensa est silo SI, ex inferiori parte pondus T sustinens, quod cochleae subjectae conversione sursum propellitur cum opus est, vel ulterius descendit. |⁺

Quibus expositis ut motus ratio, totiusque adeo inventi percipiatur (nam quae praeterea in Schemate notata apparent, postea exequemur) advertendum est in primis, quod si perpendiculum SIT per foramen R trajectum non esset, neque omnino adesset, tunc quidem clavula QR concitato motu ultro citroque jactaretur, vi ponderis ∆, omnes rotas automati agi-

1) Les grandes horloges publiques (voir la p. 62 qui suit) avaient, comme la plupart des horloges de chambre dont Huygens parle ici, la verge à palettes verticale, comme on peut le voir par l'observation de Huygens dans sa lettre à P. Petit du 1 nov. 1658 (T. II, l. 12 de la p. 273). Les horloges publiques pouvaient donc assez facilement être ‘racommodées’ par l'introduction du pendule d'après le schéma de la Fig. 8; consultez les p. 31-36 qui précèdent. Voir sur les horloges à verge horizontale la note 7 de la p. 9 et la note 3 de la p. 52.

2) Huygens donne par conséquent à la roue P le nom de ‘croonrad’ (voir l'Appendice II qui suit). Au lieu de ‘croonrad’ Huygens écrit aussi ‘kamrad’ (comparez la note 2 de la p. 75).

3) Comme on peut le voir dans la Fig. 8. La Fig. 10 que nous reproduisons dans l'Appendice II d'après le Manuscrit A (p. 21) diffère quelque peu de la Fig. 8. La roue qui correspond à la roue P de la Fig. 8 y est complètement dentée, ce qui indique peut-être que la Fig. 10 est plus ancienne que la Fig. 8.

4) La partie QR de l'automate, qu'on désigne aujourd'hui par le nom de ‘fourchette’, est appelée ‘verge’ par Huygens dans sa lettre à J. Chapelain du 28 mars 1658 (T. II, l. 7 de la p. 161); l'extrémité recourbée et percée en R y porte le nom de ‘platine’. Tandis que cette extrémité est fermée chez Huygens (comme on le voit fort bien dans les figures de la p. 160 du T. II) elle est à présent ouverte ce qui donne à cette partie la forme d'une fourchette. Ailleurs cependant Huygens semble désigner lui-même cette extrémité recourbée, seule, par le mot ‘four chette’ quoiqu'elle ne soit pas ouverte, tandis qu'il donne à la partie QR entière le nom de ‘manivelle’: le 25 février 1668 il écrit (Manuscrit C, p. 231 ou T. VI, p. 190): ‘en mettant de l'huile au pivot du pendule et à la fourchette qui sert à mener la manivelle....’ Comparez la l. 5 de la p. 328 du T. II. Les horlogers hollandais de ce temps désignent la fourchette par le mot ‘mick(e)’ ou ‘jucke’ (voir la note 4 de la p. 82 qui suit).

+ (p. 7).

[p. 60]

toutes les roues de l'automate. Mais lorsque la verge IT, avec le poids T qui y est suspendu, passe par le trou R, le mouvement de la manivelle est par ce moyen empêché de se produire, et toute l'horloge reste sans mouvement jusqu'à ce que le poids T acquière le principe d'agitation par une impulsion unique. Ceci fait, le pendule SIT se trouve animé d'un mouvement oscillatoire, parallèle au plan de la platine CD, tandis que la manivelle QR, sous l'action du poids ∆, obéit au mouvement du pendule, de telle manière que dans le cours de chacune des vibrations du pendule, elle vient à son aide durant un temps très court. De cette façon le mouvement du pendule est continué indéfiniment, tandis que, sans son adjonction à l'horloge, il faiblirait bientôt et arriverait à l'immobilité. Or, pendant chaque demi-oscillation du pendule, on percevra un coup frappé par les dents de la roue L sur chacune des palettes M, N. Tels sont les détails du mouvement de notre automate qui demandaient spécialement des explications, parce que c'est en eux que consiste toute l'invention.

Dans la figure est représentée en outre une troisième platine YZ, parallèle aux précédentes et distante de AB d'un certain intervalle. Dans cet intervalle on voit un pignon denté V, ayant le même axe que la roue E. Avec ce pignon engrènent les dents de la roue X qui porte en son milieu un tube creux Г traversant la platine YZ et menant la première aiguille Λ, qui y est attachée, de l'horloge. Dans ce tube en passe un autre serré sur la platine YZ, portant la roue X, à laquelle il sert d'axe, et livrant en même temps passage à l'arbre de la roue H qui porte une deuxième aiguille Σ plus lonque que Λ. Cette aiguille marque les secondes. En outre une aiguille des minutes Ψ beaucoup plus courte que ces deux premières est plantée à l'extrémité de l'axe DV qui traverse la platine YZ. Ce petit index se promène tout près de la platine YZ marquant les minutes sur un petit cercle. Plus haut que Ψ tourne Δ, l'aiguille des heures, avec au-dessus d'elle [par rapport au cadran] celle Σ pour les secondes dont j'ai parlé. Tout cela, comme aussi la disposition de l'ensemble des engrenages et le nombre des dents, pouvant varier de bien des manières²⁾, nous nous sommes contentés de décrire cette construction-ci comme un exemple qui s'appuie sur l'expérience. Nous indiquerons donc aussi les nombres des dents de toutes les roues qui nous ont paru être le mieux en rapport avec le modèle considéré. Sur le pourtour de chacune des roues E et H, il y a 72 dents et 6 aux pignons G et K. La roue L en a 25, O 10, et P 20, ou une partie des 20, parce que, comme

2) Comparez les Appendices I et II déjà mentionnés dans la note 7 de la p. 55 et la note 3 de la p. 58.

[p. 61]

[Fig. 8.]

tantis. Transmissa autem virgula IT, cum appenso pondere T per foramen R, impeditur eo dictus clavulae motus, totumque horologium quiescit, donec pondus T semel impulsum principium agitationis nanciscatur. Quo facto, pendulum quidem SIT oscillatorio motu fertur juxta planum laminae CD. clavula verò QR, momentum sentiens ponderis Δ, ultro obsequitur penduli motui, ita ut paulisper etiam vibrationibus hunc singulis adjuvet. Atque hoc modo perennis efficitur penduli agitatio, quae nisi illud horologio conjunctum foret, brevi deficeret vergeretque ad quietem. Ad singulos autem recursus penduli, percipientur ictus totidem ex appulsu dentium rotae L ad lamellas M, N. Et haec quidem de motu automati nostri, quae praecipue explicationem requirebant, quoniam in eo summa totius inventi vertitur.

In schemate porro tertia lamina est YZ, prioribus parallela, & à lamina AB spatio distans. quo in spatio conspicitur tympanum dentatum V, communem cum rota E axem habens. Huic congruunt dentes rotae X, quae media sui parte conjunctum habet tubulum cavum | Γ ultra laminam YZ prominentem, impositumque⁺ gerentem horologii indicem primarium Λ. Ipsi vero Γ tubulo alius itidem cavus introrsus constitutus est, laminaeque YZ consertus, axis nimirum quo rota X volvatur, & per quem simul transmittatur axis rotae H, cui impositus est index alius Σ longior indice Λ. Is secunda scrupula demonstrat. Primorum vero scrupulorum seu minutorum index prioribus illis utrisque multo brevior Ψ, extremo axi DV, ultra laminam YZ producto, affixus est. Et hic quidem indiculus, laminae, YZ¹⁾ proximus fertur, parvo in circello singula prima scrupula distinguens. Hoc verò superior index horarum Λ convertitur: & supra hunc denique Σ index, quem dixi, secundorum. Haec autem, uti & tympanorum omnium dispositio ac dentium numerus, cum multimodis variari possint²⁾, nos hunc unum in exemplum proponere satis habuimus, eumque experientia comprobatum. Itaque & dentium multitudinem in singulis tympanis designabimus, eam quae huic formae optimè convenire visa est. In circumferentia rotarum singularum EH septuageni bini sunt, seni in tympanis G & K. rota L viginti quinque habet,

+ (p. 8).

1) Lisez: ‘laminae YZ’.

2) Comparez les Appendices I et II déjà mentionnés dans la note 7 de la p. 55 et la note 3 de la p. 58.

[p. 62]

je l'ai dit, pas besoin n'est de garnir de dents cette roue tout entière. La longueur du pendule SIT est d'environ 10/12 d'un pied rhénan lequel se rapproche beaucoup du pied romain, et il exécute une vibration simple en une demi-seconde¹⁾. Il n'est pas difficile de lui donner cette longueur par des observations comparées avec le soleil ou avec une autre horloge de ce genre. Cette longueur-là correspond aux roues désignées comme alles viennent de l'être; elle offre une remarquable égalité du mouvement, fuffisante même pour les observations astronomiques. Que si, cependant, n'attachant pas de prix à la forme élégante de l'horloge, on emploie un pendule quatre fois plus long, ou même davantage, en adoptant en même temps des roues plus grandes, nous pouvons sans doute avoir encore plus de confiance aux oscillations plus lentes de ce pendule. Déjà dans quelques horloges publiques de grandes dimensions, nous avons vu employer avec un succès remarquable des pendules très longs de ce genre tels que 12 ou 20 pieds, portant des poids sphériques de 25 ou 30 livres²⁾. Mais revenant à la construction que nous venons de décrire, on voit qu'un tour de la roue E donne 12 tours de la roue H et 144 tours de la roue L. Celle-ci ayant 25 dents, c'est 3600 fois qu'elle actionne les palettes M, N et autant de fois que le pendule exécute sa double course; et comme il y a 3600 secondes en une heure, c'est dans cet espace de temps que la roue E accomplira une révolution. Par conséquent aussi le cercle sur lequel tourne l'index Ψ est divisé en 60 parties qui indiquent les minutes. Mais comme la roue H tourne douze fois en une heure, donc une fois en 5 minutes, et l'aiguille Σ avec elle, nous divisons le cercle placé en-dessous de cette aiguille en 5 parties prin-

1) En 1658 Huygens n'avait pas encore trouvé la règle pour calculer le centre d'oscillation (comparez les p. 349-376 du T. XVI); cette règle à elle seule ne permet d'ailleurs pas de déterminer pratiquement la longueur du pendule simple isochrone avec un pendule composé; elle ne devient pratiquement applicable dans certains cas que par la loi qui en résulte de l'échangeabilité du point de suspension et du point d'oscillation (T. XVI, p. 373-374). D'après le texte le pendule exécutait une vibration simple lorsque la longueur SIT, mesurée depuis le point de suspension jusqu'au point superieur T de la sphère de plomb, était environ de 10/12 × 31,39 = 26, 16 cm.
Tandis que le pied rhénan est de 31,39 cm, le pied romain, mentionné incidemment, semble avoir été de 29.57 cm; c'est du moins la valeur assez incertaine adoptée par F. Hultsch à la p. 76 de son livre ‘Griechische und Römische Metrologie’, publié en 1862 à Berlin chez Weidmann. W. Snellius dans le Cap. II du Lib. II de son ‘Eratosthenes Batavus’ de 1617, chapitre intitulé: ‘Veteris Romani pedis atque aliorum, & inter se et cum Rhijnlandico comparatio’, était arrivé à la conclusion (p. 130 et 132): ‘pedem Rhijnlandicum Romano exactè aequalem esse’, conclusion que Huygens adopte ici.

2) L'horloge de Schéveningue (voir la p. 32 de l'Avertissement) avait au tout premier commencement un pendule de plus de 50 livres (p. 125 et 161 du T. II), long de 24 pieds rhénans (p. 161), la longueur étant mesurée jusqu'à la sphère de plomb comme il a été dit dans la note précédente (comparez le deuxième alinéa de la note 1 de la p. 32). Dans la suite ce poids fut réduit, paraît-il (car il n'est pas absolument certain que Huygens parle ici de l'horloge de Schéveningue) à 30, puis à 22 livres, et la longueur du pendule à 18 pieds (T. II, p. 327). Le poids du pendule qui fut adapté en octobre 1658 à la grande horloge d'Utrecht (T. II, p. 273 et 327) était de 40 livres. La livre de la Haye est de 469, 7 gr., comme le font voir quelques poids conservés au musée communal de cette ville.

[p. 63]

[Fig. 8.]

tympanum O decem, rota P viginti, vel tantum partem horum aliquam, quia, ut dixi, totam dentibus insecari nihil opus est. Penduli longitudo SIT pedis Rhenolandici, qui ad Romanum veterem proxime accedit, dextantem circiter aequat, & cuique vibrationi. simplici impendit semiscrupulum secundum¹⁾, ad quam mensuram observationibus ad solem | vel ad aliud hujus⁺ generis horologium comparatis non difficilè perducitur. Ea longitudo rotis ita ordinatis convenit: et exquisitam motus aequalitatem, quaeque etiam Astronomicis usibus sufficiat, praestare valet. Quod si tamen concinnitate operis insuper habita, quadruplo majus pendulum adhibeatur, vel ultra etiam producatur, rotis interim majoribus quoque adsumptis, haud dubiè lentioribus oscillationibus tutius etiam fidemus. Et jam in magnis publicis Horologijs, egregio successu, perpendicula ejusmodi praelonga usurpari vidimus, alibi duodecim, alibi vicenûm pedum, cum appensa sphaera 25 vel 30 librarum²⁾. Caeterum revertendo ad ea quae hic posita fuere, apparet quidem, rota E semel circumacta, duodecies converti rotam H. centies vero quadragies & quater eam quae sequitur L. Quae cum dentes 25 habeat, 3600 vicibus alternatim impellitlamellas M, N. ac totidem recursus duplices facit pendulum SIT. Cumque 3600 scrupula secunda hora una contineantur; hinc horae spatio rota E semel convertetur. Quamobrem et circulus indici Ψ subjectus in 60 partes dividitur, quae prima scrupula significent. Rota vero H quia duodecies in hora, hoc est, semel spatio 5 scrupulorum primorum versatur, unaque index Σ, ideo circulum huic indici suppositum in 5 partes

1) En 1658 Huygens n'avait pas encore trouvé la règle pour calculer le centre d'oscillation (comparez les p. 349-376 du T. XVI); cette règle à elle seule ne permet d'ailleurs pas de déterminer pratiquement la longueur du pendule simple isochrone avec un pendule composé; elle ne devient pratiquement applicable dans certains cas que par la loi qui en résulte de l'échangeabilité du point de suspension et du point d'oscillation (T. XVI, p. 373-374). D'après le texte le pendule exécutait une vibration simple lorsque la longueur SIT, mesurée depuis le point de suspension jusqu'au point superieur T de la sphère de plomb, était environ de 10/12 × 31,39 = 26, 16 cm.
Tandis que le pied rhénan est de 31,39 cm, le pied romain, mentionné incidemment, semble avoir été de 29.57 cm; c'est du moins la valeur assez incertaine adoptée par F. Hultsch à la p. 76 de son livre ‘Griechische und Römische Metrologie’, publié en 1862 à Berlin chez Weidmann. W. Snellius dans le Cap. II du Lib. II de son ‘Eratosthenes Batavus’ de 1617, chapitre intitulé: ‘Veteris Romani pedis atque aliorum, & inter se et cum Rhijnlandico comparatio’, était arrivé à la conclusion (p. 130 et 132): ‘pedem Rhijnlandicum Romano exactè aequalem esse’, conclusion que Huygens adopte ici.

+ (p. 9).

2) L'horloge de Schéveningue (voir la p. 32 de l'Avertissement) avait au tout premier commencement un pendule de plus de 50 livres (p. 125 et 161 du T. II), long de 24 pieds rhénans (p. 161), la longueur étant mesurée jusqu'à la sphère de plomb comme il a été dit dans la note précédente (comparez le deuxième alinéa de la note 1 de la p. 32). Dans la suite ce poids fut réduit, paraît-il (car il n'est pas absolument certain que Huygens parle ici de l'horloge de Schéveningue) à 30, puis à 22 livres, et la longueur du pendule à 18 pieds (T. II, p. 327). Le poids du pendule qui fut adapté en octobre 1658 à la grande horloge d'Utrecht (T. II, p. 273 et 327) était de 40 livres. La livre de la Haye est de 469, 7 gr., comme le font voir quelques poids conservés au musée communal de cette ville.

[p. 64]

cipales et chacune d'elles en 60 subdivisions qui représentent les secondes. Enfin l'aiguille Λ doit marquer 12 heures sur son cadran; en conséquence, pour qu'elle fasse un tour dans ce laps de temps, nous attribuons 6 dents à la roue V et à la roue X, 72.

Nous expliquerons maintenant comment les poids Δ, Ξ doivent être suspendus à l'horloge. Par un artifice nouveau nous les avons disposés de telle manière que lorsqu'on remonte le poids primaire Δ, la marche de l'horloge n'est néanmoins ni interrompue ni gênée en aucune façon; ce qui était en premier lieu nécessaire dans cette invention pour empêcher qu'une certaine fraction de temps fût perdue chaque jour ou que le mouvement du pendule languît pendant le remontage du poids. On prépare à cet effet une corde sans fin, c.à.d. une corde dont les extrémités ont été adroitement réunies. Celle-ci embrasse d'abord la poulie F, garnie de pointes de fer afin que la corde y adhère d'autant mieux; d'autre part elle enveloppe la poulie à laquelle le poids primaire Δ est attaché. D'ici elle passe en remontant sur la poulie Ω, puis, redescendant de nouveau, elle soutient la deuxième poulie qui porte un poids, savoir celle à laquelle le poids plus petit Ξ est attaché; de là enfin elle retourne à F. La poulie Ω que, pour la démonstration, nous avons suspendue ici entre les platines AB, YZ (car d'habitude elle est attachée plus commodément à la cage qui contient tout le mécanisme), porte près de sa circonférence des dents en forme de scie, comme la roue L [d'échappement]; elle est munie d'un ressort Θ qui s'appuie sur les dents de façon qu'elle ne peut tourner que dans un sens - mouvement qui se produit lorsqu'on tire la corde Π et que le poids Δ remonte en conséquence - vu que l'arc-boutement du ressort sur les dents prévient le mouvement en sens inverse¹⁾. Or, il convient de donner à la gorge de cette poulie un profil tel qu'elle serre et gêne quelque peu la corde y engagée afin que celle-ci ne puisse glisser sans faire tourner la poulie; dans le même but on emploie aussi le poids Ξ [tendeur]. Ceci étant arrange de cette manière, de tout temps le poids Δ tirera de la moitié de sa force la corde Φ et sera continuer le mouvement de l'horloge même pendant qu'on le remonte en tirant sur la corde Π.

1) Comme Huygens le dit au début de cet alinéa, il s'agit ici d'une invention nouvelle. Comparez les l. 11 et 10 d'en bas de la p. 161 du T. II, où il écrit le 28 mars 1658: ‘dans ceux [les ouvrages] qui sont a contrepoids j'ay inventè cette maniere’; voir aussi la quatrième ligne d'en bas de la p. 283 du T. II (il est vrai que les horlogers Lisle et van der Thoorn de Rotterdam déclarent que cette méthode de suspension des poids était déjà connue: ‘een... manier, die voor desen is bekent en gepractiseert geweest’, tandis que, suivant eux, la méthode de suspension de leur collègue S. Douw, par laquelle il atteint le même but, serait nouvelle; voir à ce sujet la fin de la note 1 de la p. 32). Les ‘ouvrages à ressort’ pouvaient déjà être remontés sans que leur marche fût interrompue: voir les dernières lignes de la p. 271 et les premières lignes de la p. 272 du T. II, où Huygens dit: ‘les ouvrages a ressort ont toute [non pas toutes, comme on trouve à l'endroit nommé] la mesme justesse que ceux qui sont a contrepoids .... faire continuer le mouuement de l'horologe pendant qu'on le remonte; ce qui se fait a cet heure aysement, parce que l'on remonte le ressort par dedans c'est à dire par l'aissieu du tambourin qui l'enferme’. Comparez la note 6 de la p. 16 et la note 2 de la p. 72.

[p. 65]

[Fig. 8.]

primum dispescimus, & harum deinde singulas in 60 minores, quae secunda scrupula denotent. Denique index Λ in suo circulo duodecim horas distinguere debet; ac proinde, ut harum tempore semel circumeat, tympano V sex dentes tribuuntur, rotae X septuageni bini. |⁺

Nunc qua ratione pondera Δ, Ξ, horologio appendantur docebimus. Haec enim novo artificio ita ordinavimus, ut cum sursum retrahitur pondus primarium Δ, non propterea cesset aut ullatenus impediatur horologij cursus. Quod in hac inventione apprime necessarium erat, ne particula temporis aliqua quotidie subduceretur, neve penduli motus interea dum pondus attollitur languesceret. Paratur itaque funis continuus atque in se rediens, extremitatibus aptè inter se connexis. Is primo orbiculum F amplexus, aculeis ferreis asperum, quo melius funis inhaereat, parte altera trochleae, cui pondus primarium Δ alligatum est, circumvolvitur. Hinc ascendens super orbiculo Ω transit, ac rursus descendens sustinet trochleam alteram cum appenso minori pondere Ξ; unde denuo ad F redit. Orbiculus Ω (quem demonstrandi gratia hic inter laminas AB, YZ, suspendimus, nam alioqui commodius thecae quae toti horologio circumdatur affigi solet) circumferentiam versus denticulos habet, ut in rota L, serratos, ac desuper prementem elaterem Θ, quo fit ut in alteram tantummodo partem volvi possit, attracto nimirum fune Π, ac pondere propterea Δ ascendente. Nam contrarium motum elater dentibus occurrens prohibet¹⁾. Crenam autem secundum circumferentiam dicti orbiculi ita cavari oportet, ut funem immissum nonnihil coarctet constringatque, quo minus possit immoto orbiculo delabi; quem in finem etiam pondus Ξ adhibetur. His sic constitutis, semper Δ dimidia sui gravitate incumbet funi Φ, mo|tumque⁺ horologio continuabit etiam dum attracto fune Π in

+ (p. 10).

1) Comme Huygens le dit au début de cet alinéa, il s'agit ici d'une invention nouvelle. Comparez les l. 11 et 10 d'en bas de la p. 161 du T. II, où il écrit le 28 mars 1658: ‘dans ceux [les ouvrages] qui sont a contrepoids j'ay inventè cette maniere’; voir aussi la quatrième ligne d'en bas de la p. 283 du T. II (il est vrai que les horlogers Lisle et van der Thoorn de Rotterdam déclarent que cette méthode de suspension des poids était déjà connue: ‘een... manier, die voor desen is bekent en gepractiseert geweest’, tandis que, suivant eux, la méthode de suspension de leur collègue S. Douw, par laquelle il atteint le même but, serait nouvelle; voir à ce sujet la fin de la note 1 de la p. 32). Les ‘ouvrages à ressort’ pouvaient déjà être remontés sans que leur marche fût interrompue: voir les dernières lignes de la p. 271 et les premières lignes de la p. 272 du T. II, où Huygens dit: ‘les ouvrages a ressort ont toute [non pas toutes, comme on trouve à l'endroit nommé] la mesme justesse que ceux qui sont a contrepoids .... faire continuer le mouuement de l'horologe pendant qu'on le remonte; ce qui se fait a cet heure aysement, parce que l'on remonte le ressort par dedans c'est à dire par l'aissieu du tambourin qui l'enferme’. Comparez la note 6 de la p. 16 et la note 2 de la p. 72.

+ (p. 11).

[p. 66]

Et maintenant nous avons dit tout ce qui a trait à la construction de cet automate.

Il nous reste à montrer combien cette horloge est supérieure à toutes celles qui ont été en usage jusqu'à ce jour. On sait fort bien que, dans ces dernières, il y a plusieurs causes d'erreur et d'inégalité. D'abord, en effet, du moindre défaut dans la disposition et le polissage des roues provient tout de suite une notable irrégularité de la marche. En second lieu, lorsque l'huile qu'on met d'ordinaire aux axes se dessèche et s'évapore, les heures s'écoulent plus lentement. Et même si l'on suppose ces défauts absents, les horloges en question sont en tout cas sensibles aux variations des saisons et de l'air; elle les pressentent même quelquefois¹⁾. La plupart du temps elles retardent au froid et avancent au chaud. Le pendule, au contraire, ayant cette vertu et cette propriété d'avoir toujours nécessairement la même allure et de ne s'en écarter que lorsque sa longueur change, il apparaît avec évidence que, par notre invention, nous avons supprimé complètement les inconvénients nommés au point que, sauf intervention d'un obstacle assez puissant pour causer l'arrêt complet du mécanisme, il n'y a à craindre aucun retard, aucune inégalité²⁾. À vrai dire, je sais qu'à quelques personnes une double cause de doute pourra se présenter ici. D'abord parce que notre pendule, tel qu'il est, pourra sembler différer du pendule libre, vu qu'il éprouve à chaque oscillation une certaine force et impulsion de la part de la manivelle QR. D'autre part parce que, même supposé que notre pendule conserve les propriétés du pendule simple et ne lui soit inférieur en rien, des observateurs très minutieux ont remarqué chez le pendule simple lui-même une double inégalité. Nous ne nions pas à ce propos que ce qu'on dit de l'action de la manivelle est vrai. Toutefois nous savons qu'elle est très faible en raison de la gravité de T qu'on règle de telle manière que le mouvement du pendule est tout justement empêché de s'affaiblir et ne continue à se produire qu'avec une amplitude très petite et pourtant constante. Par conséquent ce mouvement n'est aucunement plus violent ou plus irrégulier que s'il n'était en aucune façon entretenu par la manivelle et que le pendule SIT, libre, était mis en mouvement par la main, comme cela s'est fait jusqu' ici³⁾. L'expérience, du reste, confirme

1) Huygens veut dire sans doute que les horloges sont sensibles à des variations légères (précurseurs dans bien des cas de variations plus grandes) qui échappent à l'observation directe.

2) Huygens ne parle pas de l'augmentation de la longueur du pendule par l'effet de la dilatation due à la chaleur. Comparez la note 5 de la p. 11 qui précède. En 1659 il écrit (T. II, p. 483) que ‘par un temps plus chaud’ les horloges à pendule ‘vont moins vite’. Toutefois en cette année aussi la dilatation des corps due à la chaleur lui était encore inconnue, comme cela résulte de sa lettre du 19 novembre 1667 à Leopoldo de Medicis qui lui avait envoyé (T. VI, p. 116) les ‘Saggi di Naturali Experienze’ de l'Académie de Florence: il écrit (T. VI, p. 161): ‘Celsitudinis Tuae industria primo [nous soulignons] repertum de phialae vitreae capacitate ex calore aucta’. En 1690 (T. IX, p. 485) il exprime l'opinion (contraire à celle de Papin qui affirme - p. 432 - que ‘tous les corps s'etendent par le chaud’) qu'il n'est pas vrai que ‘les verges des Pendules s'etendent par la chaleur sous la Ligne Equinoctiale’. Comparez la note 1 de la p. 70.

3) Comparez la note 6 de la p. 5 ainsi que les notes 1 et 2 de la p. 30.

[p. 67]

[Fig. 8.]

altum attollitur. Et hactenus quidem quae ad constructionem automati pertinent declaravimus.

Reliquum est, ut, quantum idem ijs omnibus, quae ad hanc diem in usu fuere, antecellat, perspicuum faciamus. Satis constat plurimas in his erroris & inaequalitatis causas esse. Nam & in disponendis ritè elimandisque tympanis vel levissimum peccatum, continuò motus inconstantia notabilis consequitur. Tum vero & siccato atque evanescente oleo, quod axibus addi solet, tardius horae procedunt. atque ut haec absint, varias tamen, anni tempestatum & aeris, mutationes horologia sentiunt, imo praesentiunt nonnunquam¹⁾: & frigore quidem plerunque pigriora comperiuntur, aestu plus aequo properant. Penduli vero cum sit ea vis ac proprietas, ut necessario eodem semper tenore feratur, neque ab eo nisi mutata longitudine unquam declinet; apparet sanè omnia illa quae diximus incommoda invento nostro penitus nos sustulisse, adeo ut nisi tale quod interveniat impedimentum, quo horologij motus omnis sistatur, nulla jam cursus ejus retardatio aut inaequalitas timenda sit²⁾. At enim vero non nemini duplicem hic dubitandi causam oboriri posse scio. Primum, quod differre à pendulo libero nostrum hoc videatur, quippe ad singulas vibrationes vim quandam ac nixum clavulae QR sentiens. Deinde quod, etiamsi penduli simplicis proprietates retineat, perque omnia aemuletur, hujus tamen ipsius geminae inaequalitates à nonnullis, | qui subtiliter haec perquisiverunt, animadversae⁺ sint. Hic illud quod de clavulae impressione dicitur verum esse non diffitemur. Sed levissimam utique hanc esse novimus ratione gravitatis T, quae sic temperatur, ut tantum non deficiat penduli agitatio, sed quam minimâ, & eâdem tamen latitudine perseveret. Proinde nihilo concitatior aut minus aequabilis hic ipsius motus evadit, quam si clavulae prorsus obnoxius non esset, pendulum que simplex SIT, ut adhuc fieri consuevit, manu impelleretur³⁾. Et hoc quidem

1) Huygens veut dire sans doute que les horloges sont sensibles à des variations légères (précurseurs dans bien des cas de variations plus grandes) qui échappent à l'observation directe.

2) Huygens ne parle pas de l'augmentation de la longueur du pendule par l'effet de la dilatation due à la chaleur. Comparez la note 5 de la p. 11 qui précède. En 1659 il écrit (T. II, p. 483) que ‘par un temps plus chaud’ les horloges à pendule ‘vont moins vite’. Toutefois en cette année aussi la dilatation des corps due à la chaleur lui était encore inconnue, comme cela résulte de sa lettre du 19 novembre 1667 à Leopoldo de Medicis qui lui avait envoyé (T. VI, p. 116) les ‘Saggi di Naturali Experienze’ de l'Académie de Florence: il écrit (T. VI, p. 161): ‘Celsitudinis Tuae industria primo [nous soulignons] repertum de phialae vitreae capacitate ex calore aucta’. En 1690 (T. IX, p. 485) il exprime l'opinion (contraire à celle de Papin qui affirme - p. 432 - que ‘tous les corps s'etendent par le chaud’) qu'il n'est pas vrai que ‘les verges des Pendules s'etendent par la chaleur sous la Ligne Equinoctiale’. Comparez la note 1 de la p. 70.

+ (p. 12).

3) Comparez la note 6 de la p. 5 ainsi que les notes 1 et 2 de la p. 30.

[p. 68]

exactement ce que nous affirmons à ce propos. Quant aux deux inégalités du pendule lui-même qu'on signale - et que d'autres nient - nous admettons l'une d'elles, tout en la jugeant à peine capable de produire un effet nuisible dans le cas de notre horloge; pour l'autre, nous n'hésitions pas à affirmer qu'elle est nulle. On soutient avec raison ceci, que les oscillations plus amples et plus étroites du même pendule ne se font pas dans des temps absolument égaux, mais que les premières prennent un peu plus de temps que les dernières; ce qui peut être démontré par une expérience facile. En effet, si de deux pendules, égaux en poids et en longueur, on écarte l'un beaucoup et l'autre peu de la verticale, on verra qu'abandonnés en même temps, ils ne se mouvront pas longtemps ensemble dans le même sens, mais celui dont les oscillations sont plus étroites prendra l'avance. Toutefois, comme je l'ai dit, notre horloge est moins sujette à subir les conséquences de cette inégalité parce que toutes les oscillations ont la même amplitude. Elle ne se montra pourtant pas absolument exempte de ce défaut, si nous voulons tenir compte des plus petites différences, comme cela est nécessaire dans cette question. Il peut arriver en effet que, par suite des intempéries de l'air, ou d'un vice de construction, la manivelle QR ne soit pas toujours actionnée avec la même force, d'où il résultera que les oscilllations du pendule augmenteront ou diminueront d'amplitude (quoiqu'à la vérité bien peu). Du fait que les oscillations plus amples demandent, comme je viens de le dire, plus de temps que les autres, forcément il résulte une certaine inégalité dans le mouvement de l'horloge. Et bien que cette inégalité puisse paraître négligeable, nous y apportions encore remède¹⁾ tant que les horloges étaient construites de telle manière que l'agitation du pendule était assez grande. Plus tard cependant nous avons réussi par l'emploi du pignon O et de la roue P, à faire en sorte que ce remède n'était plus nécessaire²⁾. À l'aide de ces rouages nous obtenons ce résultat que les oscillations du pendule sont arbitrairement étroites et que néanmoins l'axe MN accomplira des mouvements de va-et-vient aussi amples que cela est nécessaire. Car si nous adoptons un diamètre³⁾ de la roue P double ou triple de celui du pignon O⁴⁾, il s'ensuit que, même dans le cas de petites oscillations de P, le mouvement du pignon se fera néanmoins sur une assez grande fraction de sa circonférence. Toutes les oscillations étant de cette façon rendues plus petites, lors même

1) En ajoutant à l'horloge les arcs qui plus tard deviendront des arcs cycloïdaux. Comparez la note 3 de la p. 52, et les p. 18-19 qui font voir comment Huygens construisait ces arcs en 1657.

2) Voir encore la note 3 de la p. 52. On conçoit qu' après l'invention, en décembre 1659, des arcs cycloïdaux, destinés à réaliser un isochronisme parfait, Huygens ait cru pouvoir se passer du pignon O et de la roue P: depuis cette invention les oscillations du pendule pouvaient, semblait-il, être arbitrairement larges. Voir la forme de l'horloge décrite dans l'‘Horologium oscillatorium’ de 1673, et comparez l'horloge de 1657 (Fig. 1 etc., à la p. 14).

3) Lisez: ‘diametri’.

4) Voir la note 3 de la p. 52.

[p. 69]

[Fig. 8.]

experientia optimè comprobat. Penduli vero ipsius, quas adnotant, binas inaequalitates, alij autem contra pernegant, earum alteram admittimus, sed vix quicquam horologio nostro officientem, alteram planè nullam esse adseverare non dubitamus. Illud itaque verè asserunt, non prorsus aequali tempore latiores ejusdem penduli ac angustiores vibrationes transire, sed his illas paulo plus insumere, quod facili experimento demonstrari potest. Nam si pendula duo, pondere ac longitudine aequalia, alterum procul à perpendiculo, alterum parumper dimoveantur, simul dimissa, non diu in partes easdem unà ferri cernentur, sed praevertet illud cujus exiliores erunt recursus. Verum huic inaequalitati nostrum, uti dixi, horologium minus obnoxium est, eo quod omnes oscillationes aequali spatio à perpendiculo excurrant. Nec tamen in totum expers remansit, si minutissima quaeque, sicut hac in re sieri necesse est, consectari velimus. Contingit siquidem vel aëris intemperie, vel operis | vitio aliquo, ut⁺ non semper pari vi agitetur clavula QR, unde & oscillationes penduli (licet exiguo discrimine) crescere ac rursus imminui necesse est. Cumque ampliores recursus arctioribus, sicut modo dicebam, plus temporis impendant; idcirco nonnulla hinc in horologij motu inaequalitas existit. Et huic quidem, utut contemptibilis videri possit, remedium etiam adhibere solebamus¹⁾, quamdiu ita constructa erant horologia, ut majuscula esset penduli agitatio. Post modum verò, ne remedio opus esset, effecimus adhibito tympano O rotaque P²⁾: quibus hoc consequimur, ut quamlibet angustae sint penduli vibrationes, neque eo secius axis MN, quantum necesse est, reciproco motu convertatur. Nam cum tympani O diametro³⁾ dupla vel tripla ponatur diameter rotae P⁴⁾, sequitur ut hujus exiguâ licet oscillatione, illud tamen satis magnam circuitus partem absolvat. Sic igitur oscillationibus universis exilioribus redditis, etiamsi harum aliae alias latitudine

+ (p. 13).

1) En ajoutant à l'horloge les arcs qui plus tard deviendront des arcs cycloïdaux. Comparez la note 3 de la p. 52, et les p. 18-19 qui font voir comment Huygens construisait ces arcs en 1657.

2) Voir encore la note 3 de la p. 52. On conçoit qu' après l'invention, en décembre 1659, des arcs cycloïdaux, destinés à réaliser un isochronisme parfait, Huygens ait cru pouvoir se passer du pignon O et de la roue P: depuis cette invention les oscillations du pendule pouvaient, semblait-il, être arbitrairement larges. Voir la forme de l'horloge décrite dans l'‘Horologium oscillatorium’ de 1673, et comparez l'horloge de 1657 (Fig. 1 etc., à la p. 14).

3) Lisez: ‘diametri’.

4) Voir la note 3 de la p. 52.

[p. 70]

que certaines d'entre elles sont un peu plus grandes que d'autres, il n'en résulte pourtant, l'expérience en fait foi, aucune différence notable dans la durée de chacune. Ceci a encore pour conséquence que, lorsque le poids ∆ est augmenté, et même porté au double, le mouvement du pendule n'en est néanmoins pas accéléré, ni la marche de l'horloge altérée, tandis que le contraire a lieu dans toutes les autres horloges employées jusqu'ici. Godefroy Wendelin, homme connu par ses travaux astronomiques, a le premier et seul, je crois, mis en relief la deuxième inégalité du pendule: il écrit avoir observé que les oscillations du même pendule sont plus rapides l'hiver que l'été, et cela notablement¹⁾. Mais comme il avoue n'avoir fait usage dans cette recherche que de sabliers et de vulgaires automates, ainsi que de cadrans solaires peut-être construits avec trop peu de soin, beaucoup ont mis en doute la valeur de cette observation. Certes, je n'ai rien pu remarquer, moi, de semblable. Bien au contraire, j'ai constaté qu' aux petites horloges dont le pendule est de un demi-pied comme à celles plus grandes où il atteint près de 24 pieds, convient la même longueur pendant l'hiver qu'au milieu de l'été. Cependant cette longueur devrait être augmentée d'au moins 1/7 en hiver, si l'assertion de Wendelin était exacte¹⁾

Ayant affirmé l'egalité et la constance de notre automate sur ce point aussi, nous arrêterons notre description, laissant à l'industrie des artisans beaucoup de choses qui pourraient y être ajoutées: instruits du principe de notre invention, ils trouveront sans difficulté le moyen de l'appliquer aux horloges de divers types, même à celles qui ont été construites auparavant sous la forme ancienne. Nous mêmes avons vu,

1) Dans le chapitre ‘Temporis observandi methodvs’ de son ouvrage ‘Eclipses lunares’ - voir la note 2 de la p. 56 - Wendelin raconte (p. 25) que ce fut Mersenne qui lui fit savoir en 1631 - après l'apparition des dialogues de Galilée en 1630, où l'on trouve pour la première fois l'idée de mesurer le temps de cette manière - que ‘tempus exactissimè numerare possis funiculo trium pedum, etc.’. Il donne un aperçu de ses propres expériences sur l'isochronisme des vibrations du pendule, qu'il trouve à peu près parfait lorsque l'écart de la verticale ne dépasse pas 10^o. Il approuve donc ce moyen de mesurer le temps dans une ‘parte anni’ où les vibrations ont une durée sensiblement constante, mais il ajoute: ‘verum non est aequè diuturnas esse omnes eiusdem suspensurae Oscillationes; verum autem est, Hieme, hoc est, Sole Perigaeo plures vna horâ fieri quàm Aestate, seu Sole Apogaeo’. À la p. 21 on voit qu'il se sert pour mesurer le temps de ‘Scioterica’ (cadrans solaires), de ‘Clepsydrae Arenariae’ (sabliers) et d'‘Horisonia’ qui sont sans doute ce que Huygens appelle ici les ‘vulgaires automates’. Après 1644 Wendelin n'a plus publié d'ouvrages sur l'astronomie. C'est dans ses lettres à P. Gassendi (voir l'ouvrage de 1658 nommé à la p. 635 du T. II) que Wendelin revient sur le sujet qui nous occupe. Il écrit (lettres du 20 octobre 1643 à la p. 458 et du 25 novembre 1645 à la p. 497) avoir observé qu'un pendule faisant 458 oscillations par heure en été en faisait 473 en hiver, un deuxième 473 à 474 en été et 493 à 494 en hiver. Si l'on attribue ce prétendu phénomène à un raccourcissement, ces pendules se seraient donc raccourcis par l'hiver d'environ 1/16 et 1/12 de leurs longueurs. Nous ignorons où Wendelin peut avoir fait mention d'autres observations qui pourraient nous porter à croire que selon lui un pendule peut se raccourcir même d'un huitième de sa longueur ou davantage, de sorte qu'il faudrait augmenter sa longueur d'un septième, p.e. en tournant l'écrou qui supporte sa sphère de plomb, pour lui rendre sa longueur primitive (dans la minute de sa lettre de 1661 à D. Rembrandtsz. van Nierop, Huygens écrit également 1/7 et non pas 1/70; voir la l. 5 d'en bas de la p. 444 du T. III).
Remarquons cependant que dans les lettres nommées Wendelin n'explique pas la marche plus rapide du pendule par un raccourcissement de ce dernier: nous avons déjà dit (voir la note 2 de la p. 66) que la dilatation des corps par l'effet de la chaleur était encore inconnue en ce temps; selon Wendelin (p. 497-498) le phénomène observé provient du fait que la terre a en hiver une plus grande vitesse dans son orbite qu'en été: il y voit une preuve du mouvement de la terre autour du soleil. Huygens, qui lui aussi ne songe pas à un raccourcissement du pendule par l'effet du froid, veut donc dire: si l'assertion de Wendelin était exacte, c.à.d. si un pendule de même longueur oscillait beaucoup plus rapidement en hiver qu'en été, il faudrait augmenter considérablement sa longueur en hiver pour compenser cette prétendue variation de la période d'oscillation.

1) Dans le chapitre ‘Temporis observandi methodvs’ de son ouvrage ‘Eclipses lunares’ - voir la note 2 de la p. 56 - Wendelin raconte (p. 25) que ce fut Mersenne qui lui fit savoir en 1631 - après l'apparition des dialogues de Galilée en 1630, où l'on trouve pour la première fois l'idée de mesurer le temps de cette manière - que ‘tempus exactissimè numerare possis funiculo trium pedum, etc.’. Il donne un aperçu de ses propres expériences sur l'isochronisme des vibrations du pendule, qu'il trouve à peu près parfait lorsque l'écart de la verticale ne dépasse pas 10^o. Il approuve donc ce moyen de mesurer le temps dans une ‘parte anni’ où les vibrations ont une durée sensiblement constante, mais il ajoute: ‘verum non est aequè diuturnas esse omnes eiusdem suspensurae Oscillationes; verum autem est, Hieme, hoc est, Sole Perigaeo plures vna horâ fieri quàm Aestate, seu Sole Apogaeo’. À la p. 21 on voit qu'il se sert pour mesurer le temps de ‘Scioterica’ (cadrans solaires), de ‘Clepsydrae Arenariae’ (sabliers) et d'‘Horisonia’ qui sont sans doute ce que Huygens appelle ici les ‘vulgaires automates’. Après 1644 Wendelin n'a plus publié d'ouvrages sur l'astronomie. C'est dans ses lettres à P. Gassendi (voir l'ouvrage de 1658 nommé à la p. 635 du T. II) que Wendelin revient sur le sujet qui nous occupe. Il écrit (lettres du 20 octobre 1643 à la p. 458 et du 25 novembre 1645 à la p. 497) avoir observé qu'un pendule faisant 458 oscillations par heure en été en faisait 473 en hiver, un deuxième 473 à 474 en été et 493 à 494 en hiver. Si l'on attribue ce prétendu phénomène à un raccourcissement, ces pendules se seraient donc raccourcis par l'hiver d'environ 1/16 et 1/12 de leurs longueurs. Nous ignorons où Wendelin peut avoir fait mention d'autres observations qui pourraient nous porter à croire que selon lui un pendule peut se raccourcir même d'un huitième de sa longueur ou davantage, de sorte qu'il faudrait augmenter sa longueur d'un septième, p.e. en tournant l'écrou qui supporte sa sphère de plomb, pour lui rendre sa longueur primitive (dans la minute de sa lettre de 1661 à D. Rembrandtsz. van Nierop, Huygens écrit également 1/7 et non pas 1/70; voir la l. 5 d'en bas de la p. 444 du T. III).
Remarquons cependant que dans las lettres nommées Wendelin n'explique pas la marche plus rapide du pendule par un raccourcissement de ce dernier: nous avons déjà dit (voir la note 2 de la p. 66) que la dilatation des corps par l'effet de la chaleur était encore inconnue en ce temps; selon Wendelin (p. 497-498) le phénomène observé provient du fait que la terre a en hiver une plus grande vitesse dans son orbite qu'en été: il y voit une preuve du mouvement de la terre autour du soleil. Huygens, qui lui aussi ne songe pas à un raccourcissement du pendule par l'effet du froid, veut donc dire: si l'assertion de Wendelin était exacte, c.à.d. si un pendule de même longueur oscillait beaucoup plus rapidement en hiver qu'en été, il faudrait augmenter considérablement sa longueur en hiver pour compenser cette prétendue variation de la période d'oscillation.

[p. 71]

quandoque excedant, singularum tamen tempora, experientia teste, nullo memorabili discrimine differunt. Qua ex re & hoc contingit, ut aucto vel ad duplum pondere ∆, non propterea penduli motus acceleretur, aut horologij cursus alteretur, quod in omnibus alijs hactenus usitatis secus accidit. Alteram penduli inaequalitatem, Vir Astronomiae studijs clarus, Gothofr. Wendelinus, primus & solus, ut opinor, prodidit; expertum sese scribens ejusdem penduli velociores esse oscillationes hyemali tempore quam aestivo |idque notabili differentia¹⁾. Sed quoniam in eo examine arenaria tantum⁺ horologia, vulgariaque automata sese adhibuisse fatetur, cum sciotericis, fortasse non nimia cura descriptis; multi, quam recte se haberet haec ipsius observatio, dubitarunt. Mihi certè nihil ejusmodi licuit animadvertere. Quin contra, & minoribus horologijs, quibus semipedale est pendulum, & majoribus, in quibus 24 fere pedes aequat, eandem perpetuo longitudinem, brumae tempore ac aestate media, convenire expertus sum. Quae longitudo saltem septima sui parte per hyemem productior esse deberet, si Wendelini vera foret opinio¹⁾.

Asserta igitur & hac in parte automati nostri motus aequabilitate & constantia, sinem jam descriptioni imponemus; multa quae his addi praeterea possent, artificum industriae relinquentes, qui rationem inventi hujus edocti, non difficile reperient quo pacto illud varij generis horologijs, atque ijs etiam quae pridem ad veterem formam

1) Dans le chapitre ‘Temporis observandi methodvs’ de son ouvrage ‘Eclipses lunares’ - voir la note 2 de la p. 56 - Wendelin raconte (p. 25) que ce fut Mersenne qui lui fit savoir en 1631 - après l'apparition des dialogues de Galilée en 1630, où l'on trouve pour la première fois l'idée de mesurer le temps de cette manière - que ‘tempus exactissimè numerare possis funiculo trium pedum, etc.’. Il donne un aperçu de ses propres expériences sur l'isochronisme des vibrations du pendule, qu'il trouve à peu près parfait lorsque l'écart de la verticale ne dépasse pas 10^o. Il approuve donc ce moyen de mesurer le temps dans une ‘parte anni’ où les vibrations ont une durée sensiblement constante, mais il ajoute: ‘verum non est aequè diuturnas esse omnes eiusdem suspensurae Oscillationes; verum autem est, Hieme, hoc est, Sole Perigaeo plures vna horâ fieri quàm Aestate, seu Sole Apogaeo’. À la p. 21 on voit qu'il se sert pour mesurer le temps de ‘Scioterica’ (cadrans solaires), de ‘Clepsydrae Arenariae’ (sabliers) et d'‘Horisonia’ qui sont sans doute ce que Huygens appelle ici les ‘vulgaires automates’. Après 1644 Wendelin n'a plus publié d'ouvrages sur l'astronomie. C'est dans ses lettres à P. Gassendi (voir l'ouvrage de 1658 nommé à la p. 635 du T. II) que Wendelin revient sur le sujet qui nous occupe. Il écrit (lettres du 20 octobre 1643 à la p. 458 et du 25 novembre 1645 à la p. 497) avoir observé qu'un pendule faisant 458 oscillations par heure en été en faisait 473 en hiver, un deuxième 473 à 474 en été et 493 à 494 en hiver. Si l'on attribue ce prétendu phénomène à un raccourcissement, ces pendules se seraient donc raccourcis par l'hiver d'environ 1/16 et 1/12 de leurs longueurs. Nous ignorons où Wendelin peut avoir fait mention d'autres observations qui pourraient nous porter à croire que selon lui un pendule peut se raccourcir même d'un huitième de sa longueur ou davantage, de sorte qu'il faudrait augmenter sa longueur d'un septième, p.e. en tournant l'écrou qui supporte sa sphère de plomb, pour lui rendre sa longueur primitive (dans la minute de sa lettre de 1661 à D. Rembrandtsz. van Nierop, Huygens écrit également 1/7 et non pas 1/70; voir la l. 5 d'en bas de la p. 444 du T. III).
Remarquons cependant que dans las lettres nommées Wendelin n'explique pas la marche plus rapide du pendule par un raccourcissement de ce dernier: nous avons déjà dit (voir la note 2 de la p. 66) que la dilatation des corps par l'effet de la chaleur était encore inconnue en ce temps; selon Wendelin (p. 497-498) le phénomène observé provient du fait que la terre a en hiver une plus grande vitesse dans son orbite qu'en été: il y voit une preuve du mouvement de la terre autour du soleil. Huygens, qui lui aussi ne songe pas à un raccourcissement du pendule par l'effet du froid, veut donc dire: si l'assertion de Wendelin était exacte, c.à.d. si un pendule de même longueur oscillait beaucoup plus rapidement en hiver qu'en été, il faudrait augmenter considérablement sa longueur en hiver pour compenser cette prétendue variation de la période d'oscillation.

+ (p. 14).

1) Dans le chapitre ‘Temporis observandi methodvs’ de son ouvrage ‘Eclipses lunares’ - voir la note 2 de la p. 56 - Wendelin raconte (p. 25) que ce fut Mersenne qui lui fit savoir en 1631 - après l'apparition des dialogues de Galilée en 1630, où l'on trouve pour la première fois l'idée de mesurer le temps de cette manière - que ‘tempus exactissimè numerare possis funiculo trium pedum, etc.’. Il donne un aperçu de ses propres expériences sur l'isochronisme des vibrations du pendule, qu'il trouve à peu près parfait lorsque l'écart de la verticale ne dépasse pas 10^o. Il approuve donc ce moyen de mesurer le temps dans une ‘parte anni’ où les vibrations ont une durée sensiblement constante, mais il ajoute: ‘verum non est aequè diuturnas esse omnes eiusdem suspensurae Oscillationes; verum autem est, Hieme, hoc est, Sole Perigaeo plures vna horâ fieri quàm Aestate, seu Sole Apogaeo’. À la p. 21 on voit qu'il se sert pour mesurer le temps de ‘Scioterica’ (cadrans solaires), de ‘Clepsydrae Arenariae’ (sabliers) et d'‘Horisonia’ qui sont sans doute ce que Huygens appelle ici les ‘vulgaires automates’. Après 1644 Wendelin n'a plus publié d'ouvrages sur l'astronomie. C'est dans ses lettres à P. Gassendi (voir l'ouvrage de 1658 nommé à la p. 635 du T. II) que Wendelin revient sur le sujet qui nous occupe. Il écrit (lettres du 20 octobre 1643 à la p. 458 et du 25 novembre 1645 à la p. 497) avoir observé qu'un pendule faisant 458 oscillations par heure en été en faisait 473 en hiver, un deuxième 473 à 474 en été et 493 à 494 en hiver. Si l'on attribue ce prétendu phénomène à un raccourcissement, ces pendules se seraient donc raccourcis par l'hiver d'environ 1/16 et 1/12 de leurs longueurs. Nous ignorons où Wendelin peut avoir fait mention d'autres observations qui pourraient nous porter à croire que selon lui un pendule peut se raccourcir même d'un huitième de sa longueur ou davantage, de sorte qu'il faudrait augmenter sa longueur d'un septième, p.e. en tournant l'écrou qui supporte sa sphère de plomb, pour lui rendre sa longueur primitive (dans la minute de sa lettre de 1661 à D. Rembrandtsz. van Nierop, Huygens écrit également 1/7 et non pas 1/70; voir la l. 5 d'en bas de la p. 444 du T. III).
Remarquons cependant que dans las lettres nommées Wendelin n'explique pas la marche plus rapide du pendule par un raccourcissement de ce dernier: nous avons déjà dit (voir la note 2 de la p. 66) que la dilatation des corps par l'effet de la chaleur était encore inconnue en ce temps; selon Wendelin (p. 497-498) le phénomène observé provient du fait que la terre a en hiver une plus grande vitesse dans son orbite qu'en été: il y voit une preuve du mouvement de la terre autour du soleil. Huygens, qui lui aussi ne songe pas à un raccourcissement du pendule par l'effet du froid, veut donc dire: si l'assertion de Wendelin était exacte, c.à.d. si un pendule de même longueur oscillait beaucoup plus rapidement en hiver qu'en été, il faudrait augmenter considérablement sa longueur en hiver pour compenser cette prétendue variation de la période d'oscillation.

[p. 72]

chez celui¹⁾ auquel nous avons eu recours tout d'abord pour notre fabrication, des horloges de ce genre, ayant comme moteur non un poids mais un ressort²⁾. Tandis qu'auparavant il fallait employer dans ces dernières la fusée bien connue et la corde enroulée sur elle, chargées d'égaliser les effets du ressort au commencement et à la fin, on les supprime maintenant et on ajoute des dents au tambour dans lequel le ressort est renfermé. Car bien que dans ce système, la force du mouvement du pendule ne soit pas la même à la fin qu'au commencement, cependant les oscillations ne deviennent pas pour cela plus lentes vers la fin, comme nous l'avons fait voir plus haut. Le ressort, dans la partie voisine du centre de la spirale, est rendu raide et, de cette manière, on l'empêche d'exercer sur l'horloge, à certain moment, l'effet d'un frein. Je ne m'étendrai pas sur le fait que le même artisan¹⁾ à fabriqué aussi des automates de ce genre indiquant les heures par une sonnerie, et cela de telle manière que les deux parties, tant celle qui sert à la sonnerie que celle qui fait mouvoir l'aiguille de l'horloge, sont mises en mouvement par le même moteur (poids ou ressort). En effet, notre invention n'a d'autre rapport avec ces automates que d'en avoir fourni l'occasion et l'opportunité.

FIN.

1) Il s'agit de Salomon Coster. Comparez la p. 10, la note 2 de la p. 12 et le dernier alinéa de la note 1 de la p. 22. Les deux horloges de Coster, mentionnées aux p. 14-16, ne sonnent l'heure ni l'une ni l'autre. Il est parfaitement croyable, comme le dit Huygens, que ce soit lui qui ait inventé les horloges sonnantes à ressort moteur unique (ou à couple unique de poids moteurs) puisqu'on trouve encore des horloges de la Haye (‘Haagsche klokjes’) du dix-septième siècle possédant cette construction caractéristique pour elles. Nous connaissons p.e. une horloge sonnante de Claude Pascal (voir sur lui la note 5 de la p. 158 qui suit) ainsi construite. En tournant la clef (en sens ‘inverse’, comme dans les horloges de Coster) on remonte le ressort unique, partant l'ouvrage entier. Huygens parle aussi de cette invention de Coster dans sa lettre à P. Petit du 1 novembre 1658 (T. II, p. 273), disant: ‘Il a fait de ces horologes qui vont 7 jours et sonnent les heures, rien qu' avec un ressort.’ La dernière phrase de l'‘Horologium’ nous apprend que la construction d'horloges de ce genre par Coster n'est pas antérieure à 1657.

2) L'horloge d'Amsterdam de 1657 (voir les p. 14-16 et 31 qui précèdent) est mue par un ressort. Probablement Coster (voir les l. 18, 17 d'en bas de la p. 273 du T. II) a aussi construit des horloges à ressort du type de la Fig. 8, c. à d. avec la roue P et le pignon O et à verge à palettes verticale; mais malheureusement nous ne possédons plus d'horloges de ce genre fabriquées par lui, ni à ressort, ni à poids moteur. Comparez sur les ouvrages à ressort moteur la note 2 de la p. 10 et la note 1 de la p. 64.

1) Il s'agit de Salomon Coster. Comparez la p. 10, la note 2 de la p. 12 et le dernier alinéa de la note 1 de la p. 22. Les deux horloges de Coster, mentionnées aux p. 14-16, ne sonnent l'heure ni l'une ni l'autre. Il est parfaitement croyable, comme le dit Huygens, que ce soit lui qui ait inventé les horloges sonnantes à ressort moteur unique (ou à couple unique de poids moteurs) puisqu'on trouve encore des horloges de la Haye (‘Haagsche klokjes’) du dix-septième siècle possédant cette construction caractéristique pour elles. Nous connaissons p.e. une horloge sonnante de Claude Pascal (voir sur lui la note 5 de la p. 158 qui suit) ainsi construite. En tournant la clef (en sens ‘inverse’, comme dans les horloges de Coster) on remonte le ressort unique, partant l'ouvrage entier. Huygens parle aussi de cette invention de Coster dans sa lettre à P. Petit du 1 novembre 1658 (T. II, p. 273), disant: ‘Il a fait de ces horologes qui vont 7 jours et sonnent les heures, rien qu' avec un ressort.’ La dernière phrase de l'‘Horologium’ nous apprend que la construction d'horloges de ce genre par Coster n'est pas antérieure à 1657.

[p. 73]

fabricata sunt, applicari queat. Nos quidem apud eum, cujus opera primum in his fabricandis usi sumus¹⁾, talia quoque confecta vidimus, quae non pondere, sed elateris vi moverentur²⁾. In quibus, cum antehac pyramide illa aequatoria, chordaque huic circumvoluta opus esset, quorum ope adaequarentur primi ac postremi elateris impetus; nunc ijs omissis, ipsi tympano, cui elater inclusus est, dentes adduntur. Nam licet hoc modo non aequè in fine ac principio vigeat penduli motus, non tamen eò lentiores sub finem oscillationes efficiuntur, uti superius fuit demonstratum. Elater verò ea parte, qua ad centrum convolutus est, intenditur, atque ita cavetur ne quo temporis momento cursus horologij sufflaminetur. Mitto quod & sonitu horas edentia automata hujusmodi machinatus est¹⁾, ita ut uno eodemque, sive pondere, sive elatere, pars utraque, tam quae ad hoc comparata est, quam quae indicem horologij versat, moveretur. Etenim haec omnia ad inventum nostrum haud aliter spectant, quam quod occasionem ijs atque opportunitatem praebuerit.

FINIS.

1) Il s'agit de Salomon Coster. Comparez la p. 10, la note 2 de la p. 12 et le dernier alinéa de la note 1 de la p. 22. Les deux horloges de Coster, mentionnées aux p. 14-16, ne sonnent l'heure ni l'une ni l'autre. Il est parfaitement croyable, comme le dit Huygens, que ce soit lui qui ait inventé les horloges sonnantes à ressort moteur unique (ou à couple unique de poids moteurs) puisqu'on trouve encore des horloges de la Haye (‘Haagsche klokjes’) du dix-septième siècle possédant cette construction caractéristique pour elles. Nous connaissons p.e. une horloge sonnante de Claude Pascal (voir sur lui la note 5 de la p. 158 qui suit) ainsi construite. En tournant la clef (en sens ‘inverse’, comme dans les horloges de Coster) on remonte le ressort unique, partant l'ouvrage entier. Huygens parle aussi de cette invention de Coster dans sa lettre à P. Petit du 1 novembre 1658 (T. II, p. 273), disant: ‘Il a fait de ces horologes qui vont 7 jours et sonnent les heures, rien qu' avec un ressort.’ La dernière phrase de l'‘Horologium’ nous apprend que la construction d'horloges de ce genre par Coster n'est pas antérieure à 1657.

2) L'horloge d'Amsterdam de 1657 (voir les p. 14-16 et 31 qui précèdent) est mue par un ressort. Probablement Coster (voir les l. 18, 17 d'en bas de la p. 273 du T. II) a aussi construit des horloges à ressort du type de la Fig. 8, c. à d. avec la roue P et le pignon O et à verge à palettes verticale; mais malheureusement nous ne possédons plus d'horloges de ce genre fabriquées par lui, ni à ressort, ni à poids moteur. Comparez sur les ouvrages à ressort moteur la note 2 de la p. 10 et la note 1 de la p. 64.

1) Il s'agit de Salomon Coster. Comparez la p. 10, la note 2 de la p. 12 et le dernier alinéa de la note 1 de la p. 22. Les deux horloges de Coster, mentionnées aux p. 14-16, ne sonnent l'heure ni l'une ni l'autre. Il est parfaitement croyable, comme le dit Huygens, que ce soit lui qui ait inventé les horloges sonnantes à ressort moteur unique (ou à couple unique de poids moteurs) puisqu'on trouve encore des horloges de la Haye (‘Haagsche klokjes’) du dix-septième siècle possédant cette construction caractéristique pour elles. Nous connaissons p.e. une horloge sonnante de Claude Pascal (voir sur lui la note 5 de la p. 158 qui suit) ainsi construite. En tournant la clef (en sens ‘inverse’, comme dans les horloges de Coster) on remonte le ressort unique, partant l'ouvrage entier. Huygens parle aussi de cette invention de Coster dans sa lettre à P. Petit du 1 novembre 1658 (T. II, p. 273), disant: ‘Il a fait de ces horologes qui vont 7 jours et sonnent les heures, rien qu' avec un ressort.’ La dernière phrase de l'‘Horologium’ nous apprend que la construction d'horloges de ce genre par Coster n'est pas antérieure à 1657.