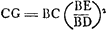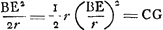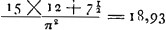Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
[pagina 253]
| |
[pagina 254]
| |
Christiaan Huygens
| |
[pagina 255]
| |
Christianus Hugenius
| |
[pagina 256]
| |
globe en liège atteint bientôt un point à partir duquel il se meut, en continuant à tomber, avec une vitesse uniforme (ce qui est nécessairement également vrai pour un globe en plomb si petit qu'il a par rapport à sa gravité autant de surface que le globe de liège, c'est-à-dire, dont le diamètre est à celui du globe de liège dans un rapport égal à celui de la gravité spécifique du liège à celle du plomb, comme je l'ai démontré ailleursGa naar voetnoot1): de même aussi j'estime à propos d'un globe en plomb arbitrairement grand que, s'il continue à tomber à travers de l'air, il parviendra enfin lui aussi à un état de mouvement uniforme, bien entendu après avoir parcouru un espace énorme, de sorte que la loi de l'accélération ne sera pas valable dans ce cas, et que par conséquent cette loi ne sera en réalité jamais observée avec une précision absolue. Ce n'est pas là pourtant une raison pour considérer la spéculation de Galilée sur ce mouvement comme peu importante et peu utile, pas plus ma foi que toute la mécanique qui traite des poids parce qu'on a coutume d'y admettre à tort que les corps pondérables tendent à tomber suivant des lignes parallèles entre elles, tandis qu'en réalité ces lignes convergent vers le centre de la terre. D'ailleurs pour la démonstration des théorèmes que nous traiterons ici, il suffit que pour des espaces arbitrairement petits l'accélération à partir du point de repos croisse suivant les nombres impairs 1, 3, 5, 7, comme Galilée l'a établiGa naar voetnoot3).  [Fig. 1.]
Ainsi lorsqu'un corps pondérable est suspendu à un fil [Fig. 1], le fil éprouve une traction pour cette raison que le corps pondérable tend à s'éloigner dans la direction du fil d'un mouvement accéléré de cette espèce. Or, par un mouvement accéléré suivant la progression enoncée un espace plus ou moins grand peut être parcouru dans le même temps comme lorsqu'un corps pondérable est maintenu sur un plan incliné AB [Fig. 2] par un fil CD parallèle à ce plan. En effet, dans ce cas aussi le corps tend à suivre une ligne DC d'un mouvement semblablement accéléré, mais non pas de telle façon qu'il parcourt en un certain laps de temps un chemin égal à celui qu'il parcourrait en ce même temps s'il avait été détaché d'un fil vertical. Il s'ensuit qu'on sent dans ce cas un moindre effort: d'autant moindre par rapport à cet autre dans la direction verticale que le corps parcourrait moins d'espace sur le plan incliné que dans la direction verticale durant le même temps. | |
[pagina 257]
| |
mis spatiis eandem rationem perfectissimè observatum iri. Nunc autem, sicut ex illa fit ut sphaera ex subere brevi eo perveniat unde aequabili deinceps celeritate decidere pergat; quod de plumbea etiam necessario verum est, minuta adeo ut pro gravitate sua tantam superficiem habeat quantam suberea, hoc est, cujus diameter sit ad diametrum illius, sicut gravitas specifica suberis ad gravitatem plumbi, ut alias ostendiGa naar voetnoot1): ita de plumbea quoque quantumvis magna existimo, si per aerem cadere pergat, perventuram quoque tandem ad aequabilemGa naar margenoot+ motum, post |Ga naar voetnoot2) immensum videlicet spatium peractum. adeo ut accelerationis ratio hîc locum non sit habitura, ac proinde revera nunquam praecisione exquisitissima servetur. Veruntamen non propterea parum egregia atque utilis Galilei de hoc motu speculatio censenda est, non magis hercle quam mechanica omnis quae circa pondera versatur quod falso in illa praesumi soleat gravia parallelis inter se lineis descendere conari quae revera ad centrum terrae vergunt. Caeterum ad illorum demonstrationem, quae nos hic tractabimus, sufficit in minimis quamlibet spatijs à quietis puncto accelerationem crescere secundum impares numeros 1, 3, 5, 7, ut Galileus statuitGa naar voetnoot3). ItaqueGa naar voetnoot4) cum grave ex filo suspensum est [Fig. 1], ideo trahitur filum, quoniam grave conatur recedere secundum lineam fili motu accelerato ejusmodi. 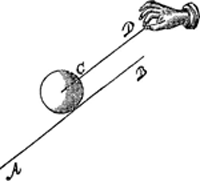 [Fig. 2.]
Potest autem motu secundum dictam progressionem accelerato majus minusve spatium eodem tempore confici. velut cum in plano inclinato AB [Fig. 2] grave sustinetur filo CD ipsi plano aequidistanti. Nam & hic conatur grave progredi per lineam DC motu similiter accelerato, sed non ut tantundem spatii percurrat certa temporis particula, quantum percurreret cadem particula si à filo perpendiculari dimissum esset. Unde & minor conatus hic sentitur, qui nempe tanto minor est altero illo conatu perpendiculari, quanto minus spatium eodem tempore in plano inclinato quam in perpendiculari grave transiturum essetGa naar voetnoot5). | |
[pagina 258]
| |
Nous admettons en outre que toutes les fois que deux corps de poids égaux sont l'un et l'autre retenus par un fil et qu'ils possèdent la tendance de s'éloigner dans la direction du fil d'un même mouvement accéléré, par lequel ils parcourraient des chemins égaux dans le même temps, l'on sent aussi la même traction de ces fils soit vers le bas soit vers le haut soit dans toute autre direction où ils sont tirés, sans qu'il fasse aucune différence de quelle cause cette tendance provient, pourvu qu'elle soit là. Or, la même tendance existe lorsque, si l'on met les corps en liberté, autrement dit si l'on ne tient pas leur tendance en échec, un même mouvement aura lieu. Et ceci ne doit être appliqué qu'au mouvement initial, en
 [Fig. 3.]
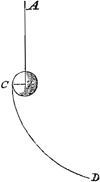
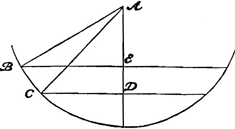
prenant un laps de temps aussi petit que possible. En effet, si par exemple le globe B [Fig. 3] est suspendu au fil AB et touche latéralement la surface concave CD, mais de telle manière que la droite menée du centre B de la sphère au point de contact soit perpendiculaire tant au fil AB qu'à la tangente à la courbe, nous savons que le globe n'est nullement supporté par la surface CD mais qu'il tire la corde AB avec autant de force que s'il ne touchait pas la surface CD mais qu'il était librement suspendu. Néanmoins s'il est détaché de la corde et qu'il tombe, il ne descendra pas de la même manière que s'il quittait la corde après avoir été librement suspendu; mais précipité sur la surface CD il n'observera pas même exactement la proportion de l'accélération indiquée par les nombres impairs 1, 3, 5, 7. Il apparaît donc qu'il ne faut pas avoir égard à ce qui arrivera au corps quelque temps après sa séparation de la corde, mais qu'il faut considérer un laps de temps aussi petit que possible après le commencement du mouvement, si nous voulons déterminer la force de la tendance au mouvement. Or, le globe B commence dans ce cas à se mouvoir après la séparation de la corde comme s'il était tombé verticalement, parce qu'au commencement il a cette inclination au mouvement qui est selon la droite AB, puisque celle-ci est parallèle à la tangente à la courbe en C. Voyons maintenant dans le cas de corps liés à un fil ou à une roue qui tourne, de quelle nature et de quelle grandeur est la tendance qui les porte à s'éloigner du centre. Supposons la roue BG [Fig. 4] qui tourne autour de son centre A parallèle au plan de l'horizon; un globule lié à la circonférence possède, lorsqu'il a atteint le point B, la tendance de continuer son mouvement suivant la droite BH qui touche la roue en B; en effet, s'il est détaché en cet endroit de la roue et qu'il s'envole, il prendra le chemin droit BH et ne le quittera pas à moins qu'il ne soit tiré en bas par la force de la gravité ou que son cours ne soit entravé par la rencontre d'un autre corps. Mais ce qui paraît à première vue difficile à comprendre, c'est pourquoi le fil AB est si fortement tendu alors que le globe a la tendance de se mouvoir | |
[pagina 259]
| |
Porro quoties duo corpora aequalis ponderis unum quodque filo retinetur, si conatum habeant eodem motu accelerato, & quo spatia aequalia eodem tempore peractura sint, secundum extensionem fili recedendi: AEqualem quoque attractionem istorum filorum sentiri ponimus, sive deorsum sive sursum sive quamcunqueGa naar margenoot+ in | partem trahantur. Neque referre qua ex causa conatus ejusmodi oriatur, dummodo adsit. Adest autem idem conatus, si data facultate seu non inhibito conatu, idem circa motum continget. Idque in initio motus tantum spectandum est, accepta parte temporis quamlibet exigua. Nam ex. gr. si globus B [Fig. 3] pendeat a filo AB, tangat autem a latere superficiem cavam CD, verum ita ut quae a centro sphaerae B ad contactum ducitur sit & filo AB & tangenti curvam perpendicularisGa naar voetnoot1), scimus jam globum neutiquam à superficie CD sustineri, sed aeque valide trahere funem AB ac si planum CD non tangeret sed libere suspensus esset. Attament si à fune separetur decidatque, non descendet eodem modo, ac si libere suspensus fune excidisset, sed per superficiem CD devolutus ne quidem accelerationis proportionem secundum numeros impares 1, 3, 5, 7 accurate servabit. Itaque apparet non illud respiciendum quid aliquandiu post separationem à fune gravi futurum sit, sed quamlibet minimam temporis particulam ab incepto motu considerandam, si vim conatus determinare velimus. Incipit autem hîc globus B, post separationem à fune, ita moveri, quemadmodum si perpendiculariter decidisset, quoniam initio eam determinationem motus habet quae est secundum rectam AB, quoniam haec tangenti curvam in C parallela est. Nunc videamus quis quantusque conatus sit corporibus filo vel rotae quae circumgyratur alligatis, ut à centro recedant. 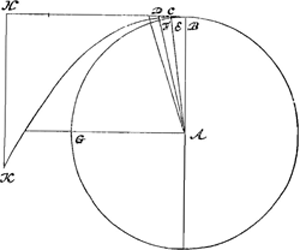 [Fig. 4.]
Sit rota BG [Fig. 4] quae circa A centrum convertatur, horizontis plano aequidistans. globulus ad circumferentiam ligatus, ubi ad B punctum venerit, conatum habet pergendi secundum rectam BH, quae rotam in B contingit: nam, si hic ab rota separetur avoletque rectam viam BH insistet, nec relinquet eam nisi vi gravitatis deorsum | trahatur, velGa naar margenoot+ occursu alterius corporis cursus ejus impediatur. Hoc vero primo intuitu difficile intellectu | |
[pagina 260]
| |
suivant la droite BH qui est perpendiculaire à AB. Mais tout s'expliquera par les considérations suivantes. Supposons cette roue très grande de sorte qu'elle emporte facilement avec elle un homme placé sur elle en B près de sa circonférence, mais attaché de sorte qu'il ne peut pas être lancé dehors lui-même; et que cet homme tienne de sa main un fil à l'autre bout duquel soit attaché une balle en plombGa naar voetnoot2). Eh bien, le fil sera tendu de la même manière, et tout aussi fortement par la force de la rotation, soit qu'il soit tenu de cette manière, soit qu'il se prolonge jusqu'en A et qu'il soit attaché là; quant à la cause de sa tension, on pourra maintenant mieux en juger. Prenons des arcs égaux BE, EF, petits par rapport à la circonférence entière, par exemple des centièmes parties ou de plus petites encore. L'homme attaché à la roue de qui nous avons parlé, parcourt donc ces arcs en des temps égaux, tandis que le plomb, s'il était abandonné à lui-même, parcourrait les droites, égales à ces arcs, BC et CD, dont les extrémités C et D ne tombent, il est vrai, pas précisément sur les droites qui relient le centre A aux points E et F, mais s'en écartent extrêment peu dans la direction vers B. Il appert maintenant que lorsque l'homme sera parvenu jusqu'en E, le plomb sera en C s'il a été lâché au point B, tandis que, lorsque l'homme aura atteint le point F, le plomb sera en D; nous dirons donc à bon droit que le plomb a cette tendanceGa naar voetnoot3). Que si les points C et DGa naar voetnoot4) étaient sur les prolongements des droites AE et AF, il serait certain que le plomb tend à s'éloigner de l'homme suivant la droite même qui émanant du centre passe par l'endroit qu'il occupe; et cela de telle façon que pendant le premier laps de temps il s'éloginerait de lui à une distance EC, et qu'après le deuxième il se trouverait à une distance FD. Or ces distances EC, FD etc. croissent de la même manière que la série des carrés depuis l'unité: 1, 4, 9, 16 etc. En effet, elles s'accordent d'autant plus exactement avec cette série que les particules BE, EF sont prises plus petites: elles doivent par conséquent être considérées comme n'en différant absolument pas au tout premier commencement. Il est donc évident que la tendance qui existe en ce cas sera tout-à-fait | |
[pagina 261]
| |
videtur, cur adeo tendatur filum AB, cum globus conctur ire secundum BH rectam quae ad AB perpendicularis est. Sed omnia hoc modo clara fient. Cogitemus
 [Fig. 4.]
maximam quampiam rotam hanc esse, ut hominem prope circumferentiam ei insistentemGa naar voetnoot1) in B, facile una secum deferat; verum ita affixum ut ne excuti ipse possit; teneat autem manu sua filum cum alligata ad caput alterum fili glande plumbeaGa naar voetnoot2). Eodem igitur modo & aeque valide filum tendetur ex vi vertiginis, sive ita contineatur, sive filum idem ad centrum usque A porrigatur, ibique deligatum sit: ratio autem ob quam tenditur manifestius jam percipi poterit. Sumantur arcus aequales BE, EF, exigui ratione totius circumferentiae, puta partes centesimae vel minores etiam. Hosce igitur arcus is quem diximus homo aequalibus temporibus pertransit rotae affixus, plumbum autem iisdem temporibus decurreret, si dimitteretur, per rectas BC, CD dictis arcubus aequales, quarum termini C, D, non quidem in eas rectas incidunt omnino, quae ex centro A per puncta E, F, ducuntur, sed minimum quid versus B ab iis lineis distant. Apparet jam, ubi homo pervenerit in E, plumbum futurum in C, si in B puncto dimissum fuisset, ubi autem ad F ille pervenerit, futurum in D. unde hunc conatum inesse plumbo rectè dicemusGa naar voetnoot3). Quod si jam puncta C, DGa naar voetnoot4) essent in rectis AE, AF productis, certum esset conari plumbum recedere ab homine per ipsam lineam quae à centro per locum ejus ducitur; & quidem ita ut prima temporis parte removeatur ab eo spatio EC, secunda autem parte temporis distet spatio FD. Haec autem spatia EC, FD &Ga naar margenoot+ caetera | deinceps ita crescunt ut quadratorum series ab unitate 1, 4, 9, 16 &c. nam tanto sanè exactius hanc seriem referunt quanto minores particulae BE, EF acceptae fuerint, ideoque in ipso initio tanquam nihil differrent consideranda sunt. | |
[pagina 262]
| |
semblable à celle qu'on sent lorsque le globe est tenu en suspension à un fil, paree que dans ce dernier cas aussi le corps tend à s'éloigner suivant la direction même du fil d'un mouvement semblablement accéléré; de sorte qu'à la fin du premier laps de temps le corps aura parcouru la petite distance 1, après deux laps de temps 4 petites distances, après trois 9 petites distances, etc. Ainsi en serait-il donc si les points C et D se trouvaient sur le prolongement des droites AE et AF. Mais maintenant comme ces points s'écartent un peu des droites nommées dans la direction de B, il s'ensuit que le globe tend à s'éloigner de l'homme non pas suivant la ligne droite qui part du centre A, mais suivant une certaine courbe qui touche cette droite à l'endroit où l'homme se trouve. En effet, si au point B un
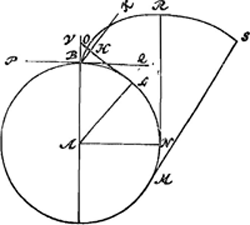 [Fig. 5.]
plan PQ [Fig. 5] touche la roue, plan que nous supposons attaché à la roue et tournant avec elle, le globe B, s'il se détache de la roue ou du plan nommé, décrira par rapport à ce plan et au point B, lesquels continuent leur mouvement, une courbe BRS qui touchera en B le prolongement du rayon AB animé du même mouvement. Si nous voulons décrire cette courbe, il suffira d'enrouler un fil quelconque sur la circonférence BNM et de mouvoir son extrémité B vers RS de telle manière que la partie qui a quitté la circonférence BNM reste toujours tendue, car par ce mouvement le fil décrira de son extrémité la dite ligne BRS, ce qu'il est facile de démontrer. Or, cette ligne possédera la propriété suivante: en quelque point, tel que N, de la circonférence qu'on mène une tangente à la circonférence coupant la courbe en R, cette droite NR sera égale à l'arc NB; ce qui est évident d'après la genèse de la courbe. Il s'agit maintenant de démontrer que la courbe et la droite AB se touchent au point B. Soit NR une tangente à la circonférence parallèle à AB. Il est certain que la partie BR de la courbe est située toute entière entre les droites parallèles AB et NR, car si l'on y prend un point quelconque tel que O et qu'on fait passer par ce point la tangente à la circonférence VOL, LO sera égale à l'arc LB et par suite plus petite que la tangente du même arc qui est LV: par conséquent il est nécessaire que le point O tombe entre V et L; et la même chose peut être démontrée pour un point quelconque situé sur BR. Si l'on dit maintenant que la droite BV ne touche pas la courbe BR en B, on pourra donc tracer à partir de B une certaine droite BK faisant avec BV un si petit angle qu'elle ne coupe pas la courbe BR; soit BK cette droite. Tirons le rayon AL parallèle à BK et soit LH perpendiculaire à cette même droite BK et | |
[pagina 263]
| |
Itaque similem planè conatum hunc fore constat illi qui sentitur cum globus filo suspensus tenetur, quoniam tunc quoque conatur recedere secundum lineamipsius
 [Fig. 4.]
fili, motu similiter accelerato; ut nempe prima temporis parte exacta peregerit spatiolum 1, duabus temporis partibus spatiola 4, tribus 9 &c. Sic igitur se res haberet si puncta C, D, essent in rectis AE, AF productis. Nunc autem quia parum versus B à praedictis lineis recedunt, contingit inde ut globus non per rectam lineam è centro A venientem conetur ab homine recedere sed per curvam quandam quae rectam illam tangit eo loco ubi homo consistit. Nempe si rotam contingat in B [Fig. 5] planum PQ, quod ei sit affixum atque una cum ipsa circumferatur, globus B, si a rota seu plano dicto separetur, describet respectu ejusdem plani punctique B porro moveri pergentium curvam BRS, quae radium AB una translatum productumque tanget in B. quam curvam si describere velimus, tantum silum aliquod circumferentiae BNM circumponendum est, ejusque caput B ducendum versus RS, ita ut semper extensa maneat pars ea quae circumferentiam BNM reliquit; hoc enim motu, extremo sui puncto, dictam lineam BRS describet; quod facile est ostendere. Erit autem haec lineae proprietas, ut si ad quodlibet circumferentiae punctum, ut N, ducatur tangens circumferentiam quae occurrat curvae in R, haec ipsa NR aequalis sit arcui NB; quod ex ortu perspicuum est. Tangere autem se mutuo curvam rectamque AB in puncto B est ostendendum.Ga naar margenoot+ Sit NR tangens circumferentiae, | parallela AB. ConstatGa naar voetnoot1) curvae partem BR totam intra rectas parallelas AB, NR jacere, nam si quodvis in ea punctum ut O sumatur, per quod tangens ad circumferentiam ducatur VOL, erit LO aequalis arcui LB ideoque minor tangente ejusdem arcus, quae est LV: unde punctum O inter V & L cadere necesse est. atque idem de quocunque puncto in BR accepto ostendi potest. Jam vero si curvam BR dicatur non tangere recta BV in B, ergo poterit duci ex B recta quaepiam BK tam exiguo angulo super BV inclinata ut curvam BR non secet. sit ea BK. Ducatur AL radius parallelus BK, sitque LH ad eandem BK perpendicularis. ideoque & ad AL. Est igitur LH aequalis sinui arcus BL ideoque | |
[pagina 264]
| |
 [Fig. 5.]
par conséquent aussi à AL. LH est donc égale au sinus de l'arc BL et par suite moindre que cet arc. Mais la droite LHO comprise entre le point de contact L et la courbe BR est égale à ce même arc. Une certaine partie de la courbe BR sur laquelle se trouve le point O tombera donc à l'intérieur de l'angle VBK quelque petit qu'on suppose cet angle. D'où il est évident que la droite BK coupe la courbe et encore que, par suite, BV la touche au point B. Comme le globe qui tourne avec la roue tend donc à décrire une courbe par rapport au rayon sur lequel il est situé, savoir une courbe telle qu'elle touche le rayon, il apparaît qu'en vertu de cette tendance le fil auquel le globe est lié ne doit pas être tendu d'autre façon que si le globe avait la tendance de se mouvoir suivant le prolongement même du rayon. Or, les distances que le globe parcourrait sur la dite courbe dans des temps croissant par portions égales, sont aussi entre elles comme la série des carrés depuis l'unité 1, 4, 9, 16 etc., bien entendu si nous portons nos regards sur le commencement du mouvement et sur des espaces très-petits; ce que la figure ci-jointe [Fig. 6] fait voir, où BE, EF, FM sont pris comme arcs égaux sur la circonférence de la roue, et où BK, KL, LN sont des droites situées sur la tangente BS égales aux dits arcs; tandis qu' EC, FD et MS sont des lignes provenant du centre. Par conséquent dans cette figure si le globe fût détaché en B de la roue tournante, au moment où le point B serait parvenu en E le globe serait en K et aurait parcouru la petite partie EK de la courbe décrite plus haut; mais à la fin du deuxième temps, lorsque B serait venu en F, le globe se trouverait en L et aurait alors parcouru la partie FL de la courbe. Et de même lorsque B serait venu en M, le globe aurait décrit la partie MN de la courbe. Or, ces parties de la ligne courbe doivent être considérées, immédiatement après la séparation du globe de la roue, comme identiques avec les droites EC, FD et MS qu'elles touchent; parce que les arcs peuvent à partir du point B être pris si menus que la petite différence qui existe entre les | |
[pagina 265]
| |
hoc arcu minor. AEqualis autem eidem arcui est recta LHO inter contactum L & curvam BR intercepta. Itaque pars aliqua curvae BR in qua est punctum O cadet intra angulum VBK, quamtumvis exiguus esse ponatur. Unde manifestum est rectam BK secare curvam, ideoque BV demum tangere eam in BGa naar voetnoot1). Cum itaque globus cum rota circumactus curvam describere conetur respectu radii in quo situs est, ac talem quidem quae radium contingat, apparet conatu hoc filum cui alligatus est, non secus tendi debere quam si secundum ipsum radium productum globus ire conetur. Sunt autem & spatia quae in dicta curva globus peracturus esset temporibus aequaliter crescentibus, sicut series quadratorum ab unitate 1, 4, 9, 16, &c. si videlicet principium motus spatiaque minima attendamus; quod apposita figura [Fig. 6] ostendit, ubi arcus aequales in circumferentia rotae accepti sunt BE, EF, FM; & [Fig. 6.]
in tangente BS rectae dictis arcubus aequales BK, KL, LN; lineae vero ex centro sunt EC, FD, MS. Hic itaque si globus à circumeunte rota divelleretur in B; tumGa naar margenoot+ ubi | punctum B pervenisset in E globus esset in K, particulamque curvae supra descriptae percurrisset EK. post secundum vero tempus exactum cum B venisset in F, globus in L reperiretur, jamque curvae partem FL percurrisset. Similiterque cum B venisset in M, globus peregisset curvae portionem MN. Hae vero curvae lineae partes tanquam eaedem cum rectis EC, FD, MS, quas contingunt, in principio separationis globi ab rota, considerandae sunt. quoniam tam parvi arcus à | |
[pagina 266]
| |
droites et ces courbes aura à leur longueur un rapport plus petit que tout rapport imaginable. Par conséquent les espaces EK, FL et MN doivent être considérés eux aussi comme croissants suivant la série des carrés depuis l'unité 1, 4, 9, 16. Et ainsi la force exercée par le globe attaché à la roue tournante ne sera pas autre que s'il tendait à se mouvoir suivant la droite qui relie le centre à lui, et cela d'un mouvement accéléré par lequel il parcourrait en des temps égaux des distances qui croissent suivant les nombres 1, 3, 5, 7, etc. En effet, il suffit que cette progression soit observée au commencement; car quand même il se mouvrait plus tard selon n'importe quelle autre loi ou par n'importe quel mouvement, ceci ne ferait aucune différence pour la tendance qui existe avant le commencement du mouvement. Mais cette tendance dont nous avons parlé est absolument semblable à celle avec laquelle les corps pondérables suspendus à un fil aspirent à descendre. D'où nous conclurons aussi que les forces centrifuges de corps mobiles inégaux, mais mus suivant des circonférences égales et avec la même vitesse sont entre elles comme les gravités ou quantités solides de ces corps. En effet, comme tous les corps pondérables tendent à tomber avec la même vitesse et d'un mouvement accéléré identique, mais que cette tendance des corps a d'autant plus de force qu'ils sont plus grands, il en doit être aussi de même pour ceux qui tendent à s'éloigner d'un centre et dont la tendance, à ce que nous avons démontré, est parfaitement semblable à celle qui résulte de la gravité. Mais tandis que la tendance à tomber est toujours la même pour un même globe toutes les fois qu'on le suspend à un fil, celle d'un globe tournant avec une roue est au contraire plus petite ou plus grande selon que la roue tournera plus lentement ou plus rapidement. Reste à examiner la grandeur ou quantité de chaque tendance pour diverses vitesses de la roue. Nous nous demanderons d'abord avec quelle vitesse il faut faire tourner la roue proposée pour que le globe tende son fil avec la même force que lorsqu'il y est verticalement suspenduGa naar voetnoot1). | |
Proposition IGa naar voetnoot2).Lorsque deux mobiles égaux parcourent en des temps égaux des circonférences inégales, la force centrifuge correspondant à la plus grande circonférence sera à celle de la plus petite circonférence dans un rapport égal à celui des circonférences elles-mêmes ou de leurs diamètresGa naar voetnoot3). | |
[pagina 267]
| |
puncto B accipi possunt ut differentiola quae est inter rectas curvasque hasce, minorem rationem habeat ad ipsarum longitudinem, quavis ratione imaginabili. Proinde igitur & spatia EK, FL, MN tanquam crescentia secundum seriem quadratorum ab unitate 1, 4, 9, 16, spectanda sunt. Atque ita conatus globi in circumeunte rota retenti haud alius erit, ac si secundum rectam quae ex centro per ipsum ducitur progredi contenderet, idque motu accelerato quo aequalibus temporibus crescentia percurreret spatia secundum numeros 1, 3, 5, 7, &c. sufficit enim initio hanc progressionem observari; nam licet postea qualibet alia ratione vel motu feratur id ad conatum qui est ante inceptum motum nihil prorsus attinet. Is autem quem diximus planè similis conatus est ei quo gravia ex filo pendentia deorsum pergere nituntur. Unde etiam concludemus vires centrifugas mobilium inaequalium sed in circulis aequalibus aequali velocitate latorum esse inter se sicut mobilium gravitates, seu quantitates solidas. Sicut enim gravia omnia eadem celeritate conantur deorsum labi motuque similiter accelerato; tanto autem amplius momenti habet hic eorum conatus quanto majora fuerint; ita in iis quoque, quae a centro tendere nituntur, evenire debet, quorum conatus planeGa naar margenoot+ similis | est ostensus conatui, qui est ex gravitate. Cum autem ejusdem globi idem semper sit conatus ad descendendum quoties ex filo suspenditur; contra verò globi in rota circumacti minor majorve conatus prout tardius celeriusve rota versabitur; superest ut magnitudinem seu quantitatem conatus cujusque in diversis rotae celeritatibus inquiramus. Et primo quidem illud investigabimus, qua celeritate rotam propositam circumagi necesse sit ut aequè validè filum suum globus intendat, atque cum perpendiculariter ab illo est suspensusGa naar voetnoot1). | |
[Propositio I.]Ga naar voetnoot2)Si mobilia duo aequalia aequalibus temporibus circumferentias inaequales percurrant; erit vis centrifuga in majori circumferentia, ad eam quae in minori, sicut ipsae inter se circumferentiae, vel earum diametriGa naar voetnoot3). | |
[pagina 268]
| |
Considérons des circonférences ayant AB et AC [Fig. 7] pour rayons, suivant lesquelles deux mobiles égaux tournent en des temps égaux. Prenons sur l'une et l'autre de très petits arcs semblables, BD et CE et sur les tangentes aux points B et C les distances BF et CG égales chacune à l'arc correspondant. Le mobile qui tourne suivant la circonférence BD a donc une tendance à s'éloigner du centre dans la direction de son fil d'un mouvement naturellement accéléré et à parcourir de ce mouvement l'espace DF en un certain laps de temps; quant à celui qui parcourt la circonférence CE, il a bien une tendance semblable à s'éloigner du centre, mais telle qu'en vertu de cette tendance il parcourrait dans le même temps l'espace EG. Par conséquent dans le cas de la plus grande circonférence le fil est tendu d'autant plus fortement que dans celui de la plus petite que DF est plus grand que EG. Or, il apparaît que FD est à GE comme BF à CG, c'est-à-dire comme BA à AC. La force centrifuge correspondant à la plus grande circonférence sera donc à celle de la plus petite comme ces circonférences elles-mêmes ou leurs diamètres. Ce qu'il fallait démontrer. | |
Proposition II.Lorsque des mobiles égaux tournent dans les mêmes ou d'égales circonférences ou roues avec des vitesses différentes mais l'un et l'autre d'un mouvement uniforme, la force centrifuge du plus rapide sera à celle du plus lent dans un rapport égal à celui des carrés des vitesses. C'est-à-dire si les fils par lesquels les mobiles sont retenus passent de haut en bas par le centre de la roue et qu'ils portent des poids par lesquels la force centrifuge des mobiles est tenue en échec et exactement équilibrée, ces poids seront entre eux comme les carrés des vitesses.
Soit donné un cercle à centre A et rayon AB, suivant la circonférence duquel se meuve d'abord un mobile plus lent avec une vitesse que représente la ligne N, ensuite un autre avec une plus grande vitesse désignée par O. Si l'on prend maintenant de très petits arcs BE et BF qui soient entre eux comme N est à O, | |
[pagina 269]
| |
Sint circuli quorum radii AB [Fig. 7], AC, per quos duo mobilia aequalia aequalibus temporibus circumferanturGa naar voetnoot1). Accipiantur in utroque arcus minimi
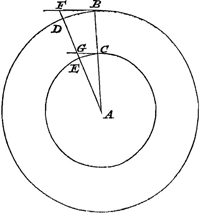 [Fig. 7.]
similes BD, CE, & in tangentibus ad puncta [Fig. 7.] B & C sumantur BF, CG singulae suis arcubus aequales. Mobile itaque in circulo BD circumlatum conatum habet recedendi a centro secundum extensionem fili sui motu accelerato naturaliter eoque motu permeandi spatium DF, certa temporis parte: in circulo autem CE circumiens similem quidem habet à centro recedendi conatum, sed quo parte illa temporis eadem conficiat spatium EG. Itaque quanto major est DF quam EG, tanto majore vi trahitur filum in majori circulo quam in minori; patet autem esse FD ad GE sicut BF ad CG, hoc est, ut BA ad AC. Erit ergo vis centrifugaGa naar margenoot+ in majori circumferentia, | ad eam quae in minori, sicut ipsae inter se circumferentiae, vel earum diametri. Quod erat demonstrandumGa naar voetnoot2). | |
[Propositio II.]Si mobilia aequalia in iisdem sive aequalibus circulis rotisve gyrentur celeritatibus in aequalibus, verum utraque motu aequabili; erit vis recedendi à centro celerioris ad vim tardioris in duplicata ratione celeritatum. Hoc est, si fila quibus illa retinentur, per centrum rotae deorsum educantur, sustineantque pondera, quibus vis mobilium centrifuga inhibeatur, atque exacte adaequetur, erunt haec pondera inter se, sicut velocitatum quadrata.
Sit circulus cujus centrum A [Fig. 8] radius AB, in cujus circumferentia feratur primum mobile tardiusGa naar voetnoot3) celeritate, quam repraesentet linea N, deinde alterum celeritate majori, quae sit O. Sumtis jam arcubus minimis BE, BF, qui sint inter se, ut N ad O, constat eadem temporis parte, qua mobile tardius | |
[pagina 270]
| |
il est évident que dans le même laps de temps pendant lequel le mobile le plus lent parcourra l'arc BE, le plus rapide parcourra l'arc BF. Supposons égales aux arcs BE et BF respectivement les droites BC et BD faisant partie de la tangente. Eh bien, il est établi que chacun des deux mobiles a une tendance à s'éloigner du centre dans la direction de son fil d'un mouvement accéléré; mais d'un mouvement tel que le mobile qui tourne le plus lentement, s'écarterait du point de la circonférence sur lequel il est placé d'un espace égal à EC, celui qui est plus rapide au contraire d'un espace FD dans le même temps. Le mobile plus rapide tire donc d'autant plus fortement que le mobile plus lent, que DF est plus grand que CE. Mais puisque nous avons pris des arcs BE et BF très petits, le rapport DF:CE doit être estimé égal à DB2:CB2, comme nous l'avons expliqué un peu plus hautGa naar voetnoot1); et comme DB est à BC, ainsi l'arc FB est à BE, c.à.d. dans le rapport O:N. Par conséquent on aura FD:EC = O2:N2; O2:N2 sera donc aussi le rapport de la force centrifuge du mobile plus rapide à la force du mobile plus lent. C.Q.F.D. | |
Proposition III.Lorsque deux mobiles égaux se meuvent avec la même vitesse suivant des circonférences inégales, leurs forces centrifuges seront inversement proportionnelles aux diamètres, de sorte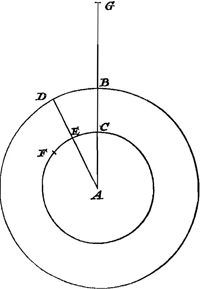 [Fig. 9.]
que dans le cas de la plus petite circonférence la force nomméeest la plus grande.
Soient donnés autour du même centre A [Fig. 9] des cercles inégaux à rayons AB et AC; des mobiles égaux se meuvent sur leurs circonférences avec une vitesse égale, c'est-à-dire que dans le temps où sur la plus grande circonférence un certain arc BD est parcouru, un arc CF égal à BD est parcouru sur la plus petite circonférence. Je dis que la force centrifuge du mobile qui circule sur la circonférence BD sera à celle que possède celui qui tourne sur la circonférence CF comme le rayon AC est à AB. Tirons le rayon AD qui coupe la plus petite circonférence en E; et soit AG troisième proportionnelle aux deux longueurs AC et AB. Imaginons-nous en outre qu'un certain mobile égal à l'un et l'autre des deux tourne sur la circonférence CF avec une vitesse telle qu'il parcoure l'arc CE dans le même temps dans lequel les deux autres décrivent les | |
[pagina 271]
| |
absolvet arcum BE, illud quod celerius est percursurum arcum BF; sint arcubus BE, BF singulis aequales in tangente positae BC, BD. Itaque & constat utrique
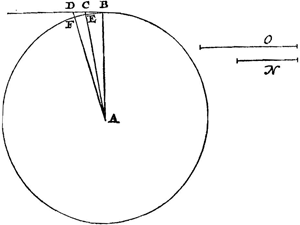 [Fig. 8.]
mobili inesse conatum recedendi a centro secundum extensionem fili sui motu accelerato; sed quo motu mobile, quod tardius fertur, recessurum sit à puncto circumferentiae, cui incumbit, quantum est spatium EC; illud vero quod celerius est, tempore aequali per spatium FD. Quanto igitur major est DF quam CE, tanto validius trahit mobile celerius tardiore. At quoniam arcus BE, BF minimos sumsimus, eadem censenda est ratio DF ad CE, quae quadrati DB ad CB, secundum ea quae paulo ante explicavimusGa naar voetnoot1);Ga naar margenoot+ estque ut DB ad BC ita arcus FB ad BE, hoc est, ita O ad N; ergo erit ut quadratum O ad quadratum N, ita FD ad EC, atque ita proinde vis centrifuga celerioris mobilis ad vim tardioris. Q.E.D. | |
[Propositio III.]Si duo mobilia aequalia in circulis inaequalibus aequali velocitate ferantur, erunt eorum vires centrifugae in ratione contraria diametrorum, ita ut in minori circumferentia dicta vis major existat.
Sunto circa idem centrum A [Fig. 9] circuli inaequales, quorum radii AB, AC; & ferantur in circumferentiis eorum mobilia aequalia celeritate aequali, hoc est, ut quo tempore in majori circumferentia percurritur arcus aliquis BD, eodem tempore in minori percurratur arcus CF ipsi BD aequalis longitudine. Dico vim centrifugam mobilis quod in circumferentia BD circumfertur, fore ad eam quam habet circumlatum in circumferentia CF sicut radius AC ad AB. Ducatur radius AD secans minorem circumferentiam in E; & sit duabus AC, AB tertia proportionalis AG. Porro intelligatur mobile quoddam utrivis duorum aequale circumferri in circumferentia CF ea celeritate, ut eodem tempore absolvat arcum CE, quo duo alia arcus BD & CF. Illius igitur assumti mobilis celeritas ad celeritatem | |
[pagina 272]
| |
arcs BD et CF. La vitesse de ce mobile supposé sera donc à celle de l'un et l'autre de ceux-là comme l'arc CE est à l'arc BD, c. à d. dans le rapport AC:AB. Or la force centrifuge du mobile qui parcourt l'arc BD sera à la force du mobile supposé qui en même temps parcourt l'arc CE, comme BA est à ACGa naar margenoot*. Mais la force centrifuge du mobile supposé sera à la force de celui qui en même temps parcourt l'arc CF dans un rapport égal à AC2:AB2Ga naar margenoot*, en d'autres termes, ce rapport sera égal à AC:AG, parce quenous avons fait voir que leurs vitesses sont dans le rapport AC::AB. En combinant les deux proportions on trouvera donc que la force centrifuge du mobile qui parcourt l'arc BD est à la force de celui qui pendant le même temps parcourt l'arc égal CF, comme BA est à AG, c'est-à-dire comme AC est à AB; ce qu'il fallait démontrer. | |
Proposition IV.Lorsque deux mobiles égaux, décrivant des circonférences inégales, ont une force centrifuge égale, le temps de révolution dans la plus grande circonférence sera au temps de révolution dans la plus petite dans un rapport égal à la racine carrée du rapport des diamètres.  [Fig. 10.]
Soient données des circonférences inégales BE et CF [Fig. 10] autour du même centre A, à rayons AB et AC, et supposons que sur chacune d'elles circule un mobile de telle manière que la force centrifuge soit la même pour les deux; je dis que le temps dans lequel la circonférence du cercle BE est parcourue est au temps dans lequel la circonférence CF est parcourue dans un rapport égal à la racine carrée du rapport AB:AC, c'est-à-dire, comme BA est à AD, moyenne proportionnelle entre AB et AC. En effet, si l'on imagine un troisième mobile égal aux deux autres, qui parcoure la circonférence CF dans le même temps dans lequel l'un des deux parcourt la circonférence BE, la force centrifuge du mobile supposé sera à celle de ce dernier comme AC est à ABGa naar margenoot*. Or, les forces centrifuges des deux premiers mobiles sont par hypothèse égales; la force centrifuge du mobile supposé sera donc à la force de celui qui par hypothèse parcourt la circonférence CF comme AC est à AB; et les forces centrifuges des mobiles qui se meuvent sur la même circonférence sont dans un rapport égal au carré du rapport des vitessesGa naar margenoot*. La vitesse du mobile supposé sera donc à celle du mobile qui par hypothèse tournait déjà sur la circonférence CF, comme AC est à | |
[pagina 273]
| |
 [Fig. 9.]
alterutrius horum erit, ut arcus CE ad arcum BD, hoc est, ut AC ad AB. Erit autem vis centrifuga mobilis, quod arcum BD percurrit, ad vim mobilis assumti, quod eodem tempore percurrit arcum CE, ut BA ad ACGa naar margenoot*. Sed vis centrifuga assumti mobilis erit ad vim ejus, quod eodem tempore percurrit arcum CF, in duplicata ratione AC ad ABGa naar margenoot*, hoc est, erit eadem quae AC ad AG, quoniam celeritates eorum ostendimus esse, ut ACGa naar margenoot+ ad AB. Ex aequa | li igitur erit vis centrifuga mobilis quod percurrit arcum BD ad vim ejus quod eodem tempore percurrit arcum aequalem CF, ut BA ad AG, hoc est, ut AC ad AB; quod erat demonstrandum. | |
[Propositio IV.]Si mobilia duo aequalia in circumferentiis inaequalibus circumlata vim centrifugam aequalem habuerint, erit tempus circuitus in majori circumferentia ad tempus circuitus in minori in subduplicata ratione diametrorum.
Sunto circuli inaequales BE, CF [Fig. 10] circa idem centrum A, quorum radii AB, AC; & in utroque mobile gyretur, ita ut eadem sit utrobique vis centrifuga; dico tempus quo circumferentia circuli BE percurritur, esse ad tempus, quo percurritur circumferentia CF, in subduplicata ratione AB ad AC, hoc est, sicut BA ad AD mediam proportionalem inter AB, AC. Si enim tertium mobile intelligatur aliis istis aequale, quod eodem tempore percurrat circumferentiam CF, quo alterum absolvit circumferentiam BE, erit assumti mobilis vis centrifuga ad vim hujus ut AC ad ABGa naar margenoot*. Ponuntur autem mobilium duorum priorum vires centrifugae aequales; ergo assumti mobilis vis çentrifuga erit etiam ad vim ejus, quod in circumferentia CF currere positum est, ut AC ad AB; sunt autem vires centrifugae eorum quae in eadem circumferentia moventur in duplicata ratione velocitatumGa naar margenoot*. Ergo velocitas assumti mobilis erit ad velocitatem ejus, quod primo positum est revolvi in circumferentia CF, sicut AC ad AD, vel ut AD ad AB. Velocitatibus autem contraria ratione respondentGa naar margenoot+ tempora lationum per eandem circumferentiam; ergo tempus circuitus | |
[pagina 274]
| |
AD ou AD à AB. Mais les temps de révolution, dans la même circonférence, sont inversement proportionnels aux vitesses; par conséquent le temps de révolution du mobile supposé, auquel est égal par hypothèse le temps de révolution du mobile parcourant la circonférence BE, sera au temps de révolution du mobile qui, à ce que nous avons dit, parcourait dès le commencement la circonférence CF comme AB est à AD. Ce qu'il fallait démontrer. | |
Proposition V.Lorsqu'un mobile décrit une circonférence de cercle avec la vitesse qu'il acquiert en tombant d'une hauteur égale à la quatrième partie du diamètre, il aura une tendance à s'éloigner du centre égale à sa gravité, c'est-à-dire il tirera le fil par lequel il est retenu avec la même force que lorsqu'il y est suspenduGa naar voetnoot1).
Soit donné un cercle [Fig. 11] à centre A et à rayon AB, parallèle à l'horizon, sur la circonsérence duquel se meuve un mobile d'un mouvement uniforme, avec une vitesse égale à celle qu'il acquerrait en tombant verticalement d'une hauteur égale à la moitié de AB, c'est-à-dire à CB; je dis que la corde par laquelle le mobile est retenu sera tendue avec la même force que s'il était librement suspendu à cette même corde. Soit BD une tangente à la circonférence, égale au rayon AB. Puisque le mobile décrit par hypothèse la circonférence de cercle avec la vitesse qu'il acquiert en tombant de la hauteur CB, c'est-à-dire avec laquelle il parcourrait d'un mouvement uniforme, dans le même temps dans lequel il a parcouru CB en tombant, un espace BD double de BC, il s'ensuit que si on le détache au point B, il parcourra dans le temps nommé ledit espace BD d'un mouvement uniforme. Considérons une très petite partie BE de cette longueur BD et tirons par le centre la droite EAH coupant la circonférence en F. Soit en outre, comme le carré de DB est au carré de BE, ainsi BC à CG en longueur. Par conséquent si le | |
[pagina 275]
| |
assumti mobilis, cui aequale est ex hypothesi tempus circuitus mobilis euntis per peripheriam BE, erit ad tempus circuitus mobilis quod in circumferentia CF initio ferri dictum est, ut AB ad AD. Quod erat demonstrandum. | |
[Propositio V.]Si mobile in circumferentia circuli feratur ea celeritate, quam acquirit cadendo ex altitudine, quae sit quartae parti diametri aequalis, Habebit conatum à centro recedendi aequalem suae gravitati, hoc est, aeque validè filum, quo retinetur, trahet, atque cum ex illo suspensum estGa naar voetnoot1). Esto circulus centro A [Fig. 11] radio AB horizonti parallelus, in cujus circumferentia feratur mobile aequabili motu, velocitate autem, quantam acquireret  [Fig. 11.]
cadens perpendiculariter ex altitudine aequali dimidiae AB, quae sit CB; dico vi centrifuga aequè validè tractum iri funem, quo mobile detinetur, ac si liberè ex eodem fune suspensum esset. Sit circuli tangens BD aequalis radio AB. Quoniam igitur mobile currit in circumferentia circuli ea celeritate, quam acquirit cadens ex altitudine CB, hoc est, qua transiret motu aequabili spatium BD ipsius BC duplum aequali tempore, quo decidit per CB; sequitur, si in B dimittatur, percursurum dicto tempore dictum spatium BD aequabili motu. Accipiatur ipsius BD pars minima quaepiam BE, & ducatur per centrum recta EAH secans circumferentiam in F. Sit porro ut quadratum DB ad quadratum BE, ita BC ad CG longitudine. Hinc igitur si tempus | |
[pagina 276]
| |
temps pendant lequel le mobile tombe d'un mouvement accéléré selon CB est par hypothèse représenté par la ligne BD, BE sera le temps du mouvement accéléré selon CG. Mais la même longueur BD sera aussi le temps pendant lequel le mobile parcourrait cette même longueur BD d'un mouvement uniforme pareil à celui qu'il possède en circulant sur la circonférence; en esfet ce temps est par hypothèse égal au temps du mouvement accéléré selon CB. BE sera donc aussi le temps dans lequel il parcourt cette même longueur BE avec la vitesse qu'il possède en vertu de sa révolution. D'où il apparaît que l'espace CG est parcouru d'un mouvement accéléré partant du repos dans le même temps que l'espace BE d'un mouvement uniforme avec la vitesse que le mobile possède par hypothèse en décrivant la circonférence. Il appert en outre que, si le mobile est détaché en B, il parviendra d'un mouvement uniforme en E au même instant où le point B de la circonférence sera venu en F; car la droite BE doit être censée égale à l'arc BF parce que BE est supposée infiniment petite. Nous dirons donc qu'il a une tendance à s'éloigner du point B d'un mouvement naturellement accéléré (car il a été démontré que ce mouvement est telGa naar voetnoot1)) en parcourant une distance FE dans le même temps dans lequel il parcourrait l'espace BE d'un mouvement uniforme avec la vitesse qu'il possède en vertu de sa révolution, c'est-à-dire dans le temps où il parcourrait d'un mouvement accéléré partant du repos la distance CG. C'est pourquoi, dès qu'il sera démontré que les espaces CG et FE sont égaux, il sera établi que la tendance du mobile suspendu à choir d'un mouvement accéléré, est absolument égale à la tendance du même mobile par laquelle, lorsqu'il décrit sa circonsérence, il s'essorce à s'éloigner de son fil d'un mouvement semblablement accéléré; parce qu'évidemment la tendance à des mouvements accélérés est égale lorsque des distances égales seraient parcourues de ces mouvements dans les mêmes laps de temps. Or l'égalité de CG et de FE se démontre de la façon suivante: comme HE est à EB ainsi EB est à EF, partant comme le carré de HE est au carré de EB, ainsi HE est à EF en longueur; d'où l'on tire en prenant les quatrièmes parties des termes antécédents: comme le carré de AF est à celui de EB, ainsi la quatrième partie de HE laquelle doit être estimée égale à ¼HF, c'est-à-dire BC, est à FE. Mais comme le carré de AF est au carré de BE, en d'autres termes comme le carré de DB est à celui de BE, ainsi d'après notre construction BC est à CG en longueur. BC sera donc à CG comme la même longueur BC est à FE, et par conséquent FE et CG sont égales entre elles; la proposition est donc démontrée. | |
Proposition VI.Étant donnée la distance qu'un mobile parcourt en un certain temps, par exemple en une seconde, en tombant verti- | |
[pagina 277]
| |
quo cadit motu accelerato per CB, repraesentari ponamus lineâ BD, erit BEGa naar margenoot+
 [Fig. 11.]
tempus motus accelerati per CG. Sed eadem BD erit quoque tempus quo transiret ipsam BD motu aequabili quantumque habet in circumferentia currens; nam hoc tempus ex hypothesi aequale est tempori motus accelerati per CB. Itaque & BE tempus erit quo transeat ipsum BE spatium celeritate, quam habet, vertiginis. Unde constat aequali tempore peragi spatium CG motu è quiete accelerato, & spatium BE motu aequabili cum celeritate, quam positum fuit habere mobile in circumferentia currens. Constat porro si mobile dimittatur in B, perventurum motu aequabili in E simul ac punctum circumferentiae B accesserit ad F; nam recta BE ipsi arcui BF aequalis censenda est, eo quod BE infinitè parva intelligitur. Itaque conatum ei inesse motu accelerato naturaliter (nam talem esse ostensum estGa naar voetnoot1)) dicemus recedendi a puncto B, per spatium FE tempore eodem quo celeritate suae vertiginis transiret spatium BE motu aequabili, hoc est, tempore eo quo percurreret motu è quiete accelerato spatium CG. Quare si ostensum fuerit spatia CG & FE esse aequalia, constabit conatum mobilis suspensi ad descendendum motu accelerato, aequalem plane esse conatui ejusdem mobilis, quo in circumferentia versatum nititur a filo suo recedere motu similiter accelerato; quoniam videlicet conatus ad motus acceleratos tunc aequalis est, cum spatia aequalia aequalibus temporibus iis motibus peragenda forent. Esse autem CG, FE aequales sic ostenditur: ut HE ad EB ita est EB ad EF, ideoque sicut quadratum HE ad quadratum EB, ita est HE ad EF longitudine. unde sumtis antecedentium subquadruplis erit, sicut quadratum AF ad quadratum EB, ita pars quarta HE, cui aequalis censenda est ¼HF, hoc est BC adGa naar margenoot+ FE; sed ut quadratum AF ad quadratum BE, sive ut quadratum | DB ad quadratum BE, ita est ex constructione BC ad CG longitudine. Ergo erit BC ad CG ut eadem BC ad FE, ideoque FE, CG inter se aequales; quare constat propositum. | |
[Propositio VI.]Data altitudine quam certo tempore, puta secundi minuti unius, mobile emetitur, cadendo ex quiete perpendiculariter; invenire circulum in cujus circumferentia mobile circumiens | |
[pagina 278]
| |
calement en partant du repos; trouver un cercle tel que si le mobile parcourt sa circonférence horizontalement en accomplissant sa révolution également en une seconde, il ait une force centrifuge égale à sa gravité.
Soit donnéc la hauteur AB qu'un mobile qui tombe en partant du repos parcourt p.e. dans le temps d'une seconde. Comme la circonférence d'un cercle est à son diamètre ainsi soit AB à la ligne C, et ainsi celle-ci à une troisième D. Décrivons alors une circonférence EFG d'un diamètre égal à cette ligne D; je dis que c'est la circonférence cherchée. En effet, divisons le rayon EF en deux parties égales par le point H. Si le mobile décrit d'un mouvement uniforme la circonférence FG avec la vitesse qu'il acquiert en tombant de la hauteur HF, il aura une force centrifuge égale à sa gravitéGa naar margenoot*. Par conséquent dès que nous aurons démontré qu'avec la vitesse nommée la circonférence totale FG est parcourue dans le temps d'une seconde, il sera établi que le cercle EFG satisfait à la proposition. Il est certain que le mobile parcourra d'un mouvement uniforme et avec la vitesse qu'il a acquise à la fin de sa chute selon HF un espace double de cette même longueur HF dans le même temps pendant lequel il est tombé le long de HF; lors donc qu'il décrira avec ladite vitesse acquise la circonférence FG d'un mouvement uniforme, le temps de sa révolution sera au temps de sa chute selon HF, comme la circonférence FG est au double de HF, en d'autres termes à EF. Et si nous prenons le double des termes conséquents, le temps du mouvement uniforme suivant la circonférence FG sera au double du temps de la chute selon HF, c'est-à-dire au temps de la chute selon D (car D est le quadruple de HF) comme la circonférence FG est au double de FE, c'est-à-dire à D; en d'autres termes, comme C est à D (car nécessairement C est égale à la circonférence FG elle-même), ou bien comme AB est à C. Mais comme AB est à C, ainsi est le temps de la chute selon AB, c'est-à-dire le temps d'une seconde, au temps de la chute selon D; parce que, comme on sait, le rapport AB:D est le carré du rapport AB:C. Par conséquent la dite période du mouvement uniforme suivant la circonférence FG sera au temps de la chute selon D, comme l'espace d'une seconde est à ce mème temps de la chute selon D. La dite période de révolution suivant la circonférence FG sera donc égale à l'espace d'une seconde; ce qu'il sallait démontrer. Comme le calculGa naar voetnoot1) fait voir que la distance AB qu'un mobile tombant vertica- | |
[pagina 279]
| |
horizontaliter, atque unoitem secundo circuitum absolvens, habeat vim centrifugam gravitati suae aequalem.  [Fig. 12.]
Sit data altitudo AB, [Fig. 12] quam perlabitur mobile cadens ex quiete tempore v. gr. unius secundi. Fiat ut circumferentia circuli ad diametrum suum, ita AB ad lineam C, & ita haec ad tertiam D. Et de scribatur diametro aequali ipsi D circulus EFG, dico hunc esse eum qui postulabatur. Dividatur enim radius EF bifariam in H. Mobile itaque in circulo FG si currat velocitate quam acquirit cadendo ex altitudine HF motuque aequabili, habebit vim centrifugam aequalem suae gravitatiGa naar margenoot*. Ideoque si tantum ostenderimus dicta velocitate percurri semel circumferentiam totam FG tempore unius secundi, jam constabit circulum EFG proposito satisfacere. Constat mobile motu aequabili atque ea celeritate quam acquisivit in fine casus per HF, transiturum spatium ipsius HF duplum, eodem tempore quo cecidit per HF. si ergo dicta acquisita celeritate feratur motu aequabili per circumferentiam FG, erit tempus quo eam absolvet ad tempus casus per HF, sicutGa naar margenoot+ circumferentia FG ad duplam HF sive ad EF. Et sum | tis consequentium duplis erit tempus motus aequabilis per circumferentiam FG ad tempus duplum casus HF, hoc est ad tempus casus per D (nam D est quadrupla HF) sicut circumferentia FG ad duplam FE, sive ad D; hoc est, sicut C ad D (nam necessario C ipsi circumferentiae FG aequalis est) hoc est, sicut AB ad C. Sed ut AB ad C ita est tempus casus per AB, hoc est tempus unius secundi ad tempus casus per D; quoniam scilicet AB ad D duplicata est ratio ejus, quae AB ad C; igitur tempus dictum motus aequabilis per circumferentiam FG erit ad tempus casus per D, ut tempus unius secundi ad idem tempus casus per D. Ergo dictum tempus per circumferentiam FG erit aequale tempori unius secundi. quod ostendere necesse erat. Quum calculusGa naar voetnoot1) doceat altitudinem AB quam uno secundo mobile cadens per- | |
[pagina 280]
| |
lement parcourt en une seconde est de 15 pieds de Rhynlande et de 7½ poucesGa naar margenoot+; et comme AB est à C comme une circonférence est à son diamètre, c'est-à-dire comme 22 à 7, suivant Archimède, partant que le rapport de C à D, c'est-à-dire au diamètre de la circonférence FG a la même valeur, ce diamètre sera de 19 oncesGa naar voetnoot2) à peu près; dont la moitié est 9 onces 6 lignes. Par conséquent si un mobile quelconque accomplit dans l'espace d'une seconde chacune de ses révolutions suivant une circonférence dont le rayon est de 9½ onces, la force centrifuge sera égale à sa gravité. | |
Lemme I.Lorsqu'un poids C est maintenu sur un plan incliné AB [Fig. 13] par un poids D librement suspendu, et que la corde CE est parallèle à l'horizon, la gravité D sera à la gravité C comme la perpendiculaire BF est à la base FA. Ceci est évident d'après la Mécanique. Par conséquent, lorsque la droite BF est prise égale à FA, la gravité D devra être égale à C. | |
Lemme II.Lorsque des poids égaux sont maintenus sur des plans diversement inclinés [Fig. 14] par des lignes parallèles à l'horizon, les puissances équilibrantes seront entre elles comme les tangentes des angles suivant lesquels les plans sont inclinés par rapport au plan de l'horizon. | |
Proposition VIIGa naar voetnoot4).Sur la surface courbe d'un conoïde parabolique à axe vertical, toutes les révolutions d'un mobile parcourant des circonférences parallèles à l'horizon, qu'elles soient grandes ou petites, seront accomplies dans des périodes égales; chacune | |
[pagina 281]
| |
labitur esse pedum Rhenoland. 15.7½ pollicumGa naar margenoot+, cumque sit AB ad C ut circumferentia ad diametrum, hoc est, ut 22 ad 7, secundum Archimedem, atque ita quoque C ad D sive ad diametrum circuli FG; fiet haec diameter 19 unciarumGa naar voetnoot2) proximè; cujus dimidium unciae 9. lin. 6. Itaque si mobile aliquod tempore secundi unius circuitus singulos absolvat in circumferentia, cujus quae ex centro est 9½ unciarum vis centrifugaGa naar voetnoot3) suae gravitati aequabitur. | |
[Lemma I.] [Fig. 13.]
Si pondus C sustineatur in plano inclinato AB [Fig. 13] a pondere Dlibere pendente, sitque funis CE horizonti parallelus; erit gravitas D ad [gravitatem] C, sicut perpendicularis BF ad basin FA. [Constat] ex Mechanicis. Hinc si BF aequalis ponatur FA, debebit gravitas Dipsi C aequalis esse. | |
Ga naar margenoot+ | [Lemma II.] [Fig. 14.]
Si pondera aequalia super planis diversimode inclinatis sustineantur [Fig. 14] retenta per lineas horizonti parallelas, erunt potentiae sustinentes inter se sicut tangentes angulorum, quibus plana ad horizontis planum inclinantur. | |
[Propositio VIIGa naar voetnoot4).][In curvaGa naar voetnoot5) superficie conoidis Parabolici, quod axim ad perpendiculum erectum habeat, circuitus omnes mobilis circumferentias Horizonti parallelas percurrentis, sive parvae, sive magnae fuerint, aequalibus temporibus peragenturGa naar voetnoot6): quae tem- | |
[pagina 282]
| |
d'elles étant égale au temps de deux oscillations d'un pendule dont la longueur est la moitié du latus rectum de la parabole engendrante.
Soit donnée une parabole HDB [Fig. 15] qui par sa révolution autour de l'axe BK engendre un conoïde parabolique. Prenons sur cet axe la longueur BA égale à ¼ du latus rectumGa naar voetnoot1), l'ordonnée correspondante AD sera égale à la moitié du latus rectum. Supposons qu'un corps en D tourne autour de l'axe AB avec une vitesse telle que la force centrifuge devienne égale à la gravité; cette force, attendu que l'angle ADE est la moitié d'un angle droit, maintiendra le corps au point DGa naar margenoot*. Mais si un corps tourne ailleurs, par exemple en H, avec le centre K et le rayon KH, la force centrifuge par laquelle il est maintenu au point H, sera égale à la force horizontale agissant selon HK par laquelle le mobile pourra être maintenu sur un plan HF tangent au paraboloïde. Or, cette dernière force sera d'après le premier Lemme à la force de la gravité comme HG est à GF, ou bien, à cause de triangles semblables, parce que HL est supposée perpendiculaire à HF, comme HK est à KL, en d'autres termes, comme HK est à AD, attendu que d'après la nature de la parabole KL est toujours égale à la moitié du latus rectum. La force centrifuge par laquelle le corps dans sa rotation est maintenu en H est donc à la gravité du corps, ou bien à la force centrifuge en D, comme HK est à DA. C'est pourquoi, d'après l'inverse de la première propositionGa naar voetnoot2), ils parcourront leurs circonférences dans le même temps. Quant au temps dans lequel les révolutions s'accomplissent, il sera déterminé de la façon suivante. Puisque nous avons supposé que le corps D tourne de telle manière qu'il possède une force centrifuge égale à sa gravité, il tournera avec la vitesse qu'il acquerrait par une chute verticale selon la moitié de ADGa naar margenoot*. Mais avec cette vitesse il parcourrait dans le temps de cette chute la ligne DA d'un mouvement uniforme. La période de la révolution est donc au temps de la chute selon la moitié de DA comme la circonférence du cercle est au rayon DA. Or le temps d'une très petite oscillation est au temps de la chute verticale d'une hauteur égale à la moitié de la longueur du penduleGa naar margenoot+, comme la circonférence d'un cercle est à son diamètre, et par conséquent le temps de deux très petites oscillations du pendule | |
[pagina 283]
| |
pora singula aequantur binis oscillationibus penduli, cujus longitudo sit dimidium lateris recti Parabolae genitricis.] [Sit Parabola HDB [Fig. 15], cujus revolutione circa axim BK, fiat Conois Parabolicum. In illo axe sumatur BA aequalis ¼ lateris rectiGa naar voetnoot1), erit ordinatim 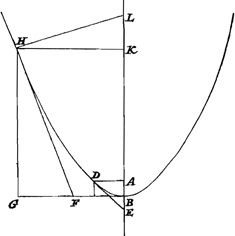 [Fig. 15.]
applicata AD aequalis lateris recti dimidio. Ponatur autem corpus in D circa axim AB circumagi ea velocitate, ut vis centrifuga fiat gravitati aequalis; quae vis ergo, cum angulus ADE sit semirectus, corpus sustinebit in puncto DGa naar margenoot+. Si vero corpus rotetur alibi, ut in H, centro K & intervallo KH, erit vis centrifuga, qua sustinetur in puncto H, aequalis vi, qua mobile per rectam HK Horizonti parallelam detineri poterit in plano HF tangente Paraboloidem. Haec autem vis ex primo Lemmate erit ad vim gravitatis, ut HG ad GF, siue, propter triangula similia, quoniam HL in HF normalis ponitur,Ga naar margenoot+ ut HK ad KL, sive, ut HK ad AD, cum ex natura Parabolae KL semper aequalis sit dimidio lateris recti. Vis ergo centrifuga, qua corpus rotando detinetur in H, est ad corporis gravitatem, sive ad vim centrifugam in D, ut HK ad DA. Quare ex conversa primaeGa naar voetnoot2) eodem tempore suas circumferentias absolvent. Tempus autem quo circuitus peraguntur ita determinabitur. Quoniam supposuimus corpus D rotari, ita ut vim centrifugam habeat gravitati aequalem, rotabitur ea velocitate, quam acquireret casu perpendiculari ex dimidia ADGa naar margenoot*. Sed ea velocitate tempore hujus descensus, absolveret lineam DA motu aequabili. Tempus ergo gyrationis est ad tempus descensus per dimidium DA; ut circumferentia circuli ad radium DA. Tempus autem oscillationis minimae est ad tempus casus perpendicularis ex dimidia penduli altitudineGa naar margenoot+, ut circumferentia circuli ad diametrum, adeoque tempus duarum oscillationum minimarum penduli DA, est | |
[pagina 284]
| |
DA est au temps de la chute selon la moitié de la hauteur DA, comme la circonférence d'un cercle est à son rayon, en d'autres termes: comme la période d'une révolution entière à ce même temps de la chute verticale d'une hauteur égale à la moitié de DA. Le temps d'une révolution dans le conoïde parabolique est donc égal au temps pendant lequel se font deux oscillations d'un pendule dont la longueur est DA, moitié du latus rectum de la parabole engendrante. C.Q.F.D. | |
Proposition VIII.Lorsque deux mobiles suspendus à des fils inégaux sont mis en rotation de telle manière qu'ils parcourent des circonférences horizontales, l'autre bout du fil demeurant immobile, et que les axes ou hauteurs des cônes dont les fils décrivent la surface par ce mouvement sont égaux, les périodes pendant lesquelles chaque mobile parcourt sa circonférence seront aussi égales.
Supposons les fils AC et AD [Fig. 16] liés en haut à un même point fixe A et qu'à eux soient attachés des mobiles en C et D respectivement lesquels tournent suivant des circonférences horizontales à rayons BC et BD. Soit encore AB l'axe commun des deux cônes que les fils AC et AD décrivent en tournant: je dis que les périodes des révolutions sont égales entre elles. Considérons d'abord des mobiles égaux; que CE soit perpendiculaire à AC et DF de même à AD. Eh bien, il est évident que c'est la force centrifuge des mobiles qui tient les fils ainsi tendus dans une direction oblique; et comme le mobile C a en vertu de sa gravité la même tendance à tomber que s'il s'appuyait sur un plan CE; et que d'autre part la force centrifuge par laquelle le corps tend à s'écarter de l'axe AB suivant BC tient cette tendance de la gravité en échec, la dite force centrifuge est nécessairement égale à la puissance, par laquelle le mobile C pourrait être maintenu sur le plan incliné CE, cette puissance agissant suivant une ligne horizontale BC. Pour la même raison la force centrifuge par laquelle le mobile D est soutenu est nécessairement égale à la puissance par laquelle ce corps pourrait être maintenu sur le plan DF, cette puissance agissant suivant une ligne également horizontale. Or cette puissance est à la première qui, à ce que nous avons dit, maintient le mobile C en place, comme la tangente de l'angle BDF est à la tangente de l'angle BCEGa naar margenoot*, c'est-à-dire comme la tangente de l'angle DAB est à la tangente de l'angle CAB, ou bien comme DB est à CB: par conséquent aussi la force centrifuge que le mobile D a dans sa circonférence sera à la force du mobile C dans la sienne comme le rayon DB est au rayon CB. D'où l'on conclut, d'après l'inverse de la Prop. IGa naar voetnoot2), que les périodes de révolution sont les mêmes. | |
[pagina 285]
| |
ad tempus casus perpendicularis ex dimidia altitudine DA, ut circumferentia circuli ad radium, hoc est; ut tempus totius gyrationis ad idem tempus casus perpendicularis per dimidiam DA. Tempus ergo gyrationis in conoidi Parabolico aequatur tempori, quo binae peraguntur oscillationes penduli, cujus longitudo sit DA, dimidium lateris recti Parabolae genitricis. Q.E.D.] | |
Ga naar margenoot+ | [Propositio VIII.]Si mobilia duo ex filis inaequalibus suspensa gyrentur, ita ut circumferentias horizonti parallelas percurrantGa naar voetnoot1), capite altero fili immoto manente, fuerint autem conorum, quorum superficiem fila hoc motu describunt, axes sive altitudines aequales, tempora quoque, quibus utrumque mobile circulum suum percurrit, aequalia erunt. Sint fila AC, AD [Fig. 16] communi vertice A religata, habeantque mobilia singula adnexa in C & D, quae gyrentur in circulis horizontalibus quorum radii 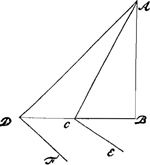 [Fig. 16.]
BC, BD. sit autem AB axis idem utriusque coni quem fila AC, AD circuitu suo ambiunt. Dicotempora circulationum esse inter se aequalia. Ponantur primo mobilia esse aequalia; sit CE perpendicularis in AC, & DF perpendicularis item in AD. Constat igitur vim centrifugam mobilium esse quae fila ita obliquè extensa sustineat; cumque mobile C conatum habeat ex gravitate sua descendendi eundem ac si plano CE incumberet; vis autem centrifuga, qua nititur recedere ab axe AB secundum BC, istum gravitatis conatum inhibeat, necesse est vim dictam centrifugam aequalem esse potentiae qua mobile C sustineretur in plano inclinato CE per lineam BC horizonti parallelam. Eadem ratione necesse est vim centrifugam, qua sustinetur mobile D, esse aequalem potentiae qua hoc idem sustineretur in plano DF per rectam item horizonti parallelam. Est autem haec potentia ad priorem illam quae sustinere dicta est mobile C, sicut tangens anguli BDF ad tangentem anguli BCEGa naar margenoot*, hoc est, sicut tangens anguli DAB ad tangentem anguliGa naar margenoot+ CAB, hoc est, ut DB ad CB: ergo & vis centrifuga quam habet mo | bile D in circulo suo, erit ad vim centrifugam mobilis C in suo circulo, ut DB semidiameter ad CB semidiametrum. Unde ex Prop. IGa naar voetnoot2) conversa, sequitur tempora circulationum esse aequalia. | |
[pagina 286]
| |
Mais si les mobiles sont inégaux, l'égalité des périodes subsistera néanmoins. En effet, si nous supposons p.e. le mobile C plus lourd qu'il n'était auparavant, il lui faudra aussi une puissance d'autant plus grande qu'il est plus lourd lui-même pour le maintenir sur le plan incliné CE, cette puissance agissant suivant une ligne horizontale, et par conséquent aussi une force centrifuge d'autant plus grande; mais pour qu'il possède cette dernière il doit parcourir la circonférence dans le même temps qu'auparavant lorsqu'il était supposé plus léger, comme cela ressort de ce que nous avons dit plus hautGa naar voetnoot2). La proposition est donc établie. | |
Proposition IX.Les périodes de révolution suivant des circonférences horizontales CD et BE [Fig. 17], l'angle de giration CAD étant le même, sont dans un rapport égal à la racine carrée de celui des longueurs des fils AC et AB.
En effet, la force centrifuge nécessaire pour maintenir une même obliquité du fil est la même dans déux parcours de ce genre; mais ladite force étant la même, suivant l'inverse de la proposition IVGa naar voetnoot3) les distances de l'axe de rotation doivent être entre elles comme les carrés des périodes de révolution. Par conséquent les carrés de ces périodes doivent être ici entre eux comme CF est à BG, c'est-àdire comme AC est à AB. C.Q.F.D. | |
Proposition X.Lorsque deux mobiles quelconques suspendus à des fils décrivent en tournant des circonférences horizontales, les périodes de révolution seront entre elles comme les racines carrées des hauteurs des cônes dont les surfaces sont parcourues par les fils.
Soient donnés les sils AC et AD [Fig. 18] auxquels sont attachés des mobiles C et D décrivant des circonférences horizontales, tandis que les bouts des sils demeurent immobiles en A. Puisse C faire circuler le fil AC suivant la surface conique dont AB est l'axe, et D le fil DA suivant la surface conique dont l'axe est AE; je dis que la période du mobile C est à la période du mobile D dans un rapport égal à la racine carrée du rapport AB:AE. En effet, imaginons-nous | |
[pagina 287]
| |
Si vero inaequalia fuerint mobiliaGa naar voetnoot1), nihilo secius eadem temporum aequalitas continget. Nam si ex. gr. mobile C gravius ponatur quam prius fuerat, tanto quoque majori potentia, quanto gravius est, indigebit, qua sustineatur in plano inclinato CE per lineam horizonti parallelam, tantoque proinde majorem vim centrifugam requiret. hanc autem ut habeat debet circulum percurrere eodem tempore, quo antea cum levius ponebatur, ut patet ex iis quae supra diximusGa naar voetnoot2). Ergo constat propositum. | |
[Propositio IX.]Tempora lationum per circulos horizontales CD, BE [Fig. 17], angulo gyrationis CAD eodem existente, sunt in subduplicata ratione longitudinum filorum AC ad AB. 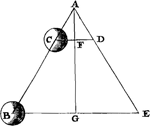 [Fig. 17.]
Eadem enim vis centrifuga est in utraque hujusmodi circulatione ad sustinendam eandem fili obliquitatem. Si autem dicta vis est eadem tunc ut quadrata temporum quibus circuli absolvuntur, ita debent esse distantiae ab axe circulationis per conversam IVGa naar voetnoot3). Ergo hic erunt sicut CF ad BG, hoc est, ut AC ad AB ita quadrata temporum circulationum. [Q.E.D.] | |
Ga naar margenoot+ | [Propositio X.]Si mobilia duo quaelibet filis suspensa gyrando describant circulos horizonti parallelos; erunt tempora circulationum in subduplicataGa naar voetnoot4) ratione altitudinum conorum, quorum superficies à filis describuntur. 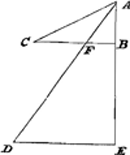 [Fig. 18.]
Sint fila AC, AD [Fig. 18] quibus annexa mobilia C & D circulos horizontales describant, dum capita filorum in A immota manent. Et C quidem ducat silum AC secundum superficiem conicam cujus axis AB, D vero filum DA per supersiciem coni cujus axis sit AE. Dico tempus circuitus mobilis C esse ad tempus circuitus mobilis D in ratione subduplicata AB ad AE. Intelligatur enim mobile aliud religatum ex filo AF, facere sua circulatione conum, cujus latus AF axis AB. Ejus igitur circulationis tempus aequale est tempori circulationis à | |
[pagina 288]
| |
qu'un autre mobile attaché à un fil AF décrive en tournant un cône à côté AF et à axe AB. La période de ce mobile est donc égale à celle du mobile CGa naar margenoot*. Or, la période du mobile F est à celle du mobile D dans un rapport égal à la racine carrée du rapport AF: ADGa naar margenoot*, ou bien de AB: AE. Par conséquent la période du mobile C elle aussi, est à celle du mobile D dans un rapport égal à la racine carrée de AB: AE. C.Q.F.D. | |
Proposition XI.Lorsqu'un mobile suspendu à un fil décrit par son mouvement, tandis que l'extrémité supérieure du fil demeure en repos, des circonférences horizontales inégales, les périodes correspondant à ces circonférences seront dans un rapport égal à la racine carrée de celui des sinus des angles suivant lesquels le fil est incliné par rapport à un plan horizontal.
Soit donné un fil AB [Fig. 19] attaché en A; et que le mobile qui y est suspendu et qui tourne horizontalement tende le fil d'abord suivant la droite AB, mais ensuite suivant la droite AC. Tirons les horizontales BE et CD coupant la verticale AD en E et en D. Par conséquent, comme AB et AC sont égales, AE représentera le sinus de l'angle ABE et AD le sinus de l'angle ACD. Je dis qu'alors les périodes correspondant aux circonférences à rayons BE et CD seront entre elles dans un rapport égal à la racine carrée du rapport AE:AD; cela ressort avec évidence de la proposition précédente. | |
Proposition XIIGa naar voetnoot2).Lorsqu'un pendule animé d'un mouvement conique décrit de très petites circonférences, les périodes correspondant à chacune d'elles seront au temps d'une chute verticale d'une hauteur égale au double de la longueur du pendule dans un rapport égal à celui d'une circonférence de cercle à son diamètre, partant égales au temps de deux oscillations latérales très petites de ce même pendule.
Soit donné un fil AC attaché en A [Fig. 20]; et que le mobile qui y est suspendu décrive en tournant une circonférence horizontale à rayon DC égal à DA, de sorte que l'angle CAD est égal à la moitié d'un angle droit; la force centrifuge en Csera égale à la gravité du mobileGa naar margenoot* et par conséquent celui-ci parcourra la circonférence décrite avec le rayon DC avec la vitesse qu'il acquerrait par une chute | |
[pagina 289]
| |
mobili CGa naar margenoot*. Est autem tempus circulationis mobilis F ad tempus circuitus mobilis D in subduplicata ratione AF ad ADGa naar margenoot*, sive AB ad AE. Ergo & tempus circulationis lationis mobilis C ad tempus mobilis D erit in subduplicata ratione AB ad AE. Q.E.D. | |
[Propositio XI.]Si mobile filo suspensum, capite fili superiore quiescente, describat motu suo circulos horizonti parallelos inaequales, erunt tempora lationum per dictos circulos in subduplicata ratione sinuum angulorum, quibus filum ad planum horizontis inclinatur. Sit filum AB [Fig. 19] religatum ad A. Mobile autem ex eo suspensum acGa naar margenoot+ circumgyratum horizontaliter exten | dat ipsum primo secundum rectam AB; 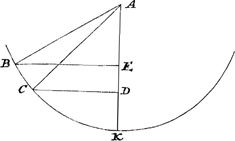 [Fig. 19.]
deinde vero secundum rectam AC; ducantur autem horizonti parallelae BE, CD, occurrentes perpendiculari AD in E & D. Ergo quia AB, AC aequales sunt, referet AE sinum anguli ABE; AD vero sinum anguli ACD; dico jam tempora lationum per circulos, quorum radii BE, CD fore inter se in subduplicata ratione AE ad AD. Patet hoc manifesto ex propositione superiori. | |
[Propositio XII.]Ga naar voetnoot2)[Si pendulum motu conico latum circuitus minimos faciat; eorum singulorum tempora, ad tempus casus perpendicularis ex dupla penduli altitudine, eam rationem habent, quam circumferentia circuli ad diametrum: ac proinde aequalia sunt tempori duarum oscillationum lateralium ejusdem penduli minimarum.]
[Sit filum AC religatum ad A [Fig. 20], ex quo suspensum mobile circumgyrando describat circulum horizontalem, cujus radius DC, aequalis ipsi DA, ita ut angulus CAD sit semirectus, erit vis centrifuga in C aequalis gravitati mobilisGa naar margenoot*, ideoque percurret circumferentiam radio DC descriptam, ea velocitate, quam acquireret mobile, casu perpendiculari ex altitudine dimidiae DC aut | |
[pagina 290]
| |
verticale d'une hauteur égale à la moitié de DC ou de DAGa naar margenoot*. Or DC est à CA comme 1 est à √2, et par conséquent le temps d'une chute verticale de la hauteur ½DC sera au temps d'une chute verticale de la hauteur ½CA (ces temps étant dans un rapport égal à la racine carrée du rapport DC:CA) dans le rapport 1:√√2. D'où l'on conclut que le temps d'une chute verticale d'une hauteur ½DC sera au temps d'une chute de la hauteur 2AC (qui est le double du temps d'une chute suivant ½AC) comme 1 est à 2√√2, ou bien comme un rayon quelconque est au double de ce rayon multiplié par √√2. Or, le temps d'une chute verticale de la hauteur ½DC est au temps de giration suivant la circonférence décrite avec le rayon DC, comme le rayon est à la circonférenceGa naar voetnoot1); et le temps d'une rotation suivant la circonférence DC est au temps d'une très petite rotation dans un rapport égal à la racine carrée du rapport AD:ACGa naar margenoot*, en d'autres termes à 1:√√2; par conséquent le temps d'une chute verticale d'une hauteur ½DC est au temps d'une très petite rotation comme le rayon est à la circonférence multipliée par √√2; le temps d'une très petite rotation du pendule AC est donc au temps d'une chute verticale d'une hauteur égale à deux fois le pendule, comme la circonférence multipliée par √√2 est au double du rayon multiplié par √√2, ou bien comme une circonférence est à son diamètre. Mais vu que le temps d'une très petite oscillation latérale du pendule AC est au temps d'une chute verticale d'une hauteur ½AC, ou, en doublant l'un et l'autre, que le temps de deux très petites oscillations latérales du pendule AC est au temps d'une chute verticale d'une hauteur 2AC, également dans un rapport égal à celui d'une circonférence à son diamètreGa naar voetnoot2), le temps d'une très petite rotation du pendule AC sera au temps d'une chute verticale d'une hauteur égale à deux fois le pendule AC, comme le temps de deux oscillations latérales très petites du pendule AC est à ce même temps d'une chute verticale le long de 2AC. Par conséquent le temps d'une très petite rotation du pendule AC sera égal au temps de deux très petites oscillations latérales du même pendule AC. C.Q.F.D. | |
Proposition XIIIGa naar voetnoot3).Lorsqu'un mobile parcourt une circonférence et accomplit chaque révolution dans le même temps dans lequel un pendule ayant pour longueur le rayon de cette circonférence pourrait parcourir d'un mouvement conique une très petite circonférence ou exécuter deux oscillations latérales très petites, il aura une force centrifuge égale à sa gravité. | |
[pagina 291]
| |
DA aequaliGa naar margenoot*. Est autem DC ad CA ut 1 ad √2, adeoque tempus casus perpendicularis
 [Fig. 20.]
ex dimidia DC ad tempus casus perpendicularis ex dimidia CA, quae tempora sunt in subduplicata ratione DC ad CA, erit in ratione 1 ad √√2. Unde tempus casus perpendicularis ex dimidia DC, ad tempus quo cadit ex dupla AC, quod temporis casus ex dimidia AC duplum est, erit, | ut 1 ad 2√√2,Ga naar margenoot+ sive ut radius quilibet ad duplum ejusdem radii ductum in √√2. Est autem tempus casus perpendicularis ex dimidia DC, ad tempus gyrationis per circumferentiam radio DC descriptam, ut radius ad circumferentiamGa naar voetnoot1); tempus autem gyrationis per circumferentiam DC est ad tempus circuitus minimi, in subduplicata ratione AD ad ACGa naar margenoot* sive ut 1 ad √√2: tempus ergo casus perpendicularis ex dimidia DC, est ad tempus circuitus minimi, ut radius ad circumferentiam ductam in √√2; tempus igitur circuitus minimi penduli AC ad tempus casus perpendicularis ex dupla penduli altitudine, ut circumferentia ducta in √√2 ad duplum radii ductum in √√2, sive ut circumferentia ad diametrum. Cum vero tempus oscillationis minimae lateralis penduli AC ad tempus casus perpendicularis ex dimidia AC, sive sumtis utriusque duplis tempus duarum oscillationum minimarum lateralium penduli AC ad tempus casus perpendicularis ex dupla AC, etiam sit, ut circumferentia ad diametrumGa naar voetnoot2), erit tempus circuitus minimi penduli AC, ad tempus casus perpendicularis ex dupla penduli AC altitudine, ut tempus duarum oscillationum lateralium minimarum penduli AC ad idem tempus casus perpendicularis ex dupla AC. Erit ergo tempus circuitus minimi penduli AC aequale tempori duarum oscillationum minimarum lateralium ejusdem penduli AC. Q.E.D.] | |
Ga naar margenoot+ | [Propositio XIII.]Ga naar voetnoot3)[Si mobile in circumferentia feratur, circuitusque singulos absolvat eo tempore, quo pendulum longitudinem semidiametri circumferentiae ejus habens motu conico circuitum minimum absolveret, vel duplicem oscillationem minimam lateralem, habebit vim centrifugam suae gravitati aequalem.] | |
[pagina 292]
| |
Soit donné un fil AC [Fig. 20] égal au rayon de la circonférence que parcourt le mobile, de sorte que l'angle CAD est égal à la moitié d'un angle droit, et supposons que la période de la révolution correspondant à CD soit 1: la période d'une très petite rotation du même pendule sera √√2Ga naar margenoot*. Or, par hypothèse la période d'une révolution suivant la circonférence à rayon AC est la même; la période correspondant à CD est donc à celle qui correspond à AC comme 1 est à √√2, en d'autres termes ce rapport est égal à la racine carrée du rapport CD:AC, d'où il résulte, d'après l'inverse de la quatrième propositionGa naar voetnoot1), que ces deux mobiles tournant de cette manière possèderont une force centrifuge égale et que par conséquent, la force centrifuge correspondant à CD étant égale à la gravitéGa naar voetnoot2), la même chose sera vraie pour la rotation suivant la circonférence à rayon AC. C.Q.F.D. | |
Proposition XIVGa naar voetnoot3).Les périodes de révolution d'un pendule quelconque animé d'un mouvement conique seront égales au temps d'une chute verticale d'une hauteur égale au fil du pendule, lorsque l'angle d'inclinaison du fil par rapport à un plan horizontal sera de 2o54′ environ. En termes précis: lorsque le sinus dudit angle sera au rayon comme un carré inscrit dans une circonférence eft au carré de la même circonférence. Soit AD = DC [Fig. 20] = a, AE = b; la circonférence d'un cercle à son rayon comme c à r. Soit 1 le temps d'une chute verticale d'une hauteur ½CD. Le temps d'une chute d'une hauteur ½AC sera alors √√2. Or, le temps correspondant à la chute suivant ½AC est à celui qui correspond à celle suivant AC comme 1 est à √2; le temps d'une chute suivant AC sera donc représenté par √√8. Mais la période de révolution correspondant à CD est au temps d'une chute de la hauteur ½CD comme c est à rGa naar voetnoot4). Par conséquent la période d'une révolution correspondant à CD sera c/r. Mais la période qui correspond à C est à celle qui correspond à un point quelconque B dans un rapport égal à la racine carrée du rapport AD:AE, ou comme √a est à √bGa naar voetnoot5). La période qui correspond à B sera donc  ; et si nous supposons maintenant AE, sinus de l'angle ABE, tel qu'il soit au rayon AB comme un carré ; et si nous supposons maintenant AE, sinus de l'angle ABE, tel qu'il soit au rayon AB comme un carré
| |
[pagina 293]
| |
[Sit filum AC [Fig. 20] aequale radio circuli, per quem mobile fertur, ita ut angulus CAD sit semirectus; sitque tempus gyrationis per CD, 1. erit tempus
 [Fig. 20.]
gyrationis minimae ejusdem penduli √√2Ga naar margenoot*. Idem autem ex hypothesi est tempus gyrationis per circumferentiam, cujus radius AC; tempus ergo gyrationis per CD est ad tempus gyrationis per AC, ut 1 ad √√2; sive in subduplicatâ ratione CD ad AC, unde ex conversa 4aeGa naar voetnoot1), habebunt haec duo mobilia ita circumlata, vim centrifugam aequalem, adeoque cum in CD vis centrifuga sit aequalis gravitatiGa naar voetnoot2), idem locum habebit, in gyratione per circulum, cujus radius AC. Q.E.D.] | |
[Propositio XIV.]Ga naar voetnoot3)[Penduli cujuslibet, motu conico lati, tempora circuitus aequalia erunt tempori casus perpendicularis ex altitudine penduli filo aequali; cum angulus inclinationis fili ad planum horizontis fuerit partium 2, scrup. 54, proxime. Exacte vero, si anguli dicti sinus fuerit ad radium, ut quadratum circulo inscriptum ad quadratum a circumferentia ejus.] [Sit AD = DC [Fig. 20], a, AE, b; circumferentia circuli ad radium, ut c ad r; tempus casus perpendicularis per | dimidiam CD sit 1. erit tempus casus perGa naar margenoot+ dimidiam AC √√2. Est autem tempus per dimidiam AC ad tempus per AC, ut 1 ad √2, erit ergo tempus per AC, ut √√8. Sed tempus gyrationis per CD est ad tempus casus per dimidiam CD, ut c ad rGa naar voetnoot4). Erit itaque tempus gyrationis per CD = c/r. Verum tempus gyrationis in C est ad tempus gyrationis in quolibet puncto B, in subduplicata ratione AD ad AE, sive ut √a ad √bGa naar voetnoot5). Erit ergo tempus gyrationis in  ; quod si nunc ponatur AE sinum anguli ABE esse ad radium AB, ut quadratum circulo inscriptum, ad quadratum circumferentiae ejus, erit b ad a√2, ita 2rr ad cc, sive bcc/arr = 2√2, vel ; quod si nunc ponatur AE sinum anguli ABE esse ad radium AB, ut quadratum circulo inscriptum, ad quadratum circumferentiae ejus, erit b ad a√2, ita 2rr ad cc, sive bcc/arr = 2√2, vel 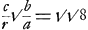 Ga naar voetnoot6): cumque c/r√b/a Ga naar voetnoot6): cumque c/r√b/a
| |
[pagina 294]
| |
inscrit dans une circonférence est au carré de cette circonférence, b sera à a√2 comme 2rr est à cc, ou bien bcc/arr = 2√2, ou bien 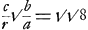 ; et comme c/r√b/a est la période de révolution correspondant au point B et √√8 le temps d'une chute de la hauteur AC, cette période correspondant à B sera égale au temps d'une chute verticale d'une hauteur égale à la longueur du fil du pendule. ; et comme c/r√b/a est la période de révolution correspondant au point B et √√8 le temps d'une chute de la hauteur AC, cette période correspondant à B sera égale au temps d'une chute verticale d'une hauteur égale à la longueur du fil du pendule.
Or, attendu que 2r:c = 7:22, on aura 4rr:cc = 49:484 ou bien 2rr:cc = 49:968. Par conséquent, 968:49 = a√2 (le rayon a étant égal à 100000): 5062 (sinus de l'angle ABE); donc l'angle ABE = 2o54′ environ. C.Q.F.D. | |
Proposition XVGa naar voetnoot2).Lorsque deux pendules égaux en poids, mais de longueur de fil différente, sont animés d'un mouvement conique et que les hauteurs des cônes sont égales, les forces avec lesquelles ils tendront leurs fils seront entre elles dans un rapport égal à celui des longueurs des fils.
Soient donnés deux pendules AB et AC [Fig. 21] de longueur différente et que deux poids égaux suspendus à leurs extrémités B et C tournent autour de l'axe commun AD. Je dis que la force avec laquelle le fil AB est tendu est à la force avec laquelle le fil AC est tendu dans un rapport égal à celui des fils AB et AC. En effet, si nous admettons que le poids B est maintenu dans cette position par une puissance en A tirant le fil AB et par une autre puissance en Gégale à la force centrifuge et tirant suivant la droite BG, il est certain d'après la Mécanique que si l'on mène BH verticalement et HL horizontalement, la force en A qui tire le fil AB sera à la gravité du poids B comme LB est à BH, ou bien comme AB est à AD. De même la force par laquelle le fil C est tendu sera à la gravité du poids C, ou bien à la gravité du poids B égal par hypothèse au poids C, comme AC est à AD. Par conséquent la force par laquelle le fil AB est tendu pendant la rotation sera à la force par laquelle le fil AC est tendu comme AB est à AC. C.Q.F.D. | |
Proposition XVIGa naar voetnoot3).Lorsqu'un pendule simple est animé de la plus grande oscillation latérale possible, c'est-à-dire lorsqu'il descend suivant | |
[pagina 295]
| |
sit tempus gyrationis in B & √√8 tempus descensus per AC, erit hoc tempus gyrationis in B, aequale tempori casus perpendicularis ex altitudine penduli filo aequali. Cum autem 2r ad c est, ut 7 ad 22, erit 4rr ad cc ut 49 ad 484, sive 2rr ad cc ut 49 ad 968. Hinc fietGa naar voetnoot1), ut 968 ad 49 ita a√2 radius = 100000 ad 5062 sinum anguli ABE gr. 2. 54′, proxime. Q.E.D.] | |
[Propositio XV.]Ga naar voetnoot2)[Si pendula duo pondere aequalia, sed inaequali filorum longitudine, motu conico gyrentur, fuerintque conorum altitudines aequales; erunt vires, quibus fila sua intendent, in eadem ratione, quae est filorum longitudinis.Ga naar voetnoot3)] [Sint duo pendula AB, AC [Fig. 21] diversae longitudinis, ex quorum extremitatibus B & C suspensa duo pondera aequalia rotentur circa communem aximGa naar margenoot+  [fig. 21.]
AD. Dico | vim qua tenditur filum AB esse ad vim qua tenditur filum AC, in ratione filorum AB ad AC. Si enim ponamus pondus B in eo situ sustineri per potentiam in A trahentem filum AB, & per potentiam aliam in G vi centrifugae aequalem trahentem secundum rectam BG constat ex Mechanicis ducta BH horizonti perpendiculari & HL eidem parallela, fore vim in A tendentem filum AB ad gravitatem ponderis B ut LB ad BH, sive ut AB ad AD. Itidem erit vis qua tenditur filum C ad gravitatem ponderis C, sive ad gravitatem ponderis B, quod aequale ipsi C positum fuit, ut AC ad AD. Erit ergo vis qua gyrando tenditur filum AB, ad vim qua tenditur filum AC, ut AB ad AC. Q.E.D.] | |
[Propositio XVI.]Ga naar voetnoot4)[Si pendulum simplex oscillatione laterali maxima agitetur, hoc est, si per totum circuli quadrantem descendat: ubi ad | |
[pagina 296]
| |
un quart de circonférence, il tendra son fil, lorsqu'il aura atteint le point le plus bas de la circonférence, avec une force trois fois plus grande que s'il y était simplement suspendu.
Lorsque le globe C [Fig. 22] attaché en A au moyen du fil AC descend suivant le quart de circonférence CB, il tendra, au moment où il sera parvenu en B, le fil AB avec une force trois sois plus grande que s'il y était simplement suspendu de sorte que son poids compterait seul. En effet, d'abord la vitesse avec laquelle il continuerait à se mouvoir suivant la ligne droite BD s'il quittait le fil en B est la même que celle qu'il aurait au point F s'il était tombé verticalement le long de CF. Là il aurait acquis une vitesse telle qu'avec cette vitesse il parcourrait d'un mouvement uniforme un espace égal au double de cette même hauteur CF dans le même temps dans lequel il est tombé de C en F. Le globe a donc en B une tendance à parcourir une ligne BD double de AB dans un temps égal à celui dans lequel il tomberait de A en B, bien entendu sans avoir égard à la force de sa gravité, par laquelle il descendrait en même temps dans le sens vertical et décrirait donc une certaine paraboleGa naar voetnoot3). Soit BGE une parabole dont AB est le demi latus rectum, et B le sommet. Parce qu'alors les écarts du globe B de la circonférence BC, tandis qu'il parcourt BD d'un mouvement uniforme, sont considérés au début près du point B commè identiques avec les écarts de la parabole BGEGa naar voetnoot4), il est manifeste que la force centrifuge que possède le globe en B en vertu de la rotation seule consiste en une tendance à s'éloigner du centre A ou de la circonférence BC d'un mouvement accéléré suivant les nombres 1, 3, 5, 7 etc.Ga naar voetnoot5) et que cette tendance est par conséquent du même genre que celle avec laquelle les corps cherchent à tomber et que nous appelons la gravité. Et cette tendance du globe B est aussi grande qu'elle le serait dans un corps égal qui parcourrait l'espace DE d'un mouvement accéléré dans le même temps pendant lequel le globe B parcourrait l'espace BD d'un mouvement uniforme, c'est-à-dire dans le même temps dans lequel le globe tomberait de A en B d'un mouvement semblablement accéléré. Par conséquent, comme DE est le double de BA, la tendance centrifuge du globe en B est le double de sa gravité. Mais il s'y ajoute ici une autre tendance due à la gravité, par laquelle le globe B, dans le même temps où il tomberait | |
[pagina 297]
| |
punctum imum circumferentiae pervenerit, triplo majori vi filum suum trahet, quam si ex illo simpliciter suspensum foret.] Si globus C [Fig. 22] ex A ligatus filo AC per quadrantem circumferentiae  [Fig. 22.]
CB descendat, ubi in B pervenerit triplo majori vi trahet silum AB, quam si simplici pondere suo suspensus essetGa naar voetnoot1). Primum enim velocitas qua pergeret moveri secundum rectamGa naar voetnoot2) lineam BD, si in B filum relinqueret, eadem est atque ea quam haberet in puncto F, si perpendiculariter per CF decidisset. Ibi autem tantam nactus esset celeritatem, ut ea spatium ipsius CF duplum consiceret motu aequabili pari tempore quo ex C decidit in F. Ergo in B conatum habet globus transeundiGa naar margenoot+ lineam BD duplam AB, pari tempore, quo ex A caderet in B; nempe non considerata vi gravitatis suae, qua deorsum quoque interim descensurus esset & Parabolam aliquam descripturusGa naar voetnoot3). Sit BGE Parabola cujus semilatus rectum AB, vertex B. Quoniam ergo recessus globi B, à circumferentia BC, dum per rectam BD aequabili motu fertur, initio prope B punctum pro iisdem habentur, cum recessibus à Parabola BGEGa naar voetnoot4); constat vim centrifugam quam ex sola circulatione habet globus in B, esse conatum recedendi à centro A vel à circumferentia BC motu accelerato secundum numeros 1, 3, 5, 7, &c.Ga naar voetnoot5) ac proinde similem esse ei conatui quo corpora descendere conantur, quem gravitatem appellamus. Est autem ille conatus in globo B tantus, quantus in corpore sibi aequali quod motu accelerato confecturum sit spatium DE, eodem tempore dum motu aequabili conficeret spatium BD, hoc est aequali tempore illi quo globus accelerato itidem motu caderet ex A in B. Ergo quia DE est dupla BA conatus centrifugus globi in B duplus est suae gravitatis. At vero conatus alius ex gravitate accedit hîc, quo globus B (pari tempore quo ex A ad B | |
[pagina 298]
| |
de A en B, aspire à parcourir maintenant aussi un espace égal en tombant verticalement d'un mouvement naturellement accéléré. En vertu des deux tendances il cherche donc à parcourir d'un mouvement accéléré suivant les nombres 1, 3, 5, 7 un espace égal à la somme de DE et de AB, en d'autres termes au triple de AB; partant la force avec laquelle il tire au point B après être descendu depuis C, est égale à trois fois la force qui résulte du simple poids du globe B librement suspendu. Ce qui est aussi exactement conforme à l'expérience. Pour savoir avec quelle force la corde AB est tendue lorsque le globe descend suivant l'arc HB: soit FN égale à la moitié de AB et construisons le rectangle BN, menons ensuite HL parallèlement à AB; je dis que la force de traction cherchée est au poids simple du globe suspendu comme HL est à LK. Par conséquent si BH est la sixième partie de la circonférence la force totale sera le double de cette force due au poids; il faudra donc, pour supporter cette force de traction, un fil deux fois plus fort que le fil simple capable de porter le globe suspendu, etc. | |
Proposition XVIIGa naar voetnoot2).Un globe attaché par un fil au centre d'un cercle vertical ne peut tourner suivant la circonférence de ce cercle, que si le fil peut supporter une tension égale à six fois le poids suspendu.
Soit BCDE [Fig. 23] un cercle vertical, au centre A duquel soit suspendu le globe B. Je dis que pour que ce globe puisse accomplir une révolution suivant la circonférence BCDE il faut un fil capable de porter le sextuple du poids B. En effet, pour que le fil reste tendu lorsque le globe passe par le point D et descend suivant l'arc DE, il faut que la vitesse du globe en ce point soit telle que, si on le détachait, il décrirait une parabole DF dont le demi latus rectum serait AD. Il doit donc avoir une vitesse égale à celle qu'il aurait au point D s'il était tombé d'une hauteur HD égale à la moitié de DAGa naar voetnoot5); pour que la dite vitesse lui reste en D après son ascension à partir de B suivant la demie circonférence BCD, il est nécessaire que la vitesse en B soit telle qu'il puisse avec cette vitesse monter verticalement jusqu'au point H. En effet, s'il possède cette vitesse en Bet qu'il parvient | |
[pagina 299]
| |
caderet) nunc quoque tantundem spatii motu naturaliter accelerato deorsum conficere nititur. Ergo utroque simul conatu, nititur conficere, motu accelerato secundum 1, 3, 5, 7, spatium aequale utrisque DE & AB, hoc est ipsius AB triplum; quamobrem etiam, erit vis, qua trahit in B puncto ex C descendens, tripla ejus quae fit ex simplici pondere globi B libere pendentis. Quod & ad amussim experientiae consentit. Si cupiam scire qua vi trahatur funis AB descendente globo per arcum HB; sit FN dimidiae AB aequalis & fiat rectangulum BN, ducaturqueGa naar voetnoot1) HL parallela AB. dico vim tractionis quaesitam esse ad pondus simplex globi pendentis, utGa naar margenoot+ HL ad LK. Unde si fuerit BH sextans | circumferentiae erit ista vis ponderis hujus dupla; eoque filo duplici opus erit ad perferendam ejus tractionis vim, cujusmodi simplici globus suspensus retineri potest, &c. | |
[Propositio XVII.]Ga naar voetnoot2)[Globus filo ex centro circuli ad horizontem perpendicularis suspensus, per circumferentiam istius circuli rotari non potest, nisi filum sextuplum ponderis appensi sustinere queat.] Sit circulus perpendiculariter ad horizontem erectus BCDE [Fig. 23], ex cujus centro A suspensus sit globus B, dico, ut hic circumgyrari possit per circumferentiam 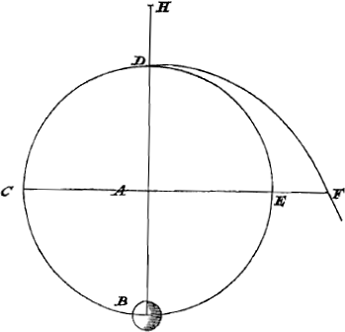 [Fig. 23.]
BCDE, opus esseGa naar voetnoot3) filo quod sextuplumGa naar voetnoot4) ponderis B appensum sustinere possit. Ut enim filum extensum maneat cum globus transit D punctum, perque arcum DE descendit, oportet velocitatem globi eam illic esse, quâ, si dimittatur, descripturus sit parabolam DF, cujus semilatus rectum sit AD. Quare tantam habere eum oportet, qualem in D habiturus esset decidens ex altitudine HD ipsius DA dimidiaGa naar voetnoot5): ut igitur ei ex B per semicirculum BCD ascendenti supersitGa naar voetnoot6) dicta celeritas in D, necesse est celeritatem in B tantam esse, qua possit ascendere perpendiculariter usque ad H | |
[pagina 300]
| |
par un chemin quelconque à la hauteur D, il lui restera toujours assez de vitesse pour qu'il puisse monter verticalement ou aussi par tout autre chemin jusqu'en H, en d'autres termes il conservera autant de vitesse qu'il en acquerrait en tombant de la hauteur HD; et c'est là la vitesse dont nous avons dit que le globe a besoin au point D. Or la vitesse avec laquelle il pourrait monter verticalement de B en H, ou bien qu'il posséderait en tombant de HB, est à la vitesse qu'il acquerrait en tombant de AB, dans un rapport égal à la racine carrée de celui de ces espaces, c'est-à-dire de √10 à 2Ga naar voetnoot1). Mais il a été démontré dans la proposition précédente que si le globe tourne dans la circonférence avec la vitesse qu'il acquiert en tombant de la hauteur AB ou bien suivant l'arc EB, la force centrifuge seule est le double du poids simple du globe. Et la vitesse avec laquelle il tourne dans la circonférence en ce point est à la vitesse dont il était question plus haut comme √10 est à 2; par conséquent les forces centrifuges sont entre elles dans un rapport égal au carré de ce rapport, c'est-à-dire comme 10 est à 4Ga naar margenoot* ou 5 à 2. La force centrifuge au point considéré est donc à la gravité du globe comme 5 est à 1. Mais à cette force centrifuge, au moment où le globe passe par le point B, il faut ajouter la force de la gravité par laquelle il tend à descendre verticalement, laquelle, à ce que nous avons dit, est à la dite force centrifuge dans le rapport 1:5. La force totale ou traction qu'éprouvera le fil, au moment où le globe passe par le point B, sera donc le sextuple de la gravité du globe. En partant de là, lorsqu'un globe attaché à un fil AB [Fig. 24] est abandonné à lui-même au point C situé à la même hauteur que A, qu'on divise AB en D de telle manière que DB = ⅖AB, et qu'on fiche en D un clou que le fil doit rencontrer lorsque le globe descend du point C, je trouve que pour cette position le globe peut précisément accomplir une révolution autour du clou D en décrivant une circonférence; mais que si le clou D est fiché plus haut, cela devient impossible. Car, attendu que la vitesse du globe en B nécessaire pour accomplir une révolution entière doit être à la vitesse qu'il acquerrait en tombant de la hauteur DB comme √10 est à 2, comme nous venons de le démontrer, il s'ensuit que les hauteurs devront être dans un rapport égal au carré de ce rapport-là, c'est-à-dire dans le rapport 10:4 ou 5:2, pour que le globe en tombant de ces hauteurs acquière l'une ou l'autre de ces vitesses. Par conséquent AB:DB = 5:2.
FIN. | |
[pagina 301]
| |
punctum. Hanc enim celeritatem in B habens, quacunque via perveniat ad altitudinem D, semper restabit ei tantum celeritatis ut possit porro perpendiculariter, vel quacunque etiam via ascendere ad H: hoc est, tanta ei supererit celeritas quantam ex altitudine HD cadens acquireret, qua illi in D opus esse diximus. Celeritas porro, qua ex B ad H perpendiculariter ascendere posset, sive quamGa naar margenoot+ haberet ex HB decidens, est ad celeritatem | quam acquireret ex AB cadens, in ratione subduplicata horum spatiorum, hoc est, ea quae √10 ad 2Ga naar voetnoot1). Est autem ostensum in praecedenti, si rotetur in circumferentia ea celeritate, quam acquirit cadens ex AB sive per arcum EB, esse vim centrifugam solam duplam ponderis globi simplicis. Estque celeritas qua hîc in eadem circumferentia rotatur ad illam, ut √10 ad 2, ac proinde vis centrifuga in ratione duplicata, hoc est 10 ad 4Ga naar margenoot*, sive ut 5 ad 2. Ergo vis centrifuga hîc erit ad globi gravitatem ut 5 ad 1. Ad hanc vero vim centrifugam, cum globus transit in B, addenda est vis gravitatis, qua deorsum tendere conatur, quae ad vim dictam centrifugam dicta est se habere, ut 1 ad 5. Ergo tota vis seu attractio quam sentiet filum transeunte globo in B erit sextuplaGa naar voetnoot2) globi gravitatis. 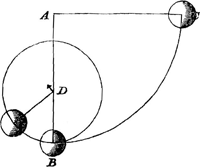 [Fig. 24.]
Hinc invenio, si globus ex AB [Fig. 24] filo ligatus dimittitur ex C, ejusdem cum A puncto latitudinis; dividatur autem AB in D, ut sit DB [=] ⅖AB, atque in D clavus figatur cui filum occurrat, globo ex C cadente: ita demum globum circa clavum D convolvi posse circulumque describere; si vero altius figatur clavus D, non posse. NamGa naar voetnoot3) cum celeritas globi in B ad circulationem integram perficiendam debeat esse ad celeritatem quam acquireret cadens ex DB ut √10 ad 2, ut modo ostensum fuit: hinc altitudines debebunt esse in duplicatâ ratione istius, nempe ut 10 ad 4 sive 5 ad 2, ex quibus cadendo diversas istas celeritates acquirat. Ergo AB ad DB ut 5 ad 2.
FINIS. |
|