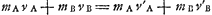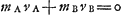Logo DBNL
Oeuvres complètes. Tome XVI. Percussion (1929)

Oeuvres complètes. Tome XVI. Percussion

(1929)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Percussion. Question de l'existence et de la perceptibilité du mouvement absolu. Force centrifuge. Travaux divers de statique et de dynamique de 1659 à 1666.

De motu corporum ex percussione.

Avertissement.

Aperçu général de la genèse du traité ‘De motu corporum ex percussione’.

On connaît la grande amitié qui liait le père de Christiaan Huygens à Descartes et l'admiration profonde que celui-ci lui inspirait1). Cette admiration fut partagée par le jeune Christiaan qui, sans doute, a rencontré plus d'une fois le philosophe français dans la maison paternelle, et subi l'ascendant de cette puissante personnalité.

Voici, en effet, comment vers la fin de ses jours Christiaan Huygens décrivit l'influence que Descartes avait exercée sur lui dans sa jeunesse2): ‘Mr. des Cartes avoit trouvè la maniere de faire prendre ses conjectures et fictions pour des veritez. Et il arrivoit a ceux qui lisoient ses Principes de Philosophie3) quelque chose de semblable qu'a ceux qui lisent des Romans qui plaisent et font la mesme impression

que des histoires veritables. La nouveautè des figures de ses petites particules et des tourbillons y font un grand agrement. Il me sembloit lorsque je lus ce livre des Principes la premiere fois que tout alloit le mieux du monde, et je croiois, quand j'y trouvois quelque difficultè, que c'étoit ma faute de ne pas bien comprendre sa pensée. Je n'avois que 15 à 16 ans. Mais y ayant du depuis decouvert de temps en temps des choses visiblement fausses, et d'autres tres peu vraisemblables je suis revenu de la preoccupation ou j'avois estè’.

En mai 1645, à l'âge de 16 ans, Christiaan entra dans l'Université de Leiden, où il rencontra le mathématicien Frans van Schooten, qui, l'année suivante, succéda à son père, du même nom, comme professeur de mathématiques à l'école des ingénieurs, dépendant de l'Université. Cet homme d'environ trente ans, grand admirateur de Descartes, fut le précepteur et bientôt l'ami de Christiaan. Il considérait comme sa vocation principale d'enseigner à ses élèves, et surtout au plus éminent d'entre eux1), les nouvelles méthodes et découvertes mathématiques du philosophe français.

En 1650 Huygens donna encore un témoignage éloquent de son admiration, à peine atteinte, pour Descartes dans les vers qu'il consacra à sa mémoire et qui finissent par la stance2):

 
‘Nature, prends le deuil, viens plaindre la première
 
Le Grand Descartes, et monstre ton désespoir;
 
Quand il perdit le jour, tu perdis la lumière,
 
Ce n'est qu'à ce flambeau que nous t'avons pu voir.’

C'est, paraît-il, en 1652 que la réaction dans l'esprit de Huygens à l'égard de Descartes se fait jour.

Le 17 janvier 1652 il écrit à van Gutschoven3) qu'il doute de la vérité des

règles de Descartes sur le choc des corps4), la première exceptée, pour ne pas dire qu'il les suspecte d'être fausses. Il pourrait apporter ses raisons, surtout contre

la quatrième1), mais il craint que cela n'intéresse pas suffisamment son correspondant.

En octobre 16522), pour illustrer la différence entre ses vues et celles de Descartes, il indique à van Schooten le cas où les deux corps se meuvent en sens contraire de manière que le produit de la masse et de la vitesse a la même valeur pour les deux. D'après lui, Huygens, les deux corps rejailliront chacun du côté d'où ils sont venus avec la même vitesse qu'ils avaient avant leur rencontre; suivant Descartes, qui dans ses règles avait omis ce cas, le plus petit n'aurait pas même la puissance de mouvoir le plus grand lorsque celui-ci serait en repos. Or, la solution indiquée ici par Huygens est précisément celle de laquelle il affirme3) dans le manuscrit de 1652, dont nous parlerons bientôt, pouvoir déduire la solution de tous les autres cas4).

Enfin, le 16 décembre 1653, il fait connaître à Kinner à Löwenthurn5) sa solution du cas où de deux corps égaux qui se choquent l'un est en repos, et lui propose le cas où le corps en mouvement rencontre un corps en repos de grandeur double. Personne, qu'il sache, n'a donné une solution acceptable dece dernier cas, ou du moins pas une qui convienne aux raisonnements qu'il avait institués à ce sujet.

 

Voilà ce que nous apprend la Correspondance de Huygens à propos de ses premières recherches sur le choc des corps. Voyons maintenant ce que les Manuscrits+ nous révèlent. Il n'y en a qu'un que l'on puisse dater de si tôt que 1652. C'est la première feuille, de 4 pages, d'un Manuscrit plus étendu dont les pages furent numérotées par Huygens. Cette feuille nous a fourni les trois premières Parties de l'Appendice I6). Sans doute contient-elle les premières recherches sur le choc des corps durs. On y voit Huygens faire fausse route au début7) pour revenir immédiatement sur ses pas et choisir une voie meilleure; en outre on trouve au milieu de la troisième page, qui a été reproduite à la fin du présent Tome en facsimilé, la minute d'une lettre à van Schooten8) à laquelle celui-ci répondit le

28 juillet 16529). Pourquoi cette minute aurait-elle été écrite à cette place si le reste de la page n'était pas déjà occupé?

Or, sur cette feuille qui doit donc dater de 1652, on rencontre déjà plusieurs des Théorèmes les plus importants du futur Traité sur le choc des corps durs10). En premier lieu le Principe de la relativité11), dont Huygens a tiré tant de profit et qui constate (pour employer l'image choisie de préférence par Huygens) que les choses se passent de même dans un bateau se mouvant avec une vitesse uniforme, qu'elles se passent sur la rive. Ensuite le beau Théorème d'après lequel dans le choc des corps durs la vitesse de la séparation est égale à celle du rapprochement12). Enfin, ce qui est très remarquable, le Théorème de la conservation de la force vive13).

Remarquons que rien sur la feuille n'indique la manière dont ce dernier Théorème a été obtenu. Il semble très improbable que la voie exposée dans le Traité14) ait été suivie: il ne reste à notre avis que la conjecture énoncée par nous dans la note 10 de la p. 95. Mais nous reviendrons plus loin sur cette question15).

En outre on trouve à la troisième page de la feuille des calculs basés sur le Principe de la conservation de la quantité de mouvement16). Il est peu vraisemblable qu'à cette époque Huygens avait déjà donné à ce Principe sa forme propre

qu'il n'a pas manqué de découvrir plus tard1), mais quoiqu'il sût déjà que le Principe interprété suivant la conception de Descartes n'est pas vrai2), il supposait, non sans raison, que dans beaucoup de cas il peut être appliqué sans amener d'erreur3). Il avait commencé par y attacher une grande valeur et ne l'a jamais rejeté entièrement4).

 

En tout cas ce que Huygens avait trouvé en 1652 suffisait pour résoudre tous les cas du choc direct des corps durs5) et l'on peut se demander pourquoi il n'a pas procédé dès lors à la publication de ses résultats.

Ce n'est certainement pas l'avis contraire de van Schooten, qui l'a retenu. Dans sa lettre du 25 octobre 16546) celui-ci opine qu'il peut croire à peine qu'un esprit si sublime et perspicace aurait publié quelque chose qui ne serait pas conforme à la vérité. Il déconseille Huygens de s'occuper de ce sujet de peur qu'il n'emploie inutilement son temps et son travail; mais Huygens lui répond7) qu'il sait bien que van Schooten n'est pas de son avis sur les régles de Descartes; mais s'il avait pris connaissance de ce que lui, Huygens, avait déjà mis par écrit, non sans labeur, sur cette matière, il jugerait bien autrement. Car si les règles de Descartes, à l'exception de la première, ne sont toutes fausses et contraires à ses propres principes, lui, Huygens, ne saurait plus discerner ce qui est vrai ou faux.

 

La véritable raison de l'ajournement, Huygens nous la révèle lui-même dans un manuscrit qui date d'une des dernières années de sa vie7a). Il y dit qu'il avait

suspendu la publication de ce qu'il avait trouvé en 1652 ou 1654, puisque, outre les lois du choc, il restait autres choses regardant la nature du mouvement qu'il n'avait pas encore suffisamment approfondies et qui exigeaient une méditation prolongée8).

On rencontre des traces de cette méditation dans la suite du Manuscrit mentionné+ à la p. 69). Elle concernait la nature et la puissance des forces qui accompagnent le choc10). Aucun instrument, dit-il11), ne surpasse en efficacité le marteau qui utilise cette puissance. Sans lui aucun édifice ne pourrait être construit, aucun coin, aucun clou enfoncé, presqu'aucun travail accompli. Ne vaut-il donc pas la peine de comprendre la puissance infinie de la percussion, si grande qu'un seul homme muni d'un marteau pourrait mettre en mouvement une sphère aussi grande que toute la terre.

Galilée, qu'il cite constamment à ce propos12), l'avait précédé dans cette recherche mais il n'avait pas fait beaucoup plus que disserter sur la difficulté du

sujet1). Huygens n'a pas réuffi non plus à pénétrer le mécanisme de la percussion. L'état imparfait de la science de la dynamique en était la cause. Des Théorèmes qui à nous, élevés dans l'école de la mécanique classique dont Newton fut le fondateur, semblent des plus élémentaires, étaient inconnus alors, et Huygens n'a pas su les découvrir. Il s'agit de l'égalité de l'impulsion Fdt reçue dans une certaine direction et de l'accroissement de la quantité de mouvement dans cette même direction2) comme aussi de l'égalité de la réaction et de l'action3), Theorèmes, d'où Huygens aurait pu déduire facilement la grande force de la percussion comme conséquence du peu de temps dans lequel elle s'accomplit, et de plus la formule véritable de la conservation de la quantité de mouvement, qu'il a fini, en effet, par trouver, mais, comme nous le montrerons plus loin4), sans bien sentir la généralité et la signification primordiale pour la dynamique du Principe en question.

 

En 16565) Huygens entreprend la tâche ardue de rédiger son Traité par axiomes ou hypothèses, lemmes, théorèmes ou propositions6), pourvus de démonstrations géométriques à la mode des anciens, comme il le jugeait alors nécessaire ou du moins très désirable. Le 20 juillet il peut écrire à de Roberval que son ouvrage est achevé7). Dans la note 1 de la p. 130 nous avons donné les+ raisons qui nous portent à croire que le Manuscrit de cet ouvrage est celui auquel nous avons emprunté l'Appendice II, p. 138-149.

Le choix des hypothèses était déjà fait depuis 1652. Il les expose8) dans sa Préface9) qu'il ne fit qu'ébaucher, mais on les retrouve, numérotées, dans le Manuscrit définitif10) qui a été reproduit dans le Traité. Les hypothèses I, III, IV11) sont faciles à accepter, II et V12) excluent les corps mous

ou demi-durs. Avec le Principe: que le centre de gravité commun ne peut pas monter par l'effet de la gravité seule, elles suffisent, ou à peu près13), aux démonstrations quelques fois très compliquées des Propositions. Quant à ces Propositions, outre celles que nous avons mentionnées plus haut comme étant déjà connues de lui en 1652, les plus remarquables sont la Prop. V (p. 47) sur la réversibilité du choc, la Prop. IX (p. 65) contenant la solution complète du choc direct des corps durs, et les belles Prop. XII (p. 81) et XIII (p. 87) sur l'effet de l'interposition d'un ou de plusieurs corps en repos entre un corps en mouvement et un autre en repos.

 

Le Manuscrit définitif du Traité, écrit d'une autre main que celle de Huygens,+ est en grande partie une copie presque textuelle de celui de 165614). Mais il présente avec ce dernier certaines différences dont nous signalons celles qui ont quelque importance:

1o. La Préface est supprimée dans le Manuscrit définitif. Elle aurait dû contenir d'après l'esquisse qu'on en trouve dans le Manuscrit de 1656, outre les hypothèses dont nous venons de parler, un aperçu des travaux antérieurs de Galilée et de Descartes et les raisons qui ont conduit Huygens à commencer ses recherches. Elle était destinée à être complétée à l'aide des annotations faites en 165415).

2o. Huygens introduit la fiction de deux hommes, l'un dans un bateau l'autre sur la rive16), joignant leurs mains et combinant leurs mouvements pour déplacer

des boules qui s'entrechoquent. On rencontre cet artifice pour la première fois dans une note1) envoyée par Huygens à la ‘Royal Society’ le 5 janvier 16692). D'après la lettre qui accompagna l'envoi il devait servir à convaincre même les plus sceptiques de la justesse du principe de la relativité3). Son emploi a nécessité un remaniement des démonstrations des trois premières et de la neuvième Proposition du Traité4). Ces démonstrations en sont devenues moins concises, mais on peut douter si elles sont plus convaincantes qu'elles ne l'étaient auparavant5).

3o. En deux endroits différents il y a des additions. Nous les avons signalées dans les notes 4 de la p. 69 et 1 de la p. 90.

4o. Il ya une omission à première vue très surprenante. Elle se rapporte à la Prop. VI (p. 49) où Huygens expose l'erreur de Descartes à propos de la conception du Principe de la conservation de la quantité de mouvement. Cette Proposition correspond au ‘Theorema 7’ (p. 147) du Manuscrit de 1656, mais dans ce dernier Manuscrit Huygens ne se borne pas à démontrer l'erreur de Descartes, il indique ensuite par quelle modification son Principe peut être rectifié6). L'omission complète et voulue de cette indication dans le Traité lui-même fait l'impression d'une injustice envers Descartes. L'un de nous à cherché à expliquer cette attitude de Huygens par le désir de porter un coup bien dirigé à la grande autorité de Descartes, qui menaçait de devenir un obstacle au progrès de la

science7). Cela est possible8), mais il y a une autre explication fondée sur la nature même du Traité qu'il se proposait de publier. Dans ce Traité rien n'est avancé qui ne soit prouvé par une démonstration rigoureuse basée sur des Hypothèses bien définies. Or, il est certain que Huygens aurait pu composer une telle démonstration du Théorème de la conservation de la quantité de mouvement dans sa vraie forme. Il suffisait à cet effet de partir de sa solution générale du problème du choc direct des corps durs9), comme il l'avait fait pour la Prop. XI (p. 73-77) sur la conservation de la force vive. Toutefois cela lui aurait coûté un certain effort pour lequel il lui manquait probablement l'inspiration, occupé comme il l'était toujours de nouveaux projets et de nouvelles découvertes qui plusieurs fois l'ont empêché de publier des résultats importants qui avaient commencé à l'intéresser moins vivement10). Et c'est sans doute cette même

raison qui l'a empêché d'incorporer dans son Traité certains autres résultats obtenus après 1656, savoir ses solutions complètes et motivées des problèmes du choc direct des corps mous et des corps semi-durs1).

 

Nous ignorons à quelle époque le Manuscrit définitif, qui a servi à la publication du Traité, en 1703, dans les ‘Opuscula postuma’2), fut composé, et par quelle main il fut écrit sous la direction de Huygens3). Nous savons seulement qu'il doit être postérieur à 16734), année dans laquelle parut l'‘Horologium oscillatorium’.

En 1669 Huygens publia ses ‘Regles du mouvement dans la rencontre des corps’ dans le Journal des Sçavans5) sans les faire accompagner d'aucune démonstration. Nous raconterons les circonstances qui ont amené cette publication dans l'Avertissement suivant. Ici nous voulons noter encore que trois ans avant sa mort Huygens n'avait pas abandonné le projet de faire paraître les démonstrations de ses règles, puisqu'il écrivit à Leibniz le 11 juillet 16926) ‘Sur la matiere du mouvement j'ay bien des choses nouvelles et paradoxes à donner, que l'on verra, quand je publieray mes demonstrations des Regles de la Percussion, insérées autrefois dans les Journaux de Paris et de Londres’.

Les corps durs de Huygens.

Des corps durs, possédant les propriétés que Huygens leur attribue, n'existent pas dans la nature.

Imaginons, en effet, deux corps parfaitement élastiques et supposons que leur choc soit un procès parfaitement adiabatique; ces corps se quitteront, excepté dans des cas très spéciaux, en exécutant des vibrations, et ces vibrations absorberont une partie plus ou moins grande, mais finie, de l'énergie de leur mouvement, de sorte qu'après le choc la somme des forces vives de leurs mouvements progressifs ne sera plus ce qu'elle était auparavant7).

La question peut être traitée à peu près rigoureusement pour le cas du choc central de deux cylindres homogènes et isotropes dont les sections sont égales et se couvrent au moment du choc, pourvu que leurs longueurs la et lb soient suffisamment grandes par rapport aux dimensions des sections, et que l'on accepte la loi de Hooke.

Supposons, en effet, que ces cylindres A et B8) (la étant égal ou supérieur à lb) ont d'abord des vitesses égales et opposées, dont la grandeur absolue est v, les axes se mouvant le long d'une même droite, et qu'au moment t = 0 les extrémités planes viennent en contact au point x = 0. Si l'axe des x pofitif est dirigé vers le cylindre B, que, pour fixer les idées, nous supposerons se trouver à droite du cylindre A, et si l'on désigne par c la vitesse de propagation des ondes de compression ou de dilatation, la solution prend la forme suivante:

Après un court intervalle de temps t la partie du cylindre B comprise entre les plans x = 0 et x = ct sera ramenée au repos et il se sera produit dans cette partie une contraction v:c par unité de longueur. D'autre part la partie au delà du plan x = ct se trouvera encore dans l'état naturel et aura conservé la vitesse -v.

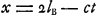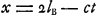Au moment t = lb:c le cylindre B tout entier se trouve en repos avec la contraction dont il vient d'être question, contraction qui disparaîtra maintenant à partir de l'extrémité droite. Tant que t est compris entre lb:c et 2lb:c on peut dire que la partie du cylindre entre x = lb et illustratie a repris sa longueur naturelle; en même temps cette partie aura acquis la vitesse +v. Quant à la partie entre x = 0 et illustratie, elle est encore en repos et on y trouve la contraction v:c.

Enfin à l'instant t = 2lb:c le cylindre entier est animé de la vitesse +v, la contraction ayant disparu dans toute son étendue.

Soit maintenant lb = la. Alors dans le cylindre A des phénomènes tout-à-fait analogues auront lieu et les deux corps seront revenus à l'état naturel au même instant t = 2la:c = 2lb:c. Comme à cet instant ils auront les vitesses -v et +v

ils se sépareront avec ces vitesses. Le résultat du choc est donc conforme à la théorie de Huygens1),

Il n'en est plus ainsi lorsque lb < la. Alors au moment t = 2lb:c où le cylindre B a atteint l'état qui vient d'être indiqué, la partie de A voisine de B se trouvera encore en repos. Toute pression qu'elle exerce sur B cessera donc et quoique les cylindres ne se séparent pas encore2) le choc peut être considéré comme fini. Le cylindre B, plus court que A, se comporte donc entièrement comme s'il avait rencontré dans les mêmes circonstances un cylindre de longueur égale lb.

Dans le cas plus général, où nous désignerons par va et vb les vitesses avant, et par v'a et v'b celles après le choc, on déduit facilement de ces résultats, pour les cylindres égaux: v'b = va et v'a = vb3) et pour les cylindres inégaux v'b = va, mais (à cause de la conservation de la quantité de mouvement)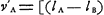 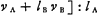illustratie illustratie.

On trouve ainsi pour la perte par le choc de l'énergie du mouvement progressif des cylindres: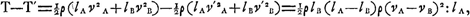



illustratie

où ρ représente la masse par unité de longueur.

Il en résulte: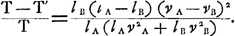



illustratie

Dans le cas va = -vb et la = 2lb on trouve p.e. ⅔ pour ce rapport4).

Bien entendu, ce qui précède est limité à des vitesses de translation v qui sont petites par rapport à la viteffe de propagation c. Dès que la fraction v:c, et par conséquent la compression produite dans les cylindres deviennent tant soit peu

considérables la loi de Hooke cesse d'être vraie et certaines simplifications dont on s'est servi dans les calculs ne sont plus justifiées.

 

La solution que nous venons d'esquisser fut trouvée par Cauchy en 18265), mais il paraît que pendant quelque temps elle fut supplantée presque complètement par la solution du même problème par Poisson6) d'après laquelle les cylindres ne se sépareront après le choc que dans le seul cas lb = la. Or, la faute dans le raisonnement de Poisson fut indiquée par de Saint-Venant7) qui élabora plus amplement la solution de Cauchy et la trouva juste. En outre, ce qui est remarquable, la bonne solution fut découverte de nouveau indépendamment par F. Neumann8), par Thomson et Tait9) et par A. Ritter10).

Bien que cette solution ne soit vérifiée que très imparfaitement par les expériences11), elle prouve du moins que la perte de force vive du mouvement pro-

gressif, causée par les vibrations que le choc excite, peut être considérable dans le cas des cylindres et que, par conséquent, la théorie de Huygens n'y peut pas rendre compte des phénomènes.

Heureusement on est conduit à une conclusion bien différente si l'on considère le choc de corps à surface convexe, qui dans leur rencontre ne se touchent que sur une petite étendue. Dans ce cas, la théorie de Huygens peut être maintenue, si seulement on suppose que les vitesses des corps sont très petites par rapport aux vitesses avec lesquelles des ondes élastiques se propagent à leur intérieur. C'est du reste une supposition sans laquelle la théorie deviendrait extrêmement compliquée.

Afin de justifier la théorie de Huygens dans les cas dont il s'agit maintenant nous pouvons nous baser sur les résultats obtenus par H. Hertz1) dans ses recherches sur le contact de corps élastiques. À cet effet il nous suffira ici de considérer des sphères à rayons égaux et formées de la même substance; on comprendra facilement que les conclusions resteront les mêmes pour des cas beaucoup plus généraux.

Voici le problème (simplifié pour ce cas) que Hertz s'est posé. Une sphère élastique est assujettie à une pression, exercée sur une petite étendue A de sa surface, dont la résultante, dirigée vers le centre, a la grandeur donnée P, et à une deuxième force de direction opposée et d'égale grandeur qui est répartie uniformément sur tout le volume du corps. Il s'établira alors un état d'équilibre

bien défini avec un aplatissement au point A que Hertz réussit à calculer à l'aide de la théorie de l'élasticité. La substance de la sphère étant considérée comme isotrope, les formules contiennent deux constantes, savoir le module de rigidité K et le coefficient bien connu de Poisson μ. Rappelons ici que, si ρ est la densité, les vitesses de propagation de vibrations transversales et longitudinales auront respectivement les valeurs:

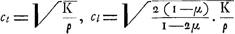illustratie

Si, au lieu d'être constantes, les forces P et -P changent d'un moment à l'autre, elles donneront lieu à des vibrations, mais la mesure dans laquelle ces mouvements intérieurs interviennent dépend entièrement de la vitesse des variations des forces. On peut négliger les vibrations et appliquer à chaque instant les formules de l'équilibre, lorsque les variations sont tellement lentes que le temps T nécessaire pour un changement appréciable de P et de -P est beaucoup plus grand que la période des vibrations propres du corps. Comme pour une sphère de rayon R cette période est de l'ordre de grandeur R:ct ou R:cl, la condition prend la forme:

 

T ≫ R/ct ou T ≫ R/cl.

 

Dans ce qui suit nous nous servirons de la première de ces inégalités, qui embrasse la deuxième, parce que cl > ct.

Dans le problème du choc la force avec laquelle l'une des sphères agit sur l'autre joue le rôle de la pression P; elle augmente à partir de zéro jusqu'à une certaine valeur maximum et diminue ensuite pour disparaître au moment de la séparation2). Il est donc clair que les vibrations seront négligeables (ce qui assurera la justesse de la théorie de Huygens) si l'intervalle de temps dans lequel ces variations ont lieu, c'est-à-dire la durée du choc satisfait à la première des conditions d'inégalité, que nous venons d'indiquer.

Or, Hertz a trouvé pour cette durée1) une formule qu'on peut mettre sous la forme:

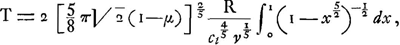illustratie

dans laquelle v désigne la vitesse relative avec laquelle l'une des sphères s'approche de l'autre et où: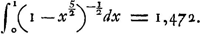

illustratie

En substituant cette dernière valeur et en prenant μ = ⅓ pour le coefficient de Poisson, on trouve: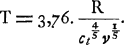

illustratie

La condition pour T devient donc:

 

(v/ct)⅕ ≪ 3,76.

 

Elle pourra être remplie si la vitesse v est suffisamment petite.

Si, par exemple, on exige que T = 20 R:ct on trouve v = 0,000235 ct. Pour l'acier la vitesse de propagation des vibrations transversales est à peu près 3,2.105 cm. par sec., donc:v = 75 cm. par sec.

On voit ainsi que des expériences sont possibles dans lesquelles la théorie de Huygens se vérifie approximativement et qu'il n'y a pas lieu de s'étonner que Huygens qui expérimenta surtout avec des sphères était sous l'impression que les résultats de sa théorie correspondaient presque parfaitement avec les expériences2).

En tout cas cette théorie peut être considérée comme rigoureusement exacte

dans un cas limite, dont on s'approche, avec des corps donnés, en diminuant les vitesses, ou bien, pour des vitesses données, en augmentant dans la pensée le module de rigidité K. Dans le choc de corps ‘parfaitement durs’, caractérisés par K = ∞, il ne se produirait aucune vibration intérieure.

Nous ne pouvons pas finir cette discussion rapide de l'applicabilité de la théorie de Huygens dans le domaine des corps physiques, sans rappeler le rôle prépondérant que ses règles du choc des corps durs ont commencé à jouer, deux siècles après leur découverte, dans le développement de la théorie cinétique des fluides.

Principe que le centre de gravité commun ne peut pas monter par la gravité seule.
Conservation de la force vive dans le choc.
Solution par Huygens du problème du choc des corps mous ou semi-durs.

Dans ses recherches sur la chaînette qui ‘ne faict point une parabole’3) et dans son merveilleux Traité sur l'équilibre des corps flottants4), Huygens avait employé le Principe que le centre de gravité commun se place aussi bas que possible5). Ce Principe ne pouvait servir sous cette forme que dans des questions de statique. C'est pourquoi il le modifie dans sa théorie du choc en lui donnant la forme nouvelle: que le centre de gravité commun ne peut pas monter par l'effet de la gravité seule. Formulé de cette façon il devient entre les mains de Huygens un instrument puissant de recherches, et il n'y a pas lieu de s'en étonner. En effet, pour tous les phénomènes réversibles ce Principe, que Huygens appela plus tard ‘le grand Principe des mechaniques’6), est équivalent à celui de la conservation de l'énergie dans un champ gravifique, où la gravité agit partout dans la même direction et avec la même intensité7).

Pour le montrer, considérons un certain nombre de corpuscules (ou de corps lorsqu'on néglige les rotations) de masses m, de vitesses v et qui se trouvent à des hauteurs h au dessus d'un certain plan horizontal. Lorsque, à l'exemple de Huygens, on convertit les vitesses en des hauteurs d'où les corpuscules peuvent être censés descendre ou jusqu'auxquelles elles peuvent s'élever en conséquence de ces vitesses, le principe employé par Huygens donne: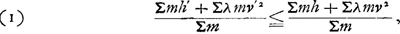



illustratie

où h' et v' représentent les hauteurs et les vitesses après le phénomène, et où λ = 1/2g.

Lorsque le phénomène est réversible on en déduit immédiatement: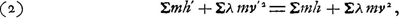



illustratie

et dans le cas du choc central de deux corps durs: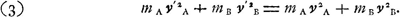



illustratie

Il est vrai que dans le Traité la déduction de cette dernière relation est beaucoup plus compliquée. Huygens n'y emploie pas la réversibilité du choc1). En vérité, il n'applique le Principe du centre de gravité commun qui ne peut pas monter qu'au cas où illustratie2). À l'aide de ce Principe et de la Prop. IV3), il arrive à la conclusion que dans le cas considéré on doit avoir v'a = -va et v'b = -vb. Puis le Principe de la relativité lui permet de remonter de ce cas spécial au cas général4), après quoi il déduit l'équation (3) des résultats obtenus pour ce dernier cas5). Mais cette déduction est de l'année 1656, lorsque Huygens composa le Manuscrit de cette date6), tandis que la Proposition qui correspond à l'équation (3) lui était connue depuis 16527) et appartenait aux

premiers résultats de ses recherches sur le choc. Peut-on croire que cette Proposition fut obtenue si tôt par la voie compliquée que nous venons d'esquisser, et n'est-il-pas beaucoup plus plausible que dès l'abord Huygens ait considéré la réversibilité du choc comme une hypothèse admissible du moins provisoirement?

 

Il est curieux de remarquer que le même Principe: que le centre commun de gravité ne peut pas monter par l'effet de la gravité, combiné avec le Principe de Huygens de la relativité, implique le Théorème de la conservation de la quantité de mouvement dans une direction donnée. Et cela sans supposer cette fois la réversibilité des phénomènes.

Concevons, en effet, qu'entre le temps t et le temps t' il se soit produit parmi les particules de masse m, ou plutôt entre les corps qu'elles composent et qu'on peut supposer durs, semi-durs ou mous, un certain nombre de chocs. Supposons d'ailleurs toutes sortes de liaisons entre eux. Ajoutons ensuite à toutes leurs vitesses v (dont vx, vy et vz soient les composantes dans trois directions rectangulaires) une vitesse commune x, parallèle aux vx; on aura donc: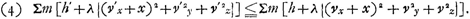



illustratie

On en déduit: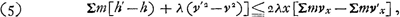



illustratie

mais cette inégalité ne peut être vraie pour toutes les valeurs de x sans qu'on ait:

 

(6) Σmvx = Σmv'x;

 

ce qu'il fallait démontrer.

Ce même raisonnement est appliqué par Huygens au choc des corps mous et semi-durs, mais seulement dans le cas particulier où illustratie8). Il

prouve qu'alors nécessairement mav'a+mbv'b s'annule aussi, d'où il suit: v'a/va = = v'b/vb = e, où e varie entre 1 (pour les corps durs) et 0 (pour les corps mous).

On reconnaîtra facilement dans cette dernière équation le résultat obtenu par Huygens dans le cas particulier en question1), auquel le cas général du choc central de deux corps semi-durs peut être facilement réduit à l'aide du Principe de Huygens de la relativité2).

Théorème de la conservation de la quantité de mouvement dans une direction donnée.

Nous n'avons pas beaucoup à ajouter aux remarques déjà faites à propos de ce Théorème3).

Huygens a commencé par l'admettre dans la forme erronée sous laquelle Descartes l'avait formulée4). Mais déjà en 1652, au début de ses efforts pour construire une théorie cohérente du choc des corps durs il avait reconnu la fausseté de cette forme dans certains cas5). Toutefois il ne douta pas de son applicabilité dans d'autres cas. Or, puisqu'il lui était impossible de construire sa théorie sans quelques hypothèses suffisamment évidentes, et qu'il n'en trouva pas ailleurs, il en emprunta deux6) au Principe énoncé par Descartes.

Deux années plus tard il avait découvert la véritable formule du Théorème7). Il la publia dans le Journal des Sçavans du 18 mars 16698), mais la forme même de cette communication montre qu'il n'avait pas reconnu le

fondement simple sur lequel nous basons ce Théorème depuis l'édition des ‘Principia’ de Newton. En effet, après l'exposition de la formule véritable9), il y parle de la ‘loy admirable de la Nature’ d'après laquelle ‘le centre commun de deux ou trois ou de tant qu'on voudra de corps, avance toûjours également vers le méme costè en ligne droite devant & aprés leur rencontre’, loi qu'il prétend pouvoir ‘démontrer en ce qui est des corps Spheriques, & qui semble estre generale en tous les autres tant durs que mols, soit que la rencontre soit directe ou oblique’10). Or, cette limitation au cas ‘des corps Spheriques’ de sa démonstration de la loi en question (qui est, de fait, entièrement identique avec le Théorème de la conservation de la quantité de mouvement) montre la nature spéciale et bornée de cette démonstration, que d'ailleurs nous ne connaissons pas.

Pour Huygens le Théorème de la conservation de la force vive prime de beaucoup celui de la conservation de la quantité de mouvement11), et il y a lieu de s'étonner qu'il ait échappé à sa perspicacité que ce dernier Théorème peut se déduire facilement du premier, dans le cas des corps durs, à l'aide du Principe de la relativité. Ajoutant aux vitesses va, vb, v'a, v'b des corps A et B, avant et après leur rencontre, la vitesse commune x, on a d'après le premier Théorème: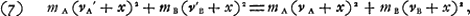



illustratie

d'où il suit: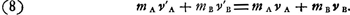



illustratie

Il est vrai qu'à cause de sa méthode géométrique Huygens aurait dû distinguer divers cas selon le sens des mouvements avant et après le choc.

Théorème de l'égalité de la vitesse de l'éloignement à celle du rapprochement.

Concevons deux mécanismes A et B d'un nombre quelconque de degrés de liberté, sans frottement, formés par des corps durs dans le sens de Huygens, et supposons que deux pièces, appartenant chacune à l'un de ces mécanismes, se rencontrent. Soient P le point de contact; π le plan tangent du point P pour les deux pièces; va et vb, au début du choc, les composantes perpendiculaires au plan tangent des vitesses du point P, considéré alternativement comme appartenant à l'un et à l'autre des pièces; v'a et v'b ces composantes à la fin du choc, on aura alors:



illustratie

Cette équation, qui dit que la vitesse relative dans la direction perpendiculaire au plan tangent commun change de sens par le choc sans changer de grandeur, permet de remplacer dans le système des équations qui peuvent servir à déterminer le mouvement après le choc, la seule équation quadratique (dépendant des forces vives) par une équation linéaire comme toutes les autres.

Or, le Théorème de Huygens de l'égalité de la vitesse de l'éloignement à celle du rapprochement, qui joue un rôle si important dans le Traité1) et qu'il a même pensé un instant à poser en axiome2), ne représente qu'un cas particulier de l'équation (9) et peut rendre le même service dans la théorie du choc direct des corps durs que le Théorème général dans le choc des mécanismes composés par ces sortes de corps.

Huygens a découvert une autre généralisation de son Théorème pour le cas du choc oblique. Elle est assez intéressante, mais bornée au cas de sphères homogènes; elle dit que par le choc la vitesse relative des centres change de direction mais pas de grandeur3).

Principe de Huygens de la relativité.

Dès le début de ses recherches4) Huygens a senti tout le profit qu'il pouvait tirer de ce Principe. Pour arriver à une théorie consistante du choc il l'a employé systématiquement et l'a suivi dans toutes ses conséquences. Il nous semble qu'on doit y attacher son nom, plutôt que celui d'un autre, pour le distinguer du Principe plus général de même appellation développé dans ces derniers temps par Einstein.

Il est vrai qu'il était déjà connu auparavant et fut employé surtout par les adhérents de la doctrine du mouvement de la Terre5). Il constituait l'un de leurs meilleurs arguments, mais ils ne l'employaient pas comme instrument de recherches. Ce mérite était réservé à Huygens.

Quant aux problèmes de métaphysique qui s'y rattachent: s'il existe un repos et un mouvement absolu et si l'on peut en reconnaître l'existence, du moins dans le cas de la rotation, Huygens n'a pas voulu s'en occuper dans la période dont nous traitons6). Plus tard, toutefois, il a changé d'attitude, comme nous le verrons dans la suite.


Vorige Volgende