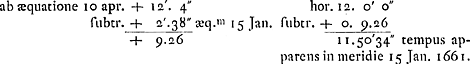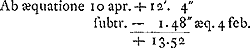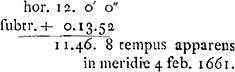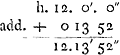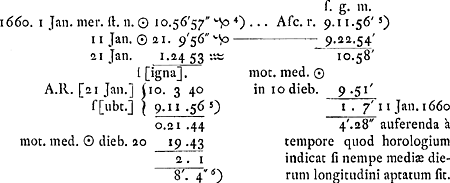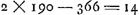singulae harum 10 secunda efficiant. Usus vero instrumenti est hujusmodi. Ponatur primum ut diametri punctum o, sursum spectet, deinde vertatur, donec orbis mobilis dies epochae, hoc est illa qua cum sole horologium convenire fecimus, vergat
[Fig. 5.]
[Fig. 6.]
ad dictum punctum o quod extento silo figuretur Ga naar voetnoot1) tunc si postea alia quavis die inquirere libeat, quantum temporis addendum vel aufer. sit horae ei quam designat horologium motu-medio et aequabili progrediens ut nempe habeatur hora temporis apparentis sive quae est in sciaterico horologio; manente orbe quem admodum positus fuit tempore epochae, move filum quousque conveniat propositae diei, et respice in semicirculis immobilibus quem minutorum et secundorum numerum idem filum indicet. Et si quidem dextram versus mouendum fuit, indicabit numerus ille quantum praecedat automaton horam sciatherii. si vero sinistrorsum filum movisti, indicabit numerus in altero semicirculo immobili quantum retardet automaton.
Hoc modo invenio, si 5 Sept. exempli gr. congruere fecero cum sole horologium, die 22 ejusdem mensis addendum ad horam horologij 5 min. et 55 secundaGa naar voetnoot2). Item si 10 Octobri cum sole conveniat horologium, 1 Martij auferendum fore ab hora horologij 26 min. 44 sec.Ga naar voetnoot3).
|
-
voetnoot1)
- La Pièce, que nous avons divisée en paragraphes, a été empruntée aux p. 212-225 du Manuscrit A. Elle contient des recherches sur l'équation du temps. Remarquons tout d'abord que cette équation est toujours appliquée dans ce qui suit comme correction au temps moyen, ce qui n'est pas conforme à l'usage moderne.
-
voetnoot2)
- D'après le lieu qu'elle occupe au Manuscrit A.
-
voetnoot3)
- Dans ce paragraphe on trouve les premiers calculs de Huygens pour déterminer l'équation du temps. Il commence par prendre pour point de départ (où l'équation est supposée nulle) le 1 janvier 1660, mais plus tard il croit faire mieux (voir le § 7, p. 542) de déplacer ce point de départ vers le 29 février 1660. À cet effet il applique aux calculs déjà accomplis, pour autant qu'ils se rapportent à des dates plus avancées que ce 29 février, une correction que nous avons marquée par des chiffres italiques.
Consultez encore, pour une explication détaillée de la méthode de calcul des § 1-3, la Pièce No. 1017 (p. 138-140 du T. IV) envoyée par Huygens à Petit en mai 1662.
-
voetnoot4)
- Longitude (280o56′57″) du Soleil le 1 janvier 1660 (style nouveau) à midi.
-
voetnoot5)
- Ascension droite (281o56′) du Soleil le 1 janv. 1660, savoir 9 ‘signa’ de 30o + 11o56′.
-
voetnoot6)
- Les 2o1′ d'ascension droite se réduisent, en effet, à 8 min. 4 sec. de temps. Ici et dans la suite l'équation du temps est toujours appliquée comme correction au temps moyen.
-
voetnoot7)
- D'après la ‘Bibliographie générale de l'astronomie’ de J.C. Houzeau et A. Lancaster, T. I, 2 (1889), p. 1570, Johann Hecker publia les éphémérides des années 1660-1670 dans l'ouvrage: ‘Motuum coelestium ephemerides ex observationibus correctis T. Brahei et J. Kepleri hypothesibus physicis, tabulisque rudolphinis ad meridianum Uraniburgicum. Gedani 1660.’
-
voetnoot5)
- Ascension droite (281o56′) du Soleil le 1 janv. 1660, savoir 9 ‘signa’ de 30o + 11o56′.
-
voetnoot5)
- Ascension droite (281o56′) du Soleil le 1 janv. 1660, savoir 9 ‘signa’ de 30o + 11o56′.
-
voetnoot8)
- Ces 8 min. 52 secondes représentent l'équation du temps du 29 février 1660, dans la supposition, employée jusqu'ici, que cette équation est nulle le 1 janvier 1660; consultez le dernier résultat du § 3 (p. 537) et comparez la note 3 de la page présente.
-
voetnoot9)
- Équation du temps lorsqu'elle est supposée nulle le 29 février 1660.
-
voetnoot9)
- Équation du temps lorsqu'elle est supposée nulle le 29 février 1660.
-
voetnoot10)
- Nous supprimons les calculs dont l'algorithme ne diffère aucunement de celui employé dans le calcul précédent.
-
voetnoot11)
- L'équation du temps étant supposée nulle le 1 janvier 1660.
-
voetnoot9)
- Équation du temps lorsqu'elle est supposée nulle le 29 février 1660.
-
voetnoot12)
- On retrouve la détermination de l'équation du temps pour cette date et pour le 20 avril qui suit aux p. 138-139 du T. IV.
-
voetnoot1)
- Un peu pêle-mêle avec les calculs du § 1 on trouve aux p. 212-213 du Manuscrit A les calculs suivants qui se rapportent à l'année 1661. Ils ont servi probablement à constater la grandeur de la différence entre les valeurs de l'équation du temps dans deux années consécutives.
-
voetnoot2)
- Longitude 281o43′27″ du Soleil au 1 janvier 1661.
-
voetnoot3)
- Ascension droite (282o45′) du Soleil à la même date; savoir 9 ‘signa’ de 30o et 12o45′.
-
voetnoot4)
- Ascension droite (281o56′) du Soleil au 1 janvier 1660.
-
voetnoot5)
- Chemin parcouru sur l'équateur par le Soleil moyen dans les trois quarts d'un jour par lesquels l'année bissextile 1660 dépasse l'année julienne.
-
voetnoot6)
- Réduction des 5′ d'ascension droite à 20 secondes de temps.
-
voetnoot7)
- Nous supprimons les calculs dont l'algorithme ne diffère aucunement de celui employé dans le calcul précédent.
-
voetnoot8)
- L'équation du temps étant supposée nulle le 1 janvier 1660.
-
voetnoot9)
- Les calculs de ce paragraphe, à l'exception du dernier (qui se rapporte au 29 février 1660), suivent un algorithme légèrement modifié, de sorte qu'ils mènent directement à la valeur de l'équation du temps dans la supposition que cette valeur est nulle le 29 février 1660.
-
voetnoot10)
- Longitude (285o48′42″) du Soleil le 5 janvier 1661.
-
voetnoot11)
- Ascension droite (287o10′) du Soleil à la même date.
-
voetnoot12)
- Ascension droite (342o18′) du Soleil le 29 février 1660.
-
voetnoot7)
- Nous supprimons les calculs dont l'algorithme ne diffère aucunement de celui employé dans le calcul précédent.
-
voetnoot12)
- Ascension droite (342o18′) du Soleil le 29 février 1660.
-
voetnoot13)
- Ascension droite (281o56′) du Soleil le 1 janvier 1660.
-
voetnoot14)
- Correction à apporter à l'équation du temps, trouvée dans la supposition qu'elle est nulle le 1 janvier 1660, pour l'accommoder à la supposition que sa valeur se réduit à zéro le 29 février de la même année. Comparez les notes 3 et 8 de la p. 534.
-
voetnoot15)
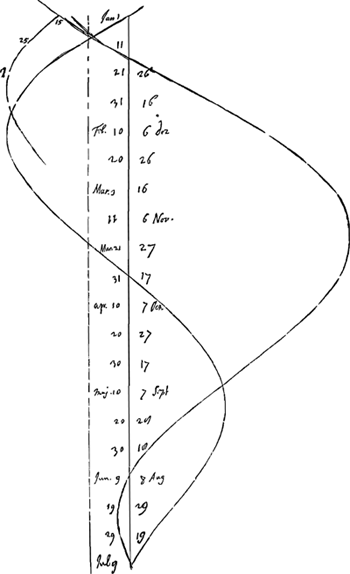
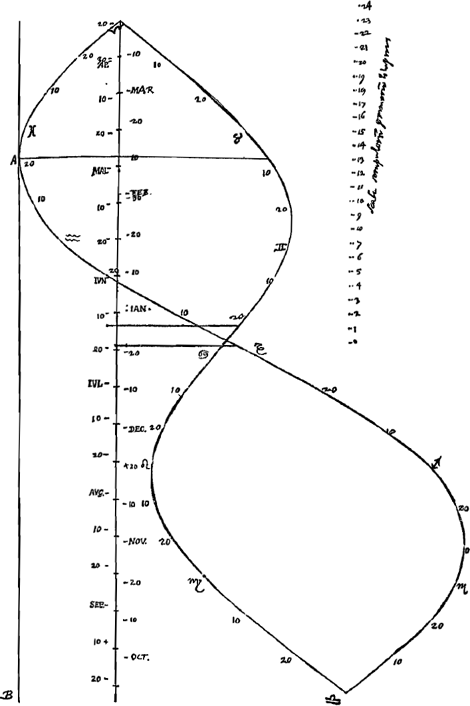
- La courbe donne une représentation graphique partielle de l'équation du temps, s'étendant du 1 janvier 1660, où l'équation est supposée nulle, jusqu'au 9 juillet de la même année, où elle devient nulle de nouveau. Consultez sur la construction et les particularités de la courbe la Fig. 2 de la page 539 et la note 1 de la p. 538.
-
voetnoot1)
- Pour pouvoir dessiner sur une seule page du Manuscrit A une représentation graphique de l'équation du temps sur une échelle pas trop petite Huygens la plie pour ainsi dire en deux, de sorte qu'à chaque point de l'axe correspondent deux dates et par suite deux valeurs de cette équation. Remarquons que les dates indiquées près de l'axe se retrouvent toutes dans les calculs du § 1. L'équation est supposée nulle au 1 janvier 1660; ensuite la courbe se tourne à gauche, indiquant que l'équation doit être soustraite du temps moyen de l'horloge pour trouver le temps vrai. Elle montre le minimum du 10 février de l'équation du temps, coupe l'axe au point qui représente le 31 mars pour indiquer ensuite un maximum correspondant au 20 mai. Huygens la continue ensuite jusqu'où elle coupe l'axe de nouveau en un point correspondant au 9 juillet, après quoi il la fait remonter, montrant le minimum secondaire de juillet et, après avoir coupé l'axe encore une fois, le maximum de la fin d'octobre, pour repasser au côté gauche de l'axe non loin d'un point correspondant au 1 janvier 1661. Enfin, afin d'enregistrer complètement les résultats pour l'année 1661 des §§ 2 et 3, Huygens la continue jusqu'en un point correspondant au 15 janvier 1661 et la fait redescendre ensuite en y ajoutant une troisième branche. Remarquons encore à ce propos que des deux dates près du même point de l'axe l'une appartient, comme nous l'avons vu, à la premîere, l'autre à la seconde branche de la courbe, de sorte que sur l'axe le 9 juillet 1660 correspond à soi-même, le 29 juin 1660 au 19 juillet 1660 et, tout en haut, le 21 janvier 1660 au 26 décembre 1660. Par suite le 1 janvier 1660 correspond au 15 janvier
1661, date qu'on trouve indiquée par le nombre 15 placé au début de la troisième branche. En effet, cette différence de 14 jours s'explique par le choix du point de rebroussement au bas de la courbe, l'intervalle du 1 janvier au 9 juillet 1660 (année bissextile) comptant 190 jours, tandis que
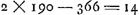 . .
Quant à la ligne interrompue parallèle à l'axe, elle désigne sans doute l'axe dont on doit se servir lorsque l'équation du temps est supposée nulle à l'équinoxe du printemps; comparez la Fig. 3 du paragraphe suivant.
-
voetnoot1)
- Voir la p. 15 de l'édition originale de l'‘Horologium oscillatorium’, ouvrage publié en 1673. L'annotation présente fut donc ajoutée après cette date.
-
voetnoot2)
- L'idée de construire une Table fondée sur ce dernier principe datait déjà de février 1662, ou de plus tôt. En effet, la Table des p. 56-57 du T. IV, envoyée à Lodewijk Huygens le 15 février et à Moray le 17 février 1662 (voir les pp. 54 et 60 du T. IV), était déjà identique à la Table de l'‘Horologium oscillatorium’.
-
voetnoot3)
- Cette figure se distingue de la précédente par ce que l'équation du temps est supposée nulle à l'équinoxe du printemps et que la longitude correspondante du Soleil est indiquée sur la courbe, la date sur l'axe. L'idée de prendre l'équinoxe du printemps comme point de départ de la table pour l'équation du temps fut énoncée par Huygens dans la lettre à Boulliau du 29 janvier 1660, p. 17 de notre T. III.
Ajoutons que l'inscription à côté de l'échelle doit être lue ‘scala scrupulorum primorum temporis.’
-
voetnoot1)
- Voir cette Table à la p. 543 et remarquons que si l'on ajoute partout aux données de cette Table 2 minutes et 2 secondes (sa voir l'équation du 28 février de la Table de l'‘Horologium oscillatorium’) elle ne diffère de celle de l'‘Horologium oscillatorium’ (qu'on trouve aussi aux p. 56-57 du T. IV) jamais plus de 3 secondes, à l'exception de la date du 11 décembre où la différence est de 4 secondes.
-
voetnoot2)
- Puisque depuis midi 29 février 1660 jusqu'à six heures de l'après-midi du 28 février 1661 on compte 36¼ jours, c'est-à-dire, à très peu près, une année tropique.
-
voetnoot3)
- Nous n'avons rien trouvé dans la Correspondance qui se rapporte à cette idée certainement
ingénieuse, et qui présente quelques avantages réels, de prendre le 28 ou le 29 février (selon les circonstances) pour point de départ d'une Table de l'équation du temps. Évidemment Huygens a bientôt abandonné cette idée en choississant pour point de départ (où l'équation est supposée nulle) l'équinoxe du printemps (voir le § 8 qui suit). Plus tard encore il préfère le choisir en sorte qu'on doit toujours ajouter et ne jamais soustraire l'équation pour déduire le temps vrai du temps moyen (voir l'annotation au-dessus de la Fig. 3 de la p. 541).
-
voetnoot4)
- Comparez le cinquième calcul de la p. 535.
-
voetnoot5)
- On lisait primitivement 2′.48″; comparez le sixième calcul de la p. 535. Nous ne connaissons pas la cause de ce changement et des autres indiqués dans les notes 6-9, 11-13, 15-19.
-
voetnoot6)
- On lisait primitivement 5.48 (comparez la liste de la p. 535), et ensuite 5.46.
-
voetnoot8)
- Primitivement 9.0; comparez la liste de la p. 535.
-
voetnoot11)
- Primitivement 16.24; comparez la liste de la p. 535.
-
voetnoot12)
- Primitivement 17.20; comparez la liste de la p. 535.
-
voetnoot13)
- Primitivement 12.44; comparez la liste de la p. 535.
-
voetnoot15)
- Primitivement 10.32; comparez la liste de la p. 536.
-
voetnoot16)
- Primitivement 13.8; comparez la liste de la p. 536.
-
voetnoot17)
- Primitivement 16.20; comparez la liste de la p. 536.
-
voetnoot18)
- Primitivement 29.48; comparez la liste de la p. 536.
-
voetnoot18)
- Primitivement 29.48; comparez la liste de la p. 536.
-
voetnoot19)
- Primitivement 6.40; comparez le premier calcul du § 3, p. 537.
-
voetnoot20)
- Comparez le deuxième calcul du § 3, p. 537.
-
voetnoot1)
- Consultez à propos de la Table qui suit la lettre à Boulliau du 29 janvier 1660 à la p. 17 de notre T. III. Nous ne connaissons pas les calculs à l'aide desquels elle a été composée. Probablement Huygens s'est servi des Éphémérides mentionnées dans la note 7 de la p. 534. Alors ces calculs auront ressemblé beaucoup à ceux des § 1-3 aux p. 534-537. La Table n'a pas été achevée, probablement parce que Huygens, pour les raisons qu'on trouve dans sa lettre à Paget du 23 octobre 1665 (p. 509-510 du T.V), s'était résolu à donner plutôt une Table arrangée d'après les jours de l'année, comme celle dont il est question dans les dernières lignes de la note 3 de la p. 542.
-
voetnoot2)
- Dans la lettre du 29 janvier 1660 à Boulliau, citée dans la note précédente, cette valeur de l'équation est donnée comme correspondant à 24o de ♑, mais parce que l'équation s'y trouve dans le voisinage d'un maximum il est clair qu'elle ne change que très peu pour un seul degré de l'écliptique. De plus, puisqu'elle change beaucoup moins de 20o ♑ à 25o ♑ que de 25o ♑ à 30o ♑ ce maximum précédait probablement la longitude de 25o ♑. La donnée en question peut donc très bien avoir été empruntée à la Table présente.
-
voetnoot1)
- Comparez la Fig. 2 (p. 539) où les maxima et les minima indiqués par la courbe correspondent à ces dates. Plus tard Huygens a ajouté ici en marge ‘25.0′.♉. 3.18.♌. 9.43.♏. 22.19♒’; voir la Fig. 3 (p. 541) et la Table de la p. 544. Remarquons toutefois que pour trouver ces longitudes avec une précision qui va jusqu'aux minutes de nouveaux calculs ont été nécessaires. En effet, pour la première de ces quatre longitudes on trouve ces calculs dans la Pièce V qui suit (voir les p. 553-556), pour les trois autres ils nous manquent.
-
voetnoot2)
- Voir dans la Fig. 2 (p. 539) le point d'inflexion qui correspond à cette date.
-
voetnoot2)
- Voir dans la Fig. 2 (p. 539) le point d'inflexion qui correspond à cette date.
-
voetnoot2)
- Voir dans la Fig. 2 (p. 539) le point d'inflexion qui correspond à cette date.
-
voetnoot2)
- Voir dans la Fig. 2 (p. 539) le point d'inflexion qui correspond à cette date.
-
voetnoot3)
- La Table de l'‘Horologium oscillatorium’ qui fut envoyée à Lodewijk Huygens le 15 février 1662 (voir les pp. 54, 56 et 57 du T. IV) donne 31′55″. Elle n'avait donc pas encore été construite lors de la rédaction du texte présent.
-
voetnoot4)
- Voici le passage en question, tel qu'ou le lit dans l'ouvrage de Copernic ‘De revolutionibus orbium coelestium, Libri VI’ de 1543 (cité dans la note 21 de la p. 9 de notre T. I) p. 96 verso-97 recto du ‘Caput XXVI: De Νυχϑήμερῳ, hoc est diei naturalis differentia’ du ‘Lib. III’: ‘Placuit autem Mathematicis diei naturalis principium non ab ortu vel occasu, sed à meridie vel media nocte accipi. Nam quae ab horizonte sumitur differentia, multiplicior existit, utpote quae ad aliquot horas sese extendit, & praeterea quod ubique non est eadem, sed secundum obliquitatem sphaerae multipliciter uariatur. Quae uero ad meridianum pertinet, eadem ubique est atque simplicior. Tota ergo differentia, quae ex ambabus iam dictis causis, cum propter Solis apparentem progressum inaequalem, tum etiam ob inaequalem circa meridianum transitum constituitur, ante Ptolemaeum quidem à medietate Aquarij diminutionis sumens principium, & à principio Scorpij accrescendo, tempora [de 4 minutes] VIII. & trientem unius [33 m. 20 s.] colligebat, Quae nunc à uigesimo gradu Aquarij vel prope, ad decimum Scorpij diminuendo: à decimo vero Scorpij ad uigesimum Aquarij crescendo, contracta est in tempora septem, scrup. XLVIII [28 m. 48 s.]. Mutantur enim & haec propter perigaei & eccentrotetis instabilitatem cum tempore. Quibus demum si maxima quoque differentia praecessionis aequinoctiorum comparata fuerit, poterit tota dierum naturalium differentia supra decem tempora se extendere sub aliquo annorum numero. In quo tertia causa inaequalitatis dierum latuit hactenus, eo quòd aequinoctialis circuli reuolutio ad medium aequaleque aequinoctium aequalis inuenta est, non ad apparentia aequinoctia, quae ut satis patuit, non sunt admodum aequalia.
Decem igitur tempora [40 m.] duplicata efficiunt horam unam cum triente, quibus aliquando dies maiores excedere possunt minores. Haec circa annuum Solis progressum caeterarumque stellarum tardiorem motum citra errorem manifestum poterant forsitan contemni. Sed propter Lunae celeritatem, ob quam in dimidio gradu & tertia possit error committi, nullatenus sunt contemnenda.’
Quant au passage correspondant des ‘Magnae Constructions Lib. XIII’ de Ptolemée (voir l'ouvrage cité dans la note 19 de la p. 8 du T. I), on le trouve dans le neuvième Chapitre ‘Περὶ τῆς τῶν νυχθημέρων ὰνισότητος (De inaequalitate dierum naturalium)’ du troisième Livre. Boulliau donne une traduction latine de ce Chapitre aux p. 78-83 de son ‘Astronomia philolaica’ de 1645; voir l'ouvrage cité dans la note 7 de la p. 230 de notre T. I.
-
voetnoot4)
- Voici le passage en question, tel qu'ou le lit dans l'ouvrage de Copernic ‘De revolutionibus orbium coelestium, Libri VI’ de 1543 (cité dans la note 21 de la p. 9 de notre T. I) p. 96 verso-97 recto du ‘Caput XXVI: De Νυχϑήμερῳ, hoc est diei naturalis differentia’ du ‘Lib. III’: ‘Placuit autem Mathematicis diei naturalis principium non ab ortu vel occasu, sed à meridie vel media nocte accipi. Nam quae ab horizonte sumitur differentia, multiplicior existit, utpote quae ad aliquot horas sese extendit, & praeterea quod ubique non est eadem, sed secundum obliquitatem sphaerae multipliciter uariatur. Quae uero ad meridianum pertinet, eadem ubique est atque simplicior. Tota ergo differentia, quae ex ambabus iam dictis causis, cum propter Solis apparentem progressum inaequalem, tum etiam ob inaequalem circa meridianum transitum constituitur, ante Ptolemaeum quidem à medietate Aquarij diminutionis sumens principium, &
à principio Scorpij accrescendo, tempora [de 4 minutes] VIII. & trientem unius [33 m. 20 s.] colligebat, Quae nunc à uigesimo gradu Aquarij vel prope, ad decimum Scorpij diminuendo: à decimo vero Scorpij ad uigesimum Aquarij crescendo, contracta est in tempora septem, scrup. XLVIII [28 m. 48 s.]. Mutantur enim & haec propter perigaei & eccentrotetis instabilitatem cum tempore. Quibus demum si maxima quoque differentia praecessionis aequinoctiorum comparata fuerit, poterit tota dierum naturalium differentia supra decem tempora se extendere sub aliquo annorum numero. In quo tertia causa inaequalitatis dierum latuit hactenus, eo quòd aequinoctialis circuli reuolutio ad medium aequaleque aequinoctium aequalis inuenta est, non ad apparentia aequinoctia, quae ut satis patuit, non sunt admodum aequalia. Decem igitur tempora [40 m.] duplicata efficiunt horam unam cum triente, quibus aliquando dies maiores excedere possunt minores. Haec circa annuum Solis progressum caeterarumque stellarum tardiorem motum citra errorem manifestum poterant forsitan contemni. Sed propter Lunae celeritatem, ob quam in dimidio gradu & tertia possit error committi, nullatenus sunt contemnenda.’
Quant au passage correspondant des ‘Magnae Constructions Lib. XIII’ de Ptolemée (voir l'ouvrage cité dans la note 19 de la p. 8 du T. I), on le trouve dans le neuvième Chapitre ‘Περὶ τῆς τῶν νυχθημέρων ὰνισότητος (De inaequalitate dierum naturalium)’ du troisième Livre. Boulliau donne une traduction latine de ce Chapitre aux p. 78-83 de son ‘Astronomia philolaica’ de 1645; voir l'ouvrage cité dans la note 7 de la p. 230 de notre T. I.
-
voetnoot1)
- Savoir 14′13″-9′9″; voir la Table de la p. 543.
-
voetnoot2)
- Savoir 5′4″ + (21′30″-18′0″); voir la même Table.
-
voetnoot3)
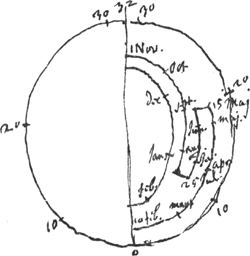
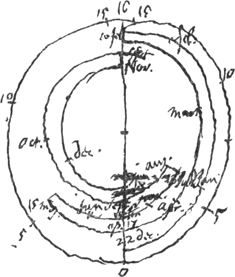
- Voir la Fig. 5, qui représente la ‘construction mechanique’, dont il est question dans la lettre de Huygens à Boulliau du 26 février 1660 (p. 25 du T. III) et ‘par la quelle’ on peut ‘scavoir incontinent combien il faut adjouster on oster de l'heure de l'horloge à chasque jour de l'an, estant donnè celuy au quel j'ay adjustè l'horloge avec le soleil ou avec un sciaterique. Ce que l'on ne peut pas faire par le moyen d'une table sans un peu de calcul ou bien elle ne servira qu'a une seule Epoche’, c'est à dire pour une seule supposition sur la date où l'équation du temps est nulle.
-
voetnoot4)
- Voir les traits marqués sur la ligne brisée, formée par des arcs de cercle et de petits segments de rayons.
-
voetnoot5)
- Ce nombre a été choisi par Huygens à propos de la plus grande valeur (31 min. 53 sec.) que l'équation du temps peut prendre dans une Table construite sur le principe indiqué à la p. 541. Il néglige la différence entre cette valeur et 32 minutes entières.
-
voetnoot6)
- Afin de compléter l'explication de cette figure, commencée dans les premières lignes de ce paragraphe, il suffira de renvoyer à la Table des p. 56-57 du T. IV. On comprendra facilement que le petit segment de la ligne brisée qui se trouve sur le rayon vertical aboutissant au point marqué o correspond à la date du 10 février, époque où l'equation du temps est nulle. De ce petit segment partent deux arcs de cercle. L'arc extérieur correspond aux dates du 10 février jusqu'au 15 mai où l'équation atteint un premier maximum de 19 min. 29 sec. Vient ensuite un petit segment menant à un arc qui s'arrête à un point qui correspond au minimum du 25 juillet de 9 min. 46 sec. Après cela suivent encore deux autres arcs dont le premier représente l'intervalle du 25 juillet jusqu'au 1 novembre lorsque l'équation atteint sa valeur maximum d'à peu près 32 min., et le second l'intervalle du 1 novembre jusqu'au 10 février de l'année suivante.
-
voetnoot7)
- Cette figure est du même genre que la précédente. Seulement elle se rapporte à une Table où l'époque, où l'équation du temps est nulle, a été choisie de sorte que cette équation varie de + 16 min. à - 16 min. De plus le cercle entier y est utilisé.
-
voetnoot2)
- La Table des p. 56-57 du T. IV donne 5 min. 52 sec.
-
voetnoot3)
- 26 min. 47 sec. d'après la Table mentionnée dans la note précédente.
|

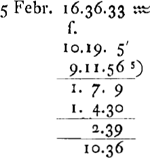
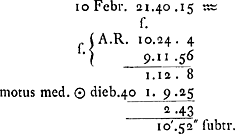
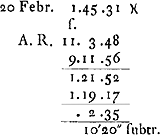
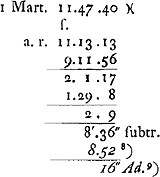
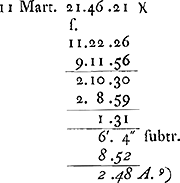
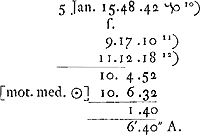
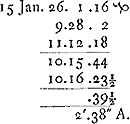
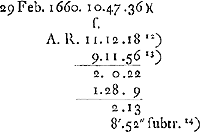
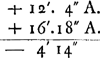
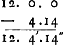 tempus apparens in meridie horologij die 7 Sept.
tempus apparens in meridie horologij die 7 Sept.