Oeuvres complètes. Tome XV. Observations astronomiques

[p. 527]

I¹⁾.
[1658?]

§ 1²⁾.

Inquirendum an aliqua sit dierum inaequalitas. nam si 12′ vel plura minuta mediò tempori addenda aliquando vel auferenda longitudinum scientia ea de causa perfecta non erit nisi vera noscatur aequatio. Haec autem ipsius horologij ope invenienda est: Quod ad medium tempus primo est componendum hoc modo. aliqua ex fixis inter duo perpendicula observetur, eo cum redierit postridie, debebit index horologij

[Fig. 1.]

non idem tempus quod in priori observatione ostendere, sed fere 3′.56½″ minus, tantumque in dies singulos. quod si aequo citius incessisse comperiatur, longiori pendulo est opus. Ergo ut quadr. temporis horologij ad quadr. temporis 24 horarum ita fiat longitudo penduli ad aliam: ea tempori medio conveniet. Cochleae³⁾ ad hoc noscenda est quantitas, quantum scilicet singulis conversionibus promoveatur. Item penduli longitudo quae alio pendulo examinari poterit aequales alteri oscillationes faciente.

1) La Pièce, que nous avons divisée en paragraphes, a été empruntée aux p. 41-44 du Manuscrit K. Huygens s'y occupe de diverses applications astronomiques de l'horloge à pendule.

2) Dans ce paragraphe Huygens se propose de donner une méthode pour déterminer expérimentalement l'équation du temps à l'aide de son horloge à pendule nouvellement inventée. Il parle d'un tel projet dans sa lettre du 1 nov. 1658 à Petit (voir la p. 272 de notre T. II), mais il ne l'a jamais exécuté et on le verra bientôt (voir la Pièce III aux p. 534-537) suivre une autre voie. Toutefois il paraît avoir réussi à vérifier à l'aide de ses horloges l'existence de cette équation et d'en contrôler la grandeur obtenue d'autre façon; voir les pp. 21, 36, 389, 438 du T. III, 71 et 134 du T. IV, 259 du T. VI et 545 du T. VII, comme aussi la p. 14 de l'édition originale de 1673 de l'‘Horologium oscillatorium’.

3) Savoir l'écrou placé au-dessous du poids du pendule, écrou qui sert à hausser ou à baisser ce poids; voir la p. 6 de l'édition originale de 1658 de l'‘Horologium’.

[p. 528]

§ 2.

Sciatericum ope nostri horologij construi posset, nulla molestia in quibusvis planis superficiebus; Mendies tantum accurate cognoscendus est; eo cum venerit sol, notanda est puncti fixi umbra, caeteris vero horis omnibus ad horologium. Hoc si diversis duobis anni temporibus fiat, per bina quaeque puncta umbrae notata, lineae horariae ducentur. Harum vero concursus stili quoque locum indicabit; stili positus legitimus erit, cum umbra ipsius aliquam ex horarijs lineis conteget.

§ 3.

Alas ut minus diu moveatur¹⁾. Pendulum breve et grave.

1) S'agit-il des petits arcs à apporter pour rendre isochrones les oscillations du pendule? Consultez la lettre du 1 novembre 1658 à Petit à la p. 271 du T. II.

§ 4.

Ex ortus solis tempore vel occasus, horam diei supputare, explorata in meridie poli altitudine. vel tabulas ad hoc conficere.

[Fig. 2.]

Supputatur hoc modo. Sicut sinus totus ad tangentem elevationis poli, ita tangens declinationis solis ad sinum arcus aequatoris: qui in tempus conversus indicat quot horis ante vel post horam sextam sol in loco observationis oriatur vel occidat²⁾. Nempe si declinatio solis et latitudo loci utraque borea est vel austrina, auferendum est tempus calculo inventum ab horis 6. ut prodeat hora exortus. Addendum vero ijsdem 6 horis ut habeatur occasus hora. At si diversa est declinatio ac latitudo loci obs.^is addendo ortus momentum; auferendo occasus prodibit. per logarithmicas sinuum tabulas expeditissimus est calculus, ut tabulis proinde non sit opus. nisi declinationis solis.

Quoniam vero non semper oriens vel occidens sol spectari potest utile foret ad nonnullas solis altitudines tabulas condi, velut si ad 3 graduum altitudinem tabula conscribatur, ex qua quovis loci, modo data sit poli altitudo cum solis declinatione, constet quota hora sit cum sol tribus gradibus supra horizontem ascendit. nam calculus hîc paulo prolixior est; quo nimirum ex tribus trianguli sphaerici lateribus

2) Soit P le pôle, Z le zénith, ☉ le soleil qui soit situé dans l'horizon, on trouve alors la règle en question en appliquant au triangle ZP☉ à côté droit Z☉ la formule: cos ZP☉ = - cot ZP × cot P☉.

[p. 529]

datis angulus horarius inquiritur. Primum latus est distantia solis à polo. alterum, distantia solis a puncto verticali, sive complementum altitudinis solis. tertium denique distantia poli à puncto verticali, hoc est, complementum poli altitudinis.

Sic item ad 6 et novem gr^.m altitudinem tabulae construantur.

Incertiores autem sunt temporis supputationes ex observationibus ijs quibus prope in meridie sol deprehensus fuerit, nisi si meridiana linea accurate explorata sit, tum enim exquisite tempus definiri poterit, observata applicatione solis ad eam lineam. Verum haec inter navigandum certo constitui non potest, nam acus magnetae illita exigua est et instabilis, et alioqui infida propter declinationem variabilem. Altitudo tamen poli satis exacte ex meridiana solis altitudine indagabitur, ut satis notum est.

In observatione solis orientis occidentisve cavendum est ne fallat refractio aeris, qua fit ut interdum ½ gradu sol sublimior spectetur. caeterum in ea orbis parte quae inter tropicos continetur parum periculi hinc esse arbitror. Si quod tamen est, resciri id potest inspecto sole per vitra nostra fumo infecta. nam si rotundus sol prope horizontem conspicitur nullam patitur refractionem. sin ellipticus fuerit pro modo ellipseos refractio aestimari poterit. Meridiana solis altitudo inprimis quotidie tentanda est, aliae autem praeter hanc altitudines eo fine annotandae, quo tempore horologij sese obtulerint, ut si forte ortus vel occasus conspici nequeat, liceat tamen instituto calculo, longitudinem ex medijs istis observationibus experari. Quanquam si tabulae ad diversas altitudines solis (ut modo dictum est) praesto sint, raro continget ut alijs observationibus quam quae ad tabulas istas pertinent sit opus.

§ 5.

Stellarum omnium situs ope horologij et binorum perpendiculorum describi poterunt si poli altitudo et meridianus loci exactè cognitus fuerit³⁾.

Primum namque ascensiones rectae facile inquirentur hoc modo aliqua ex primarijs stellis, puta canis major observetur cum ad meridianam lineam applicatur, inde prout quaeque reliquarum stellarum eodem pervenerit annotetur quanto tempore post canem majorem meridianum occupet; et convertantur temporum differentiae in gradus aequatoris. Oportet autem horologium ad mensuram

3) Huygens ajoute ici en marge: ‘Ad hanc rem etiam Wilhelmus Lantgravius horologiis usus est.’ Comparez la note 2 de la p. 521; mais remarquons que Wilhelm IV n'employa ses horloges qu'à la détermination des ascensions droites.

[p. 530]

diei stellaris accommodatum esse qui brevior est die solari medio, fere 3′56″. Sic enim cuique horae 15 gradus tribuentur. minuto temporis quindecim minuta gradus. &c. Attamen et ordinaria horologij constitutione ratio iniri potest, addendo adhuc

[Fig. 3.]

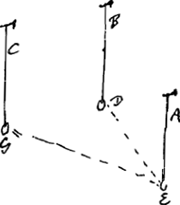
in singulas horas, 2′28″ unius gr. circ.¹⁾ in singula minuta temporis 2″28‴ gradus. Sic itaque omnium ascensiones rectae cognoscentur si una data fuerit. Porro ad declinationem stellarum inveniendam, opus est alio adhuc perpendiculo praeter id quod meridianam ostendit. Illud vero in certo angulo ad meridianam lineam disponatur, veluti si perpendicula A et B in meridianam congruant DE: aliud suspendatur C, ita ut ang. DEG sit 60 vel alio numero graduum. Hoc facto observetur quo temporis intervallo secundum horologium, stella aliqua a meridiano circulo perveniat eousque ut contegatur à duobus simul perpendiculis, A, C. Vel primum ab his contecta, quanto post tempore tegatur à duobus simul A, B. Idem in quotcunque stellis inquiratur, ac deinde calculus instituatur ex hoc fundamento. Sit [Fig. 4] in sphaera descripta meridianus circulus PZA. Poli P et A. AEquator AEQ, horizon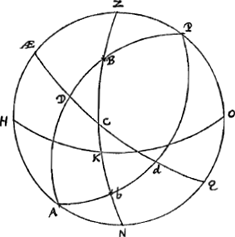

[Fig. 4.]

HO. Altitudo poli OP exempli gr. 52.5′ quanta hic Hagae est. ZKN verticals circulus. arcus HK ponatur ex gr. 60. grad. Stella aliqua B observata sit, ope perpendiculi, in circulo verticali ZKN, hora 7^a vespertina, ad horologium diei solari medio adaptatum. hora autem 9^a in meridiano circulo PZH. Hinc declinatio stellae ut supputetur designetur per polos P, A et stellae locum B circulus PDA, secans aequatorem in D. Est igitur declinatio stellae arcus BD, qui sic invenitur. Primum in triang. ZAEC datum est latus ZAE aequale PO, hoc est 52.5′. adhoc angulus Z gr. 60 quoniam totidem est arcus

1) En effet, la rotation de la sphère céleste s'élève à 15^o (1+1/365¼), soit 15^o2′28″ par heure de temps moyen.

[p. 531]

HK. Rectus autem ang. AE. Itaque fit ang. C. gr. 57.51²⁾. latus vero AEC gr. 53.48′³⁾. Quia vero punctum aequatoris D simul cum stella B ad meridianum accedit. necesse est arcum DAE esse 30 gr. 4′56″ quoniam duabus horis praeterlabitur ut constat ex ante dictis⁴⁾. Arcus autem AEC inventus est gr. 53.48. Itaque DC gr. 23.43′. Sed in triangulo DBC etiam cognitus est ang. DCB gr. 57.51′ et ang. D est rectus. Itaque hinc facile invenitur latus DB⁵⁾, quod exhibet declinationem stellae quaesitam. Cum autem austrina est stellae declinatio qualis b, auferendus est arcus AEC ex AEd qui ex temporis quantitate innotuit, et reliqua eodem modo exequenda. Notandum quod arcus AEC, itemque angulus ZCAE semper ijdem maneant quamdiu eodem perpendiculorum situ ad observandum utimur.

Inventio anguli AECZ. per logar.

sin. totus ad sin. compl. lateris ZAE 52.5′, ut sin. ang. AEZC gr. 60 ad sin compl. ∠ AECZ

Inventio lateris AEC.

sin. totus ad sin lateris ZAE. 52.5′. ut tang. ang. AEZC 60′⁶⁾ ad t. lat. AEC.

2) Voir le premier des calculs qui suivent.

3) Voir le deuxième calcul.

4) Comparez les premières lignes de la p. 530.

5) Voir le calcul de la p. 532.

6) Lisez: 60^o.

[p. 532]

Invent. lateris DB in ∆DBC.

¹⁾²⁾

Brevius haec absolvi poterant considerando tantum ∆^oZPB. In quo dantur angulus Z 120 gr. Angulus P 30.4′.56″. et latus ZP. 37.55′. unde noscitur latus PB, cujus complementum BD est stellae declinatio quaesita.

Ricciolus alios modos investigandi declinationes huic praefert³⁾; nescio quare. nam refractionis certè hic nullum incommodum est⁴⁾.

1) Comparez la l. 3 de la p. 531.

2) Lisez: 32^o37′.

3) Dans le ‘Caput XI. De Fixarum Declinatione & Ascensione Recta obseruandis, aut ex observatione colligendis’ du ‘Liber sextus’ du T. I de l'‘Almagestum novum’ Riccioli décrit (p. 431-432) diverses methodes pour déterminer les déclinaisons des étoiles sous les suscriptions suivantes: Problema 1. Data Vera Altitudine Meridiana Sideris, & Altitudine Poli, Declinationem eiusdem Sideris Inquirere; Problema 2. Declinationem Sideris Inuestigare, Data Poli Altitudine, & obseruatis Sideris Altitudine & Azimutho vero; Problema 3. Declinationem Sideris Inquirere, Data Poli Altitudine, & obseruatis aut Altitudine vera & momento Temporis; aut Azimutho & momento Temporis.
Comme on voit la méthode décrite par Huygens est conforme à la dernière des méthodes mentionnées par Riccioli (savoir la deuxième du ‘Problema 3’) et la seule de ses méthodes qui est indépendante de la réfraction atmosphérique. Or, à la p. 432, Riccioli s'exprime comme suit sur les mérites relatifs des méthodes en question: ‘Sed suadeo vt Declinationes Fixarum capias per Problema 1. vt nos fecimus, potiùs quam per 2. aut si quando non possis illo vti, vtaris secundo potiùs quàm tertio.’

4) Quoique Huygens ne possédàt encore, pendant la rédaction de la Pièce présente (voir le dernier alinéa du § 4), que des notions assez vagues sur la réfraction atmosphérique, on voit combien d'importance il attachait à l'élaboration d'une méthode indépendante de cette source d'erreurs.
Ajoutons qu'on trouve la description d'une méthode analogue, fondée cette fois sur l'emploi d'un instrument inventé par O. Römer pour observer les passages par le premier vertical, dans l'ouvrage de Horrebow ‘Basis astronomiae sive Astronomiae pars mechanica, in qua describuntur observatoria, atque instrumenta astronomica Roemeriana Danica; simulque eorundem usus, sive methodi observandi Roemerianae,’ etc. (Voir les p. 237-239 du T. III des ‘Opera mathemarico-physica Petri Horrebowii, Havniae, 1741, sumptibus Jacobi Preussii.’) Au § 480 (p. 239 des ‘Opera’) il est proposé de déterminer la grandeur de la réfraction à diverses hauteurs au-dessus de l'horizon par la comparaison des déclinaisons trouvées par cette méthode (sur laquelle ou peut consulter encore la p. 521 de l'‘Avertissement’ qui précède) avec celles obtenues par l'observation directe au cercle méridien.