Logo DBNL
Oeuvres complètes. Tome XV. Observations astronomiques (1925)

Oeuvres complètes. Tome XV. Observations astronomiques

(1925)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Avertissement.

Les Pièces I-XII, qui suivent, sont des notes d'importance très inégale, que l'on trouve disséminées dans les Manusscrits A, B, C et K1); elles datent de la première période d'activité astronomique de Christiaan Huygens à la Haye.

Il y traite des questions de portée diverse, au fur et à mesure que tel ou tel sujet l'occupe; tantôt le désir d'appliquer sa belle invention des horloges à pendule à la détermination de la longitude le conduit à des recherches étendues sur l'équation du temps2), tantôt ce sont des observations ou des études théoriques de ses contemporains qui lui fournissent son sujet, tantôt enfin l'origine de la Pièce est moins évidente.

Ainsi on le voit s'intéresser à la dépression de l'horizon (Pièce II)3), à la position de Mercure d'après les tables de la ‘Nederduytsche Astronomia’ de

Rembrantsz. van Nierop (P. IV)1), au rapport entre le temps solaire moyen et le temps sidéral (P. VI)2), au cadran solaire (P. IX)3), à la période synodique des planètes (P. X)4), au diamètre apparent de l'ombre de la terre à l'endroit où la lune la traverse (P. XI)5), à l'ombre des satellites de Jupiter (P. XII)6).

L'avant-dernière question fut déjà discutée par Hipparque, qui déduisit la relation remarquable q + S = p + P, où q est la moitié du diamètre en question, S le demi-diamètre apparent du Soleil, p + P la somme des parallaxes horizontales de la Lune et du Soleil. Comme Huygens place le Soleil à l'insini - ‘immensa distantia’ - la formule se réduit à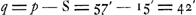 illustratie, d'où l'on obtient 1o24′ pour la valeur cherchée7).

 

La Pièce IV8) nous est une véritable énigme. Dans quel but Huygens a-t-il voulu connaître la longitude de Mercure le 23 novembre 1644 à 7 heures du matin? Ce calcul a-t-il quelque rapport avec le passage sur le disque du Soleil qui a eu lieu au commencement de novembre de cette même année? Huygens a-t-il eu l'intention d'étudier par avance le passage du 3 mai 1661 qui plus tard l'a intéressé si vivement9), et a-t-il, asin de s'y préparer, commencé par le calcul d'une position quelconque de Mercure suivant l'‘Astronomia’ de van Nierop10)? Ou a-t-il voulu simplement soumettre à une épreuve l'exactitude de sa ‘tabula lignea’?11).

Et pourquoi a-t-il choisi l'ouvrage de van Nierop pour le calcul en question? Il est vrai qu'il s'en était servi en 1658 pour le calcul de la position de Saturne, mais bientôt après il en avait abandonné l'usage pour l'emploi des Éphémérides12).

Comment expliquer enfin la négligence avec laquelle les calculs ont été exécutés comme en témoignent les erreurs et les contradictions qu'ils contiennent13)?

Nous ne savons pas répondre à ces questions.

Toutefois, il convient de nous occuper un moment, sans entrer dans les détails, de la méthode plutôt grossière dont van Nierop se sert pour le calcul du lieu géocentrique des planètes. À son avis14) on peut se dispenser de la théorie correcte, mais compliquée et laborieuse, de Kepler et s'en tenir à l'idée des anciens astronomes que les planètes se meuvent uniformément autour du ‘Punctum aequans’; ce qui permet d'employer dans le calcul les longitudes moyennes.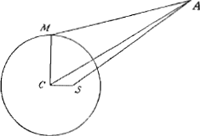



illustratie

Soit donc dans la figure ci-contre A la Terre, S le Soleil, M Mercure et C le centre de l'orbite de cette planète. On trouve évidemment la position géocentrique AM de Mercure en partant de la longitude du Soleil, déterminée par AS, et en appliquant deux corrections, savoir la ‘middelpuntsachtring’ SAC, qui détermine la direction AC, et l'élongation MAC (dite ‘wechsachtring’) tabulée à l'aide de l'angle MCA pour la valeur maximum de la distance CA. Pour la valeur minimum de cette distance il faudra augmenter l'élongation d'un certain accroissement (‘toevoeging’) dont on prendra dans les cas intermédiaires une partie proportionnelle à l'‘indeiling’. Pour plus dedétails nous renvoyons à l'ouvrage en question.

 

Les Pièces I, III, V, VII et VIII sont plus intéressantes que les autres. Huygens, ardent observateur en ces jours, fournit des contributions importantes à l'Astronomie Pratique, Science qui avait pris un nouvel essor depuis l'invention de la lunette. En effet, nous savons que Huygens joua un rôle prépondérant dans les progrès de cet instrument: non seulement il tailla de ses propres mains, en collaboration avec son frère Constantyn, de nombreuses lentilles, mais encore

il fit des recherches profondes sur la théorie de la dioptrique1). Ce n'est pas tout. Poussé par le désir de connaître les diamètres des planètes, il ajouta aux lunettes des micromètres de construction diverse2). Enfin, en 1657, il dota l'humanité en général, l'Astronomie en particulier, de son invention de l'horloge à pendule, suivie, dix-huit années plus tard, de l'horloge à balancier; inventions qui le remplirent de joie et dont il était fier3). Et pour cause! ‘Par cette invention précieuse [l'horloge à pendule] il commença la grande révolution [dans l'Astronomie Pratique] qui fut complétée quelques années après par l'application des lunettes aux instruments astronomiques’4).

En effet, grâce à l'heureuse idée de placer des fils dans le foyer de l'objectif, Auzout et Picard réussirent, en 1667, à substituer, pour fixer la direction exacte d'un astre observé, la lunette aux pinnules en usage jusqu'alors.

Mais retournons à l'époque de l'invention de l'horloge à pendule.

Immédiatement après cette invention, Huygens s'efforce d'appliquer le nouvel instrument aux observations astronomiques. En 1658 il détermine grâce à lui le champ d'une de ses lunettes5), ce qui lui fournit son premier micromètre. Ensuite, pour pouvoir appliquer les horloges à la détermination de la longitude, comme il en avait eu l'intention dès l'abord6), il entreprend une étude de l'équation du temps, sur laquelle nous reviendrons plus loin. Enfin, ce qui n'est pas moins important, son invention de l'horloge à pendule met les astronomes à même de remplacer la mesure des hauteurs par l'observation des passages7), et c'est précisément cette nouvelle méthode qui allait développer l'Astronomie Pratique d'une manière tout-à-fait imprévue dans la seconde moitié du dix-septième siècle. En effet, on sait que, vers 1689, l'illustre astronome danois Ole Römer construisit l'instrument de passage, précurseur du cercle méridien8), et que c'est encore Römer qui au moyen des passages de Véga et de Sirius essaya de trouver la parallaxe annuelle de ces deux étoiles.

Quant à la mesure des hauteurs, elle était peu exacte en 1658. D'une part on avait toujours recours aux pinnules pour fixer la direction de l'astre observé, la lunette directrice n'ayant pas encore été inventée, comme nous l'avons vu; d'autre part on se méfiait beaucoup des valeurs obtenues à cause de la réfraction9), phénomène peu connu, dont l'astronome Alhazen avait donné la première idée encore assez vague, et que Tycho Brahé prétendait encore différer pour le Soleil, la Lune, et les étoiles. Bien que Kepler reconnût le vrai caractère de la réfraction10), on n'en avait vers le milieu du dix-septième siècle que des notions assez incorrectes et un peu naïves. Elle ne serait pas à redouter dans les régions équatoriales de la terre11). Elle n'aurait pas grande importance quand le soleil se montre circulaire et dans le cas d'un soleil elliptique, la valeur même de l'ellipticité mettrait en état d'évaluer la réfraction12). Idée bien ingé-

nieuse mais qui fait voir comment, en 1658, Huygens se trompa sur la portée du phénomène.

Ce n'est qu'en 1662 que J.D. Cassini construisit une table détaillée de la réfraction1), basée sur la loi des sinus; mais l'incertitude sur les meilleures valeurs à prendre demeurait très grave. Pour une distance zénithale de 45o on trouve les valeurs 47″ (Kepler), 59″ (Cassini), 71″ (La Hire), etc., tandis que la plupart des astronomes (van Lansbergen, Gassendi, Riccioli, Hevelius, van Nierop) admettent, comme Tycho Brahé, que la réfraction ne commence à devenir sensible qu'au-dessous de 45o.

Il semble que même après l'application de la lunette aux instruments astronomiques l'incertitude de la réfraction ait encore retardé le développement de l'art de mesurer les hauteurs. On avait, il est vrai, pour déterminer l'heure une méthode à peu près indépendante de la réfraction. C'était la méthode des hauteurs correspondantes, appliquée dès l'antiquité, mais il fallait qu'il y eût un assez long laps de temps entre les deux observations, celle de l'Est et celle de l'Ouest, et on n'était sûr ni de la constance de l'instrument et de sa position, ni, ce qui comptait davantage, de l'état de l'atmosphère.

Le passage d'une étoile par un plan vertical est absolument indépendant de la réfraction, et c'est bien un des plus grands avantages de cette méthode, qui du reste est simple et, depuis que l'on dispose des horloges à pendule, très exacte. Dans le cas où le plan vertical est celui du méridien, l'observation des passages d'une étoile brillante et du Soleil fournit l'ascension droite de cette étoile (celle du Soleil étant calculée à l'aide de la déclinaison supposée connue), d'où l'ascension droite de toute autre étoile peut être déduite en observant la différence des temps de passage à l'aide d'une horloge réglée sur le temps sidéral2).

On sait que la méthode d'établir des instruments fixes notamment dans le méridien était déjà pratiquée par les astronomes arabes au moyen âge, et

qu'elle fut persectionnée par Tycho Brahé, dont le colossal quadrant mural sournissait des observations d'une précision inconnue auparavant.

Huygens reprend l'idée, mais il lui donne une extension importante et remarquable3). Deux perpendiculaires A et B devaient fournir le plan du méridien4); il en ajoute une troisième C, située dans un azimut de 60o par rapport à A, et il démontre que l'observation du passage d'un astre par les deux plans AB et AC ne donne pas seulement l'ascension droite mais encore la déclinaison de l'astre.

L'idée de Huygens ne s'est pas réalisée tout de suite, que nous sachions5), et ce n'est que vers 1689, trente ans plus tard, que Römer construisit son instrument de passage qui pouvait être orienté, soit dans le méridien, soit dans le plan du premier vertical. Il est vrai que Römer ne semble avoir destiné le second instrument6) (celui qui se mouvait dans le premier vertical) qu'à la détermination de la déclinaison du Soleil7), notamment lors de son passage par les équinoxes (ce qui explique la dénomination ‘Instrumentum aequinoctiorum’), mais il n'en est pas moins vrai que dès ce temps l'Astronomie possède un instrument et une méthode permettant de déterminer d'une manière générale les déclinaisons par passages au lieu de hauteurs. D'ailleurs la méthode n'a guère été employée et tomba bientôt dans l'oubli, jusqu'à ce que Bessel la fit revivre en 18248).

Or, Huygens a aussi contribué au perfectionnement, tant théorique que pratique,

de la mesure des hauteurs. À notre connaissance il fut le premier à remarquer que pour la détermination de l'heure, la plus grande précision est atteinte dans le premier vertical1), où, comme il le démontre, la distance zénithale d'une étoile varie le plus rapidement possible par rapport au temps, et cela indépendamment de la déclinaison.

En outre, le problème, très discuté à cette époque, de la détermination de la longitude sur haute mer éveille son intérêt pour l'arbalète, instrument portatif de vieille date, servant à mesurer la hauteur du Soleil. Huygens se rend compte2) des désavantages sérieux de cet instrument grossier, soit sous la forme d'une simple croix à bras mobile, soit transformé de manière à permettre à l'observateur de tourner le dos au Soleil en mesurant sa hauteur3). D'une manière ingénieuse Huygens réussit à ébaucher un instrument portatif qui semble exempt des principaux défauts des arbalètes ordinaires; dans le Manuscrit B cet instrument est représenté sans description4). Nous reproduisons ici cette figure en y ajoutant, pour faciliter l'explication, quelques lettres, quelques lignes interrompues et l'indication 50o.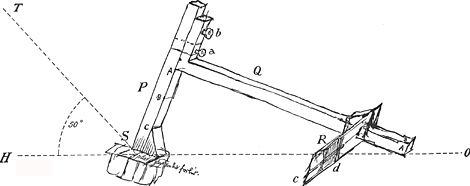



illustratie

La pièce coudée Q peut être fixée, au moyen de deux vis a et b, perpendiculairement sur le bras P, dans trois positions, A, B, C. La pièce R glisse sur Q; on y voit une fente c couverte à moitié par le verre noir d. L'oeil de l'observateur, placé en O, regarde l'horizon de la mer à travers la fente (direction OH) et

reçoit en même temps le rayon lumineux provenant du Soleil et réfléchi par le ‘plat glas sonder foelie’5) S sur le verre noir d. Dans le cas représenté par la Figure la hauteur du Soleil est de 50o environ; évidemment la moitié de cet angle, soit 25o, se calcule à l'aide du rapport des longueurs lues sur P et Q. Pour la mesure de plus petites hauteurs on place la pièce Q dans les positions B ou C.

 

Nous avons déjà dit6) que le désir d'appliquer ses horloges à la détermination de la longitude a poussé Huygens vers des études étendues sur l'équation du temps.

Vers le milieu du dix-septième siècle la détermination de cette équation était encore un sujet de controverse. On sait qu'elle peut être considérée pratiquement comme la somme algébrique de deux corrections dont l'une, la ‘réduction à l'équateur’, est causée par l'inclinaison de l'écliptique sur l'équateur, et l'autre, l'‘équation du centre’, par l'excentricité de l'orbite terrestre. Tycho Brahé dans la ‘Tabula aequationis temporis’ qu'on trouve dans ses ‘Astronomiae instauratae progymnasmata’7) ne s'occupe que de la première de ces deux causes, Kepler tient compte de toutes le s deux dans ses ‘Tabulae Rudolphinae’8), Boulliau dans son ‘Astronomia philolaica’ prétend qu'on ne doit compter qu'avec la moitié de l'équation du centre9).

Or, Huygens n'hésite pas dans l'attitude à prendre envers ces théories. Il écrit à Boulliau le 21 février 1660 qu'il s'est déja aperçu clairement à l'aide de ses horloges de l'inégalité des jours et qu'il croit même qu'à l'avenir il pourra la mesurer ‘et demonstrer par expérience qu'il saut joindre les deux causes entieres, des quelles vous rejettez la moitiè de l'une’1).

Lorsqu'en janvier 1660 il commence la construction d'une Table de l'équation du temps, il suit d'ailleurs une méthode différente de celles de ces prédécesseurs en se basant sur les éphémerides de Hecker2), calculées d'après les Tables dites Rudolphines de Kepler. Cette méthode est si simple qu'il ne semble pas nécessaire de l'expliquer ici; on la trouve appliquée dans la Pièce III, p. 534-537. D'ailleurs Huygens lui-même en a donné une exposition admirable dans une Pièce envoyée à Petit en mai 16623).

Tandis que Boulliau prétendait que l'équation du temps avait son ‘Epoque’ naturelle4), Huygens soutient que le choix du point de départ, où l'équation est supposée nulle, n'a aucune importance puisqu'il s'agit seulement des différences de l'équation de jour en jour. Aussi prend-il d'abord le 1 janvier pour l'époque5), plus tard le jour de l'équinoxe du printemps6), ensuite, afin de se

débarrasser de la complication des années bissextiles, le 29 février7). Enfin le plus rationnel lui paraît de faire coïncider le temps moyen et le temps vrai au 10 février ou bien au 1 novembre, dates où l'équation du temps atteint ses valeurs extrêmes8). C'est, en effet, sur cette considération qu'il fonde sa Table définitive, qu'on rencontre dans l'‘Horologium oscillatorium’9), où l'équation s'annule au 10 février.

D'après cette Table la plus grande valeur de la correction à apporter au temps moyen pour le réduire au temps vrai est de 31m 55s10). Au 10 février et au 1 novembre, aussi bien qu'au 14 mai11) et au 25 juillet, dates d'un maximum et d'un minimum plus faibles, le jour vrai égale le jour moyen. Du 10 février jusqu'au 14 mai11) et du 25 juillet jusqu'au 1 novembre le jour vrai est plus court que le jour moyen, tandis qu'il est plus long pour le reste de l'année. Le 18 septembre le jour vrai a une durée minimum, tandis que le 25 décembre la durée est maximum12).

La Pièce III aboutit13) à la description d'un instrument qui peut servir à trouver sans calcul la correction à apporter à l'heure de l'horloge pour en déduire le temps vrai14).

Dans la Pièce V (p. 553-556) Huygens discute, d'un point de vue théorique, le problème de trouver, notamment au printemps, la date où le mouvement du Soleil en ascension droite passe par sa valeur moyenne. À cette date, où le jour vrai égale le jour moyen, l'équation du temps atteint, comme nous venons de le constater, une valeur maximum. Si le Soleil possédait une vitesse uniforme le long de l'écliptique, la solution du problème serait donnée par la règle de l'astronome Geber: cos2 δ = cos ε1), où ε est l'inclinaison de l'écliptique sur l'équateur et δ la déclinaison du Soleil à la date cherchée. À cause de l'irrégularité du mouvement solaire le problème devient plus compliqué et doit être abordé par la méthode des approximations successives; le résultat obtenu de cette manière par Huygens est 55o o′ pour la longitude cherchée2), ce qui correspond assez bien avec la date du 15 mai trouvée auparavant dans la Pièce III3).


Vorige Volgende