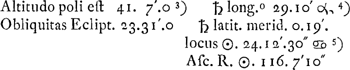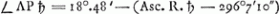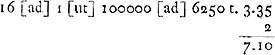Oeuvres complètes. Tome XV. Observations astronomiques

[p. 383]

Appendice IX¹⁾
À l'ouvrage: ‘Systema Saturnium’.
1667.

[Première Partie.]²⁾

1667.

Parisijs 16 Jul. h. 13.15′ a meridie. Saturni major diameter observabatur parallela horizonti. quaeritur quo angulo inclinata fuerit ad parallelum aequatoris per ♄ transeuntem. Item quo angulo planum annuli Saturnij inclinetur ad planum aequatoris, et ad planum Eclipticae.

³⁾⁴⁾⁵⁾

Tempus a meridie reductum in gr. aequ. 198.48′.0⁶⁾ ∞. 18.48′ + 180^o.

1) Dans cet Appendice nous réunissons des travaux de Huygens concernant l'observation de Saturne du 16 juillet 1667. On peut consulter encore à propos de la même observation les p. 139-142 du T. VI et la p. 93 du Tome présent.

2) Nous commençons par reproduire les p. 192-193 du Manuscrit C, où l'on trouve outre les données de l'observation, un exposé des calculs à exécuter pour déduire de ces données e.a. l'angle de la ligne des anses avec une parallèle à l'équateur ainsi que les angles du plan de l'anneau avec ceux de l'écliptique et de l'équateur terrestre.

3) Lisez 48.53′.0 (= 90^o-41^o7′.0″), puisqu'il s'agit de la latitude de Paris.

4) Savoir 299^o10′ de longitude.

5) Savoir 114^o12′30″ de longitude.

6) L'heure de l'observation étant 13^h 15^m, on trouve 198^o45′; mais comparez la p. 139 du T. VI. Pourquoi ‘les 3′’ furent-elles ajoutées? Nous n'avons pas su en découvrir la raison. Remarquons toutefois qu'à la page citée le calcul est fait comme s'il y avait 198^o45′.

[p. 384]

[Fig. 1.]

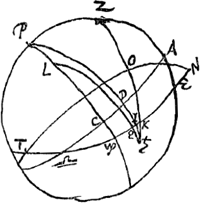
Sit PZA merid. A♎ aequator E♎ eclipt. P polus aequ. L. polus eclipt. PL♑ colurus solstitij. ♄ locus Saturni. Q locus ♄ ad eclipt. reductus.

Oportet primum invenire arc. P♄.

In ∆^oLP♄, datur latus LP 23.31′.0. Et latus L♄ 90.19′. Et ang. PL♄ qui est compl. ad 2 rectos ∠ⁱ♑LQ 29.10′. Ergo ∠ PL♄ 150.50′. hinc ergo invenietur latus P♄.

In eodem ∆PL♄ invenietur et ∠ P. cujus mensura est arc. CD, qui additus ad C♎ indicat asc. r. ♄¹⁾.

Gradus AEquatoris oppositus asc. r. ☉²⁾ est 116.7′.10 [+] 180 [∞] 296.7′.10″, qui ablatus ab asc. r. ♄ relinquet.... qui ablati ab 18.48′ qui respondent 1 h. 15′ reliquum erit ∠ AZ♄³⁾. ergo datur et ∠ PZ♄⁴⁾, et ∠ PZ⁵⁾ 41.7. et latus P♄. Ergo invenietur ang. P♄Z, qui est idem quo major diam. ♄ inclinatur ad parall. aequatoris.

In ∆PL♄ invenietur et ang. ♄, qui additus ad ∠ P♄Z facit ∠ Q♄K sed et latus Q♄ datum est 19′. et ∠ KQ♄ est rectus. Ergo invenitur et ∠ QK♄, unde OKN. Itemque invenietur latus QK. Quo ablato à QN quae data est cum N sit gr. 20.30′. ♓⁶⁾. Ergo in ∆OKN rectang.^o ad O⁷⁾, datur preterea latus KN et ∠ K. Ergo invenietur et ∠.N, quo planum annuli inclinatur ad planum Eclipt.

Nota NOT esse circulum magnum quem facit planum annuli ♄ⁱ productum, qui circulus necessario ad ang. rectos secare debet circulum azimut ZO, quia diam. saturni magna eundem azimut ad ang. rectos secare cernebatur.

Hoc modo calculus exactus instituendus esset. Sed cum latitudo ♄ⁱ 19′ tuto negligi possit, cum neque observatio prorsus exquisita haberi queat, considerare licebit ♄^m tanquam in ecliptica positum, ac tum calculus multo fit brevior.

1) Savoir en ajoutant 180^o.

2) Il s'agit de l'ascension droite du point de l'écliptique opposé au soleil.

3) Lisez AP ♄. On a en effet

4) En vérité cet angle n'est pas encore connu, mais on connaît dans le triangle PZ ♄, l'angle ZP ♄ et les côtés P ♄ et PZ , ce dernier étant égal au complément de la latitude de Paris.

5) Lisez plutôt arc. PZ.

6) TN représente le plan parallèle à l'anneau de Saturne; voir pour la longitude du noeud N le deuxième alinéa de la p. 327. On a ♑N = 80^o30′, mais ♑Q = 29^o10′ et par suite QN = = 51^o20′.

7) Huygens va le démontrer dans l'alinéa suivant.

[p. 385]

[Fig. 2.]

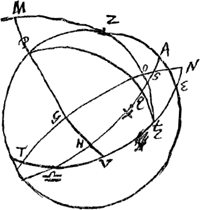
Quaeratur⁸⁾ ♄ⁱ declinatio ♄Q, quae addita ad QP 90^o. dat arcum ♄P.

Quaeratur et ☉ asc. R. cui addetur 180^o. et habebitur punctum X notans asc.^m R. loci soli oppositi Quae auferatur ab asc. R. ♄ⁱ. fit arcus aequacoris XQ. Sed AX est 18.48′. quia est hora 1¼ post mediam noctem⁹⁾. Ergo auferendo XQ ab AX relinquetur arc. QA qui mensurat ∠ APQ.

Jam in ∆PZ♄ notus est ∠ P. et latera PZ 41.7′ et P♄. Ergo invenietur ∠ P♄Z, quo ♄ major diameter inclinatur ad parallelum horizontis¹⁰⁾.

Porro in ∆♎♄Q rectangulo ad Q, datur latus ♎♄ et latus Q♄. unde invenitur ∠ ♎♄Q. cui additus P♄Z, facit ∠ ♎♄O unde et ∠ O♄N dabitur. Sed et latus ♄N datur, cum N sit in gr. 20.30 ♓. et ∠ ♄ON est rectus. Ergo invenitur et ∠ ♄NO quo planum annuli inclinatur ad planum eclipticae.

Denique in ∆♎NS, quia datur ∠ N et ∠ ♎ 23.31′. et latus ♎N, invenietur et ∠ S. unde et ∠ TS♎ datus erit, quo planum annuli inclinatur ad planum aequatoris.

Producatur azimut ♄OZ, qui transibit per polum circuli NOT aequatoris ♄ⁱ. Sit is polus M. Et ducatur circulus magnus MPGHV. qui necessario secabit ad angulos rectos tum aequatorem ♄ⁱ NOT, tum aequatorem telluris ♎A, videlicet in G et H. Occurrat autem eclipticae in V. Ergo hoc loco positus ♄, habebit majorem diametrum aequatori parallelam. itemque in puncto eclipticae huic opposito. Ad inveniendum vero punctum V in ecliptica, quaerendum latus S♎ in ∆♎NS; à quo ablato arcu SH (qui necessario est 90^o. quia circulus MGH secat in G et H ad ang. rectos circulos SG, SH) relinquitur arcus H♎. Et ∠ H♎V datus est 23.31′. et ∠ H rectus. ergo invenietur hypotenusa ♎V, atque ita punctum V datum erit.

Ut autem inveniatur quibus duobus eclipticae locis saturni major diam. maxime inclinabitur ad parallelum aequatoris¹¹⁾ quaerenda puncta circiter quadrante circuli ab V et illi opposito distantia ad quorum singula ductis magnis circulis a polis P et M, hi faciant angulos maximos ad dicta puncta. quae puncta nequaquam praecise distabunt quadrante eclipticae a punctis V et illi opposito. Neque etiam sibi

8) Dans cet alinéa et les deux suivants Huygens reprend les calculs qui précèdent dans la supposition simplifiée que Saturne se meut dans l'écliptique.

9) Comparez la note 6 de la p. 383.

10) Lisez ‘aequatoris’.

11) Il s'agit donc maintenant du problème mentionné dans la note 1 de la p. 372 qui précède; mais cette fois il se présente dans sa forme la plus générale puisque, dans le cas présent, les distances des pôles de l'équateur terrestre et du plan de l'anneau au pôle de l'écliptique ne sont plus supposées égales.

[p. 386]

mutuo erunt opposita. Et majori angulo poterit inclinari magna illa diameter ad parallelum aequatoris quam est ang. GSH.

[Deuxième Partie.]¹⁾

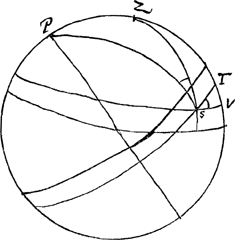[Fig. 3.]

16 Jul. h. 13, m. 15 a meridie Saturni major diam. parallela horizonti observabatur. quaeritur quo angulo inclinata fuerit ad parallelum aequatoris per Saturnum transeuntem.

Sit PZV meridianus, P polus. Z zenit S locus Saturni in 29.10′ capric.²⁾

TS parallelus aequatoris.

VS parallelus horizontis.

Quaeritur ergo angulus TSV, cui aequalis ang. ZSP. nam PST et ZSV sunt recti. a quibus demto communi ang. ZST, supersunt aequales inter se TSV, ZSP.

locus solis in 24.10′. Cancri³⁾ unde inv. angulus ZPS, 13.30′⁴⁾ et fit ∠ ZSP sive TSV 8.49′.

Cum in meridiano circulo esset Saturnus, capiebatur utcunque angulus quem longior diameter faciebat cum horizonte grad. 7.10′ ut proinde eundem quoque cum aequatore fecerit⁵⁾.

1) Dans cette deuxième Partie, empruntée à une feuille séparée, Huygens expose deux méthodes différentes pour calculer, à l'aide des données de l'observation du 16 juillet 1667 (voir la p. 383), les angles du plan de l'anneau de Saturne avec l'écliptique et l'équateur. La deuxième de ces méthodes est identique à celle de la première Partie; mais cette fois Huygens a noté plusieurs fois la valeur numérique des arcs et des angles. On trouve aux p. 180-183 du Manuscrit C des traces, très confuses et difficiles à reproduire, des calculs qui ont amené ces valeurs.

2) Savoir 299^o10′ de longitude.

3) Savoir 114^o10′ de longitude.

4) Voir pour la méthode de calcul de cet angle et du suivant le deuxième et le troisième alinéa de la p. 385.

5) Nous n'avons pas rencontré dans les Manuscrits une telle observation exécutée lorsque Saturne se trouvait dans le méridien. Quant à la valeur de 7^o10′, on rencontre à la p. 180 du Manuscrit C le petit calcul qui suit:







Ajoutons qu'à la même page on rencontre une figure analogue à notre Fig. 3; mais où l'angle TSV est bissecté par un grand cercle du sphère.

[p. 387]

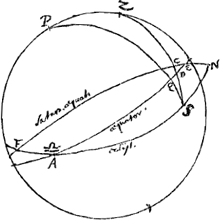
Sit porro inquirendus angulus quo planum annuli Saturnij, sive Saturni aequator, inclinatur ad aequatorem nostrum; et ad Eclipticae planum. Constat ex

[Fig. 4.]⁷⁾

ijs quae in Saturni Systemate examinavi, planum annuli secare eclipticam in gr. 20.30′ virg. et ♓⁶⁾.

Sit AE aequator; FS ecliptica; in qua Saturnus ponatur in S, nam exiguae latitudinis min. 19. rationem non habemus. Princ. librae in A.

Quia autem Saturni major diam. in S parallel. cernebatur horizonti, necesse est planum annuli secare azimut ZS ad angulos rectos. Sit ergo circulus magnus secundum planum annuli, sive aequator Saturni FC. secans aequatorem nostrum in E. Ergo angulus FCS rectus. Quaeritur vero ang. CED. Item AE.

In triang. rectang. AQS datur QS declin. ♄, 20.27′. Item QA ascens. recta. Ergo invenietur ang. QSA 102.0, cui additus ZSP 8.49 facit ang. DSA 110.49. Sed et DAS datur. 23.30′. Et latus SA, cum detur locus Saturni 29.10′ capric.²⁾ Ergo invenietur hinc lat. DS.

Rursus in triang. FSC, datur ang. FSC idem cum ASD invento. et ang. FCS rectus et latus FS, quia F in 20.30 virg.⁸⁾ Ergo invenitur lat. SC, a quo ablato SD, reliquum est DC. Jam in triang. DCE, datur lat. DC et ang. CDE aequ. ADS, et DCE est rectus. Ergo invenitur ang. CED. Itemque latus DE quod additum ad DA facit AE. dato ang.^o E in ∆^o FAE, et ang. A et latere FA 9 30′ invenitur ang. EFA inclinatio plani annuli ad Eclipticae planum.

Ang. F vel N quo inclinatur Saturnij annuli planum ad planum eclipticae potest et hoc modo inveniri. Cognito ut ante ang.^o ASD 110.49., habetur et DSN 69.11′, datur autem et latus SN 51.20′ in ∆^oSCN, cum N sit in gr. 2030′, piscium⁹⁾. Et ang. C est rectus. Ergo invenitur et ∠ SNC quaesitus 31.22′.

Rursus in triang. NEA, dantur ang.ⁱ N et A et latus AN. Unde invenietur et ang. E quaesitus, cujus nempe compl. ad 2 rectos est ∠ DEC. 8.58′.

Sin. 31.22 ad rad. ut 52 ad 100. Ergo haec est proportio minoris diametri annuli ad majorem. diam. annuli ad diam. globi debet esse proximè ut 7 ad 3¹⁰⁾.

7) Il s'agit évidemment d'une correction à apporter.

6) Savoir 170^o30′ et 350^o30′; voir le deuxième alinéa de la p. 327.

2) Savoir 299^o10′ de longitude.

8) Savoir 170^o30′ de longitude.

9) Savoir 350^o30′ de longitude.

10) Comparez à propos de cette valeur du rapport en question la p. 479 qui suit.

[p. 388]

Circa 28.56 ♒ et ♌¹⁾ maxime ad aequatorem inclinabitur ♄ⁱ major diam. circiter 8.58′. at in 28.56 ♍ et ♉²⁾ parallela erit aequatori.

1) Savoir 328^o56′ et 148^o56′ de longitude; comparez l'alinéa qui commence en bas de la p. 385.

2) Savoir 238^o56′ et 58^o56′.

[Troisième Partie.]³⁾

Sin. 31.22⁴⁾ ad radium ut 52051 ad 100000 sive proxime ut 52 [ad] 100 itaque haec est proportio minoris diametri annuli ♄ ad majorem in phasi latissima.

diameter annuli ad diametrum globi proxime debet esse ut 7 ad 3⁵⁾.

[Fig. 5.]

phasis latissima, circa gr. 20.30 ♐ et ♊⁶⁾.

haec correctior in libro D⁷⁾.

3) Dans cette Partie, empruntée à la p. 183 du Manuscrit, Huygens applique la valeur trouvée pour l'angle du plan de l'anneau avec l'écliptique pour construire la phase de la largeur maximum de l'anneau.

4) Voir la cinquième ligne d'en bas du texte de la p. 387.

5) Voir la note 10 de la p. 387.

6) Savoir 260^o30′ et 80^o30′; comparez la p. 315.

7) Cette remarque fut ajoutée plus tard. La figure en question se trouve à la p. 106 du



Manuscrit D. Elle n'est accompagnée d'aucun commentaire. D'après la place qu'elle occupe elle doit dater de l'un des derniers mois de 1668. Nous croyons utile de la reproduire ici. On peut d'ailleurs constater la similitude géométrique presque parfaite des deux figures.