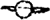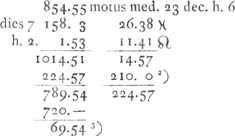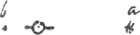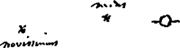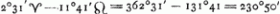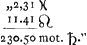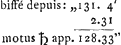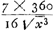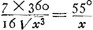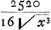Oeuvres complètes. Tome XV. Observations astronomiques

X¹⁰⁾.
(Manuscrit D).
1672-1673.

[Fig. 108.]¹¹⁾

d. lunae, 18 Jul. 1672¹²⁾, hora dimidia post mediam noctem. Saturnus observatus cum brachijs, quae jam 5 Junij renata observaverat D. Cassinus¹³⁾, et jam ab illo tempore valde clara ac con-

10) Cette section contient les observations qu'on trouve aux pp. 313, 316-317, 360, 365, 367 et 368 du Manuscrit D.

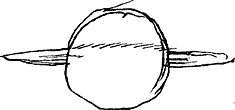
11) Dans le Manuscrit K la raie obscure inférieure manque sur le globe de Saturne; voir à la page suivante la Fig. 108a que nous empruntons à ce Manuscrit. De plus on trouve une figure analogue à la p. 237 du T. VII. Dans le Manuscrit D Huygens a tâché d'effacer la raie inférieure à l'aide d'un couteau.

12) On retrouve cette observation et les suivantes jusqu'à celle du 16 août 1672 incluse aux p. 94-96 du Manuscrit K.

13) Consultez sur cette observation de Cassini les p. 179-180 du T. VII.

[p. 110]

spicua erant. Mihi hac observatione videbantur non aeque lucida ac¹⁾ reliquum

[Fig. 108a.]

Saturni corpus. Tractus obscurus paulo inferior brachiorum linea cernebatur, hoc est revera superior²⁾, boream versus, quia telescopium evertit situm³⁾.

Cum autem visus noster altius supra planum annuli quam sol elevatus fuerit, non potest ista fuisse annuli umbra. Quare ipsa annuli margo fuisse videtur, radios solis non reflectens vel debiliter certe, sicut in Systemate a nobis positum fuit⁴⁾.

[Fig. 109.]

Comes a parte dextra adstabat fere in maxima distantia.

Vera positio⁵⁾.

^6)7)8)9)

1) Le Manuscrit K donne: ‘paulo minus lucida videbantur quam’.

2) C'est, en effet, ce qui devait arriver suivant la note 2 de la p. 106 puisqu'en juillet 1672 la terre avait passé au côté sud de l'anneau. Donc ici encore (comparez la note 6 de la p. 108) Huygens a dessiné la position vraie. Du reste pour le satellite ce fait est constaté expressément.

3) ‘invertit positionem’ (Manuscrit K).

4) Voir les p. 61-62 de l'édition originale.

5) Ces mots manquent dans le Manuscrit K.

6) Cette indication est empruntée au Manuscrit K. Consultez toujours, pour l'explication de ces calculs de la distance du satellite à son apogée, les p. 30-33 du ‘Systema’.

7) Lisez: 533.45.

8) Lisez 55 au lieu de 35. En appliquant la correction indiquée à la p. 45 on trouve donc 289^o52′; ce qui est conforme à l'observation.

9) Mot hollandais = donc. Le mouvement orbital de Saturne se calcule à 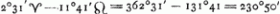. Dans le Manuscrit K ce calcul se retrouve sous la forme suivante: 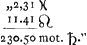où par mégarde le signe du Bélier est remplacé par celui des Poissons. Remarquons que dans le Manuscrit D on trouvait primitivement le calcul suivant, 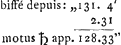Le résultat erroné de ce calcul avait d'abord servi dans le calcul de la distance du satellite à son apogée. Combiné avec d'autres erreurs de calcul qu'on ne peut plus préciser parce que les chiffres ont été biffés de manière à devenir illisibles, ce résultat avait amené 122^o36′ pour cette distance; valeur qu'on retrouve dans la Fig. 110, et qui était peu conforme à l'observation représentée par la Fig. 109.

[p. 111]

[Fig. 110.]¹⁰⁾

comes¹¹⁾ secundum calculum. Ergo minus remotus debuisset apparere quam revera observatus fuit enim in B vel in C. Itaque motus medius pauxillo augendus erit¹²⁾.

10) Dans la figure correspondante du Manuscrit K on ne retrouve sur le cercle, qui représente l'orbite, que l'indication du résultat corrigé, pourvue de l'annotation: ‘comes sec. calculum qui cum observatione optime convenit.’ Tout le reste a été omis.

11) Ce passage, biffé par l'auteur dans le Manuscrit D, ne figure pas dans le Manuscrit K, d'où l'on peut inférer de nouveau que celui-ci ne contient certainement pas l'observation originale.

12) Nous avons vu (voir la note 9) que cette conclusion reposait sur un calcul erroné et que le résultat obtenu plus tard (voir la p. 110) convenait très bien à l'observation. C'est probablement à propos de cette circonstance que Huygens ajouta à l'article qui parut dans le ‘Journal des Sçavans’ du 12 décembre 1672 (voir les p. 235-237 du T. VII) l'alinéa suivant: ‘Avant que de sinir j'ajoûteray que la Table que j'ay donnée du mouvement de la petite Lune ou Estoile qui accompagne Saturne & qui tourne autour de luy en 16 jours moins 47 minutes, s'est jusqu' icy trouvée si conforme aux observations, que je ne sçaurais encore voir s'il y faut ajoûter ou diminuer quelque chose.’
Remarquons toutefois que la conformité si parfaite entre les tables de Huygens et le mouvement du satellite que Huygens croyait pouvoir constater reposait sur une illusion comme nous l'avons montré aux p. 44-45 du Tome présent.

[p. 112]

1672, 6 Aug. hora 11.

Saturnus visus cum brachijs, nondum perforatis. linea obscura eodem modo se habebat atque in observatione superiori 18 Jul.¹⁾

[Fig. 111.]

Comes non apparebat, ut conjunctum Saturno fuisse oporteat²⁾. Unde³⁾ etiam liquet observatione praecedenti fuisse eum loco B⁴⁾ orbitae suae.

Eadem hora.

Mars observatus, in cujus disco maculae quaedam, sed tam parum obscuritate

[Fig. 112.]⁵⁾

sua a caeteris disci partibus distinctae, ut figura earum bene notari non posset. Verum in australi parte, quo loco forsan alter polorum situs est, macula quaedam reliquo disco multò lucidior, quae ad B situ everso notata est, conspiciebatur; quam nec ego nec alius quisquam quod sciam antea animadvertit⁶⁾.

1) Voir la Fig. 108^a de la p. 110.

2) Dans le Manuscrit K Huygens ajoute: ‘vel prope conjunctum’.

3) Cette phrase fut biffée dans le Manuscrit D. Elle manque dans le Manuscrit K.

4) Voir la Fig. 110.

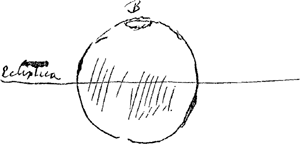
5) Dans la figure correspondante du Manuscrit K l'indication vague des taches obscures manque entièrement. On y trouve seulement le contour de la tache polaire marquée, comme ici, par la lettre B. La figure n'a pas été reproduite dans le mémoire de F. Terby, cité à la p. 31; M. van de Sande Bakhuyzen ne connaissait que la figure, telle qu'elle se trouve dans le Manuscrit K (voir la p. 56 de son mémoire mentionné dans la note 5 de la p. 33).

6) Le Manuscrit K fait suivre: ‘Postea Cassino quoque hoc tempore observatam ab ipso didici’. Or, nous n'avons pas pu trouver cette observation de Cassini. Ni Terby, dans le mémoire mentionné dans la note précédente, ni M. Flammarion dans ‘La planète Mars’ ne nous renseignent sur ce point. Il paraît donc qu'elle n'a pas été publiée par Cassini. Dans l'ouvrage de Cassini de 1666, cité en premier lieu dans la note 9 de la p. 47 de notre T. VI, il se trouve un croquis de Cassini, reproduit dans le ‘Journal des Sçavans du Lundy 24 mai 1666’ (Fig. A de la planche vis à vis de la p. 474 du Tome premier), dans les ‘Philosophical Transactions’ N^o. 14 du 2 juillet 1666 (voir la planche vis à vis de la p. 231 du Vol. I) et dans l'ouvrage de Flammarion, où l'on voit quatre taches blanches dont deux polaires. Mais l'aspect de la planète est bien différent de celui que nous montrent les lunettes d'aujourd'hui, et les croquis de Huygens l'emportent de beaucoup.

[p. 113]

1672, 13 Aug. h. 10½.

Saturnus visus ut supra, ac rursus sine comite.

[Fig. 113.]⁷⁾

Eodem tempore.

Mars observatus in quo macula lucida ad polum rursus ut supra apparebat. Macula obscura autem hac fere forma versus inferiorem disci partem cernebatur⁸⁾.

7) La figure correspondante du Manuscrit K fut reproduite dans le mémoire de Terby, mentionné dans la note 5 (voir sa Fig. 2) et discutée d ans celui de M. van de Sande Bakhuyzen, mentionné dans la même note (voir la p. 57 de ce mémoire). Elle avait déjà été choisie par F. Kaiser parmi les dessins de Huygens de la planète Mars, qu'il trouvait dans le Manuscrit K, pour la reproduire dans ses ‘Untersuchungen über den Planeten Mars bei dessen Oppositionen in den Jahren 1862 und 1864’ (p. 1-86 des ‘Annalen der Sternwarte in Leiden, Bd. 3, 1872’; voir la Fig. 7 de la pl. III). Elle lui semblait éminemment propre à être employée dans la détermination de la durée de la rotation de la planète; voir la p. 61 de son mémoire.

8) Dans le Manuscrit K la dernière phrase se lit comme suit: ‘Macula vero obscura hac fere forma versus inferiorem (revera superiorem) disci partem cernebatur.’

dominica. 14 Augusti hora 10½

Mars eandem fere maculam ostendebat. Saturnus rursus sine comite. nubes⁹⁾ impediebant observationem.

9) Le Manuscrit K intercale: ‘aliquantum’.

[p. 114]

16 Aug. hora 10½.

[Fig. 114.]

Saturni comes vero situ, ad dextram paulo altior linea brachiorum et in distantia fere magna.

Martis diameter observata per telescopium inspiciente oculo altero, altero extra telescopium inspectante¹⁾ circulum chartaceum 3 poll. diametro, is²⁾ marti aequalis apparebat remotus pedibus 22 ab oculo. distantia³⁾ ad diametrum circuli est ut 88 ad 1. Unde Mars apparuit in telescopio, 39′. auget autem telescopium in ratione 120 ad 1⁴⁾. Ergo Martis diameter apparens fuerit hic 19″½. Erat autem in ♓ gr. 22.4′. unde⁵⁾ accepta ad tellurem distantia in Tabula nostra Planetaria⁶⁾ est ad minimam possibilem a terra distantiam ut 246 ad 226. Ergo maxima apparens diameter Martis fit 21″,14‴. Quam tamen olim 30″ taxavi⁷⁾.

Videndum accuratè qua proportione telescopium augeat⁸⁾ res visas. Cassinus et Picardus menses [sic] sept. in maxima ♂ proximitate diametrum hanc 25″ aut 26″ sibi observatam affirmant⁹⁾. filis prope lentem ocularem usi¹⁰⁾.

situs inversus.

23 Dec. h. 6 post merid¹¹⁾.

[Fig. 115.]

[30 Dec. h. 8 post merid.

[Fig. 116.]

1) Le Manuscrit K donne ‘intuente’.

2) Après le mot ‘diametro’ le Manuscrit K fait suivre: ‘lucernae ad moto lumine illustratum. Hic’.

3) ‘quae distantia’ (Manuscrit K).

4) Le Manuscrit K ajoute ‘secundum diam.’

5) ‘Ubi’ (Manuscrit K).

6) Probablement la ‘tabula lignea’; comparez la note 8 de la p. 57.

7) Comparez la p. 66.

8) Ce qui suit après ce mot jusqu' à la fin de cette annotation manque dans le Manuscrit K. Ajoutons que tout ce passage, à l'exception du premier alinéa ‘Saturni comes’ etc. et jusqu'au mot ‘augeat’ inclus, fut cité par Kaiser à la p. 15 du mémoire mentionné dans la note 3 de la p. 36.

9) Il s'agit probablement d'une communication verbale.

10) Auzout donne une description du micromètre à vis dans son ‘Traité du Micromètre’ de 1667 (voir la note 7 de la p. 198 de notre T. V et la correction qui y fut apportée dans la note 11 de la p. 63 du T. VI). Ce traité fut réimprimé p. 413-422 des ‘Divers ouvrages de mathématique et de physique, par Messieurs de l'Académie Royale des Sciences’ de 1693 et de même p. 97-112 (deuxième pagination) du T. VII, Première Partie, des ‘Mémoires de l'Académie Royale des Sciences. Depuis 1666 jusqu'à 1699’ de 1729. L'heureuse idée de placer des fils mobiles au foyer de la lunette fut déjà pratiquée auparavant (en 1640) à l'insu des astronomes français par Gascoigne; voir la lettre de R. Towneley dans le N^o. 25 des ‘Philosophical Transactions’ de 1667, p. 457-458 du Vol. II, et l'article de W. Derham dans le N^o. 352 des mêmes ‘Transactions’ de 1717, p. 603-610 du Vol. XXX.

11) Cette observation du satellite Rhéa de Saturne, faite le soir même de sa découverte par Cassini, ainsi que la suivante du 30 Dec. sont sans doute identiques avec les observations de ces dates qui figurent sur la planche II, Fig. II, qui accompagne l'article de Cassini dans les ‘Philosophical Transactions’ du 25 mars 1673, cité dans les notes 1 et 2 de la p. 268 du T. VII. Dans cet article Cassini atteste expressément (p. 5181 du Vol. VIII) que Huygens, Picard, Mariotte et Römer étaient présents à l'occasion de l'observation du 23 décembre 1672 et il semble probable que Huygens assista de même à celle du 30 décembre. Il est vrai que Huygens donne ici 6 heures du soir pour l'heure de l'observation du 23 décembre et Cassini environ 7 heures du soir (p. 5183).

[p. 115]

quaeritur periodicum tempus novi comitis, item ratio ejus distantiae a Saturno ad distantiam mei comitis¹²⁾.

NB. novus hoc spatio y dierum sesquiperiodum absolverat, quod non putabam. Tempus periodi proxime est 4½ dierum¹³⁾.

12) L'annotation que nous reproduisons est, en effet, suivie de quelques calculs où Huygens s'efforce de trouver ces desiderata dans la supposition que les deux observations se rapportaient à une même période de révolution du nouveau satellite que Cassini croyait être identique avec le satellite Japet, le plus éloigné de tous, qui fut découvert par lui en octobre 1671, mais qu'il avait bientôt perdu de vue (voir les p. 5178-5181 de l'article cité dans la note précédente).
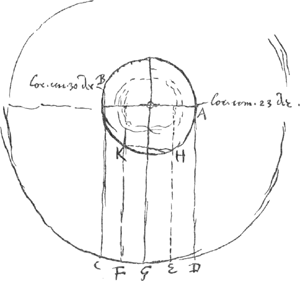
Quoique ces calculs se trouvent dans un état assez confus, on peut bien en déchiffrer la portée générale. Soit donc x le rapport du rayon de l'orbite CFGED (Fig. 117) du nouveau satellite à celui de l'orbite BKHA parcouru par le satellite de Huygens en environ 16 jours. La durée de la révolution du nouveau satellite est alors de 16 √x³ jours et l'arc FE parcouru entre le 23 et le 30 décembre mesure 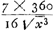degrés. Or, Huygens évalue l'arc KH à 55^o et l'arc FE à 55^o/x. On a donc 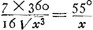, ou, comme Huygens l'exprime: ‘1 [ad] x (proport orbit^m contraria) [ut] 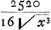(gr. com. novi) [ad] 55 (gr. comitis mei qui aequantur dimidio radij cum dimidio sin. 69 gr.)’
La dernière partie de cette proportion nous montre comment l'évaluation de l'arc KH a été obtenue. Évidemment Huygens suppose que le satellite nouveau se trouvait à chaque observation environ à mi-chemin entre le sien et la planète, de sorte que la corde KH est à-peu-près perpendiculaire à la droite qui passe par le périgée et l'apogée, et qu'elle ne diffère pas sensiblement de l'arc KH.
Dans ces conditions il est facile de calculer approximativement la longueur de la corde KH et par suite celle de l'arc KH (prenant pour unité le rayon de l'orbite AHKB) lorsqu'on connaît les distances à l'apogée du satellite de Huygens au 23 et au 30 décembre. Or, par les calculs qui suivent dans le texte, Huygens avait trouvé pour ces distances, en degrés entiers, respectivement 270^o et 69^o.
Ajoutons que Huygens résume le résultat de ses calculs dans la phrase suivante, biffée depuis: ‘Ergo radius orbitae comitis novi ad radium orbitae mei comitis saturnij ut 8⅕ ad 1. Tempus vero periodicum novi comitis circiter dierum 375. Distantia apparens maxima 27′.’

13) Cette annotation a été ajoutée évidemment après que Cassini avait découvert par les observations de janvier 1673 la véritable durée (d'environ 4½ jours) des révolutions de Rhéa autour de Saturne; voir les notes 6 et 7 qui suivent.

[p. 116]

¹⁾²⁾³⁾

²⁾³⁾

[Fig. 117.]

duorum planetarum, in eodem vortice circumlatorum, tempora periodica sunt inter se ut radices quadratae cuborum a distantijs eorum a centro vorticis. hoc de planetis circa solem primus observavit Keplerus⁴⁾. deinde de comitibus jovis Wendelinus⁵⁾.

1) Comparez à propos des calculs qui suivent et qui se rapportent au satellite découvert par Huygens la note 6 de la p. 110.

2) Différence en longitude des signes ♓ (330^o et ♌ (120^o).

3) En appliquant la correction indiquée à la p. 45 on doit retrancher environ 13^o de la distance à l'apogée.

2) Différence en longitude des signes ♓ (330^o et ♌ (120^o).

3) En appliquant la correction indiquée à la p. 45 on doit retrancher environ 13^o de la distance à l'apogée.

4) Voir l'ouvrage de 1619 cité dans la note 2 p. 475 de notre T. II.

5) Voici ce qu'on lit à la p. 492 de l'‘Almagestum novum’ de Riccioli: ‘Non minùs Keplerianâ ingeniosa est Vendelini sagacissimi Astronomi animaduersio de propositione periodorum & interuallorum Iouialium satellitum, quam ille mihi per summam liberalitatem, praelonga & doctissimà Epistola communicauit. Sicut enim in Planetis majoribus distantiae Planetarum mediae à Sole sunt ad inuicem in ratione sesquialtera suorum temporum periodicorum; ita distantiae horum Planetulorum Iovialium à Ioue, quae sunt 3′.5′.8′.14′. sunt inter se in ratione sesquialtera periodicorum’. Voir sur Godesried Wendelin la note 23 de la p. 304 du T. II.

[p. 117]

[Fig. 118.]

10 Jan. hora 7.⁶⁾

situs inversus ut in telescopio.

[Fig. 119.]

15 Jan.⁷⁾ inter h. 6 et 9. fere per duas horas exiguus comes b in eadem ad Saturnum distantia perstitit cum Saturni motus apparens diurnus esset 5′. ideoque intervallo duarum horarum debuerit recedere a stellula hac si sixa fuisset spatio 25″, hoc est duplicasse fere distantiam primo visam, nam diametro sphaerae Saturni cum uno brachio aequalis erat distantia⁸⁾.

Ergo constat planetam esse.

[Fig. 120.]⁹⁾

6) On retrouve cette observation dans l'article de Cassini, mentionné dans la note 11 de la p. 115; voir la p. 5182 de cet article et la Fig. II de la planche II qui l'accompagne. Le satellite intérieur est Rhéa qui a accompli quatre révolutions en 18 jours (du 23 déc. 1672 au 10 janvier 1673). C'est à cette occasion que Cassini s'étonna de trouver le nouveau satellite, qu'il avait pris d'abord pour celui (Japet) qu'il avait découvert en octobre 1671, pour la troisième fois entre Saturne et le satellite (Titan) découvert par Huygens.

7) Cette observation se retrouve de même dans l'article de Cassini et dans la Fig. II de la planche II qui l'accompagne. Elle finit par persuader Cassini qu'on avait à faire à un satellite (Rhéa) dont l'orbite se trouvait à l'intérieur de celle du satellite de Huygens; voir la p. 5182 de l'article mentionné.

8) Vu la distance qui séparait Saturne de la Terre à l'époque de l'observation, la somme des diamètres apparents du globe et de l'anneau est 55″.4, dont la moitié, c'est-à-dire le diamètre du globe augmenté de la longueur de l'un des bras, est 27″.7.

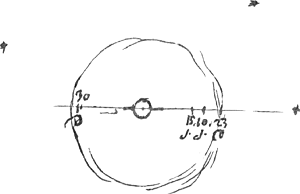
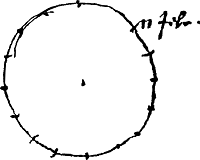
9) Dans cette figure Huygens a résumé évidemment les observations du 23 et du 30 décembre 1672, et du 10 et 15 janvier 1673. Les trois points marqués en dehors du cercle indiquent les positions (de droite à gauche) de Titan dans son orbite an 23 décembre, au 10 janvier, au 30 décembre et au 15 janvier, ces dernières positions ne différant pas sensiblement. Dans le manuscrit on voit très distinctement le cercle, tracé avec la pointe d'un compas, qui passe par ces trois points.

[p. 118]

Tertij comitis¹⁾ prope Saturnum observationes.

11 febr. hora 6½.²⁾

[Fig. 121.]

ipse observavi cum Picardo.

[Fig. 122.]³⁾

12. febr. hor. 6½²⁾

[Fig. 123.]

1) Ce ‘tertius comes’, indiqué dans les Fig. 121 et 123 par ‘novissimus’, n'est autre que le satellite (Japet) découvert par Cassini en octobre 1671. Toutefois, lorsque le 6 février 1673 Cassini retrouva ce satellite, ne l'ayant pas revu avec certitude depuis le 6 novembre 1671, il n'était pas facile d'en constater l'identité dans les premiers jours qui suivirent. Quant à Huygens, il paraît avoir eu des doutes sérieux sur l'interprétation des observations d'octobre 1671, puisqu'il écrivit le 4 décembre 1671 à son frère Constantyn (voir la p. 122 du T. VII) ‘Monsieur Cassini croioit dernierement avoir decouuert un nouveau Satellite de Saturne, mais a ce que l'on a pu juger par le peu d'observations qu'il en a, (car le temps sombre ne luy a pas permis d'en faire du depuis) ce ne peut estre que quelque petite comete sans queue.’

2) Dans l'article cité dans la note 11 de la p. 115 Cassini dit expressément (p. 5184) que les observations de février 1673 furent faites quelquefois en compagnie de Huygens et de Mariotte. On retrouve les observations du ‘novissimus’ du 11 et du 12 février dans la Fig. I de la planche II qui accompagne l'article.

3) Évidemment cette esquisse représente la position de Titan dans son orbite au 11 février 1673.

2) Dans l'article cité dans la note 11 de la p. 115 Cassini dit expressément (p. 5184) que les observations de février 1673 furent faites quelquefois en compagnie de Huygens et de Mariotte. On retrouve les observations du ‘novissimus’ du 11 et du 12 février dans la Fig. I de la planche II qui accompagne l'article.