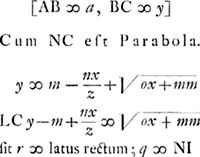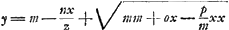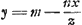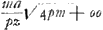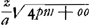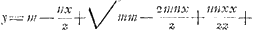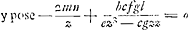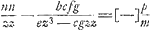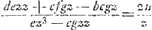Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 423]
| |
AppendiceGa naar voetnoot1)
| |
[pagina 424]
| |
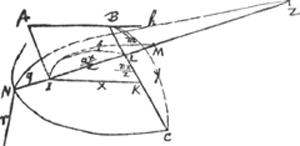 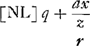 Ga naar voetnoot1) 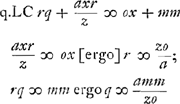 quoniam volo distantiam IN, et latus rectum r ita esse comparata, ut sumpta AB x quantâcumque semper sit rq + arx/z ∞ ox + mm, omnino necesse est terminum arx/z esse ∞ ox et reliquum proinde reliquo. Si enim sit ar/z inaequalis o, puta major, fiet ut quo major sumetur x, eo amplius terminus arx/z superet term.m ox. Ergo oporteret tanto quoque semper majorem esse excessum termini mm supra rq. quod fieri non potest cum sint quantitates determinatae.
Cum NC Ellipsis. 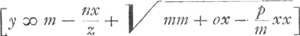 Sit IM ∞ f; lat. rectum ∞ r; lat. transv. NZ ∞ h. | |
[pagina 425]
| |
 Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5) Si mm fuerit ∞ 0 erit tertia aequatio 1/4 rh - rff/h ∞ 0 unde r ∞ oz/a ut Cartesius | |
[pagina 426]
| |
 aitGa naar voetnoot1). At si ox ∞ 0 erit in tertiaGa naar voetnoot2) aequatione etiam f ∞ zho/2ar sive nihilo. ergo in primaGa naar voetnoot3) aequatione tantum 1/4 rh ∞ mm et r ∞ 4mm/h: sed inventum fuit h ∞ mraa/pzz in secunda aequatione. igitur r ∞ 4mmpzz/mraa et rr ∞ 4mpzz/aa, et r ∞ 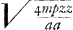 ut refert Cartesius ibidemGa naar voetnoot1). ut refert Cartesius ibidemGa naar voetnoot1).
Quod pro fractione 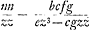 scribit p/mGa naar voetnoot4) id quidem facilitatis causa in sequentibus facit quod denominatorem ponit m, eandem quantitatem cujus est quadratum mm, verum et difficultatem aliquam idem affert cum termino pxx/m nulla fractio adhaeret etenim tum nusquam quidem apparet p et tamen in terminis qui centrum et latera docent reperitur neque pro nihilo istic habendum sed cogitandum quod p ∞ m ut recte notat Florim. de BauneGa naar voetnoot5). Sed, quidni loco fractionis prioris posuit 2n/m potius quam 2n/zGa naar voetnoot6), nam et hoc magno usui fuisset in sequentibus? Exprimetur enim ea ratione linea IN per am/o quae prius erat amm/ozGa naar voetnoot7). Et IM per ao/2pGa naar voetnoot8) quae fuerat aom/2pz latus rectum per scribit p/mGa naar voetnoot4) id quidem facilitatis causa in sequentibus facit quod denominatorem ponit m, eandem quantitatem cujus est quadratum mm, verum et difficultatem aliquam idem affert cum termino pxx/m nulla fractio adhaeret etenim tum nusquam quidem apparet p et tamen in terminis qui centrum et latera docent reperitur neque pro nihilo istic habendum sed cogitandum quod p ∞ m ut recte notat Florim. de BauneGa naar voetnoot5). Sed, quidni loco fractionis prioris posuit 2n/m potius quam 2n/zGa naar voetnoot6), nam et hoc magno usui fuisset in sequentibus? Exprimetur enim ea ratione linea IN per am/o quae prius erat amm/ozGa naar voetnoot7). Et IM per ao/2pGa naar voetnoot8) quae fuerat aom/2pz latus rectum per 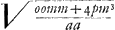 (sed hoc parvum quidem prodest) latus transversum per (sed hoc parvum quidem prodest) latus transversum per 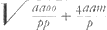 . vel per . vel per 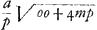 . In parabola latus rectum erit om/a.
Ego itaque formulam universalemGa naar voetnoot9) hanc ponerem . In parabola latus rectum erit om/a.
Ego itaque formulam universalemGa naar voetnoot9) hanc ponerem 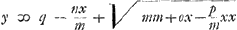 ubi hoc tantum observandum quod si terminus nx/m defuerit, erit a ∞ mGa naar voetnoot10) et m ubique illius loco substituendum. Alterum autem ibidem ut in Cartesiana formula observandum, nempe si termino p/m xx fractio desit, quod ubi hoc tantum observandum quod si terminus nx/m defuerit, erit a ∞ mGa naar voetnoot10) et m ubique illius loco substituendum. Alterum autem ibidem ut in Cartesiana formula observandum, nempe si termino p/m xx fractio desit, quod
| |
[pagina 427]
| |
tunc p ∞ m et m illius quoque loco substituendum. At hisce observationibus non erit opus si formula universalis haec statuatur 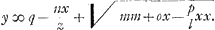 . Erit vero lat. rectum . Erit vero lat. rectum 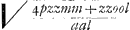 sive sive 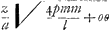 transversum transversum 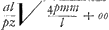 ratio horum quae pzz ad aal. Si pro termino nx/z habeatur x, oportet sumere KL ∞ IK vel AB et ducere IL. Ratio autem lineae IK vel KL ad IL tunc erit ea quae z ad a. Itaque in terminis qui centrum et latus rectum transversumque docent retinendae z et a, pro quibus quaelibet duae lineae sumendae quae rationem habeant quam IK ad IL. Si terminus nx/z desit delendum ubique z et aGa naar voetnoot11). ratio horum quae pzz ad aal. Si pro termino nx/z habeatur x, oportet sumere KL ∞ IK vel AB et ducere IL. Ratio autem lineae IK vel KL ad IL tunc erit ea quae z ad a. Itaque in terminis qui centrum et latus rectum transversumque docent retinendae z et a, pro quibus quaelibet duae lineae sumendae quae rationem habeant quam IK ad IL. Si terminus nx/z desit delendum ubique z et aGa naar voetnoot11).
|
|