Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 409]
| |
Contributions aux commentaires de Van Schooten sur la ‘Geometria’ de Descartes.
| |
[pagina 411]
| |
Avertissement.Quelques-uns des résultats mathématiques obtenus par Huygens qui ne furent pas publiés par lui-même, parurent parmi les Commentaires que van Schooten ajouta à sa traduction latine de la ‘Géométrie’ de DescartesGa naar voetnoot1). C'est pourquoi nous croyons devoir reproduire ici les passages de ces Commentaires qui se rapportent aux travaux de Huygens. On connaît les relations amicales qui existaient entre le professeur van Schooten et son élève depuis l'arrivée de ce dernier à Leiden, en mai 1645, jusqu'au décès de van Schooten, en janvier 1661. Or, van Schooten aimait beaucoup à faire ressortir les mérites de ses élèves. Ainsi déjà en 1649, dans la première édition de la ‘Geometria’, il inséra une ‘invention’ du jeune Huygens en la | |
[pagina 412]
| |
faisant précéder de quelques mots de louange qui montrent qu'il avait pressenti de bonne heure le grand avenir de son élèveGa naar voetnoot1). Cette invention de Huygens consiste dans la remarque, elucidée par un exemple, qu'un problème peut quelquefois se transformer en théorème; savoir dans le cas où tous les points situés à l'extérieur ou à l'intérieur d'une figure donnée satisfont aux conditions posées dans le problème. C'est à l'âge de 15 ans que Huygens avait fait cette remarque. En effet, on la retrouveGa naar voetnoot2) sur une des premières pages du Manuscrit No. 17, dont nous avons déjà parlé dans l'Avertissement pour les ‘Travaux divers de Jeunesse’Ga naar voetnoot3). Lors de la rédaction de cet Avertissement, nous ignorions si ce petit manuscrit avait été commencé avant ou après le départ de Christiaan, en 1645, pour Leiden. Depuis, nous avons été mieux renseignés, grâce à feu M.J.A. Worp, qui a publié, en 1913, des annotations de Constantijn Huygens père, sur les progrès des études de ses filsGa naar voetnoot4). On y lit sous l'année 1644: ‘Dans cette même année je mis Constantyn et Christiaan sous la direction de Stampioen pour leur enseigner les mathématiques. Le succès était singulier, quoique ce fût surtout Christiaan qui excellait. Non seulement qu'il comprenait et retenait facilement toute chose, mais il inventait quotidiennement toutes sortes de choses ingénieuses, qu'il assemblait dans un livret (“Boeckjen”), de sorte qu'il y avait lieu de s'en étonner grandement’. Or, ce ‘boeckje’ qu'il désigna plus tard dans les mêmes termes à son frère ConstantijnGa naar voetnoot5) était sans doute le manuscrit No. 17Ga naar voetnoot6).
La participation de Huygens à la seconde édition, de 1659, de la ‘Geometria’ | |
[pagina 413]
| |
était beaucoup plus active. En effet, comme nous le verrons, elle ne s'est pas limitée aux endroits où elle est expressément mentionnée par van SchootenGa naar voetnoot7). Aussitôt après que Louis Elsevier avait fait savoir à van Schooten, qu'il voulait préparer une nouvelle édition de la ‘Geometria’, celui-ci s'adressa à Huygens pour le prier de lui communiquer les corrections ou modifications qu'il jugerait opportun d'apporter à cet ouvrageGa naar voetnoot8). En réponse, Huygens lui envoya, en octobre ou novembre 1654, une copie des annotations qu'il avait faites en marge de son exemplaireGa naar voetnoot9). Outre celles qui se rapportent aux passages que nous reproduisons dans le texte qui suit, on trouve dans cette copie plusieurs autres annotations, plus ou moins importantes, qui ont été utilisées également par van Schooten. Nous en signalons deux, dont l'une a occasionné la note volumineuse CC, p. 182-206 de l'édition de 1659; nous avons citée celle-ci dans la note 3 de l'Appendice, p. 423. L'autre concerne les points d'intersection d'une parabole et d'un cercleGa naar voetnoot10). Huygens y traite du cas où trois de ces points coïncident, et fait remarquer que dans ce cas les deux courbes se coupent au point de coïncidence, nonobstant qu'elles y possèdent une tangente commune. On retrouve cette observation à la p. 339 de l'édition en question de la ‘Geometria’. Au mois de mars 1655, Huygens attira l'attention de van Schooten sur une petite inadvertance commise par Descartes dans sa ‘Géométrie’ et lui proposa de la corriger dans le texte de la nouvelle édition de la ‘Geometria’ ou de l'indiquer dans ses CommentairesGa naar voetnoot11). C'est la première de ces alternatives qui fut suivie par van Schooten aux p. 28-29 de l'édition de 1659. Enfin il y a encore la note BB, p. 179-181, qui fut ajoutée sur l'instigation de Huygens. En effet, celui-ci reçut, en juillet 1656, une lettre de Roberval, où ce savant lui indiqua ce qu'il considérait comme une faute importante commise par | |
[pagina 414]
| |
Descartes, savoir que Descartes n'avait pas compris que la solution complète du problème de Pappus à quatre lignes ‘demande deux sections à la fois, et chacune toute entiere’Ga naar voetnoot1). Huygens trouva les remarques de Roberval ‘tres belles et veritables’ et il envoya sa lettre à van Schooten avec la recommandation d'utiliser ses remarques pour les CommentairesGa naar voetnoot2). Or, pour un fervent admirateur de Descartes, comme van Schooten, la manière dont Roberval parla du ‘bon-homme’ Descartes était difficile à digérer. Ainsi, dans sa réponse, il ne manqua pas de prendre ardemment la défense de DescartesGa naar voetnoot3); toutefois, quelques mois plus tard, après avoir reçu une lettre très détaillée de HuygensGa naar voetnoot4), où celui-ci renouvela sa recommandation, van Schooten résolut de se conformer à l'avis de HuygensGa naar voetnoot5); mais il le sit d'assez mauvaise grâce, puisque dans la note BB il ne nomme ni Huygens, ni Roberval, quoiqu'il suive de très près la lettre de HuygensGa naar voetnoot6).
Nous ne voulons pas passer sous silence une conjecture proposée par Uylenbroek à la p. 3 de ses ‘Exercitationes mathematicae et philosophicae, Fasc. II’Ga naar voetnoot7) de 1833. D'après cette conjecture on doit lire Hugenius au lieu de Huddenius à la p. 367 de l'édition de 1659 de la ‘Geometria’. Il s'agit d'expliquer la manière dont les règles de Cardan pour la résolution des équations cubiques auraient pu être trouvéesGa naar voetnoot8). Or, dans une lettre du 29 mai 1655, van Schooten avait prié | |
[pagina 415]
| |
Huygens de lui communiquer ce qu'il avait imaginé à ce sujetGa naar voetnoot9). En réponse, Huygens exposaGa naar voetnoot10) à van Schooten une méthode pour la résolution de l'équation 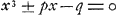 qui ne diffère pas essentiellement de celle qu'on trouve aux p. 367-368 de la ‘Geometria’. qui ne diffère pas essentiellement de celle qu'on trouve aux p. 367-368 de la ‘Geometria’.
La conjecture d'Uylenbroek semble donc bien plausible. Toutefois nous devons faire observer qu'une méthode tout-à-fait analogue fut développée par Hudde lui-même aux p. 499-501 de l'‘Epistola prima de Reductione AEquationum’ d'avril 1658; épître qui fut insérée par van Schooten dans la nouvelle édition de la ‘Geometria’. Et Hudde ne manque pas d'observer, à l'endroit cité, que la règle de Cardan ‘aurait pu être trouvée de la manière indiquée, quoique peut-être elle fût découverte par d'autres considérations’Ga naar voetnoot11). On voit donc que Hudde s'était occupé du même sujet. Il est vrai que le mot ‘olim’ dans le passage en questionGa naar voetnoot12) paraît exclure une communication si récente qu'avril 1658 et s'accorde mieux avec la date du 5 juin 1655 de la lettre de Huygens, mais il est possible que Hudde eût expliqué verbalement sa méthode à van Schooten bien avant 1658. |
|

