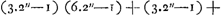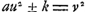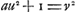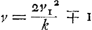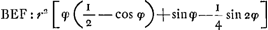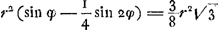Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 183]
| |
Avertissement.Aperçu général des travaux mathématiques de 1655 à 1659.Les années 1655-1659 ont été fertiles, pour Huygens, en recherches mathématiques de genres très différents. Parmi les travaux qui datent de cette période on en trouve qui se rapportent à la théorie des nombres et surtout à l'équation dite de PellGa naar voetnoot1); d'autres contiennent la rectification de la parabole et la quadrature des surfaces courbes des conoïdes parabolique, elliptique et hyperboliqueGa naar voetnoot2), ou la discussion d'un certain nombre de courbes diverses, de leur quadrature, de la cubature de leurs surfaces de révolution et de divers centres de gravité qui se présentent dans leur étudeGa naar voetnoot3); d'autres encore traitent, à l'occasion des problèmes sur la cycloïde proposés par Pascal, des propriétés de cette courbeGa naar voetnoot4) et d'une application cyclométrique de l'une de ces propriétésGa naar voetnoot5). Il y en a de très | |
[pagina 184]
| |
importants qui exposent et appliquent la théorie des développées et des courbes parallèlesGa naar voetnoot1) et d'autres plus élémentaires qui donnent la solution d'un problème, ou bien la démonstration d'un théorème, d'arithmétiqueGa naar voetnoot2), de planimétrieGa naar voetnoot3), de stéréométrieGa naar voetnoot4) ou de géométrie analytiqueGa naar voetnoot5). Il ne semble pas nécessaire d'analyser ici toutes ces Pièces. Nous nous bornerons donc à parler des principales. D'ailleurs pour les autres les notes que nous y avons ajoutées suffiront pour en faire connaître la genèse et la portée. Disons encore que beaucoup des résultats les plus importants trouvés par Huygens pendant l'époque qui nous occupe ont été publiés par lui dans son ‘Horologium oscillatorium’ de 1673; mais sans démonstrations et sans faire connaître aucunement la manière dont ils furent obtenus. Or, les Pièces qui suivent fournissent les démonstrations qui manquent dans cet ouvrage, et jettent une vive lumière sur les méthodes employées par Huygens pour découvrir les résultats qu'il y énonce. | |
Recherches sur la théorie des nombres. Équation dite de Pell.Huygens n'a été que rarement sous l'influence du charme que la théorie des nombres a exercé sur tant de mathématiciens célèbres. On peut même dire que s'il s'est occupé quelquefois de cette théorie, c'était un peu malgré lui. Ainsi, en mai 1656, Huygens écrit à MylonGa naar voetnoot6), qui lui fait parvenir deux problèmes de Fermat sur les nombres, que ces problèmes ‘sont tout a fait beaux dans le gendre, et mal aisez à resoudre,’ qu'‘au moins ils me semblent tels a moy qui | |
[pagina 185]
| |
ne me suis gueres exercè dans les questions des nombres, parce que j'ay toujours pris plus de plaisir à celles de Geometrie. Toutefois j'essayeray encore si j'en puis devenir maistre’. Deux années plus tard, en septembre 1658, il s'exprime bien plus fortement dans une lettre à Wallis en disant qu'il ne comprend pas qu'on s'occupe avec tant d'animation de ces sortes de problèmes auxquels on ne devrait consacrer ‘ses bonnes heures’ que lorsque les questions importantes comme on en trouve tant dans la géométrie viendraient à manquerGa naar voetnoot7). Et Huygens a persévéré longtemps dans cette attitudeGa naar voetnoot8). C'est seulement vers la fin de sa vie qu'il communique à Leibniz un jugement plus favorable lorsqu'il lui écritGa naar voetnoot9): ‘Dans la recherche des nombres, le plus utile seroit de s'arrester aux Theoremes dont il y en a des beaux et qui peuvent servir dans des rencontres’. Quel est donc le motif qui a poussé Huygens en 1657 et 1658 à s'occuper plus activement de problèmes sur les nombres? Il nous le révèle dans une de ses lettresGa naar voetnoot10), où l'on lit: ‘Je n'adjousteray rien touchant le traité de Monsieur FrenicleGa naar voetnoot11) si non que je suis marry de n'avoir pas sceu, auparavant que de veoir la solution de ces problemes, que Monsieur de Fermat la jugeoit de telle importance. Car encore que je ne me sois jamais guere appliquè aux questions purement arithmetiques je n'aurais pas laissè d'entreprendre celles cy, afin de meriter s'il m'eust estè possible l'estime de ce grand homme’Ga naar voetnoot12). | |
[pagina 186]
| |
Ajoutons qu'une fois lancé dans cette voie, qui n'était pas de celles qu'il préférait suivre mais où ses relations avec les géomètres français de son époque l'avaient poussé, il n'a pas manqué de faire des remarques ingénieuses sur l'équation de Pell, d'inventer un bel algorithme pour trouver le résidu de la division d'un grand nombre p.e. par le nombre 7Ga naar voetnoot1) et d'indiquer de nouveaux caractères pour reconnaître si un nombre donné est un non-carréGa naar voetnoot2).
Déjà en 1646 le père Mersenne tâcha, mais avec peu de succès, d'intéresser le jeune Huygens, âgé alors de dix-sept ans, aux problèmes sur les nombresGa naar voetnoot3). En 1656, après son premier séjour à ParisGa naar voetnoot4), l'influence des mathématiciens français commence à se faire sentir. Il croit être agréable à Mylon en lui mandantGa naar voetnoot5) que van Schooten lui a ‘monstrè une reigle de Monsieur des CartesGa naar voetnoot6) pour trouver des nombres qu'on appelle amicabiles’. Il s'est lui-même appliqué à cette recherche et il veut savoir si Mylon a quelque règle semblableGa naar voetnoot7). Nous ne savons pas quels étaient ces deux problèmes de Fermat envoyés en mai 1656 dont il fut question plus hautGa naar voetnoot8). Ce ne fut qu'en mars de l'année suivante | |
[pagina 187]
| |
que Huygens reçut le célèbre problème qui a occupé tant de mathématiciensGa naar voetnoot9), savoir celui de trouver des nombres entiers satisfaisant à l'équation 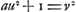 , où a est un nombre entier donné; équation à laquelle on a associé bien à tort le nom de PellGa naar voetnoot10).
Voici les résultats obtenus par Huygens dans ses recherches sur cette équation: 1o. il montra que chaque solution de l'une des équations , où a est un nombre entier donné; équation à laquelle on a associé bien à tort le nom de PellGa naar voetnoot10).
Voici les résultats obtenus par Huygens dans ses recherches sur cette équation: 1o. il montra que chaque solution de l'une des équations 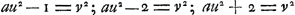 en amène une autre de l'équation en questionGa naar voetnoot11); 2o il remarqua qu'il en est de même pour chaque solution d'une équation en amène une autre de l'équation en questionGa naar voetnoot11); 2o il remarqua qu'il en est de même pour chaque solution d'une équation 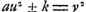 , pourvu que k satisfasse à une certaine conditionGa naar voetnoot12); 3o. il indiqua une solution dans les cas particuliers où , pourvu que k satisfasse à une certaine conditionGa naar voetnoot12); 3o. il indiqua une solution dans les cas particuliers où 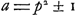 , ou p2 ± 2Ga naar voetnoot13); 4o. il montra qu'ayant trouvé une solution quelconque de l'équation de Pell on en peut déduire une infinité d'autresGa naar voetnoot14). , ou p2 ± 2Ga naar voetnoot13); 4o. il montra qu'ayant trouvé une solution quelconque de l'équation de Pell on en peut déduire une infinité d'autresGa naar voetnoot14).
On voit donc, qu'excepté dans les cas particuliers prémentionnés, Huygens n'avait d'autre moyen, pour trouver une solution d'une équation de Pell donnée, que d'essayer diverses valeurs de u l'une après l'autre afin d'examiner si elles satisfaisaient à l'équation de Pell elle-même ou à l'une des équations auxiliaires. Il est vrai que, dans cette besogne, les caractères qu'il avait trouvésGa naar voetnoot15) pour reconnaître très vite dans un grand nombre de cas qu'un nombre donné est un non-carré, lui pouvaient être utiles; mais cela n'empêchait pas que sa méthode ne fût très laborieuse et ne pût pas servir dans les cas fréquentsGa naar voetnoot16) où la plus petite | |
[pagina 188]
| |
solution est un nombre aslez grand. Sans douce Fermat et Frenicle possédaient des méthodes plus puissantes, mais ils ont eu le tort de ne pas les faire connaîtreGa naar voetnoot1). Or, ayant reçu, en septembre 1658, le ‘Commercium epistolicum’ de WallisGa naar voetnoot2), Huygens y trouva une méthode due à Brounker qui conduit au but avec sûreté, même dans les cas les plus compliqués, comme p.e. dans celui de a = 109, où la plus petite solution égale 15140424455100Ga naar voetnoot3). Quoique cette méthode soit encore loin de l'élégance et de la perfection obtenues plus tard dans cette matière par les mathématiciens modernesGa naar voetnoot4), on comprend que Huygens, après en avoir éprouvé l'efficacité, ne manqua pas de témoigner à Wallis de son admiration pour cette invention, tout en y apportant, bien à raison, cette restriction: qu'il n'en resulte pas, comme Wallis le prétendait, que chaque équation de Pell doit admettre une solutionGa naar voetnoot2). | |
Rectification de la parabole et quadrature des surfaces des conoïdes parabolique, elliptique et hyperbolique.Les problèmes de la rectification de la parabole et de la quadrature de la surface du conoïde parabolique étaient présents dans les esprits des mathématiciens au temps où Huygens commença sa carrière scientifique. En 1646 déjà, lorsqu'il était âgé de 17 ans, il rencontra dans les ‘Cogitata physico-mathematica’ de MersenneGa naar voetnoot5) une fausse quadrature de la surface du conoïde paraboliqueGa naar voetnoot6). De même, en 1656, Huygens reconnut la fausseté de la rectification de la parabole, proposée par HobbesGa naar voetnoot7). | |
[pagina 189]
| |
Ainsi l'on comprend que, lorsque, le 27 octobre 1657, il trouva la solution des deux problèmes pour autant qu'elle était possible, savoir leur réduction respectivement à la quadrature de l'hyperbole et à celle du cercle, il fit sortir de sa plume le fameux ‘εὕρηϰα’Ga naar voetnoot8) dont il avait coutume de marquer dans ses manuscrits les endroits où il venait d'exposer une découverte importante. Ensuite il se mit à rédiger à la mode archimédienne les démonstrations des théorèmes qu'il avait trouvésGa naar voetnoot9); sans doute avec l'intention de les faire paraître dans un nouveau traité géométrique du genre de ceux qu'il avait déjà publiés. Vers le même temps il communiqua à de SluseGa naar voetnoot10) et à van SchootenGa naar voetnoot11) les résultats de sa quadrature de la surface du conoïde parabolique pour quelques cas particuliers, sans toutefois leur saire connaître ni sa méthode, ni la solution du cas général. De la lettre qu'il avait reçue, van Schooten donna lecture à van HeuraetGa naar voetnoot12). Huygens nous assureGa naar voetnoot13), et il n'y a pas lieu d'en douter, que ce fut cette lecture qui inspira à van Heuraet son article ‘De transmutatione curvarum linearum in rectas’Ga naar voetnoot14), où, en trois pages, il expose une méthode générale pour réduire la rectification d'une courbe à la quadrature d'une autre et l'applique à la rectification de la parabole cubique et à la réduction de celle de la parabole ordinaire à la quadrature de l'hyperbole. À la suite de cette communication, van Heuraet fit bientôt parvenir à Huygens sa solution à lui du problème de la quadrature de la surface du conoïde paraboliqueGa naar voetnoot15). Elle correspond à celle de Huygens pour le fond, mais en diffère beaucoup par la formeGa naar voetnoot16). Or, Huygens avait obtenu son résultat d'une manière assez détournée, moitié algébrique, moitié géométrique, se basant sur une propriété | |
[pagina 190]
| |
de la suite des nombres carrés impairs 1, 9, 25, etc., et, en fin de compte, sur la cubature du conoïde hyperbolique obtenue déjà par ArchimèdeGa naar voetnoot1). Il n'était pas probable que van Heuraet eût suivi la même voie. Il fallait donc qu'il en existât une autre plus directe et Huygens ne tarda pas à la découvrir; en la suivant il retrouva le résultat de van Heuraet dans la forme même dans laquelle celui-ci l'avait énoncéGa naar voetnoot2). De plus, il aperçut que la méthode qu'il venait de trouver pouvait s'appliquer également à la quadrature des surfaces des conoïdes hyperboliques et elliptiques. En effet, la nouvelle méthode apprenait à réduire la quadrature de la surface de révolution engendrée par une courbe méridienne donnée à la quadrature d'une courbe plane. Lorsque la première courbe était une parabole, la courbe adjointe l'était égalementGa naar voetnoot3); lorsqu'elle était une hyperbole ou une ellipse l'adjointe était, dans le premier cas une hyperboleGa naar voetnoot4), dans le second, selon les circonstances, une hyperboleGa naar voetnoot5) ou une ellipseGa naar voetnoot6). Cela signifiait qu'on pouvait réduire la détermination du rayon d'un cercle dont l'aire est égale à celle de la surface d'un conoïde hyperbolique ou elliptique, ou bien à la quadrature de l'hyperbole et, par conséquent, aussi à la rectification de la parabole, ou bien à la quadrature du cercle. C'était là une invention importante qui valait la peine d'être poursuivie en détail. Et, en effet, Huygens réussit bientôt à trouver des constructions très élégantes pour le rayon de ce cercle d'aire égaleGa naar voetnoot7). Évidemment ces nouvelles découvertes méritaient d'être insérées dans le traité que Huygens avait projeté. Mais une difficulté se présenta. Jusqu' ici, en rédigeant ses ouvrages géométriques, Huygens avait toujours suivi scrupuleusement dans ses démonstrations la méthode des anciens de laquelle il donne, dans une annotation de 1659Ga naar voetnoot8), une analyse, remarquable par sa généralité. Or, pour appliquer cette méthode on devait circonscrire aux grandeurs en question (longueurs, aires ou volumes) d'autres qui ne les surpassent que d'une quantité | |
[pagina 191]
| |
aussi petite qu'on le veut, et on devait prouver rigoureusement qu'il en est ainsi, en partant de postulats bien définisGa naar voetnoot9). Par des artifices souvent très ingénieuxGa naar voetnoot10), Huygens avait réussi jusqu' à présent à satisfaire à ces exigences, mais il prévoyait que pour les résultats nouvellement obtenus cela demanderait un travail très pénible et d'une valeur douteuse. Il se décida donc à une sorte de compromisGa naar voetnoot11); c'est-à-dire il résolut de se servir quelquefois des ‘indivisibles’Ga naar voetnoot12), se bornant en ce cas à fournir non pas une démonstration rigoureuse, mais seulement ‘le fondement d'une telle démonstration, de sorte qu'apres l'avoir examiné ceux qui s'y connaissent ne sauraient douter de la possibilité d'une démonstration rigoureuse’. Toutefois il ne changera pas les parties qu'il a déjà rédigéesGa naar voetnoot13). Elles pourront ‘servir de preuve et en quelque sorte d'exemple pour montrer que les autres parties auraient pu être arrangées de la même façonGa naar voetnoot14)’. | |
[pagina 192]
| |
Conformément à ces intentions Huygens rédigea la partie du traité projeté qui se rapporte à l'étude détaillée des courbes adjointes de la parabole, de l'hyperbole et de l'ellipseGa naar voetnoot1). Ensuite il cessa de s'en occuper; probablement parce que la première ardeur de l'invention était passée et qu'il était attiré par d'autres travauxGa naar voetnoot2). Enfin, en 1673, il se contenta de donner dans son ‘Horologium oscillatorium’Ga naar voetnoot3) les principaux résultats qu'il avait obtenus, sans y joindre de démonstrations; ce qu'il jugea alors d'autant moins nécessaire que Wallis avait publié dans ses ‘Tractatus duo’ de 1659, les quadratures de surfaces courbes de conoïdes avec les déductionsGa naar voetnoot4).
Nous n'avons pas encore parlé de la deuxième Partie (p. 324-334) de la Pièce N.o X; elle occupe une place à part dans les recherches de Huygens sur la quadrature des surfaces des conoïdes hyperboliques et elliptiques. Soit, afin d'en montrer la portée, h1, la hauteur, S1 l'aire de la surface courbe d'un conoïde elliptique découpé d'un sphéroïde aplati dont 2a1 est le plus grand axe et 2b1 le plus petit, qui est l'axe de révolution; soit de plus h2 la hauteur d'un | |
[pagina 193]
| |
conoïde hyperbolique, S2 l'aire de sa surface courbe appartenant à un hyperboloïde dont 2a2 est l'axe réel et de révolution, et 2b2 l'axe imaginaire. Posons encore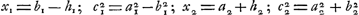 . On a alors: . On a alors:
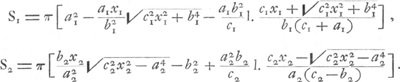 Si l'on prend la somme S1 + S2 de ces expressions, il est évident que dans certains cas les termes logarithmiques peuvent disparaître, de sorte que l'expression pour S1 + S2 devient purement algébrique. 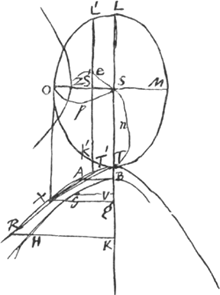 Or, dans la Partie qui nous occupe, Huygens a réussi à découvrir un de ces cas par des raisonnements géométriques. Pour y parvenir, il suppose en premier lieu que la courbe méridienne LOTMGa naar voetnoot5) du sphéroïde aplati, de révolution autour de OM, et celle HGB du conoïde hyperbolique, de révolution autour de TK, possèdent la même courbe adjointe RXT. Dans nos notations cela conduit aux relations: 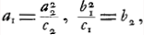 et l'on remarquera que ces relations amènent l'égalité des coefficients
et l'on remarquera que ces relations amènent l'égalité des coefficients 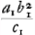 et et 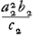 des termes logarithmiques dans les expressions pour S1 et S2. des termes logarithmiques dans les expressions pour S1 et S2.
Ensuite Huygens emploie une construction que nous allons expliquer. Consi- | |
[pagina 194]
| |
dérons
 à cet effet le conoïde correspondant au segment OLʹKʹO. Sa surface courbe est égale à l'espace mixtiligne OXATʹSʹO multiplié par 2π. De même la surface courbe du conoïde hyperbolique engendré par HGBK est égale à l'espace KRXABK multiplié également par 2π. Or, le premier de ces espaces est égal à un trapèze moins le segment hyperbolique XATʹX, et le second à un trapèze plus le segment RXAR. On peut donc, lorque ces segments sont égaux, construire avec la règle et le compas une ligne ρ, telle que 1/2 ρ2 est égal à la somme des espaces OXATʹSʹO et KRXABK, et cette ligne constituera alors le rayon d'un cercle dont l'aire est égale à la somme des aires des deux surfaces courbes conoïdales. Tout dépend ainsi de la construction de la corde AR qui, partant du point donné A, découpe de l'hyperbole TTʹAXR un segment ARXA égal au segment donné TʹAXTʹ; construction que Huygens apprend à exécuter à la p. 327Ga naar voetnoot1). C'est là en principe la découverte de Huygens; mais il reste à dire 1o qu'il se borne au cas du demi-sphéroïde LOTL, 2o qu'il remplace vers la fin ce demisphéroïde par un sphéroïde entier dont les axes sont à ceux du demi-sphéroïde comme 1 à √2Ga naar voetnoot2), 3o qu'il s'occupe surtout du cas particulier où les points X et A de la présente figure coïncidentGa naar voetnoot3). | |
[pagina 195]
| |
Ce cas exige BS = OX, c'est-à-dire 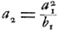 . Combinée avec . Combinée avec 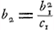 et avec et avec 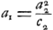 Ga naar voetnoot4), cette relation nous donne: Ga naar voetnoot4), cette relation nous donne:
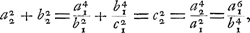 ou bien: 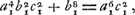 ou enfin: 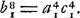 De cette derniere équation on déduit 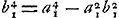 ; ce qui donne ; ce qui donne 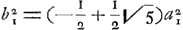 .
Si l'on écrit cette dernière équation sous la forme: .
Si l'on écrit cette dernière équation sous la forme: 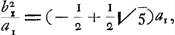 , elle nous dit que le ‘latus rectum’ de l'ellipse LOTM (par rapport à l'axe LT) est le plus grand segment de cet axe divisé en extrême et moyenne raison; résultat dont Huygens ne manqua pas de faire mention dans l'‘Horologium oscillatorium’Ga naar voetnoot5). , elle nous dit que le ‘latus rectum’ de l'ellipse LOTM (par rapport à l'axe LT) est le plus grand segment de cet axe divisé en extrême et moyenne raison; résultat dont Huygens ne manqua pas de faire mention dans l'‘Horologium oscillatorium’Ga naar voetnoot5).
Ajoutons encore, avant de passer à d'autres sujets, que déjà le 15 février 1658Ga naar voetnoot6), Huygens donna à de Sluse un aperçu de ses nouvelles découvertes, y comprise celle que nous venons d'expliquer. Il fit suivre cet aperçu le 26 févrierGa naar voetnoot7) par une description des constructions qui servent à la quadrature des sphéroïdes avec la recommandation de ne pas les montrer à d'autres personnes. Toutefois, l'année suivante, il résolut de faire ‘connaître partout’ son théorème sur la rectification de la paraboleGa naar voetnoot8). Il le fit, en effet, en y joignant ses inventions sur la quadrature des surfaces des conoïdes et sphéroïdes, en janvier et février 1659, à de Carcavy, à Wallis, à Pascal, à van Schooten et à BoulliauGa naar voetnoot9) et, encore, en septembre et octobre 1659, à Grégoire de St. Vincent et à Kinner à Löwen- | |
[pagina 196]
| |
thurnGa naar voetnoot1). Évidemment Huygens croyait avoir trouvé ainsi le moyen le plus efficace de se réserver la priorité de ses découvertes, en attendant qu'il aurait le loisir de les publier. Aussi fait-il un appel, dans l'‘Horologium oscillatorium’Ga naar voetnoot2), à sa correspondance avec de Sluse, Pascal, Wallis et d'autres pour constater cette priorité. Nous avons déjà vu quel a été l'esset de la communication à WallisGa naar voetnoot3). Pascal loua beaucoup les inventions de Huygens dans une lettre à de CarcavyGa naar voetnoot4) et dans la ‘Lettre de A. Dettonville a Monsieur Hugguens de Zulichem’Ga naar voetnoot5) qu'il publia en février 1659. En même temps il fit parvenir à Huygens une esquisse de sa méthode pour la solution du cas du conoïde parabolique, en y ajoutant que les cas du conoïde hyperbolique et des sphéroïdes lui semblaient bien difficiles; ‘ainsy’ poursuivit-il ‘ie n'y penseray pas seulement car ie suis persuadé qu'il y a plustot du blame que de l'honneur a accquerir en trauaillant sur les ouurages d'autruy et principalement quand ils sont traittez par des personnes excellentes comme Monsieur Hugguens’Ga naar voetnoot6). À Fermat Huygens avait seulement fait demander par l'intermédiaire de de CarcavyGa naar voetnoot7) si sa méthode s'étendait à trouver la dimension des surfaces courbes des conoïdes et des sphéroïdes. Fermat répondit affirmativement et afin que Huygens n'en pût douter il donna quelques indications sur les résultats, assurant qu'il les avait obtenus sans connaître ceux de HuygensGa naar voetnoot8). Il ajouta qu'il avait trouvé de même la quadrature de la surface courbe engendrée par la révolution d'une parabole autour de son appliquéeGa naar voetnoot9); savoir qu'elle se réduit à la quadrature de l'hyperbole. | |
[pagina 197]
| |
À ce propos Huygens écrivit à de CarcavyGa naar voetnoot10) qu'il croyait bien que ‘Monsieur de Fermat n'avoit veu’ aucune de ses propositions ‘puis qu'il l'assure’, mais que ‘d'autres peut estre seraient plus incredules, si en les donnant au public il n'allegue celuy a qui il les aie fait veoir auparavant. La mesure de la superficie du conoide que fait la parabole autour de l'appliquée laquelle il promet en supposant la quadrature de l'hyperbole sera quelque chose de nouveau si elle est vraye’. En réponse de Carcavy rassura Huygens sur les intentions de FermatGa naar voetnoot11) et lui fit parvenirGa naar voetnoot12) de la part de celui-ci le résultat de la quadrature en question, laquelle fut trouvée ‘subtile’ par Huygens qui pria de Carcavy d'exhorter Fermat à publier sa méthode si elle était nouvelleGa naar voetnoot13). | |
Recherches sur les paraboles et hyperboles de divers degrés, sur la conchoïde, la cissoïde et sur d'autres courbes.
| |
[pagina 198]
| |
résultatsGa naar voetnoot1), et aussi à en donner des démonstrations ‘Euclideo more’Ga naar voetnoot2). Il commence, à cet esset, par déterminer les tangentes des courbes prémentionnées qu'il appelle ‘paraboloïdes.’ Ensuite il emploie d'une manière ingénieuse les propriétés de ces tangentes pour obtenir les quadraturesGa naar voetnoot3) et les cubatures cherchées dont il sait déduire enfin la situation des centres de gravité. Il résume ses résultats en six règlesGa naar voetnoot4) dont les trois premières correspondent exactement aux règles générales empruntées par Mersenne à Fermat qui, à ce qu'il paraît, était aussi en possession des autres règlesGa naar voetnoot5). Après donc avoir trouvé à sa satisfaction les règles pour les ‘paraboloïdes’, Huygens s'aperçut que ses raisonnements étaient applicables avec peu de modifications aux ‘hyperboloïdes’, savoir aux courbes xbya = k. Il étudia donc ces courbes et s'occupa surtout de ce qui les distingue des ‘paraboloïdes’, c'est-à-dire des espaces qui s'étendent jusqu'à l'infini entre les courbes et leurs asymptotesGa naar voetnoot6). Ajoutons encore que Huygens mentionne ses recherches sur les ‘paraboloïdes’ et les ‘hyperboloïdes’ dans l'‘Horologium oscillatorium’, p. 90 de l'édition originale.
Les travaux de la Pièce No. IX doivent pour la plupart leur origine à la correspondance assidue qui eut lieu entre Huygens et de Sluse dans les années 1657 et 1658. Ils peuvent servir à expliquer plusieurs passages dans les lettres de Huygens à son ami. | |
[pagina 199]
| |
D'abordGa naar voetnoot7) les deux correspondants s'occupent des ‘perles de de Sluse’, savoir des courbes dont les équations sont comprises dans l'équation générale 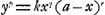 . Ils les complètent, si c'est nécessaire, par leurs symétriquesGa naar voetnoot8) . Ils les complètent, si c'est nécessaire, par leurs symétriquesGa naar voetnoot8) 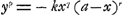 , afin d'obtenir des boucles fermées dont ils déterminent les tangentes, les points d'inflexion, les quadratures et les centres de gravité, comme aussi les cubatures de leurs solides de révolution. Ensuite c'est le tour de la conchoïdeGa naar voetnoot9) et de la cissoïdeGa naar voetnoot10). Quelquefois d'autres mathématiciens, van SchootenGa naar voetnoot11), HuddeGa naar voetnoot12), van HeuraetGa naar voetnoot13), WallisGa naar voetnoot14) et MylonGa naar voetnoot15), participent à la discussion de ces mêmes sujets. , afin d'obtenir des boucles fermées dont ils déterminent les tangentes, les points d'inflexion, les quadratures et les centres de gravité, comme aussi les cubatures de leurs solides de révolution. Ensuite c'est le tour de la conchoïdeGa naar voetnoot9) et de la cissoïdeGa naar voetnoot10). Quelquefois d'autres mathématiciens, van SchootenGa naar voetnoot11), HuddeGa naar voetnoot12), van HeuraetGa naar voetnoot13), WallisGa naar voetnoot14) et MylonGa naar voetnoot15), participent à la discussion de ces mêmes sujets.
Ce qui intéresse beaucoup Huygens et de Sluse, ce sont ces espaces dont nous avons déja parlé à propos des ‘hyperboloïdes’, qui s'étendent à l'infini entre les courbes et leurs asymptotes et dont toutefois les aires, ou les volumes des solides de révolution, sont parfois finisGa naar voetnoot16). C'est de Sluse qui donne à cet intérêt l'expression la plus pittoresque lorsqu'il se vante de pouvoir donner la mesure d'un vase de poids médiocre mais que, cependant, le plus grand glouton ne pourrait viderGa naar voetnoot17). | |
[pagina 200]
| |
Remarquons encore l'importance que Huygens et de Sluse, et surtout ce dernier, attachent aux réductions à la quadrature du cercle ou de l'hyperbole. Chaque problème dont la solution amènerait en même temps une de ses quadratures est appelé par de Sluse une ‘ἀπαγωγὴν’; et les nombreuses quadratures et cubatures de ce genre qui se présentent dans sa correspondance avec Huygens, il les considère principalement comme des ‘ἀπαγωγάς’ plus ou moins intéressantesGa naar voetnoot1). | |
Recherches sur les propriétés géométriques de la cycloïde.C'était le père Mersenne qui, comme sur tant d'autres sujets, fournit à Huygens, en 1646, les premiers renseignementsGa naar voetnoot2) en partie inexactsGa naar voetnoot3) sur des travaux existants concernant la cycloïde; mais ces communications ne semblent pas avoir donné lieu du côté du jeune Huygens à des recherches originales. Il en fut autrement, lorsque, douze années plus tard, Boulliau lui envoyaGa naar voetnoot4) les deux lettres circulaires dans lesquelles Pascal, sous le pseudonyme Dettonville, proposa ‘à tous les géomètres de l'univers’ les problèmes suivants: Trouver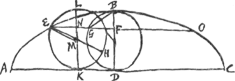 l'aire d'un demi-segment cycloïdal EBFGa naar voetnoot5) et la situation de son centre de gravité, les volumes des solides engendrés par la révolution de ce segment autour de BF et autour de EF, ainsi que | |
[pagina 201]
| |
les centres de gravité de ces solides et aussi des solides partiels qu'on obtient en les coupant par un plan passant par leur axe de révolution. Pascal, d'ailleurs, n'exigeait pas que tous les calculs fussent exécutés; il se contenterait, écrivit-il, de chaque solution qui établirait, soit à la manière des anciens, soit par la méthode des indivisibles, comment on pourrait déterminer toutes les choses demandées. Toutefois il réclamait la démonstration complète, ou le calcul complet, dans les cas particuliers où le point F se confond avec le point D, ou avec le centre du cercle générateur BGD. Les prix seraient décernés à ceux qui, avant le 1er octobre 1658, auraient résolu les questions proposéesGa naar voetnoot6). Ensuite dans sa seconde lettre circulaire il avertit qu'il suffirait de calculer la situation du centre de gravité du solide engendré par une demi-révolution de l'espace ABD autour de la base ADGa naar voetnoot7) Huygens, ayant pris connaissance de ces problèmes, ne tarda pas à se mettre à l'oeuvre. Il trouva d'abord l'aire BEF dans les deux cas particuliers signalés par PascalGa naar voetnoot8). Ensuite il détermina l'aire du segment EBO dans le cas généralGa naar voetnoot9) et | |
[pagina 202]
| |
découvrit à cette occasion un cas remarquable où ce segment est carrable sans
 supposer la quadrature du cercleGa naar voetnoot1). Enfin il trouva, dans les deux cas particuliers, la distance du centre de gravité du segment EBO à sa base EO et en déduisit le volume du solide engendré par la révolution autour de cette baseGa naar voetnoot2). Il put mander, à Boulliau, le 25 juillet 1658, qu'il avait obtenu ces résultatsGa naar voetnoot3). Il ajouta qu'ayant manqué le reste, il ne pouvait aspirer au prix proposé par l'auteur; d'ailleurs les problèmes lui ‘semblent si difficiles pour la pluspart, qu'il doubte fort si celuy mesme qui les a proposez les pourroit tous resoudre’. Toutefois ces problèmes et surtout celui signalé en particulier dans la seconde circulaire, ne lui laissaient pas de repos. Il reprit donc ce dernier problème et il réussit, en effet, par des artifices des plus ingénieux à déterminer la distance du centre de gravité du solide en question au plan ABDGa naar voetnoot4), de sorte que pour connaître complètement la situation du centre de gravité demandé il ne lui manqua plus que la distance au plan décrit par BDGa naar voetnoot5). Il communiqua à BoulliauGa naar voetnoot6) ce résultat qui était faussé par des erreurs de calculGa naar voetnoot7), en ajoutant de nouveau qu'il croyait à peine ‘que tous les dits problemes estoyent possibles’. | |
[pagina 203]
| |
En janvier 1659 les recherches de Huygens sur la cycloïde reçurent une nouvelle impulsion. Pascal lui avait fait parvenir son ‘Historia cycloidis’Ga naar voetnoot8). Il y mentionne la rectification de la cycloïde par Wren et propose quelques nouveaux problèmes relatifs au centre de gravité d'un arc cycloïdal, comme EBO, et aux dimensions et centres de gravité des surfaces engendrées par la révolution d'un tel arc autour de sa flèche ou de sa cordeGa naar voetnoot9). Huygens admira beaucoup l'invention de WrenGa naar voetnoot10), quoiqu'il ne sût pas encore si sa rectification s'appliquait à un arc quelconque - ce qui était bien le casGa naar voetnoot11) - ou seulement à la cycloïde entière. Il réussit bientôt à retrouver le résultat de WrenGa naar voetnoot12) et à résoudre le premier des nouveaux problèmes, savoir celui de déterminer le centre de gravité de l'arc EBOGa naar voetnoot13). Il fut agréablement surpris.Ga naar voetnoot14) par la simplicité du résultat, indiquant que le centre de gravité de cet arc divise toujours la flèche BF dans la raison de 2 à 1. Toutes ces dernières recherches partaient de la connaissance de la tangente à la cycloïde, qui, en tout point E, est parallèle à la corde BG. Huygens avait rencontré cette propriété dans l'édition de van Schooten de la ‘Geometria’ de DescartesGa naar voetnoot15), mais il n'était pas entièrement content de la manière dont elle y est déduite. Il s'appliqua donc à en donner une nouvelle démonstrationGa naar voetnoot16) basée sur le postulat qu'une droite qui passe par un des points d'une courbe | |
[pagina 204]
| |
est tangente à cette courbe lorsque les points de la courbe qui se trouvent de part et d'autre du point considéré et dans son voisinage, sont situés du même côté de la droite; postulat qu'il emploie souvent dans ces sortes de démonstrationsGa naar voetnoot1).
Quoique Pascal tâchât de faire parvenir à Huygens aussitôt qu'il lui fût possibleGa naar voetnoot2) la célèbre ‘Lettre de A. Dettonville à Monsieur de Carcavy suivie de traités de géométrie’Ga naar voetnoot3) publiée en décembre 1658, Huygens ne la reçut que le 8 mai 1659Ga naar voetnoot4). Il y trouva, du moins en principe, la solution de tous les problèmes proposés. En effet, dans la lettre elle-même et dans les traités qui l'accompagnent, Pascal sait se procurer, pour le cas spécial de la cycloïde, presque toutes les ressources, nommément l'intégration par parties, dont dispose aujourd'hui le mathématicien moderne. Par suite, ses méthodes sont plus générales et plus puissantes que celles de Huygens, qui pour chaque nouveau problème devait chercher de nouveaux artifices; mais, comme Huygens s'exprimeGa naar voetnoot5) ‘il faut avouer que c'est un labyrinthe lors que l'on veut faire la construction de quelque probleme, et pour cela je voudrois qu'il eust partout pris seulement un cas le plus facile pour en donner le calcul tout du long et non seulement le dernier facit, ou bien un exemple a chaque Theoreme’. C'est pourquoi Huygens choisit, pour y appliquer la méthode de Pascal, deux cas particuliers de l'un des problèmes qu'il n'avait pas pu résoudre auparavant. Il envoya sa solution du cas le plus compliqué à de CarcavyGa naar voetnoot6), le priant de lui dire s'il avait ‘bien supputè’. Quant à la solution de l'autre cas, nous la reproduisons dans la Cinquième Partie de la Pièce No. XI, p. 376Ga naar voetnoot7). Par l'application du théorème de Guldin on en déduit facilement la | |
[pagina 205]
| |
cubature trouvée par RobervalGa naar voetnoot8) déjà avant 1646 et mentionnée par nous dans la note 3 de la p. 201. Encore en août 1693, Huygens témoigna à de la Hire de son admiration pour cette invention de RobervalGa naar voetnoot9). Ajoutons que vers le commencement de mars 1660 Huygens reçutGa naar voetnoot10) le traité ‘De cycloide’ de WallisGa naar voetnoot11), où celui-ci résoud les problèmes de Pascal à l'aide des méthodes de l'‘Arithmetica infinitorum’Ga naar voetnoot12). Wallis s'y plaint violemment des procédés de Pascal. Dans la polémique qui s'ensuivit, Huygens, sans y prendre une part active, servit d'intermédiaire entre Wallis et de CarcavyGa naar voetnoot13). | |
Théorie des développées et des courbes parallèles. À propos des recherches sur la cycloïde, dont nous venons de traiter, nous avons dû constater une certaine infériorité des méthodes de Huygens, comparées à celles de Pascal et de Wallis. Par ses travaux sur la théorie des développées, Huygens a pris, pour ainsi dire, une revanche éclatante. En effet, en développant cette théorie, il a ajouté à l'analyse des courbes planes un chapitre intéressant et beau dont la priorité lui appartient sans contestation. Il faut en chercher l'origine dans l'emploi des petits arcs BA et CDGa naar voetnoot14) que Huygens appliqua en 1658 à ses horloges à pendule afin de rendre la période des oscillations indépendante de leur largeur. Il est clair que ces arcs sont | |
[pagina 206]
| |
 avec la courbe décrite par la masse pesante dans la relation d'une développée à sa développante. D'abord c'était à l'expérience que Huygens demanda ‘de quelle maniere et combien’ il devait ‘les plier pour esgaler entre eux les coups des plus larges jusqu'aux plus menus’. Il y réussit si bien avec ‘deux Horologes de cette façon, qu'en trois jours il n'y eust jamais entre elles la difference d'autant de secondes: quoyque cependant’ il en changeât ‘souvent les poids, les rendant plus ou moins pesants’Ga naar voetnoot1). C'est au 1 décembre 1659Ga naar voetnoot2) que Huygens découvrit le tautochronisme de la cycloïde, et déjà le 6 décembre il put écrire à van SchootenGa naar voetnoot3) qu'il avait trouvé ces jours ce qu'il n'avait jamais espéré de connaître, c'est-à-dire la forme exacte qu'il faut donner aux arcs AB, CD afin d'égaliser absolument les oscillations. Cette invention lui sembla la plus heureuse de toutes celles qui se soient jamais présentées à luiGa naar voetnoot4). Ayant trouvé une méthode générale pour déterminer la développée d'une courbe donnée, Huygens l'appliqua non seulement à la cycloïdeGa naar voetnoot5), mais aussi aux coniques et aux paraboles et hyperboles de divers degrés. Dans la Pièce No. XV nous avons reproduit ses recherches de 1659 sur les développées de l'ellipse et de l'hyperboleGa naar voetnoot6). Elles nous apprennent comment Huygens a obtenu les résultats qui sont mentionnés dans l'‘Horologium oscillatorium’ sans qu'on y trouve leur déductionGa naar voetnoot7). Nous faisons suivre dans la même Pièce la théorie générale des développées telle qu'elle fut inventée par Huygens dans cette même annéeGa naar voetnoot8). L'exposition | |
[pagina 207]
| |
s'écarte en plusieurs points de celle qu'il donna plus tard dans l'‘Horologium oscillatorium’Ga naar voetnoot9). Elle en diffère surtout en ce qu'elle est accompagnée de considérations sur les courbes parallèles et équidistantes, qui manquent entièrement dans cet ouvrage. Disons encore que dans le manuscrit dont nous avons emprunté la Pièce No. XV on trouve aussi quelques calculs incomplets sur les développées des paraboles et hyperboles de divers degrés qui montrent que les résultats qui se rapportent à ces courbes dans l'‘Horologium oscillatorium’Ga naar voetnoot10), furent découverts eux aussi en cette année 1659. |
|