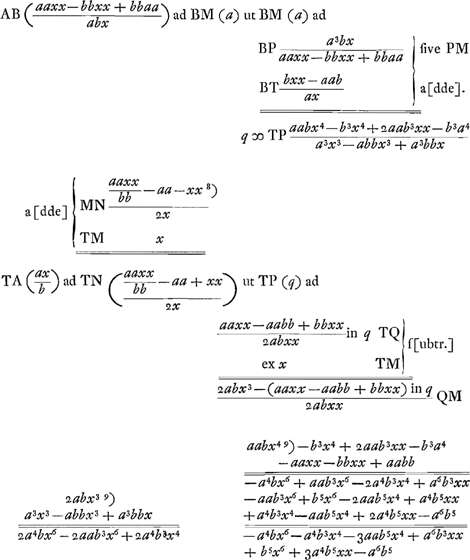
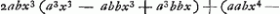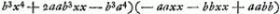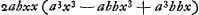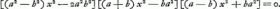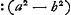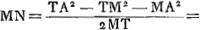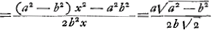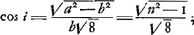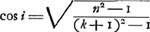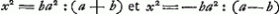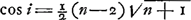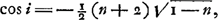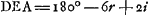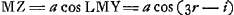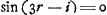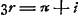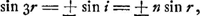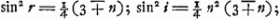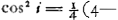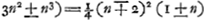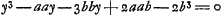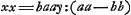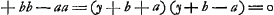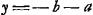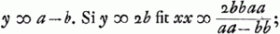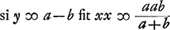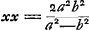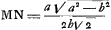numeris exhibita fuerit. dein ex xx radicem extrahendo habebitur valor x, quae representat lineam MT, quando numerus a etiam radium MA significat. Porro ut b ad a ita sit x ad aliam, ea erit TA. Et ex tribus lateribus trianguli MTA, faciendo ut MT ad summam TA, AM ita eorum differentia ad aliam, et ab ea auferendo TM, et accepto residui semisse habebitur MN. Jam ut AM ad MN ita sit radius in canone sinuum ad aliam quae erit sinus anguli MAN et ejus complimenti AMN sinus erit AN. Ut autem a ad b ita sit sinus AN ad alium, is erit MR sinus anguli MAR. Denique angulus MAN una cum triplo MAR auferatur a duobus rectis; reliquum bis sumtum dabit angulum semidiametri Iridis secundariaeGa naar voetnoot14). |
-
voetnoot1)
- La pièce a été empruntée aux p. 148-151 du Manuscrit C.
-
voetnoot2)
- Le même problème fut traité par Descartes au lieu cité dans la note 3, p. 146 du Tome présent. Consultez sur sa méthode la note 4, p. 147. La table, dont il est question dans cette note, contient de même les valeurs de l'angle DEA de notre figure, et Descartes trouve de cette manière 51o 54′ pour sa valeur minimum dans le cas de l'eau.
-
voetnoot3)
- Huygens annota en marge ‘haec melius folio sequenti’. Voir, à ce propos, l'‘Appendice IX’, p. 169 du Tome présent, qui donne une autre leçon de beaucoup simplifiée du début de la pièce présente jusqu' au commencement des calculs.
-
voetnoot4)
- Il s'agit de l'‘Appendice II’, p. 146 du Tome présent. En effet, puisque l'angle CBH est égal à l'angle BAE, HB représentera le rayon incident dont BC est le rayon réfracté. On peut donc identifier HB avec le rayon PF de la figure de la p. 146 et DE avec le rayon KO de cette même figure; mais alors la relation ∠OKN = 2∠DAB, démontrée à la p. 147, se réduit à celle du texte, c'est-à-dire, à ∠EDK = 2∠CMO. Quant à la relation ∠EDK = 2∠BML, pour la déduire il faut observer que EDK est l'angle qu'un rayon comme HB ou EA fait avec le rayon qu'il engendre après deux réfractions et une réflexion. En identifiant ensuite EA avec le rayon PF de la figure de la p. 146, on voit que la relation mentionnée, ∠OKN = 2∠DAB, amène cette fois ∠EDK = 2∠BML.
-
voetnoot5)
- On a DKE = BHA = ABC = 2SBM et KDE = 2BML = 2SMB.
-
voetnoot6)
- De cette manière ΔMBP devient isocèle et MP parallèle à CB.
-
voetnoot7)
- Comparez la Prop. II de la p. 15 du Tome présent.
-
voetnoot8)
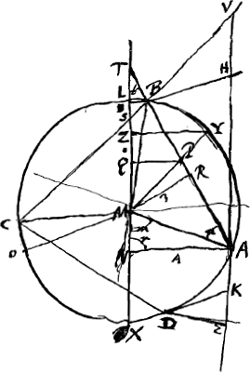
- MN est calculé à l'aide du ΔAMT dont les trois côtés sont connus.
-
voetnoot9)
- Il s'agit ici du calcul du numérateur de l'expression pour QM, après substitution de la valeur de q.
-
voetnoot9)
- Il s'agit ici du calcul du numérateur de l'expression pour QM, après substitution de la valeur de q.
-
voetnoot10)
- L'expression trouvée pour le numérateur
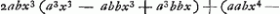 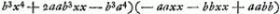 est divisée par b puisque ce facteur apparait dans le dénominateur est divisée par b puisque ce facteur apparait dans le dénominateur 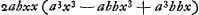 . .
-
voetnoot11)
- Voici donc la grandeur qui doit être rendue maximum; pour en trouver la condition Huygens applique la règle exposée en 1659 par Hudde à la p. 511 de l'ouvrage cité dans la note 5, p. 360 du Tome II.
-
voetnoot12)
- Plus tard Huygens ajouta: ‘potest dividi. vid. lib.’ En effet, l'équation dont il s'agit peut s'écrire
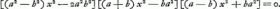
Or, des trois valeurs pour x2 auxquelles cette équation conduit, la première x2 = 2a2b2: 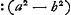 , est la seule qui puisse servir. Elle amène , est la seule qui puisse servir. Elle amène
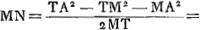
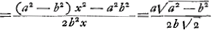
c'est-à-dire, si i représente l'angle d'incidence XMA, et n l'indice de réfraction:
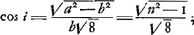
ce qui est conforme à la formule générale:
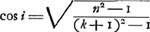
pour l'angle d'incidence qui appartient au kième arc-en-ciel (voir p.e. J.M. Perntner, Meteorologische Optik, Wien, Braumüller, 1906, p. 498-502).
Quant aux racines 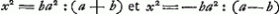 qui, en posant a = n, b = 1, conduisent aux valeurs: qui, en posant a = n, b = 1, conduisent aux valeurs:
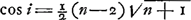 et et
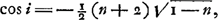 elles s'expliquent par le fait que Huygens n'a pas déterminé directement la valeur minimum de l'angle
elles s'expliquent par le fait que Huygens n'a pas déterminé directement la valeur minimum de l'angle 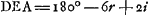 (où r est l'angle de réfraction MAB); mais celle du segment (où r est l'angle de réfraction MAB); mais celle du segment 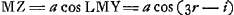 . .
De cette manière il introduit nécessairement dans sa solution les valeurs de i qui satisfont à la relation 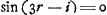 ; dont on déduit 3r = i ou ; dont on déduit 3r = i ou 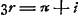 , ou bien , ou bien
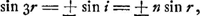
d'où il résulte successivement: 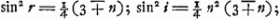 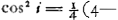 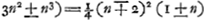 ; conforme aux valeurs fausses indiquées quelques lignes plus haut. ; conforme aux valeurs fausses indiquées quelques lignes plus haut.
Ajoutons que l'endroit cité par Huygens, où il expose la réductibilité de l'équation en x se trouve dans le Manuscrit G, à la page 25, sous la suscription: ‘aequatio ad secundam Iridem seu Exteriorem inveniendam ex refractionis proportione data, quae est inventa in libro C. Hanc ibi non videram quomodo posset dividi.’ Il y commence par réduire cette équation a la forme 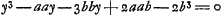 à l'aide de la substitution à l'aide de la substitution 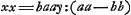 ; ensuite il divise par y-2b; ce qui amène yy+2by+ ; ensuite il divise par y-2b; ce qui amène yy+2by+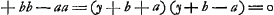 . Rejetant enfin la solution . Rejetant enfin la solution 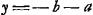 , sans doute parce qu'elle cond uit à une valeur imaginaire pour x, il conclut: ‘Ergo y ∞ 2b vel , sans doute parce qu'elle cond uit à une valeur imaginaire pour x, il conclut: ‘Ergo y ∞ 2b vel 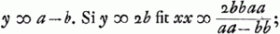 ; ;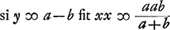 .’ .’
D'après le lieu où elle se trouve cette annotation doit dater de 1688 ou de 1689.
-
voetnoot13)
- Comme nous l'avons montré dans la note précédente, Huygens, s'il avait réussi à écarter les racines inefficaces de cette équation, aurait pu la simplifier à la forme:
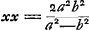 et trouver ensuite et trouver ensuite 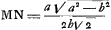 . .
-
voetnoot14)
- La page 151 du manuscrit contient encore quelques calculs qui se rapportent au cas de l'eau a = 4, b = 3, mais qui n'ont pas abouti.
|
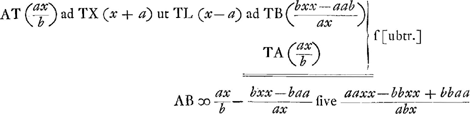
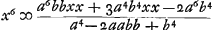 postquam in
postquam in