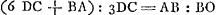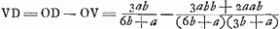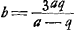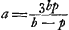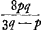Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 157]
| |
Appendice VIGa naar voetnoot1)
| |
[pagina 158]
| |
Ang. AES aequ. angulo EAB. Et ang. SEG aeq. ango. EKB. Ergo ang. AES ad angulum SEG ut DK ad BA. Hoc est ut tripla DC ad BA. et angulus AEG ad
 ang. AES ut 3 DC+BA ad 3 DC. Sed ang. AEO aequ. ango. AEG. et ang. EAO aequ. ango. AES. Ergo ang. AEO ad ang. EAO ut 3 DC+BA ad 3 DC. Ergo AO ad OE (OB) ut 3 DC+BA ad 3 DC. Ergo AB ad BO ut 6 DC+BA ad 3 DC. neglecta autem lentis crassitudine eadem est BO ac DO. Fit porro alia refractio in X, atque inde radius tendit secundum rectam XV, concurrens cum axe in V. Quod punctum invenitur faciendo ut OK ad OC ita OD ad OVGa naar voetnoot4). Et auferendo OV ab OD relinquitur DV distantia à lente quaesita puncti concursus parallelorum reflexorum.
Sit AB ∞ a; CD ∞ b. Ergo DK ∞ 3b. 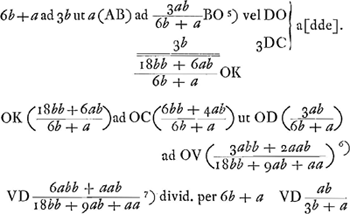 Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7) Si a ∞ b fit VD ∞ ¼ a. Si a infinite magna fit VD ∞ b. Si b infinite magna fit VD ∞ 1/3 a. fit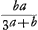 distantia concursus cum radij in superficiem BE primum incidunt, descripta ex VD mutatis invicem a in b. distantia concursus cum radij in superficiem BE primum incidunt, descripta ex VD mutatis invicem a in b.
| |
[pagina 159]
| |
Cum sit 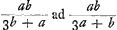 ut 3a+b ad 3b+a, apparet si a major quam b, etiam ut 3a+b ad 3b+a, apparet si a major quam b, etiam 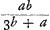 majorem fore quam majorem fore quam 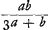 , hoc est, concursum tum longius distare cum convexior superficies soli obvertitur. , hoc est, concursum tum longius distare cum convexior superficies soli obvertitur.
Si lens planoconvexa sit, et convexa superficies radijs exponatur, fit distantia concursus aequalis radio convexi. Sed si plana radios primum excipiat fit eadem distantia concursus aequalis 1/3 radij convexitatis. 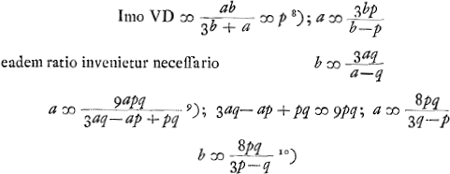 Ga naar voetnoot8)Ga naar voetnoot9)Ga naar voetnoot10) Ergo a ad b ut 3p-q ad 3q-p. bon ad cognoscendas convexitates lentis datae per reflexionem. |
|