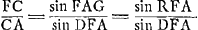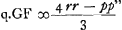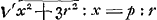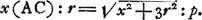Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 146]
| |
Appendice IIGa naar voetnoot1)
| |
[pagina 147]
| |
mam definit; Estque diversus pro diversa proportione refractionis quam habet materia sphaerae diaphanae. Si ex aqua constat angulus OKN cum maximus est aequat grad. 41. 30′Ga naar voetnoot4) atque ea est semidiameter quoque iridis caelestis. At si vitrea est, idem angulus NKO est 21 gr. 52′Ga naar voetnoot5) circiter. Data igitur refractionis proportione investigandum sit quantus maximus esse possit angulus NKO. Jungatur AD, et producatur donec occurret producto radio PF in R, et jungatur RK. Ea igitur erit in directum ipsi KO. Nam quia FD, DK aequales sunt, eadem quantitate refringitur radius DK egrediendo densum, atque PF ingrediendo. ideoque angulus DKO aequalis angulo DFP: sed et angulus DKR angulo DFR aequalis est, quia triangula KDR, FDR habent angulos ad D et latera eos comprehendentia aequalia, ergo duobus simul angulis DFP et DFR hoc est duobus rectis aequales sunt anguli DKO et DKR; ideoque RKO linea recta. Est autem angulus OKN aequalis angulo KRF quia KN parallela RF. estque angulus KRF duplus anguli ARF sive DAB. Igitur et angulus OKN anguli DAB duplus. Ergo ut angulus OKN sit maximus qui esse possit, oportet angulum BAD quoque maximum esse. Est autem data ratio lineae FDCGa naar voetnoot6) ad CA, nam haec eadem est quae ratio refractionisGa naar voetnoot7), quia FD ponitur refractio radij PF ipsi AC paralleli, sicut in dioptricis ostendimusGa naar voetnoot8). Igitur huc tota res redit ut quaeratur punctum F in circumferentia MFB, ejusmodi, ut ductâ FC quae ad CA datam habeat rationem, abscindatur arcus BD maximus qui hoc modo abscindi potest. ducantur ad MB perpendiculares FG, DL. Ergo AL minimam oportet esse, quae possit. Vocetur semidiam. AM, r; et proportio refractionis sit quae est lineae p ad r, et AC sit x. Ergo quia ut r ad p ita est AC ad CF erit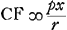 , et per 13 l. 1. Elem.Ga naar voetnoot9) erit , et per 13 l. 1. Elem.Ga naar voetnoot9) erit
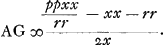
| |
[pagina 148]
| |
Fiat deinde ut
 Ga naar voetnoot1). Ga naar voetnoot2) Ponatur jam x+y ∞ x et substituantur potestates ejus in locum potestatum x, ut rursus habeatur AL, quae cum praecedenti compareturGa naar voetnoot3).  | |
[pagina 149]
| |
Post alternas multiplicationes per denominatorem utrumque omnia dividenda per y; quo facto eae quantitates quibus adhuc y aderit
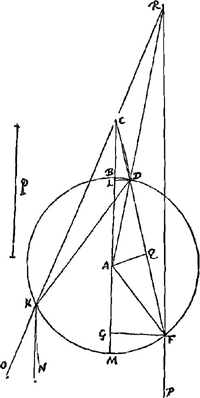 omnes delendae sunt, sed quae deleri debere constat non opus est scribere ut hic erunt omnia praeterquam quibus simplex y ineritGa naar voetnoot4). 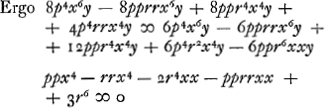 dividitur per xx-rr et fit ppxx-rrxx-3r4 ∞ ∞ 0 non tamen xx ∞ rr proposito convenit sed 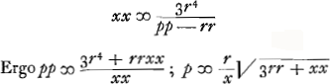 Verùm ut q.AB (rr) ad pp hoc est 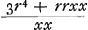 ita est q.AC (xx) ad q.CF ita est q.AC (xx) ad q.CF
 Ga naar voetnoot5) Ergo 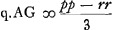 . Itaque cognitis p et r facile cognoscitur AG, et hinc angulus NKO. Nam ex sinu AG datur angulus AFG, cujus complementum angulus GAF. ergo datur et sinus GFGa naar voetnoot6). Habet autem GF ad AQ perpend. in FD proport. refractionis eandem scilicet quam FC ad CA quae data est. Ergo hinc datur AQ sinus anguli AFQ; cujus complementum angulus QAF. Hic autem bis sump- . Itaque cognitis p et r facile cognoscitur AG, et hinc angulus NKO. Nam ex sinu AG datur angulus AFG, cujus complementum angulus GAF. ergo datur et sinus GFGa naar voetnoot6). Habet autem GF ad AQ perpend. in FD proport. refractionis eandem scilicet quam FC ad CA quae data est. Ergo hinc datur AQ sinus anguli AFQ; cujus complementum angulus QAF. Hic autem bis sump- | |
[pagina 150]
| |
tus, addito angulo FAG, constituit angulum GAD quo ablato ex duobis rectis restat angulus DAB, cujus duplus est NKO, sub
 quo semidiameter iridis conspicietur ut superius dictum fuitGa naar voetnoot1). dato autem angulo NKO refractionis proportionem invenire solidumGa naar voetnoot2) est. Dato enim angulo NKO datur quoque dimidium ejus nempe angulus DAB. Ergo data est AL, quae vocetur a: et sit AC sicut prius ∞ x. Inventum autem fuit quod cum angulus NKO maximus est, AG est rr/x, Et tota CG ∞ 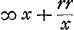 . Sed haec aliter quoque nunc exprimetur atque inde habebitur aequatio.
Sciendum itaque quod CD est ad CF ut ▭ FCD ad qu. FC. Est autem ▭ FCD ∞ ▭ MCB hoc est differentiae quadratorum AC, AB sive xx-rr; et antea inventum fuit qu. FC ∞ 3rr+xx. Ergo CD ad CF ut xx-rr ad 3rr+xx sed ut CD ad CF ita CL ad CG; estque CL ∞ x-a. Ergo erit . Sed haec aliter quoque nunc exprimetur atque inde habebitur aequatio.
Sciendum itaque quod CD est ad CF ut ▭ FCD ad qu. FC. Est autem ▭ FCD ∞ ▭ MCB hoc est differentiae quadratorum AC, AB sive xx-rr; et antea inventum fuit qu. FC ∞ 3rr+xx. Ergo CD ad CF ut xx-rr ad 3rr+xx sed ut CD ad CF ita CL ad CG; estque CL ∞ x-a. Ergo erit 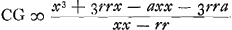 aequalis aequalis 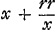 prius inventae. prius inventae.
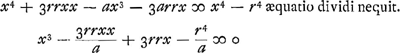 ad auferendum secundum terminum ponatur 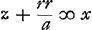 Ga naar voetnoot3)
Et invenitur Ga naar voetnoot3)
Et invenitur
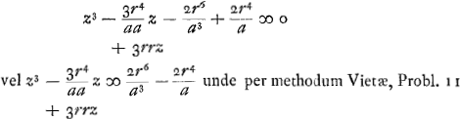 | |
[pagina 151]
| |
de Numerosa Potest. Res. radix extraheturGa naar voetnoot4), redactis prius omnibus ad numeros. Sic igitur inventa quantitate z, addendum est rr/a (quae est secans anguli DAB) et habebitur x, unde porro p innotescet, nam inventum est superius 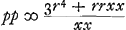 . Ergo inventa erit proportio refractionis nam ea est ut p ad r. . Ergo inventa erit proportio refractionis nam ea est ut p ad r.
Si rr/a secans anguli DAB quae data est vocetur s. Erit AEquatio haec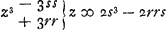
Et rursus si ss-rr vocetur tt, (est enim ss-rr ∞ quo. tangentis anguli DAB) Erit AEquatio haec z3-3ttz ∞ 2tts. Itaque dato angulo sub quo semidiameter Iridis maxima spectatur, proportio refractionis invenietur per regulam sequentem: Regula: Inveniatur numerus qui ductus in quadratum suum multatum triplo quadrato tangentis dimidij anguli dati, fiat aequalis quadrato ejusdem tangentis, ducto in duplam secantem suam (quod fiet per methodum à Vieta traditam Probl. XI de numerosa potestatum affect. Resolutione;) atque is numerus dictae secanti addatur. Habebit radix quadr. ducta ex quadrato ejus summae et triplo quadrato radij ad ipsam summam proportionem eam quae est RefractionisGa naar voetnoot5).
Exempli gratia proponatur invenienda proportio refractionis aquae ex eo quod semidiameter Iridis caelestis maxima conspicitur sub angulo 41 gr. 30′. Dimidium ejus anguli est 20. 45′ hujus tangens 37886. hujus quadratum 1435348996. triplum ejus 4306046988. secans autem 20. 45′ est 106936 cujus duplum 213872 ductum in quadratum tangentis 1435348996 facit 306980960472512. Si igitur numerus inveniendus vocetur x erit aequatio ista; | |
[pagina 152]
| |
 Ga naar voetnoot1)Ga naar voetnoot2)Ga naar voetnoot3) Ergo 133689 ad 100000 est proportio refractionis aquae quae proxime est | |
[pagina 153]
| |
eadem quam 250 ad 187 et paulo major quam 4 ad 3 sicut et Cartesius ipsam ex Iride invenit, sed ope tabulae ad hoc constructaeGa naar voetnoot4). Contra autem cum proportio refractionis data est invenietur angulus sub quo semidiameter Iridis maxima spectari debeat per Regulam hujusmodi. Regula. Ut minor proportionis terminus ad majorem ita sit radius circuli qui est in Canone ad alium numerum. Ejus numeri quadratum auferatur à quadruplo quadrato radij. Et e triente residui eliciatur radix quadr aticaGa naar voetnoot5). Porro ut major proportionis terminus ad minorem ita sit radix inventa ad alium numerumGa naar voetnoot6) et quaeratur cujus anguli sit sinus hic numerus in canone. Nam si ab anguli hujus duplo auferatur angulus cujus sinus est radix praedicta, reliquum bis sumptum dabit angulum semidiametri Iridis quaesitumGa naar voetnoot7). Exempli gratia sit data proportio refractionis aquae quae est 250 ad 187. 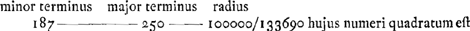
17873016100 quod ablatum à quadruplo quadr. radij nempe 40000000000, relinquit 22126983900 cujus tertia pars est 7375661300. Hujus radix quadr.a est 85881 sub quo semidiam. Iridis maxima spectaturGa naar voetnoot8). |
|