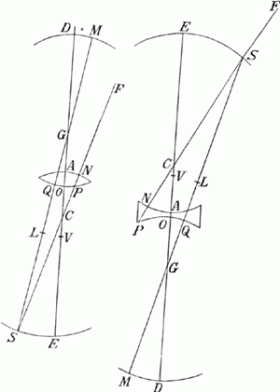
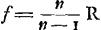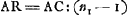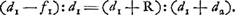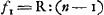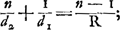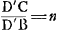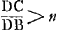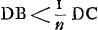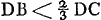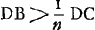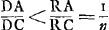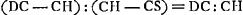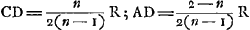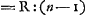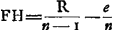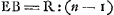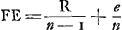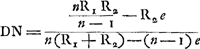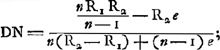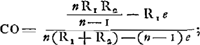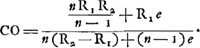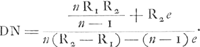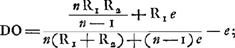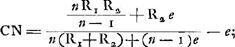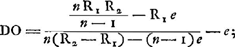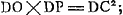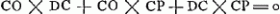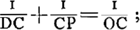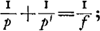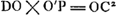Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 2]
| |||||||||||||||||||||||||||||||||||||
La DioptriqueGa naar voetnoot1).
| |||||||||||||||||||||||||||||||||||||
[pagina 3]
| |||||||||||||||||||||||||||||||||||||
DioptricaGa naar voetnoot1).
| |||||||||||||||||||||||||||||||||||||
[pagina 4]
| |||||||||||||||||||||||||||||||||||||
lequel il considérait un anneau vu sous l'eauGa naar voetnoot1); l'auteur y parlait sans doute de cette flexion des rayons et de l'illusion optique qui en résulte. Mais les lois que suivent les rayons réfractés ont été trouvées plus tard; c'est de nos jours seulement qu'on les a découvertes. L'expérience a montré que ces lois sont les suivantes: 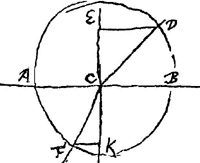 [Fig. 1.]
Considérons un corps transparent liquide ou solide, se trouvant du côté de K, et possédant une surface plane, qui est coupée suivant la ligne AB par un autre plan, celui dans lequel est dessinée la figure. Un rayon oblique DC tombe sur cette surface, faisant avec la droite ECK, qui y est perpendiculaire, un angle DCE. Ce rayon pénètre dans l'eau ou dans le verre suivant la droite CF faisant avec CK un angle moindre que l'angle DCE. Le phénomène obéit à la loi suivante: les sinus des deux angles, c'est-à-dire les perpendiculaires DE, FK correspondant à ces angles et abaissées chacune d'un point de la circonférence dont C est le centre sur la droite EK, ont entre elles une proportion bien déterminée et invariable. Or, cette mesure des réfractions par la proportion non pas des sinus, mais des angles mêmes, avait été définie anciennement par Alhazen l'Arabe et VitellionGa naar voetnoot2), et confirmée plus ou moins par quelques expériences. Mais comme, dans des inclinaisons plus grandes, cette proportion se trouvait différer de la proportion | |||||||||||||||||||||||||||||||||||||
[pagina 5]
| |||||||||||||||||||||||||||||||||||||
aquis visoGa naar voetnoot1), in quo procul dubiò de flexu isto radiorum agebatur, nataque inde visus fallacia. Leges vero, quas ita affecti radij sequuntur, serius, ac nostro demum oevo repertoe sunt. Quas hoc modo sese habere experientia docuit. Sit liquidi vel solidi diaphani corporis versus K existentis superficies plana, quoe ab alio plano, in quo figura hoec descripta intelligitur, secetur secundum rectam AB. In hanc incidat radius obliquus DC, qui ad rectam ECK, superficiei propositoe perpendicularem, faciat angulum DCE; is in aqua vitrove perget secundum CF minori angulo ad CK inclinatam, quam sit angulus DCE. atque ea lege ut sinus utriusque anguli, hoc est perpendiculares eorum DE, FK ex circumferentia circuli centro C descripti in rectam EK demissoe certam, eandemque semper inter se rationem servent. Hoec autem refractionum mensura, non sinuum, sed angulorum ipsorum proportione ab Alhaseno Arabe et VitellioneGa naar voetnoot2) olim definita fuerat, et experimentis quibusdam utcunque confirmata. Sed cum in majoribus radiorum inclinationibus a vero discrepare proportio illa reperiretur, diligentius sibi eandem rem recen- | |||||||||||||||||||||||||||||||||||||
[pagina 6]
| |||||||||||||||||||||||||||||||||||||
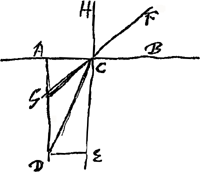
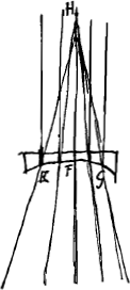
véritable les modernes ont jugé qu'il leur fallait examiner la chose avec plus de soin. Parmi eux Kepler, après plusieurs vains effortsGa naar margenoot*, n'a pas trouvé, il est vrai, la véritable loi; mais par ses conjectures et ses différentes tentatives il a beaucoup contribué aux études de ses successeurs. Après lui Willebrord Snellius, lorsque l'importance de la chose était devenue plus manifeste, vu que le télescope avait été inventé, parvint avec beaucoup de peine et après avoir fait de nombreuses expériences, à mesurer convenablement la grandeur des réfractions, sans toutefois comprendre sufissamment ce qu'il avait trouvé. Car en prenant par exemple comme surface de l'eau le plan AB, et comme objet visible sous l'eau le point D, que l'oeil placé en F doit alors apercevoir sur la droite FC,
 [Fig. 2.]
Snellius prolongeait cette droite FC, jusqu' à ce qu'elle rencontrât la droite DA au point G, DA étant perpendiculaire à la surface de l'eau. Ayant fait cette construction, il affirmait que l'image de l'objet vu apparaît en G, et que les droites CD et CG ont entre elles une proportion déterminée, savoir pour l'eau 4:3. C'est là en effet la vraie proportion de ces droites, et cela s'accorde avec cette loi de la réfraction que nous venons d'expliquer. Car CD est à CG, suivant la doctrine des triangles, comme le sinus de l'angle DGC ou AGC ou HCF est au sinus de l'angle CDG ou DCE. Mais Snellius n'a aucunement fait attention à cette proportion des sinus. Il se figurait que la chose dépend si complètement de l'image apparente qu'il croyait reconnaître même dans un rayon perpendiculaire, tel que HC, l'effet de la réfraction, consistant, comme il pensait à tort, en un raccourcissement du rayon visuelGa naar voetnoot2). Il était trompé par le fait que lorsqu'on regarde d'en haut un vase rempli d'eau, le fond semble partout s'élever. Or, la vraie cause de ce phénomène doit être cherchée | |||||||||||||||||||||||||||||||||||||
[pagina 7]
| |||||||||||||||||||||||||||||||||||||
tiores investigandam existimarunt. In quibus Keplerus, plurimis frustra tentatisGa naar margenoot*, ipsam quidem rei veritatem non est assecutus; conjecturis tamen suis, varijsque molitionibus non parum sequentium studia adjuvit. Post eum vero Willebrordus Snellius, cum jam majus operoe pretium appareret, quippe exorto telescopij invento, multo labore multisque experimentis eo pervenit ut veras quidem refractionum mensuras teneret, nec tamen quod invenerat satis intelligeret. Nam positâ, ex. gratia, aquoe superficie AB, visibili vero sub aqua in D, quod oculo in F posito appareat quasi in recta FC, continuabat hanc FC, donec in G puncto occurreret rectoe DA, ad superficiem aquoe perpendiculari; hisque ita descriptis, statuebat imaginem rei visoe apparere in G, rectoeque CD ad CG certam esse rationem, veluti in aqua sesquitertiam. Quoe rectarum inter se ratio vera est, ac convenit prorsus cum ea quam paulo ante explicuimus refractionis lege; quia CD est ad CG, ex doctrina triangulorum, ut sinus anguli DGC, vel AGC, seu HCF, ad sinum angi. CDG, sive DCE. Verum ad hanc sinuum proportionem nequaquam attendit Snellius et usque adeo ab apparente imagine rem omnem pendere existimavit, ut etiam in radio perpendiculari qualis HC, effectum refractionis, seu, ut falso opinatur, decurtationem radij visorij agnoscatGa naar voetnoot2). deceptus eo quod etiam rectà | |||||||||||||||||||||||||||||||||||||
[pagina 8]
| |||||||||||||||||||||||||||||||||||||
en considérant les rayons de lumière qui se dirigent vers les deux yeux. Tout ceci, exposé par Snellius dans un livre entier sur la réfraction, est resté inédit. Nous avons vu ce livre autrefoisGa naar voetnoot1) et nous avons appris que Deseartes l'a vu également. C'est peut-être de ce livre que Descartes a tiré sa loi des sinusGa naar voetnoot2), dont il s'est servi fort heureusement dans l'explication de l'arc-en-cielGa naar voetnoot3) et dans la recherche de la forme des lentillesGa naar voetnoot4). La valeur numérique de ce rapport des sinus, lorsque le rayon tombc de l'air dans l'eau, ou dans le verre, ou dans d'autres corps transparents, peut être cherchée à l'aide d'un prisme, comme Descartes l'indiqueGa naar voetnoot5), ou par d'autres procédés, que celui qui aura bien compris ce qui précède n'aura pas de peine à trouver. Quant à nous, les procédés que je vais décrire nous ont paru être plus commodes que les autres. Si la matière transparente est liquide, il faut remplir avec ce liquide un vase de verre dont la paroi a la forme d'un cylindre ou tout au moins celle d'une surface de révolution autour de l'axeGa naar voetnoot6). Plus ce vase est volumineux, et plus le verre en est mince, mieux il convient à l'expérience. Soit
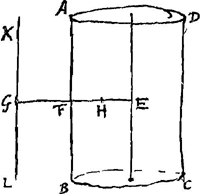 [Fig. 3.]
ABCD ce vase. Plaçons-le de telle manière que son axe soit perpendiculaire à la direction des rayons solaires ou à celle des rayons venant d'une source lumineuse lointaine. Ces rayons, s'ils tombent sur le vase du côté DC, convergeront de l'autre côté du vase après avoir traversé le verre et l'eau qui y est contenue, et si le vase a une forme cylindrique, ils engendreront une ligne lumineuse telle que KL, sur une surface plane parallèle aux génératrices du cylindre. Lorsqu'on aura obtenu la ligne la plus brillante et la moins large possible, on prendra au compas la distance GF qui sépare la surface plane du vase, et on marquera cette distance | |||||||||||||||||||||||||||||||||||||
[pagina 9]
| |||||||||||||||||||||||||||||||||||||
desuper in vas aqua plenum inspicienti, fundus omni parte attolli videtur. Cujus rei vera causa ex radijs ad utrumque oculum tendentibus petenda est. Hoec autem omnia quoe de refractionis inquisitione volumine integro Snellius exposuer at inedita mansere, quoe et nos vidimus aliquandoGa naar voetnoot1) et Cartesium quoque vidisse accepimus, ut hinc fortasse mensuram illam quoe in sinibus consistit, elicueritGa naar voetnoot2); quâ in explicanda IrideGa naar voetnoot3) & vitrorum figuris investigandisGa naar voetnoot4) felicissimè est usus. Cujusmodi vero sit illa Refractionis in sinibus proportio cum radius ex aere in aquam, vitrumve, aut alia corpora diaphana defertur, id vel prismate, ut Cartesius proecipitGa naar voetnoot5) inquiri potest, vel alijs modis; quos qui proecedentia intellexerit, non difficulter inveniet. Nobis hi, quos jam docebo, coeteris faciliores visi sunt. nam si liquida diaphani materia data sit, ea vitreum vas impleatur, quod vel cylindri formam habeat, vel ejusmodi solum quae circa axem rotunda sitGa naar voetnoot6); quo autem capacius erit, quòque tenuiori vitri, eo melius. Esto illud ABDC, atque ita collocetur, ut axem habeat solaribus radijs, vel ab lumine longinquo venientibus, directè oppositum. Hi igitur radij si cadant in latus DC, concurrent ex parte altera vasis, postquam et vitrum et aquam eo contentam transierint, et, si cylindraceum vas fuerit, lineam quandam lucidam signabunt ut KL in plana superficie vasis lateri parallela. Ea ubi perfectissima contigerit linea minimaeque latitudinis, circino capiatur distantia GF qua planum a vase abest, eaque distantia in chartam annotetur: atque apponatur deinde semidiameter vasis FE à centro ad | |||||||||||||||||||||||||||||||||||||
[pagina 10]
| |||||||||||||||||||||||||||||||||||||
sur une feuille de papier. On y ajoutera le rayon FE du vase, c'est-à-dire la distance du centre à la surface extérieure. Soit H le point qui partage ce rayon en deux parties égales. L'indice de réfraction de l'eau ou en général du fluide considéré sera alors le rapport EG:GH; ce sera toujours ce rapport qu'on trouvera entre les deux sinus, comme je l'ai dit plus haut. Mais les rayons, après avoir traversé le verre, convergeront plus exactement si nous ne laissons passer que ceux-là seulement qui pénètrent dans le vase cylindrique par le milieu; il faut donc couvrir les deux côtés jusqu' à une certaine distance du milieu. On trouvera la démonstration de ce qui vient d'être dit dans la suite de ce traité, au théorème XIII du premier livreGa naar voetnoot1). On verra en outre, d'après le théorème XXV du livre IGa naar voetnoot2), que les réfractions qui ont lieu dans le verre ne nous empêchent nullement de considérer le cylindre ABCD comme formé entièrement d'eau. Et si l'on veut obtenir par un procédé tout aussi rapide l'indice de réfraction du verre ou du cristal, il faut prendre une lentille formée de cette substance et possédant une surface plane et une surface convexe telle que la lentille ABC. On exposera la surface plane aux rayons du soleil ou à ceux d'une lampe placée à grande distance de sorte que les rayons tombent perpendiculairement sur cette surface. Derrière la lentille on placera une surface plane et on l'éloignera de la lentille à une distance telle que les rayons, en convergeant vers cette surface, y engendrent l'image la plus nette possible du soleil ou de la flamme. Soit cette image en E. Que l'on mesure alors la distance EB de cette image à la surface convexe de la lentille, et que l'on sache que l'indice de réfraction du verre ou du cristal considéré est égal au rapport de la somme du rayon de courbure DB de la surface convexe et de la longueur mesurée BE, c'est-à-dire de DE d'une part, et de la longueur BE elle-même d'autre part. Cette proposition sera démontrée au théorème IX du premier livreGa naar voetnoot3). Il sera avantageux de couvrir les bords de la lentille jusqu' à une certaine distance du centre, afin qu'elle donne une image plus nette de la source lumineuse. Je pourrais aux méthodes décrites en ajouter d'autres plus laborieuses, conduisant plus subtilement à la connaissance de ce même indice de réfraction. Mais comme il n'est pas fort important de chercher la valeur numérique de cet indice avec une grande précision, et que cette valeur est quelque peu différente, comme je l'ai déjà ditGa naar voetnoot6), pour diverses sortes de verres ou d'eaux, il me semble inutile de faire connaître d'autres procédés. J'ajoute toutefois que l'indice de réfraction de l'eau de pluie, mesuré avec précision, s'est trouvé avoir la valeur 250:187, peu supérieure à la fraction 4/3; c'est ce que Descartes a inféré ingénieusement de la considération du diamètre de l'arcen-cielGa naar voetnoot7). D'après cette même méthode, nous avons calculé l'indice de réfraction du verre, en nous servant d'une petite sphère solide de cette substance, et en observantGa naar voetnoot8) à l'aide de cette sphère que le rayon d'un arc-en-ciel pour une | |||||||||||||||||||||||||||||||||||||
[pagina 11]
| |||||||||||||||||||||||||||||||||||||
extimam superficiem, quae bifariam secetur in H. Jam proportio refractionis aquae, vel quicunque liquor fuerit, habebitur ea quae est EG ad GH, quae nempe eadem semper in sinibus existet ut superius exposui. Accuratius autem radij post vitrum colligentur si tantum eos transire sinamus qui circa medium cylindrum penetrant, lateribus utrinque aliquousque contectis. Ac demonstratio quidem hujus in sequentibus invenietur, libri primi propos. [XIII]Ga naar voetnoot1). nec refractiones quae in vitro hic accidunt quicquam obesse, quo minus cylindrus ABCD velut totus aqueus censeatur, patebit ex ijs, quae dicentur lib. [I] propos. [XXV]Ga naar voetnoot2). Quod si vitri aut crystalli refractiones simili compendio inquirere libeat, lentem ex ea materia formatam accipe, superficie altera plana, altera convexa, qualis hic est lens ABC. Superficiem planam soli oppone vel lucernae procul positae ut [Fig. 4.]
radij incidant ad rectos angulos: post lentem vero adhibe planum aliquod, ac tantum remove, ut in eo radij coeuntes imaginem solis aut flammae quam nitidissimam depingant: Esto in E. Tum distantiam hujus imaginis ab lentis convexa superficie metire EB, et quam rationem habet semidiameter convexitatis ABC puta DB unà cum inventa longitudine BE, hoc est, tota DE ad hanc ipsam BE, eandem scito esse refractionis vitri vel crystalli propositae. hoc enim demonstrabitur lib. I. prop. [IX]Ga naar voetnoot3). Lentem vero circa latera aliquatenus texisse proderit, ut imaginem lucidi eo nitidiorem referat. Alios modos adjungere his possem operosiores, quibus proportio eadem refractionis subtiliusGa naar voetnoot4) colligatur, sed cum non multum intersit scrupulose eam definiriGa naar voetnoot5) et in diversi generis vitris aquisve, ut jam dixiGa naar voetnoot6), diversa aliquantum deprehenditur, operae pretium non videtur plura de his praecipere. Aquae tamen pluviae refractio, ut hoc addam, accuratè dimensa reperta est ut 250 ad 187, paulo scilicet major sesquitertia; idque ex Iridis amplitudine Cartesius subtiliter sane collegitGa naar voetnoot7). Similique ratione, adhibita sphaerula vitrea solida, inventaque ex observationeGa naar voetnoot8) semidiametro iridis in pluvia vitrea, si qua | |||||||||||||||||||||||||||||||||||||
[pagina 12]
| |||||||||||||||||||||||||||||||||||||
pluie de verre, si jamais une telle pluie venait à tomber, serait de 21o 45′. Nous expliquerons ce calculGa naar voetnoot1) dans le traité des ParéliesGa naar voetnoot2). Quant à la valeur de l'indice, nous avons trouvéGa naar voetnoot3) qu'elle est supérieure à 114/76, c'est-à-dire à 3/2, mais inférieure à 115/76. Il est donc permis de prendre la valeur 3/2; l'erreur ainsi commise est négligeable. D'ailleurs nous n'avons nullement, dans les théorèmes qui suivent, eu égard à cette valeur là plutôt qu' à aucune autre, et il faut savoir que ce que nous établirons dans ces théorèmes est vrai, indépendamment de la valeur numérique de l'indice de réfraction. Les trois théorèmes suivants, dont nous ferons par la suite un fréquent usage, découlent aisément de la loi des réfractions, que nous venons d'exposer. | |||||||||||||||||||||||||||||||||||||
Proposition IGa naar voetnoot6).Soit donnée une surface quelconque AB, bornant un corps transparent existant du côté C, et soit AC le rayon réfracté provenant du rayon DA qui tom be de l'extérieur sur ce corps. Prolongeons DA vers F et CA vers E. Imaginons-nous ensuite que le corps transparent change de place de telle manière qu'il reste borné par la même surface AB, mais qu'il v ienne se trouver de l'autre côté de cette surface, c'est-à-dire du côté E. Je dis qu' alors le rayon réfracté, provenant du rayon FA, sera AE. 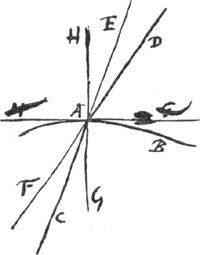 [Fig. 5.]
En effet, soit HAG qui coupe la surface au point A, une perpendiculaire à cette surface. Le rayon DA et le rayon réfracté AC sont par conséquent dans le même plan passant par HG. Vu que le rayon DA, lorsque le corps transparent est situé du coté G, fait avec la perpendiculaire HG le même angle que le rayon FA, lorsque le corps transparent est situé du côté H (car DAF est par hypothèse une ligne droite), les rayons réfractés provenant de chacun de ces rayons feront aussi avec HG des angles égaux. Or, le rayon réfracté AC, provenant du rayon DA, fait avec AG l'angle CAG. Le rayon réfracté provenant du rayon FA fera donc un angle égal avec HA, c'est-à-dire un angle de grandeur | |||||||||||||||||||||||||||||||||||||
[pagina 13]
| |||||||||||||||||||||||||||||||||||||
talis caderet, grad. 21.45′; proportionem refractionis vitri inde calculoGa naar voetnoot1) subduximus, cujus ratio in ijs, quae de Pareliis, explicabiturGa naar voetnoot2), comperimusque majorem quam 114 ad 76, sive quam 3 ad 2, minorem vero quam 115 ad 76. ut sesquialteram usurpare absque errore liceatGa naar voetnoot3). CoeterumGa naar voetnoot4) non ad hanc magis quam ad aliam quamlibet in sequentibus theorematis respeximus quoeque ijs definiemus omnia eodem modo se habitura sciendum estGa naar voetnoot5), quaecunque demum fuerit refractionis proportio. Porro ex lege refractionum modo explicata tria haec Theoremata facile deducuntur, quorum in caeteris frequens usus erit. | |||||||||||||||||||||||||||||||||||||
Propositio [I]Ga naar voetnoot6).Si fuerit superficies quaelibet AB, terminans diaphanum versus C existens, sitque radij DA extrinsecus in illam incidentis refractio AC, et producatur DA versus F, et CA versus E. Et intelligatur deinde diaphanum ita transponi ut eadem superficie AB terminetur, sed existat ad partem ejus contrariam, ubi nempe est E. Dico jam radij FA refractionem fore AE. Sit enim recta HAG quae penetret superficiem AB ad angulos rectos in A. Sunt ergo in eodem plano per HG ducto tum DA tum refractio ejus AC. Quia vero radius DA ad perpendicularem HG existente diaphano versus G eodem angulo inclinatur, quo radius FA, existente diaphano versus H, est enim DAF, ex hypothesi, linea recta, etiam refractiones utriusque cum ipsa HG angulos aequales constituent. Radij autem DA refractio AC facit angulum CAG, ergo | |||||||||||||||||||||||||||||||||||||
[pagina 14]
| |||||||||||||||||||||||||||||||||||||
HAE, CAE étant une ligne droite. Mais de plus FA et AE se trouvent dans le même plan passant par la droite HG, vu que FA est le prolongement de DA, et AE de CA. Il est donc évident que le rayon réfracté provenant du rayon FA n'est autre que AE, lorsque le corps transparent se trouve du côté H. C'est ce qu'il fallait démontrer. | |||||||||||||||||||||||||||||||||||||
Proposition II.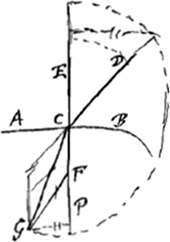 [Fig. 6.]
Soit AB la surface d'un corps transparent, la forme de cette surface étant arbitraire. Soit DC un rayon oblique tombant du dehors sur cette surface, CG le rayon réfracté, et la droite ECP une normale à la même surface. Prenons un point quelconque F sur cette normale, à l'intérieur du corps transparent, et tirons FG parallèle au rayon DC. Je dis que cette parallèle coupe le rayon réfracté CG et que le rapport CG:GF est égal à l'indice de réfraction. Car l'angle FCG est plus petit que l'angle DCE à cause de la réfraction; cet angle sera donc aussi plus petit que l'angle PFG; c'est pourquoi les droites CG et FG se couperont nécessairement. De plus, selon la loi des réfractions exposée plus haut le rapport du sinus de l'angle DCE au sinus de l'angle FCG est égal à l'indice de réfraction. Or, le sinus de l'angle DCE est le même que celui de l'angle DCF ou CFG. Par conséquent dans le triangle CFG le rapport du sinus de l'angle CFG au sinus de l'angle FCG est égal à l'indice de réfraction. La même chose sera donc vraie pour le rapport du côté CG au côté GF, car dans tout triangle les côtés sont entre eux comme les sinus des angles opposés. Il est clair que la réciproque de cette proposition est également vraie. C'est-à-dire, lorsque FG est parallèle au rayon DC et rencontre la droite CG, et que le rapport CG:GF est égal à l'indice de réfraction, CG sera le rayon réfracté qui correspond au rayon DC. | |||||||||||||||||||||||||||||||||||||
[pagina 15]
| |||||||||||||||||||||||||||||||||||||
huic aequalem angulum efficiet refractio radij FA cum ipsa HA, hoc est aequalem angulo HAE, est enim CAE linea recta. Sed et in eodem plano, per rectam HG ducto, sunt FA et AE, quum sint in directum ipsis DA, CA. Ergo patet radij FA refractionem fore ipsam AE quando diaphanum est a parte H. quod erat dem. | |||||||||||||||||||||||||||||||||||||
Propositio [II].Si fuerit diaphani superficies quaelibet AB, in quam extrinsecus cadat obliquus radius DC, qui refringatur secundum CG; sitque recta ECP secans diaphani superficiem ad angulos rectos, et sumatur in ea intra diaphanum punctum quodvis F, unde ducatur FG parallela radio DC. dico hanc occurrere refractioni CG, et habere CG ad GF rationem eam quae est refractionis. Quia enim propter refractionem angulus FCG minor est quam DCE, idem quoque minor erit quam PFG, ideoque CG, FG necessario concurrent. Porro quia secundum refractionum legem superius expositam, sinus anguli DCE ad sinum anguli FCG rationem habet eam, quae est refractionis. Sinus autem anguli DCE idem est qui anguli DCF seu CFG. Ergo in triangulo CFG habebit sinus anguli CFG ad sinum anguli FCG rationem refractionis. Quare eandem quoque habebit latus CG ad latus GF. Quia nempe in omni triangulo, latera inter se eandem proportionem servant, quam sinus angulorum, quibus illa subtenduntur. Patet autem et conversae hujusGa naar voetnoot1) veritas. Nempe si FG parallela existente radio DC, rectaeque CG occurrente, fuerit CG ad GF ratio eadem quae est refractionis, tunc CG fore refractionem radij DC. | |||||||||||||||||||||||||||||||||||||
[pagina 16]
| |||||||||||||||||||||||||||||||||||||
Proposition III.Soit AB [Fig. 7] la surface d'un corps transparent, la forme de cette surface étant arbitraire. Le corps transparent se trouve du côté L. Soit DC un rayon à l'intérieur de ce corps. Ce rayon sort du corps au point C et est réfracté selon CH. Soit ECP une normale à la surface. Prenons sur cette normale un point quelconque L et tirons de là une parallèle LH au rayon DC. Je dis que cette parallèle coupe le rayon réfracté CH, et que le quotient LH:HC est égal à l'indice de réfraction. Car le rayon DC quitte le corps après avoir été réfracté à la surface; l'angle PCH sera donc plus grand que l'angle LCD, c'est-à-dire que l'angle CLH. Il en résulte manifestement que les droites CH et LH se coupent. 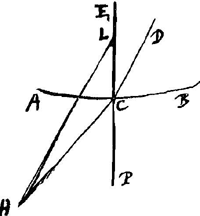 [Fig. 7.]
De plus, suivant la loi des réfractions, le rapport du sinus de l'angle PCH au sinus de l'angle LCD ou CLH est égal à l'indice de réfraction. Or, le sinus de l'angle PCH est le même que celui de l'angle LCH. Par conséquent dans le triangle LHC le rapport du sinus de l'angle LCH au sinus de l'angle CLH sera égal à l'indice de réfraction. La même chose sera donc vraie pour le rapport des côtés LH et HC. Ce qu'il fallait démontrer. Ici aussi la réciproque de la proposition est évidemment vraie. C'est-à-dire, lorsque LH est parallèle au rayon DC et rencontre la droite CH, et que le rapport LH:HC est égal à l'indice de réfraction, CH sera le rayon réfracté qui correspond au rayon DC.
Nous expliquerons dans la suite comment on trouve les points où se réunissent les rayons après avoir été réfractés par quelque surface plane, convexe ou concave, ou bien ceux où les rayons, dispersés par cette réfraction, se coupent lorsqu'on les prolonge en sens inverse. Nous les appellerons points de concours ou points de dispersion. Toutefois, comme nous désignerons également par ce nom des points auxquels ne correspondent pas exactement, comme on le fera voir, tous les rayons réfractés, nous devons dire en peu de mots ce qu'il faut alors entendre par là. Lorsqu'il peut être démontré que les rayons qui tombent parallèlement sur la lentille ABC [Fig. 8] coupent tous l'axe DBE, après la réfraction, en-deçà d'un certain point E, ou bien qu'ils coupent tous l'axe au-delà de ce point, et cela de telle façon que plus un rayon incident est proche de l'axe, plus le point où le rayon réfracté, qui y correspond, coupe l'axe est proche du point E, et que cette | |||||||||||||||||||||||||||||||||||||
[pagina 17]
| |||||||||||||||||||||||||||||||||||||
Propositio [III].Si fuerit diaphani superficies quaecunque AB [Fig. 7], terminans diaphanum versus L existens: radius autem intra diaphanum sit DC, qui in C egrediensGa naar voetnoot1), refringatur in CH. Et ducta ECP, quae superficiem secet ad angulos rectos, sumatur in ea punctum quodvis L, unde ducatur LH parallela radio DC. dico hanc occurrere refractioni CH, atque esse LH ad HC rationem eam quae est refractionis. Quia enim radius DC refractus exit à diaphano, erit angulus PCH major angulo LCD, hoc est, angulo CLH. Unde manifestum est rectas CH, LH concurrere. Porro autem, quia secundum legem refractionis, sinus anguli PCH ad sinum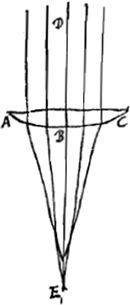 [Fig. 8.]
anguli LCD sive CLH, proportionem refractionis habet, sinus autem anguli PCH idem est qui sinus anguli LCH, habebit itaque in triangulo LHC, sinus anguli LCH ad sinum anguli CLH proportionem refractionis. Quare eandem quoque habebit latus LH ad latus HC. quod erat probandum. Rursus autem et conversa propositionis hujus manifesta est. Nempe si LH parallela existente radio DC, rectaeque CH occurrente, fuerit LH ad HC ratio ea quae refractionis, etiam CH fore refractionem radij DC.
Nunc quomodo puncta ea inveniantur, ad quae radij, postquam in superficie aliqua plana convexa aut cava refracti fuerint, colliguntur, vel ad quae dispersi respiciunt, deinceps exponemus; quae quidem puncta concursus vel dispersus vocabimus. Quoniam veroGa naar voetnoot2) hoc nomine etiam illa puncta designabimus ad quae tamen radios omnes refractos non accuratè pertinere ostensum fuerit, id quomodo tunc intelligendum sit paucis declarandum est. Ergo si radios parallelos in lentem ABC [Fig. 8] incidentes omnes post refractionem convenire ostendatur cum axe DBE citra punctum quoddam E, vel omnes ultra idem punctum, verùm hoc pacto ut quo quisque radius axi propinquior fertur eo refractus concurrat propius ad punctum E, idque ad distantiam tandem quavis data minorem, tum | |||||||||||||||||||||||||||||||||||||
[pagina 18]
| |||||||||||||||||||||||||||||||||||||
dernière distance finit par devenir plus petite qu'une grandeur donnée quelconque,
 [Fig. 9.]
alors aussi le point E sera appelé le point de concours. Et de même pour une lentille concave KFG [Fig. 9], lorsque nous aurons démontré que les rayons parallèles venant du côté H sont dispersés après la réfraction de telle façon que prolongés en sens inverse ils rencontrent tous l'axe FH soit en-deçà soit au-delà d'un certain point H, et cela avec les mêmes conditions que nous avons aussi posées pour la lentille convexe, alors le point H sera appelé le point de dispersionGa naar voetnoot1). Même nous considérons dans la plupart des cas ces points comme déterminant exactement le concours ou la dispersion des rayons; nous pourrons le faire en ayant égard seulement aux parties centrales des lentilles ou des surfaces, parties dont les dimensions, par rapport aux diamètres de la convexité ou de la concavité, doivent être assez faibles pour que ce qui est imparfait dans le sens géométrique paraisse parfait à nos yeux. Car il est certain que les dimensions latérales des lentilles satisfont à cette condition; cela est vrai aussi bien pour les lentilles que nous voyons donner dans l'obscurité une image des objets que le soleil éclaire endehors, que pour celles dont se composent les lunettes ou les télescopes: s'il en était autrement, on n'obtiendrait pas avec ces lentilles des effets aussi remarquables. 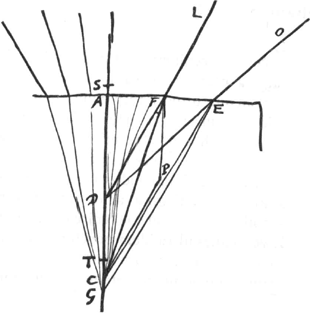 [Fig. 10.]
| |||||||||||||||||||||||||||||||||||||
Proposition IV.
| |||||||||||||||||||||||||||||||||||||
[pagina 19]
| |||||||||||||||||||||||||||||||||||||
quoque punctum E concursus punctum dicetur. Similiterque in lente cava KFG [Fig. 9], si parallelos radios à parte H venientes post refractionem ita spargi ostenderimus, ut retrorsum producti conveniant cum axe FH omnes citra punctum quoddam H, vel omnes ultra, ijsdemque etiam conditionibus quas in convexa posuimus, tum punctum H dicetur punctum dispersusGa naar voetnoot1). Quin etiam haec puncta plerumque sic accipiemusGa naar voetnoot2), tanquam concursum aut dispersum radiorum exactè determinarent; medias videlicet lentium aut superficierum partes respicientes, quarum satis exigua sit proportio ad convexitatis vel cavitatis diametros, ut quantum ad sensum oculorum attinet perfectum videatur quod geometrica ratione est imperfectum. Ita enim sese habere lentium latitudines certum est, tum earum quibus in tenebris picturam representari videmus rerum quae foris a Sole illuminantur, tum quibus perspicilla seu telescopia constant; neque enim alioqui tam insignes earum effectus cernerentur. | |||||||||||||||||||||||||||||||||||||
[Propositio IV.]
| |||||||||||||||||||||||||||||||||||||
[pagina 20]
| |||||||||||||||||||||||||||||||||||||
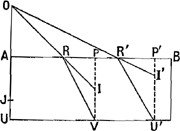
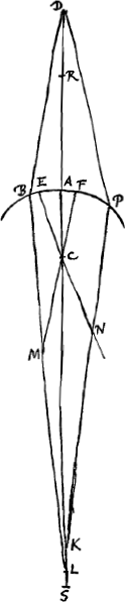
toutes les droites qui apparaissent dans la figure soient situées dans un plan passant par AD. Prolongeons AD et choisissons le point T de telle manière que le rapport TA:AD soit égal à l'indice de réfraction. Je dis que ce point T sera le point de concours cherché. Or, en premier lieu je démontrerai qu' aucun rayon réfracté ne rencontre l'axe AD en-deçà du point T. Soit en effet FC le rayon réfracté provenant du rayon LF. Achevons la construction du parallélogramme CDFP. FP sera donc perpendiculaire à la surface AE et PC sera parallèle au rayon LF et rencontrera le rayon réfracté provenant de ce rayon en C. Le rapport FC:CP sera donc égal à l'indice de réfractionGa naar margenoot*. Or, FD est égale à CP. Par
 [Fig 10.]
conséquent le rapport CF:FD sera lui aussi égal à cet indice de réfraction, c'est-à-dire à TA:AD. Le carré de CF est donc aussi au carré de DF, comme celui de TA est à celui de AD. Le carré de CF est donc au carré de DF, comme une quantité plus grande est à une quantité moindre. Par conséquent, soustrayant des deux côtés le carré de AF, on voit que le rapport CA2::AD2 est plus grand que le rapport CF2:DF2, c'est-à-dire que le rapport TA2:AD2. Le carré de CA sera donc plus grand que celui de TA, et la ligne CA elle-même sera plus grande que TA: d'où il appert que le rayon réfracté FC rencontre l'axe AD au-delà du point T. Il faut démontrer en second lieu que les rayons réfractés provenant de rayons situés plus près de la droite AD la rencontrent en un point plus rapproché du point T que ceux provenant de rayons plus éloignés de cet axe. Soit, en effet, le rayon OE plus éloigné de l'axe que le rayon LF, et soit EG le rayon réfracté correspondant à ce rayon-là. Joignons les points C et E par une droite. Le carré de CE surpasse alors le carré de ED d'une quantité égale à la différence des carrés de CF et de DF, vu que cette différence, ainsi que la première, est égale à la sommeGa naar margenoot+ du carré de CD et de deux fois le rectangle sur les lignes CD et DA. Or, le carré de CE est plus grand que celui de CF. Le rapport CE2:ED2 est donc plus petit que le rapport CF2:FD2. C'est pourquoi le rapport CE:ED est aussi inférieur au rapport CF:FD. Mais CF est à FD comme GE à ED. En effet, on peut démontrer pour les lignes GE et ED, comme cela a été démontré pour les lignes CF et FD, que leur rapport est égal à l'indice de réfraction: cela résulte de ce | |||||||||||||||||||||||||||||||||||||
[pagina 21]
| |||||||||||||||||||||||||||||||||||||
quae in schemate apparent intelligantur in plano per AD ducto. Producatur AD et habeat TA ad AD rationem eam quae est refractionis. Dico T fore punctum concursus quaesitum. Et primo quidem ostendam nullius radij refractionem concurrere cum AD citra punctum T. Sit enim FC refractio radij LF; et perficiatur parallelogrammum CDFP. Erit igitur FP superficiei AE ad angulos rectos, et PC parallela radio LF, ejusque refractioni occurrens in C. Quare FC ad CP habebit proportionem quae est refractionisGa naar margenoot*. Est autem FD aequalis CP. Ergo etiam CF ad FD proportionem refractionis habebit, hoc est, eam quam TA ad AD. Ergo et quadratum CF ad quadr. DF, ut quadr. TA ad quadr. AD. Ergo ratio quadrati CF ad quadr. DF est majoris ad minus. Quare auferendo utrinque quadratum AF, erit ratio quadrati CA ad quadr. AD major quam quadrati CF ad quadr. DF, hoc est quam quadrati TA ad quadr. AD. Itaque quadratum CA majus erit quadrato TA, et CA linea major quam TA: unde apparet refractionem FC convenire cum axe AD ultra punctum T. Secundo loco ostendendum est radiorum rectae AD propinquiorum refractiones propius concurrere ad punctum T quam remotiorum. Sit enim radius OE remotior radio LF, et refractio ejus sit EG: et jungatur EC. Quadratum igitur CE excedit quadr. ED, quantum CF quadratum excedit quadr. DF, quia utrorumque differentia est aequalis quadrato CD et duplo rectangulo CDAGa naar voetnoot2)Ga naar margenoot*. Est autem quadratum CE majus quadrato CF. Ergo minor est ratio quadrati CE ad quadr. ED, quam quadrati CF ad quadratum FD. Quare et lineae CE ad ED minor ratio quam CF ad FD. Ut autem CF ad FD ita est GE ad ED. Nam sicut de lineis CF, FD ostensum fuit, ostendi etiam potest de lineis GE, ED, habere eas rationem quae est refractionis, quia scilicet EG statuitur esse refractio radij OE tendentis ad D. Igitur minor erit ratio CE ad ED quam GE ad ED: ac proinde GE major quam CE. Unde facile perspicitur AG quoque majorem esse quam CA; adeoque concursum refracti radij OE longius abesse a puncto T quam radij LF. Denique ostendere oportet aliquos radios refractos convenire cum AD producta in puncto quod dato quolibet intervallo minus distet à puncto T. Sumatur punctum C, dato intervallo propius situm puncto T et ulterius distans ab A quam ipsum T; et sicut differentia quadratorum TA, AD ad quadr. AD, ita sit differentia quadratorum CA, AD ad quadr. DS. Ergo quia differentia prior minor est posteriore, erit et quadratum AD minus quam quadra- | |||||||||||||||||||||||||||||||||||||
[pagina 22]
| |||||||||||||||||||||||||||||||||||||
que EG est par hypothèse le rayon réfracté provenant du rayon OE dont le prolongement passe par le point D. Le rapport CE:ED sera donc inférieur au rapport GE:ED; par conséquent GE est plus grande que CE. On voit donc aisément que AG aussi est plus grande que CA, et que le point où le rayon OE coupe l'axe après avoir été réfracté est par conséquent plus éloigné du point T que le point sur l'axe qui correspond au rayon LF. Il faut enfin faire voir que quelques rayons réfractés rencontrent le prolongement de AD en un point situé du point T à une distance inférieure à un intervalle donné quelconque. Prenons un point C situé à une distance moindre du point T que la distance donnée et plus éloigné du point A que le point T lui-même. Comme la différence de TA2 et AD2 est à AD2, ainsi soit la différence de CA2 et AD2 à DS2. Par conséquent, comme la première différence est inférieure à la seconde, le carré de AD sera aussi plus petit que celui de DS; et la ligne DA sera plus petite que DS. Ainsi, si l'on décrit une circonférence avec le centre D et le rayon DS, cette circonférence coupera la droite AF par exemple enF. Joignons le point F aux points C et D, et prolongeons DF jusqu'en L. Vu qu' alors la différence de TA2 et AD2 est à AD2 comme la différence de CA2 et AD2 est à DS2 ou à DF2, on aura, par composition, TA2 est à AD2 comme la différence de CA2 et AD2, augmentée de DF2, est à DF2. Or, la différence CA2 - AD2, c'est-à-dire CD2+2 CD. DA, ajoutée à DF2 donne une somme égale à CF2. Par conséquent, TA2:AD2 = CF2:DF2. Et CF:DF = TA:AD. Or TA:AD est égal à l'indice de réfraction. Dans le triangle CFD on a donc CF:FD égal à ce même indice; et il en est de même pour le rapport des sinus des angles CDF ou ADF d'une part, FCD d'autre part. Or, l'angle ADF est l'angle entre le rayon incident LF et la perpendiculaire, et l'angle FCD est celui entre la même perpendiculaire et la ligne FC. Il est donc certain que FC est le rayon réfracté provenant du rayon LF. Nous avons ainsi démontré que le rayon réfracté provenant d'un certain rayon incident coupe l'axe AD en un point situé du point T à une distance plus petite qu'un intervalle quelconque. A cause de tout cela le point T sera le point de concours cherché. | |||||||||||||||||||||||||||||||||||||
Proposition V.
| |||||||||||||||||||||||||||||||||||||
[pagina 23]
| |||||||||||||||||||||||||||||||||||||
tum DS:Et linea DA minor quam DS. Ideoque si centro D intervallo DS, circumferentia describatur, ea secabit rectam AF. Secet in F, et jungatur CF, itemque DF, quae producatur versus L. Quoniam igitur differentia quadratorum TA, AD est ad quadr. AD ut differentia quadratorum CA, AD ad quadratum DS vel DF; erit, componendo, quadratum TA ad quadr. AD ut differentia quadratorum CA, AD una cum quadrato DF ad quadratum DF. Est
 [Fig. 10.]
autem differentia quadratorum CA, AD, hoc est, quadr. CD cum duplo rectangulo CDA, addita quadrato DF aequalis quadrato CF. Ergo sicut quadr. TA ad quadr. AD, ita quadr. CF ad quadr. DF. Et linea CF ad DF ut TA ad AD. Est autem ratio TA ad AD ea quae refractionis. Ergo in triangulo CFD habet latus CF ad FD proportionem refractionis; ac proinde eandem quoque habebit sinus anguli CDF vel ADF, ad sinum anguli FCD. Est autem angulus ADF quo radius incidens LF inclinatur ad perpendicularem, et angulus FCD quo ad eandem perpendicularem inclinatur linea FC. Ergo constat radij LF refractionem esse FC. Atque ita ostensum est alicujus radij refractionem quolibet intervallo propius concurrere ad punctum T cum axe AD. Erit igitur propter haec T punctum concursus quaesitum. | |||||||||||||||||||||||||||||||||||||
[Propositio V.]
| |||||||||||||||||||||||||||||||||||||
[pagina 24]
| |||||||||||||||||||||||||||||||||||||
perpendiculaire à la surface AE. Prolongeons-la, et soit TA:AD égal à l'indice de réfraction. Je dis que T sera le point de dispersion cherché, c'est-à-dire que les rayons réfractés, tels que FN, provenant de rayons issus du point D, tels que DF, ont dans le corps transparent la direction qu'ils auraient en venant du point T. En effet, prolongeons DF du côté L et joignons les points F et T. Alors il sera clair par ce qui précède que si, contrairement à notre hypothèse, nous nous figurons que la surface AE limite un corps transparent situé du coté D, les rayons, qui se dirigent vers le point D ont après la réfraction leur point de concours en T, de sorte que FT sera le rayon réfracté provenant du rayon LF. Or, FD est le prolongement de LF, et FN est celui de TF. Par conséquent, FN sera ici le rayon réfracté provenant du rayon DFGa naar margenoot*. Le rayon DF a donc après la réfraction la même direction que s'il provenait du point T; c'est pourquoi le point T sera le point de dispersion cherché. Il est évident qu'en vérité les rayons réfractés, prolongés en sens inverse, coupent l'axe AD au-delà du point T. | |||||||||||||||||||||||||||||||||||||
Proposition VI.
| |||||||||||||||||||||||||||||||||||||
[pagina 25]
| |||||||||||||||||||||||||||||||||||||
et producatur, habeatque TA ad AD proportionem refractionis. Dico T fore punctum dispersus quaesitum: Hoc est radiorum ex D procedentium refractiones, sicut FN est radij DF, intra diaphanum
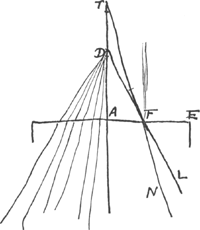 [Fig. 11.]
ita ferri, quasi venirent ex puncto T. Producatur enim DF versus L, et jungatur FT. Igitur si superficiem AE, contra quam hîc positum est, terminare imaginemur diaphanum versus D existens, manifestum est per praeced. radiorum ad D tendentium refractiones concurrere ad punctum T: ita ut radij LF refractio futura sit FT. Est autem FD in directum ipsi LF, et FN in directum ipsi TF. Ergo et FN erit hic refractio radij DFGa naar margenoot*. Itaque radius DF refractus ita fertur quasi ex puncto T manaret, ideoque erit T punctum dispersus quaesitum. Patet autem ejusmodi esse, ut radiorum refractiones retro productae ultra ipsum T, cum recta AD conveniant. | |||||||||||||||||||||||||||||||||||||
[Propositio VI.]
| |||||||||||||||||||||||||||||||||||||
[pagina 26]
| |||||||||||||||||||||||||||||||||||||
de réfraction. Par conséquent le rayon FL sera inversement le rayon réfracté provenant du rayon TF; car telle est la loi des réfractions, comme cela a été exposé plus haut. D est donc le point de dispersion cherché. Ce point sera tel que tous les rayons réfractés rencontrent l'axe en-deça de D, c'est-à-dire en un point plus rapproché que D lui-même de la sursace A. Cela peut facilement être démontré à l'aide des considérations du problème 1. | |||||||||||||||||||||||||||||||||||||
Proposition VII.
| |||||||||||||||||||||||||||||||||||||
Lemme 1.Ga naar voetnoot1)Soit ABC [Fig. 14] un triangle possédant un angle obtus A. Une droite partant de B rencontre AC, prolongée du côté C, au point D. Je dis que le rapport BD:DA est plus petit que BC:CA. En effet, soit CE une parallèle à DB. Comme l'angle A est par hypothèse | |||||||||||||||||||||||||||||||||||||
[pagina 27]
| |||||||||||||||||||||||||||||||||||||
portio refractionis. Igitur vicissim radij TF refractio erit FL; haec enim refractionum lex est ut supra fuit expositum. Igitur D est punctum dispersus quaesitum. Erit autem ejusmodi ut radiorum refractiones omnes citra D concurrant, hoc est ut concursus earum minus distet a superficie A quam punctum D. Quod facile probari potest ex iis quae habentur in Probl. [1]. | |||||||||||||||||||||||||||||||||||||
[Propositio VII.]
| |||||||||||||||||||||||||||||||||||||
Lemma [1.]Ga naar voetnoot1)Sit triangulum BAC [Fig. 14] angulum A obtusum habens, et ducatur ex B quae occurrat AC, versus C productae in D. Dico minorem esse rationem BD ad DA quam BC ad CA. Sit enim ducta CE parallela DB. Quoniam ergo angulus A obtusus est; angu- | |||||||||||||||||||||||||||||||||||||
[pagina 28]
| |||||||||||||||||||||||||||||||||||||
obtus, et que l'angle BEC est égal à la somme des angles A et ECA, BEC sera un angle obtus, et par conséquent dans le triangle BEC le côté BC sera plus grand que le côté EC. C'est pourquoi on aura EC:CA < BC:CA. Or, EC:CA = BD:DA. Donc aussi BD:DA < BC:CA. Ce qu'il fallait démontrer. | |||||||||||||||||||||||||||||||||||||
Lemme 2.Réciproquement, si nous considérons de nouveau un triangle BAC [Fig. 14] possédant un angle obtus A, et que BD est opposée à ce même angle et rencontre la droite AC ou son prolongement, de telle manière que le rapport BD:DA soit plus petit que le rapport BC:CA, je dis que DA est plus grande que CA. En effet, si nous admettons que DA est plus petite que CA, on aura par le lemme précédent BD:DA > BC:CA. Or, par hypothèse BD:DA < BC:CA. Par conséquent, DA n'est pas plus petite que CA. Elle ne peut pas non plus lui être égale. La seule possibilité qui reste c'est que DA soit plus grande que CA. Ce qu'il fallait démontrer. | |||||||||||||||||||||||||||||||||||||
Lemme 3.Soit un triangle ABC [Fig. 15] possédant un angle obtus B. Une droite partant de B rencontre AC, prolongée du côté C, au point D. Je dis qu'on aura AD:DB < AC:CB.  [Fig. 15.]
En effet, soit CE parallèle à DB. Vu que l'angle B du triangle CBE est obtus, le côté CE sera plus grand que le côté CB. Par conséquent, AC:CE < AC:CB. Or, AC:CE == AD:DB. Doncaussi AD:DB < AC:CB; ce qu'il fallait démontrer. | |||||||||||||||||||||||||||||||||||||
Lemme 4.Considérons de nouveau le triangle ABC [Fig. 15] possédant un angle obtus B. Tirons BD de manière à ce que cette droite coupe AC ou son prolongement en D, et que l'angle ABD soit également obtus; soit en outre AD:DB < AC:CB. Je dis que AD est plus grande que AC. En effet, soit AD < AC, il résultera alors du lemme précédent que le rapport | |||||||||||||||||||||||||||||||||||||
[pagina 29]
| |||||||||||||||||||||||||||||||||||||
lus autem BEC aequalis utrisque simul,
 [Fig. 14.]
angulo A et ECA:Erit et BEC angulus obtusus, ideoque in triangulo BEC latus BC majus latere EC. quare minor ratio erit EC ad CA quam BC ad CA. ut autem EC ad CA ita BD ad DA. Ergo minor quoque ratio BD ad DA quam BC ad CA. Quod erat propositum. | |||||||||||||||||||||||||||||||||||||
Lemma 2.Contra autem, posito ut ante, triangulo BAC [Fig. 14], angulum A obtusum habente, si ducatur BD eidem obtuso angulo subtensa, occurensque rectae per AC, ita ut minor sit ratio BD ad DA, quam BC ad CA; dico DA majorem esse quam CA. Si enim DA minor dicatur quam CA, erit per praeced. lemma major ratio BD ad DA quam BC ad CA. Ponitur autem minor esse. Ergo DA non erit minor quam CA, sed nec aequalis potest esse. Ergo superest ut DA sit major quam CA. quod erat propositum. | |||||||||||||||||||||||||||||||||||||
Lemma 3.Sit triangulum ABC [Fig. 15] angulum B obtusum habens, et ducatur ex B quae productae AC versus C occurrat in D. Dico minorem fore rationem AD ad DB quam AC ad CB. Sit enim CE parallela DB. Quoniam ergo trianguli CBE obtusus est angulus B, Erit latus CE majus latere CB:ac proinde minor ratio AC ad CE quam AC ad CB. Ut autem AC ad CE ita est AD ad DB. Ergo minor quoque ratio AD ad DB quam AC ad CB. quod erat propositum. | |||||||||||||||||||||||||||||||||||||
Lemma 4.Sit denuo triangulum ABC [Fig. 15] angulo B obtuso, et ducatur BD occurrens rectae per AC in D, ita ut et angulus ABD existat obtusus, sitque ratio AD ad DB minor ratione AC ad CB. Dico AD majorem esse quam AC. Si enim AD minor dicatur quam AC, sequetur ex lemmate praecedenti, ratio- | |||||||||||||||||||||||||||||||||||||
[pagina 30]
| |||||||||||||||||||||||||||||||||||||
AC:CB est plus petit que le rapport AD:DB. Mais ici nous avons posé AD:DB < AC:CB. Par conséquent AD n'est pas plus petite que AC. Elle ne lui est pas non plus égale, vu que BC et BD sont par hypothèse différentes l'une de l'autre. Donc AD > AC. Ce qu' il fallait démontrer. | |||||||||||||||||||||||||||||||||||||
Lemme 5.Soit une ligne droite AB divisée en C de telle manière que AC > CB. Prolongeons cette droite du côté B, et soit AD:DB = AC:CB. Décrivons avec CD comme diamètre la circonférence de cercle CED. Si des lignes droites AE, BE sont menées d'un point quelconque E de cette circonférence, je dis qu'on aura AE:EB == AC:CB. Cela a été démontré par Eutocius dans son Commentaire aux Coniques d'ApolloniusGa naar voetnoot1). Et mieux par le professeur Fr. van Schooten, dans sa restitution des lieux plans d'ApolloniusGa naar voetnoot3). Mais si un point, tel que H, est pris en dehors du cercle, et que ce point est réuni par des droites à A et à B, je dis qu'on aura AH:HB < AC:CB.  [Fig. 16.]
En effet, tirons la droite AK, K étant le point où la droite BH coupe la circonférence. On a donc AK:KB = AC:CB; partant AK > KB. C'est pourquoi, si l'on ajoute des deux côtés KH, on aura AK+KH:HB < AK:KB. Mais HA < < HK+KA, ou 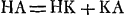 , si H est pris sur la ligne CD prolongée du côté D. On aura donc aussi AH:HB < AK:KB, c'est-à-dire < AC:CB. Ce qu'il fallait démontrer. , si H est pris sur la ligne CD prolongée du côté D. On aura donc aussi AH:HB < AK:KB, c'est-à-dire < AC:CB. Ce qu'il fallait démontrer.
Si nous prenons au contraire un point tel que L à l'intérieur de la circonsérence, et que nous joignons ce point par des droites à A et à B, je dis qu'on aura AL:LB > AC:CB.En effet, supposons que le prolongement de BL rencontre la circonférence en M. Joignons les points A et M. On a donc AM:MB = AC:CB, et par conséquent AM > MB. Mais 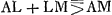 , l'égalité ayant lieu si le point L est pris sur la ligne BD. Par conséquent, on aura aussi , l'égalité ayant lieu si le point L est pris sur la ligne BD. Par conséquent, on aura aussi 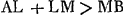 . .
| |||||||||||||||||||||||||||||||||||||
[pagina 31]
| |||||||||||||||||||||||||||||||||||||
nem AC ad CB minorem esse quam AD ad DB. hic autem ratio AD ad DB minor ponitur quam AC ad CB. Non est igitur AD minor quam AC. Sed nec aequalis, cum BC, BD diversae ponantur. Ergo major est AD quam AC, quod erat propos. | |||||||||||||||||||||||||||||||||||||
Lemma [5].Esto linea recta AB [Fig. 16] divisa in C, ut AC sit major quam CB. Et producatur versus B, habeatque AD ad DB rationem eandem quam AC ad CB: Et describatur circa CD diametrum circulus CED. Si ad quodvis circumferentiae punctum ut E ducantur rectae AE, BE. Dico esse AE ad EB ut AC ad CB. Demonstratum hocest ab Eutocio in comm. ad Conica Apoll.Ga naar voetnoot1) Et melius a Clariss. Viro Fr. Schotenio, in locis planis Apollonij ab ipsoGa naar voetnoot2) restitutisGa naar voetnoot3). Quod si vero extra descriptum circulum sumatur punctum ut H, ad quod rectae inflectantur à punctis A, B; dico AH ad HB minorem rationem habere quam AC ad CB. Ducatur enim AK ad intersectionem circumferentiae et rectae BH. Est igitur AK ad KB ut AC ad CB: ideoque AK major quam KB. Quare addita utrique KH, erit AKH ad HB minor ratio quam AK ad KB. Sed HA minor est quam HKA vel ipsi aequalis, si H sumtum fuerit in linea CD versus D prolongata. Ergo et AH ad HB minorem rationem habebit quam AK ad KB, hoc est, quam AC ad CB. quod erat propositum. Rursus si intra circulum sumatur punctum ut L ad quod rectae inflectantur è punctis A et B. Dico AL ad LB rationem majorem esse quam AC ad CB. Producta enim BL occurrat circumferentiae in M, et jungatur AM. Est ergo AM ad MB ut AC ad CB, ideoque AM major quam MB. Sed ALM major est quam AM, vel eidem aequalis, si punctum L sumtum fuerit in linea BD. Ergo ALM quoque major erit quam MB. Quare si utrinque auferatur LM, fiet | |||||||||||||||||||||||||||||||||||||
[pagina 32]
| |||||||||||||||||||||||||||||||||||||
Et, en retranchant des deux côtés LM, le rapport du reste AL au reste LB sera donc plus grand que celui
 [Fig. 16.]
de AL+LM et de MB. Or, 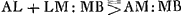 . Le rapport AL:LB sera donc en tout cas plus grand que le rapport AM:MB. La vérité de notre proposition est donc é tablie. . Le rapport AL:LB sera donc en tout cas plus grand que le rapport AM:MB. La vérité de notre proposition est donc é tablie.
Et il est clair que la réciproque des deux propositions est également vraie. C'est-à-dire que, si AH:HB < AC:CB, le point H tombe en-dehors de la circonférence CED décrite de la manière indiquée. Mais, si AL:LB > AC:CB, le point L est situé à l'intérieur de cette circonférence. | |||||||||||||||||||||||||||||||||||||
Proposition VIII.
| |||||||||||||||||||||||||||||||||||||
[pagina 33]
| |||||||||||||||||||||||||||||||||||||
major ratio reliquae AL ad reliquam LB quam ALM ad MB. Ratio autem ALM ad MB major est vel eadem cum ratione AM ad MB. Ergo ratio AL ad LB major utique erit quam AM ad MB. quare constat propositum. Patet autem et conversum utriusque horum. Nempe si AH ad HB minorem rationem habeat quam AC ad CB, punctum H cadere extra circulum CED dicto modo descriptum. Si autem AL ad LB majorem habeat rationem quam AC ad CB, punctum L intra eundem circulum cadere. | |||||||||||||||||||||||||||||||||||||
[Propositio VIII.]
| |||||||||||||||||||||||||||||||||||||
[pagina 34]
| |||||||||||||||||||||||||||||||||||||
En second lieu nous ferons voir que les rayons réfractés provenant de rayons situés plus près de l'axe AC coupent l'axe en des points moins éloignés du point Q que ceux provenant de rayons situés à plus grande distance de l'axe. En effet, soit OB un rayon situé plus près du dit axe AC que le rayon NP, et soit PK le rayon réfracté qui y correspond. Tirons les droites CP et KB. On verra de la même manière que plus haut, que les rapports BL:LC et PK:KC sont chacun égal à l'indice de réfractionGa naar voetnoot*. Or, BK > PK. Par conséquent, BK:KC > PK:KC, c'est-à-dire > BL:LC. Or, l'angle BCL, opposé à la fois à la ligne BL et à la ligne BK, est nécessairement un angle obtus. On aura donc CL > CKGa naar margenoot*. Et ainsi il est évident que le rayon réfracté provenant du rayon OB rencontre l'axe en un point plus rapproché du point Q que celui qui correspond au rayon réfracté provenant du rayon NP. Nous démontrerons enfin que quelques rayons réfractés coupent AC en un point éloigné du point Q à une distance inférieure à un intervalle quelconque donné. En effet, considérons d'abord l'un quelconque NP des rayons incidents et le rayon réfracté PK qui y correspond. Prenons entre K et Q un point L éloigné du point Q à une distance moindre que l'intervalle donné. Prenons en outre un point T tel que CQ:QA = CL:LT, et joignons les points P et L. Vu qu'alors l'angle PCL est obtus, et CL > CK, on aura PL:LC < PK:KCGa naar margenoot*. Or, le rapport PK:KC est égal à l'indice de réfraction, puisque PK est par hypothèse le rayon réfracté provenant du rayon NP. Par conséquent, comme le rapport PL:LC est plus petit que le rapport PK:KC, il sera également inférieur au rapport TL:LC, car, en vertu de notre construction, on a TL:LC = AQ:QC, c'est-à-dire = PK:KC. PL est donc plus petite que TL. Mais TL < AL; car CT < CA, vu que CL < CQ. La circonférence décrite du centre L avec le rayon LT doit donc nécessairement couper la circonférence AP entre A et P. Admettons qu'elle la coupe en B. Tirons BO parallèle à AC, et joignons B avec L et avec C. Comme CB est alors perpendiculaire à la surface AB, et que le rapport BL:LC, c'est-à-dire TL:LC, est égal à l'indice de réfraction, BL sera le rayon réfracté correspondant au rayon OB, parallèle à la droite AC. On voit ainsi que les rayons réfractés provenant de ce rayon-là et de tous ceux qui seront situés plus près de l'axe, coupent l'axe en des points éloignés du point Q à une distance plus petite que l'intervalle donné. Et pour cette raison Q sera le point de concours des rayons réfractés, ce qu'il s'agissait de trouver. | |||||||||||||||||||||||||||||||||||||
Proposition IX.
| |||||||||||||||||||||||||||||||||||||
[pagina 35]
| |||||||||||||||||||||||||||||||||||||
Secundo loco ostendetur radiorum axi AC propiorum refractiones propius accedere ad punctum Q quam remotiorum. Sit enim radius OB dictae AC propior quam radius NP, atque hujus refractio sit PK. Et jungantur CP, KB. Eâdem igitur ratione qua modò, et BL ad LC et PK ad KC habebit proportionem refractionisGa naar margenoot*. Est autem BK major quam PK. Ergo major ratio BK ad KC quam PK ad KC, hoc est, quam BL ad LC. Angulus autem BCL necessario est obtusus, cui utraque linearum BL, BK subtenditur. Ergo major erit CL quam CKGa naar margenoot*. Atque ita apparet, refractionem radij OB propius concurrere ad punctum Q quam refractionem radii NP. Denique ostendemus aliquos radios refractos convenire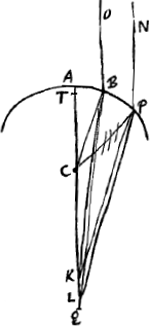 [Fig. 17.]
cum AC ad punctum quolibet dato intervallo minus distans à puncto Q. Sit enim primò quilibet radius parallelus incidens NP, et refractio ejus PK, et sumatur inter K et Q punctum L dato intervallo propinquius puncto Q. Quam autem rationem habet CQ ad QA, eam habeat CL ad LT, et jungatur PL. Quoniam igitur angulus PCL obtusus est, et CL major quam CK, erit minor ratio PL ad LC quam PK ad KCGa naar margenoot*. Est autem ratio PK ad KC eadem quae refractionis, quia PK ponitur esse refractio radij NP. Ergo cum ratio PL ad LC sit minor quam PK ad KC, eadem quoque minor erit ratione TL ad LC, nam per constr. est TL ad LC ut AQ ad QC, hoc est, ut PK ad KC. Igitur PL minor quam TL. Sed TL minor est quam AL; est enim CT minor quam CA, quia CL minor quam CQ. Ergo circumferentia descripta centro L, radio LT, necesse est ut secet circumferentiam AP inter A et P. Secet ergo in B, et ducatur BO parallela AC, jungantur BL, CB. Quia igitur CB ad superficiem AB perpendicularis est, habetque BL hoc est TL ad LC proportionem refractionis, erit BL refractio radij OB, rectae AC paralleli. Itaque patet et hujus radij, et omnium qui ab axe AC minus distabunt refractiones concurrere ad puncta dato intervallo minus remota à puncto Q. Et ob haec quidem erit Q punctum concursus radiorum refractorum, quod invenire oportebat. | |||||||||||||||||||||||||||||||||||||
[Propositio IX.]
| |||||||||||||||||||||||||||||||||||||
[pagina 36]
| |||||||||||||||||||||||||||||||||||||
transparent, sur laquelle tombent du dedans des rayons parallèles, trouver le point de concours des rayons réfractésGa naar voetnoot1). Soit AB [Fig. 18] la surface convexe, et C son centre où passe CA parallèle aux rayons incidents. Prolongeons cette droite jusqu'en R, et soit le rapport CR::RA égal à l'indice de réfraction. Je dis que R est le point de concours cherché. Nous démontrerons donc en premier lieu qu' aucun rayon réfracté ne rencontre le prolongement de CA au-delà du point R. En effet, soit BL le rayon réfracté provenant du rayon OB parallèle à la droite CA. Joignons B et C. Comme CB est perpendiculaire à la surface AB, et CL parallèle au rayon OB, le rapport CL:LB sera égal à l'indice de réfractionGa naar margenoot*, c'est-à-dire à CR:RA. Mais LA < LB. Par conséquent, on aura CL:LA > CL:LB, c'est-à-dire > CR:RA, et, par partage, CA:AL > CA:AR. Donc AL < AR, et il est clair que le rayon réfracté provenant du rayon OB coupe l'axe en-deçà du point R. Il faut faire voir en second lieu que les rayons réfractés provenant de rayons situés plus près de la droite CA coupent l'axe plus près du point R. Soit donc le rayon OB plus près de CA que le rayon NP, et soit PK le rayon réfracté provenant du rayon NP. Joignons les points B et K d'une part, C et P d'autre part. Le rapport CK:KP sera donc égal à l'indice de réfraction, et le rapport CL:LB de même. Mais comme KB < KP, on aura CK:KB > CK:KP, c'est-à-dire > CL:LB. Et les angles CBL et CBK sont nécessairement obtus. On aura donc CL > CK, ce qui démontre notre proposition. Il faut enfin démontrer qu'un des rayons réfractés coupe le prolongement de CA en un point éloigné du point R à une distance plus petite qu'un intervalle donné. Soit NP l'un quelconque des rayons parallèles et PK le rayon réfracté qui y correspond. Prenons un point L entre K et R, tel que LR soit inférieure à l'intervalle donné. Soit le rapport CL:LT égal à l'indice de réfraction, c'est-à-dire à CR:RA. Vu qu'alors AL < AR, on aura CA:AL > CA:AR. Et, par composition, CL:LA > CR:RA, c'est-à-dire > CL:LT; d'où l'on tire LT > LA. Joignons les points L et P. Alors, comme l'angle CPK est obtus et que CL est par hypothèse plus grande que CK, l'angle CPL sera également obtus: et partant on aura CK:KP > CL:LPGa naar voetnoot*. Or, CK:KP = CL:LT, car ces rapports sont chacun égal à l'indice de réfraction. Par conséquent, CL:LT > CL:LP et LT < LP. Mais on a démontré que cette même longueur LT est plus grande que LA. Si l'on décrit du centre L et avec le rayon LT une circonférence, celle-ci | |||||||||||||||||||||||||||||||||||||
[pagina 37]
| |||||||||||||||||||||||||||||||||||||
radij intrinsecus occurrant, invenire punctum concursus refractorumGa naar voetnoot1).Sit superficies convexa AB, centro C, per quod 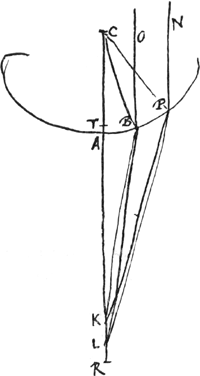 [Fig. 18.]
ducta sit CA radijs incidentibus parallela. Producatur ea ad R, et habeat CR ad RA proportionem refractionis. Dico R esse punctum concursus quaesitum. Primùm ergo demonstrabimus nullius refractionem radij convenire cum producta CA ultra punctum R. Sit enim radij OB ipsi CA paralleli refractio BL, et jungatur BC. Ergo cum CB ad superficiem AB perpendicularis sit, et CL parallela radio OB, habebit CL ad LB proportionem refractionisGa naar voetnoot*, hoc est, eam quam CR ad RA. Sed LA minor est quam LB. Igitur CL ad LA majorem habebit rationem quam ad LB, hoc est quam CR ad RA: Et dividendo CA ad AL majorem quam CA ad AR. Ergo AL minor quam AR. patetque radij OB refractionem concurrere citra punctum R. Porro ostendendum est radiorum rectae CA propinquiorum refractiones propius pervenire ad punctum R. Sit itaque radius OB quam NP propior CA, et refractio radij NP sit PK; et jungantur BK, CP. Habebit igitur CK ad KP refractionis proportionemGa naar margenoot* aeque ac CL ad LB. quia autem KB minor est quam KP, erit major ratio CK ad KB quam CK ad KP, hoc est, quam CL ad LB. Suntque anguli CBL, CBK uterque necessario obtusi. Ergo major erit CL quam CK, ex quo propositum patet. Denique est ostendendum, alicujus radij refractionem occurrere CA productae in puncto, quod dato quolibet propius sit puncto R. Sit aliquis è parallelis radijs NP, cujus refractio PK:Et sumatur punctum L inter K et R, dato intervallo propius puncto R, et habeat CL ad LT rationem refractionis, eandem nempe quam CR ad RA. Quia ergo AL minor est quam AR, erit CA ad AL ratio major quam CA ad AR. Et componendo major ratio CL ad LA quam CR ad RA, hoc est quam CL ad LT. Quare LT major erit quam LA. Jungatur LP. Itaque quia angulus CPK est obtusus, et ponitur CL major quam CK, erit quoque obtusus angulus CPL: ac proinde major ratio CK ad KP quam CL ad LPGa naar margenoot*. Ut autem CK ad KP ita est CL ad LT, nam utraque est ratio eadem quam refractionis. Ergo major ratio CL ad LT quam CL ad LP, ac proinde LT minor quam LP. Sed eadem LT major est ostensa quam LA. Ergo si centro L, | |||||||||||||||||||||||||||||||||||||
[pagina 38]
| |||||||||||||||||||||||||||||||||||||
coupera donc la circonférence AP entre A et P, par exemple en B. Soit BO parallèle à AC. Joignons en outre le point B avec les points L et C. Comme alors CL:LT, c'est-à-dire CL:LB, est égal à l'indice de réfraction, et que CB est perpendiculaire à la surface AB, BL sera le rayon réfracté qui correspond au rayon OBGa naar margenoot*). Il est donc démontré qu'un certain rayon réfracté, provenant d'un rayon parallèle à CA, coupe le prolongement de cette même droite AC en un point éloigné du point R à une distance plus petite qu'un intervalle quelconque donné. Pour ces raisons le point R sera le point de concours cherché. | |||||||||||||||||||||||||||||||||||||
Proposition X.Étant donnée la surface sphérique concave d'un corpstransparent sur laquelle tombent du dehors des rayons parallèles, trouver le point de dispersion des rayons réfractésGa naar voetnoot1).Soit AB la surface concave faisant partie d'une sphère à 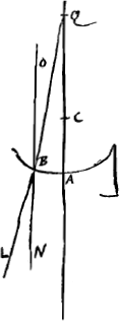 [Fig. 19.]
centre C. Sur cette surface tombent des rayons parallèles à la droite CA, tels que OB. Prolongeons AC et prenons un point Q tel que le rapport AQ:QC soit égal à l'indice de réfraction. Je dis que Q est le point de dispersion cherché, autrement dit, que par la réfraction les rayons changent leur direction de telle manière qu'ils semblent provenir du point Q. En effet, menons la droite QB et prolongeons-la du côté L; prolongeons aussi le rayon OB du côté N. Alors, de même que, lorsque la surface AB est convexe, c'est-à-dire lorsque le corps transparent est situé du côté C, BQ est le rayon réfracté provenant du rayon NBGa naar margenoot*, de même ici, le corps transparent étant situé de l'autre côté, BL sera le rayon réfracté provenant du rayon OBGa naar margenoot*, vu que BO est le prolongement de NB et BL celui de BQ. Il faut savoir pourtant que le rayon réfracté BL et tous les autres rayons réfractés, lorsqu' on les prolonge en sens inverse, ne coupent pas l'axe au point Q lui-même, mais un peu en-deçà de ce point, parce que le rayon réfracté provenant du rayon NB, considéré comme rayon incident tombant sur une surface convexe, coupe lui aussi l'axe en-deçà du point QGa naar margenoot*. Mais nous négligeons ici cette petite différence, comme je l'ai déjà dit plus hautGa naar voetnoot2); cela tient à ce que nous considérons surtout les rayons qui sont situés à une faible distance de l'axe AC. Il ressort manifestement de cette proposition, que les rayons qui se dirigent vers | |||||||||||||||||||||||||||||||||||||
[pagina 39]
| |||||||||||||||||||||||||||||||||||||
semidiametro LT circumferentia describatur, ea
 [Fig. 18.]
secabit circumferentiam AP inter A et P. Secet in B puncto, et sit BO parallela AC, et jungantur LB, BC. Quia ergo CL ad LT, hoc est, ad LB habet proportionem refractionis, estque CB ad superficiem AB perpendicularis, erit BL refractio radij OBGa naar margenoot*. Quare ostensum est alicuius radij rectae CA paralleli refractionem concurrere cum eadem AC producta, in puncto quod dato quolibet intervallo minus absit à puncto R. Atque ob haec erit R punctum concursus quaesitum. | |||||||||||||||||||||||||||||||||||||
Propositio [X].Data diaphani superficie sphaerica cava in quam radij paralleli extrinsecus incidant, invenire punctum dispersus refractorumGa naar voetnoot1). Sit [Fig. 19] superficies cava AB ex sphaera cujus centrum C, incidantque in eam radij rectae CA paralleli ut OB. Producatur AC, et habeat AQ ad QC proportionem eam quae est refractionis. Dico Q esse punctum dispersus quaesitum: hoc est, radios ita refractione inflecti ut pergant tanquam ex puncto Q promanantes. Jungatur enim QB et producatur versus L, et radius OB versus N. Itaque sicut superficie AB convexa existente, id est, diaphano ad partem ubi est C collocato, radij NB refractio est BQGa naar margenoot*: ita hîc ubi diaphanum ad contrariam partem situm est, erit radij OB refractio BLGa naar margenoot*, quia BO est in directum ipsi NB, et BL ipsi BQ. Sciendum tamen refractionem BL atque omnes alias retro productas non ad ipsum punctum Q concurrere, sed paulo citra, quoniam etiam radij NB in convexam superficiem incidentis refractio citra punctum Q cum axe AC concurritGa naar margenoot*. Verum exiguum discrimen pro nullo hîc habemus, sicut supra jam admonuiGa naar voetnoot2); quia videlicet illos radios praecipuè respicimus qui proximi sunt axi AC. Manifestum autem est ex propositione hac, radios tendentes ad punctum | |||||||||||||||||||||||||||||||||||||
[pagina 40]
| |||||||||||||||||||||||||||||||||||||
le point Q, tels que LB, et qui tombent du dedans sur la surface concave AB, deviennent après la réfraction parallèles à l'axe AC. Car si le rayon réfracté, provenant du rayon OB, est BL, alors BO sera aussi le rayon réfracté provenant du rayon LB. | |||||||||||||||||||||||||||||||||||||
Proposition XI.Étant donnée la surface sphérique concave d'un corps transparent, sur laquelle tombent du dedans des rayons parallèles, trouver le point de dispersion des rayons réfractésGa naar voetnoot1.Sur la surface concave AB, dont C est le centre, tombent des  [Fig. 20.]
rayons parallèles à la droite AC, tels que OB. Prolongeons CA, et prenons un point R tel que le rapport CR:RA soit égal à l'indice de réfraction. Je dis que R est le point de dispersion cherché. En effet, joignons R et B et prolongeons RB du côté L; prolongeons aussi OB du côté N. Si la surface AB était convexe, le rayon NB serait réfracté suivant BRGa naar margenoot*. De même, cette surface étant concave, BL sera le rayon réfracté provenant du rayon OBGa naar margenoot*, vu que OBN et RBL sont des lignes droites. On voit par là que les rayons qui se dirigent vers R, tels que LB, sont réfractés de telle maniere par la surface concave AB, qu'ils deviennent parallèles à la droite AC. Car BL étant le rayon réfracté provenant du rayon OB, BO sera le rayon réfracté provenant de LB. | |||||||||||||||||||||||||||||||||||||
Définition.Nous dirons que les rayons incidents ou les rayons réfractés correspondent au point vers lequel ils se dirigent ou dont ils proviennent ou semblent provenir. | |||||||||||||||||||||||||||||||||||||
Proposition XII.Étant donnée la surface sphérique convexe ou concave d'un corps transparent et le point auquel correspondent les rayons qui tombent sur cette surface; construisons sur l'axe, qui passe par le centre et par le point donné, une quatrième proportionnelle à trois longueurs ayant chacune une extrémité en ce point. La première de ces longueurs est la distance du point donné au point auquel correspondraient les rayons réfractés provenant de rayons parallèles à l'axe venant de l'autre côté. La seconde est la distance du point à la surface | |||||||||||||||||||||||||||||||||||||
[pagina 41]
| |||||||||||||||||||||||||||||||||||||
Q, ut LB, incidentesque intrinsecus in superficiem cavam AB, refractione facta, evadere parallelos axi AC. Nam si radij OB refractio est BL, erit et radij LB refractio BO. | |||||||||||||||||||||||||||||||||||||
Propositio [XI].Data diaphani superficie sphaerica cava, in quam radij paralleli intrinsecus incidant, invenire punctum dispersus refractorumGa naar voetnoot1). Ad superficiem cavam AB [Fig. 20] cujus centrum C, accidant radij paralleli rectae AC, ut OB. Producatur CA, et habeat CR ad RA proportionem refractionis. Dico R esse punctum dispersus quaesitum. Jungatur enim RB et producatur versus L, itemque OB versus N. Si igitur superficies AB esset convexa, radius NB refringeretur in BRGa naar margenoot*. Itaque eâdem cava existente, erit quoque radij OB refractio BLGa naar margenoot*, quandoquidem OBN, RBL sunt lineae rectae. Hinc vero manifestum est radios ad R tendentes ut LB, ita refringi ad eandem cavam superficiem AB, ut postea fiant rectae AC paralleli. Nempe quia BL est refractio radij OB, etiam BO erit refractio radij LB. | |||||||||||||||||||||||||||||||||||||
Definitio.Pertinere ad punctum illud radij vel radiorum refractiones dicuntur, ad quod tendunt, vel a quo exeunt, vel ad quod eo modo se habent, ac si inde prodijssent. | |||||||||||||||||||||||||||||||||||||
Propositio [XII].Data diaphani sphaerica superficie convexa, vel cava, et puncto, ad quod pertinentes radij superficiei dictae occurrant; si tribus ab illo puncto distantijs quarta proportionalis constituatur, in axe qui per centrum superficiei et punctum ipsum transit; quarum distantiarum prima sit à puncto dato ad illud quo pertinerent refractiones radiorum axi parallelorum à contraria parte advenientium; secunda ad superficiem refringentem, tertia ad centrum illius; terminus quartae | |||||||||||||||||||||||||||||||||||||
[pagina 42]
| |||||||||||||||||||||||||||||||||||||
réfringente. La troisième est la distance au centre de cette surface. La quatrième s'étendra alors jusqu'au point qui correspond aux rayons réfractés. Cette quatrième distance doit être prise à partir du point donné dans un sens tel que toutes les quatre soient dans le même sens ou bien deux dans un sens, deux dans l'autreGa naar voetnoot1). Nous diviserons ce Théorème en huit parties, car la surface sphérique est convexe ou concave, et dans chacun de ces deux cas les rayons peuvent venir du dehors ou du dedans; ils peuvent en outre venir d'un point donné ou bien se diriger vers un point donné. Et dans la plupart des huit parties il y a encore lieu de distinguer plusieurs cas. | |||||||||||||||||||||||||||||||||||||
Première partie.La surface est convexe et les rayons qui partent du point donné tombent du dehors sur la surface. Soit [Fig. 21] AB la surface sphérique convexe du corps transparent, et C son centre. Soit D le point d'où partent les rayons tels que DB qui tombent sur cette surface. Menons une droite par les points D et C et prenons sur elle un point R tel que le rapport CR:RA soit égal à l'indice de réfraction. R est donc le point de concours des rayons parallèles venant de l'autre côtéGa naar margenoot*. Or, le point D pourra être à plus grande ou bien à plus petite distance de la surface convexe que le point R; car s'il coincide avec R, les rayons qui en partent seront estimés parallèles, ainsi qu'il résulte de la prop. IX; en effet, cela se tire de ce que, comme nous l'avons dit, des rayons parallèles qui viennent du côté C se dirigent, après avoir traversé la surface AB, vers le point R. Soit donc d'abord le point D à plus grande distance de la surface que le point R, et comme DR est la première des distances dont nous avons parlé, DA la seconde et DC la troisième, faisons en sorte qu'on ait DR:DA = DC:DS. Je dis que S sera le point de concours des rayons provenant du point D. En effet, nous démontrerons d'abord qu'aucun rayon réfracté ne rencontre l'axe AC au-delà du point S, et cela de la façon suivante. Soit BL le rayon réfracté provenant d'un rayon quelconque DB. Tirons | |||||||||||||||||||||||||||||||||||||
[pagina 43]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 21.]
distantiae erit punctum quo pertinebunt radij refracti. Haec autem quarta distantia in eam dati puncti partem sumenda est, ut vel omnes eodem versus habeantur, vel binae utrimqueGa naar voetnoot1). Hoc Theorema in partes octo distribuemus, nam superficies sphaerica vel convexa est vel cava, et utrique vel extrinsecus, vel intrinsecus radij occurrunt, et vel a dato, vel ad datum punctum tendentes. Partes vero pleraeque suos casus habebunt. | |||||||||||||||||||||||||||||||||||||
Pars 1.Cum superficies est convexa, et a puncto venientes radij extrinsecus in eam deferuntur. Esto diaphani superficies sphaerica convexa AB, cujus centrum C, et punctum D a quo venientes radij in illam deferantur ut DB. Agatur recta per DC, inque ea signetur punctum R, ita ut CR ad RA habeat proportionem refractionis. Est igitur R punctum concursus radiorum parallelorum à contraria parte venientiumGa naar margenoot*. Punctum autem D aut magis aut minus à convexo distabit quam punctum R; nam si in ipsum R incidit, radij ab illo venientes pro parallelis habentur, ut ex. prop. [IX] manifestum est; quia nempe uti diximus paralleli ex parte C venientes a superficie AB detorquentur ad punctum R. Primò igitur sit punctum D remotius quam R, et quandoquidem DR est prima dictarum distantiarum, DA secunda, DC tertia, fiat ut DR ad DA ita DC ad DS. Dico S fore punctum concursus radiorum ex D procedentium. Nam primùm quidem, nullius radij refractionem cum axe AC ultra punctum S convenire, sic ostendemus. Sit radij cujusvis DB refractio BL, et ducatur CM parallela DB, et producatur versus C | |||||||||||||||||||||||||||||||||||||
[pagina 44]
| |||||||||||||||||||||||||||||||||||||
CM parallèle à DB et prolongeons-la du côté C jusqu'à ce qu'elle rencontre la surface AB en F. Vu qu' alors FM qui passe par le centre de la surface convexe est parallèle au rayon DB, et que BM est le rayon réfracté qui y correspond, il est certain que FM sera plus petite que CRGa naar margenoot*Ga naar voetnoot1), et CM par conséquent plus petite que AR. Or, DB > DA. On a donc DB:CM ou DL:LC > DA:AR; et, par conversion, LD:DC < AD:DR ou SD:DC. Par conséquent, DL sera plus petite que DS. On voit donc que BL, le rayon réfracté qui provient du rayon DB, coupe l'axe AC en-deçà du point S, et qu'il en est de même pour tous les autres rayons. Nous démontrerons en second lieu que les rayons qui sont à plus petite distance de l'axe AC, se rapprochent davantage du point S, après avoir été réfractés. Supposons que le rayon DP est plus éloigné de l'axe que le rayon DB, et soit PK le rayon réfracté qui y correspond. Menons la droite CN parallèle à DP; cette parallèle rencontre la surface en E. L'angle ADP ou ACE est alors plus grand que l'angle ADB ou ACF. Mais la partie AP de la circonférence est aussi plus grande que AB. Ainsi l'arc EP sera à plus forte raison plus grand que l'arc FB. Il est donc évident que le point de concours du rayon DP réfracté avec la droite ECN est plus rapproché du centre C que le point de concours du rayon DB réfracté avec la droite FMGa naar margenoot*. Par conséquent, CN < CM. Mais DP > DB. On aura donc DP:CN ou DK:KC > DB:CM ou DL:LC. Et, par partage, DC:CK > > DC:CL. Donc CK < CL, ce qu'il fallait démontrer. Enfin on peut démontrer que certains rayons réfractés coupent l'axe AC en des points éloignés du point S à une distance plus petite qu'un intervalle quelconque. En effet, on a DL:LC = DB:CM et l'on peut obtenir, en rapprochant le rayon DB de l'axe DAC, que la différence entre DB et DA devienne plus petite qu'une longueur quelconque donnée; il en sera de même de la différence entre CM et AR; car l'excès de AR sur CM sera d'autant plus petit que l'arc BF sera plus petit. Il paraît donc qu'on peut obtenir que le rapport DB:CM, c'est-à-dire DL:LC diffère aussi peu qu'on le voudra du rapport DA:AR. Et partant, par conversion, on obtiendra que la valeur du rapport LD:DC se rapproche autant qu'on le voudra de celle du rapport AD:DR ou SD:DC. Et ainsi DL sera à peu près égale à DS, c'est-à-dire le point L où le rayon DB coupe l'axe AC sera aussi près qu'on le voudra du point S. Pour ces raisons S sera le point de concours des rayons qui proviennent du point D. Soit maintenant [Fig. 22] le point donné D situé entre les points A et R. Faisons de nouveau DR:DA = DC:DS, la distance DS étant portée dans le sens DR, et non pas dans le sens DC. Je dis que les rayons qui tombent du point D sur la | |||||||||||||||||||||||||||||||||||||
[pagina 45]
| |||||||||||||||||||||||||||||||||||||
quousque occurrat superficiei AB in F. Cum igitur FM per centrum convexi ducta sit parallela radio DB, sitque refractio hujus BM, constar FM minorem fore quam CRGa naar margenoot*Ga naar voetnoot1), et CM proinde minorem quam AR. DB autem
 [Fig. 21.]
major est quam DA. Itaque major ratio DB ad CM, hoc est, DL ad LC, quam DA ad AR; ideoque per conversionem rationis minor ratio LD ad DC quam AD ad DR, hoc est, quam SD ad DC. Ergo DL minor erit quam DS. Patet igitur radij DB refractionem BL convenire cum axe AC citra punctum S, ac proinde reliquorum quoque omnium. Deinceps demonstrabimus radios eos qui minus distant ab axe AC, refractos propius accedere ad punctum S. Esto radius DP remotior quam DB, et refractio illius sit PK. Ducatur CN parallela DP, et occurrat superficiei in E. Angulus itaque ADP, hoc est ACE major est quam ADB sive ACF. Sed et circumferentiae pars AP major est quam AB. Itaque arcus EP major omnino erit arcu FB. Quare constat concursum radij DP refracti cum recta ECN propiorem esse centro C quam concursum radij DB refracti cum recta FMGa naar margenoot*. Ergo CN minor quam CM. Sed DP major est quam DB. Ergo major ratio DP ad CN, hoc est, DK ad KC quam DB ad CM, hoc est, quam DL ad LC. Et dividendo, major DC ad CK, quam DC ad CL. Ergo CK minor quam CL, quod ostendere oportebat. Denique aliquos radios refractos cum axe AC concurrere ad puncta quolibet intervallo propiora puncto S hinc erit manifestum. Etenim quia DL est ad LC ut DB ad CM, potestque fieri appropinquando radium DB ad axem DAC ut differentia inter DB et DA sit qualibet data minor, ut et ea quae est inter CM et AR; nam excessus AR super CM eo minor erit quo minor fuerit arcus BF; apparet fieri posse ut ratio DB ad CM, hoc est DL ad LC quamlibet proxime eadem evadat quae DA ad AR; ac proinde per conversionem rationis ratio LD ad DC quamlibet proxime eadem quae AD ad DR, hoc est quam SD ad DC. Atque ita DL proximè aequalis DS. hoc est ut punctum L ubi radius DB convenit cum axe AC quamlibet propinquum fiat puncto S. Propter haec igitur erit S punctum concursus radiorum ex D manantium. Esto autem nunc punctum D [Fig. 22] inter A et R datum; et fiat rursus ut DR ad DA ita DC ad DS; accipiatur autem DS non versus C sed versus | |||||||||||||||||||||||||||||||||||||
[pagina 46]
| |||||||||||||||||||||||||||||||||||||
surface AB changent de direction après la réfraction de telle manière qu'ils semblent provenir du point S, en d'autres termes, S sera, dis-je, le point de dispersion des rayons réfractés. En effet, nous démontrerons d'abord que tous les rayons réfractés dont nous avons parlé, rencontrent l'axe, lorsqu'on les prolonge en sens inverse, à une distance plus grande que AS du point A. Soit DB un rayon incident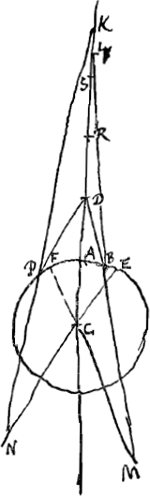 [Fig. 22].
et BM le rayon réfracté qui y correspond, lequel prolongé en sens inverse coupe l'axe AC en L. Bien entendu, il faut que DB soit plus petite que les deux tiers de DCGa naar voetnoot1), pour que le rayon réfracté BM prolongé en sens inverse coupe l'axe AC; s'il en était autrement, ce rayon serait parallèle à l'axe ou il le couperait après avoir été prolongé dans le sens direct, comme cela ressort de ce qui a été démontré plus haut (prop. IX)Ga naar voetnoot2). Donc, CM étant menée parallèle à DB, on aura de nouveau, comme dans le cas précédent, CM < AR. Mais DB > DA; c'est pourquoi DB:CM ou DL:LC > DA:AR. Et, par inversion, CL:LD < RA:AD et, par partage, CD:DL < RD:DA ou CD:DS. C'est pourquoi DL > > DS. Par conséquent, le point de rencontre L est plus éloigné du point A que le point S. Il faut observer qu' en prenant le point D fort près du point R on pourrait avoir DB > CM, et qu'ainsi les rayons réfractés provenant de certains rayons suffisamment éloignés de l'axe le couperaient au-delà du point CGa naar voetnoot3). On démontre de la même manière que dans le cas précédent que les rayons réfractés provenant de rayons plus rapprochés de l'axe AC, prolongés en sens inverse, coupent l'axe plus près du point S. Il n'y a entre cette démonstration et celle du cas précédent que cette seule différence qu' après avoir démontré que DK:KC > DL:LC, nous en conclurons maintenant, par inversion et par partage, que CD:DK < CD:DL, et, par conséquent, que CK > CL, d'où l'on tire DK > DL. Enfin on fait voir, de nouveau comme dans le cas précédent, que les rayons réfractés provenant de certains rayons incidents coupent l'axe en des points éloignés du point S à une distance plus petite qu'un intervalle quelconque donné. S sera donc le point de dispersion des rayons provenant du point D. | |||||||||||||||||||||||||||||||||||||
[pagina 47]
| |||||||||||||||||||||||||||||||||||||
R. Dico radios ex puncto D in superficiem AB incidentes post refractionem ita inflecti quasi venirent ex puncto S, sive S fore punctum dispersus radiorum refractorum. Etenim primo ostendemus omnes dictas refractiones retro productas concurrere longius ab A quam sit punctum S. Sit radius incidens DB, ejusque refractio BM, quae producta retro occurrat axi AC in L. Oportet autem DB minorem esse duabus tertiis DCGa naar voetnoot1), ut refractio BM retro producta conveniat cum axe AC, nam alioqui vel parallela illi fieret, vel occurreret prorsum producta, ut manifestum est ex demonstratis prop. [IX]Ga naar voetnoot2). Ducta igitur CM parallela DB, erit rursus, sicut in casu praecedenti CM minor quam AR; at DB major quam DA; ideoque major ratio DB ad CM, hoc est, DL ad LC, quam DA ad AR; Et invertendo minor CL ad LD quam RA ad AD; et dividendo minor CD ad DL quam RD ad DA, hoc est, quam CD ad DS. Quare DL major quam DS. ideoque occursus L ulterius distat ab A quam punctum S. Sumpto autem puncto D valde propinquo ipsi R posset fieri DB major quam CM, et sic refractio radiorum quorundam ab axe remotiorum concurrere simul cum axe ultra punctum CGa naar voetnoot3). Porro quod radiorum axi AC propiorum refractiones retro productae propius concurrunt ad punctum S, demonstratur quemadmodum in casu praecedenti; nisi quod hîc, ubi ostenderimus majorem esse rationem DK ad KC quam DL ad LC, inde sequatur, invertendo et dividendo, rationem CD ad DK minorem esse quam CD ad DL, ideoque CK majorem esse quam CL, unde DK major quam DL. Denique aliquorum radiorum refractiones quolibet intervallo propius concurrere ad punctum S eodem quoque modo ostenditur atque in casu priori. Erit igitur S punctum dispersus radiorum ex D promanantium. | |||||||||||||||||||||||||||||||||||||
[pagina 48]
| |||||||||||||||||||||||||||||||||||||
Deuxième Partie.La surface est convexe et les rayons qui se dirigent vers le point donné tombent du dehors sur cette surface. 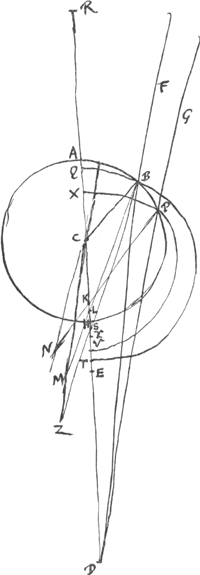 [Fig. 23.]
Soit donnée la surface convexe AB du corps transparent et le point D où se dirigent des rayons tels que FB et GP, au moment où ils tombent du dehors sur la dite surface. Soit C le centre de courbure, et DCA une droite passant par ce centre. Prolongeons DA, et prenons un point R tel que le rapport CR:RA soit égal à l'indice de réfraction. R sera donc le point de concours des rayons parallèles venant de l'autre côté. Construisons ensuite une quatrième proportionnelle DS à DR, DA et DC. Je dis que S est le point auquel correspondent les rayons réfractés qui se dirigeaient avant la réfraction vers le point D. La construction est universelle, la même pour tous les cas; mais pour la démonstration, il faut faire une différence entre trois cas. Car le rapport de DC au rayon CH est plus grand que l'indice de réfraction, ou plus petit, ou égal à cet indice. Et dans ce dernier cas il mérite d'être remarqué que tous les rayons se réunissent exactement au point unique S, comme je l'ai déjà remarqué il y a longtemps, lorsque j'indiquais que dans un cas particulier une des ovales, que Descartes avait imaginées pour réunir les rayons, se réduit à une circonférence de cercle, ce que Franc. van Schooten a inséré dans ses Commentaires sur la géométrie de DescartesGa naar voetnoot3). Parcourons par ordreGa naar voetnoot4) les trois cas que j'ai nommés. Soit d'abord [Fig. 23] le point D situé de telle manière que le quotient DC:CH soit supérieur à l'indice de réfraction, c'est-à-dire plus grand que CR:RA. Et soit S le point trouvé de la manière que nous venons d'indiquer. Supposons que le rayon réfracté provenant d'un rayon quel- | |||||||||||||||||||||||||||||||||||||
[pagina 49]
| |||||||||||||||||||||||||||||||||||||
Pars 2.Cum superficies convexa est, et ad punctum tendentes radij extrinsecus illi occurrunt. Esto data convexa diaphani superficies AB, et punctum D, quo tendentes radij ut FB, GP, exterius incidant in dictam superficiem. Centrum autem convexitatis sit C, per quod ducta sit recta DCA. Producatur DA, et habeat CR ad RA proportionem refractionis. Erit ergo R concursus parallelorum à contraria parte venientium. Deinde tribus hisce DR, DA, DC, inveniatur quarta proportionalis DS. Dico punctum S esse quo pertinent radij refracti ad D tendentes. Et constructio quidem universalis est ad omnes casus pertinens; in demonstratione autem triplex spectanda est differentia. Nam DC ad radium CH vel majorem rationem habet quam sit refractionis ratio, vel minorem, vel eandem. Atque hoc ultimo casu animadversione dignum est radios omnes perfectè coireGa naar voetnoot1) ad punctum unum SGa naar voetnoot2), ut jam olim adverteram cum Ovalem quandam ex ijs quas Cartesius excogitaver at ad colligendos radios uno casu circulum fieri admonui; quod suis in Cartesij geometriam commentarijs Franc. Schotenius inseruitGa naar voetnoot3). Ut autem tres quos diximus casus ordineGa naar voetnoot4) persequamur, sit primo [Fig. 23] punctum D ita positum, ut major sit ratio DC ad CH, ratione refractionis, hoc est quam CR habet ad RA. Sitque S punctum repertum eo modo quo diximus. Radius autem quilibet ut FB tendens ad punctum D, refractus conveniat cum | |||||||||||||||||||||||||||||||||||||
[pagina 50]
| |||||||||||||||||||||||||||||||||||||
conque tel que FB, se dirigeant vers le point D, coupe l'axe en L après la réfraction. Alors je démontrerai d'abord que le point L tombe en-deçà du point S. Joignons B et S par une droite et prolongeons cette droite, ainsi que BL. Les deux droites prolongées couperont la droite CMZ parallèle au rayon FBD, la première en Z, la seconde en M. Prenons ensuite un point E tel qu'on ait DA:AS = DE:ES. Vu qu' alors DC:CH ou DC:CA > CR:RA, on aura aussi, par permutation, DC:CR > CA:AR. Et, par compofition, DR:RC > CR:RA. Pour cette raison le rapport du reste DC au reste AC est plus grand que le rapport DR:RCGa naar margenoot*. Or, on a DR:RC = DA:AS. Car comme on a DR:DA == DC:DS, on aura par permutation et par conversion de cette proportion DR:RC = DA:AS. Par conséquent, on a aussi DC:CA > DA:AS. Or, DA:AS = DE:ES; donc la somme de DA et DE est à celle de AS et SE, c'est-à-dire à AE, comme DA est à AS. Par conséquent, DC:CA ou DC:CH > (AD+DE):AE. Et, par partage, DH:HC > 2DE:EA. Et, en prenant le double du deuxième et du quatrième terme DH:HA > 2DE:2EA ou DE:EA. Le point E tombe donc en-dehors de la circonférence ABH; par conséquent, si l'on décrit une circonférence, ayant EA comme diamètre, le point B sera situé à l'intérieur de cette circonférence. Mais, DE:ES = DA:AS. Donc on aura DB:BS > DA:ASGa naar margenoot*. Or, DB:BS = CZ:ZS, et DA:AS = DR:RC; cela a été démontré plus haut. On aura donc CZ:ZS > DR:RC. Or, le rapport DR:RC est composé des rapports DR:RA et RA:RC, et DR:RA = DC:CS, parce que nous avons pris le point S de telle façon que DR:DA = DC:DS. Le rapport CZ:ZS est donc plus grand que celui qui se compose des rapports DC:CS et RA:RC. Or, le rapport CZ:ZS est égal au produit des rapports CZ:ZB et ZB:ZS. Le produit de ces deux derniers rapports sera donc plus grand que le produit des rapports DC:CS et RA:RC. C'est pourquoi, si l'on divise les deux produits par BZ:ZS et DC:CS respectivement, lesquels rapports sont égaux entre eux, le rapport CZ:ZB sera encore plus grand que le rapport RA:RC. Et, par inversion, BZ:ZC < CR:RA. Or le rapport CR:RA, égal à l'indice de réfraction, est égal à BM:MCGa naar margenoot*, vu que BM est le rayon réfracté provenant du rayon FB, auquel on a mené la parallèle CM. Par conséquent, BZ:ZC < BM:MC. Or l'angle BCZ, étant égal à l'angle FBC, est nécessairement obtus; et chacune des lignes BM, BZ est opposée à cet angle. On aura donc CM < CZGa naar margenoot*, et par conséquent l'angle CBM < CBZ. | |||||||||||||||||||||||||||||||||||||
[pagina 51]
| |||||||||||||||||||||||||||||||||||||
axe AC in L. Ostendam igitur primo punctum L cadere citra S. Jungatur BS, et producatur, ut et BL, et occurrat utraque rectae CMZ radio FBD parallelae,
 [Fig. 23.]
nempe BS in Z, BL in M. Sicut autem DA ad AS ita sit DE ad ES. Quia ergo ratio DC ad CH sive ad CA major quam CR ad RA; et permutando major erit DC ad CR quam CA ad AR. Et componendo DR ad RC major quam CR ad RA. Quare reliquae DC ad reliquam AC major ratio quam DR ad RCGa naar margenoot*. Ut autem DR ad RC ita est DA ad AS. nam quia ut DR ad DA ita DC ad DS, erit permutando et per conversionem rationis DR ad RC ut DA ad AS. Itaque ratio DC ad CA major quoque quam DA ad AS. Ut autem DA ad AS ita DE ad ES, ideoque duae simul DA, DE ad duas AS, SE, hoc est ad AE, ut DA ad AS. Igitur major ratio DC ad CA, sive ad CH, quam ADE ad AE:Et dividendo major ratio DH ad HC quam duplae DE ad EA. Et sumtis consequentium duplis; major DH ad HA, quam duplae DE ad duplam EA, hoc est quam DE ad EA. Itaque punctum E cadit extra circulum ABH, ideoque si circa EA diametrum circulus describatur, is intra se complectetur punctum B. Est autem DE ad ES ut DA ad AS. Itaque major erit ratio DB ad BS quam DA ad ASGa naar margenoot*. Ut autem DB ad BS ita est CZ ad ZS, et ut DA ad AS ita DR ad RC, fuit enim hoc antea ostensum. Major itaque erit ratio CZ ad ZS quam DR ad RC. Componitur autem ratio DR ad RC ex rationibus DR ad RA et RA ad RC, quarum DR ad RA est eadem quae DC ad CS, quia fecimus ut DR ad | |||||||||||||||||||||||||||||||||||||
[pagina 52]
| |||||||||||||||||||||||||||||||||||||
C'est pourquoi CL est aussi plus petite que CS. L'on voit ainsi que tous les rayons réfractés, provenant de rayons qui se dirigent vers le point D, coupent l'axe en-deçà du point S.  [Fig. 23.]
Nous démontrerons maintenant que de plus les rayons réfractés provenant de rayons situés à plus petite distance de l'axe AC, coupent l'axe plus près du point S, et cela de telle manière que la distance du point de rencontre au point S peut devenir plus petite qu'un intervalle quelconque donné. En effet, considérons un rayon quelconque GP se dirigeant vers le point D et rencontrant la surface AB; soit PK le rayon réfracté correspondant. Le point de concours K est donc entre les points C et S, d'après ce qui a déjà été démontré. Prenons ensuite entre K et S un point quelconque L, et divisons DL en T de telle manière que DT:TL = DC. AR:LC. CR, le premier produit étant plus grand que le second. En effet, on a DC:CL > DC:CS ou DR:RA (car l'égalité de ces deux derniers rapports a été démontrée plus haut), partant le rapport DC:CL est beaucoup plus grand que le rapport CR:RA, et ainsi le produit DC..AR est plus grand que le produit CL. CR. Comme on a donc DT > TL, on peut prendre sur la ligne DL, prolongée du coté L, un point Q tel que DQ:QL = DT:TL. Supposons que ce point ait été trouvé et qu'on ait décrit une circonférence de cercle sur le diamètre QT. Cette circonférence coupera la circonférence AP entre A et P, comme cela sera démontré plus loin. Supposons qu'elle la coupe au point B. Tirons la ligne droite DBF et joignons les points B et L; prolongeons BL jusqu' à ce qu' elle rencontre la droite CM, qui doit être menée parallèle à la dite droite DBF. Vu qu'alors le point B est situé sur la circonférence dont TQ est le diamètre, et que DT:TL = DQ:DL, on aura DB:BL = = DT:TLGa naar margenoot*, c'est-à-dire égal à DC. AR:LC. CR. Or, le rapport DB:BL ou CM:ML est le produit des rapports CM:MB et MB:ML ou DC:CL, | |||||||||||||||||||||||||||||||||||||
[pagina 53]
| |||||||||||||||||||||||||||||||||||||
DA ita DC ad DS. Ergo ratio CZ ad ZS major quam quae componitur ex rationibus DC ad CS et RA ad RC. Ratio autem CZ ad ZS eadem est compositae ex rationibus CZ ad ZB et ZB ad ZS. Ergo quae ex duabus hisce componitur ratio major erit composita ex rationibus DC ad CS et RA ad RC. quare ablatis utrinque rationibus aequalibus, hinc DC ad CS, inde BZ ad ZS, major adhuc erit ratio CZ ad ZB quam RA ad RC. Et invertendo ratio BZ ad ZC minor quam CR ad RA. Sicut autem CR ad RA, quae est ratio refractionis, ita est BM ad MCGa naar margenoot*, quoniam BM est refractio radij FB, cui parallela ducta est CM. Igitur minor est ratio BZ ad ZC quam BM ad MC. Angulus autem BCZ, quoniam aequalis est angulo FBC, necessario est obtusus; eique utraque linearum BM, BZ subtensa est. Ergo CM minor erit quam CZGa naar margenoot*, et angulus proinde CMB minor angulo CBZ. Quare et CL minor quam CS. Itaque apparet omnium radiorum ad D tendentium refractiones cum axe AC convenire citra punctum S. Nunc porro ostendemus refractiones radiorum axi AC propinquiorum concurrere propius ad punctum S, idque ad intervallum minus quolibet dato. Sit enim radius aliquis GP tendens ad D, inque superficiem AB incidens, qui refringatur in PK. Est igitur concursus K inter C et S, ex jam demonstratis. Porro inter K et S quodvis punctum sumatur L: et dividatur DL in T, ut DT ad TL habeat rationem eam quam rectangulum DC, AR, ad rectangulum LC, CR; quae quidem erit majoris ad minus. Major enim est ratio DC ad CL quam DC ad CS, hoc est, quam DR ad RA (nam has easdem esse supra ostensum est) ideoque multo major ratio DC ad CL quam CR ad RA, ac proinde rectangulum DC, AR majus rectangulo CL, CR. Quoniam igitur ratio DT ad TL est majoris ad minus, potest in linea DL continuata versus L, sumi punctum Q, ita ut DQ ad QL habeat eandem rationem quam DT ad TL. Esto itaque inventum, sitque ad diametrum QT descripta circuli circumferentia. Ea secabit circumferentiam AP inter A et P, ut postea demonstrabitur. Secet ergo in B, et ducatur recta DBF, et jungatur BL, eaque producatur, et occurrat rectae CM, quae ducenda est ipsi DBF aequidistans. Quoniam igitur punctum B est ad circuli circumferentiam cujus diameter TQ, estque DT ad TL ut DQ ad QL; erit ratio DB ad BL eadem quae DT ad TLGa naar margenoot*, hoc est, quae rectanguli DC, AR ad rectangulum LC, CR. Ratio autem DB ad BL, hoc est, CM ad ML componitur ex ratione CM ad MB et MB ad ML, hoc est, et DC ad CL. Rectangulum vero DC, AR ad rectangulum LC, CR compositam habet rationem ex DC ad CL et AR ad RC. Ergo eadem est ratio quae componitur ex rationibus CM ad MB et DC ad CL, compositae ex rationibus DC ad CL et AR ad RC. Quare ablata | |||||||||||||||||||||||||||||||||||||
[pagina 54]
| |||||||||||||||||||||||||||||||||||||
et le rapport DC. AR:LC. CR est égal au produit des rapports DC:CL et AR:RC. Par conséquent, le produit des rapports CM:MB et DC:CL est égal au produit des rapports DC:CL et AR:RC. C'est pourquoi, en divisant les deux produits par le rapport DC:CL, on aura CM:MB = AR:RC et, par inversion, BM:MC = CR:RA, ce qui est égal à l'indice de réfraction. Par conséquent, comme CM est parallèle au rayon FB, BLM sera le rayon réfracté correspondant à ce rayon-là. Or, le point L a été pris arbitrairement entre K et S. Il est donc établi que le rayon réfracté provenant d'un certain rayon incident, coupe la droite CS en un point éloigné du point S à une distance plus petite qu'un intervalle quelconque donné. Mais on a démontré aussi que le rayon qui, après avoir été réfracté, parvient au point L, est situé plus près de l'axe AC que celui qui, après avoir été réfracté, rencontre l'axe au point K. Il en résulte que les rayons réfractés qui coupent l'axe plus près du point S, proviennent de rayons situés plus près de l'axe AC. Et il est clair que la réciproque est également vraie, c'est-à-dire que les rayons réfractés provenant de rayons situés plus près de l'axe AC coupent cet axe plus près du point S. Pour ces raisons S sera le point de concours des rayons provenant du point D. Quant à notre affirmation d'après laquelle la circonférence décrite avec QT comme diamètre coupe la circonférence APH entre A et P, la vérité en peut être démontrée comme suit. D'abord, comme CS > CL, on aura AC:CL > AC:CS, et, par composition, AL:LC > AS:SC. Or, le rapport AS:SC est le produit des rapports AS:SD et SD:SC, dont le premier AS:SD est égal à RC:CD, vu que par construction DR':DC = DA:DS. On a aussi SD:SC = DA:AR. Le rapport AL:LC sera donc plus grand que le produit des rapports RC:CD et DA:AR, c'est-à-dire, que le produit des rapports CR:RA et DA:DC. C'est pourquoi si l'on divise des deux côtés par le rapport DA:DC, on voit que le produit de AL:LC et DC:DA ou de LA:AD et DC:CL est plus grand que CR:RA. Et, en divisant de nouveau par le rapport DC:CL, on voit que LA:AD est plus grand que le produit des rapports CR:RA et LC:CD. Et, par inversion, on trouve que le rapport DA:AL est plus petit que le produit de DC:CL et de AR:RC, c'est-à dire, que le rapport du produit DC. AR au produit CL. CR, c'est-à-dire, que le rapport DQ:QL. Donc aussi, par partage, DL:LA < DL:LQ. Il en résulte LQ < LA. Or, DC:CL > DQ:QL, car DC:CL > DC. AR:CL. CR, vu que AR. < CR. Il est donc évident que le point Q tombe entre les points A et C. Divisons ensuite DK en deux parties par le point V de telle façon qu'on ait DV:VK = DC. AR:KC. CR. Le premier de ces produits est plus grand que le second; en effet, cette inégalité peut être démontrée de la même manière que, plus haut, celle des produits DC. AR et LC. CR. Choisissons ensuite le point X de telle façon qu'on ait DV:VK = DX:XK. Le point X tombera alors entre A et C, de même que le point Q, car ceci aussi peut être démontré de la même manière. Décri- | |||||||||||||||||||||||||||||||||||||
[pagina 55]
| |||||||||||||||||||||||||||||||||||||
communi ratione DC ad CL, erit eadem ratio CM ad MB quae AR ad RC. et invertendo BM ad MC eadem quae CR ad RA, quae est ratio refractionis. Ergo cum CM sit parallela radio FB, erit BLM ejusdem radij refractio.  [Fig. 23.]
Sumtum autem fuit punctum L pro arbitrio inter K et S. Itaque constat alicujus radij refractionem quolibet dato intervallo propius accedere ad punctum S, in linea CS. Sed et ostensum est radium, cujus refractio pervenit ad punctum L, propiorem esse axi AC, quam cujus refractio ad punctum K concurrit. Ergo constat eas refractiones, quae propius conveniunt ad punctum S, pertinere ad radios axi AC propiores. Cujus conversum quoque verum esse liquet, nimirum radiorum axi AC propinquiorum refractiones propius concurrere ad punctum S. Ergo ob haec erit S punctum concursus radiorum ex D venientium. Quod autem dictum est circumferentiam circa QT diametrum descriptam secare circulum APH inter A et P, sic ostendetur. Primò quia CS major quam CL, erit major ratio AC ad CL quam AC ad CS, et componendo, major AL ad LC quam AS ad SC. Ratio autem AS ad SC componitur ex rationibus AS ad SD et SD ad SC; quarum AS ad SD eadem est quae RC ad CD, quia ex constr. est DR ad DC ut DA ad DS. Item ratio SD ad SC est eadem quae DA ad AR. Major itaque erit ratio AL ad LC quam composita ex ratione RC ad CD et DA ad AR: hoc est, quam composita ex ratione CR ad RA et DA ad DC. Quare ablata utrinque ratione DA ad DC, erit composita ex ratione AL ad LC et DC ad DA, sive composita ex LA ad AD et DC ad CL major quam CR ad RA. Ablataque rursus utrinque ratione DC ad CL, erit LA ad AD major quam composita ex rationibus CR ad RA et LC ad CD. Et invertendo ratio DA ad AL minor compositâ ex ratio- | |||||||||||||||||||||||||||||||||||||
[pagina 56]
| |||||||||||||||||||||||||||||||||||||
vons une circonférence avec le diamètre XV. Elle coupera la circonférence AP précisément au point P où nous avons dit que le rayon GP rencontre la surface convexe AB. En effet, prolongeons PK et menons CN parallèle à GPD; cette parallèle
 [Fig. 23.]
coupera le prolongement de PK. Par conséquent, comme nous avons supposé que PK est le rayon réfracté provenant du rayon GP, auquel CN qui passe par le centre est parallèle, le rapport PN:NC sera égal à l'indice de réfraction. On a donc CN:NP = AR:RC. En partant de là, nous raisonnerons de la manière suivante. Le rapport CN:NK est le produit des rapports CN:NP et NP:NK ou DC:CK; par conséquent, le rapport CN:KN ou DP:PK est le produit des rapports AR::RC et DC:CK, ou, si l'on veut, le rapport des produits AR. DC et RC. CK. On aura donc DP:PK = AR. DC:RC. CK; donc aussi DP:PK = DV:VK = DX:XK. C'est pourquoi la circonférence dont le diamètre est XV passera par le point PGa naar margenoot* comme nous le disions. Or, comme DT:TL = AR. DC:RC. CL et que DV:VK = AR. DC:RC. CK, on aura DT:TL < DV:VK; en effet, RC. CL >> RC. CK. Par conséquent, le rapport DT:TK est à plus forte raison plus petit que le rapport DV:VK; car DK est par hypothèse plus grande que DL. Il apparaît donc que le point T tombe entre D et V. Je dis de plus que le point Q tombe entre A et X. En effet, prenons un point Y tel qu'on ait DQ:QL = DX:XY. Alors, vu que par construction XK:XD = RC. CK:AR. DC, et que DX:XY = DQ:QL = AR. DC:RC. CL, on aura en combinant ces deux équations XK:XY = RC. CK:RC. CL ou CK:CL. Donc XK:KY = CK:KL. Mais, XK > CK, comme nous l'avons dit plus haut. Par conséquent, on a aussi KY > KL, partant DY < DL. Or, nous avions DX:XY = DQ::QL et, par conversion, DX:DY = DQ:DL. Par conséquent, comme DY << DL, on aura aussi DX < DQ. Le point Q tombera donc nécessairement entre | |||||||||||||||||||||||||||||||||||||
[pagina 57]
| |||||||||||||||||||||||||||||||||||||
nibus DC ad CL et AR ad RC; hoc est, ratione rectanguli DC, AR ad rectangulum CL, CR, hoc est, ratione DQ ad QL. Quare et dividendo ratio DL ad LA minor erit ratione DL ad LQ. Unde patet LQ minorem esse quam LA. Est autem ratio DC ad CL major quam DQ ad QL, nam DC ad CL ratio major est quam rectanguli DC, AR, ad rectangulum CL, CR, quia AR minor est quam CR. Itaque patet punctum Q cadere inter A et C. Jam porro dividatur DK in V, ut habeat DV ad VK rationem eam quam rectangulum DC, AR ad rectangulum KC, CR. Haec autem est majoris ad minus, siquidem hoc eadem ratione ostenditur qua supra ostensum fuit rectangulum DC, AR majus esse rectangulo LC, CR. Deinde fiat ut DV ad VK ita DX ad XK, cadetque punctum X inter A et C, aequè ac punctum Q, nam hoc similiter quoque demonstrari potest. Sit autem circuli circumferentia circa XV diametrum descripta. Ea secabit circulum AP in ipso puncto P ubi radius GP convexo AB occurrere dictus est. Producatur enim PK, et occurrat ei CN parallela GPD. Ergo quia PK posita est esse refractio radij GP, cui parallela ex centro ducta est CN, habebit PN ad NC rationem refractionis. Est igitur CN ad NP ut AR ad RC. Unde sic porro argumentabimur. Ratio CN ad NK componitur ex rationibus CN ad NP et NP ad NK, hoc est, et DC ad CK; igitur ratio CN ad NK, hoc est, DP ad PK, componitur ex rationibus AR ad RC et DC ad CK, ex quibus componitur quoque ratio rectanguli AR, DC ad rectangulum RC, CK. Igitur DP ad PK erit ut rectangulum AR, DC ad rectangulum RC, CK. ac proinde etiam sicut DV ad VK, nec non ut DX ad XK. Quare circumferentia cujus diameter XV, transibit per punctum PGa naar margenoot*, ut dicebamus. Jam quia ratio DT ad TL est eadem quae rectanguli AR, DC ad rectangulum RC, CL; ratio vero DV ad VK eadem quae rectanguli AR, DC ad rectangulum RC, CK; minor erit ratio DT ad TL quam DV ad VK, quia rectang. RC, CL majus est rectangulo RC, CK. Itaque multo minor ratio DT ad TK quam DV ad VK; nam DK major est posita quam DL. Apparet igitur punctum T cadere inter D et V. Punctum vero Q dico cadere inter A et X. Sit enim ut DQ ad QL ita DX ad XY. Ergo quia XK ad XD per constr. ut rectang. RC, CK ad rectangulum AR, DC; DX autem ad XY ut DQ ad QL, hoc est ut rectang. AR, DC ad rectangulum RC, CL: erit ex aequo XK ad XY ut rectang. RC, CK ad rectang. RC, CL, hoc est, ut CK ad CL. Et XK ad KY ut CK ad KL. Est autem XK major quam CK, ut superius dictum fuit. Ergo KY major quoque quam KL, ideoque DY minor quam DL. Erat autem DX ad XY ut DQ ad QL, et per conversionem rationis DX ad DY ut DQ ad DL. Ergo quum DY sit minor quam DL, erit et DX minor quam DQ. Unde necessario punctum Q cadet inter A et X, nam quod inter A et C cadat jam ante ostensum fuit. Sed punctum T ostendimus distare ab A ultra punctum V. Ergo manifestum est circumferentiam QBT secare circulum APH inter A et P. Quod demonstrandum supererat. Sit nunc ratio DC ad CH minor ratione refractionis, hoc est ratione CR | |||||||||||||||||||||||||||||||||||||
[pagina 58]
| |||||||||||||||||||||||||||||||||||||
A et X, car nous avons déjà démontré que ce point tombe entre A et C. Mais nous avons fait voir que le point T est plus éloigné du point A que le point V. Il est donc évident que la circonférence QBT coupe la circonférence APH entre A et P. C'est ce qui restait à démontrer. Supposons maintenant que le rapport DC:CH est plus petit que l'indice de réfraction, c'est-à-dire que CR:RA. Et soit le point D situé, soit en-dehors de la circonférence ABH [Fig. 24], soit en-dedans de cette circonférence [Fig. 25], de telle manière toutefois que ce point soit plus éloigné du point A que le centre C. Car si ce point est situé entre A et C, on aura encore un autre cas particulier que nous examinerons bientôt. FB étant un rayon qui se dirige vers le point DGa naar voetnoot1) et qui, après la réfraction, rencontre l'axe AC au point L, je dis que L est plus éloigné de A que le point S. En effet, joignons B et S et menons CM parallèle à FD; supposons que cette parallèle rencontre les prolongements de BS et de BL en Z et en M respectivement; et prenons un point E tel que DA:AS == DE:ES. Si alors le point D est pris à l'intérieur de la circonférence ABH, le point E lui aussi tombera nécessairement à l'intérieur. Mais si le point D est pris en-dehors de la dite circonférence, le point E tombera néanmoins à l'intérieur, comme cela résulte de la démonstration suivante. Vu que DC:CH ou DC:CA < CR:RA, on aura aussi par permutation DC:CR < CA:AR et, par composition, DR:RC < CR:RA; c'est pourquoi le rapport du reste DC au reste CA sera plus petit que le rapport DR:RC ou DA::AS; l'égalité de ces deux derniers rapports se démontrant de la même manière que dans le cas précédentGa naar voetnoot2). Or, on a par construction DA:AS = DE:ES, donc aussi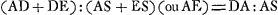 . Par conséquent, DC::C Aou DC:CH < (AD+DE):AE, et, par partage, DH:HC < 2DE:EA. Et, en prenant le double du deuxième et du quatrième terme DH:HA < 2DE::2EA ou DE:EA. Le point E tombera donc à l'intérieur de la circonférence ABH. . Par conséquent, DC::C Aou DC:CH < (AD+DE):AE, et, par partage, DH:HC < 2DE:EA. Et, en prenant le double du deuxième et du quatrième terme DH:HA < 2DE::2EA ou DE:EA. Le point E tombera donc à l'intérieur de la circonférence ABH.
Dans les deux cas nous continuerons à raisonner de la façon suivante. Vu que le point E tombe entre A et H, le point B sera en-dehors d'une circonférence décrite avec AE comme diamètre. Or, DA:AS = DE:ES. On aura donc DB:BS < DA::ASGa naar margenoot*. De plus DB:BS = CZ:ZS, et DA:AS = DR:RC. On a donc CZ:ZS << DR:RC. Or, le rapport DR:RC est égal au produit des rapports DR:RA et RA:RC, dont le premier est égal à DC:CS, vu que par construction DR::DA = DC:DS. Par conséquent le rapport CZ:ZS sera plus petit que le produit des rapports DC:CS et RA:RC. Or, le rapport CZ:ZS est égal au produit des rapports CZ:ZB et ZB:ZS. En divisant des deux côtés par des rapports égaux, savoir par BZ:ZS d'un côté et par DC:CS de l'autre, le rapport restant, savoir CZ:ZB, sera aussi plus petit que le rapport RA:RC. Et, | |||||||||||||||||||||||||||||||||||||
[pagina 59]
| |||||||||||||||||||||||||||||||||||||
ad RA, sitque punctum D vel extra circulum ABH [Fig. 24] vel intra [Fig. 25], ita tamen ut ultra centrum C distet ab A. Nam cum inter A et C positum est adhuc singularis est casus, quem mox videbimus. Radio igitur existente FBGa naar voetnoot1), qui tendat ad punctum D, conveniatque refractus cum axe AC in puncto L: dico L distare ab
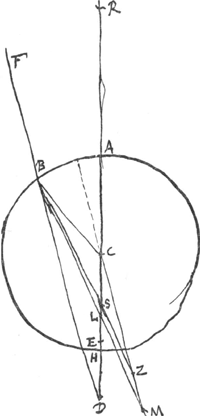 [Fig. 24.]
A ulterius quam punctum S. Jungatur enim BS, et ducatur CM parallela FD, quae occurrat productis BS, BL in Z et M; Et sicut DA ad AS ita sit DE ad ES. Si igitur punctum D intra circulum ABH ponatur, cadet necessario et E intra eundem. Si vero D extra dictum circulum ponatur, tamen E punctum intra circulum cadere sic ostenditur. Quia enim minor ratio DC ad CH, vel DC ad CA quam CR ad RA, permutando quoque minor erit DC ad CR quam CA ad AR, et componendo, minor DR ad RC quam CR ad RA; quare reliquae DC ad reliquam CA minor erit ratio quam DR ad RC, hoc est, quam DA ad AS, namque has easdem esse sicut in casu praecedenti ostenditurGa naar voetnoot2). Ut autem DA ad AS ita est DE ad ES ex constr. ideoque et duae simul AD, DE ad duas simul AS, SE, hoc est ad AE, ut DA ad AS. Igitur minor ratio DC ad CA, vel DC ad CH, quam ADE ad AE:Et dividendo minor ratio DH ad HC quam duplae DE ad EA. Sumtisque consequentium duplis, minor DH ad HA quam duplae DE ad duplam EA, hoc est, quam DE ad EA. Ergo punctnm E cadet intra circulum ABH. Jam utroque casu sic porro argumentabimur. Quoniam E cadit inter A, H, si circa AE diametrum circulus describatur, extra eum erit punctum B. Est autem ut DA ad AS ita DE ad ES. Ergo erit DB ad BS minor ratio quam DA ad ASGa naar margenoot*. Ut autem DB ad BS ita est CZ ad ZS; et ut DA ad AS ita DR ad RC. Ergo minor est ratio CZ ad ZS quam DR ad RC. Ratio autem DR ad RC componitur ex rationibus DR ad RA et RA ad RC, quarum DR ad RA est eadem quae DC ad CS, quia ut DR ad DA ita DC ad DS ex constr. Ergo ratio CZ ad ZS minor erit compositâ ex rationibus DC ad CS et RA ad RC. Ratio autem CZ ad ZS eadem est compositae ex rationibus CZ ad ZB et ZB ad ZS. Itaque ablatis utrinque rationibus aequalibus, hinc BZ ad ZS, inde DC ad | |||||||||||||||||||||||||||||||||||||
[pagina 60]
| |||||||||||||||||||||||||||||||||||||
par inversion, on aura BZ:ZC > CR:RA; mais le rapport CR:RA qui est égal à l'indice de résraction est égal aussi à BM:MCGa naar margenoot*, vu que BLM est le rayon réfracté provenant du rayon FB, auquel CM est parallèle. Par conséquent, BZ:ZC > BM:MC. Mais l'angle BCM, opposé à la fois à BM et à BZ, est nécessairement obtus, étant égal à l'angle FBC. Par conséquent, CZ sera plus petite que CMGa naar margenoot*, et l'angle CBM > CBZ. Donc aussi CL > CS. Ce qu'il fallait démontrer. On pourrait ensuite faire voir par une démonstration à peu près pareille à celle employée dans le premier casGa naar voetnoot2), que les rayons réfractés provenant de rayons situés à une plus petite distance de l'axe AC (j'entends par cela des rayons qui coupent la circonférence plus près du point A) rencontrent l'axe plus près du point S, et cela de telle manière que la distance du point de rencontre au point S soit plus petite qu'un intervalle quelconque donné. Mais nous ne répéterons pas ici cette argumentation prolixe. Nous nous contenterons de faire voir que certains rayons réfractés rencontrent l'axe en des points rapprochés autant qu'on le voudra du point S. Cela se démontre de la façon suivante. Supposons que le prolongement [Fig. 26.]
de MC rencontre la circonférence en N [Fig. 25]. Les triangles LDB et LCM sont semblables, d'où l'on tire DB:CM = DL:LC; et l'on peut obtenir, en rapprochant le rayon FB de l'axe AC, que la différence de longueur des lignes DB et DA devienne plus petite qu'une grandeur quelconque donnée, et de même aussi celle des lignes CM et AR; en effet, cette différence sera d'autant plus petite que l'arc BN sera plus petit, ainsi qu'il appert par le problème 5Ga naar voetnoot3), eu égard à ce que BM::MC = CR:RA. Il en résulte qu'on peut obtenir que le rapport DB:CM ou DL:LC acquière une valeur différant aussi peu qu'on le voudra de celle du rapport DA:AR ou DS:SC, et qu' ainsi le point L, où le rayon réfracté FB coupe l'axe AC, se rapproche indéfiniment du point S. Soit maintenant le point donné D [Fig. 26] situé entre A et C. Dans ce cas aussi BL, le rayon réfracté provenant du rayon FB, tombera entre D et C. Je dis que le point de concours L sera de nouveau situé à plus grande distance du point A que le point S. Prolongeons BL et supposons que CM, parallèle à FBD, rencontre ce prolongement au point M. Vu qu' alors le point D se trouve sur le diamètre entre A et le | |||||||||||||||||||||||||||||||||||||
[pagina 61]
| |||||||||||||||||||||||||||||||||||||
CS, minor quoque erit reliqua ratio CZ ad ZB quam RA ad RC:Et invertendo, major BZ ad ZC quam CR ad RA. Sicut autem CR ad RA quae est ratio refractionis ita est BM ad MCGa naar margenoot*, quoniam BLM est refractio radij FB, cui parallela ducta est et CM. Igitur major est ratio BZ ad ZC quam BM ad MC. Angulus autem BCM, cui utraque BM, BZ subtenditur, necessario est obtusus, quippe aequalis angulo FBC. Ergo CZ minor erit quam CMGa naar margenoot*, atque angulus proinde CBM major angulo CBZ. Quare et CL major quam CS; quod erat probandum.  [Fig. 25.]
Porro simili fere demonstratione, atque in casu primoGa naar voetnoot2), ostendi posset refractiones radiorum axi AC propinquiorum (intelligo autem propinquiores qui minimam circumferentiae partem versus A abscindunt) propius coire ad punctum S, idque ad intervallum quolibet dato minus. Sed prolixam argumentationem hîc non repetemus. Illud tamen, quod ad puncta quamlibet proxima puncto S, radiorum aliquorum refractiones concurrunt, hoc modo evinci potest. Producta MC occurrat circumferentiae in N [Fig. 25]. Quoniam ergo propter triangula similia LDB, LCM, sicut DB ad CM, ita DL ad LC; potestque fieri appropinquando radium FB ad axem AC, ut differentia longitudinis linearum DB, DA evadat qualibet data minor, ut et ea quae est inter CM et AR; (haec enim differentia eo minor erit quo minor continget arcus BN, ut patet ex problemate [5]Ga naar voetnoot3), quia nempe ratio BM ad MC est eadem quae CR ad RA) apparet hinc fieri posse ut ratio DB ad CM, hoc est, DL ad LC, quamlibet propeGa naar voetnoot4) eadem efficiatur quae DA ad AR, hoc est, quae DS ad SC. atque sic punctum L, quo nempe radius FB refractus cum axe AC convenit, quamlibet propinquum fiat puncto S. Sit jam punctum D inter A et C datum [Fig. 26], cadet autem et hîc radij FB refractio BL inter D et C. Dico concursum L rursus hic distare longius ab A quam punc- | |||||||||||||||||||||||||||||||||||||
[pagina 62]
| |||||||||||||||||||||||||||||||||||||
centre C, DB sera plus grande que DA. Mais CM < AR, ainsi qu'il ressort de la propos. VIII, vu que CM est parallèle au rayon FB, auquel correspond le rayon réfracté BM. On a donc BD:CM ou DL:LC > DA:AR. Or, DA::AR = DS:SC. Par conséquent DL:LC > DS:SC, et, par composition, DC:CL > DC:CS. Donc CL < CS. Il est évident par là que le point L est plus éloigné que le point S du point A. On démontre ensuite, de la même manière que dans le cas précédent, que dans ce cas aussi certains rayons réfractés se rapprochent indéfiniment du point S. Par conséquent, S sera le point de concours des rayons qui se dirigent vers le point D. Reste à démontrer la proposition dans le dernier cas, celui où le point D est placé en-dehors de la sphère ABH [Fig. 27] de telle manière que l'on ait DC::CH = CR:RA, ce qui est égal à l'indice de réfraction. Nous avons dit que dans ce cas les rayons réfractés provenant de tous les rayons qui se dirigent vers le point D se coupent exactement au point S qui est situé de telle façon que l'on ait DR:DA = DC:DS. En effet, ayant placé le point D comme nous l'avons dit, supposons que FBD soit un rayon quelconque se dirigeant vers ce point et rencontrant la surface au point B. Joignons le point B au point S. Je dis que BS est précisément le rayon réfracté provenant du rayon FB. En effet, prolongeons BS et menons CM parallèle à FBD; cette parallèle coupera le prolongement de BS. Joignons les points B et C. Vu qu' alors DC:CH ou DC:CA = CR:RA, la ligne entière DR sera aussi à RC, comme CR est à RA. Or, DR:RC = DA:AS, parce qu'on a par construction DR:DA = DC:DS. Par conséquent, on a aussi DA:AS == CR:RA ou DC:CH. En retranchant DC de DA, et CH (ou CA) de AS, le reste CA, ou CH, sera au reste CS comme DC est à CH. Or, CB = CH. Donc aussi BC:CS = DC:CB et, par conséquent, les triangles DCB et BCS sont semblables, attendu que ces triangles ont aussi en commun l'angle C compris entre les côtés proportionnels. Par conséquent, le troisième côté DB du premier triangle sera au troisième côté BS du second triangle, comme DC est à CB ou à CH, et l'angle SBC sera égal à l'angle BDC. Il en résulte que, dans les triangles DBS et BMC, l'angle MBC sera égal à l'angle BDS. Mais l'angle BMC est de plus égal à l'angle DBS, à cause du parallélisme des droites BD et CM. Par conséquent, les dits triangles DBS et BMC seront aussi semblables, et l'on aura donc BM:MC = DB:BS ou CD:CH ou CR:RA. Le rapport BM:MC est donc égal à l'indice de réfraction, et CM est parallèle au rayon FB. Par conséquent, BSM est le rayon réfracté provenant du rayon FBGa naar margenoot*, ce qu'il fallait démon- | |||||||||||||||||||||||||||||||||||||
[pagina 63]
| |||||||||||||||||||||||||||||||||||||
tum S. Producatur BL, et occurrat ei CM parallela FBD in M. Quia itaque punctum D est in diametro inter A et centrum C, erit DB major quam DA. Sed CM minor est quam AR ut constat ex propos. [VIII], quia CM parallela est radio FB cujus refractio est BM. Ergo major est ratio BD ad CM, hoc est, DL ad LC, quam DA ad AR. Sicut autem DA ad AR ita est DS ad SC. Ergo major ratio DL ad LC quam DS ad SC; et componendo, major DC ad CL quam DC ad CS. Ergo CL minor quam CS. Unde liquet punctum L ulterius quam S distare ab A.  [Fig. 27.]
Porro autem, eodem modo quo in casu praecedenti, ostenditur hîc quoque radiorum aliquorum refractiones propius concurrere. ad punctum S, qualibet data distantia. Erit igitur et hîc S punctum concursus radiorum ad D tendentium. Ultimus casus demonstrandus restat, cum punctum D extra sphaeramGa naar voetnoot1) ABH [Fig. 27] sic collocatum est, ut DC ad CH habeat rationem eandem quam CR ad RA, hoc est, rationem refractionis. Quo casu diximus omnium radiorum ad D tendentium refractiones accurate colligi in puncto S: quod nempe invenitur faciendo ut sicut DR ad DA ita sit DC ad DS. Puncto igitur D sicut dictum est posito, sit quilibet radius illuc tendens FBD et ab occursu B ducatur ad punctum S recta BS. Dico radij FB refractionem esse ipsam BS. Producatur enim BS et occurrat ei CM parallela FBD, et jungatur BC. Quia igitur DC ad CH sive CA, ut CR ad RA, erit quoque tota DR ad RC ut CR ad RA. Ut autem DR ad RC ita est DA ad AS, quia videlicet ex constr. est ut DR ad DA ita DC ad DS. ItaqueGa naar voetnoot2) et DA ad AS ut CR ad RA, hoc est ut DC ad CH. Ergo si à DA auferatur DC et ab AS auferatur CH sive CA, habebit et reliqua CA, seu CH, ad reliquam CS eandem rationem quam DC ad CH. Est autem CB aequalis CH. Ergo et BC ad CS ut DC ad CB: ideoque trianguli DCB, BCS similes, quoniam et angulum ad C communem habent qui à lateribus proportionalibus comprehenditur. Igitur et latus illius reliquum DB erit ad hujus trianguli latus reliquum BS ut DC ad CB sive CH, et angulus SBC erit aequalis angulo BDC. Hinc jam igitur in triangulis DBS, BMC, angulus MBC aequabitur angulo BDS. Est autem et angulus BMC aequalis angulo DBS, propter parallelas BD, CM. Igitur dicti trianguli DBS, BMC similes quoque erunt, ac proinde BM ad MC ut DB ad BS, hoc est, ut DC ad CH, hoc est, ut CR ad RA. Itaque BM ad MC rationem eam habet quae est refractionis; estque CM radio FB parallela. Ergo BSM est refractio radii FBGa naar margenoot*. quod erat osten- | |||||||||||||||||||||||||||||||||||||
[pagina 64]
| |||||||||||||||||||||||||||||||||||||
trer. Tous les rayons qui se dirigent vers le point D et qui rencontrent la surface convexe AB convergeront donc, après la réfraction, vers le point unique S. Il est manifeste que, si nous supposons construites autour du centre C deux surfaces sphériques avec les rayons CD et CS et que nous prenons sur elles deux points quelconques K et P situés sur le même rayon CK, tous les rayons qui se dirigent vers le point K sont réfractés par la surface ABH du corps transparent de telle manière qu'ils convergent exactement vers le point P: aucune surface autre qu'une surface sphérique ne peut présenter ce phénomène. Nous pourrons maintenant, à l'aide des résultats obtenus, attendu que nous avons appris à connaître à fond la réfraction produite par le verre et qu'une surface sphérique est facile à polir, fabriquer des lentilles qui font converger en un point donné les rayons qui se dirigent vers un autre point donné. Et de même des lentilles qui réfractent les rayons venant d'un point donné de telle manière qu'ils semblent provenir d'un autre point donné. En effet, soient donnés les points A et B [Fig. 28] et supposons qu'il faille faire converger en B les rayons qui se dirigent vers le point A. Divisons AB en deux parties par le point C de telle manière que le [Fig. 29.]
rapport AC:CB soit égal à l'indice de réfraction du verre, c'est-à-dire à 3/2. Prolongeons ensuite AB jusqu' en D, de telle manière qu'on ait CD:DB = AC:CB. Décrivons une circonférence EFG avec le centre D et le rayon DC, et une deuxième circonférence EHG avec le centre B et le rayon BH, un peu plus petit que BF. Cette circonférence coupera nécessairement la première, mettons aux points E et G: et la lunule EFGH représentera la forme de la lentille cherchée coupée par le milieuGa naar voetnoot1). En effet, les rayons qui se dirigent vers le point A en tombant sur la surface EFG se dirigeront après y avoir été réfractés vers le point B, d'après ce que nous venons de démontrerGa naar voetnoot2), et y parviendront, vu qu'ils ne seront pas réfractés de nouveau par la surface EHG, dont le centre est précisément le point B. Et la même lentille pourra nous servir pour réfracter des rayons qui proviennent du point B de telle manière qu'ils semblent provenir du point A. De la même manière, étant donnés les points A et B [Fig. 29], si, après avoir trouvé la circonférence | |||||||||||||||||||||||||||||||||||||
[pagina 65]
| |||||||||||||||||||||||||||||||||||||
dendum. Omnes igitur radij ad D tendentes atque occurrentes superficiei convexae AB, refracti concurrent ad punctum unicum S. Manifestum autem est, si circa centrum C duae sphaericae superficies intelligantur semidiametris CD, CS. atque in illis duo quaepiam puncta sumantur K, P, radio eodem CK connexa, omnes radios ad K tendentes refringi in diaphani superficie ABH, ut exactè concurrant ad punctum P: quod quidem nulla alia quam sphaerica supersicies praestare queat.  [Fig. 28.]
Poterimus porro per haec, cum et refractionem vitri penitus cognitam habeamus, sitque sphaerica superficies expolitu facilis, lentes conficere quae radios ad datum punctum tendentes ad datum aliud punctum concurrere faciant. Item quae venientes ex dato puncto ita inflectant quasi ex alio puncto dato promanent. Dentur enim puncta A, B [Fig. 28], oporteatque efficere ut radij tendentes versus A colligantur in B. Dividatur AB in C ut habeat AC ad CB rationem quae est refractionis vitri, hoc est, sesquialteram. Deinde producatur AB usque in D, ut sit CD ad DB sicut AC ad CB, et centro D radio autem DC describatur circumferentia EFG; et alia EHG, centro B, radio BH, paulo minori quam est BF. Haec autem priorem circumferentiam necessario secabit, velut in punctis E, G: et meniscus EFGH figuram quaesitae lentis per medium sectae exhibebitGa naar voetnoot1). Radij enim tendentes ad A et in superficiem EFG incidentes ibique refracti vergent ad punctum B, secundum ea quae modo ostensa fueruntGa naar voetnoot2), atque eò quidem pervenient cum nullam amplius patiantur refractionem in superficie EHG, quippe cujus centrum est ipsum B punctum. Eadem vero lens efficiet etiam, ut radij ex B venientes inflectantur quasi ex A venirent. Similiter datis punctis A B [Fig. 29], inventaque circumferentia EFG sicuti | |||||||||||||||||||||||||||||||||||||
[pagina 66]
| |||||||||||||||||||||||||||||||||||||
EFG comme nous l'avons dit, nous décrivons avec le centre B et le rayon BN, un peu plus grand que BF, une autre circonférence LNM, la figure ELNMGF représentera la section d'une seconde lentille dont on se servira pour faire converger en A les rayons qui se dirigeaient vers le point B. En effet, puisque EFG, étant une surface convexe du verre, fait converger vers B les rayons qui se dirigeaient vers A; il en résulte que cette même surface, étant, comme c'est le cas ici, une surface concave, doit faire converger vers A les rayons qui se dirigeaient vers B; c'est ce qui ressort clairement de la propos. IGa naar voetnoot1). Quant à la surface LNM elle ne change rien ici au cours des rayons qui se dirigent vers le point B, attendu que cette surface a le point B comme centre. Et la même lentille concave réfractera les rayons qui proviennent du point A de telle manière qu'ils semblent provenir du point B. | |||||||||||||||||||||||||||||||||||||
Troisième partie.La surface est convexe, et les rayons qui proviennent d'un point donné rencontrent cette surface en venant de l'intérieur. Soit AB la surface convexe du corps transparent et S le point donné, d'où proviennent des rayons tels que SB tombant sur cette surface; en sortant du corps transparent ces rayons seront réfractés, à moins que S ne coïncide avec le centre C de la surface convexe. Mais, en outre, le cas doit être divisé en deux parties. En effet, tirons la droite SC et prolongeons-la jusqu' à ce qu'elle coupe la circonférence AB au point A. Si nous choisissons alors le point Q de telle manière que le rapport AQ:QC soit égal à l'indice de réfraction, le point S sera ou bien plus près ou bien plus éloigné du point A que le point Q. Car s'il coïncide avec le point Q, il est évident d'après la propos. VIIIGa naar voetnoot2), que les rayons réfractés ne convergent pas vers un point mais sont considérés comme parallèles: en effet, Q est le point de concours des rayons parallèles tombant du dehors sur la surface AB. Supposons donc d'abord que le point S est plus éloigné du point A que le point Q [Fig. 30]. Et prenons le point D de telle manière que l'on ait SQ:SA = SC::SD. Je dis que D sera le point de concours des rayons réfractés qui atteignent la surface AB, étant partis du point S. Pour le démontrer, prenons AR = CQ, de telle manière que A tombe entre R et C. Alors le rapport CR:RA sera égal à l'indice de réfraction, de même que le rapport AQ:QC. Et il est manifeste en outre que le point R tombe entre A et D. Car, comme on a SQ:SA = SC:SD, on aura, par permutation et par partage, SQ:QC = SA:AD; partant, comme SQ << SA, QC ou AR sera aussi plus petite que AD. De plus, comme SA:AD = SQ::QC ou SQ:AR, le reste QA ou CR sera aussi au reste RD comme SA est à ADGa naar margenoot*. | |||||||||||||||||||||||||||||||||||||
[pagina 67]
| |||||||||||||||||||||||||||||||||||||
diximus, si centro B, intervallo autem BN paulo majori quam BF alia circumferentia describatur LNM: figura ELNMGF sectionem alterius lentis referet, quae efficiet ut radij tendentes ad punctum B dirigantur versus A. Si enim convexa existens vitri superficies EFG radios ad A tendentes deflectere facit ad B, necesse est ut eadem superficies cava existens ut hîc, radios ad B tendentes mittat versus A: ut facile colligere est ex propos. [I]Ga naar voetnoot1). Superficies autem LNM nulla refractione hîc radios inflexit ad B tendentes, quoniam hoc centrum habet. Eadem vero lens cava radios ex A venientes ita franget ut videantur procedere ex puncto B. | |||||||||||||||||||||||||||||||||||||
Pars 3.Cum convexa est superficies, et à puncto egredientes radij intrinsecus illi occurrunt.  [Fig. 30.]
Sit convexa diaphani superficies AB et punctum S, ex quo in illam perveniant radij ut SB, qui quidem egredientes diaphanum refringentur, nisi S sit idem cum convexi centro C. Est autem praeterea quoque duplex casus. Junctâ enim SC, eademque productâ, ac circumferentiam AB secante in A, si fecerimus ut AQ ad QC habeat rationem quae est refractionis, erit punctum S vel propius puncto A quam punctum Q, vel ulterius remotum. Nam si convenit cum puncto Q, perspicuum est ex propos. [VIII]Ga naar voetnoot2) radios post refractionem non concurrere ad punctum aliquod, sed pro parallelis haberi: est enim Q punctum concursus radiorum parallelorum extrinsecus in superficiem AB incidentium. Sit igitur primo punctum S ulterius distans ab A quam punctum Q [Fig. 30]. Et fiat ut SQ ad SA ita SC ad SD. Dico D fore punctum concursus radiorum refractorum qui à puncto S procedunt ad superficiem AB. Ponatur enim AR aequalis CQ, ita ut A inter R et C cadat. Ergo et CR ad RA proportionem refractionis habebit aeque ac AQ ad QC. Et praeterea manifestum est punctum R cadere inter A et D. Nam quia ut SQ ad SA ita SC ad SD, erit permutando et dividendo, ut SQ ad QC ita SA ad AD; unde, cum SQ sit minor SA, erit et QC, hoc est, AR minor quam AD. Porro quoniam est SA ad AD ut SQ ad QC, hoc est AR, erit et reliqua QA, hoc est, CR ad reliquam RD ut SA ad ADGa naar margenoot*. Et componendo CD ad DR ut | |||||||||||||||||||||||||||||||||||||
[pagina 68]
| |||||||||||||||||||||||||||||||||||||
Et, par composition, CD:DR = SD:DA, et, par inversion et permutation, DR::DA = DC:DS. Par conséquent, d'après la première partie de la proposition présente, les rayons qui proviennent du point D seront réfractés de telle manière à la surface AB qu'ils convergeront vers S. Réciproquement, les rayons qui proviennent du point S seront donc réfractés par la même surface de telle manière qu'ils convergeront vers D. Ainsi D sera le point de concours cherché, et cela dans le même sens que le point S dans les propositions précédentes. C'est-à-dire, les rayons ne convergeront pas exactement ici vers le point D, mais tous en-deçà de ce point; cela se démontre de la façon suivante. Un rayon quelconque provenant du point D, tel que DB, après avoir été réfracté à la surface AB, rencontre la droite DC en-deçà du point SGa naar margenoot*, par exemple en P. C'est pourquoi BD sera réciproquement le rayon réfracté provenant du rayon PB. Par conséquent, le rayon réfracté BN provenant du rayon SB rencontrera l'axe en-deçà du point D. En effet, attendu que les rayons PB et SB se dirigent vers le même point de la surface, il est nécessaire que ces rayons se coupent après la réfraction, comme cela se déduit aisément de la première propriété des réfractions. Soit maintenant S [Fig. 31], le point donné, situé de telle manière que sa distance du point A soit plus petite que QA. Il sera donc situé soit entre Q et C, soit entre C et A. Car s'il coïncide avec C, aucune réfraction n'aura lieu, comme [Fig. 31.]
nous l'avons déjà dit. Supposons d'abord que le point S soit entre Q et C; et faisons de nouveau SQ:SA = SC:SD; portons cette dernière distance du côté opposé au centre C. Je dis que D sera le point de dispersion des rayons réfractés qui proviennent du point S. En effet, prenons, comme plus haut, AR égale à CQ. Alors le rapport CR:RA, étant égal au rapport AQ:QC, sera aussi égal à l'indice de réfraction. Et comme on a SQ:SA = SC:SD, on aura aussi, par composition, QA (ou RC):AS = CD:DS. C'est pourquoi la somme de RC et CD, c'est-à-dire DR, sera aussi à la somme de AS et DS, c'est-à-dire à DA, comme DC est à DS. Par conséquent, S sera le point de concours des rayons qui se dirigent vers D et qui sont réfractés par la surface convexe ABGa naar margenoot*. Réciproquement, D sera donc le point de dispersion des rayons qui tombent du point S sur la même surface AB, mais en venant du dedans. Or, dans un seul cas D sera exactement le point de dispersion; savoir lorsque le rapport AC:CS sera égal au rapport AQ::QC, c'est-à-dire à l'indice de réfractionGa naar voetnoot1). En effet, si l'on a AQ:QC = AC:CS, et qu'on retranche AC de AQ et CS de QC, le rapport du reste CQ au reste QS sera aussi égal à AQ::QC. Comme on a en outre QA:AS = CD:DS, ainsi que cela a été démontré antérieurement, on aura aussi, par conversion de cette proportion, AQ:QS = | |||||||||||||||||||||||||||||||||||||
[pagina 69]
| |||||||||||||||||||||||||||||||||||||
SD ad DA, et invertendo et permutando DR ad DA ut DC ad DS. Quare per propos. [hujus part. 1.] radij ex puncto D fluentes in superficie AB ita
 [Fig 30].
refringentur ut tendant ad S. Ideoque et vice versa, qui veniunt ab S puncto, ad eandem superficiem ita refringentur ut tendant ad D. Igitur D erit punctum concursus quaesitum. Ea nempe ratione qua punctum S in propositionibus antecedentibus. Etenim non perfectè ad D radij hîc concurrent sed omnes citra; quod sic ostenditur. Radius quilibet ex D veniens ut DB atque a superficie AB refractus, convenit cum recta DC citra punctum SGa naar margenoot*, velut in P. Quare et vicissim radij PB refractio erit BD; Ideoque radij SB refractio puta BN, concurret citra punctum D. quia cum ad idem superficiei punctum tendant radij PB, SB, necesse est ut post refractionem fiat intersectio, ut facilè colligitur ex prima refractionum proprietate. Sit nunc punctum S datum [Fig. 31], ut minus distet ab A quam punctum Q. Erit autem vel inter Q et C vel inter C et A. nam cum in C incidit nullam fieri refractionem jam diximus. Sit primo inter Q et C punctum S; et fiat rursus ut SQ ad SA ita SC ad SD quae sumatur in partem à centro C aversam. Dico D fore punctum dispersus radiorum refractorum qui ab S puncto egrediuntur. Sumatur enim, ut ante, AR aequalis CQ. Erit ergo et CR ad RA proportio refractionis, eadem nempe quae AQ ad QC. Et quoniam SQ ad SA ut SC ad SD, erit et componendo QA, hoc est, RC ad AS ut CD ad DS. quare et utraque simul RC, CD hoc est DR ad utramque simul AS, DS, hoc est ad DA ut DC ad DS. Ergo radiorum ad D tendentium et in convexa superficie AB refractorum punctum concursus erit SGa naar margenoot*. Quare et vicissim radiorum ex puncto S in superficiem eandem AB, sed intrinsecus, incidentium, punctum dispersus erit D. Erit autem D punctum dispersus accuratè uno casu, cum nempe ratio AC ad CS erit eadem quae AQ ad QC, sive quae refractionisGa naar voetnoot1). Si enim ut AQ ad QC ita AC ad CS; auferendo AC ab AQ et CS ab QC erit et reliquae CQ ad reliquam QS eadem ratio quae AQ ad QC. Quia porro QA ad AS ut CD ad DS, uti antea ostensum est, erit et per conversionem rationis AQ ad QS ut DC ad CS. Sed CS ad CA ut CQ ad AQ; ergo erit ex aequo in proportione pertur- | |||||||||||||||||||||||||||||||||||||
[pagina 70]
| |||||||||||||||||||||||||||||||||||||
= DC:CS. Mais CS:CA = CQ:AQ. On aura donc par la règle de la proportion dérangéeGa naar voetnoot1), DC:CA (ou CH) = CQ:QS, ou AQ:QC, rapport qui est égal à l'indice de réfraction. Comme donc le rapport DC:CH lui-aussi est égal à cet indice, et que DR:DA = DC:DS, comme nous l'avons démontré ici, il est clair que tous les rayons qui se dirigent vers le point D et qui sont réfractés par la surface convexe AB, se réunissent exactement au point SGa naar voetnoot2). Réciproquement, les rayons qui proviennent du point S seront donc réfractés de telle manière par la même surface qu'ils semblent provenir du point D. Et si le rapport AC:CS est plus petit que le rapport AQ:QC, tous les rayons réfractés provenant de rayons issus du point S couperont l'axe AC, lorsqu'on les prolonge en sens inverse, au-delà du point D. Si l'on a au contraire AC:CS > AQ:QC, tous ces prolongements couperont l'axe en-deçà du point D, comme cela se déduit aisément de la deuxième partie de la proposition présente. Enfin, le cas où le point donné S se trouve entre A et C [Fig. 32], conduit à la même construction que le dernier cas considéré et la démonstration est la même également. En effet, comme on a SQ:SA = SC:SD, on aura par composition QA (ou RC):AS = CD:DS. C'est pourquoi, si nous retranchons CD de RC et DS de AS, le reste DR sera au reste DA comme DC est à DS. Nous en tirerons les mêmes conclusions que dans le cas précédent. Ainsi D sera le point de dispersion en ce sens que tous les rayons réfractés, prolongés en sens inverse, coupent l'axe en-deçà de ce point, c'est-à-dire entre D et A. | |||||||||||||||||||||||||||||||||||||
Quatrième Partie.La surface est convexe, et les rayons qui se dirigent vers un point donné rencontrent la surface en venant de l'intérieur. Soit AB la surface convexe du corps transparent et S le point donné où se dirigent des rayons tels que LB au moment où ils rencontrent la surface en venant de l'intérieur. Soit C le centre de la surface convexe. Tirons la droite SC et supposons qu'elle coupe la surface en A. Prolongeons-la jusqu'au point Q de telle manière que le rapport AQ:QC soit égal à l'indice de réfraction, et prenons un point D tel qu'on ait SQ:SA = SC:SD. Je dis que D est alors le point de concours des rayons réfractés provenant de rayons qui se dirigeaient vers le point S. En effet, soit AR = CQ. Alors le rapport CR:RA sera lui-aussi égal à l'indice de réfraction. Et comme on a SQ:SA = SC:SD, on aura, par partage, QA (ou CR):SA = CD::DS. C'est pourquoi, en retranchant CD de CR et DS de SA, nous trouverons que le reste DR est au reste DA comme DC est à DS. Par conséquent, comme les rayons qui, issus du point D, tombent sur la surface convexe AB et y sont réfractés, | |||||||||||||||||||||||||||||||||||||
[pagina 71]
| |||||||||||||||||||||||||||||||||||||
bataGa naar voetnoot1) DC ad CA sive CH ut CQ ad QS, hoc est, ut AQ ad QC, quae est proportio refractionis. Cum autem DC ad CH habet proportionem refractionis, estque DR ad DA ut DC ad DS, ut hic esse ostendimus, constat radios omnes ad punctum D tendentes, atque ad supersiciem convexam AB refractos, colligi exactè ad punctum SGa naar voetnoot2). Ergo et vicissim qui veniunt ex puncto S,
 [Fig. 32.]
ad eandem superficiem ita refringentur, ut a puncto D procedere videantur. Quod si vero minor ratio fuerit AC ad CS quam AQ ad QC, omnium radiorum ex S venientium refractiones retro productae ultra punctum D concurrent cum axe AC; si autem ratio AC ad CS major fuerit quam AQ ad QC, eaedem omnes citra punctum D concurrent, ut ex propos. [hujus parte 2] facile colligitur. Casus denique is quo punctum S inter A et C datum est [Fig. 32], eodem modo construitur quo novissime praecedens nec dissimilem demonstrationem habet. Nempe cum sit SQ ad SA ut SC ad SD, erit componendo, QA, hoc est RC ad AS ut CD ad DS. Quare auferendo CD ab RC, et DS ab AS, erit et reliqua DR ad reliquam DA ut DC ad DS. Unde reliqua eodem modo concludemus. Erit autem D punctum dispersus ejusmodi, ut refractiones omnes retro productae citra ipsum concurrant, hoc est inter D et A. | |||||||||||||||||||||||||||||||||||||
Pars 4. [Fig. 33.]
Cum superficies convexa est, et ad punctum tendentes radij intrinsecus superficiei occurrunt. Esto diaphani convexa superficies AB, et datum punctum S, quo tendant radij, ut LB intrinsecus superficiei occurrentes, centrum vero convexi sit C. Jungatur SC secetque superficiem in A, et producatur ad Q, ut AQ ad QC habeat proportionem refractionis; et ut SQ ad SA ita sit SC ad SD. Dico D esse punctum concursus radiorum refractorum qui ad S punctum pergunt. Sit enim AR aequalis CQ; ergo et CR ad RA habebit proportionem refractionis. Et quia SQ ad SA ut SC ad SD, erit dividendo, QA, hoc est, CR ad SA ut CD ad DS. Quare auferendo CD à CR, et DS ab SA, erit et reliqua DR ad reliquam DA ut DC ad DS. Ergo quum radij ex D in | |||||||||||||||||||||||||||||||||||||
[pagina 72]
| |||||||||||||||||||||||||||||||||||||
ont de point SGa naar margenoot* pour point de dispersion; réciproquement les rayons qui se dirigent vers le point S seront réfractés par la même surface de manière à se diriger vers le point D. Toutefois, ils ne se dirigeront pas rigoureusement vers ce point. Les rayons qui proviennent du point D, prolongés en sens inverse, ne se coupent pas exactement au point S, mais rencontrent tous l'axe à une plus grande distance du point A. Par conséquent, les rayons qui se dirigent vers le point S rencontreront l'axe en des points différents, non pas au point Dlui-même mais seulement à petite distance de ce point entre A et D. Ces points seront d'autant plus rapprochés du point D que le rayon incident sera plus rapproché de l'axe CA. | |||||||||||||||||||||||||||||||||||||
Cinquième Partie.La surface est concave et les rayons qui proviennent d'un point donné tombent sur cette surface du côté extérieur.  [Fig. 34.]
Soit AB [Fig. 34 et 35] la surface sphérique concave et C son centre. Supposons que des rayons issus du point D, tels que DB, tombent sur cette surface. Tirons DC et admettons que son prolongement coupe la surface en A. Choisissons le point R de telle manière que le rapport CR:RA soit égal à l'indice de réfraction. R sera donc le point de dispersion des rayons parallèles venant du côté opposé. Prenons un point S tel qu'on ait DR:DA = DC:DS. Je dis que S sera le point de dispersion des rayons issus du point D après leur réfraction par la surface AB. En effet, si nous joignons les points S et B par une droite et que nous prolongeons cette droite vers L, et DB vers N, il est clair que BS serait le rayon réfracté provenant du rayon NB, si la surface AB était convexe. Par conséquent, maintenant qu' elle est concave, c'est-à-dire qu' elle limite un corps transparent placé de l'autre côté, BL sera le rayon réfracté provenant du rayon DB, puisque NBD et SBL sont des lignes droitesGa naar margenoot*. Ainsi S sera le point de dispersion des rayons issus du point D. Or, il y a trois cas. Car le point D peut être donné de telle manière que le rapport DC:CA est ou plus grand que le rapport CR:RA, ou plus petit, ou bien égal à ce rapport. Et si le rapport DC:CA est égal au rapport CR:RA, c'est-à-dire à l'indice de réfraction, S sera le point auquel correspondront exacte- | |||||||||||||||||||||||||||||||||||||
[pagina 73]
| |||||||||||||||||||||||||||||||||||||
convexum AB incidentes refractique habeant punctum dispersus SGa naar margenoot*; vicissim qui ad S tendunt ab eadem superficie inflectentur versus punctum D. Non tamen accurate; sed quia qui ex D veniunt refracti, retroque producti, non in ipsum punctum S concurrunt, sed omnes ulterius ab A, idcirco et ij qui tendunt ad punctum S, tantum prope D inter A, D, concurrent ad puncta diversa, quae eo propiora erunt puncto D, quo radius incidens propior fuerit axi CA. | |||||||||||||||||||||||||||||||||||||
Pars 5.Cum superficies cava est, et radij a puncto venientes extrinsecus ei occurrunt.  [Fig. 35.]
Sit superficies sphaerica cava AB [Fig. 34 et 35] cujus centrum C, incidantque in eam radij a puncto dato D procedentes, ut DB. Jungatur DC, et producta secet superficiem in A, et habeat CR ad RA proportionem refractionis. Erit ergo R punctum dispersus radiorum parallelorum ab opposita parte venientium. Jam sicut DR ad DA ita sit DC ad DS. Dico S fore punctum dispersus radiorum ex D egredientium postquam in superficie AB refracti fuerint. Junctâ enim SB, productâque versus L, et DB versus N: constat radij NB refractionem fore BS, si superficies AB convexa esset. Ergo cum cava nunc sit, hoc est, diaphanum ab contraria parte positum terminet, cumque NBD, SBL sint lineae rectae, erit radij DB refractio BLGa naar margenoot*. Itaque erit S punctum dispersus radiorum ex D manantium. Sunt autem casus tres. Nam punctum D ita datum est, ut ratio DC ad CA sit major ratione CR ad RA, vel minor, vel aequalis. Et si quidem eadem est ratio DC ad CA quae CR ad RA, sive quae refractionis, erit S punctum quo exacte omnes radij refracti pertinebunt. Si vero ratio DC ad CA major, refractiones omnes retro productae citra S punctum cum axe AC convenient. Si minor, | |||||||||||||||||||||||||||||||||||||
[pagina 74]
| |||||||||||||||||||||||||||||||||||||
ment tous les rayons réfractés. Mais si le rapport DC:CA est plus grand, tous les rayons réfractés prolongés en sens inverse rencontreront l'axe AC en-deçà du point S. S'il est plus petit, au-delà de ce point. Tout ceci résulte clairement de ce qui est contenu dans la deuxième partie de cette propositionGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||
Sixième Partie.La surface est concave et les rayons qui se dirigent vers le point donné coupent cette surface en venant du dehors.Soit AB [Fig. 36 et 37] la surface sphérique, C son centre. Supposons que les rayons, tels que OB, qui se dirigent vers le point donné D, tombent sur cette surface. Menons une droite par les points D et C qui coupe la surface  [Fig. 36.]
en A. Prenons les points R et S de telle façon que le rapport CR:RA soit égal à l'indice de réfraction et que l'on ait DR:DA = DC:DS. Je dis que dans le premier cas [Fig. 36], lorsque R tombe entre A et D, le point S sera le point de dispersion des rayons qui se dirigeaient vers le point D. Et dans le second cas [Fig. 37], lorsque D tombe entre A et R, je dis qu'au contraire S sera leur point de concours. Mais si D coïncide avec le point R, les rayons qui tendent vers D, deviendront après la réfraction parallèles entre eux et à l'axe AC, comme cela a été observé dans les propos. [IX et I]Ga naar voetnoot2). Dans les cas ici considérés la démonstration est la suivante. Tirons la droite SB et prolongeons-la du côté L. Les lignes SBL et DBO sont droites et il a été démontré plus haut dans la première partie de la proposition présenteGa naar voetnoot3) que les rayons provenant du point D et réfractés par la surface convexe AB se coupent au point S de manière que, DB étant un rayon incident, BS devient le rayon réfracté correspondant. Il en résulte que dans le cas actuel le rayon réfracté provenant du rayon OB qui se dirige vers le point D et qui tombe sur la surface concave AB est BLGa naar margenoot*. Toutefois, pour parler exactement, lorsque S est le point de dispersion, le rayon réfracté provenant de OB coupera l'axe AC en-deçà du point S; et lorsque S est le point de concours, il coupera l'axe au-delà de ce point. | |||||||||||||||||||||||||||||||||||||
Septième Partie.La surface est con cave et les rayons qui proviennent d'un point donné tombent du dedans sur cette surface. | |||||||||||||||||||||||||||||||||||||
[pagina 75]
| |||||||||||||||||||||||||||||||||||||
ultra. Quae omnia ex ijs quae propositionis hujus parte secundaGa naar voetnoot1) habentur manifesta sunt. | |||||||||||||||||||||||||||||||||||||
Pars 6.Cum superficies cava est, et radij ad punctum tendentes extrinsecus illi occurrunt.Sit superficies sphaerica cava AB [Fig. 36 et 37], centro C; incidantque in eam radij ad punctum datum D tendentes, ut OB. Agatur recta per DC, secans superficiem in A, et habeat CR ad RA proportionem refractionis. Et ut DR ad DA ita sit DC ad DS. Dico priore casu [Fig. 36],  [Fig. 37.]
cum R cadit inter A, D, punctum S fore punctum dispersus radiorum qui ad D tendebant. Altero verò casu [Fig. 37], cum D cadit inter A, R, eventurum contra ut S sit punctum eorum concursus. Si autem D fuerit idem quod punctum R, radij eo tendentes, post refractionem fient inter se et axi AC paralleli, ut in propos. [IX et I]Ga naar voetnoot2) annotatum fuit. Casus autem hîc propositi demonstrabuntur ductâ SB, eâdemque versus L extensâ. Quia enim rectae sunt lineae SBL, DBO, estque superius demonstratum, propos. [hujus pars 1]Ga naar voetnoot3) radiorum ex D venientium ad superficiem AB convexam refractiones concurrere ad S punctum, ita ut si DB sit radius incidens refractio ejus fiat BS; necesse est hîc radij OB ad D tendentis atque in cavam superficiem AB incidentis refractionem esse BLGa naar margenoot*. Quamquam exacta ratione tamen radij OB refractio concurret cum AC citra punctum S, quando S est punctum dispersus. Sed ultra, quando contingit S esse punctum concursus. | |||||||||||||||||||||||||||||||||||||
Pars 7.Cum superficies cava est et radij à puncto venientes intrinsecus illi occurrunt. | |||||||||||||||||||||||||||||||||||||
[pagina 76]
| |||||||||||||||||||||||||||||||||||||
Soit AB [Fig. 38] la surface concave et C son centre; et soit S le point d'où proviennent des rayons tels que SB qui rencontrent la surface en venant de l'intérieur. Menons une droite par les points S et C qui coupe la surface en A, et supposons que le rapport AQ:QC soit égal à l'indice de réfraction. Q est alors le point auquel correspondraient des rayons parallèles venant de l'autre côté. Par conséquent, soit SQ:SA = SC:SD. Je dis que D sera le point de dispersion des rayons qui proviennent du point S: en d'autres termes que, si l'on joint les points D et B et qu'on prolonge DB du côté de L, BL sera le rayon réfracté provenant du rayon SB. En effet, si l'on prolonge également SB du côté de N, il est clair que BD est le rayon réfracté provenant du rayon NB, si la surface AB est supposée convexeGa naar margenoot*. De même ici, le corps transparent se trouvant de l'autre côté de la surface AB, BL sera le rayon réfracté provenant de SBGa naar margenoot*. Par conséquent, D sera le point de dispersion des rayons provenant du point S, et cela de telle manière que tous les rayons réfractés coupent l'axe en-deça de ce point, c'est-à-dire plus près de la surface AB. | |||||||||||||||||||||||||||||||||||||
Huitième Partie. [Fig. 39.]
La surface est concave et les rayons qui se dirigent vers un point donné tombent du dedans sur cette surface. Soit AB [Fig. 39, 40 et 41] la surface concave du corps transparent, et C son centre; et soit S le point donné où se dirigent des rayons tels que OB au moment où ils rencontrent la dite surface, en venant de l'intérieur. Menons la droite SC qui coupe la surface en A, et supposons que le rapport AQ:QC soit égal à l'indice de réfraction. Soit en outre SQ:SA = SC::SD. Je dis que dans le premier cas [Fig. 39], lorsque le point Q tombe entre A et S, D sera le point de dispersion des rayons qui se dirigent vers le point S. Mais dans les deux cas suivants [Fig. 40 et 41], où S tombe entre A et Q, je dis que D sera le point de concours de ces mêmes rayons. Joignons les points D et B et prolongeons DB du côté de L. Alors, si nous supposons que AB est une surface convexe de sorte que le corps transparent se trouve du côté de C, il est clair que le rayon réfracté provenant du rayon SB est DB dans le premier cas et le prolongement de DB, c'est-à-dire BL, dans les deux cas suivantsGa naar margenoot*. Réciproquement, le corps transparent étant actuellement placé de l'autre côté de la surface, BL sera le rayon réfracté provenant du rayon OB dans le premier cas, et BD sera le rayon réfracté dans | |||||||||||||||||||||||||||||||||||||
[pagina 77]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
Sit superficies cava AB, cujus centrum C; et punctum S, unde digressi radij ut SB intrinsecus in superficiem ferantur. Ducatur recta per SC, secans superficiem in A, et habeat AQ ad QC proportionem refractionis. Erit igitur punctum Q quo pertinerent radij paralleli à parte contraria advenientes. Quare ut SQ ad SA ita sit SC ad SD. Dico D fore punctum dispersus radiorum ab S manantium: hoc est, si jungatur DB et producatur versus L, futuram BL refractionem radij SB. Si enim et SB producatur versus N, constat radij NB refractionem esse BD, si superficies AB convexa intelligaturGa naar margenoot*. Itaque hîc, cum diaphanum ad alteram partem superficiei AB positum sit, erit et BL refractio radij SBGa naar margenoot*. Ideoque D punctum dispersus radiorum ab S venientium. Est autem ejusmodi ut refractiones omnes citra ipsum cum axe conveniant, hoc est minus proculGa naar voetnoot1) a superficie AB. | |||||||||||||||||||||||||||||||||||||
Pars 8. [Fig. 40.]
 [Fig. 41.]
Cum superficies cava est, et radij ad punctum tendentes intrinsecus illi occurrunt. Sit diaphani cava superficies AB [Fig. 39, 40 et 41]; centrum ejus C; et punctum datum sit S quo tendentes radij ut OB, intrinsecus dictae superficiei occurrant. Ducatur recta per C, secans superficiem in A, habeatque AQ ad QC proportionem refractionis. Porro ut SQ ad SA ita sit SC ad SD. Dico priore casu [Fig. 39], cum punctum Q cadit inter A et S, futurum D Punctum dispersus radiorum ad S tendentium. Posterioribus vero duobus [Fig. 40 et 41] quibus S cadit inter A, Q, dico D fore eorundem radiorum punctum concursus. Jungatur DB et versus L producatur. Itaque si superficies AB convexa ponatur, ut diaphanum sit versus C, constat radij SB refractionem esse DB priori casu, duobus verò reliquis in producta DB, hoc est BLGa naar margenoot*. Quare è diverso hîc, | |||||||||||||||||||||||||||||||||||||
[pagina 78]
| |||||||||||||||||||||||||||||||||||||
les deux autres casGa naar margenoot*. En effet, OBS et DBL sont des lignes droites. Par conséquent, D est dans le premier cas le point de dispersion des rayons qui se dirigent vers le point S, et leur point de concours dans les deux autres cas. Du reste, il peut arriver que D devienne exactement le point de concours; cela aura lieu lorsque le rapport AC:CS [Fig. 41] est précisément égal à l'indice de réfraction, donc aussi au rapport AQ:QC. Mais dans les cas où D est le point de dispersion, les rayons réfractés prolongés en sens inverse couperont toujours l'axe en-deçà du point D.
Ayant appris à connaître par ce qui a été démontré jusqu'ici la façon dont chacune des surfaces considérées réfracte les rayons, nous pourrons maintenant trouver les points de concours ou de dispersion pour des lentilles convexes ou concaves quelconques ou pour des lentilles composées de diverses façons de surfaces convexes, concaves ou planes; et cela tout aussi bien dans le cas où les rayons incidents sont parallèles que lorsqu'ils partent d'un point donné ou se dirigent vers un point donné. Et dans la construction de ces points de concours ou de dispersion nous pourrons souvent aussi faire usage de méthodes plus rapides, comme cela deviendra manifeste dans ce qui suit. | |||||||||||||||||||||||||||||||||||||
Proposition XIII.Étant donnée une sphère composée d'une substance transparente, trouver le point de concours d'un faisceau de rayons parallèles tombant sur cette sphère. Soit donné une sphère dont C est le centre. Soit BA l'axe et la circonférence BPA une section centrale. Supposons que les rayons incidents, tels que OP, soient parallèles à l'axe BA. Divisons le rayon CA en deux parties égales par le point E et prolongeons ce rayon de telle manière que le rapport CD:DE soit égal à l'indice de réfraction de la matière dont se compose la sphère. Par exemple, si la sphère considérée est de cristal ou de verre, il faut que le rapport CD:DE soit environ égal à 3/2, mais si elle est d'eau, à 4/3. Je dis que D sera le point de concours cherchèGa naar voetnoot1). En effet, prenons sur l'axe AB prolongé des deux côtés les points S et Q de telle manière que les rapports BS:SC et AQ:QC soient l'un et l'autre égal à l'indice de réfraction, c'est-à-dire au rapport CD:DE. On aura alors CS = CQ. Les rayons parallèles à l'axe BA, tels que OP, seront donc réfractés de telle manière en entrant dans la sphère qu'ils se dirigeront vers le point SGa naar margenoot*. Ensuite, comme on a CD:DE = BS:SC, on aura aussi par partage CE (ou EA):ED = BC (ou CA):CS. Donc aussi EA:AD = CA:AS. Or, EA est la moitié de CA, par | |||||||||||||||||||||||||||||||||||||
[pagina 79]
| |||||||||||||||||||||||||||||||||||||
ubi diaphanum à parte altera superficiei collocatum est, erit radij OB refractio BL in casu primo, in reliquis vero BDGa naar margenoot*. Quia videlicet OBS, DBL sunt rectae lineae. Est igitur priori casu D punctum dispersus radiorum ad S tendentium, reliquis duobus punctum concursus. Potest autem fieri ut fiat D punctum concursus accuratè; nempe si AC ad CS [Fig. 41] habeat rationem eam quae est refractionis, hoc est eandem quam AQ ad QC. Quandocunque autem D sit punctum dispersus semper radij refracti retro producti convenient cum axe citra punctum D.
Cognita singularum superficierum refractione ex his quae hactenus demonstrata sunt, poterimus jam lentium quarumlibet convexarum vel cavarum vel quae ex convexis, cavis, planisque superficiebus diversimode componuntur, puncta concursus vel dispersus invenire, aequè cum paralleli radij incidunt, atque cum ex dato vel ad datum punctum feruntur: Qua in re saepe etiam compendia quaedam sequi licebit, ut in sequentibus manifestum fiet. | |||||||||||||||||||||||||||||||||||||
Propositio [XIII].Sphaera data quae sit ex materia diaphana, invenire punctum concursus radiorum parallelorum in illam incidentium. 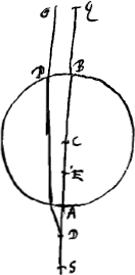 [Fig. 42.]
Esto sphaera cujus centrum C axis BA, sectio per centrum circulus BPA. Incidant autem radij paralleli axi BA, ut OP. Dividatur semidiameter CA bifariam in E, et producatur, et habeat CD ad DE proportionem refractionis, eam nempe quae convenit materiae ex qua sphaera componitur. Veluti si crystallina aut vitrea sphaera proponatur oportet rationem CD ad DE esse sesquialteram proximè, si vero ex aqua, sesquitertiam. Dico D fore punctum concursus quaesitumGa naar voetnoot1). Signentur enim in axe AB utrinque producto puncta S et Q, ut tam BS ad SC quam AQ ad QC habeat proportionem refractionis, hoc est, eandem quam CD ad DE: fientque inter se aequales CS, CQ. Radij igitur axi BA paralleli, ut OP, in ingressu ita frangentur, ut tendant ad punctum SGa naar margenoot*. Porro autem quia CD ad DE ut BS ad SC, erit et dividendo CE sive EA ad ED, ut BC sive | |||||||||||||||||||||||||||||||||||||
[pagina 80]
| |||||||||||||||||||||||||||||||||||||
conséquent AD est aussi précisément la moitié de AS. Mais SC est aussi la moitié de SQ. Donc SQ:SC = SA:SD, où il est permis d'échanger le deuxième et le troisième terme. Mais Q est le point de concours des rayons parallèles tombant de l'autre côté sur la surface A. Par conséquent D sera le point de concours des rayons qui se dirigent vers le point S et qui sont réfractés par la même surface AGa naar margenoot*. Nous avons déjà dit qu' après la première réfraction qui a lieu à la surface BP, les rayons se dirigent vers le point S. Il est donc évident qu' après avoir passé par la sphère entière les rayons ont le point D pour point de concours. Ce qu'il fallait démontrer. Il faut savoir que ceci ne doit être estimé vrai que pour les rayons situés à fort petite distance de l'axe BA, comme dans la plupart des cas traités antérieurement. Ce sont ces rayons, en effet, qui ont le pouvoir de brûler, lorsque la sphère est exposée au soleil et qui peuvent produire une image des objets à la distance AD. Cette distance sera à peu près égale au quart du diamètre pour une sphère de verre, à la moitié du diamètre pour une sphère d'eauGa naar voetnoot2). On comprendra maintenant la raison de l'artifice servant à mesurer l'indice de réfraction, que j'ai fait connaître au commencementGa naar voetnoot4). En effet, la démonstration donnée ici s'applique également à un cylindre ou à un autre vase rond quelconque coupé perpendiculairement à son axe. | |||||||||||||||||||||||||||||||||||||
Proposition XIV.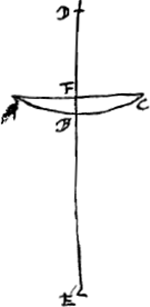 [Fig. 43.]
Etant donnée une lentille qui possède une surface plane et une surface convexe, trouver le point de concours des rayons parallèles à l'axe. Soit donnée une lentille dont ABC [Fig. 43 et 44], partie d'une sphère à centre D, soit la surface convexe, et AFC la surface plane. Et supposons d'abord [Fig. 43] que cette dernière surface soit opposée aux rayons parallèles. Tirons la droite DBE qui représente l'axe de la lentille, c'est-à-dire qui coupe le plan AFC à angles droits; prolongeons-la jusqu'en E de telle manière que le rapport DE:EB soit égal à l'indice de réfraction qui est toujours supposé connu. Il est clair que E sera alors le point de concours cherchéGa naar voetnoot5). En effet, les rayons parallèles à l'axe DF ne seront nullement réfractés en tombant à angles droits sur la surface plane AC. Ils seront donc encore parallèles en atteignant la surface ABC où ils seront réfractés de telle manière qu'ils se dirigeront vers le point E d'après la proposition IXGa naar voetnoot6). | |||||||||||||||||||||||||||||||||||||
[pagina 81]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 42.]
CA ad CS. Unde et EA ad AD ut CA ad AS. Est autem EA dimidia ipsius CA, ergo et AD dimidia erit ipsius AS. Sed et SC est dimidia ipsius SQ. Ergo ut SQ ad SC ita SA ad SD, et permutando. Est autem Q punctum concursus radiorum parallelorum à parte contraria in superficiem A incidentium. Itaque erit D punctum concursus radiorum ad S tendentium atque ad superficiem eandem A refractorumGa naar margenoot*. Diximus autem radios parallelos post primam refractionem in superficie BP tendere ad punctum S. Ergo totâ sphaerâ penetratâ liquet eos concurrere ad punctum D. quod erat demonstrandum. Sciendum autem est de radijs axi BA proximis haec intelligenda, ut superius quoque plerumque factum est. Qui quidem radij et comburendi facultatem habent, sphaerâ soli expositâ; Et rerum imagines pingendi ad distantiam AD. Haec autem erit proximè quarta pars diametri in sphaera vitrea, in sphaera aquea vero semissisGa naar voetnoot2). Unde jam artificijGa naar voetnoot3) ejus ratio manifesta est, quo proportionem refractionis initio inquirere docuiGa naar voetnoot4). Quoniam haec demonstratio ad cylindrum quoque pertinet, vel ad aliud omne vas rotundum cujus sectio ad axem recta sit. | |||||||||||||||||||||||||||||||||||||
Propositio [XIV].Data lente quae superficiem unam planam habeat, alteram convexam, invenire punctum concursus radiorum axiparallelorum. Sit data lens cujus superficies convexa ABC [Fig. 43 et 44], ex sphaera quae centrum habeat D. Plana autem superficies sit AFC. Atque haec primò [Fig. 43] radijs parallelis opposita sit. Ductâ igitur DBE recta, quae axem lentis referat, hoc est, quae superficiem AFC secet ad angulos rectos, eâque producta ad E, ita ut DE ad EB habeat proportionem refractionis, quae semper data intelligitur: manifestum est E fore punctum concursus quaesitumGa naar voetnoot5). Radij enim axi DF paralleli, cum in superficiem planam AC incidant ad rectos angulos, nullam refractionem ibi patientur, ac proinde paralleli venient ad superficiem ABC. cujus refractione ad E punctum flectentur per [prop. IX]Ga naar voetnoot6). | |||||||||||||||||||||||||||||||||||||
[pagina 82]
| |||||||||||||||||||||||||||||||||||||
Or, la distance BE sera égale au diamètre de la surface convexe ou au double de DB si la lentille est en verre, vu que le rapport DE:EB est alors égal à 3/2. Supposons en second lieu que la surface convexe ABC soit opposée aux rayons [Fig. 44]. Si nous prolongeons maintenant l'axe BD jusqu'en G de telle manière que le rapport BG:GD soit égal à l'indice de réfraction, G sera le point où se dirigent les rayons après la première réfraction qui a lieu à la surface ABCGa naar margenoot*. Divisons GF par le point H de telle manière que le rapport GF:FH soit égal lui aussi à l'indice de réfraction. Je dis que H sera le point de concours des rayons parallèles après que ceux-ci auront traversé les deux surfaces de la lentilleGa naar voetnoot2). En effet, puisque les rayons se dirigent vers le point G après la réfraction qui a lieu à la surface ABC et qu'ils tombent du dedans sur la surface plane AFC ayant cette direction, cette surface les dirigera ensuite vers le point HGa naar margenoot*, attendu que le rapport GF:FH est égal à l'indice de réfraction. Or, il est évident que la distance FH n'est inférieure que de peu à la distance BE trouvée plus haut, et qu'elle est à cette dernière comme GF est à GB. Partant, si nous négligeons l'épaisseur FB de la lentille, on aura FH = BE, en d'autres termes FH sera égale au diamètre de la sphère dont ABC est une partie, si la lentille est en verre. On verra en considérant exactement la façon dont les rayons réfractés par cette lentille se réunissent sur l'axe et en faisant un calcul là dessus, qu'ils se réunissent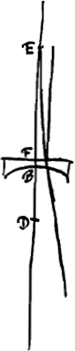 [Fig. 45.]
un peu mieux, c'est-à-dire que les points où ils coupent l'axe sont situés un peu plus près d'un point unique, dans la deuxième position de la lentille, c'est-à-dire, lorsque la surface convexe est opposée aux rayons incidents, que lorsque la surface plane leur est opposéeGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||
Proposition XV.Étant donnée une lentille qui possède une surface concave et une surface plane, trouver en avant de cette lentille le point de dispersion des rayons parallèles. Soit donnée une lentille de la forme indiquée, dont B [Fig. 45 et 46] soit la surface concave, D étant le centre de la concavité, et F la surface plane. Si donc la surface plane est opposée aux rayons incidents [Fig. 45], prolongeons DB jusqu' en E, de telle manière que le rapport DE: EB soit égal à l'indice de réfraction. E sera alors le point de | |||||||||||||||||||||||||||||||||||||
[pagina 83]
| |||||||||||||||||||||||||||||||||||||
Erit autem BE distantia diametro convexi sive duplae DB aequalis si lens vitrea fuerit quia ratio DE ad EB est sesquialtera. 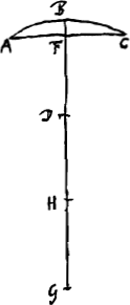 [Fig. 44.]
Sit nunc superficies convexa ABC radijs opposita [Fig. 44]. Si igitur axis BD producatur ad G, ut BG ad GD habeat proportionem refractionis, erit punctum G quo tendent radij post primam refractionem in superficie ABCGa naar margenoot*. Dividatur autem GF in H, ita ut GF ad FH habeat quoque refractionis proportionem. Dico H fore punctum concursus radiorum parallelorum postquam utramque superficiem lentis transierintGa naar voetnoot2). Quia enim post refractionem in superficie ABC tendunt ad punctum G, atque ita occurrunt intrinsecus superficiei planae AFC, haec eos diriget porro ad punctum HGa naar margenoot*, quoniam GF ad FH proportio est refractionis. Manifestum autem est distantiam FH paulo tantum minorem esse quam BE supra inventam, rationemque ad eam habere quam GF ad GB. Unde, si crassitudo lentis FB pro nulla habeatur, erit FH ipsi BE aequalis, hoc est, diametro sphaerae cujus portio est ABC si lens vitrea fuerit. Patebit autem, si concursus radiorum ab hac lente refractorum exactè expendatur atque ad calculos revocetur, accuratius aliquanto eos propiusque ad unum punctum convenire hoc posteriore lentis situ, nempe cum superficies convexa venientibus opposita est radijs, quam si plana ad illos convertaturGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||
[Propositio XV.]Data lente quae cavam et planam superficiem habeat, invenire ante ipsam punctum dispersus radiorum parallelorum. Esto lens ejusmodi cujus cava superficies sit B [Fig. 45 et 46], centrum cavitatis habens D, plana autem F. Quod si ergo superficies plana radijs advenientibus obversa est [Fig. 45], producatur tantum DB in E, ut DE ad EB sit proportio ea quae est refractionis; | |||||||||||||||||||||||||||||||||||||
[pagina 84]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 46.]
dispersion cherché, comme cela résulte de la prop. XIGa naar voetnoot1). En effet, aucune réfraction n'a lieu à la surface plane F parce que, par supposition, les rayons tombent perpendiculairement sur cette surface; ils seront donc encore parallèles en atteignant la surface B. Mais si la lentille est retournée [Fig. 46], il faut prolonger BD jusqu' en G de telle manière que le rapport BG:GD soit égal à l'indice de réfraction. Ensuite il faut diviser GF par le point E de telle manière qu' aussi le rapport GF:FE soit égal à ce même indice de réfraction. Ainsi on aura de nouveau trouvé le point de dispersion EGa naar voetnoot2). En esset, les rayons parallèles, après avoir été réfractés à la surface concave B, auront ensuite le point G pour point de dispersion, suivant la prop. XGa naar voetnoot3). Mais les rayons qui, venant du point G, atteignent la surface plane, y sont réfractés une seconde fois, et continuent leur route comme s'ils étaient issus du point E, suivant la prop. VIGa naar voetnoot4). Par conséquent, E est le point de dispersion cherché. Mais comme on a GF:FE = BG:GD, et que GF > BG, on aura aussi FE > GD, trandis que la ligne BE du premier cas est égale à cette même GD. En retranchant des deux côtés l'épaisseur BF de la lentille, on verra aussi que la distance BE est plus grande dans le second cas que FE dans le premier cas. | |||||||||||||||||||||||||||||||||||||
Proposition XVI.Étant donnée une lentille convexe à surfaces égales ou inégales, les deux pouvant être convexes ou l'une convexe et l'autre concave, la concavité étant dans ce dernier cas moindre que la convexité, trouver le point de concours d'un faisceau de rayons parallèles. | |||||||||||||||||||||||||||||||||||||
[pagina 85]
| |||||||||||||||||||||||||||||||||||||
eritque E punctum dispersus quaesitum, uti manifestum est ex prop. [XI]Ga naar voetnoot1). Nulla siquidem contingit refractio in superficie plana F quum radij ad angulos rectos in hanc incidere ponantur, ideoque paralleli perveniant in superficiem B. Si vero aliter conversa fuerit lens [Fig. 46], producenda est BD ad G, ita ut BG ad GD sit proportio refractionis; deinde dividenda GF in E ut et GF ad FE proportionem refractionis habeat eandem; atque ita rursus inventum erit dispersus punctum EGa naar voetnoot2). Radij enim paralleli refracti in superficie cava B, habebunt inde punctum dispersus G, per [Prop. X]Ga naar voetnoot3). qui vero ex G venientes incidunt in superficiem planam, secundò ibi refractionem subeunt, perguntque deinceps quasi ex puncto E procederent, per [Prop. VI]Ga naar voetnoot4). Itaque E est punctum dispersus quaesitum. Quia vero GF ad FE ut BG ad GD, estque GF major quam BG, erit et FE major quam GD, cui aequalem esse constat BE in casu priori. Unde ablata utrinque BF crassitudine lentis, etiam distantia BE in posteriori casu major erit quam FE in priori. | |||||||||||||||||||||||||||||||||||||
[Propositio XVI.]Data lente convexa parium vel disparium superficierum, sive utraque convexa sit, sive altera cava; sed cavitas sit convexitate minor; invenire punctum concursus parallelorum. | |||||||||||||||||||||||||||||||||||||
[pagina 86]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 48.]
Soit CD [Fig. 47 et 48] l'une quelconque des lentilles décrites, et soit A le centre de la surface C, B celui de la surface D. Joignons A et B et prolongeons AB des deux côtés. Faisons en sorte que les rapports CE:EA et DL:LB soient l'un et l'autre égal à l'indice de réfraction. Prenons ensuite un point N tel qu'on ait EL:ED = EB:EN, la longueur EN étant portée dans le sens indiqué dans la prop. XIIGa naar voetnoot1). N sera alors le point de concours de rayons parallèles à l'axe qui viennent du côté de CGa naar voetnoot2). En effet, de tels rayons, réfractés premièremetn par la surface C, se dirigent après cette réfraction vers le point E, comme cela a été démontré à la prop. VIIIGa naar voetnoot3). Mais les rayons qui se dirigent vers le point E sont réunis au point N après avoir été réfractés à la surface D. Cela résulte de la quatrième partie de la prop. XIIGa naar voetnoot4), et, si la section de la lentille a la forme d'une lunule [Fig. 48], de la huitième partie de la prop. XIIGa naar voetnoot5). De la même manière, si nous faisons LE:LC = LA:LO, O sera le point de concours des rayons parallèles qui viennent du côté de DGa naar voetnoot6). Et il faut observer que les distances DN et CO sont à peu près égales entre elles et que l'unique cause de leur inégalité consiste dans le fait que la lentille a une certaine épaisseur. Et si la surface D fait partie d'une plus grande sphère que la surface C, c'est-à-dire si BD est plus grande que AC, la distance CO sera plus grande que DNGa naar voetnoot7), ce qui se démontre comme suit. Attendu qu'on a DL:LB = CE:EA, on aura aussi par conversion de cette proportion et par inversion DB:DL = CA:CE. Or, DB > CA, donc aussi DL > CE. Si l'on retranche DC de chacune de ces lignes dans le cas de la lentille biconvexe, tandis que dans le cas de la lunule on ajoute la même longueur DC à DL et qu'on la retranche de CE; il sera évident que dans les deux cas le rapport LC:DE devient plus grand que le rapport LD:CE ou LB:AE. C'est pourquoi le rectangle LC.AE sera plus | |||||||||||||||||||||||||||||||||||||
[pagina 87]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 47.]
Sit lens utravis harum CD [Fig. 47 et 48], et superficiei C centrum A, B vero superficiei D. Jungatur AB et producatur utrimque et fiat ut tam CE ad EA, quam DL ad LB rationem habeant quae est refractionis. Deinde sicut EL ad ED ita sit EB ad EN, haec autem EN in partem eam sumenda est, quam praecipit prop. [XII]Ga naar voetnoot1). Eritque N centrum concursus radiorum axi parallelorum qui veniunt a parte CGa naar voetnoot2). Refracti enim primò in superficie C pertinent inde ad punctum E, ut ostensum est Prop. [VIII]Ga naar voetnoot3). qui autem ad E pertinent refracti in superficie D colliguntur in puncto N, [per part. 4. Prop. XII]Ga naar voetnoot4) et in menisco [Fig. 48] per [part. 8. Prop. XII]Ga naar voetnoot5). Eadem ratione si fiat ut LE ad LC ita LA ad LO, erit O punctum concursus parallelorum qui adveniunt a parte DGa naar voetnoot6). Et notandum quod distantiae DN et CO proximè inter se sunt aequales, causamque inaequalitatis oriri tantum a crassitudine lentis. Et si quidem superficies D sit ex majori sphaera quam superficies C, hoc est, si BD sit major quam AC, erit CO distantia major quam DNGa naar voetnoot7); quod sic ostenditur. Quia ut DL ad LB ita CE ad EA, erit et per conversionem rationis et invertendo ut DB ad DL ita CA ad CE. Estque DB major quam CA, ergo et DL major quam CE. In casu igitur lentis utrinque convexae, si ab utraque harum auferatur DC; in menisco autem si eadem DC addatur ad DL, auferatur vero à CE; patet utrobique majorem fieri rationem LC ad DE, quam sit LD ad CE, hoc est, quam LB ad AE. quamobrem rectan- | |||||||||||||||||||||||||||||||||||||
[pagina 88]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 50.]
grand que le rectangle DE.LB. Or, le rect. LC. AE est égal au rect. LE.CO, vu qu'on a LE:EA = LC:CO. Et le rect. DE.LB est égal au rect. EL.DN, attendu qu'on a EL:LB = ED:DN. Le rect. LE.CO est donc plus grand que le rect. LE.DN, et par conséquent CO > DN. Mais si nous négligeons l'épaisseur CD de la lentille, comme nous le ferons presque toujours dans ce qui suit, je dis que O et N, les points de concours des rayons parallèles, sont situés à égale distance de la lentille. Remplaçons les points D et C par le point unique D [Fig. 49 et 50], situé au milieu de la lentille. Vu qu'alors LE:LA = LD:LO, on aura aussi LE:EA = LD:DO, donc LE.DO = EA.LD. Or, le rectangle DE.LB est égal à ce dernier rectangle, attendu qu'on a DE:EA = DL:LB, et d'autre part DE.LB = EL.DN, parce que EL:LB = ED:DN. Par conséquent, les rectangles LE.DO et EL.DN sont égaux, partant DO = DN. Ce qu'il fallait démontrer. Et nous pourrons maintenant trouver plus aisément les points O et N. En effet, il suffit de trouver le seul point L, ce qui se fait de la même manière qu' auparavant, c'est-à-dire en rendant le quotient DL:LB égal à l'indice de réfraction, et de faire ensuite BA:AD = LB:DN (ou DO)Ga naar voetnoot1). En effet, comme DL:LB = DE:EA, on aura par conversion LD:DB = ED:DA et, par permutation, LD:DE = BD::DA. Donc aussi LE:ED = BA:AD. Mais nous avons pris le point N de telle manière que BA:AD = LB:DN. Par conséquent, LE::ED = LB:DN. Et, par permutation, EL:LB = ED:DN. Donc aussi EL:EB = ED:EN, et N est par conséquent le point de concours cherché; car cela a été démontré antérieurement. Pour une lentille en verre on aura donc le théorème suivant. La somme des rayons de courbure des deux surfaces convexes, ou bien pour la lunule la différence des deux rayons de courbure, est à l'un des deux rayons comme le double de l'autre est à la distance du foyer. En effet, LB devient alors le double du rayon BD, parce que DL:LB = 3:2, ce qui est l'indice de réfraction pour le verre. Dans le cas où les deux surfaces convexes ont le même rayon on trouve que la distance focale sera égale à ce rayon. | |||||||||||||||||||||||||||||||||||||
Proposition XVII.Étant donnée une lentille concave à deux surfaces sphériques trouver le point de dispersion des rayons parallèles. | |||||||||||||||||||||||||||||||||||||
[pagina 89]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 49.]
gulum LC, AE majus erit rectangulo DE, LB. Rectangulum autem LC, AE aequale est rectangulo LE, CO, quia ut LE ad EA ita LC ad CO; et rectangulum DE, LB aequale est rectangulo EL, DN, quia ut EL ad LB ita ED ad DN. Ergo majus est rectang. LE, CO rectangulo LE, DN, ideoque CO major quam DN. At si crassitudinem lentis CD pro nulla habeamus, uti fere semper in sequentibus fiet, dico puncta concursus parallelorum O et N aequaliter a lente remota esse. Sit enim nunc punctum medium lentis D pro utrisque D et C [Fig. 49 et 50]. Quia ergo LE ad LA ut LD ad LO, erit et LE ad EA ut LD ad DO, unde rectang. LE, DO aequale rectangulo EA, LD. huic autem aequale est rectang. DE, LB, quia DE ad EA ut DL ad LB, et rursus rectangulo DE, LB aequale rectang. EL, DN, quia ut EL ad LB ita ED ad DN. Ergo rectang. LE, DO aequabitur rectangulo EL, DN; ac proinde DO ipsi DN; quod erat probandum. Puncta autem O vel N faciliori ratione nunc invenire licebit. Etenim solum inveniendum est punctum L sicut antea, faciendo nimirum ut DL ad LB sit proportio ea quae est refractionis; ac deinde ut BA ad AD ita LB ad DN vel DOGa naar voetnoot1). Quia enim DL ad LB ut DE ad EA, erit per conversionem rationis LD ad DB ut ED ad DA, et permutando LD ad DE ut BD ad DA. Unde et LE ad ED ut BA ad AD. Ut autem BA ad AD ita fecimus LB ad DN. Igitur LE ad ED ut LB ad DN. et permutando, EL ad LB ut ED ad DN. Unde et EL ad EB ut ED ad EN, ideoque N punctum concursus quaesitum; nam hoc antea fuit ostensum. Itaque, in lente vitrea, sicut duae simul convexitatum semidiametri; in menisco autem ut earum differentia, ad alterutram ipsarum, ita reliqua bis erit ad foci distantiam. fit enim tunc LB dupla radij BD, quia DL ad LB ut 3 ad 2 quae in vitro est proportio refractionis. Quod si autem superficies utraque fuerit aequaliter convexa, apparet jam foci distantiam semidiametro convexitatis aequalem fore. | |||||||||||||||||||||||||||||||||||||
[Propositio XVII.]Data lente cava duarum superficierum sphaericarum, punctum dispersus radiorum parallelorum invenire. | |||||||||||||||||||||||||||||||||||||
[pagina 90]
| |||||||||||||||||||||||||||||||||||||
Soit donnée la lentille CD possédant deux surfaces concaves [Fig. 51] ou bien une surface convexe et l'autre concave [Fig. 52], la première étant celle qui fait partie de la surface sphérique la plus grande. Soient AC et
 [Fig. 52.]
BD les rayons de courbure des deux surfaces; prolongeons-les jusqu' aux points L et E de telle manière que les rapports CE:EA et DL::LB soient l'un et l'autre égal à l'indice de réfraction. Et prenons un point N tel qu'on ait EL:ED = EB:EN. Je dis que N sera le point de dispersion des rayons parallèles qui arrivent du côté CGa naar voetnoot1). En effet, les rayons qui tombent parallèlement sur la surface C et y sont réfractés, correspondent ensuite au point E, suivant la prop. XGa naar voetnoot2), vu que le rapport CE:EA est égal à l'indice de réfraction. Mais comme on a EL:ED = EB:EN, les rayons qui proviennent du point E auront après avoir été réfractés par la surface D, le point N pour point de dispersion, d'après la prop. XII, part. 7 et part. 3Ga naar voetnoot4). Le point N est donc le point de dispersion des rayons parallèles après la double réfraction produite par la lentille CD. Cependant, dans le cas de la lentille cavoconvexe, il est nécessaire que le rayon BD surpasse le rayon AC suffisamment pour que l'on trouve le point L plus éloigné de la lentille que le point E. Car, s'il en est autrement, les rayons qui viennent du point E, ne pourront pas diverger après la réfraction due à la surface D, comme cela est manifeste par la prop. XII part. 3. Ensuite, si l'on choisit un point O tel que LE:LC = LA::LO, ce point sera le point de dispersion des rayons parallèles qui viennent du côté DGa naar voetnoot7). En effet, après la première réfraction, celle due à la surface D, ces rayons correspondront au point L, d'après les prop. X et VIIIGa naar voetnoot8). Et, comme on a LE:LC == LA:LO, après la deuxième réfraction qui est due à la surface C, les rayons seront dispersés comme s'ils provenaient du point O, d'après la prop. XII part. 7 et part. 8Ga naar voetnoot9). Or, DO sera plus petite que CN si AC | |||||||||||||||||||||||||||||||||||||
[pagina 91]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 51.]
Sit data lens CD quae superficiem utramque cavam habeat [Fig. 51], vel alteram earum convexam [Fig. 52], sed quae majoris sit sphaerae quam cava. Sint autem semidiametri superficierum AC, BD, quae producantur ad L et E; ut tam CE ad EA quam DL ad LB habeat proportionem quae refractionem metitur. Et ut EL ad ED ita sit EB ad EN. Dico N fore punctum dispersus radiorum qui paralleli incident a parte CGa naar voetnoot1). Qui enim paralleli advenientes refringuntur in superficie C, exinde pertinent ad punctum E, per [prop. X]Ga naar voetnoot2); quia CE ad EA est proportio refractionis. Sed quia ut EL ad ED ita EB ad EN, ideo qui ad E, vel qui ex E veniuntGa naar voetnoot3), refracti à superficie D, habebunt punctum dispersus N, ut constat ex prop. [XII. part. 7. et p. 3]Ga naar voetnoot4). Igitur punctum N est punctum dispersus radiorum parallelorum post geminam in lente CD refractionem. Oportet autem in lente cavoconvexa, ut semidiameter ACGa naar voetnoot5) tanto saltem major sit semidiametro BD, ut punctum E ulterius quam L a lente remotum inveniatur. Nam alioqui radij qui ad E tenduntGa naar voetnoot6), refracti in superficie D non poterunt dispergi, ut constat ex prop. [XII. part. 3]. Porro si siat ut LE ad LC ita LA ad LO, erit O punctum dispersus parallelorum qui adveniunt a parte DGa naar voetnoot7). Primum siquidem per refractionem supersiciei D, pertinebunt radij ad punctum L, per [prop. X. et VIII]Ga naar voetnoot8). Et quia LE ad LC ut LA ad LO, ideo post alteram refractionem in superficie C, dispergentur quasi procederent è puncto O, per [prop. XII. p. 7. et 8]Ga naar voetnoot9). Erit autem jam DO | |||||||||||||||||||||||||||||||||||||
[pagina 92]
| |||||||||||||||||||||||||||||||||||||
est plus petite que BDGa naar voetnoot1), et réciproquementGa naar voetnoot2). Car, puisqu'on a BD:AC == DL:CE et que BD a été supposée plus grande que AC, on aura
 [Fig. 52.]
aussi DL > CE. Par conséquent si, dans le cas de la lentille biconcave, on ajoute à chacune des deux dernières lignes l'épaisseur DC de la lentille, et que, dans le cas de la lentille cavoconvexe, on retranche DC de DL et qu'on l'ajoute à CE, dans l'un et l'autre cas on aura LC:DE < LD:CE ou LB:AE. Par une argumentation semblable à celle dont nous nous sommes servis plus haut dans le cas de la lentille convexe, on prouvera que le rectangle LE.CO est plus petit que le rectangle LE.DN, et par conséquent CO < DN; la différence est toutefois petite: elle provient de l'épaisseur de la lentille. Car si nous négligeons cette épaisseur, de sorte que les deux points D et C coïncident au point D, les distances DN et DO deviendront égales entre elles, ce qui se démontre de la même manière que dans le cas de la proposition précédente se rapportant à la lentille convexe. Or, ici aussi les points de dispersion O et N pourront maintenant être trouvés plus rapidement; il suffit de faire en sorte que le rapport DL:LB soit égal à l'indice de réfraction, comme auparavant, et qu'on ait ensuite BA:AD = BL:DN ou DOGa naar voetnoot3). La démonstration est également la même que pour la lentille convexe. Il est évident que si les deux surfaces concaves [Fig. 51] ont la même courbure, donc si AD = DB, DN ou DO sera égale à la moitié de LB et par conséquent, si la lentille est en verre, précisément égale au rayon AD ou BD. Et cela pour la même raison que celle qui a servi pour le point de concours de la lentille convexe. | |||||||||||||||||||||||||||||||||||||
[pagina 93]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 51.]
minor quam CN, si AC fuerit minor quam BDGa naar voetnoot1), et contraGa naar voetnoot2). Quia enim BD ad AC ut DL ad CE, poniturque BD major quam AC, erit et DL major quam CE. Itaque in casu lentis utrimque cavae si addatur utrisque DC lentis crassitudo, in casu vero cavoconvexae, si auferatur DC à DL, eadem vero addatur ad CE, fiet utrobique minor ratio LC ad DE quam LD ad CE, hoc est, quam LB ad AE. Unde simili argumentatione ac supra in lente convexa efficietur recttangulum LE, CO minus esse rectangulo LE, DN, ideoque CO minorem quam DN; differentia vero est exigua, quae oritur ex crassitudine lentis. Namque si pro nulla habeatur lentis crassitudo, ita ut pro punctis D et C sit unum D, jam distantiae DN, DO inter se aequales fient, quod eodem modo demonstratur atque superiori propositione in lente convexa. Poterunt autem hic rursus puncta dispersus O vel N brevius nunc inveniri, faciendo tantum ut DL ad LB habeat refractionis proportionem, sicut prius; ac deinde sicut BA ad AD ita BL ad DN vel DOGa naar voetnoot3); cujus eadem quoque est demonstratio quae fuit in lente convexa. Liquet autem, si utraque superficies fuerit aequaliter concava [Fig. 51], hoc est, si AD aequalis DB, quod DN vel DO erit aequalis dimidiae LB: ac proinde, si lens vitrea fueritGa naar voetnoot4), aequalis ipsi AD vel BD semidiametro. Eadem scilicet ratione qua id in lente convexa de concursus puncto ostensum fuit. | |||||||||||||||||||||||||||||||||||||
[pagina 94]
| |||||||||||||||||||||||||||||||||||||
Proposition XVIII.Trouver une lentille possédant une surface convexe égale à une surface donnée, et ayant son point de concours des rayons parallèles à une distance donnée.  [Fig. 53.]
 [Fig. 54.]
Soit donnée l'une des surfaces de la lentille C, c'est-à-dire son rayon de courbure AC. Soit CO la distance donnée. On demande de trouver une seconde surface qui, jointe à la première, puisse constituer une lentille capable de réunir les rayons incidents parallèles au point O. Prolongeons AC jusqu'en P de telle manière que le rapport AP:PC soit égal à l'indice de réfraction. Alors si la distance OC est trouvée être précisément égale à la distance CP, la deuxième surface de la lentille devra être plane, ainsi que cela est manifeste par la prop. XIVGa naar voetnoot1). Mais si OC et CP sont inégales, on prendra un point B tel que leur différence PO sera à OC comme AC est à CBGa naar voetnoot2). Cette dernière longueur sera portée du côté P, si PC > CO, et de l'autre côté si PC < CO. Et dans le premier cas [Fig. 53] la deuxième surface de la lentille sera convexe et aura BC pour rayon; dans le deuxième cas [Fig. 54] cette surface sera concave, de sorte que la section de la lentille aura alors la sorme d'une lunule. La preuve de ce que nous venons de dire est la suivante. Comme on a AC:CB = PO::OC, on aura par composition, dans le premier cas, AB:BC == PC:CO, et le même résultat sera obtenu dans le second cas en prenant la différence des termes dont nous prîmes tantôt la somme. Or, le rapport AP:PC est égal à l'indice de réfraction. Par conséquent, O est le point de concours des rayons qui tombent parallèlement sur la lentille C, d'après la prop. XVIGa naar voetnoot3). On voit donc que la lentille qui satisfait au problème a été trouvée. | |||||||||||||||||||||||||||||||||||||
[pagina 95]
| |||||||||||||||||||||||||||||||||||||
[Propositio XVIII.]Lentem invenire cujus superficies altera convexa sit eadem datae, quaeque punctum concursus parallelorum habeat ad datam distantiam. Sit lentis C superficies altera data, hoc est semidiameter ejus convexitatis AC. deturque distantia CO, oporteatque invenire superficiem alteram quae juncta priori, lentem efficiat quae radios parallelos cogat ad punctum O. Producatur AC usque in P, ut sit AP ad PC proportio refractionis. Tum si quidem distantia OC ipsi CP aequalis inveniatur, debebit altera lentis superficies plana esse, ut ex [prop. XIV]Ga naar voetnoot1) manifestum est. Si vero OC, CP inaequales fuerint, fiat sicut differentia earum PO ad OC, ita AC ad CBGa naar voetnoot2); quae accipiatur versus P, si PC major fuerit quam CO; at versus partem alteram si minor PC quam CO. Eritque priore casu [Fig. 53] superficies lentis altera convexa à semidiametro BC; posteriore [Fig. 54] autem cava, adeo ut tunc meniscus habeatur. Demonstratio autem est hujusmodi. Quoniam est AC ad CB ut PO ad OC, erit componendo in priorè casu, in altero vero per conversionem rationis contrariam ut AB ad BC ita PC ad CO. Est autem AP ad PC proportio refractionis. Igitur erit O punctum concursus radiorum qui paralleli incidunt in lentem C, ut constat ex prop. [XVI]Ga naar voetnoot3). Patetque lentem, qualis requirebatur, esse inventam. | |||||||||||||||||||||||||||||||||||||
[pagina 96]
| |||||||||||||||||||||||||||||||||||||
Proposition XIX. [Fig. 56.]
Étant donnée une lentille possédant deux surfaces convexes inégales ou à section en forme de lunule, trouver une autre lentille équivalente ayant une surface convexe et une surface plane ou bien deux surfaces convexes de même courbureGa naar voetnoot1). Soit donnée une lentille D biconvexe [Fig. 55] ou à section en forme de lunule [Fig. 56]. Et soient A et B les centres des surfaces. Prenons un point K tel qu'on ait BA:AD = BD:DK. Je dis que DK est le rayon de courbure de la surface convexe d'une lentille dont la seconde surface est plane et qui est équivalente à la lentille DGa naar voetnoot1). En effet, prenons les points L et N de telle manière que le rapport DL:LB soit égal à l'indice de réfraction, et qu'on ait BA:AD = LB:DN. N sera donc le foyer de la lentille D, d'après ce qui a été démontré à la prop. XVIGa naar voetnoot2). Mais on a aussi BA:AD = BD::DK; par conséquent, BD:DK = LB:DN. Et, par permutation, BD:BL = DK:DN. Donc on aura, par composition, DL:LB = KN::ND. C'est pourquoi aussi le rapport KN:ND sera égal à l'indice de réfraction. Par conséquent, si une lentille est placée en D possédant une surface convexe à rayon de courbure KD, et une deuxième surface plane du côté K, son foyer sera le point N, comme cela est manifeste d'après la prop. XIVGa naar voetnoot3). Mais si KD est doublée, on aura par là le rayon de courbure de la lentille biconvexe symétrique, d'après la prop. XVI. | |||||||||||||||||||||||||||||||||||||
[pagina 97]
| |||||||||||||||||||||||||||||||||||||
[Propositio XIX.] [Fig. 55.]
Datae lenti inaequaliter convexae vel menisco, lentem aliam aequivalentem invenire, quae convexam et planam superficiem habeat vel utramque convexam aequaliter. Sit data lens D qualem diximus [Fig. 55] vel meniscus [Fig. 56]. Et centra superficierum sint A et B. Fiat ut BA ad AD ita BD ad DKGa naar voetnoot1). Dico DK esse semidiametrum convexi, lentis quae alteram superficiem planam habeat, quaeque paria faciat cum lente D. Habeat enim DL ad LB proportionem quae est refractionis, et ut BA ad AD ita sit LB ad DN. Erit ergo N focus lentis D, per ea quae in prop. [XVI]Ga naar voetnoot2) demonstrata sunt. Verum ut BA ad AD ita quoque est BD ad DK; ergo BD ad DK ut LB ad DN. Et permutando BD ad BL ut DK ad DN. Et componendo igitur erit ut DL ad LB ita KN ad ND. quare et KN ad ND erit refractionis proportio. Itaque si in D lens constituatur quae superficiem alteram convexam habeat semidiametro KD, alteram vero versus K planam, ejus erit focus punctum N, ut ex prop. XIV]Ga naar voetnoot3) manifestum est. Si vero KD duplicetur, habebitur semidiameter convexitatis ad lentem duarum aequalium supersicierum, ut patet ex prop. [XVI]. | |||||||||||||||||||||||||||||||||||||
[pagina 98]
| |||||||||||||||||||||||||||||||||||||
Proposition XX. [Fig. 57.]
 [Fig. 58.]
 [Fig. 59.]
Étant donnée une lentille quelconque convexe ou concave, possédant soit deux surfaces sphériques soit une surface sphérique et une surface plane; étant donné de plus sur l'axe de cette lentille un point où se dirigent ou d'où proviennent des rayons lumineux qui tombent sur la lentille: si l'on construit une troisième proportionnelle à deux longueurs, dont la première est la distance du point donné au point auquel correspondent les rayons réfractés provenant de rayons incidents parallèles venant de l'autre côté, et la seconde la distance du point donné à la lentille elle-même, alors l'extrémité de la troisième, portée sur l'axe à partir du point donné dans le même sens que la première longueur, sera le point de concours ou de dispersion des rayons qui proviennent du point donné ou qui se dirigent vers luiGa naar voetnoot1). Soit CGa naar voetnoot2) la lentille, dont nous négligerons ici l'épaisseur, et soit D le point donné sur l'axe AC de la lentille d'où proviennent ou vers lequel se dirigent les rayons qui tombent sur la lentille C. Et soit O le point auquel correspondent les rayons réfractés provenant de rayons incidents parallèles venant de | |||||||||||||||||||||||||||||||||||||
[pagina 99]
| |||||||||||||||||||||||||||||||||||||
[Propositio XX.] [Fig. 60.]
 [Fig. 61.]
 [Fig. 62.]
Posita quavis lente convexa vel cava, sive utraque superficie sphaerica constet, sive altera plana; datoque in axe ejus puncto, à quo vel ad quod radij tendentes lenti occurrant: Si duabus ab eo puncto distantijs tertia proportionalis statuatur, quarum distantiarum prima sit ad punctum quo pertinent refractiones parallelorum a contraria parte incidentium, secunda ad lentem ipsam; erit terminus tertiae distantiae, sumendae à puncto dato in partem eandem cum prima, punctum concursus vel dispersus radiorum à dato puncto vel ad datum tendentiumGa naar voetnoot1). Sit lens CGa naar voetnoot2), cujus quidem crassitudinem tanquam si nulla esset hic considerabimus, in axe autem lentis AC datum sit punctum D, a quo vel ad quod tendentes radij lenti C occurrant. Sitque O punctum quo pertinent refractiones radiorum parallelo- | |||||||||||||||||||||||||||||||||||||
[pagina 100]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 66.]
 [Fig. 67.]
 [Fig. 68.]
l'autre côté. Prenons DP égale à la troisième proportionnelle à DO et DC; cette distance DP étant toujours prise dans le même sens que DO. Je dis que P sera le point de çoncours ou de dispersion des rayons qui proviennent du point D ou qui se dirigent vers lui. Le cas où D coïnciderait avec O est exclu, vu que dans ce cas les rayons qui proviennent du point D ne seront pas réunis en un point par la réfraction due à la lentille, mais qu'ils deviendront parallèles, d'après la prop...Ga naar voetnoot1). La preuve du théorème, lorsque les deux surfaces de la lentille sont sphériques, sera la suivante. Soit A le centre de courbure de la surface sphérique que les rayons incidents rencontrent la première, et B celui de la deuxième surface. Construisons les points E et L de telle manière que les rapports CE:EA et CL:LB soient l'un et l'autre égal à l'indice de réfraction. Prenons CR égale à AE, et portons-la sur l'axe de l'autre côté de la lentille. Il en résultera que AR::RC = CE:EA. Cherchons ensuite une quatrième proportionnelle DN à ces trois grandeurs DR, DC et DA et portons-la dans un sens tel que les quatre longueurs aient ou bien toutes le même sens à partir du point D ou bien deux d'entre elles un sens et deux l'autreGa naar voetnoot2). Et dans le cas où D coïncide avec le point A, il faudra se représenter N comme coïncidant également avec les deux points nommés. Mais si R coïncide avec D, nous aurons un cas qui sera traité à-partGa naar voetnoot3). Jamais d'ailleurs N ne coïncidera avec L, si D diffère de OGa naar voetnoot4), comme nous avons dit que cela doit être. Comme donc les rapports CE:EA et CL:LB sont égaux l'un et l'autre à l'indice de réfraction, et que le point O est celui qui correspond aux rayons réfractés provenant de rayons parallèles, ces quatre longueurs LE, LA, LC et LO formeront une proportion géométriqueGa naar margenoot*. Il en résulte qu'on aura LE:EA == LC:CO et, par permutation, LE:LC = EA (ou CR):CO. Donc aussi LE:EC = CR:RO. Vu que de plus, par construction, DR:DA = DC::DN, on aura aussi DR:RA (ou EC) = DC:CN et, par inversion, NC:CD == EC:DR. Par conséquent, NE:RC = EC:DR. Mais nous avons dit que RC:RO = LE:EC. On aura donc, par la règle de la proportion déran- | |||||||||||||||||||||||||||||||||||||
[pagina 101]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 63.]
 [Fig, 64.]
 [Fig. 65.]
rum a contraria parte incidentium. Et ponatur duabus DO, DC tertia proportionalis DP, ita ut DO, DP semper sint versus partem eandem. Dico P fore punctum concursus vel dispersus radiorum ex D vel ad D procedentium. Debet autem D non incidere in O, quia tunc radij ex D venientes refractione lentis non cogentur ad punctum, sed paralleli evadent, ut constat ex prop....Ga naar voetnoot1). Demonstratio autem, quando utraque lentis superficies sphaerica est, erit hujusmodi. Sit A centrum sphaericae superficiei cui primum incidentes radij occurrunt; B vero centrum reliquae. Et inveniantur puncta E et L, ut tam CE ad EA quam CL ad LB habeat proportionem refractionis. Et ponatur ipsi AE aequalis CR ad partem lentis alteram; unde AR erit ad RC sicut CE ad EA. fiat quoque tribus hisce DR, DC, DA quarta proportionalis DN, sumenda in eam partem ut vel quatuor omnes à puncto D eodem versus habeantur vel binae utrimqueGa naar voetnoot2). Quod si D sit idem quod A punctum, etiam N cum hisce coincidere cogitandum est. Si vero R cadat in D, is casus seorsim demonstrabiturGa naar voetnoot3). Nunquam vero N cadet in L, cum D diversum sit ab OGa naar voetnoot4), uti diximus esse debere. Quia igitur CE ad EA, item CL ad LB est proportio refractionis, punctumque O quo pertinent refractiones parallelorum; erunt proportionales hae quatuor LE, LA; LC, LOGa naar margenoot*. quare et LE ad EA ut LC ad CO, et permutando LE ad LC ut EA sive CR ad CO. Unde et LE erit ad EC ut CR ad RO. Quia porro ex constructione proportionales sunt DR, DA; DC, DN, erit et DR ad RA seu EC ut DC ad CN; et invertendo | |||||||||||||||||||||||||||||||||||||
[pagina 102]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 57.]
 [Fig. 58.]
 [Fig. 59.]
 [Fig. 60.]
 [Fig. 61.]
 [Fig. 62.]
géeGa naar voetnoot1), EN:RO = LE::DR. Et, par permutation et inversion, LE:EN == DR:RO. D'où encore LE:LN = DR:DO, et par suite rect. LE.DO == rect. LN.DR. Or on a DO:OC = rect. DO.LE::rect. OC.LE. On aura donc DO:OC = rect. LN.DR:rect. OC.LE ou rect. LC.RC. En effet, nous avons dit auparavant que LE:LC = CR:CO. Mais DO:OC = DC:CP, vu que, par construction, DO, DC et DP forment une proportion géométrique. Par conséquent DC:CP = LN.DR::LC.CR. Or, LC.CR == LB.AR, vu que, par construction, CL:LB == AR:RC. Par conséquent, DC:CP = DR..LN:LB.AR, où le dernier rapport est composé des rapports DR:RA et LN:LB. Mais le rapport DC:CP est composé des rapports DC:CN et CN:CP; donc (DR:RA)×(LN:LB) = (DC:CN)×(CN:CP). Or, DC:CN = DR:RA parce que par construction DR:DA == DC:DN. On en conclut l'égalité des rapports qui restent, LN:LB = CN::CP. Donc aussi NL:NB = NC:NP. Par conséquent, comme DR:DA = DC:DN, on voit en premier lieu, d'après la prop. XIIGa naar voetnoot2), que les rayons qui proviennent du point D ou qui se dirigent vers lui, sont réfractés par la surface dont A est le centre, de telle manière qu'ils correspondent ensuite au point N. Mais comme on a aussi NL:NB = NC:NP, les rayons qui se dirigent vers N ou qui proviennent de ce point, correspondront en second lieu au point P, après avoir été réfractés par la deuxième surface dont B est le centre, comme cela est manifeste d'après la même propositionGa naar voetnoot3). Il paraît | |||||||||||||||||||||||||||||||||||||
[pagina 103]
| |||||||||||||||||||||||||||||||||||||
NC ad CD ut EC ad DR. Quare et NE ad RC ut EC ad DR. Sed ut RC ad RO ita diximus esse LE ad EC. Ergo ex aequali in ratione perturbataGa naar voetnoot1),
 [Fig. 63.]
 [Fig. 64.]
erit ut EN ad RO ita LE, DR. Et permutando et invertendo, ut LE ad EN ita DR ad RO. Hinc vero et LE ad LN ut DR ad DO, ac proinde rectang. LE, DO aequale LN, DR. Est autem sicut DO ad OC ita rectang. DO, LE ad OC, LE. Ergo erit DO ad OC ut rectang. LN, DR ad OC, LE, hoc est ad rectang. LC, RC. Dictum enim fuit antea quod LE ad LC sicut CR ad CO. Est autem ut DO ad OC ita DC ad CP, quia ex constr. proportionales sunt DO, DC, DP. Ergo DC ad CP sicut rectang. LN, DR ad LC, CR. Rectangulum autem LC, CR aequale est LB, AR, quia CL ad LB ex constr. ut AR ad RC. Ergo DC ad CP rationem habet quam rectang. DR, LN ad LB, AR, hoc est, compositam ex rationibus DR ad RA et LN ad LB. Ratio autem DC ad CP componitur quoque ex rationibus DC ad CN et CN ad CP. Ergo eadem est ratio composita ex rationibus DR ad RA et LN ad LB, compositae ex rationibus DC ad CN et CN ad CP. Ratio autem DC ad CN est eadem quae DR ad RA, quia ex constr. proportionales sunt DR, DA; DC, DN. Ergo et reliqua ratio LN ad LB eadem est reliquae CN ad CP. Unde proportionales quoque erunt NL, NB; NC, NP. Primum itaque quia proportionales sunt DR, DA; DC, DN constat ex prop. [XII]Ga naar voetnoot2) radios qui ex puncto D vel ad D feruntur, refringi a superficie cujus centrum A, ut exinde pertineant ad punctum N. At quia porro proportionales quoque sunt NL, NB; NC, NP; ideo qui ad N vel ex N feruntur, refracti in superficie altera cujus centrum B, pertinebunt ad punctum P, ut ex eadem prop. manifestum estGa naar voetnoot3). Itaque patet P esse punctum concursus vel dispersus radiorum qui ex D puncto promanant, vel eo tendunt; quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||||
[pagina 104]
| |||||||||||||||||||||||||||||||||||||
donc que P est le point de concours ou de dispersion des rayons qui émanent du point D ou qui se dirigent vers ce point. Ce qu'il fallait démontrer.  [Fig. 69.]
 [Fig. 70.]
Mais lorsqu'il arrive que les points D et R coïncidentGa naar voetnoot1), la démonstration, après que nous aurons construit [Fig. 69 et 70] le reste comme auparavant, excepté le point N, sera la suivante. Nous avons dit qu'on a EL:LC = RC:CO. On aura donc RO (ou DO):OC = EC:CL. Mais DO:OC = DC:CP, et EC::CL = RC:LB, vu que, par construction, CE:EA (ou CR) = CL:LB. Par conséquent, DC:CP = RC (ou DC)::LB. La distance CP est donc égale à LB. Et en ajoutant des deux côtés BC, on aura aussi BP = LC. Le rapport BP:LB ou BP:PC est donc égal au rapport CL:LB. Mais c'est là, par construction, l'indice de réfraction. D'après les prop. XI et IXGa naar voetnoot2), on voit donc en premier lieu, attendu que le rapport AR:RC est supposé égal à l'indice de réfraction, que les rayons qui correspondent à R ou à D et qui sont réfractés par la surface dont A est le centre, auront tous la même direction à l'intérieur de la lentille. Mais ces rayons, tombant parallèlement sur la surface dont B est le centre, correspondront ensuite au point P, vu que le quotient BP:PC est égal à l'indice de réfraction. Par conséquent, P est le point de concours ou de dispersion des rayons qui émanent du point D ou qui se dirigent vers ce point. Ce qu'il fallait démontrer. Mais si l'une des deux surfaces de la lentille est sphérique et l'autre plane, l'une ou l'autre sera exposée aux rayons incidents. Et si c'est la surface sphérique dont A est le centre qui leur est exposée [Fig. 71-76], il faut construire à DO, DA et DC une quatrième proportionnelle DN et la porter sur l'axe de telle manière que ces quatre lignes aient ou bien toutes le même sens ou bien deux d'entre elles un sens et deux l'autre. On aura donc DO:OA = DC:CN et, par permutation, DO:DC = OA:CN. Mais on a aussi DO:DC = OC:CP, vu que, par construction, DO, DC et DP forment une proportion géométrique. Par | |||||||||||||||||||||||||||||||||||||
[pagina 105]
| |||||||||||||||||||||||||||||||||||||
Cum vero contingit puncta D et R in unum coireGa naar voetnoot1), constructis [Fig. 69 et 70] caeteris ut prius, praeter punctum N, demonstratio erit hujusmodi. Nimirum quia dictum fuit esse EL ad LC ut RC ad CO, erit RO seu DO ad OC ut EC ad CL. Sicut autem DO ad OC ita est DC ad CP, et ut EC ad CL ita RC ad LB, quia ex constr. est CE ad EA sive CR ut CL ad LB. Itaque DC ad CP ut RC seu DC ad LB. ac proinde CP ipsi LB aequalis. Et addita utrique BC, erit quoque BP aequalis LC. Ergo eadem ratio BP ad LB seu PC quae CL ad LB. Haec autem est ratio refractionis ex constructione. Quia itaque primum AR ad RC posita est refractionis proportio, constat ex prop. [XI et IX]Ga naar voetnoot2) quod radij ad R,
 [Fig. 71.]
 [Fig. 72.]
 [Fig. 73.]
 [Fig. 74.]
 [Fig. 75.]
 [Fig. 76.]
hoc est, ad D pertinentes, atque in superficie cujus centrum A refracti, paralleli intra lentem incedent. Qui autem paralleli occurrunt superficiei cujus B centrum est, pertinebunt deinceps ad punctum P, quia BP ad PC est proportio refractionis. Itaque P est punctum concursus vel dispersus radiorum ex D vel ad D tendentium; quod erat dem. Quod si vero superficierum lentis altera sphaerica fuerit altera plana, erit vel haec vel illa radijs venientibus exposita, ac si quidem sphaerica ijs exponatur, cujus centrum A [Fig. 71-76] fiat tribus DO, DA, DC quarta proportionalis DN, quae accipiatur in eam partem ut vel omnes quatuor eodem versus habeantur vel binae utrimque. Erit igitur et DO ad OA ut DC ad CN, et permutando DO ad DC ut OA ad CN. Sed et DO ad DC est sicut OC ad CP, quia ex constr. proportionales sunt DO, DC, DP. Itaque OA ad CN ut OC ad CP; et permutando AO ad OC ut NC ad CP. Ratio | |||||||||||||||||||||||||||||||||||||
[pagina 106]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 75.]
 [Fig. 76.]
conséquent, OA:CN = OC:CP et, par permutation, AO::OC = NC:CP. Or, le rapport AO:OC est égal à l'indice de réfraction, attendu que O est le point auquel correspondent les rayons réfractés provenant de rayons parallèlesGa naar margenoot*. Le rapport NC:CP sera donc aussi égal à l'indice de réfraction. Et comme nous avons fait DO:DA = DC:DN, il paraît donc que tous les rayons qui se dirigent vers le point D ou qui proviennent de ce point, sont réfractés à la surface dont A est le centre de telle façon qu'ils correspondent ensuite au point NGa naar margenoot*. Mais comme le rapport NC:CP est égal à l'indice de réfraction, les rayons qui correspondent au point N, après avoir été réfractés à la surface plane de la lentille, correspondront ensuite au point PGa naar margenoot*. Dans ce cas le théorème est donc également vrai. Mais si les rayons tombent d'abord sur la surface plane de la lentille [Fig. 77-82], et que A est de nouveau le centre de la surface sphérique, il faut prendre le rapport CE:EA égal à l'indice de réfraction, et de même aussi le rapport MC:CD. Puisque donc O est le point auquel correspondent les rayons parallèles, CO sera égale à AEGa naar margenoot*, et on aura donc aussi CE::CO = CE:EA, ou MC:CD. C'est pourquoi aussi ME::OD = MC:CD. Mais OD:OC = DC:CP, vu que, par construction, DO, DC et DP forment une proportion géométrique. En combinant les deux proportions, on trouve donc ME::OC (ou EA) = MC:CP, et par conséquent, ME:MA == MC:MP. Comme nous avons pris le rapport MC:CD égal à l'indice de réfraction, les rayons qui proviennent du point D ou qui se dirigent vers lui, correspondront au point M après avoir été réfractés à la surface plane de la lentilleGa naar margenoot*. Et comme on a ME:MA = MC:MP, il est prouvéGa naar margenoot(*) que les rayons qui correspondent au point M, après avoir été réfractés à la surface dont A est le centre correspondront ensuite au point P. C'est ce qui restait à démontrer. Il résulte clairement de ce qui précède que, en ce qui regarde la distance des points de concours ou de dispersion des rayons qui émanent de points quelcon- | |||||||||||||||||||||||||||||||||||||
[pagina 107]
| |||||||||||||||||||||||||||||||||||||
autem AO ad OC est ea quae refractionis, quia O est punctum quo pertinent refractiones radiorum parallelorumGa naar margenoot*. Igitur et NC ad CP erit refractionis proportio. Quia itaque fecimus proportionales DO, DA; DC, DN; apparet radios omnes qui ad D vel ex D feruntur, refringi in superficie cujus centrum A, ut exinde pertineant ad punctum NGa naar margenoot*. Sed quia NC ad CP rationem habet quae est refractionis, ideo qui ad punctum N pertinent, refracti in plana lentis superficie, pertinebunt inde ad punctum PGa naar margenoot*. Ergo et hic constat propositum.  [Fig. 77.]
 [Fig. 78.]
 [Fig. 79.]
 [Fig. 80.]
 [Fig. 81.]
 [Fig. 82.]
Si vero in planam lentis superficiem primum radij incidant [Fig. 77-82], rursusque centrum superficiei sphaericae sit A; fiat ut CE ad EA proportionem refractionis habeatGa naar voetnoot4), atque item MC ad CD. Quia igitur O punctum est quo pertinent refractiones parallelorum, erit CO aequalis AEGa naar margenoot*; ideoque et CE ad CO ut CE ad EA, hoc est, ut MC ad CD. Quare et ME ad OD erit ut MC ad CD. Est autem ut OD ad OC ita DC ad CP, quia ex constr. proportionales sunt DO, DC, DP. Igitur ex aequo, ut ME ad OC sive EA ita MC ad CP; ac proinde ut ME ad MA ita MC ad MP. Quia igitur posita est ratio MC ad CD eadem quae refractionis, ideo radij ex D vel ad D tendentes, post refractionem in supersicie lentis plana, pertinebunt ad punctum MGa naar margenoot*. Et quia proportionales sunt ME, MA; MC, MP, constatGa naar margenoot* radios qui ad M punctum pertinent, refractos in super- | |||||||||||||||||||||||||||||||||||||
[pagina 108]
| |||||||||||||||||||||||||||||||||||||
ques ou qui se dirigent vers des points quelconques, il ne fait aucune différence de tourner l'une ou l'autre des surfaces de la lentille vers le côté des rayons incidents. On voit aussi que des lentilles à surfaces différentes, mais possédant des points de concours ou de dispersion des rayons parallèles situés à égale distance, sont équivalentes sous les autres rapports. Cela résulte de ce fait que dans la construction on n'a pas égard aux centres de courbure des deux surfaces de la lentille, mais seulement aux points de concours ou de dispersion des rayons incidents parallèlesGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||
Proposition XXI.Placer en un lieu donné une surface sphérique capable de réunir en un point donné les rayons provenant d'un autre point donné ou se dirigeant vers un tel pointGa naar voetnoot2).  [Fig. 83.]
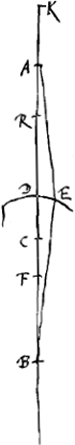 [Fig. 84.]
Soient A, B et D [Fig. 83-87]Ga naar voetnoot3) les points donnés, situés sur une ligne droite, et soit demandé de placer au point D une surface sphérique capable de réunir au point B les rayons qui proviennent du point A ou qui se dirigent vers ce point. Il faut savoir qu'en un seul cas on ne trouve pas une surface sphérique mais, au lieu d'elle, une surface plane. Cela aura lieu lorsque le point A est situé entre B et D, et que le rapport BD:DA est égal à l'indice de réfraction, comme dans le premier des cas considérés [Fig. 83]. Car si l'on fait passer par le point D une surface plane limitant un corps transparent qui se trouve du côté de A, cette surface forcera les rayons qui se dirigeaient vers le point A de se réunir au point B, comme cela a été démontré plus hautGa naar voetnoot4). Dans les autres cas [Fig. 84-87], la construction sera la suivante. Prolongeons DA jusqu' en K de telle manière que le quotient KD:DA soit égal à l'indice de réfraction, et construisons une quatrième proportionnelle BC à BK, BA et BD. Portons-la sur la droite donnée dans un sens tel que les quatre longueurs aient ou bien toutes la même direction ou bien deux d'entre elles une direction et les deux autres la direction opposée. Si nous décrivons alors | |||||||||||||||||||||||||||||||||||||
[pagina 109]
| |||||||||||||||||||||||||||||||||||||
ficie, cujus centrum A, pertinere porro ad punctum P. Quod demonstrandum supererat. Manifestum autem ex his est, quantum ad distantiam punctorum concursus vel dispersus radiorum, à quibusvis vel ad quaelibet puncta tendentium, nihil interesse utra lentis alicujus superficies radijs incidentibus obvertatur. Item diversarum superficierum lentes, quae puncta concursus vel dispersus parallelorum aeque remota habent, etiam ad caetera aequivalentes esse. Nempe quia in constructione non attenduntur centra singularum lentis superficierum, sed tantummodo punctum concursus vel dispersus radiorum parallelorumGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||
[Propositio XXI.]In dato loco superficiem sphaericam constituere, quae radios ex dato vel ad datum punctum pergentes, ad punctum aliud datum concurrere faciatGa naar voetnoot2). Sint data puncta A, B et D [Fig. 83-87]Ga naar voetnoot3) in linea recta et oporteat ad D superficiem sphaericam constituere quae radios ex A vel ad A tendentes colligat in puncto B. Sciendum quod uno casu superficies sphaerica non invenitur, sed plana ejus loco. Nempe cum punctum A inter B et D situm est, habetque BD ad DA rationem quae est refractionis, ut in casu horum primo [Fig. 83]. Nam si per punctum D plana superficies ducatur diaphanum terminans quod sit a parte A, ea radios versus A punctum tendentes coget ad punctum B, ut supra demonstratum fuitGa naar voetnoot4). In caeteris autem casibus [Fig. 84-87] haec erit constructio. Producatur DA ad K, ut KD ad DA sit eadem quae refractionis ratio; et tribus hisce BK, BA, BD, inveniatur quarta proportionalis BC, ponaturque in eam partem ut vel omnes in eandem tendant, vel binae in utramque. Jam si centro C circumferentia describatur DE, ea sectionem quaesitae superficiei exhibebit, diaphanum habentis a | |||||||||||||||||||||||||||||||||||||
[pagina 110]
| |||||||||||||||||||||||||||||||||||||
une circonférence DE avec C pour centre, cette circonférence représentera la section de la surface cherchée, le corps transparent étant placé du côté de B. Cette
 [Fig. 85.]
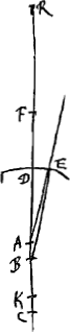 [Fig. 86.]
surface sera convexe dans tous les cas, excepté un seul [Fig. 87] où elle sera concave, savoir le cas où le point A est placé entre D et B de telle manière que le rapport BD:DA est plus grand que l'indice de réfraction. Quant à la démonstration, elle est la suivante. Posons DF = AK, d'où résulte que l'on aura en même temps FA == DK, et faisons en sorte que le rapport CR:RD soit égal à l'indice de réfraction, c'est-à-dire au rapport KD:DA. Comme BK:BA = BD:BC on aura donc BK:KA == BD:DC et, par permutation, BK:BD = KA (ou DF)::DC. Donc aussi KD (ou AF):DB = FC:CD; et, par permutation et inversion, FC:FA = DC:DB. Ensuite, comme FA = KD par construction, on aura FA:AD == KD:DA ou CR:RD. Donc aussi, par conversion, AF::FD = RC:CD. Mais nous avions FC:FA = DC:DB. On aura donc, par la règle de la proportion dérangéeGa naar voetnoot1), FC:FD = RC:DB. De plus, comme FA:AD = CR::RD, on aura, par partage, FD:DA = CD:DR et, par permutation, FD:CD = DA:DR. Donc aussi FD::FC = DA:AR. Et, par inversion, FC:FD = AR:AD. Mais nous avions démontré FC:FD = RC:BD. Donc aussi AR:AD = RC:BD. Et, par permutation, AR:RC = AD:BD. Par conséquent, AR, AC, AD et AB forment également une proportion géométrique. Il en résulte que les rayons qui correspondent au point A sont réfractés de telle manière par la surface DE qu'ils se réunissent au point BGa naar voetnoot2). Ce qu'il fallait démontrer. Or, si l'on ajoute à la surface trouvée une deuxième surface à centre B et de rayon inférieur à BD, les deux surfaces formeront ensemble une lentille capable de produire l'effet désiré; car aucune réfraction n'aura lieu à la deuxième surface, vu que les rayons se dirigent vers son centreGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||
Proposition XXII.Chercher les points de concours ou de dispersion des rayons qui correspondent à un axe de la lentille faiblement incliné par rapport à l'axe principal, et démontrer que la distance | |||||||||||||||||||||||||||||||||||||
[pagina 111]
| |||||||||||||||||||||||||||||||||||||
parte B. Quae quidem caeteris casibus convexa, uno vero cava erit [Fig. 87], nempe si punctum A positum fuerit inter D et B, et major ratio BD ad DA ratione refractionis. 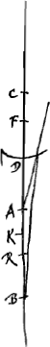 [Fig. 87.]
Ad demonstrationem autem, ponatur DF aequalis AK, ut simul fiat FA aequalis DK. et habeat CR ad RD rationem quae est refractionis, hoc est, quam habet KD ad DA. Quia igitur BK ad BA ut BD ad BC, erit et BK ad KA ut BD ad DC, et permutando, BK ad BD ut KA seu DF ad DC. Quare et KD seu AF ad DB, ut FC ad CD; et permutando et invertendo FC ad FA ut DC ad DB. Porro quia FA aequalis KD ex constructione, erit FA ad AD ut KD ad DA, hoc est, ut CR ad RD. Igitur et per conversionem rationis, AF ad FD ut RC ad CD. Sed ut FC ad FA ita erat DC ad DB. Igitur ex aequali in proportione perturbataGa naar voetnoot1), erit FC ad FD ut RC ad DB. Insuper quia ut FA ad AD ita CR ad RD, erit et dividendo, FD ad DA ut CD ad DR; et permutando, FD ad CD ut DA ad DR. Ergo et FD ad FC ut DA ad AR. et invertendo FC ad FD ut AR ad AD. Sed ut FC ad FD ita ostensa fuit RC ad BD. Igitur et AR ad AD ut RC ad BD:Et permutando AR ad RC ut AD ad BD. Ideoque et proportionales AR, AC; AD, AB. Unde liquet radios ad punctum A pertinentes, ita refringi in superficie DE ut congregentur in puncto BGa naar voetnoot2). Quod erat demonstrandum. Si vero inventae superficiei altera jungatur centro B, semidiametro minore quam BD; constituent simul lentem, quae propositum efficiet; nam in posteriori superficie nulla amplius continget refractio, quum radij ad ipsius centrum feranturGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||
[Propositio XXII.]RadiorumGa naar voetnoot4), qui ad axes lentium pertinent ab axe primario paulum declinantes, puncta concursus vel dispersus investigare. Et ostendere eandem fere horum esse a lente di- | |||||||||||||||||||||||||||||||||||||
[pagina 112]
| |||||||||||||||||||||||||||||||||||||
de ces points à la lentille est à-peu-près la même que celle des points qui appartiennent à des rayons correspondant à l'axe principal, si ces rayons étaient parallèles ou émanaient de points situés à la même distance de la lentille.Jusqu' ici nous avons examiné des systèmes de rayons parallèles aux axes des 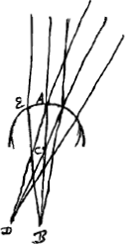 [Fig. 88.]
lentilles ou correspondant à des points situés sur ces axes. Mais il est nécessaire d'avoir égard aussi aux rayons qui correspondent à des points situés en-dehors de l'axe, attendu que les merveilleux phénomènes qui se présentent dans l'oeil et dans les instruments optiques de toute espèce dépendent également de ces rayons-là. Il faut examiner d'abord ce qui a lieu à une seule surface, parce que, ceci étant connu, la chose sera aussi plus facile pour les lentilles. Soit EA [Fig. 88] une surface sphérique convexe, C son centre, AC son rayon de courbure. Prolongeons ce rayon jusqu' au point B, de telle manière que le rapport AB:BC soit égal à l'indice de réfraction. Imaginons-nous de plus une sursace sphérique concave BD, avec le même centre C, qui recevra les rayons. Alors non seulement les rayons parallèles à la droite CB et tombant sur la surface AE se réuniront en B, comme cela a été démontré à la Prop. VIIIGa naar voetnoot1), mais ceux qui se mouvront parallèlement à la droite CD, formant un angle quelconque avec CB, se réuniront de la même manière au point D. En second lieu, si les rayons qui proviennent d'un point quelconque G [Fig. 89] ou qui se dirigent vers un tel point [Fig. 90], et qui sont réfractés à la surface sphérique AE, ont un point de concours H, lequel est trouvé à l'aide de la Prop. XII, p. 1 et 4Ga naar voetnoot3), et que nous nous figurons les surfaces sphériques GK, HL à centre C, alors les rayons qui proviennent de K, point de la surface GK, ou qui se dirigent vers K, se réuniront de la même manière en un point de la surface HL, tel que L. Cela est évident par soi-même dans tous les cas. | |||||||||||||||||||||||||||||||||||||
[pagina 113]
| |||||||||||||||||||||||||||||||||||||
stantiam ac eorum quoe ad puncta radiorum in axe positorum pertinent, si vel paralleli vel oeque procul distantibus punctis radij fuerint egressi. Hactenus complexus radiorum examinavimus qui ad axes lentium referuntur. Sed necesse est eos quoque inspicere qui ad puncta extra axem posita pertinent, quoniam ab his radijs oeque ac ab illis pendent tum oculi tum omnis generis perspicillorum miri effectus. ac videndum primò, quid fiat in superficiebus singulis, quia hoc cognito, etiam de lentibus res erit facilior. Sit superficies sphaerica convexa EA [Fig. 88], cujus centrum C, semidiameter convexitatis AC, quae producatur ad B, ut sit ratio AB ad BC eadem quae est refractionis. Intelligatur porro superficies sphaerica cava, radios exceptura, [Fig. 89.]
 [Fig. 90.]
BD; centrum idem habens C. Jam non tantum radij paralleli rectae CB, in superficiem AE incidentes, convenient in B, ut in [Prop. VIII]Ga naar voetnoot1) demonstratum est, sed et ij qui rectae CD, angulum qualemcumque cum CB constituenti, paralleli ferentur, eodem modo ad D concurrent. Rursus si à puncto [Fig.89] vel ad punctum aliquod G [Fig. 90] tendentes radij fractique in superficie sphoerica AEGa naar voetnoot2), habuerint punctum concursus H; hoc autem invenitur per [Prop. XII, part. 1 et 4]Ga naar voetnoot3) et centro C intelligantur superficies sphaericae GK, HL, tunc radij ex K puncto superficiei GK venientes, vel ad K tendentesGa naar voetnoot4), concurrent similiter ad punctum in superficie HL, ut L. atque haec per se manifesta sunt in quibuscunque casibusGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||
[pagina 114]
| |||||||||||||||||||||||||||||||||||||
ConsidéronsGa naar voetnoot1) maintenant une lentille convexe AO [Fig. 91], avec BAE comme
 [Fig. 91.]
axe, sur lequel se trouvent donc les centres des sursaces AN et OP, c'est-à-dire, les points C et G. Les rayons qui proviennent du point B et qui rencontrent la surface AN, y sont réfractés de manière à se diriger vers le point E; ensuite, après avoir été réfractés de nouveau à la surface OP, ils se dirigent vers le point V. SupposonsGa naar voetnoot2) de même que des rayons issus d'un point D situé en-dehors de l'axe et se trouvant à égale distance que le point B | |||||||||||||||||||||||||||||||||||||
[pagina 115]
| |||||||||||||||||||||||||||||||||||||
PonaturGa naar voetnoot1) nunc lens convexa AO [Fig. 91] cujus axis B AE, in quo nempe centra supersicierum AN, OP sint C et G. Radij autem a puncto B manantes in superficiem AN, franguntur ut inde tendant ad punctum E; atque iterum fracti in superficie OP pergant ad punctum V. ItemGa naar voetnoot2) a puncto D extra axem, quodque tantundem ac B distet à supersicie AN, vel à centro ejus C, egressi radij in super- | |||||||||||||||||||||||||||||||||||||
[pagina 116]
| |||||||||||||||||||||||||||||||||||||
de la surface AN, c'est-à-dire de son centre C, tombent sur elle. Nous trouvons
 [Fig. 91.]
de la manière suivante le point de concours L de ces rayons après les deux réfractions dues à la lentille. Tirons la droite DC, qui coupera la surface AN perpendiculairement en N et cherchons sur le prolongement de cette même ligne le point S où se réunissent les rayons qui proviennent de D après avoir été réfractés à la surface AN, d'après ce qui a été exposé plus haut. Or, il appert que les distances CS et CE seront égales. Joignons maintenant les points S et G par une droite qui coupera la surface OQ normalement en Q. Par conséquent, le point de concours L des rayons qui après la première réfraction se dirigent vers S et qui sont réfractés de nouveau à la surface OQ, se trouve sur cette même droite SG. Ce point de concours peut donc être trouvé d'après ce qui a été dit plus haut. Et que le point L est à peu près à la même distance de la lentille que le point V, on le démontre de la manière suivante. Si les points E et S, sommets des cônes lumineuxGa naar voetnoot1), étaient à égale distance de la surface OQ, qui par sa réfraction change ces cônes en d'autres dont les sommets sont L et V, ces deux derniers sommets seraient eux aussi à égale distance de cette surface. Or, les distances QS et OE sont à-peuprès égales: elles ne diffèrent l'une de l'autre que d'une fort petite quantité, savoir de l'excès de GE ou de la somme de GC et CS sur GS. Par conséquent, les distances LQ et VO elles aussi seront à-peuprès égales. Mais comme nous supposons que les droites qui joignent les points B et D d'une part et les points V et L d'autre part, sont fort petites et que ces points eux-mêmes sont à égale distance de la lentille, elles peuvent être considérées comme perpendiculaires à l'axe BE de la lentille. | |||||||||||||||||||||||||||||||||||||
[pagina 117]
| |||||||||||||||||||||||||||||||||||||
ficiem hanc incidant. Horum punctum concursus L post binas in lente refractiones ita invenimus. Ducatur recta DC, quoe secabit superficiem AN in N, ad rectos angulos: invenieturque in eadem linea producta punctum S quo concurrunt radij ex D venientes post refractionem in superficie AN, per superius exposita. Et apparet distantias CS, CE fore oequales. Jungatur jam SG; quoe superficiem OQ normaliter secabit in Q; eritque propterea in ipsa SG punctum concursus L, radiorum ex prima refractione tendentium ad S, ac rursus refractorum in superficie OQ, atque invenietur inde istud concursus punctum ex superioribus. Quod autem punctum L proxime eandem distantiam habebit à lente ac punctum V, hinc constabit. Si enim puncta E, S, vertices nempe conorum radiosorumGa naar voetnoot1) oequaliter distarent a superficie OQ, cujus refractione mutantur hi coni in conos quorum vertices L et V; etiam hi vertices oequaliter distarent ab hac superficie. Sunt autem distantioe QS, OE proximè oequales, quippe minimo quopiam differentes, quanto nimirum GE sive duoe simul GC, CS superant GS. Ergo et distantioe LQ, VO proximè oequales erunt. Rectoe autem qua puncta B, D, itemque V, L, conjungunt, quia minimoe esse censentur, et puncta ipsa oequaliter a lente distant, possunt tanquam ad axem lentis BE perpendiculares haberi. Hoec autem non difficulter ad cavas quoque lentes, et ad eas quoe alteram superficierum planam habent, omnemque casuum diversitatem, facile transferri possunt radios parallelos tanquam ad punctum infinite distans considerando. | |||||||||||||||||||||||||||||||||||||
[pagina 118]
| |||||||||||||||||||||||||||||||||||||
Or, ceci peut être étendu sans difficulté aux lentilles concaves et à celles qui ont une surface plane et à tous les autres différents cas; les rayons parallèles étant considérés comme correspondant à un point infiniment distant. La seconde figure [Fig. 92] explique cette affirmation par un seul exemple, celui de la lentille planconcave. En effet, la surface plane AN de cette lentille reçoit les rayons qui se dirigent vers le point B de l'axe, et de même d'autres rayons qui se dirigent vers le point D situé à petite distance de l'axe et à la même distance de la surface AN que le point B. Or, si nous supposons que les rayons qui se dirigeaient vers le point B, deviennent parallèles à l'axe AE après la deuxième réfraction à la surface OQ, autrement dit, qu'ils tendent à se réunir au point V situé sur l'axe à une distance infinie, alors les rayons qui se dirigent vers le point D deviendront eux aussi parallèles par la deuxième réfraction due à cette même surface OQ; autrement dit, ils correspondront à un point L situé sur la ligne QGS à une distance infinie. Cette ligne est trouvée de la même manière que dans le cas précédent; et l'on démontre aussi de la même manière qu' après la deuxième réfraction les rayons deviennent parallèles tant pour le deuxième faisceau incident que pour le premier, avec cette différence que dans ce cas-ci, des deux grandeurs GE et GS qui sont considérées comme égales, la première est un peu plus petite que GS; en effet, AE et NS sont égales. De plus il ressort clairement de ce qui précède que les cônes lumineux, obliques ou droites, transmis par deux ou plusieurs lentilles, ont leurs derniers sommets à égale distance de la dernière lentille, si les rayons se rapportent primitivement à des sommets de cônes également distants de la première. La vérité de ce qui a été démontré ici est confirmée par l'expérience de l'image formée par une lentille placée devant une ouverture en un lieu obscur. En effet, cette image est vue avec une netteté admirable non seulement sur l'axe de la lentille, mais aussi autour de l'axe sur une étendue assez considérable de manière que les plus petits détails sont clairement aperçus dans l'image. Et les effets remarquables obtenus avec des télescopes composés de deux, de trois ou de quatre lentilles montrent aussi la vérité de notre théorème. | |||||||||||||||||||||||||||||||||||||
Proposition XXIII.A l'intérieur de toute lentille possédant deux surfaces convexes, ou deux surfaces concaves, il existe un point déterminé tel qu'un rayon quelconque passant par ce point a | |||||||||||||||||||||||||||||||||||||
[pagina 119]
| |||||||||||||||||||||||||||||||||||||
Quod uno etiam exemplo in lente planoconcava schema alterum [Fig. 92] explicat.  [Fig. 92.]
Hujus enim lentis plana superficies AN radios ad punctum axis B tendentes excipit, itemque alios tendentes ad punctum D, ab axe exiguo distans, et oeque ac B à superficie AN. Quod si jam ponamus eos qui ad B tendebant, post alteram refractionem in superficie OQ fieri parallelos axi AE; sive ad punctum V in axe infinite distans concurrere, fient etiam qui ad D tendunt, ejusdem superficiei OQ altera refractione, inter se paralleli, sive ad punctum L in linea QGS infinitè distans pertinebunt. Quoe linea invenitur eodem modo ac in casu proecedenti; eademque est demonstratio, qua ostendatur ex postrema refractione radios utrobique fieri parallelos, nisi quod hoc casu è duabus GE, GS, quoe ut oequales censentur, GE nunc pauxillo minor est quam GS, quippe cum oequales sint AE, NS. Porrò ex his manifestum est, etiam per binas pluresve lentes transmissos conos radiosos tam obliquos quam rectos, oequali distantia à lente postrema vertices suos ultimos habere, si ad oeque remotos conorum vertices radij primitus spectent. Comprobat autem quoe hic ostensa sunt experimentum picturoe, quam lens foramini opposita in loco tenebroso exhibet, cum non tantum in axe lentis, sed et circùm amplo satis spatio hoec pictura mirabili nitore conspiciatur, ut minima quoeque distinctè exprimat. Eadem vero et telescopiorum ex binis, ternis, quaternisve lentibus compositorum egregij effectus vera esse ostendunt. | |||||||||||||||||||||||||||||||||||||
Propositio [XXIII].In omni lente, duarum convexarum aut concavarum superficierum, punctum quoddam est intus, per quod radius quilibet transiens ante et post lentem sibi ipse parallelus in- | |||||||||||||||||||||||||||||||||||||
[pagina 120]
| |||||||||||||||||||||||||||||||||||||
la même direction avant d'entrer dans la lentille et après l'avoir traversée. Mais un point de ce genre est trouvé à l'extérieur de la lentille, du côté de la plus petite sphère, lorsque la section de la lentille a la forme d'une lunule, ou que sa surface concave a un rayon de courbure plus petit que sa surface convexeGa naar voetnoot2). 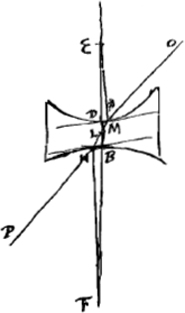 [Fig. 94.]
Supposons que la lentille soit une de celles [Fig. 93-96] dont l'une des deux surfaces est décrite du centre E avec le rayon ED, l'autre du centre F avec le rayon FB, et que de ces deux rayons FB soit le plus grand; tirons la droite FE qui coupe la lentille en D et en B. Or, si nous posons: BL est à LD comme le rayon FB est au rayon ED, de telle manière que le point LGa naar voetnoot4) (si la lentille est biconvexe [Fig. 93] ou biconcave [Fig. 94]) tombe sur la droite BD même qui fait connaître l'épaisseur de la lentille, mais que ce point tombe en-dehors de la lentille de côté de la plus petite sphère, dans le cas où la section de la lentille a la forme d'une lunule et dans les autres cas; je dis que tout rayon, comme PNMO, qui pénètre dans la lentille de telle manière que la partie NM de ce rayon contenue dans la lentille passe par le point L ou correspond à ce point, suivra après avoir traversé la lentille une direction parallèle à la direction que ce rayon avait avant d'atteindre la lentille, c'est-à-dire, la partie PN sera parallèle à la partie MO. 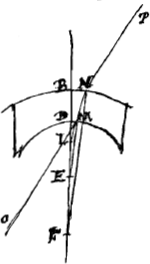 [Fig. 96.]
En effet, tirons FN et EM et figurons-nous les plans qui touchent les deux surfaces sphériques de la lentille aux points N et M. On aura FB:ED = BL:LD et, par permutation, FB:BL = ED:DL. Donc aussi BF (ou NF):FL = DE (ou ME):EL. Comme les triangles NFL et MEL ont, par conséquent, la même proportion des côtés qui avoisinent les angles E et F respectivement, qu'ils ont des angles égaux au point L et que ces angles L [Fig. 93 et 96] ou bien les angles M et N [Fig. 94 et 95] sont obtus (car on voit facilement qu'il en est nécessairement ainsi), ces triangles sont forcément semblables. C'est pourquoi les angles compris entre les côtés proportionnels seront aussi égaux, je veux dire que l'angle NFL sera égal à l'angle MEL. Par conséquent, les droites FN et EM seront aussi parallèles. Mais ces droites | |||||||||||||||||||||||||||||||||||||
[pagina 121]
| |||||||||||||||||||||||||||||||||||||
cedit. In menisco autem, et in illa quae minori cavo quam convexo constat, punctum ejusmodiGa naar voetnoot1) extra lentem, a parte sphaerae minoris reperiturGa naar voetnoot2). 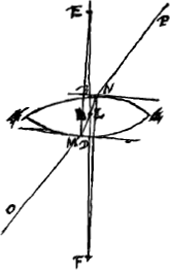 [Fig. 93.]
Sit lens quaelibet istarum [Fig. 93-96], cujus superficies altera descripta sit centro E, radio ED, altera centro F, radio FB, quorum FB sit major altero: et jungatur FE, quae secet lentem in D et B. Quod si jam sicut radius FB ad radium ED ita ponatur BL ad LD; ut cadatGa naar voetnoot3) punctum LGa naar voetnoot4), (si quidem duarum convexarum [Fig. 93] vel concavarum [Fig. 94] superficierum fuerit lens) in ipsa linea BD, quae lentis crassitudinem definit; extra lentem vero, versus sphaeram minorem, in menisco et casibus reliquis; dico radium omnem qui lentem penetrat, ut PNMO, ita ut pars ejus NM intra lentem contenta transeat per punctum L, vel ad ipsum pertineat, sibi ipsi, ante ingressum et post egressum ex lente, parallelum ferri, hoc est partem PN parti MO. 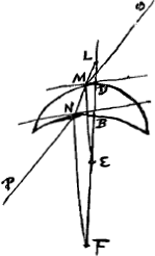 [Fig. 95.]
Jungantur enim FN, EM, et intelligantur planae superficies in punctis N et M utrasque lentis superficies sphaericas tangentes. Quia igitur ut FB ad ED ita BL ad LD; erit et, permutando, FB ad BL ut ED ad DL. Unde et BF sive NF ad FL ut DE sive ME ad EL. Cum itaque triangula NFL, MEL, latera circa angulos E et F proportionalia habeant, angulosque aequales ad L, qui vel ipsi obtusi sunt [Fig. 93 et 96] vel reliqui ad M et N [Fig. 94 et 95], (hoc enim necessario ita esse facile perspicitur) similia proinde triangula haec esse necesse est. Quare et anguli lateribus proportionalibus comprehensi aequales erunt, angulus nempe NFL angulo MEL; ideoque parallelae inter se rectae FN, EM. Hae autem ad angulos rectos sunt planis quae superficies lentis | |||||||||||||||||||||||||||||||||||||
[pagina 122]
| |||||||||||||||||||||||||||||||||||||
sont perpendiculaires aux plans que nous supposons tangents aux surfaces de la lentille aux points N et M. Ces plans sont donc aussi parallèles entre eux. C'est pourquoi il est nécessaire que le rayon NM qui fait des angles égaux avec ces deux plans, soit dévié par le même angle en sortant de la lentille que lorsqu'il y entrait. L'angle PNM est donc égal à l'angle NMO. Or ce sont des angles alternes: il est donc certain que PN et MO sont parallèles, ce qu'il fallait démontrer. Nous n'avons pas mentionné les lentilles planconvexes et les lentilles planconcaves. Il ressort de ce qui a éte démontré que pour ces lentilles le point L tombe au milieu de la surface sphérique de la lentille. | |||||||||||||||||||||||||||||||||||||
Proposition XXIV.Le diamètre de l'image d'un objet quelconque qui est tormée dans un plan situé derrière une lentille convexe, est à celui de l'objet comme la distance de l'image à la lentille est à celle de l'objet à la lentilleGa naar voetnoot1).Soit ADCB [Fig. 97] la lentille convexe. Soit la droite KF l'objet. Supposons que l'axe de la lentille est perpendiculaire à cette droite et passe par son milieu E. Partant des points K, E et F et de tous les autres points qu'on peut se figurer sur  [Fig. 97.]
cette droite, des rayons tomberont donc sur toute la lentille ABC et après une double réfraction, je veux dire la réfraction aux deux surfaces de la lentille, ils se réuniront en un même nombre de points du plan IHG. Ceux qui proviennent de K, de E et de F se réuniront en G, en H et en I respectivement; pour autant que nous supposons que l'image est distincte. Or, comme la lumière qui émane du point K passe par tous les points qui se trouvent à l'intérieur de la lentille ABC, il adviendra nécessairement qu'un rayon déterminé parmi ceux qui partent de K pour se réunir en G passe par le point L de la lentille, c'est-à-dire par le point dont nous avons parlé dans la proposition précédente, et ce rayon suivra avant d'atteindre la lentille et après l'avoir traversée une même direction. Et comme un autre rayon se meut de la même manière de F vers I, il apparaît que l'un et l'autre de ces rayons peuvent être considérés comme des lignes droites qui se coupent au centre de la lentille, l'épaisseur de la lentille étant négligée. Ils forment donc de cette façon deux triangles isocèles semblables, dont KF et IG sont les bases; c'est pour- | |||||||||||||||||||||||||||||||||||||
[pagina 123]
| |||||||||||||||||||||||||||||||||||||
in punctis N et M contingere intelliguntur. Ergo et plana ista inter se parallela erunt. Quamobrem cum radius NM aequalibus angulis ad illa inclinetur, necesse est eum aequali angulo flecti, ubi lentem egreditur atque ubi intrabat, hoc est, angulum PNM esse aequalem angulo NMO. Sunt autem alterni: itaque constat PN, MO esse parallelas, quod erat dem. Lentes planoconvexas et planoconcavas hic non recensuimus, in quibus tamen per haec ipsa constat punctum L cadere in mediam lentis superficiem sphaericam. | |||||||||||||||||||||||||||||||||||||
Propositio [XXIV].Pictura cujusque visibilis quae fit in plano post lentem convexam, ad visibile ipsum eam habet rationem, secundum diametrum, quam picturae distantia a lente ad visibilis ab ea distantiamGa naar voetnoot1). Sit lens convexa ADCB [Fig. 97]. Visibile vero linea recta KF, quam axis lentis mediam secet, atque ad angulos rectos, in E.A punctis igitur K, E, F aequè ac ab alijs omnibus, quae in proposita linea imaginari licet, radij ferantur in totam lentem ABC, qui post geminam refractionem, in utraque nimirum lentis superficie, colliguntur in totidem punctis tabulae IHG; nempe qui ex K in G, qui ex E in H, et qui ex F in I; quatenus quidem distinctam ponimus existere hanc picturam. Quum igitur lux à puncto K manans, omnia puncta quae sunt intra lentem ABC pervadat fiet necessariò utGa naar voetnoot2) aliquis radiorum ex K manantium, atque in G collectorum, transeat per punctum lentis L, illud nimirum quo de egimus propos. superiori; atque is radius ante et post lentem sibi ipsi parallelus feretur; quumque similiter aliquisGa naar voetnoot3) transeat ab F ad I, apparet utrosqueGa naar voetnoot4) pro lineis rectis haberi posse, in centro lentis sese intersecantibus; non considerata videlicet lentis crassitudine. Cumque hoc modo duos triangulos isosceles similes efficiant, quorum bases KF et IG; hae utique eandem inter se rationem servabunt quam triangulorum | |||||||||||||||||||||||||||||||||||||
[pagina 124]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 97.]
quoi ces bases auront entre elles la même proportion que les hauteurs des triangles; c'est-à-dire que les distances des bases à la lentille ABCD. Ce qu'il fallait démontrer. Mais si nous ne négligeons pas l'épaisseur de la lentille et qu'on demande d'indiquer plus exactement le sommet du triangle formé derrière la lentille, il faut diviser l'intervalle LD qui sépare le point L de la surface postérieure de la lentille, par le point V, de telle manière que le quotient LD:DV soit égal à l'indice de réfraction: V sera alors le sommet cherché. Cela résulte de la prop. VIGa naar voetnoot3), vu que la petite partie de la surface ADC qui est interceptée entre les rayons qui se croisent en L, peut ici être considérée comme une surface planeGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||
Proposition XXVGa naar voetnoot5).Deux corps transparents qui possèdent des pouvoirs réfringents différents se touchent suivant une surface commune; un rayon qui vient du corps le moins réfringent et qui pénètre dans celui qui réfracte plus fortement, est incliné du côté de la perpendiculaire, l'indice qui correspond à cette réfraction étant le quotient des indices de ces deux corps par rapport à l'air. Il est établi par voie expérimentale que lorsque la surface de l'eau ou d'un autre liquide transparent est recouverte par une mince lame de verre, tout rayon qui tombe du dehors sur cette lame subit, en passant à l'intérieur du liquide qui se trouve au-dessous d'elle, le même changement de direction que lorsqu' aucune substance n'est interposée, et que le rayon est, par conséquent, réfracté uniquement à la surface du liquide. C'est à cause de cette même propriété que dans une sphère de verre mince remplie d'eau, on observe les mêmes réfractions que dans les gouttes d'eau qui possèdent une forme sphériqueGa naar voetnoot7). Il faut pourtant observer que, quelque mince que soit la lame de verre, elle a néanmoins deux surfaces et que, par conséquent, les réfractions sont aussi au nombre de deux; on peut donc considérer une lame de ce genre comme fort épaisse, les angles de réfraction n'en seront pas moins les mêmes. | |||||||||||||||||||||||||||||||||||||
[pagina 125]
| |||||||||||||||||||||||||||||||||||||
ipsorumGa naar voetnoot1) altitudines; hoc est, quam distantioe basiumGa naar voetnoot2) à lente ABCD. quod erat dem. Quod si vero lentis crassitudo etiam consideretur, apexque trianguli post lentem effecti accuratius designandus sit, oportet dividere intervallum LD inter punctum L et superficiem lentis posteriorem, in V, ut sit LD ad DV ratio eadem quae est refractionis, eritque punctum V apex quaesitus; quod quidem manifestum est ex prop [VI]Ga naar voetnoot3) quoniam superficiei ADC particula inter radios decussatos intercepta tanquam plana hic censuri potestGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||
Propositio [XXV]Ga naar voetnoot5).Diaphanis duobus diversae refractionis communi superficie inter se conjunctis, radius e minus refringente in id quod magis refringit penetrans, versus perpendicularem inclinatur eamque servat refractionis proportionem, qua differunt inter se proportiones utriusque diaphani in aereGa naar voetnoot6). Experimento constat cum aquae aut alterius liquidi diaphani superficies lamina tenui vitrea terminatur, quemvis radium extrinsecus incidentem eodem modo intra subjacens liquidum deflecti, ac si nulla re interposita, tantum ad liquidi superficiem refractus fuisset. Hinc quoque fit ut in sphaera ex tenui vitro aqua plena, eaedem refractiones animadvertantur, quae in aquae guttis, sphaerae formam habentibusGa naar voetnoot7). Sciendum vero quod quantumvis tenui existente lamina vitrea duae tamen ejus sunt superficies, totidemque propterea fiunt refractiones ac proinde laminam ejusmodi ut valde crassam considerari posse, nec tamen ob hoc alios fieri refractionum angulos. | |||||||||||||||||||||||||||||||||||||
[pagina 126]
| |||||||||||||||||||||||||||||||||||||
Soit donc donnée une lame de ce genre, dont les deux surfaces, vues de côté, soient représentées par les lignes parallèles AB et DK [Fig. 98]; supposons que la même surface DK limite aussi un autre corps transparent placé au-dessous d'elle et doué d'un pouvoir réfringent moindre. Soit CB un rayon qui se meut dans l'air et qui, après avoir été réfracté, suivra à l'intérieur du premier corps transparent la direction BD. Ce rayon passe ensuite dans le corps transparent inférieur et prend la direction DF; et, après avoir tiré BE et HDQ perpendiculaires aux surfaces DK et AB, on peut mener au rayon BC les parallèles DE et HP, BH étant parallèle à DF. Or, comme l'expérience enseigne que la droite DF, ou la droite BH qui lui est parallèle, forme avec CB un angle égal à celui qui serait formé par le rayon incident et le rayon réfracté si CB était réfracté directement par un corps transparent semblable à celui qui se trouve au dessous de DK, il est évident que BH est plus éloignée que BD de la perpendiculaire BE. L'angle HBE est donc plus grand que l'angle DBE, mais l'angle FDQ est égal à l'angle HBE, et l'angle BDH à l'angle DBE. Par conséquent, l'angle FDQ est aussi plus grand que l'angle BDH. Donc, le rayon BD qui vient du corps transparent le plus réfringent et qui pénètre dans celui qui réfracte moins fortement, s'écarte de la perpendiculaire DQ. Réciproquement, DB est le rayon réfracté qui provient du rayon FD venant du corps transparent le moins réfringent. Il paraît donc que ce rayon réfracté se rapproche de la perpendiculaire DH, vu qu'on a démontré que l'angle HDB est plus petit que l'angle QDF. Soit maintenant L:M l'indice de réfraction du corps transparent ABKD par rapport à l'air, et N:M celui du corps transparent qui se trouve au dessous de DK. Le rapport L:M diffère donc du rapport N:M par le rapport L:N, vu que . Il faut donc démontrer: sin FDQ: sin BDH = L:N. . Il faut donc démontrer: sin FDQ: sin BDH = L:N.
Donc, comme BD, à l'intérieur du corps transparent ABDK, est le rayon réfracté provenant du rayon CB, et que DE est tracée parallèlement à cette même CB et rencontre la perpendiculaire BE en E, le rapport BD:DE sera d'après la prop. IIGa naar voetnoot1) égal à l'indice de réfraction du corps transparent ABDK par rapport à l'air, c'est-à-dire égal à L:M. Pareillement, comme la droite BH, parallèle à DF, forme avec le rayon BC le même angle que si elle représentait le rayon réfracté, provenant de BC, lorsque ce rayon tombe sur un corps transparent semblable à celui qui se trouve au dessous de DK, et comme HP est parallèle à BC, le rapport BH:HP sera, d'après la même prop. Il, égal à l'indice de réfraction du corps transparent au dessous de DK par rapport à l'air, c'est-à-dire à N:M. D'où l'on tire, par conversion, PH:HB = M:N. Comme on a donc BD:DE = L::M, et DE (ou HP):HB = M:N, on obtient, en combinant ces deux équations, BD:BH = L:N. Mais comme DB est à BH, ainsi est le sinus de l'angle | |||||||||||||||||||||||||||||||||||||
[pagina 127]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 98.]
Sit igitur lamina hujusmodi, cujus duae superficies a latere inspectae, referantur lineis parallelis AB, DK [Fig. 98] ac superficies quidem DK eadem quoque terminet diversi generis subjectum diaphanum, quod minoris sit refractionis. Feratur autem in aere radius CB, cujus intra superius diaphanum refractio sit BD; inde vero inferiori se immittat secundum rectam DF; ductisque BE, HDQ, perpendicularibus ad superficies DK, AB, sint DE, HP parallelae radio BC; BH vero parallela DF. Quum igitur experimentum doceat rectam DF, sive ei parallelam BH, ita inclinari ad CB, uti inclinaretur ipsius CB refractio intra diaphanum simile ei quod sub DK; manifestum est BH minus ad perpendicularem BE accedere quam BD; hoc est, angulum HBE majorem esse angulo DBE, angulo autem HBE aequalis est FDQ, et angulo DBE aequalis BDH. Ergo et angulus FDQ major quam BDH. Radius igitur BD ex diaphano magis refringente in id quod minus refringit penetrans a perpendiculari DQ recedit. Est autem vicissim radij FD, ex diaphano minoris refractionis veniente, refractio DB. Ergo hanc ad perpendicularem DH accedere apparet, cum angulus HDB minor ostensus sit quam QDF. Sit jam proportio refractionis in aere diaphani ABKD, ea quae L ad M, diaphani vero sub DK ea quae N ad M. Excedit itaque ratio L ad M rationem N ad M, ratione L ad N; quandoquidem ratio L ad N addita rationi N ad M componit rationem L ad M. Quare ostendendum est sinum anguli FDQ esse ad sinum anguli BDH sicut L ad N. Quia ergo radij CB, intra diaphanum ABDK, refractio est BD, ipsi verò CB parallela ducta est DE, occurrens perpendiculari BE in E; erit ex prop. [II]Ga naar voetnoot1) ratio BD ad DE eadem quae refractiones metitur diaphani ABDK in aere constituti; hoc est, ea quae L ad M. Eadem ratione, cum BH parallela DF, ita inclinetur ad radium BC ac si esset ejus refractio in diaphanum simile ei, quod sub DK, incidentis; sitque HP ipsi BC parallela; erit ex eadem prop. [II] ratio BH ad HP similis ei quae refractiones metitur diaphani sub DK in aere existentis, hoc est ea quae N ad M. Unde et convertendo PH ad HB sicut M ad N. Cum sit igitur BD ad DE ut L ad M; DE vero sive illi aequalis HP ad HB ut M ad N; erit ex aequo BD ad BH ut L ad N. Sicut autem DB ad BH, ita sinus anguli DHB, ad sinum anguli HDB, sicut L ad N, quod erat ostendendum. | |||||||||||||||||||||||||||||||||||||
[pagina 128]
| |||||||||||||||||||||||||||||||||||||
DHB à celui de l'angle HDB. Ces deux sinus sont donc dans le rapport L:N; ce qu'il fallait démontrer. Il résulte de ces considérations que sous l'eau l'indice de réfraction du verre est égal à 9:8. En effet, si le corps transparent ABKD est en verre, on aura L:M = 3:2 ou = 9:6, parce que nous avons trouvé que telle est la grandeur de l'indice du verre par rapport à l'airGa naar voetnoot1). Mais l'indice de réfraction N:M du corps transparent sous DK sera, au cas que ce corps soit de l'eau, égal à 4:3Ga naar voetnoot2) ou à 8:6. D'où l'on tire L:N = 9:8. | |||||||||||||||||||||||||||||||||||||
Proposition XXVI.Expliquer la construction de l'oeil et la manière dont se fait la visionGa naar voetnoot3).  [Fig. 99.]
Après avoir bien réfléchi à ce que nous avons démontré à la proposition XXII, il ne serait pas absurde de supposer que l'oeil aurait pu être construit de la façon suivante. La figure d'un hémisphère aurait pu être donnée à sa partie extérieure ABC, laquelle doit être transparente partout, et le fond de l'oeil aurait pu avoir également la forme d'un hémisphère DEF, opposé au premier, mais concentrique avec lui, le rayon ME étant pris égal à trois fois le rayon MB du plus petit hémisphère; ensuite toute la cavité DABCFED aurait pu être remplie d'une humeur aqueuse. Car de cette façon les rayons émanant de points H, G, I quelconques faisant partie d'objets fort éloignés pourraient se réunir, après avoir été réfractés à la surface ABC, en autant de points de l'hémisphère concave DEF; ceux qui proviennent de G en E, ceux qui partent de H et de I en L et en K respectivementGa naar margenoot*. Mais comme la façon dont une surface sphérique rassemble les rayons n'est pas suffisamment parfaite, excepté seulement pour les rayons qui se meuvent dans le voisinage immédiat de l'axe il fallait remédier à cet inconvénient, ce qui pouvait fort bien se faire en couvrant toute la base AC du plus petit hémisphère à l'exception de la partie près du centre M, où il fallait laisser une ouverture de gran- | |||||||||||||||||||||||||||||||||||||
[pagina 129]
| |||||||||||||||||||||||||||||||||||||
 [Fig. 98.]
Ex his manifestum fit proportionem refractionis vitri sub aqua esse eam quae novem ad octo. Si enim diaphanum ABKD sit vitrum, erit L ad M ut 3 ad 2, sive 9 ad 6, quia hanc invenimus esse proportionem refractionis vitri in aereGa naar voetnoot1). Diaphani autem sub DK, siquidem aqua fuerit, refractionis proportio, hoc est N ad M, erit ea quae 4 ad 3Ga naar voetnoot2), sive 8 ad 6. Unde fit L ad N ut 9 ad 8. | |||||||||||||||||||||||||||||||||||||
[Propositio XXVI.]Oculi constructionem et quae sit videndi ratio explicareGa naar voetnoot3). PerpensisGa naar voetnoot4) quae superius Prop. [XXII] exposuimus, videatur hoc modo non absurde oculum fabricari potuisse; nempe hemisphaerij figuram tribuendo parti ejus exteriori ABC [Fig. 99], quae tota sit pellucida. fundum vero oculi alterum hemisphaerium faciendo DEF, priori oppositum, sed idem centrum habens, semidiametrum vero ME triplam ponendo semidiametri MB minoris hemisphaerij; ac totam deinde cavitatem DABCFED aqueo humore replendo. Hoc pacto enim radij, à quibuslibet rerum procul positarum punctis manantes ut H, G, I, fractique in superficie ABC, ad totidem puncta cavi hemisphaerij DEF collecti fuissent; nempe qui ex G in E, qui ex H in L, qui ex I in KGa naar margenoot*. Quoniam autem non satis perfecta est, quae fit a sphaerica superficie, radiorum collectio, nisi eorum tantum qui axi proximi incedunt; oportune remedium ei rei adhiberi poterat, obvelando totam hemisphaerij minoris basin AC, praeterquam circa centrum M, | |||||||||||||||||||||||||||||||||||||
[pagina 130]
| |||||||||||||||||||||||||||||||||||||
deur convenable. Car ceci vaut beaucoup mieux que de couvrir la surface extérieure ABC en laissant une ouverture autour du point B, vu qu' alors la sursace ABC n'aurait pas été aussi propre à recevoir les rayons venant des points H et I qu' à recevoir ceux qui viennent de G, tandis que, l'ouverture étant auprès de M, elle est également propre à recevoir tous les rayons nommés. De prime abord cette construction de l'oeil pourrait donc sembler convenable. Nous verrons cependant plus loin que la providence de l'auteur suprême y a sagement apporté quelques changements et y a aussi ajouté certaines choses nécessaires, quoique, en faisant cela, elle se soit servie de procédés si subtils qu'il ne nous est pas donné de comprendre son oeuvre dans tous ses détails. Le premier changement est le suivant. L'auteur suprême n'a pas voulu faire usage de tout l'hémisphère ABC; il en a conservé la partie supérieure, mais en a beaucoup ôté aux côtés, sans toutefois diminuer par là l'étendue du champ que l'oeil embrasse d'un seul regard. La raison qu'il avait pour ôter cette partie de l'hémisphère ABC était celle-ci: il voulait également enlever une partie de l'hémisphère DEF, en ramenant vers l'intérieur les points D et F et leur entourage, et il désirait de cette façon donner à l'oeil une forme qui se rapprochât le plus possible de la forme sphérique. Car il voulait que l'oeil fût mobile et pût tourner de tous les côtés dans la cavité qui le contient. Il lui donna donc une forme extérieure telle qu'elle a été indiquée dans la deuxième figure ci-jointe [Fig. 100], laquelle représente l'oeil humain coupé par un plan passant par l'axe. Les dimensions de toutes les parties y ont été doublées pour les rendre mieux visibles. Dans cette figure la partie transparente de la cornée est ABC; le reste AXYC, qui compose la tunique extérieure de l'oeil, est de plus faible courbure et opaque. Au dedans de cette tunique les anatomes en distinguent deux autres, dont l'intérieure est appelée rétine; elle est formée d'un tissu de fibres extrêmement fines du nerf optique VT, et présente une couleur blanchâtre auprès du fond KEL de l'oeil. Il faut savoir de plus que l'auteur a rempli la cavité de l'oeil non pas d'un seul fluide, mais de trois fluides différents; dont celui qui est contenu dans l'espace ABCFNORDA est tout-à-fait fluide, tandis que celui qui se trouve dans l'espace DRPNFLKD est un peu plus épais comme l'albumine d'un oeuf. Quant au troisième qui forme une petite lentille RONP adhérente au deuxième fluide et attachée par des filaments DR, NF, étendus tout autour d'elle, il est en quelque sorte dur, comme du blanc d'oeuf bouilli, mais en même temps parfaitement transparent comme les deux autres. Il diffère aussi de ces deux autres par son indice de | |||||||||||||||||||||||||||||||||||||
[pagina 131]
| |||||||||||||||||||||||||||||||||||||
ubi foramen modicum relinquendum erat. Hoc enim multo melius quam si exterior superficies ABC contegatur, relicto circa B foramine; quia tunc superficies ABC non aequè benè comparata fuisset ad excipiendos radios a punctis H et I venientes atque ad illos ex G, ad quos omnes nunc eodem modo sese habet, facto foramine ad M. Haec igitur oculi constructio non aliena primà fronte censeri posset: in qua tamen aliqua prudenter mutasse summi opificisGa naar voetnoot1) providentiam, aliqua etiam necessario addidisse, deinceps videbimus, etsi adeo subtili ratione in his versata sit, ut non in omnibusGa naar voetnoot2) artificium ejus assequi liceat. Ac primum quidem non totum hemisphaerium ABC adhibere voluit, sed, retenta parte superiori, circa latera multum abstulit, nequeGa naar voetnoot3) eo tamen spatium quod uno obtutu visus comprehendit angustius effecit. Causa autem auferendi erat ut et hemisphoerij DEF partes circa D et F introrsum reduceret, atque ita oculum ad sphaerae rotunditatem, quatenus id fieri posset, formaret. Volebat enim mobilem esse ut inGa naar voetnoot4) cavo quo continetur quaquaversum convolvi
possetGa naar voetnoot4). Figuram igitur exteriorem dedit hujusmodi qualem schema hoc alterum exhibet [Fig. 100], quod oculum hominis per axem dissectum refert, duplicata omnium magnitudine quo clarius pateant.
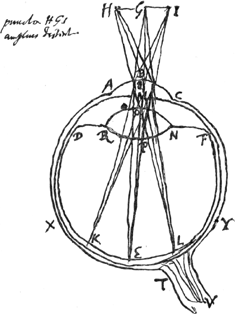 [Fig. 100.]
Hîc corneae pars pellucida est ABC reliqua majoris sphaeraeGa naar voetnoot5) et opaca AXYC, quae exteriorem oculi tunicam componit. Intra hanc duas alias anatomici distinguunt, quarum intima ex tenuissimis nervi optici VT fibris contexta, ac circa fundum oculi KEL albescens, retina dicitur. Caeterum cavitatem oculi non uno liquore, sed tribus inter se diversis complevit; quorum qui spatio ABCFNORDA continetur plane fluidus est, qui vero spatio DRPNFLKD paulo crassior instar ovi albuminis. tertius autem qui lenticulam constituit RONP, secundo liquori adhaerentem, et filamentis, DR, NF circum undique extentis affixam, durus quodammodo, sicut albumen igni coctum; verum pellucidus plane, uti reliqui duo. Differt autem ab illis etiam refractione, quam aliquanto majorem habet, unde | |||||||||||||||||||||||||||||||||||||
[pagina 132]
| |||||||||||||||||||||||||||||||||||||
réfraction, qui est un peu plus grand; d'où il résulte que les rayons venus du dehors des points H, G, I et qui convergeaient déjà après avoir été réfractés à la surface ABC de la cornée, souffrent de nouveau une faible réfraction aux deux surfaces de la lentille OP. Cette réfraction les fait converger encore un peu davantage, de telle manière qu'ils forment l'image des points H, G, I d'où ils sont venus en autant de points L, E, K situés au fond de l'oeil. Et il est possible que cette seconde réfraction produite par la lentille RN suffise pour donner aux rayons une direction telle que la surface concave KEL puisse servir à recevoir l'image des objets. Si cette réfraction n'existait pas, la surface KEL devrait faire partie d'une sphère plus grande telle qu'elle a été représentée dans la figure précédente. Mais il existait une autre raison plus forte pour faire usage de cette lentille: il fallait rendre l'oeil capable de distinguer les objets lointains aussi bien que les objets situés à faible distance; laquelle propriété faisait défaut à cet oeil imaginé par nous, dont nous avons parlé plus haut. Or cela peut être obtenu de deux manières; d'abord en diminuant la distance entre la surface de la cornée et la dite lentille lorsque nous voulons regarder des objets situés à faible distance; et en second lieu en donnant à la lentille une forme un peu plus convexe; ou aussi en combinant les deux moyens. S'il est vrai que la lentille se rapproche de la cornée, ce mouvement doit être le résultat d'une pression exercée par les muscles sur les surfaces latérales de l'oeil et en même temps sur le liquide vitreux auquel la lentille RN adhère, comme nous l'avons dit. MaisGa naar voetnoot1) si nous admettons que la lentille change de forme et devient plus convexe lorsque nous regardons des objets rapprochés, il semble qu'il faut en chercher la cause dans une détente des filaments DR, NF due à la pression exercée sur l'oeil par les muscles: la tension de ces filaments, agissant partout sur la lentille, lui donnalt auparavant une forme plus plate. Mais, comme je l'ai déjà dit, il est possible aussi que les deux causes agissent simultanément. De plus, la providence a placé la pupille M non pas, comme nous l'avons fait plus haut, au centre de la surface convexe ABC, mais un peu plus près d'elle. La raison de ce déplacement nous semble incertaine. Il est possible toutefois que ce changement ait pu contribuer aussi quelque peu à rendre la surface KEL de la rétine, possédant sa courbure actuelle, apte à recevoir les images, tandis que autrement elle aurait dû faire partie d'une plus grande sphère. Je trouve que le diamètre AL de la sphère entière est environ la douzième partie d'un pied de LeydeGa naar voetnoot2) | |||||||||||||||||||||||||||||||||||||
[pagina 133]
| |||||||||||||||||||||||||||||||||||||
fit ut radij, qui extrinsecus a punctis H, G, I, venientes, atque in corneae superficie ABC fracti, jam convergebant, exiguam iterum refractionem patiantur in utraque lentis OP superficie; qua quidem paulo magis adhuc convergunt, atque ita ut in totidem punctis L, E, K, in fundo oculi referant illa, unde venerunt,
 [Fig. 100.]
puncta H, G, I. Ac fortasse quidem, secunda illa refractione in lente RN, ita radij diriguntur ut recipiendae rerum picturae apta jam sit cavitas superficiei KEL, quae alioqui e majori sphaera esse deberet, sicut in priori figura efficta fuit. Verum et alia major fuit necessitas adhibendae lentis hujus, nempe ut ejus auxilio aeque ad res longinquas, ac in proximo sitas, oculus adaptaretur; quod in nostro illo superius exposito oculo deerat. Hoc autem fieri potest duobus modis, ut vel accedat propius ad corneae superficiem dicta lens cum res prope positae contuendae sunt, vel ut in formam paulo convexiorem colligatur; vel etiam ut utrumque accidat. Quod si accedit ad corneam, id fieri oportet prementibus oculi latera musculis, atque una humorem vitreum cui lens RN inhaerere dicta est. At siGa naar voetnoot1) figuram mutare lens eadem dicatur, rotundiorque fieri cum ad res prope admotas respicimus, videtur presso à musculis oculo remitti filamenta DR, NF, quae prius undique eam tendentia planiorem efficiebant. Potest autem, ut jam dixi, et utrumque horum simul fieri. Porro pupillae M locum, non ita ut nos supra, in centro convexitatis ABC statuit, sed propius paulo illi admovit, incertum qua de causa, nisi quod et hoc aliquid facere potest, quo superficies retinae KEL, ea qua nunc est cavitate, apta sit recipiendis imaginibus, cum alioqui amplioris sphaerae esse debuisset. Diametrum sphaerae totius AL invenio unciam circiter esse pedis nostri LugdunensisGa naar voetnoot2), | |||||||||||||||||||||||||||||||||||||
[pagina 134]
| |||||||||||||||||||||||||||||||||||||
qui est a peu près le même que l'ancien pied des RomainsGa naar voetnoot1); et que le diamètre de la sphère dont la cornée ABC fait partie est égal à ⅗ pouce. Quant à la pupille M, sa largeur n'a pas de dimension fixe: en effet, comme tout-lemonde peut s'en assurer par l'expérience, cette largeur est d'autant plus grande que la lumière qui éclaire l'oeil a une moindre intensité, et la vue d'un objet vivement éclairé suffit pour causer sa contraction. Le même phénomène se passe lorsque nous tâchons de regarder des objets placés près de l'oeil. C'est avec un art merveilleux que la pupille a été construite de manière à rester toujours ronde lorsque sa grandeur change. Mais l'examen de ces propriétés de l'oeil ne fait pas partiede notre plan. Nous tâcherons encore moins de répondre à la question de savoir comment l'image des objets visibles qui se forme au fond de l'oeil, parvient de là à notre cerveau et à notre esprit, comment, étant renversée, elle nous fait cependant voir les objets debout, et comment il se fait, qu'en regardant avec les deux yeux, nous ne voyons pas les objets doubles. D'ailleurs, toutes ces questions sont à mon avis trop obscures pour que des mortels, quels qu'ils soient, puissent en trouver la solution. | |||||||||||||||||||||||||||||||||||||
Proposition XXVII.Porter secours aux yeux des vieillards et des myopes à l'aide d'une lentille en verre. D'après l'explication que nous avons donnée de la construction de l'oeil et des conditions de la vision, il est facile de conclure ensuite en quoi la condition des yeux de ceux qui, comme les vieillards, ne voient distinctement que les objets éloignés, s'écarte de la condition ordinaire; et de même pour ceux qui ne distinguent que les objets fort rapprochés, savoir les myopes. Car comme le point de concours des rayons qui viennent d'un objet peu éloigné est nécessairement à plus grande distance de la surface extérieure de l'oeil que celui de ceux qui viennent d'un point fort distant, une image parfaite d'un objet fort distant et celle d'un objet peu éloigné ne pourront être formées dans le même oeil à moins que celui-ci ne soit doué de la faculté de pouvoir changer quelque peu la forme ou la position du liquide crystallin, et de s'ajuster de cette manière tantôt aux objets rapprochés tantôt aux objets éloignés. C'est pourquoi il est certain que ceux dont les yeux sont également bons pour toutes les distances, ont reçu des yeux qui possèdent cette propriété. Mais les yeux des vieillards, et aussi ceux de bien des gens qui ne sont pas encore âgés, sont plus rigides et moins mobiles à l'intérieur; chez eux, seuls les rayons qui viennent de loin ou pour le moins d'une distance de deux ou trois pieds, se réunissent exactement sur la surface intérieure au fond de l'oeil. Au contraire les myopes, autrement dit ceux qui ont la vue | |||||||||||||||||||||||||||||||||||||
[pagina 135]
| |||||||||||||||||||||||||||||||||||||
qui pene idem est ac vetus RomanorumGa naar voetnoot1); unciae vero tres quintas habet diameter convexitatis corneae ABC. Pupillae M latitudo certam mensuram non habet; est enim, uti quivis experiendo explorare potest, major cum minor lux oculo affulget: soloqueGa naar voetnoot2) lucidae rei aspectu contrahitur, vel item cum ea quae prope oculo admoventur intueri conamur. Insigni autem artificio ita fabricata est ut, mutata magnitudine, semper sibi constet rotunditas. Sed in haec inquirere non est nostri instituti, multoque minus quomodo quae in fundo oculi pictura visibilium formatur, inde ad cerebrum mentemque nostram perferatur, cumque inversa sit rectas tamen res nobis videri faciat, utque oculis duobus, non tamen duplices. quae et obscuriora omnia arbitror, quam ut mortalium ulli pervestigari queant. | |||||||||||||||||||||||||||||||||||||
[Propositio XXVII].Senum et myopum oculis auxilium comparare lente vitrea. Ex hisGa naar voetnoot3) quae de constructione oculi ac videndi ratione explicuimus, facile est porro colligereGa naar voetnoot4) quomodo affecti esse debeant oculi eorum qui tantum remota distincte cernunt, ut senes; vel qui tantum proxima, ut myopes. Cum enim radiorum e propinquo puncto venientium concursus necessario longius absit a summa oculi superficie quam eorum qui a longe remoto adfluunt, non poterit et longinquae rei et propinquae in eodem oculo perfecta imago depingi, nisi ea facultate praeditus sit ut humoris crystallini vel figuram vel situm aliquatenus immutare possit, atque ita nunc ad has nunc ad illas res se accommodet. Quare quibus ad omnia aeque oculi valent, ijs tales obtigisse certum est. Senibus vero ac multis quoque citra senectutem rigidiores sunt, parumque intus mobiles, quibus proinde tantum qui à longinquo veniunt radij, aut certe à duorum vel trium pedum intervallo, accuratè in fundo oculi coguntur. At myopes seu luscitiosi propinqua omnia, | |||||||||||||||||||||||||||||||||||||
[pagina 136]
| |||||||||||||||||||||||||||||||||||||
faible, voient clairement tous les objets rapprochés pourvu qu'ils ne soient pas à une distance supérieure aux deux tiers d'un pied et même moins, d'où il suit qu'ils peuvent peut-être accommoder un peu la forme de leurs yeux aux distances diverses des objets visibles, mais non pas jusqu'au point de réunir en un même point de la rétine des rayons incidents parallèles ou venant d'un objet situé à grande distance. Mais, à cause d'une trop grande convexité, ils réunissent ces rayons avant qu'ils n'aient atteint le fond de l'oeil. Et ce qui rend la vérité de ces propositions manifeste, c'est précisément le fait que le défaut, tant des uns que des autres, peut être corrigé en approchant de l'oeil des lentilles d'une certaine forme. Car une lentille concave diminue la trop grande convexité chez le myope, l'oeil du presbyte au contraire est corrigé par une lentille convexe. Pour trouver la forme la plus efficace des lentilles pour les yeux de chaque homme, il faut d'abord examiner la constitution de ces yeux et la mesure de leur défaut. C'est ce qu'on peut faire de la façon suivante. Si l'on veut porter secours à un vieillard, il faut éloigner lentement de ses yeux un objet visible quelconque, jusqu'au moment où il commence à l'apercevoir distinctement et sans effort, et noter cette distance, parce qu'elle détermine avec certitude la constitution de sa vue. Car si l'on a trouvé une longueur AB [Fig. 101] pour la dite distance et que celui auquel cette distance se rapporte et qui est placé en A, tâche de voir un point C plus rapproché; il arrivera bien que, lorsqu'il dirige le regard de ses deux yeux vers C, un petit changement a lieu à l'intérieur d'eux par rapport à la disposition qui leur servait à regarder au loin, mais néanmoins ils ne parviendront à voir distinctement que les objets situés à la distance AB. Il leur faut donc une lentille qui, placée devant l'oeil, change la direction des rayons qui viennent du point C de telle manière qu'ils semblent provenir du point B. Prenons donc un point O tel qu'on ait BC:CA = CA:CO. Alors la distance entière AO sera le rayon de la surface d'une lentille en verreGa naar voetnoot5) de forme symétrique qui satisfait au problème. Et toute lentille de forme quelconque ayant AO pour distance focale y satisfera également. En effet, comme on a, en vertu de la construction, CO:CA = CA:CB, et que CO et CB sont situées du même côté du point C, tandis que O est le foyer de la lentille située en A, il s'ensuit de la proposition XXGa naar voetnoot6) que les rayons qui émanent du point C, sont réfractés par la lentille en A de telle manière qu'ils semblent provenir du point B. C'est pourquoi, pour l'oeil dont nous parlons, chaque objet éloigné à une distance AC sera clairement aperçu à l'aide de lentilles de ce genre. D'autre part, s'il faut construire pour un myope une lentille qui lui permette de bien discerner les objets éloignés, il suffit de chercher la plus grande distance à laquelle il voit distinctement un objet qu'on approche de lui; cette distance sera précisément la longueur du rayon de la surface sphérique en forme de laquelle il | |||||||||||||||||||||||||||||||||||||
[pagina 137]
| |||||||||||||||||||||||||||||||||||||
dummodo non ultra certum terminum, puta pedis duas tertiasGa naar voetnoot1) aut etiam minus, recesserint, distinctè conspiciunt; unde parumper forsanGa naar voetnoot2) formam oculorum accommodare possunt diversis visibilium distantijsGa naar voetnoot3), sed non eousque ut radios parallelos, sive a procul dissita re venientes, in retina ad punctum colligant. Sed ob nimiam convexitatem ante eos colligant quam ad oculi fundumGa naar voetnoot4) pervenerint.
 [Fig. 101.]
Et haec quidem ita se habere eo ipso manifestum est, quod vitium utrumque, admotis oculo certae figurae lentibus, emendari potest. Myopi enim nimiam convexitatem minuit lens cava, presbytis vero convexa contraria ratione medetur. Quarum itaque lentium figura ut cujusque oculis quam aptissima inveniatur, primùm constitutio eorum et defectus quantitas hoc modo exploranda est. Si seni auxilium quaeratur, visibile aliquod paulatim ab oculis ejus removere oportet, quo ad primum distincte illud absque incommodo suo cernat; atque eam distantiam signare, quia visus constitutionem certo determinat. Si enim dicta distantia sit inventa AB [Fig. 101], atque is ad quem pertinet positus in A, conetur videre punctum propinquum C; fiet, dirigendo oculum utrumque ad C, ut simul utrique intrinsecus quidem aliquantum mutentur ab ea dispositione quam habebant ad longinqua conspiciendum, sed hoc tantummodo consequentur ut distincte contueantur ea quae sunt ad distantiam AB. Itaque lente ejusmodi opus est, quae oculo admota radios ex C puncto venientes inflectat quasi veniant ex B. Sit igitur ut BC ad CA ita CA ad CO. Eritque tota AO semidiameter superficiei lentis vitreaeGa naar voetnoot5) utrinque aequaliter convexae, quae propositum efficiet. Vel idem quoque efficiet lens quaevis quae focum seu punctum concursus parallelorum habebit ad distantiam AO. Quia enim, ex constructione, CO est ad CA ut CA ad CB; suntque CO et CB ad eandem partem puncti C; O vero punctum concursus parallelorum lentis in A; sequitur ex propos. [XX]Ga naar voetnoot6) radios a C puncto manantes, post refractionem in lente A, ita flecti ac si venirent ex B. Quare oculo illi quem diximus, cuncta intervallo AC remota, ejusmodi lentium ope distincte percipientur. Rursus si myopi comparandum sit conspicillum quo longinqua perfecte discernat, quaerenda est tantum distantia maxima, ex quaGa naar voetnoot7) visibile admotum videat | |||||||||||||||||||||||||||||||||||||
[pagina 138]
| |||||||||||||||||||||||||||||||||||||
faut construire les deux surfaces concaves de la lentille en verre. Ou, si l'on désire qu'elle soit concave d'un côté seulement et plane de l'autre, il faut que le rayon de la surface concave soit la moitié du rayon précédent. Car chacune de ces lentilles, placée devant son oeil, aura pour effet de réfracter les rayons incidents parallèles (car on estime parallèles les rayons qui viennent de points fort éloignés) de telle manière qu'ils semblent provenir du foyer de la lentille, dont la distance à l'oeil sera précisément celle à laquelle il voit distinctement, comme cela résulte des propositions XV et XVIIGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||
Proposition XXVIII.Trouver une lentille en verre qui permette de voir clairement aux personnes placées sous l'eau. Il est certain que ni les poissons tirés de l'eau ni les autres animaux submergés dans l'eau ne peuvent voir distinctement quoi que ce soitGa naar voetnoot2). Car quant aux yeux de ces derniers, vu que le liquide aqueux qui se trouve au-dessous de la cornée possède environ le même indice de réfraction que l'eau, comme cela a été trouvé par expérience, il s'ensuit nécessairement que, lorsqu'ils sont submergés, aucune réfraction des rayons incidents ne se produit à l'entrée de l'oeil. Le fait que le pouvoir réfringent de la cornée elle-même a une valeur différente, n'a aucune influence car puisque ses deux surfaces sont parallèles, et qu'elle se trouve entre deux milieux transparents de même pouvoir réfringent, elle transmettra tous les rayons sans changement de direction appréciable. Par conséquent, les rayons qui, lorsque l'oeil se trouvait hors de l'eau, étaient réfractés à la surface de la cornée et se dirigeaient de là en convergeant vers le liquide crystallin, atteindront maintenant ce dernier en suivant des routes parallèles; et le pouvoir réfringent du liquide crystallin ne sera pas suffisant pour les amener, comme d'habitude, à se réunir au fond de l'oeil, mais leur point de concours sera situé plus loin: de là la vision confuse. D'autre part dans l'oeil des poissons il y aura hors de l'eau une forte réfraction à la surface extérieure, réfraction qui sous l'eau était nulle ou du moins beaucoup plus faible, et ainsi dans leurs yeux le concours des rayons aura lieu avant que ceux-ci n'aient atteint le fond. Il en résulte qu'ils ne pourront rien voir si ce n'est confusément. Mais pour corriger la vision d'un homme sous l'eau, il faut trouver une lentille qui, placée devant l'oeil, transmette les rayons au liquide crystallin en les faisant converger autant que lorsqu'ils ont été réfractés à la surface extérieure de l'oeil chez ceux qui se trouvent en-dehors de l'eau. Ce problème est facile à résoudreGa naar voetnoot4), vu que nous savons que l'indice de réfraction du verre par rapport à l'eau a la valeur 9/8 (en effet, cet indice est le pro- | |||||||||||||||||||||||||||||||||||||
[pagina 139]
| |||||||||||||||||||||||||||||||||||||
distinctè, atque ea ipsa erit longitudo semidiametri sphaerae secundum quam ab utraque parte lentem vitream excavare oportet. Vel si ab altera tantum parte cava, ab altera plana desideretur oportet ejus cavitatis semidiameter sit prioris subdupla. Quaevis enim harum lentium oculo admota efficiet ut radij incidentes paralleli (tales enim censentur a longinquis punctis venientes) inflectantur tanquam venirent a puncto dispersus, cujus distantia ab oculo erit eadem, quae illi distincte videndi mensura erat, ut apertum est ex propos. [XV et XVII]Ga naar voetnoot1). | |||||||||||||||||||||||||||||||||||||
Propositio [XXVIII].Lentem vitream invenire qua sub aquis positi distincte videant. Certum est nec pisces ex aqua extractos, nec animalia caetera sub aquam demersa, distinctè quidquam cernere posseGa naar voetnoot2). In horum namque oculis, quoniam humor aqueus, qui corneae tunicae subjacet, fereGa naar voetnoot3) eandem aquae refractionem habet, sicut experientia compertum est, necesse est sub aquam mersis nullam in primo oculi introitu fieri radiorum extrinsecus incidentium refractionem. nec refert quidem an corneae ipsius refractio diversa sit, quia cum duabus superficiebus constet parallelis, atque utrimque aequalis refractionis diaphano tangatur, radios omnes quasi rectos transmittet. Radij itaque qui, oculo extra aquam posito, ad corneae superficiem refracti, inde jam convergentes tendebant ad humorem crystallinum, ij nunc in eum paralleli deferentur; neque sufficiet humoris crystallini refractio ad cogendos eos in fundo oculi, sicut solet, sed ulterius situm erit eorum concursus punctum, unde videndi confusio. Piscibus autem, extra aquam, magna continget in exteriore oculo refractio, quae sub aquis vel nulla erat, vel certe multo minor. Atque ita in eorum oculis concursus radiorum fiet antequam ad fundum pervenerint, unde nihil nisi confuse conspicere eos posse consequitur. Caeterum hominis visus sub aqua ut emendetur, ejusmodi lens invenienda est, quae oculo admota radios aeque convergentes ad humorem crystallinum transmittat, atque a supersicie oculi exteriore venire solent extra aquam agentibus. Quod quidem facileGa naar voetnoot4) est, cum refractionis vitri sub aqua sciamus eam esse proportionem | |||||||||||||||||||||||||||||||||||||
[pagina 140]
| |||||||||||||||||||||||||||||||||||||
duit de l'indice du verre par rapport à l'air, qui a la valeur 3/2, et de l'inverse de l'indice de l'eau par rapport à l'air qui a la valeur ¾. Car cela s'accorde avec l'expérienceGa naar voetnoot1) et aussi avec la théorie physique que nous avons exposée dans le Traité de la LumièreGa naar voetnoot2). Suivant cette théorie, le rapport de la vitesse de la lumière dans l'eau à celle dans l'air étant pris égal à ¾, et celui de la vitesse dans l'air à la vitesse dans le verre à 3/2, il faut conclure que la vitesse dans l'eau est à celle dans le verre comme 9 est à 8), et que nous connaissons le rayon de courbure de la cornée à l'endroit où elle est transparente. En effet, c'est une partie d'une surface sphérique dont le diamètre est égal à ⅗ pouce de notre pied ou du vieux pied romain, comme nous l'avons indiqué dans la description de l'oeilGa naar voetnoot3). Soit donc AC [Fig. 102] la surface convexe extérieure de l'oeil, et AB son rayon. Admettons que l'indice de réfraction du liquide aqueux est égal à celui de l'eau, c'est-à-dire 4/3Ga naar voetnoot5). Si nous prenons donc BD égale à trois fois le rayon AB, il est certain que les rayons parallèles, l'oeil étant hors de l'eau, sont réfractés de telle manière à la surface AC qu'ils doivent se réunir après avoir parcouru la distance ADGa naar voetnoot7). Mais lorsque l'oeil est submergé, aucune réfraction ne se produit à la surface AC; il faut donc placer devant cette surface une lentille en verre qui par sa [Fig. 102.]
réfraction sous l'eau puisse réunir au point D les rayons parallèles à l'axe AB. Soit FAK cette lentille ayant une surface plane tandis que l'autre, qui doit être à fort petite distance de l'oeil, est convexe et a un rayon HA. Si donc par cette lentille les rayons incidents parallèles sont réunis au point D, le rapport HD:DA sera égal à l'indice de réfraction, comme cela résulte de la prop. XIVGa naar voetnoot8). Or cet indice, celui du verre placé dans l'eau, est égal à 9/8. Par conséquent HD:DA = 9:8, et, par partage, HA:AD = 1:8. Mais DA:AB = 4:1 ou == 8:2. Donc, en combinant les deux proportions, HA::AB = 1:2. Or, AB était de 3/10 pouce. Par conséquent HA est de 3/20 pouce, et la forme de la lentille FAK est donc connue. Mais si, au lieu d'elle, nous en désirons une autre G également convexe des deux côtés, il paraît que ses deux surfaces auront la même convexité que la surface AC de la cornée; c'est-à-dire qu' elles feront partie d'une sphère ayant un diamètre de ⅗ pouce.
FIN DU PREMIER LIVRE. | |||||||||||||||||||||||||||||||||||||
[pagina 141]
| |||||||||||||||||||||||||||||||||||||
quae 9 ad 8 (quae nempe componitur ex proportione refractionis vitri in aere, quae est 3 ad 2, et aquae in aere inversa, quae est 3 ad 4. Hoc enim cum experientiae consentitGa naar voetnoot1), tum rationi physicae, quam in libro de LuceGa naar voetnoot2) exposimus. Quandoquidem posita celeritate lucis in aqua ad celeritatem ejus in aere, sicut 3 ad 4; itemque celeritate in aere ad celeritatem in vitro, sicut 3 ad 2, sequitur celeritatem in aqua ad celeritatem in vitro esse ut 9 ad 8) cumque et corneae tunicae qua diaphana est, convexitatem cognitam habeamus. Est enim sphaericae superficiei portio cujus diameter 3/5 unciae pedis nostratis seu Romani veteris, ut in oculi descriptione annotavimusGa naar voetnoot3). Sit jam igiturGa naar voetnoot4) AC [Fig. 102] exterius oculi convexum cujus semidiameter AB. et ponatur ratio refractionis humoris aquei eadem quae est aquae, id est, 4 ad 3Ga naar voetnoot5). Igitur sumptaGa naar voetnoot6) BD triplâ semidiametri AB, certum est radios parallelos, oculo extra aquam posito, ita flecti ad superficiem AC ut cogantur ad distantiam ADGa naar voetnoot7). Demerso autem oculo nulla ad AC fit refractio; quare opponenda ibi est lens vitrea quae refractione sua sub aqua, radios parallelos axi AB colligat in puncto D. Sit ea lens FAK, superficie una plana, altera vero, quae proxime oculo admoveatur, convexa semidiametro HA. Si igitur hac lente radij paralleli colliguntur ad punctum D, habebit HD ad DA proportionem refractionis, ut constat ex propos. [XIV]Ga naar voetnoot8). Est autem proportio haec, refractionis nempe vitri sub aqua, quae 9 ad 8. Itaque HD ad DA ut 9 ad 8. et dividendo HA ad AD ut 1 ad 8. Sed DA est ad AB ut 4 ad 1, sive ut 8 ad 2. Ergo, ex aequo HA ad AB ut 1 ad 2. Erat autem AB 3/10 unciae. Ergo HA 3/20 unciae, atque ita nota jam est forma lentis FAK. Quod si vero in locum ejus aliam desideremus uti G aequaliter utrinque convexam, apparet ejus superficies utrasque ejusdem fore convexitatis cujus est corneae superficies AC. hoc est è sphaera cujus diameter habeat unciae 3/5.
[FINIS PRIMI LIBRI.] |
|