Oeuvres complètes. Tome VIII. Correspondance 1676-1684

N^o 2193.
G.W. Leibniz à Christiaan Huygens.
Appendice au No. 2192.

La pièce se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek et par G.J. Gerhardt¹⁾.

J'ay trouué quelques Elemens d'une nouuelle characteristique tout a fait differente de l'Algebre et qui aura des grands avantages pour representer à l'esprit exactement et au naturel quoyque sans figures tout ce qui depend de l'imagination, L'Algebre n'est autre chose que la characteristique des nombres indeterminés ou des grandeurs. Mais elle n'exprime pas directement la situation, les angles, et le mouuement: d'ou vient qu'il est souuent difficile de reduire dans un calcul ce qui

1) Uylenbroek l'a séparée de la lettre et imprimée dans le Fasciculus II (pp. 6 et suiv.) de sa publication.
Consultez, sur l'écriture de cette lettre, la note 19 de la lettre précédente. Nous avons rigoureusement conservé, dans notre texte, l'orthographe et la ponctuation du manuscrit, quoique les points, qui, sans règle, suivent les lettres majuscules se rapportant aux figures, n'ayent aucune signification.

[p. 220]

est dans la figure et qu'il est encor plus difficile de trouuer des demonstrations et des constructions geometriques asses commodes lors meme que le calcul d'Algebre est tout fait. Mais cette nouuelle characteristique suivant des figures de veue ne peut manquer de donner en même temps la solution et la construction et la demonstration Geometrique; le tout d'une maniere naturelle, et par une analyse, c'est a dire par des voyes determinées. l'Algebre est obligée de supposer les Elemens de Geometrie, au lieu que cette caracteristique pousse l'analyse jusqu'au bout: si elle estoit achevée de la maniere que je la conçois on pourroit faire en caracteres qui ne seront que des lettres de l'alphabet la description d'une machine quelque composée qu'elle pourroit estre, ce qui donneroit moyen à l'esprit de la connoistre distinctement et facilement avec toutes les pieces et même avec leur usage et mouuement, sans se servir de figures ny de modelles et sans gêner l'imagination: et on ne laisseroit pas d'en avoir la figure presente dans l'esprit autant que l'on se voudroit faire l'interpretation des caracteres. On pourroit faire aussi par ce moyen des descriptions exactes des choses naturelles comme par exemple des plantes et de la structure des animaux et ceux qui n'ont pas la commodité de faire des figures, pourveu qu'ils ayent la chose presente deuant eux ou dans l'esprit se pourront expliquer parfaitement, et transmettre leur pensees ou experiences a la posterité ce qui ne se sçauroit faire aujourdhuy, car les paroles de nos langues ne sont pas assés arrestées ny asses propres pour se bien expliquer sans figures. Mais c'est la moindre utilité de cette caracteristique, car s'il ne s'agit que de la description il vaudra tousjours mieux quand on en peut et veut faire la depense d'avoir les figures et mesme les modelles, ou plustost les originaux des choses. Mais l'utilité pricipale consiste dans les consequences et raisonnemens qui se peuuent faire par les operations des caracteres qui ne se sçauroient exprimer par des figures (et encor moins par des modelles) sans les trop multiplier ou sans les brouiller par un trop grand nombre de points et de lignes: d'autant qu'on seroit obligé de faire une infinité de tentatives inutiles: au lieu que cette methode meneroit seurement et sans peine. je croy qu'on pourroit manier par ce moyen la mecanique presque comme la geometrie et qu'on pourroit mesme venir jusqu'à examiner les qualites des materiaux, par ce que cela depend ordinairement de certaines figures de leur parties sensibles. Enfin je n'espere pas qu'on puisse aller asses loin en Physique avant que d'avoir trouuer un tel abrege pour soulager l'imagination. car nous voyons par exemple quelle suite de raisonnemens geometriques est necessaire pour expliquer seulement l'arc en ciel: qui est un des plus simples effects de la nature par ou nous pouuons juger combien de consequences seroient necessaire pour penetrer dans l'intieur des mixtes dont la composition est si subtile que le microscope qui en découure bien plus que la centmillieme partie ne l'explique pas encor assés pour nous aider beaucoup. Cependant il y a quelque esperance d'y arriver en partie, quand cette analyse veritablement Geometrique sera établie. Mais comme je ne remarque pas que quelque autre ait jamais eu la même pensée ce qui me fait craindre quelle ne

[p. 221]

se perde si je n'ay pas le temps de l'acheuer. J'adjouteray icy un essay qui me paroist considerable et qui suffira au moins à rendre mon dessein plus croyable et plus aisée à concevoir, afin que si quelque hazard en empeche la perfection a present, cecy serve de monument a la posterite et donne lieu a quelque autre d'en venir a bout.

Or il est constant qu'il n'y a rien de plus important dans la Geometrie que la consideration des lieux: c'est pourquoy j'en exprimeray quelques uns des plus simples par cette maniere de caracteres. Les lettres de l'Alphabet signifieront ordinairement les points des figures. Les premiers lettres comme A.B. exprimeront les points donnés; les derniers, comme X. Y les points demandés. Et au lieu qu'on se sert des égalités ou equations dans l'algebre, je me sers icy des congruités que j'exprime par ce caractere: ȣ. par exemple dans la premiere figure ABC ȣ DEF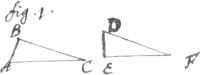



veut dire qu'il y a de la congruite entre les deux triangles ABC et DEF suivant l'ordre des points; qu'ils peuuent occuper exactement la même place, et qu'on peut appliquer ou mettre l'un sur l'autre sans rien changer dans ces deux figures que la place ainsi en appliquant D sur A, et E sur B. et F sur C les deux triangles (estans posés égaux et semblables) seront manifestement coincidents. Mais sans parler des triangles, on en peut dire autant en quelque façon des points sçavoir ABC. ȣ DEF dans la seconde figure; c'est à dire on pourra mettre en mesme temps A sur D et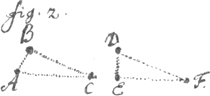



B sur E et C sur F. sans que la situation des trois points ABC entre eux ny des trois points DEF entre eux soit changée supposant les trois premiers joints par quelques lignes inflexibles (droites ou courbes, n'importe:) et les trois autres de même: apres cette explication des caracteres, voicy les lieux. Soit A ȣ Y dans la fig. 3. c'est a dire soit un point donné A. on demande le lieu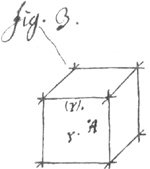



de tous les point Y ou (Y) etc. qui ont de la congruite avec le point A. je dis que le lieu de tous les Y sera l'espace infini de tous costés, car tous les points du monde ont de la congruité entre eux: C'est à dire l'un se peut tousjours mettre à la place de l'autre. Or tous les points du monde sont dans un même espace. On peut aussi exprimer ce lieu ainsi: Y ȣ .(Y). tout cela est trop manifeste, mais il falloit commencer par le commencement.

Soit (dans la figure 4) A.Y. ȣ A. (Y) le lieu de tous les Y. sera la surface de la sphere dont le centre est A et

[p. 222]

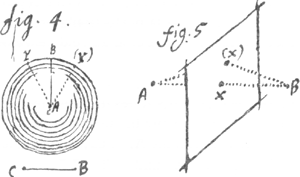le rayon AY tousjours le meme en grandeur ou égal à la donnée AB ou CB c'est pourquoy on peut aussi exprimer le mesme lieu ainsi A.B ȣ AY ou C.B. ȣ A.Y.

Soit (dans la 5 figure) A.X. ȣ B.X. le lieu de tous les X sera le plan deux points A et B estant donnés, on demande un troisieme X qui ait la mesme situation à l'egard du point A, qu'il a à l'égard du point B. [c'est a dire que A.X soit egale ou (par ce que toutes les droites egales sont congruentes) congruente à B.X. ou que le point B se puisse appliquer au point A gardant la mesme situation qu'il avoit à l'égard du point X] je dis que tous les points X. (X) d'un certain plan seul continué à l'infini satisferont à la question car comme A.Y²⁾ ȣ B.Y²⁾. de mesme A. (Y)²⁾ ȣ B(Y)³⁾. Mais il n'y en aura point qui satisfasse hors de ce plan. C'est pourquoy ce plan continué à l'infini sera le lieu commun de tous les points du monde qui sont situés à l'egard de A comme à l'egard de B [il s'en suit que ce plan passera par le milieu de la droite AB, qui luy est perpendiculaire].

Soit dans la 6 fig. A.B.C. ȣ ABY le lieu de tous les Y sera la circulaire. C'est à dire il y a trois points donnés, A.B.C. on demande un quatriême Y qui a la même situation que C. à l'egard de A.B. je dis qu'il y a une infinité de points qui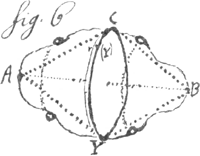



peuuent satisfaire et le lieu de tous ces points est la circulaire. Cette description ou definition de la ligne circulaire ne presuppose pas le plan, (comme celle d'Euclide) ny mêmes la droite. Cependant il est manifeste que son centre est D au milieu entre A et B. on pourroit aussi dire ainsi. A.B.Y. ȣ .A.B.(Y) car alors le lieu seroit un cercle mais qui ne seroit pas donné. C'est pourquoy il faut adjouter un point donné l'on se peut imaginer que les points AB demeurant fixes et que le point C. attache à eux par quelques lignes inflexibles (droites ou courbes) et par consequent gardant la même situation à leur egard soit tourné à l'entour de A.B pour décrire la circulaire C.Y. (Y) On peut juger par là que la situation d'un point à l'egard d'un autre peut estre conçue sans exprimer la ligne droite pour veu on les conçoiue joints par quelque ligne que ce soit. Et si la ligne

2) Lisez: X.

2) Lisez: X.

2) Lisez: X.

3) Lisez: (X).

[p. 223]

est posée inflexible la situation des deux points entre eux sera immutable. Et deux points peuuent estre conçus avoir la même situation entre eux que deux autres points, si les uns peuuent estre joints par une ligne qui puisse estre congrue avec la ligne qui joint les autres. Je dis cecy à fin qu'on voye que ce que j'ay dit jusqu'icy ne depend pas encore de la ligne droite (dont je vay donner la definition) et qu'il y a difference entre A.C situation de A et C entre eux et la droite AC.

Soit (dans la 7 figure). A.Y ȣ .B.Y.ȣ.C.Y.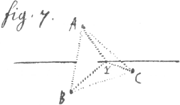



le lieu de tous les Y sera la droite. C'est à dire trois points estants donnés; On demande un point Y qui a la mesme situation à l'egard de A. qu'il a à l'egard de B et qu'il a à l'égard de C. Je dis que tous ces points tomberont dans la droite infinie. Y. (Y) si tout estoit dans un même plan, deux points donnés suffiroient pour determiner ainsi la droite.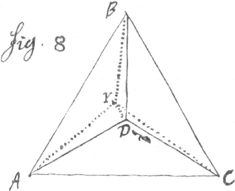

Soit enfin dans l'huictieme figure A.Y. ȣ BY. ȣ .C.Y ȣ .D.Y. le lieu sera un seul point. car on demande un point Y qui ait la mesme situation à l'égard de quatre points donnes A.B. C D c'est à dire que les droites A.Y.B.Y.C.Y.D.Y⁴⁾ soient égales entre elles et il n'y a qu'un seul qui puisse satisfaire.

Ces mesme lieux se peuvent exprimer en plusieurs autres façons mais celles cy sont des plus simples et des plus fecondes et peuvent passer pour des definitions. Et pour faire voir que ces expressions servent au raisonnement, je monstreray par les caracteres avant que de finir ce qui est produit par l'intersection de ces lieux: premierement l'inter section de deux surfaces spheriques est une ligne circulaire. Car puis que l'expression de la circulaire est A.B.C. ȣ A.B.Y. nous aurons A.C. ȣ A.Y. et B.C. ȣ .B.Y dont les lieux sont deux surfaces spheriques l'une ayant le centre A et le rayon A.C. l'autre de⁵⁾ centre B et le rayon BC. De mesme l'inter section d'un plan et de la spherique est une ligne circulaire⁶⁾. Car l'expression d'une spherique est A.C. ȣ A.Y. et celle d'un plan est A.Y. ȣ .B.Y et par consequent A.C. ȣ B.C. par ce que le point C est un des points Y: or B.C estant ȣ A.C et A.C estant ȣ A.Y nous aurons

4) Lisez: AY, BY, CY, DY.

5) Lisez: le.

6) Les deux dernières phrases ont été omises par mégarde dans la publication de Gerhardt.

[p. 224]

B.C ȣ A.X et A.Y estant ȣ B.Y. nous aurons⁷⁾ B.C ȣ .BY. joignons ces con gruités et nous aurons.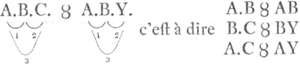

Or A.B.C ȣ A.B.Y est à la circulaire donc l'intersection d'un plan et d'une surface spherique donne la circulaire. Ce qu'il falloit demonstrer par cette sorte de calcul. de la même façon il paroistra que l'inter section de deux plans est une droite. car soyent deux congruités, l'une, A.Y. ȣ B.Y pour un plan, l'autre A.Y. ȣ C.Y pour l'autre plan, nous aurons A.Y ȣ B.Y. ȣ C.Y dont le lieu est la droite. Enfin l'inter section de deux droites est un point car soit AY. ȣ B.Y. ȣ C.Y et B.Y ȣ C.Y. ȣ D.Y nous aurons A.Y. ȣ B.Y. ȣ C.Y. 8 .DY.

Je n'ay qu'une remarque à adjouter, c'est que je voy qu'il est possible d'entendre⁸⁾ la caracteristique jusqu'aux choses qui ne sont pas sujettes à l'imagination: mais cela est trop important, et va trop loin pour que je me puisse expliquer la dessus en peu de paroles⁹⁾.

7) Les mots ‘B.C .A. X et A.Y, estant ȣ B.Y. nous aurons’ sont intercalés en marge par Leibniz lui-même.

8) Lisez: étendre.

9) En bas de la dernière page. Chr. Huygens a noté: quadrature arithm. équation x^x - 24 ∞ o. niveau. Dioptrique.