Oeuvres complètes. Tome VI. Correspondance 1666-1669

N^o 1622.
E. Mariotte à Christiaan Huygens.
Appendice au No. 1621.
[janvier 1668].

La pièce se trouve à Leiden, coll. Huygens.
Elle a été publiée dans Mariotte Oeuvres T.H.

Du mouuement des pendules. Premier principe naturel.

Vn mesme poids fait le commencement de sa descente auec vne mesme vistesse en quelque lieu accessible de l'air qu'on le laisse tomber.

Ce principe se prouue par experience et doibt estre admis comme on admet

[p. 179]

dans les mechaniques que les cordes des balances sont parallelles a cause de la grande distance de la surface de la terre a son centre, quelle que soit la cause du mouuement vers le centre.

2^e principe naturel.

Si vn corps est porté d'vne vistesse vniforme par vn petit espace par quelque cause que ce soit, ceste cause cessant il continuera son mouuement de mesme part auec la mesme vistesse par vn espace esgal au premier s'il n'est point empesché par vne autre cause.

Ce principe est accordé par Descartes et Galilée, et il est facile de le prouuer par experience, nous appellerons ceste puissance par laquelle le corps continue son mouuement puissance acquise ou mouuement acquis.

Premiere proposition.

Jl est jmpossible qu'vn poids qu'on laisse tomber dans l'air continue sa descente auec vne vistesse vniforme, mais il acquiert a chasque moment esgal de temps, vn nouueau degré esgal de vistesse.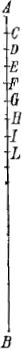

Soit AB vne ligne perpendiculaire a vn plan horisontal diuisee en plusieurs petites parties esgales es points C, D, E, F, G, H, I &c. et qu'ayant laissé tomber vn poids du point de repos A il descende d'vne vistesse vniforme s'il se peut jusques au point C, par sa puissance naturelle de descendre vers le Centre de la terre, en vn certain temps que nous appellerons vn moment, donc par le 2^e principe naturel il continuera sa descente auec la mesme vistesse par l'espace CD, et dans le 2^e moment de temps esgal au premier il arriueroit au point D par sa puissance acquise, encor que la puissance naturelle de descendre l'eut abandonné au point C, mais parce qu'il la conserue tousjours esgale en quelque lieu qu'il soit de la ligne AB par le premier principe, dans ce 2^e moment de temps il parcourra par ceste puissance vn autre petit espace esgal a AC, donc par ces deux puissances ensemble il passera les deux petits espaces CD, DE au 2^e moment et par les mesmes raisons dans le 3^e moment il ira de E en G par la puissance acquise puisqu'au moment precedent il est descendu de C en E et par la puissance naturelle qui ne le quitte point, il descendra encor en ce 3^e moment vn espace esgal a AC par le premier principe, donc dans ce 3^e moment il paruiendra au point H et ainsy de suitte cest a dire que si au 1^er moment il passe

[p. 180]

l'espace AC au 2^e il passera le double de AC au 3^e le triple au 4^e le quadruple &c. donc sa vistesse augmentera a proportion des temps de sa descente, et si on entend que la ligne AB soit diuisée en de plus petites parties a l'jnfiny, et le temps aussy a l'jnfiny ceste acceleration de mouuement sera enfin vniforme, et la vistesse augmentera a proportion des temps, ce qui estoit a prouuer.

2^e proposition.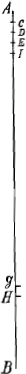

Soit AB vne perpendiculaire qu'vn poids ayt passée dans vn certain temps tombant du point de repos A et que ce poids estant arriué au point B change de direction et remonte vers le point A commencant son mouuement de bas en haut selon la vistesse acquise au point B je dis qu'il remontera jusques au point A et que le temps de sa montée sera esgal a celuy de sa descente. Car soit supposé le temps de sa descente estre diuisé en 10 moments esgaux, et la ligne AB en 55 parties esgales entre elles et que le poids passe la 1^ere au premier moment par vne vistesse vniforme, donc par ce qui a esté dit en la precedente au 10^e moment il passera en descendant 10 de ces petites parties, mais en remontant au 11^e moment auec la mesme vistesse il passera aussy 10 de ces petites parties par la puissance acquise par le 2^e principe, et par la puissance naturelle il en descendroit vne dans ce mesme 11^e moment qui sera le 1^er de la montée, donc par les 2 puissances ensemble le poids ne remontera que 9 parties cest a dire que si B g est esgale a 10 de ces parties et g H a vne, le poids ne montera en ce 1^er moment que jusques au point H et dans le 2^e moment deuant parcourir 9 de ces parties par la puissance acquise, il n'en parcourra que 8 a cause que la puissance naturelle de descendre luy en ostera vne en ce 2^e moment et ainsy des autres espaces; donc la progression des espaces ou petites parties esgales de sa montée au 1^er, 2^e, 3^e, 4^e moment &c. sera 9, 8, 7, 6, 5 &c. et au lieu d'en passer 2 au 9^e moment, il n'en passera que vne et enfin debuant monter vne de ces petites parties au 10^e moment par la puissance acquise, et en descendre vne par la puissance naturelle dans le mesme 10^e moment ces deux puissances s'effaceront precisement l'vne l'autre et le dernier terme de la montée sera au 9^e moment. donc le temps de la montee du poids estant de 9 moments et celuy de sa descente de 10, leur difference sera 1/10 et la descente estant de 55 parties telles que B g en est 10 la montée ne sera que de 45 cest a dire enuiron ⅕ moins que la descente, mais si le temps est supposé diuisé en 100 moments et la ligne AB en 5050 parties esgales et que le poids au 1^er moment passe par vne vistesse vniforme vne de ces parties en descendant, il parcourra les 5050 parties dans les 100 moments, mais parce que nous venons de dire le temps de la montée deffaudra d'vn de ces 100 moments et lespace deffaudra de 100 de ces petites parties

[p. 181]

cest a dire enuiron 1/50 de toute la ligne AB, que si ceste diuision de temps et d'espace est continuée a l'jnfiny, ces deffautz diminueront toujours et en fin la difference des temps sera moindre qu'aucun moment de temps donné et celle des espaces moindre qu'aucune grandeur donnée cest a dire comme rien, donc le poids remontera jusques au point ou il a commencé sa descente &c. ce qui estoit a prouuer.

Jl sensuit de ceste proposition que si on jette en l'air perpendiculairement vn poids comme vne balle de plomb, le temps de sa montée depuis le point ou il quitte la main jusques au point de repos, et celuy de sa descente jusques au point ou il a quitté la main seront esgaux et que la vistesse de la balle diminuera vniformement en montant jusques a son repos a proportion des temps de la montée.

3^e proposition.

Soit AB vne ligne perpendiculaire qu'vn poids ayt passée en descendant du point de repos A. comme il a esté demonstré dans les propositions precedentes, et qu'au mesme temps quelque autre mobile parcoure la ligne CD esgale a AB par vne vistesse vniforme je dis que ceste vistesse sera esgale a la moitié de la vistesse acquise par le poids au point B.

Car soit supposé le temps de la descente par AB estre diuisé en 100 moments esgaux et la ligne AB en 5050 parties esgales et que le poids passe la 1^ere moment par vn mouuement vniforme, par ce qui a esté dit en la 1^ere paroposition le poids parcourra au 50^e moment 50 de ces parties et 100 au 100^e et l'aggregé de toutes ces parties sera 5050, nombre esgal a 50 auec le produit de 50 par 100, mais si pendant chacun de ces moments l'autre mobile parcourt en la ligne CD 50 de ces parties par vne vistesse vniforme ceste vistesse sera esgale a la moitié de la vistesse acquise par le mouuement acceleré au point B de la ligne AB puisqu'au dernier moment de la descente le poids a parcouru 100 de ces parties, et l'aggregé des parties parcourues dans les 100 moments par ceste vistesse vniforme sera esgal au mesme produit de 100 par 50 cest a dire 5000 et la difference des espaces passez par ces 2 mobiles en mesme temps sera 50 qui est 1/100 de tout l'espace passé par le mouuement vniforme, mais si le temps est supposé estre diuisé en 1000 moments et la ligne AB en 500500 petites parties esgales &c. on monstrera par les mesmes raisons que les espaces parcourus par le mouuement acceleré et par l'vniforme seront differents de 1/1000 et si on diuise le temps et la ligne AB en de plus petites parties ceste difference diminuera tousjours, donc si elles sont diuisées a l'jnfiny ceste difference sera en fin comme rien et les 2 mobiles dont l'un descend par vn mouuement acceleré jusques au point B et l'autre se meut par vne

[p. 182]

vistesse vniforme esgale a la moitié de celle acquise au point B passeront en temps esgaux les 2 lignes esgales AB, CD, donc &c. ce qui estoit a prouuer.

proposition 4^e.

Si vn poids passe en descendant des espaces jnesgaux en diuers temps, les espaces passez seront l'vn a l'autre en raison doublée des temps de leur descente.

Soit la ligne AB, dont la partie AC soit passée par vn poids descendant du point de repos A dans le temps DE et toute la ligne AB dans le temps DE je dis que comme le quarré de DE est au quarré de DF ainsy l'espace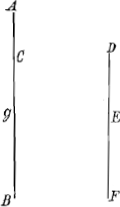



AC est a l'espace AB. Car soit supposé comme dans les propositions precedentes le temps DE estre diuisé en 10 moments esgaux et l'espace AC en 55 parties esgales dont le poids en passe vne auec vne vistesse vniforme au 1^er moment donc par la 1^ere proposition il en passera 10 au 10^e et si DF est double de DE le temps DF sera composé de 20 de ces moments et au 20^e moment il parcourra 20 petites parties esgales a celles de AC, donc l'aggregé de toutes les parties passees dans le temps DF sera esgal au produit de 10 par 20 auec 10 et celuy des parties passées dans le temps DE sera esgal a 5 auec le produit de 5 par 10, or ces produits sont nombres semblables donc ils sont l'vn a l'autre en raison doublée de leurs costez homologues scauoir 10 et 20 ou DE, DF, mais dautant que le nombre 10 adjousté au premier produit n'est pas au nombre 5 adjousté au dernier en raison doublee de 10 a 20 mais en la simple raison de DE a DF, l'aggregé des parties passees dans le temps DF sera moindre que le quadruple des parties de AC et la difference sera 10 scauoir 1/21 de toute la ligne passée dans le temps DF, mais si on suppose les temps et les espaces estre diuisez a l'jnfiny, la proportion de ceste difference diminuera tousjours comme il a esté monstré cy dessus et en fin sera comme rien, donc AB passé dans le temps DF sera quadruple de AC lorsque l'acceleration du mouuement sera vniforme, on fera la mesme preuue, si DF est supposée triple ou quadruple de DE ou en quelque autre raison, donc &c. ce qui estoit a prouuer.

Jl sensuit que si on prend Ag moyenne proportionnelle entre AC, AB, que comme AC a Ag ainsy le temps par AC au temps par AB.

5^e proposition.

Soit BC vne ligne horisontale CA perpendiculaire a BC et AB jnclinée, je dis que

[p. 183]

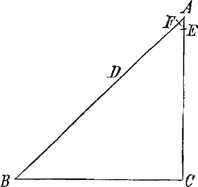si on laisse tomber vn mesme poids du point A que le temps de sa descente par AB sera au temps de sa descente par AC comme AB est a AC car d'autant que la pesanteur totale du poids est a sa pesanteur sur la ligne jnclinee AB comme AC a AB²⁾, et que la pesanteur n'est autre chose qu'vne puissance de descendre selon vne certaine vistesse, jl sensuit que si on entend que le poids descende auec vne vistesse vniforme vn trespetit espace comme AE en la ligne AB³⁾ pendant vn certain moment de temps et que dans le mesme moment vn autre poids esgal parcoure d'vne vistesse vniforme l'espace AF dans la ligne AB, que comme le poids en AB est a son poids total par AC ainsy AF sera a AE, si donc on entend AC estre diuisée en plusieurs parties esgales a AE et qu'il y ait en AB vn esgal nombre de parties dont chacune soit esgale a AF et que l'aggregé de ces parties soit AD, AD sera a AC comme AF a AE cest a dire comme le poids en AB a son poids total, ou comme AC a AB, et par ce qui a esté dit dans les precedentes le temps par AD sera esgal au temps par AC puis qu'en autant de moments jnfiniment petits que l'espace AC sera parcouru, AD le sera aussy, mais par la 4^e proposition ou sa suitte, comme AB a AC moyenne proportionnelle entre AB et AD ainsy le temps par AB au temps par AD, et le temps par AD est esgal au temps par AC, donc le temps par AB sera au temps par AC, comme AB a AC, je dis encor que la vistesse acquise au point B est esgale a la vistesse acquise au point C. car par la 1^ere proposition comme le temps par AD au temps par AB cest a dire comme AD a AC ainsy la vistesse en D a la vistesse en B, mais aussy comme nous venons de monstrer la vistesse en D est a la vistesse en C comme AD a AC ou AF a AE car la vistesse en C est autant multiple de celle en E comme celle en D de celle en F, donc la vistesse en D a mesme raison aux vistesses en C et en B, donc ces 2 dernieres sont esgales ce qu'il falloit prouuer.

2) Lisez: comme AB à AC.

3) Lisez: AC.

6^e proposition.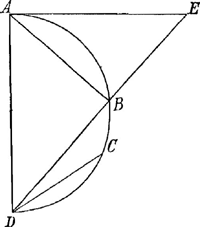

Soit ABD vn demy cercle et deux jnscrites BD, CD et soit AD le diametre perpendiculaire a la tangente horisontale AE, je dis que des poids esgaux descendants de B en D et de C en D auront les temps de leur descente esgaux. Car soient tirées les lignes AB et DBE donc les triangles EDA, ADB seront equiangles et par consequent comme ED a DA ainsy DA a DB donc par la suitte de la 4^e proposition comme ED a AD ainsy le temps par ED du repos en E au temps par BD du repos

[p. 184]

en B, mais par la precedente comme ED a DA ainsy le temps par ED au temps par AD donc le temps par ED a mesme raison au temps par BD et au temps par AD donc ces deux derniers temps seront esgaux, on prouuera de mesme que le temps par CD est esgal au temps par AD, donc les temps par BD et par CD seront esgaux ce qui estoit a prouuer.

7^e proposition.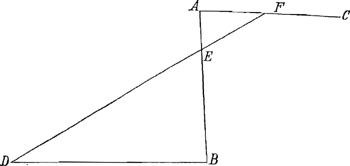

Soit AB perpendiculaire a l'horison AC, BD perpendiculaire a AB et AE le quart de la ligne et soit FED quelconque ligne entre les 2 parallelles AC, BD, je dis que le temps par FE, EB sera esgal au temps par AE, ED, mais si AE est moindre que le quart de AB le temps par AE, ED sera plus grand que par FE, EB, mais si AE est plus que le quart le temps par FE, EB sera le plus grand. Car estant prises Fg et AH⁴⁾ moyennes proportionnelles entre FE, FD et AE, AB, le temps par EB du repos en A ou en F sera EH par la 5^e proposition et par la 4^e, et celuy par ED sera Eg, or au 1^er cas AE sera esgale a EH et FE a Eg, donc FE, EH temps par FED⁵⁾ sera esgal a AEg temps par AED, au 2^e cas gE sera plus grande que EF et HE que EA et a cause de la similitude des triangles AFE, EBD gE sera a EF comme HE a EA, donc gE, EA ensemble, la plus grande et la plus petite, seront plus grandes que HE, EF ensemble, donc le temps par AED sera plus grand que par FEB et au 3^e cas par de semblables raisons FE, EH seront ensemble plus grands que AE, Eg, et par consequent le temps par FE, EB sera le plus grand, ce qui estoit a prouuer.

On prouuera le mesme si les 2 lignes AEB, FED sont toutes deux jnclinées, et l'on peut conclurre par ce qui est dit au 3^e cas qu'vn poids commencant sa descente par vne ligne perpendiculaire ou peu jnclinée et la finissant par vne beaucoup jnclinée fait le temps plus court que s'il commencoit et finissoit au contraire, si la perpendiculaire et l'jnclinée sont esgales et mesme quand la perpendiculaire et l'jnclinee seroient vn peu plus grandes, que l'jnclinee et la perpendiculaire.

4) Les points H et g, qui doivent se trouver sur les droites EB et ED, sur une droite parallèle à BD, ont été omis dans la figure du manuscrit.

5) Lisez: FEB.

[p. 185]

8^e proposition.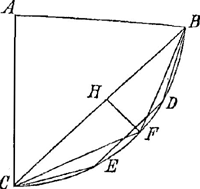

Soit ABC vn quart de cercle dont le centre soit A, et AC perpendiculaire a l'horison, BC costé du quarré jnscrit dans le cercle, BD, DE, EC trois costez du dodecagone et BF, FC 2 costez de l'octogone, je dis que le temps par BF, FC de suitte, sera plus court que par BC car estant tirée FH perpendiculaire a BC, BH moitié de BC est plus jnclinée que BF, mais HC est moins jnclinée que FC, et les 2 BF, FC ne sont a BC que comme 27 a 25 a peu pres, donc par ce qui a esté dit a la fin de la precedente le temps par BFC sera vraysemblablement plus court que par BC et par les mesmes raisons le temps par les 3 costez BD, DE, EC sera encor plus court, et si on reduit en nombres ces temps, on trouuera que si le temps par BC est 100000 celuy par BFC sera 93758 et celuy par BEFC⁶⁾, 93072 a peu pres d'ou lon peut conclurre que le temps par quatre soustendantes de suitte sera encor plus court et en fin que par la Circonference BC il sera le plus court de tous et pourroit estre au temps par BC comme 93 a 100 ou 13 a 14 a peu pres.

6) Lisez: BDEC.

Conclusion.

Dans toutes les propositions precedentes on fait abstraction de la resistance de l'air, mais estant supposée comme elle le doibt estre pour rendre raison de ce qui nous paroit dans le mouuement des pendules &c. voicy ce qu'on en peut dire, si le poids de la pendule est de bois et que la resistance de lair augmente le temps de sa descente par l'arc de 90 degrez d'vn 1 1/7, si le poids est de plomb ceste augmentation de temps sera moindre et encor moindre s'il est d'or, et parce qu'vn arc d'vne seconde ou d'vne tierce est pris ordinairement pour auoir mesme jnclination et mesme grandeur que sa corde a cause de leur trespetite difference, si le temps par le costé du quarré est 100000, celuy par l'arc dvne tierce sera aussy 100000 puisque par sa corde il est esgal a 100000 par la 6^e proposition, donc le temps par l'arc de 90 degrez sera a celuy par l'arc d'vne tierce comme 12 a 13 selon la proposition precedente si on fait abstraction de la resistance de l'air, mais l'air resistant plus aux grands mouuements qu'aux petits, la resistance de l'air au poids qui se meut par l'arc d'vne tierce sera comme rien donc si par tout l'arc, de 90 degrez ceste resistance augmente le temps d'vn ⅛, le temps qui estoit 12 sera 13½ et le temps par l'arc d'vne tierce sera encor 13 puisque la resistance de l'air ne le change point et par consequent le temps des grandes vibrations et celuy des plus petites, sera comme 27 a 26, mais si le poids est d'or et que la resistance de l'air n'augmente le temps de sa cheute par 90 degrez que d'vn 1/13 les grandes et les peti-

[p. 186]

tes vibrations seront esgales, mais soit que le poids soit de bois ou de plomb &c. les vibrations par vn arc de 30 degrez et au dessous seront sensiblement esgales; et pour les poids qui tombent librement vers le centre si le principe de leur mouuement est esgal pres et loin du centre, il augmentera sa viste sse jusques au point ou la resistance de l'air esgalera ce 1^er principe de mouuement, ou puissance naturelle de descendre et de ce point il continuera jusques au centre auec vne vistesse vniforme et passera au dela aussy loin qu'est lespace depuis le point de repos jusques au point de l'vniformité du mouuement s'il y auoit vne ouuerture pleine d'air jusques aux antipodes que si ceste puissance est comme celle du fer a l'esgard de l'aymant, qui est plus forte plus l'aymant est proche, le poids augmentera sa vistesse au commencement de sa cheute comme au cas precedent jusques a vn point au de la du quel sa vistesse commencera a deuenir sensiblement vniforme quoy qu'elle s'augmente tousjours vn peu jusques au centre, et en fin si la 1^ere puissance est comme celle des cordes de lut ou des ressorts qui est plus forte loin du repos que pres, la vistesse augmentera comme cy dessus au commencement de la cheute jusques a vn point d'ou elle commencera a diminuer peu a peu jusques au centre &c. ce qui est facile a prouuer.

Jl est encor tres facile de prouuer par la 4^e et par le commencement de ceste conclusion que si les longueurs des pendules sont entre elles, comme nombre quarré a nombre quarré et qu'on prenne leur moyenne proportionnelle que le nombre des vibrations de la petite pendule sera au nombre de celles de la grande en mesme temps comme la moyenne proportionelle a la plus petite pendule du moins si les vibrations se font par des arcs moindres que 30 degrez.