Oeuvres complètes. Tome VI. Correspondance 1666-1669

N^o 1600.
[Buot]¹⁾ à Christiaan Huygens.
août 1667.

La pièce se trouve à Leiden, coll. Huygens.

1) Cette pièce est écrite de la main de Buot.

L'obseruation faite par Messieurs Huguens, Picart, Buot et Richer²⁾. Pour trouuer l'Inclination des plans de l'anneau de ♄. auec le plan de lequateur et auec le plan de l'Ecliptique.

Le 15 aoust 1667. sur les 11. heures du soir, ♄ fut enuiron le meridien, lors que la teste d'Andromede estoit distante du Zenith de 49. 50′.

2) Jean Richer mourut à Paris en 1696. Il était un des cinq jeunes gens qui furent adjoints aux Académiciens en 1666 pour les aider dans leurs travaux, et se rendit en 1671 à Cayenne afin d'y faire diverses observations: il obtint un grand succès et revint en 1674. Il observa aussi le retard du pendule sous l'équateur. Après son retour de ce voyage, dont sa santé avait beaucoup souffert, il se retira et depuis ne vint que rarement aux séances de l'Académie.

[p. 144]

♄ fut obserué parallele a lhorison, lors que Andromede estoit distante du Zenith de 40. 55′.

Au temps de cette derniere obseruation ∠ du vertical de ♄. auec la meridienne vers loccident estoit de 13^o26′.20″. Si on se pouuuoit asseurer de cette obseruation, ou lobseruateur tenoit vn de ses aplombs a la main, qui est sujette a varier et qui oblige a tenir loeil trop proche du filet; car les costez comprenant ∠ estant de 3000. la base auoit 702. dont la moitié 351, la quelle donne pour le sinus du demy angle du sommet 11700, auquel repond 6.43′10.″ dont le double fait ∠ requis de 13.^o.26.′20.″

Lascension droitte du chef d'Andromede est^3)	358.^o 0.′ 0.″
Sa declinaison septentrionale^4)	27. 17.
Le lieu du Soleil	22. 47. ♌.
Son ascension droitte	145. 9.
Le lieu de ♄	27. 2. ♑.
Sa latitude Meridionale	0. 21.
Son ascension Droitte	299. 10.
Sa declinaison meridionale	21. 9. 40.
La difference des ascensions du ☉ et de ♄ est	154. 1. 0.
Ou repond pour lheure quon pretend auoir obserué ♄ au meridien	10.h.16.′ 4.″

3) L'ascension droite de α Andromède était en 1667: 358^o 49′.

4) La déclinaison de α Andromède était en 1667: 27^o 15′.

Examen de la mesme heure par la hauteur d'Andromede.

les 3. costez du Δ a resoudre, sont la distance du pole au Zenith	41.^o 7.′
la distance d'Andromede au pole 62. 43. et la distance d'Andromede au Zenith. obseruée tres justement de 49. 50.′ par lesquels on trouue pour la distance d'Andromede au meridien	59.^o 9. 0.
quil faut oster de lascension droitte de la mesme Andromede	358. 0.
et reste pour lascension droitte du MC	298. 51.
dou ostant lascension droitte du lieu du ☉	145. 9.
reste la distance du soleil au meridien passée depuis le midy precedent	153. 42.
ou repond pour lheure juste quand ♄ estoit au meridien	10.h.12.′ 3.″

Scauoir 4′. 1.″ dheure plustost que lobseruation par les filets.

[p. 145]

Calcul de lheure au temps de la 2. obseruation.

au Δ a resoudre les 3. costez donnez sont la distance du pole au Zenith 41. 7.′ la distance d'Andromede au pole 62. 43. et la distance obseruée dAndromede au Zenith 40. 55. par lesquels on trouue pour la distance dAndromede au meridien 45^o. 28′. a oster de son ascension droitte 358. 0.′ et reste lascension droitte du MC	312. 32.′
dou ostant lascension droitte du ☉	145. 9.
reste la distance du ☉ au meridien	167. 23.
ou repond 11 heures 9′. 32.″ pour lhure de lobseruation.

Examen de lobseruation de lazimuth de ♄ occidental. au temps de ceste 2. obseruation.

Lascension droitte du MC. est par la precedente	312. 32.
lascension droitte de ♄ Occidental est	299. 10.
donc la distance de ♄ au meridien vers l'occident est	13. 22.

et partant au Δ PZ ♄ ou son opposé pz ♄ nous auons pz. 41. 7., p♄. complement



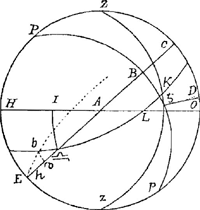de 21. 9. 40″. scauoir de la declinaison B ♄ auec ∠ p. 13. 22.″ distance de ♄ au meridien et on demande ∠ ♄ zp.

Au Δ. rectangle ♄ Dp ∠ p. et lhypothenuse p♄. sont donnez et partant on trouue la base Dp. du 1^er Δ rectangle 68. 18.′ 10.″ a la quelle si on adjouste zp. 41. 7.′ on aura la base du 2e Δ. zD. 109. 25.′ 10.

Mais comme le sinus de la base du 2e. Δ zD /⁵⁾ Sinus de la base du 1^er pD. // la tangente de ∠ de la base p. du ie Δ / a la Tangente de ∠ de la base z. du 2. Δ.

Scauoir lazimuth de ♄. 13^o. 10′. 30″. plus petit que celuy qui a esté obserué par les filets de 15′. 50″ de degré, scauoir denuiron ¼ de degré.

Nous auons donc lascension droitte de MC. a 11 heures 9′. 32″ de 312.^o 32.′ d'ou ostant le quart occidental de lequateur CA. scauoir

90. 0.

5) Cette notation a / b // c / d désigne la même chose que a∶ b=c∶d.

[p. 146]

jl restera la descension oblique du point A	222. 30^6).
desquels ostant encore le demi Equateur dentre ♈ et ♎	180. 0.
restera larc de lequateur ♎ A	42. 32.
auec lequel, et auec leleuation du pole de Paris, on trouuera par calcul ou par les tables ∠ KLO. scauoir ∠ de l'ecliptique sur lhorison ou la hauteur du 90^e degré de lecliptique de	27. 51. 10.″
et le point de lEcliptique de lhorison occidental A^7) de	12. 5. ⇸
qui auec 3 signes, donne le 90e degré de lecliptique a	12. 5. ♓.
lieu de ♄ a oster	27. 2. ♃
reste larc de lEcliptique depuis ♄. jusques au 90e degré	45. 3.

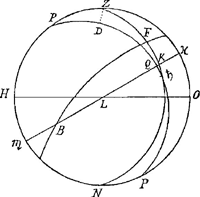C'est pourquoy dans cette figure ou HPZO. est le cercle nonagenaire, P. le pole de lEcliptique ♏ ♓, et Z et N. le Zenith et le nadir, qui sont les poles de lhorison. On à le Δ obliquangle PZ ♄. auquel PZ ∥⁸⁾ ♓ O. hauteur du 90^e degré est de 27. 51′. 10″. auec P♄. de 90. 21′. par ce quil est composé du quart PQ et de la latitude de ♄. de 0. 21′. auec ∠ compris P. mesuré par larc Q ♓ de 45″. 3′ et jl faut trouuer ∠ a ♄.

1^o au Δ PDZ rectangle en D. on a.

Comme le rayon / a la Tangente de PZ 27. 51. 10′.

// Sinus Complement de ∠ P. 45. 3′.

/ a la Tangente de la base PD. quon trouue de 20^o. 28′. 20″ qu'il faut oster de P ♄. 90. 21′. 0″. et reste la base du 2. Δ scauoir DQ⁹⁾. de 69. 52. 40″.

Mais comme le Sinus de la base du 2 Δ. / Sinus de la base du 1^er.

// la tangente de ∠ de la base du 1^er. Δ a la tangente de ∠¹⁰⁾ la base du 2 Δ. Ou repond 20. 27. 40″. pour ∠ a ♄.

Maintenant pour trouuer ∠ B. compris du plan de l'anneau sur le plan de lEcliptique. jl faut resoudre 1^nt. le petit Δ rectangle QHK¹¹⁾. auquel ∠ Q. est droit. ∠ ♄. est connu par la precedente de 20. 27′. 40″. auec ⊥¹²⁾ Q ♄. scauoir la latitude de ♄ 0. 21′. dou vient ∠ K. de 69. 32′. 20″. et la ⊥ KQ. de 7′. 50″.

6) Lisez: 32′.

7) Lisez: L

8) C'est le signe d'égalité.

9) Lisez: D♄

10) Intercalez: de

11) Lisez: Q♄K

12) Le signe ⊥ désigne la cathète.

[p. 147]

Mais par les donnez le plan de l'anneau coupe lEcliptique

en B. a 20. 30′. de ♍^13)	ou 5^s. 20^o. 30′.
Q longitude de ♄ 27. 2 ♑	ou 9. 27. 2
donc larc de lEcliptique BQ. est 126. 32′	4. 6. 32
au quel si on adjoute QK	7. 50″. on aura
pour tout BK	126. 39. 50″.

C'est pourquoy au Δ BFK. rectangle en F. par lobseruation du parallelisme du grand diametre de l'anneau a lhorison, nous auons lhypotenuse BK. 126. 39′. 50″. dont le supplement est 53. 20′. 10″. auec le supplement de ∠ BKF 69^o. 32. 20. et partant on trouue ∠ B. 32^o. 0′. pour ljnclination de lanneau sur lEcliptique.

Pour auoir ljnclination du plan du mesme anneau sur le plan de lequateur prenons dans la 1^re. figure le Δ h b ♎ au quel larc de lEcliptique b ♎. est 9. 30′. et ∠ ♎ 23. 31. et ∠ b supplement de ljnclination des plans de lecliptique et de lanneau 148. 0′. C'est pourquoy on trouue ∠ du sommet du 1^er. Δ rectangle d b ♎

de	66. 46′. 20″.
lequel osté de tout ∠ b	148. 0. 0.
Reste	81. 13. 40″.

pour ∠ du sommet du 2. Δ h b d. et ensin on trouue pour ∠ h. compris du plan de lanneau sur lequateur 9. 32. 50″.

13) Cette valeur de la longitude du noeud de l'anneau de Saturne est celle qui est indiquée par Huygens dans son Systema Saturnium. La longitude de ce noeud était en 1667 environ 15^o de ♍.