Oeuvres complètes. Tome IV. Correspondance 1662-1663

N^o 965.
W. Brouncker à Christiaan Huygens.
[janvier 1662.]
Appendice au No. 964.

La pièce se trouve à Leiden, coll. Huygens.

A Demonstration of the Equality of Vibrations in a Cicloid-Pendulum^a).

Imagine the Curve H X C¹⁾ to bee made vp of an infinite Number of equall sides or streight lines (as Hb, bd, df, &c.) so inclining that their perpendicular altitudes (ab, cd, ef, &c.) are in an arithmetical progression from an horizontall to a vertical position. I say first a bullet moving in such a Curve falls from all parts thereof in equall time. (as from f to H, b to H, d to H, x²⁾ to H, &c., all in the same

a) ℞ 7 Febr. 1662.
Demonstratio Domini Brouncker a Domino Moray missa Londino, qua nostrum inventum aequabilis motus in Cycloide probare conatus est, sed nihil effecit. Vitiosa enim est omnis haec argumentatio qua aequalia tempora descensus in exposita linea ostendere nititur, ipsa vero linea quin Cyclois sit non dubito, etsi et in hoc demonstrando aliquid peccatum sit. [Chr. Huygens.]

1) Consultez la planche ci-contre.

2) Lisez: X.

[p. *3]

[p. 29]

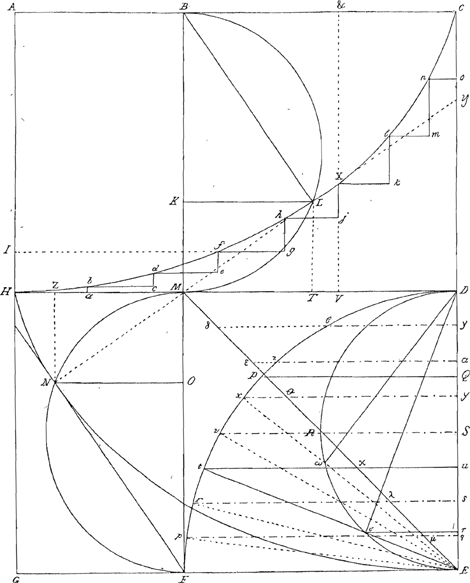
time.) for it passeth every following line or side in the same space of time yt it doth the first from whence it fell. (as being let fall from X, in the same time that it passeth from X to H³⁾, in the same it passeth from h to f, from f to d, from d to b, and from b to H.) Because the first velocity is alwayes in proportion to the distance. as Xh being the fifth side from H X, Xj is to ba as 5 to 1, and consequently the Bullets velocity at X being let fall there, is to the Bullets velocity at b, if thence let fall, as 5 to 1. and the retardation arising from the inclination of the following lines or sides, is still equall to the accelleration arising from the continuance of the motion. (as Xh having five degrees of velocity, hf has but foure because Xj is to hg as 5 to 4, and so one degree of velocity is lost by the greater inclination of the side hf: but because there is one moment of time past since the motion begun, when the Bullet is fallen to h from X, therefore one degree of velocity is acquired from that continuance of motion or second impulse; and therefore one degree onely being lost by the position of the side, and an other got in lieu thereof by the continuance of the motion; the velocity remaines still the same at h that it had at X, and the like of all the rest.) And so in a Circle the versed sines of small arches, equally increasing are so very neare that they may well bee said to have the proportion of squares; and therefore their differences as odd numbers, that is to encrease equally, or in an arithmeticall progression. And because the first difference, if the arches bee infinitely small, or lesse then any assignable quantity, is not onely absolutely, but in respect to those arches also, lesse then any assignable quantity or infinitely small, as is easie to demonstrate and hath been don already in my paper of recoyling. therefore after an infinite progression, as in the curve H X C, and not before, these differences do equally increase vnto an equallity with the first arch. And indeed this Curve is no other then what results from the continuance of that series vnto which at the beginning of thè quadrant (where the vibrations are at least physically equall) there is so great a neerenesse that in respect to themselves the difference is lesse then any assignable quantity.

I proceed therefore and say next that this Curve is a Cicloid: For in the triangle MDE, MD, & DE, being equall to DC and divided into as many equall parts Eq, qs, su &c, as there are sides in the Curve HXC and the Radiaus of the Quadrant DPF, which is also equall therevnto, divided in the same manner: the sides of the triangles Epq, Ers, Etu, &c. are proportionall to the triangles Hba, bdc, dfe, &c., and therefore pq. μq (=Eq.)∷ Ha. ab and rs. λs (=Es) ∷ bc. cd, &c. so of the rest. And therefore HI = ab + cd + ef. If = Ha + bc + de ∷ μq + λs + ϰu. pq + rs + tu that is, the number being infinit, HI the intercepted diameter is to If the ordinate ∷ as the respective triangle Eϰu, to the respective portion F tuE. And therefore AH. HI ∷ Δ EMD. Δ Eϰu. But

3) Lisez: h.

[p. 30]

Δ EMD. Δ Eϰu ∷ Ed × Ed⁴⁾. Eu × Eu. And Eu × Eu = ED × Eτ (ED. Eu. Eτ ∺⁵⁾ as will presently appeare) Therefore EMD. Eϰu ∷ ED × ED. ED × Eτ ∷ ED. Eτ. Therefore AH. HI ∷ ED. Eτ. But AH = ED. Therefore HI = Eτ. and Eu the side of the respective Δ is the meane proportionall between AH and HI.

Now because Eu is the meane proportionall between ED and Eτ; therefore Eτ × ½ ED equals the Δ Eϰu. And because DRE is a semicircle, therefore DσE is a rectangle Δ. And because DEt is an angle common to both Δ (DEσ and tEu;) and the hypothenuse of both are equall (tE = ED): therefore Dσ = tu and Eσ = Eu. therefore ED. Eσ = Eu. Eτ. are in continuall proportion (as was said above). And the two rectangle Δs DσE and tuE are equall. but the Δ DσE = σ τ × ½ ED; therefore the Δ tuE = στ × ½ ED. And because tF = the arch σ E; therefore tF × ½ ED = the arch σ E × ½ ED. but tF × ½ ED equals the Secter tEF; therefore the secter tEF = the arch σ E × ½ ED. Therefore the portion EFtu (= the secter tEF + Δ tuE) = the arch σ E × ½ ED + σ τ × ½ ED. therefore Δ Eϰu is to the portion EFtu, as Eτ × ½ ED is to σE × ½ ED + στ × ½ ED ∷ Eτ. σ E + σ τ. But Eτ = HI the intercepted Diameter, therefore τ σ + σ E = If the ordinate. But in a cycloid Eτ being the intercepted Diameter, τ σ + σ E is the ordinate, therefore this Curve is a Cicloide.

But if the Cheekes of a Pendulum bee a Cicloid of the altitude of half the Pendulum, the Bullet vibrates or is carried in a Cicloid.

For Xh being infinitly small that is but a point, Xh continued that is XM is the tangent to that point, that is to ye point X (and because XV is to XM as Xj is to Xh; and Xj is to Xh as the side of the respective Δ is to the Diameter; and the side of the respective Δ is to the Diameter as the intercepted diameter is to the side of the respective Δ, that is as XV to the meane proportionall between the diameter & it, therefore XM is the meane proportionall betweene the diameter and it. that is XM is the meane proportionall between AH or & V and XV). And because the aggragate of all the termes ab, cd, ef, &c. vsque ad jX equals XV therefore so many times Xj = twice XV, and therefore as many times Xh (that is the Curve HX) = twice XM. (and therefore if the diameter bee divided according to the odd numbers 1. 3. 5. 7. &c. and ordinats drawne through those points, the Cicloid HXC is divided by these ordinates into equall parts,) therefore LM being a tangent to ye curve at ye point L, MN = LM. therefore the point N is in the semicircle MNF = MLB and because the angle HMN is equall to the angle VMX which is the Complement of the angle LBC; and HM = AB the Complement of

4) Lisez: ED × ED.

5) Cela signifie que ED, Eu, Eτ sont en proportion continuelle.

[p. 31]

BC = MD. therefore MN cuts ye semicircle at the intersection thereof with the Cicloid. therefore N is in ye Cicloid HNE. therefore all ye vibrations of a Cicloid Pendulum so proportiond as before are of equall time. Quod &c.