Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 646.
R.F. de Sluse à [Christiaan Huygens].
5 août 1659.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par C. le Paige dans le Bull. di Bibliogr. T. 17.

Leodij 5^ta Aug^ti 1659.

Nobilissime Domine

Quod ominatus fueram cum ad Te libellum meum transmisi id reipsâ nunc experior, fore nimirum vt viam inuenires quam illi¹⁾ in opere perficiendo ingressus sum. Fateor enim cum primum incepj occurrisse mihi cogitationes ijs similes quas ad me misistj²⁾. Sed vt agam ingenue, aliâ demum ac faciliorj methodo vsus sum, quam sj porro pergas vt coepisti reperturum Te non dubito. Addis, non solum illum circulum adhiberj posse quj rectangulum ex duabus extremis includit sed alios quoque numero infinitos, de quo ne προπετῶς iudicium feram, rogo vt rem accuratius explices, et exemplo aliquo illustres, magno enim opere me obligabis si id feceris. Cartesio plurimum faueo, fuit enim acutus supra quam dici potest Geometra, sed συντ Ἀδραστείᾳ λέγω, non ita multum debeo. Eram enim in locorum consideratione priusquam eius Geometriam vidissem. Nam quid tandem sunt loca nisj figurarum proprietates, quas ex analysi venarj ea demum Geometrae laus est, quae sane Cartesio in primis debetur. Quid vero ab illius methodo mea discrepet videbis in alio opere, immo in hoc ipso si quas antea tibi significaui propositiones 3^am et 6^tam inter se conferas. Si quid interim eâ de re scribendum mihj sit, et si quid vltra desi-

1) Lisez: illo.

2) Dans nos collections cette lettre manque.

[p. 450]

derem, id fiet sine vllius nedum viri illius magni reprehensione, sum enim minime omnium ϕιλόψογος. Ex his satis, vt opinor, perspicis opus non esse vt symbolis Cartesianis vtar: praeterquam enim quod scripta mea recudere ac reformare deberem, (quod quidem difficile foret et erroribus obnoxium) id nihil omnino vtilitatis adferret, nam licet plerumque in conclusionibus pari passu ambulemus, in constructionibus tamen saepe δὶς διὰ πασῶν, vt aiunt, differimus. Arbitror autem characteres meos non ita a Cartesianis abire vt negotium vel tironi exhiberi possint. De Typographo optime mones, et doleo nobis non esse felicioris ingenij artifices: Tu succurre, et consilium suggere quod in alio opere sequi debeam. Exemplum adiungo methodj meae in planis, non illud quidem alicuius momentj, sed tantum vt in eiusdem Analysim inquiras. Proponatur dato semicirculo



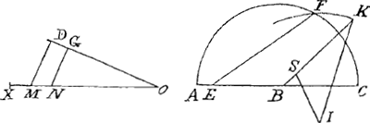AFC inuenire in Diametro AC punctum E, a quo si in angulo dato ducatur EF, rectangulum AEC ad quadratum EF habeat rationem datam. Vnicum casum construo. Data sit ratio XO ad NO, angulus ONG. diuidatur XN bifariam in M et ex punctis M et N cadant in OG normales MD, NG. Tum facto in centro angulo CBS, aequali dato GNO, sumatur BS aequalis DG, et eidem ad rectos SI aequalis MD. Deinde producatur BS in K ita ut SK possit vtramque CB, BS³⁾. Demum centro I, interuallo IK, describatur arcus KF, secans semicirculum datum in F puncto ex quo ducatur FE ad diametrum parallela BS. Dico rectangulum AEC ad quadratum EF, habere rationem datam XN ad NO⁴⁾, esseque in angulo dato. Unde cum rectae MD, DG continuo variari possint, si rectae XO, NO varientur in eadem ratione, patet infinitos circulos⁵⁾ satisfacere proposito.

Audi nunc aliud. Accepi a Clarissimo Gutiscovio nostro libellum Thomae Angli ex Albijs⁶⁾ (Chrysaspidem vocat) mole non magnum, sed qui magna promittat. Quadraturam nempe circulj et his παραπλήσια. Cum ab anno exercitationem⁷⁾ edidisset auctor, qua conatus fuerat ostendere spiralem primae reuolutionis aequa-

3) De Sluse veut dire: SK² = CB² + BS².

4) Lisez: NO ad XO.

5) C'est-à-dire que, dans la construction, le cercle TK peut être remplacé par une infinité d'autres cercles.

6) Thomas White (qui se nomma tour à tour Candidus, Albius, de Albis, Bianchi, Richworth) naquit en 1588 et mourut en 1680. Il fut prêtre catholique anglais, et résida en Portugal et en France; il se jeta dans le mysticisme et ses livres furent mis à l'index en 1658.

7) Exercitatio de geometria indivisibilium et proportione Spiralis ad Circulum. Auct. Th. de Albis. Londini. 1658. in-8^o.

[p. 451]

lem esse semiperiferiae suj circulj, eum monui per amicum⁸⁾ hunc errorem olim a Guldino admissum et correctum esse. Ille nunc obfirmato animo in Guldinum inuehitur⁹⁾, eumque ignorantiae arguit quod neglecta demonstratione vt putat Geometricâ, calculo arithmetico fidem habuerit. Miserer me Geometriae cum talia video, sed magis auctoris, qui quam in studijs sublimioribus famam adeptus est, hoc libello multum imminuit. Sed nihilne Geometrae vestri in meo reprehensione dignum adnotarunt? Si quid intellexisti sac me certiorem, atque insuper si quod Problema planum aut solidum habes cuius constructionem difficilem arbitraris, mitte sodes vt in eo methodj meae periculum faciam. Vale interim Vir praestantissime ab eo qui pleno affectu est

Tuj obseruantissimus Renatus Franciscus Slusius.

8) Peut-être Francis Hall, qui écrivait sous le nom de Thomas Line (Linus); il naquit à Londres en 1595 et mourut à Liège le 5 novembre 1675. Reçu Jésuite en 1623, il vint plus tard enseigner l'hébreu et les mathématiques au Collège Anglais à Liège. Il est connu par la dispute qu'il eut avec Newton au sujet de la théorie des couleurs. Après la mort de Linus, la controverse fut continuée par son disciple Gascoigne et par Lucas, successeur de Linus. C'est par erreur que Brewster, dans son ouvrage: ‘Memoirs of the Life, Writings and Discoveries of Sic Isaac Newton’, désigne Linus, anglais de naissance, comme ‘Dutch philosopher’. Hall publia l'ouvrage:
De Pseudo-quadratura circuli Dom. Thomae Viti. Auct. Th. Lino. Londini. [1659.] in-8^o:

9) White répondit à ses adversaires par l'écrit intitulé:
Apologia pro doctrina sua ad calumniatores. Auth. Th. de Albis. Londini. 1660. in-8^o, que Hall fit suivre par l'anticritique:
Th. Line, Refutation of the attempt to square the circle. London. 1660. in-8^o.