Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 450.
R.F. de Sluse à Christiaan Huygens.
8 janvier 1658.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 446. Chr. Huygens y répondit par le No. 451.
Elle a été publiée par C. le Paige dans le Bull. di Bibliogr. T. 17.

Nobilissime Domine

Gratissimas Tuas 3^a huius anni datas, vna cum acutis εὑρήμασιν Clarissimi Heuratij nudiustertius accepi, quem vel ex hoc specimine doctum Geometram, ὡς ἐξ ὄνυχος τὸν λέοντα, satis agnouj. Atque vt tandem, quod facturum me receperam, quid circa curuam meam illamque Huddenianarum primam vlterius obseruauerim, palam faciam, altius mihj res repetenda est. Ego olim cum id otij mej ratio pateretur, parabolarum infinitarum exemplo, Hyperbolas etiam ac circulos vel ellipses infinitas excogitaueram, leuiter variatâ aequatione. Quod exemplo declarasse sufficiet.



Sit recta AB, et curua BD, in quâ sumpto quolibet puncto D, ducatur applicata DC, quam in terminis analyticis voco x, et BC y, AB vero a. habeatur autem perpetuo haec aequatio ay + yy ∞ ax. Hanc vocaui Hyperbolarum infinitarum primam. 2^dam statuj ay + yy ∞ xx. Altiorem ayy + y³ ∞ aax vel ayy + y³ ∞ axx et ita in infinitum, quod nullo negotio



fieri posse satis animaduertis. Transfer hoc ad circulos mutato nempe signo + in - et fiet ay - yy ∞ ax, ay - yy ∞ xx, ayy - y³ ∞ aax vel ayy - y³ ∞ axx &c. Jn harum proprietates cum inquirerem, vidj statim primam et secundam Hyperbolarum vel Ellipsium praedictarum, esse parabolam, circulum, Ellipsim vel Hyperbolam Apollonij, caeteras non ita, qua-

[p. 122]

rum interim dimensionem vel solida demonstraui, saepe etiam (quod ad te scripsisse meminj) ἀπαγωγὰς ad circulj quadraturam ex ijs deduxj. Harum Ellipsium vna est curua quam proposueram, vt scis, nempe haec ayy - y³ ∞ aax. Primam autem Huddenij deprehendj postea partem esse Hyperbolae illius quae his terminis explicatur ayy + y³ ∞ aax. Quod vt planum fiat paucas meae proprietates mecum



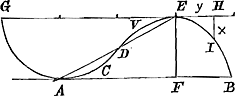considera. Sit in illâ, ad axem AB applicatarum maxima EF, et iungatur AE, quae vtique curuam secabit in D puncto vbi flexus mutatur. Aio spatium curuâ ACD et recta AD comprehensum, ei aequale esse, quod recta DE et curuâ DVE continetur, imo idem omnino esse sed inuerse positum. Vt quemadmodum recta GE tangit curuam in E ita pariter recta BA tangat eandem in A. Vnde sequitur vlterius, si illa prout exigit, producatur, occurrere ipsi GE in G, et curuam DAG esse plane eandem ipsi DEB sed inuersé positam. At si vltra punctum E, quaelibet applicetur a parte exteriori curuae vt HI, sitque illa x, et EH y, haberj aio perpetuo hanc aequationem ayy + y³ ∞ aax. Itaque curuam EB esse vnam Hyperbolarum infinitarum quas superius descripsi, quae cum versus B produci possit in infinitum (idem intelligendum versus G). apparet efformarj latinum sigma, ad quod appenditur illa quam primo loco nobis proposuit Clarissimus Huddenius, quemadmodum etiam aliunde deduxit. Quaenam igitur tandem est haec curua? inquies, Dicerem nisj Te scirem id Tuo Marte inuestigare malle, et Platonis praecepto in tuo praedio ὀρύττειν μεχρὶ τῆς ϰεραμίτιδος γῆς antequam a vicino aquam petas. Hoc itaque Tibi propositum esto, et per Te Clarissimis illis viris (si tanti esse censeas) qui tam docté hactenus illam examinarunt. Gratulor interim Tibj, quod Parabolarum infinitarum areas et solida Geometrice demonstraris. Ego quoque me in illo campo lusisse meminj cum Romae essem, et similes tuis ac fortasse easdem in schedis meis ibidem latere demonstrationes. Video enim nos eandem saepe viam insistere: idque etiam in dimensione Huddenianarum primae arbitratus fueram, cum idem συμπέρασμα nobis occurrisset; sed ex Tuis animaduertj, te tribus spatijs quorum vnum est rectilineum, vtj, Ego vero vnico curuilineo, methodo mihi peculiarj, rem confecj. Eadem nempe qua in dimetiendis illis Hyperbolis et Ellipsibus vsus fueram. Accipe etiam ab eodem fonte quando ita iubes, ἀπαγωγὴν pro circulj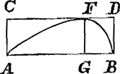



quadratura. Super AB esto curua in quâ sumpto quolibet puncto F, et applicatâ FG, si illa sit x, et AG y, AB a, fiat perpetuo aequatio ay³ - y⁴ ∞ aaxx. Hoc spatium si fueris dimensus, scias te circulum ipsum facile metiri posse^a). Quod si eidem circumscriptum intelligas parallelogrammum AD, et ex vtriusque reuolutione circa axem AB gigni cylindrum, et solidum inscriptum, Aio habere hoc ad illud rationem notam, quam, sj quando vacabit et si operae pre-

a) fallitur. [Chr. Huygens.]

[p. 123]

tium esse videatur inuestigandam Tibj propono, aut si mauis, earn cum iusseris a me accipies. De Tuis motus regulis censeo et hortor vt breuj edantur in lucem. Nec est quod diuersa sentientium autoritas te moueat; frustra enim hominum praeiuditijs condemnatur, quem ratio absoluit. Prodeant itaque cum bono Deo, a quo Tibi felix anni noui principium, feliciora incrementa precor ex animo. Vale Vir Clarissime et ama

Tui obseruantissimum Renatum Franciscum Slusium.

Leodij 8 Aⁱ. 1658.

Nobilissimo Clarissimoque Domino Domino Christiano Hugenio de Zulichem &c. A la Haye.

VI