Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 447.
H. van Heuraet à Fr. van Schooten.
Appendice au No. 446.

Cette pièce se trouve à Leiden, coll. Huygens¹⁾.

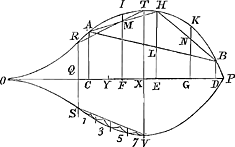
Ducatur intra curvam quomodocunque recta AB, et ex A et B cadant perpendiculares in axem AC, BD. Dividatur deinde CD in quatuor equalia punctis F, E, G, et agantur rectae FI, EH, GK, parallelae AC. et jungantur AH, HB. Investigetur jam ratio quam habet HL ad utramque simul IM, KN, quam reperio ut 2 ad 1. Atque inde segmentum AIHKBA ad inscriptum triangulum AHB, ut 4 ad 3.

Inveni porro curvam hanc ex contrarijs flexibus constare duobus, punctumque hos definiens reperiri, sumtâ OQ ∞ ⅓ OP, ductaque RS ad OP perpendiculari. Quod si jam ex R et S duae aequales rectae intra curvam subtendantur, ut RT, SV, eaeque in partes quotlibet aequales dividantur rectis quae aequedistent ipsi TV, et jungantur puncta curvae in quae dictae lineae incidunt. Erunt segmenta ita abscissa in continua ratione numerorum imparium ab unitate 1, 3, 5, 7, 9, 11 &c. Hinc invenio centrum gravitatis duorum segmentorum rectis SV, RT abscissorum cadere in Y, ita ut divisâ lineá QX in 15 partes, statuatur QY octonis ipsarum aequalis.

1) Cette traduction d'une partie de la Lettre N^o. 435 est de la main de Chr. Huygens.