Briefwisseling. Deel 1: 1608-1634

730. J. Golius⁶⁾. (K.A.)

Cum eruditi viri benevolentiam mihi paras, et quidem parvulo adeo officio meo, quam ego affectare maxime cupio, benevolentiae erga me tuae testimonio me luculento beas. At vereor, ne felicitati meae obsistat debiti obsequii mora, nisi te atque illum, cordatos ingenuosque viros, plus moveat ipsum infortunium meum, culpâ vacuum, quod nempe, hesterno demum die, et quidem Hagae, mihi redditae sunt tuae literae, quae biduo ante, absente me, Leidam frustra latae fuerant. Optem uberiorem in hoc campo materiem mihi dari, quo promptiore operâ hoc quidquid est damui resarcire aut compensare nitar, et quidem, si institutum scriptoris nossem, plura hujus generis nunc sponte adderem. Quod autem ad Byzantii latitudinem attinet, Imperatoris Osmanici astronomus⁷⁾ testatus iterum atque iterum mihi fuit, se observatis proprijs, et quidem repetitis, eam comperisse graduum dumtaxat XLI, miratus Arabas, qui ad gradum XLV

6) Eenige zinnen uit den brief zijn uitgegeven door Dr. D.J. Korteweg in Verslagen en Meded. der Kon. Akad. v. Wetensch., Afd. Natuurk., 3^de reeks, IV, 1888, blz. 258, waar ook over de belangrijkheid van dezen brief wordt gesproken.

7) Nl. Aben Marufi; zie blz. 262.

[p. 372]

extulissent; quem errorem, in gente dissita semel receptum, putabat per manus esse traditum. Ad eandem hanc quaestionem memini me respondisse alias viro literarum orientalium et mathematum perquam gnaro, Wilhelmo Schikardo¹⁾, Academiae Tubingensis insigni lumini, qui nunc geographiam novam adornat, occasione data, dum Abilfedae²⁾, geographi Arabis, versioni et editioni operam navat. Ut autem locorum meridianos situsque certius connectat, et ad coeli normam terras exigat, solis et lunae eclipses varias et poli elevationes accurate observatas captat et conquirit undique; idemque in ejus gratiam factitat vir quidem nostras vere magnus³⁾, interposita propriae famae auctoritate, quippe qui illius doctrinae, studijs atque virtutibus merito magno favet. Quamobrem conjectare audeo, ab ijs quaestionem hanc moveri, praesertim quia haud videbar tunc temporis Schikardi expectationi aut votis satisfecisse. Unde vereri subit, ut satisfaciam Ampl. Tuae, aut speratae gratiae quidquam responso consequar, utve etiam D. legatus Haga⁴⁾ dubitationem possit tollere, quia haud alius ibi, quod quidem sciam, astronomus degit, illo, quem dixi, celebrior aut rerum peritior. Secundariâ itaque tentabo viâ, num tueri spem meam et benevolum affectum tuum possim auctario aliquo. Id autem officio postulato reliquo optabilius esse, tibique fore gratius confido, pro quo fidem ante menses aliquot operamque obstrinxi meam⁵⁾, nisi forte et hic quoque mihi fraudi sit longa cunctatio; quod tamen ut minus metuam, facit tum difficultas et momentum rei, tum aequitas et facilitas animi tui. Neque enim asserere hactenus fui ausus ingeniosi Desecartis inventum, quod tamen, seu praesagio, seu affectu quodam, apud te jactare non extimueram, scilicet refractionis leges, ab illo descriptas, quas veras esse et ipsius naturae, me credere visus et ratio nunc cogunt. Cepi nuper experimenta quaedam incidique paulo post in Snelliana plurima, quae ambiguitatem et scrupulum exemerunt omnem. Ambo illi, qui dici merentur magni mathematici, haud unquam inter se cogniti, diversis locis et temporibus contrarias ingressi vias, per principia et causas Gallus, per effectus et observata Batavus, alijs et diversis verbis concluserunt prorsus idem. Quod neque celare Ampl. tuam, neque sine studio divulgare velim, quo et tibi mea constet observantia et inventoribus sua in solidum gloria. Snellius, venerandae memoriae praeceptor meus, cum ex Vitellionis⁶⁾ calculo et tabulis, tum ex proprijs ad observata plurima, eaque saepius et diverso modo repetita, subductis, hoc formavit theorema opticum.

Si duplex fuerit medium, densitate et raritate differens, radius quivis incidentiae verus ad suum apparentem in ejus generis medio eandem servat rationem.

1) Wilhelm Schickard (1592-1635), sedert 1619 professor te Tübingen, was een beroemd mathematicus, orientalist en geograaf en heeft verscheidene werken geschreven.

2) Eerst in 1650 heeft John Greaves uitgegeven Chorasmiae, et Mawaralnahrae, hoc est Regionum extra fluvium Oxvm, Descriptio, ex Tabulis Abvlfedae Ismaelis, Principis Hamah. Londini.

3) Zeker Willem Blaeu; zie blz. 264.

4) Zie blz. 368.

5) Zie blz. 349.

6) Witelo, of Vitellio, was een Pool, die in de 13^de eeuw leefde. Hij schreef Perspectivae libri decem, gedrukt in 1533.

[p. 373]

Esto medij



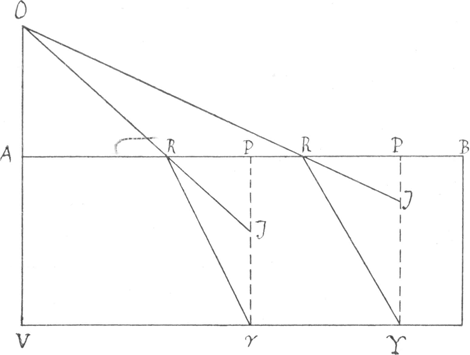densioris terminus AB, visibile γ, radius incidentiae γ R, refractus in rariore medio R O, oculi situs in puncto O. Videbitur itaque imago rei visibilis in concursu radij refracti O R continuati et perpendicularis incidentiae, quae sit γ P et punctum concursus J. In eodem itaque medio, scilicet hic densiore, radius incidentiae verus erit γ R, suusque apparens R J. Docent observata quae ratio est γ R ad R J, semper obtinere eandem inter quoscunque radios similes, ut Υ R et R J, quia in ipso radio perpendiculari et irrefracto γ A, ubi incidentis ipsius pars est radins apparens. Neque enim res visibilis γ spectata perpendiculariter suo apparet loco, sed superiore in J, et ut y A ad A J, ita γ R se habet ad R J. Unius itaque radij obliquatione, aut perpendicularis contractione cognitâ, quod modis pluribus facile fieri potest, cognoscetur ratio caeterorum incidentium et apparentium omnium. Quae, exempli gratia, in aqua est ut 4 ad 3, in vitro ut 3 ad 2, quando scilicet utrobique oculus consistit in aëre.

Nobilis ille Gallus Desecartes mira subtilis ingenij sagacitate a principijs simplicibus et manifestis exorsus, continua demonstrationum serie, trajectionum, quae per diversa fiunt media, generalem stabilivit legem, quam in Opticis hoc speciali expressit theoremate:

Si duplex fuerit medium, densitate et raritate differens, radij cujusque incidentis in medio uno, et refracti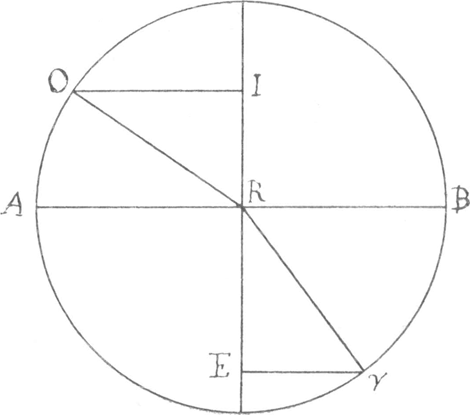



sui in altero puncta a refractionis puncto aeque dissitas distantias habent a perpendiculari refractionis in eadem semper ratione.

Esto medij cujusvis densioris terminus A B, visibile γ, radius incidentiae γ R, refringatur in O; et γ R, R O sunt aequales, per punctum autem R ducatur perpendicularis refractionis E I, et ab ea punctorum y et O distantiae sunto γ E et O I, inter radios similes semper eadem servabitur distantiarum ratio, undecunque et quocunque procedant.

[p. 374]

Ita esto corporis densioris terminus A B C D per quod a punctis γ, V, Y in eundem incidant



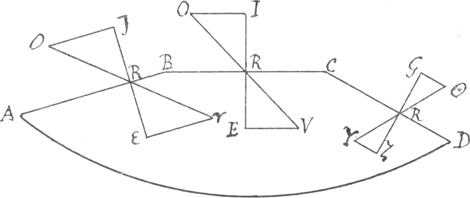radij γ R, V R et Y R, quibus aequentur sui refracti R O, R O et R Θ, erit ut perpendicularis γ ε ad perpendicularem O J, ita V E ad O I, et Y ζ ad Θ G, eademque in ijsdem duobus medijs erit distantiarum fere perpendicularium similium ratio.

Experimento ad illustrandam potius, quam probandam veritatem uno atque altero contentus fuit, nixus firmitudine necessariae, seu mathematicae, demonstrationis, ita ut, plura inter se conferre, visum illi fuerit tempus perdere. Eodem autem redire inventum utriusque, demonstrabo theoremate tali.

Si radius incidentiae in medio uno et refractus in altero sint acquales, extremorum a perpendiculari refractionis distantiae sunt incidenti et apparenti in eodem medio radijs reciproce proportionales.

Esto rursus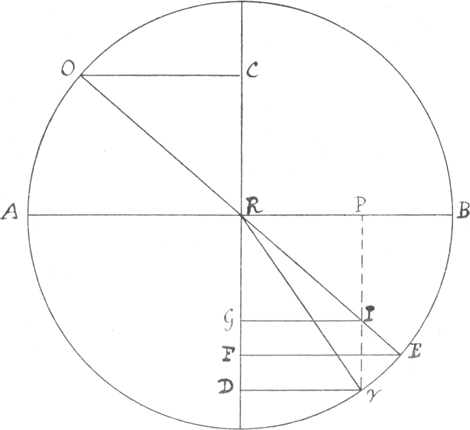



medij densioris terminus A B, visibile γ, radius incidentiae in medio densiore γ R, refractus suus in rariore R O, ijque inter se aequales. Per punctum R ducta sit perpendicularis refractionis C D; erunt itaque γ D et O C punctorum γ et O ab eadem perpendiculari distantiae. Oculus situs in puncto O, qui spectabit imaginem in concursu radij refracti O R continuati et perpendicularis incidentiae γ P in puncto I; eruntque γ R radius incidentiae, et R I radius apparens in eodem medio; dico esse, ut γ P ad O C, ita γ R ad R I.

[p. 375]

Nam in centro R intervallo R O describatur peripheria, quae transibit per γ, quia O R et γ R sunt aequales. O R producta in I porro producatur ad punctum peripheriae E, et ab E et I ducantur perpendiculares in perpendicularem refractiones duae, nempe E F et I G, quae duabus distantijs O C et γ O sigillatim aequales erunt; est autem, ut I G ad E F, ita I R ad R E; ergo erit, ut γ O ad O C, ita γ R ad R I.Q.e.d.

Haec eadem Snelliana reflectionis quoque omnis norma est, ita ut totius visionis compositae praecipua et summaria doctrina comprehendatur pauculis hisce verbis.

In visione composita radius quivis incidentiae verus et suus apparens in eodem obliquativo eandem servant rationem.

Hic finem itaque facio, ne pluribus magnas seriasque occupationes tuas interpellem peccemque in publica commoda, neve consummato ingenio tuo injuriam faciam, quo facile tibi fuerit totam nunc catoptricam atque dioptricam perficere. Cuncta enim naturae et artis mysteria, huc facientia, ex hac scaturigine derivari, perque hoc elementum a geometra et arithmetico demonstrari possunt. Tanti est in mathematibus mixtis caeterisque disciplinis deprehendisse primos fontes! Tantum est quod nesciunt homines, ut rem oculis omnium maxime obviam, a tot seculis hactenus, quod quidem constat, nullus viderit! Tamque semper pueri sunt, ut quae incognita admirati sint et suspexerint maxime, eadem inventa despiciant et tantum non rideant! Quod vereri videtur suae physicae naturae genius Desecartes, ea quippe tota mechanica, seu potius mathematica est; adeo palpabilem fecit, ex materia infinite dividua et motu, tanquam solis principijs, derivatam. At sapientiores et generosae animae ob facilitatem et necessarium rerum ordinem multo magis perspicient atque respicient summam Creatoris potentiam et sapientiam, ac mirabuntur amabilem per se maxime pulchritudinem. Ita de se testatur nobis ipse philosophus, cujus dulcissima consuetudine pridem mihi licuit per biduum frui; ingenue fateor, quanto magis tracto atque cognosco, tanto magis miror et amo. Neque enim in eo minor est animi bonitas probitasque vitae, quam ingenij felicitas et doctrinae praestantia. Opus autem, quod molitur, ad humanae animae, cujus originem a Deo petit, philosophiam nunc perductum, extremam expectat manum; erit autem breve et pressum, ut attentionem et in philosophando diligentiam majorem excitet. Ipse nunc Daventriam secessit, ut se turbae et compellationibus eximat et postea se fructuosius omnibus impertiat. Prima occasione data salutem illi nunciabo tuo nomine, quam fore illi gratissimam scio, et utrique vestrum amicitiam mutuam, si unquam vos congredi contingat. Vale, vir amplissime, et me benevolentia tua fovere et beare perge. Dabam Lugd. in Bat., ipsis Kal. (1) Nov. CIƆIƆCXXXII.