De bouwstenen van de schepping

Een zoektocht naar het allerkleinste

[p. 31]

4 Duizelingwekkende snelheden

Honderdduizend keer zo klein als het atoom zelf is het harde pitje dat er midden in zit: de atoomkern. Door zijn massa, maar nog meer door zijn elektrische lading bepaalt het alle eigenschappen van het atoom. Door de ongenaakbaarheid van de atoomkernen lijken de atomen die onze dagelijkse wereld opbouwen onveranderlijk, ook als ze onderlinge interacties aangaan waarbij ze de scheikundige verbindingen vormen. Maar wat onbreekbaar lijkt, kán wel stuk. Als atomen met duizelingwekkende snelheden op elkaar afstormen kan het gebeuren dat de kernen elkaar raken, en dan kunnen deze uiteenspatten of samensmelten. Er komen dan subatomaire deeltjes vrij. De nieuwe natuurkunde van de eerste helft van de twintigste eeuw werd beheerst door de nieuwe raadsels waar deze deeltjes ons mee opscheepten.

Maar we hebben toch de quantummechanica, zult u zeggen, en die is toch overal van toepassing? Wat was dan de moeilijkheid? Inderdaad, de quantummechanica is zeker van toepassing op de subatomaire deeltjes, maar er is meer. De krachten waarmee deze deeltjes op elkaar inwerken en die de atoomkernen bij elkaar houden zijn zo groot dat de snelheden waarmee ze om elkaar bewegen in en buiten die kernen, in de buurt komen van de lichtsnelheid, ongeveer 300.000 km/sec. Wanneer zulke snelheden een rol spelen is er een tweede wijziging nodig in de natuurwetten van de negentiende eeuw: dan hebben we rekening te houden met de speciale relativiteitstheorie van Albert Einstein.

Ook dit is een resultaat van een publicatie door Einstein in 1905. Zijn uitgangspunt was dat een experiment uitgevoerd in een laboratorium in de vrije ruimte uitkomsten moet geven die er niet van afhangen hoe snel en in welke richting het laboratorium zich in de ruimte beweegt, ook niet als men in dat labora-

[p. 32]

torium de snelheid van het licht meet. Dat is vreemd, want stel dat het laboratorium zich in een ruimteschip bevindt dat een snelheid heeft van 50.000 km/sec. Dan zou je verwachten dat de waargenomen lichtsnelheid in één richting 350.000 km/sec zal bedragen en in de tegenovergestelde richting slechts 250.000 km/sec. Ook in de loodrechte richtingen zou je een kleine afwijking verwachten.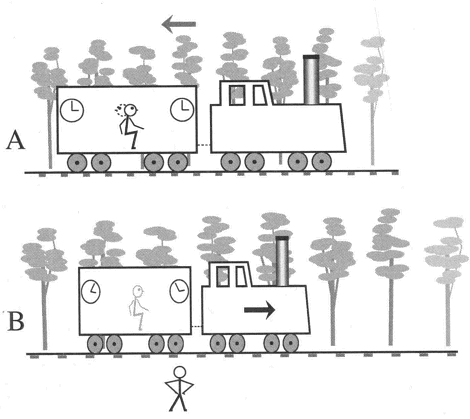

Figuur 5. Volgens Einsteins speciale relativiteitstheorie hangt de wijze waarop wij lengte en tijd waarnemen af van waar wij ons bevinden en hoe wij zelf bewegen. Iemand die zich in een rijdende trein bevindt (a) kan zijn klokken hebben gelijkgezet en de lengte van de trein hebben gemeten. De waarnemer buiten (b) zal vinden dat diezelfde klokken niet gelijk lopen en dat de trein wat korter lijkt, terwijl voor hem de bomen wat verder uit elkaar staan.

[p. 33]

Echter, zo'n experiment is afhankelijk van het bestaan van goede klokken en lengtemetingen. Bovendien moeten diverse klokken gelijkgezet worden. Dat klokken en linialen heel goed door de snelheid van het laboratorium beïnvloed zouden kunnen worden, was al in 1893 geopperd door de Nederlander Hendrik Antoon Lorentz (1853-1928), en onafhankelijk van hem door de Ier G.F. Fitzgerald. In Nederland is Lorentz overigens ook om andere redenen bekend geworden: hij was voorzitter van de Zuiderzeecommissie, die de waterstromingen moest uitrekenen welke zouden ontstaan als er ergens een afsluitdijk zou worden aangelegd. In aanmerking nemend dat er toen nog geen computers bestonden, bleken zijn berekeningen later opmerkelijk nauwkeurig te zijn.

Lorentz dacht echter nog in termen van stilstaande en bewegende linialen; ten gevolge van hun beweging zouden linialen kunnen krimpen. Einstein was het die zich realiseerde dat hierdoor stilstand en beweging alle relatief zijn geworden. Er bestaat niet zoiets als absolute rust, of een absoluut referentiepunt ten opzichte waarvan men de lichtsnelheid kan meten.

Er moest nog veel meer relatief worden. Massa en energie hangen nu ook van de snelheid af, en tevens elektrische en magnetische veldsterkte. Einstein ontdekte dat de massa van een deeltje altijd evenredig is met zijn energie, als je daarbij een zeer grote hoeveelheid ‘rustenergie’ optelt. Deze rustenergie is evenredig met de massa van het deeltje als het in rust verkeert:

E = M × c²

Hierin is E de energie, M de massa en c de snelheid van het licht.

Mede door deze voorspelling, dat in kleine deeltjes enorme hoeveelheden energie opgeslagen moeten zitten, werd de rela-

[p. 34]

tiviteitstheorie voor de natuurkunde (en voor de samenleving!) erg belangrijk. Ook voor deze theorie geldt dat zij alleen maar werkt als zij ‘holistisch’ is: alles en iedereen moet onderworpen zijn aan de relativiteit van beweging. Niet alleen klokken gaan anders lopen wanneer men ze grote snelheden geeft, ook alle andere levenloze en levende mechanismen zoals het menselijke hart. Anders zou de experimentator immers wel de absolute snelheid waarmee zijn laboratorium beweegt kunnen vaststellen!

Einstein zag snel in dat daarom ook de wetten van de zwaartekracht aangepast moesten worden aan het relativiteitsbeginsel. Nu herinnert u zich dat voor kleine objecten de zwaartekracht een zeer ondergeschikte rol speelt. Voor de subatomaire deeltjes is de zwaartekracht verschrikkelijk zwak. Voor ons verhaal doet de zwaartekracht er dus niet veel toe. Toch zal ik later in dit boek weer tegen deze merkwaardige en uiterst fundamentele kracht aanlopen. Het probleem waarvoor Einstein zich geplaatst zag zou ook belangrijk zijn voor het begrijpen van andere krachten tussen de kleine deeltjes. Daarom vermeld ik nu vast waar hij, pas na tien jaar, de oplossing vond.

Teneinde het relativiteitsbeginsel van toepassing te doen zijn op de zwaartekracht moest het principe worden uitgebreid. Niet alleen de eigen snelheid van een laboratorium is niet meer te achterhalen, ook veranderingen in die snelheid niet; die zijn niet te onderscheiden van de invloeden van zwaartekrachtsvelden.

Het gevolg hiervan was dat de zwaartekracht met ruimte en tijd hetzelfde doet als wat vocht doet met een stuk glad papier: er komen bobbels en rimpels in, die niet meer zijn glad te strijken. De wiskunde van gekromde ruimtes bleek reeds bekend te zijn, maar het toepassen van zulke abstracte wiskunde voor het formuleren van de natuurwetten was in Einsteins tijd iets geheel nieuws, en het duurde verscheidene jaren voordat hij er vertrouwd mee was. Nu, driekwart eeuw later, vinden natuur-

[p. 35]

kundigen het heel gewoon te flirten met uiterst geavanceerde wiskunde. Ook nu geldt echter nog dat vaak niet de wiskunde zelf het moeilijkste probleem is; het vinden van de juiste wiskundige benadering voor nieuwe theorieën, dat is meestal de moeilijkste schakel.

Einsteins theorie voor de zwaartekracht noemen we de algemene relativiteitstheorie. We komen erop terug, eerst omdat deze theorie als voorbeeld zal dienen voor andere theorieën voor fundamentele krachten, en ten slotte omdat voor objecten die nog veel kleiner zijn dan de subatomaire deeltjes de zwaartekracht weer een rol kan gaan spelen. Maar voorlopig kunt u de zwaartekracht en de algemene relativiteitstheorie weer vergeten. We gaan eerst de subatomaire deeltjes bespreken.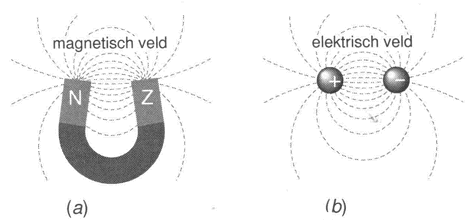

Figuur 6. Volgens de vergelijkingen van Maxwell vormen de magnetische veldlijnen bij een magneet hetzelfde patroon als de elektrische veldlijnen bij twee tegenovergestelde elektrische ladingen.

[p. 36]

__________

De elektromagnetische kracht

De elektrische kracht is de kracht waarmee twee elektrisch geladen deeltjes elkaar afstoten (als ze gelijke ladingen hebben), of elkaar aantrekken (als de ladingen een tegengesteld teken hebben).
De magnetische kracht is de kracht die een snel bewegend elektrisch geladen deeltje ondervindt in een magneetveld. Een magneetveld ontstaat als elektrisch geladen deeltjes snel bewegen, bijvoorbeeld als ze door de wikkelingen van een spoeltje stromen.
James Clerk Maxwell slaagde er in 1873 in de volledige vergelijkingen voor de elektrische en magnetische krachtvelden op te schrijven. Het werd een ‘geünificeerde’ theorie, die nu elektromagnetisme genoemd wordt. Zie figuur 6, blz. 35.
Kenmerkende eigenschappen van deze kracht, zoals ze op de elementaire deeltjes inwerkt, zijn:

•	De kracht grijpt op universele wijze aan op elektrische lading.
•	De kracht heeft een zeer grote reikwijdte (magnetische velden kunnen de enorme afstanden tussen sterren overbruggen).
•	De kracht is vrij zwak. Bepalend voor de sterkte is de verhouding tussen het kwadraat van de lading van een elektron en 2hc (2 × de constante van Planck maal de lichtsnelheid). Deze verhouding is ongeveer 1 : 137, 036.
•	De ‘drager’ van de kracht is het foton, een deeltje met massa 0 en spin^1. Het foton heeft zelf geen elektrische lading.

Algemeen is de reikwijdte van een kracht omgekeerd evenredig met de massa van zijn drager.

__________

1 Het begrip ‘spin’ wordt in het volgende hoofdstuk verder toegelicht.

[p. 37]

__________

De zwaartekracht

De zwaartekracht is een zeer fundamentele kracht waarvan Einstein in 1915 de gedetailleerde structuur wist te ontrafelen, en die hij in verband bracht met kromming in ruimte en tijd. Echter ook nu nog weten wij niet hoe deze wetten te verenigen zijn met de wetten van de quantummechanica.

•	De zwaartekracht grijpt uitsluitend aan op de massa van de deeltjes.
•	De kracht heeft een zeer grote reikwijdte (werkt door tot de verste uithoeken van het heelal).
•	De kracht is zo uiterst zwak dat het wel nooit mogelijk zal zijn direct de zwaartekrachtswerking tussen twee elementaire deeltjes onderling experimenteel te detecteren. De kracht merken wij alleen doordat deze collectief is: alle deeltjes trekken dezelfde kant op.
•	De drager is het hypothetische ‘graviton’. Hoewel nog nooit ontdekt, weten we wat de quantummechanica erover zal zeggen: het heeft massa 0 en spin 2.

Een algemene wet voor alle krachten is dat als de drager even spin heeft, de kracht tussen twee gelijksoortige ladingen aantrekkend is en tussen tegengestelde ladingen afstotend. Heeft de drager oneven spin dan is dit andersom.

__________