Geschiedenis van de wetenschappen in België van de Oudheid tot 1815

[p. 113]

Paul Bockstaele
De wiskunde

Het uit de laat-Romeinse tijd overgeleverde quadrivium - aritmetica, geometrie, astronomie en muziek - diende ook in de 16de eeuw nog als schema voor het onderwijs van wat men de mathematische wetenschappen noemde. Dat zijn alle wetenschappen die de kwantiteit als object hebben. In 1602 publiceerde Adriaan van Roomen onder de titel Universae Mathesis Idea een werkje over de natuur, de waarde en het nut van de mathematica. Hij onderscheidt de ‘mathematica pura’ of zuivere wiskunde die zich bezig houdt met de kwantiteit in abstracto, en waartoe de aritmetica en de geometrie behoren, en de ‘mathematica mixta’ of gemengde wiskunde die concrete kwanti-

Portret van Joachim Sterck van Ringelberg. Foto uit privé-bezil ▪

teiten bestudeert. Dit kan de hemelsfeer zijn, wat voert tot de kosmologie, astronomie, astrologie, chronologie en tijdmeting, of het kunnen aardse kwantiteiten zijn, die worden bestudeerd in de geodesie en de cartografie, de geografie, de optica, de muziek, de mechanica, enz. In de volgende hoofdstukken komen enkele takken van de gemengde wiskunde aan de beurt. In dit hoofdstuk gaat het uitsluitend over de geschiedenis van de zuivere wiskunde. We willen ons hierbij niet beperken tot de belangrijke figuren die op een of andere manier tot de ontwikkeling van de wiskunde hebben bijgedragen, maar ook aandacht schenken aan alle aspecten van het mathematisch gebeuren. Zowel het onderwijs van de eenvoudige rekenmeester als dat aan de universiteit, zowel het elementaire leerboek als de geleerde verhandeling, hebben een rol gespeeld en verdienen een plaats in de geschiedenis van de wiskunde en in ons verhaal.

▪ Mathematica aan de Leuvense universiteit omstreeks 1500

In de allereerste statuten van de Leuvense universiteit, daterend uit 1426-27, wordt voorde mathematische vakken het volgende voorgeschreven: het voorlezen van een traktaat over de hemelsfeer, boek I van Euclides' Elementen, een traktaat over aritmetica en een traktaat over muziek. Meer dan tachtig jaar later, in 1512, publiceerde de artesfaculteit, na lange discussies, vernieuwde statuten, die echter niet bewaard bleven. De inhoud ervan kennen we slechts ten dele via een nieuwe redactie, waarschijnlijk uit 1567-68. Wat de mathematica betreft, worden onder de te lezen traktaten alleen nog de aritmetica en een werk over de hemelsfeer vermeld. Van geometrie is er geen sprake meer, afgezien van enkele zeer elementaire begrippen in het traktaat over de sfeer.

Een duidelijker beeld van de inhoud en de omvang van dit onderwijs geeft ons misschien het werk van de

[p. 114]

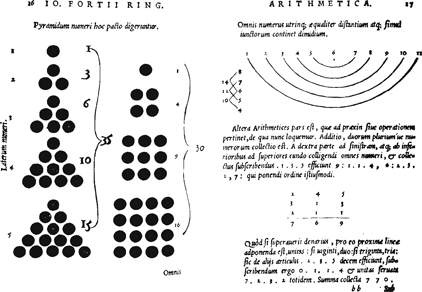
Joachim Sterck van Ringelberg. Arithmetica, Lyon, 1531. Foto uit privé-bezit ▪

humanist Joachim Sterck van Ringelberg. Geboren te Antwerpen in 1499, kwam hij als twaalfjarige knaap aan het hof van keizer Maximiliaan I. In 1516 of 1517 kwam hij naar Leuven, maar pas in 1519 vinden we zijn naam in de matrikels van de universiteit. Vermoedelijk bleef hij in de universiteitsstad tot 1527, het jaar waarin hij zijn rondreis langs verschillende Europese steden begon. Begin 1531 verbleef hij in Lyon. Daarna verliest men zijn spoor. Waarschijnlijk is hij dat jaar of kort daarna overleden. Over zijn doen en laten gedurende de circa tien jaren dat hij in Leuven verbleef weten we weinig. Hij zou zich hebben beziggehouden met kalligrafie, tekenen en schilderen en het maken van kopergravures. Bovendien gaf hij private lessen over allerlei onderwerpen, waaronder wiskunde en astronomie. Zijn encyclopedisch oeuvre omvat onder meer traktaten over aritmetica, geometrie, perspectief, astronomie, astrologie, horoscopen, kosmologie, chronologie en geomantiek. Sommige zijn duidelijk voor het onderwijs bedoeld en onderstellen, wegens hun uiterste beknoptheid, mondelinge aanvullingen. Een voorbeeld hiervan is zijn Arithmetica. In de uitgave Lyon 1531 beslaat het traktaatje zeventien bladzijden. Het eerste deel ervan is een samenvatting op vier bladzijden van Boëthius' De institutione arithmetica. Het begint met de definitie van even en oneven getallen, en van volmaakte en onvolmaakte getallen. Hierop volgt de terminologie gebruikt voor het aanduiden van de verschillende soorten verhoudingen, en ten slotte iets over figuratieve getallen. Het tweede deel behandelt het praktisch rekenen, zowel met gehele getallen als met breuken. Het werkje sluit met iets over rekenen met penningen.

In een paar van Ringelbergs werkjes vindt men ook iets over meetkunde. Zijn Sphaera bijvoorbeeld begint met enkele grondbegrippen als punt, lijn, oppervlak, lichaam, cirkel en bol. In een werk met de zonderlinge titel Chaos mathematicum geeft hij enkele eenvoudige geometrische constructies, waarschijnlijk ontleend aan het werk Geometriae introductionis libri sex (Parijs, 1503) van Charles de Bouvelles (ca. 1470-ca. 1553), professor van theologie en kanunnik te Noyon. Hierop volgen een aantal regeIs voor het berekenen van de oppervlakte van meetkundige figuren, dit alles zonder

[p. 115]

enige uitleg of bewijs. Te vermelden blijft nog een traktaatje met de misleidende titel Optica; het handelt in werkelijkheid over perspectief en schijnt, direct of indirect, afhankelijk te zijn van het werk De artificiali perspectiva (1505) van de Fransman Jean Pélerin of Viator (1435/40-1524).

▪ Rekenen en meten voor landmeters, wijnroeiers en kooplui

Ook buiten de in het Latijn docerende en schrijvende universitaire wereld ondervond men reeds vroeg dat enige wiskundige kennis nuttig en zelfs onontbeerlijk was. Stimulerend werkten hier de noden van de groeiende steden en de zich snel ontwikkelende koophandel. Administratie en boekhouding, landmeterij of het werk op de bouwwerf eisten enige vaardigheid in rekenen en meten. De uitbreiding van de wijnhandel van de Vlaamse steden met Frankrijk en Duitsland maakte het omrekenen van maten noodzakelijk. De inning van cijnzen op bier en wijn of andere waren onderstelde de mogelijkheid de inhoud van vaten en tonnen te controleren. Rond dit alles hadden zich vanaf de 14de eeuw tal van diensten en officies ontwikkeld zoals ijker, wijnmeter, korenmeter, landmeter, boekhouder, enz. Groot was de mathematische kennis van deze ambtenaren, bouwmeesters en kooplieden niet. Vaak was hun enige scholing de praktijk. Als leerjongen namen ze de vakkennis en tradities over van hun meester. Het toenemend belang van die officies in de loop van de 15de eeuw stimuleerde de vraag naar betere scholing en leermiddelen. Voor de nog jonge boekdrukkunst opende deze groeiende belangstelling voor direct bruikbare en nuttige kennis bij het begin van de 16de eeuw een veelbelovend werkterrein. Dat hier zaken te doen waren schijnt onder meer de Brusselse jonker Thomas van der Noot te hebben begrepen. Geboren circa 1475, vestigde hij zich omstreeks 1508 als drukker te Brussel. Tussen 1508 en 1523 legde hij rond de veertig boeken ter perse, op weinige uitzonderingen na alle in het Nederlands, waaronder verschillende volkswetenschappelijke werkjes door hemzelf vertaald of samengesteld uit Latijnse, Franse, Duitse of andere bronnen. Ten dienste van kooplieden, landmeters, wijnroeiers, en voor allen die iets meer wensten te weten over rekenen of meetkunde, publiceerde hij twee werkjes: een aritmetica in 1508 en een meetkundeboekje in 1513.

Het rekenboekje kreeg als titel Die maniere om te leeren cyffren na die rechte consten Algorismi. Int gheheele ende int ghebroken. Zoals de titel aangeeft leert het rekenen, zowel met gehele getallen als met breuken. Aansluitend volgen een aantal toepassingen, onder meer op de regel van drieën. Het werkje, waarschijnlijk door van der Noot zelf samengesteld, is uiterst elementair. Het schijnt wel enig succes te hebben gekend. Circa 1510 bezorgde de Antwerpse drukker Willem Vorsterman een nieuwe uitgave, vermeerderd met een hoofdstuk over het rekenen met penningen. Bij dezelfde drukker verscheen in 1529 een Franse vertaling onder de titel La maniere pour aprendre a cyfrer et compter par plumes et gectz selon la vraie science de Algorisme en nombre entier et rompu. Vermeldenswaard is nog dat het oudste in het Engels gedrukte rekenboekje, verschenen in 1537 bij John Herford te Saint Albans, uitvoerige stukken bevat die vertaald zijn uit Die Maniere.

Het tweede wiskundeboekje dat van der Noot publiceerde is Die waerachtige const der Geometrien

Thomas van der Noot, Die waerachtige const der Geometrien, 1513. Voorpagina. Foto uit privé-bezit ▪

[p. 116]

leerende hoemen alderhande breydden, lingden, dicten, ende hoochden der velden beemden bosschen berghen metselrien paveyselen torren huysen kercken ende alderhande dinghen meten sal. Hoemen oock maken sal die wynroede, om daer mede te roeden alderhande tonnen vaten cuypen backen ende diergelijcke. Deze lange titel geeft duidelijk aan voor wie het werkje in de allereerste plaats was bestemd: de landmeters en de wijnroeiers. In de eerste zeven hoofdstukken, het inleidende theoretisch deel van het werkje, vindt men definities van allerlei meetkundige figuren. In de volgende hoofdstukken leert men oppervlakten en inhouden berekenen. Het is een opsomming van regels, gepresenteerd zonder enige verklaring. Ze vormen een merkwaardig mengsel van juiste en onjuiste voorschriften, die reeds generaties lang kritiekloos werden overgeleverd. Voor de man van de praktijk, de landmeter of de wijnroeier, zijn vooral de laatste tien hoofdstukken van belang. Men leert er de constructie van drie instrumenten: de wijnroede of vizierstok waarmee men

Gielis vanden Hoecke, Een sonderlinghe boeck in dye edel conste Arithmetica, Antwerpen, 1537. Foto uit privé-bezit ▪

de inhoud van vaten en tonnen meet, de jakobsstaf en het geometrisch kwadrant, gebruikt door landmeters voor het meten van hoeken en het bepalen van hoogten of afstanden.

Hoe groot het succes is geweest van dit allereerste gedrukte Nederlandse meetkundeboek is moeilijk te achterhalen. Zeker is dat het decennialang in de Nederlanden het enige in de volkstaal geschreven handboek voor praktische geometrie is gebleven. De Antwerpse drukker Jan Roelants bezorgde in 1547 een nieuwe druk.

▪ De eerste kennismaking met de algebra

Op het gebied van de mathematische wetenschappen is de Renaissance gekenmerkt door de opkomst van de algebra. Anders dan in andere takken van de wiskunde is dit niet het gevolg van de herontdekking van de oude Griekse werken, maar de voortzetting van een middeleeuwse traditie. Vanaf de 15de eeuw verspreidde de algebra zich vanuit Italië naar Duitsland, en van daar naar Frankrijk en de Nederlanden. Het eerste werk waarin de algebra uitvoerig aan bod komt is de Summa de Arithmetica Geometria Proportioni et Proportionalita uit 1494 van Luca Pacioli (1445-1517). Deze omvangrijke compilatie, geschreven in de volkstaal, geeft een overzicht van wat in de 15de eeuw aan wiskundige kennis voorhanden was. Achtereenvolgens worden de aritmetica, de algebra, de meetkunde en het boekhouden behandeld. Een belangrijke rol in de ontwikkeling van het algebraïsch symbolenschrift speelde Etienne de la Roche's Larismethique, gepubliceerd te Lyon in 1520. Vooral in Duitsland verschenen in het eerste kwart van de 16de eeuw verschillende aritmetica's, waarin ook de ‘regula coss’ of algebra wordt behandeld. Tot de belangrijkste behoren Henricus Grammateus' Eyn new künsdich behend und gewiss Rechenbuchlin (1518, vele herdrukken) en Christoff Rudolffs Behend unnd hübsch Rechnung durch die kunstreichen regeln Algebre (1525).

Waar en wanneer men in de Zuidelijke Nederlanden voor het eerst heeft kennisgemaakt met algebra is moeilijk te achterhalen. Uit terloopse aanwijzingen in vroeg-16de-eeuwse werken kan men opmaken dat gedrukte literatuur toen reeds een vlugge verspreiding kende. Het is waarschijnlijk dat reeds voor 1530 sommige van de hierboven genoemde werken hun weg

[p. 117]

hadden gevonden naar belangstellenden te Leuven of elders. Het duurde echter tot 1537 vooraleer er iets over algebra in druk verscheen. In dat jaar bezorgde de Antwerpse drukker Simon Cock de uitgave van Een sonderlinghe boeck in dye edel conste Arithmetica, geschreven door Gielis vanden Hoecke. Over de auteur is weinig bekend. De opdracht van zijn boek dateert hij: ‘Gandavi ex nostra officina tertio Calendas Novembreis’ (30 oktober), en hij ondertekent als ‘AEgidius Hoecke’. Iets meer vernemen we uit de registers van de Leuvense universiteit. Onder de studenten ingeschreven op 29 augustus 1521 in de pedagogie De Lelie vinden we: ‘Egidius, zoon van Johannes Houck uit Gent’. Onderstellende dat hij toen circa vijftien jaar oud was, moet Gielis vanden Hoecke rond 1505 in Gent geboren zijn. Hoe lang hij in Leuven bleef is niet meer te achterhalen. Vermoedelijk slechts twee jaar, de duur van de studies in de artesfaculteit. Een laatste gegeven levert ons een Almanack ende Pronosticatie voor het jaar 1536, die hij liet drukken bij Pieter de Keysere te Gent. Daaruit vernemen we dat hij te Gent woonde op de Zandberg, waar hij zijn kalenders verkocht. Vermoedelijk was hij er ook als schoolmeester werkzaam.

Vanden Hoecke draagt zijn Sonderlinghe boeck in dye edel conste Arithmetica op aan de prior van de Sint-Michielsabdij te Antwerpen, de premonstratenzer Guilhelmus Rhetius of Willem van Rethy, die hij prijst om zijn geleerdheid en in het bijzonder om zijn mathematische kennis. Het boek begint met het aanleren van de vier hoofdbewerkingen, zowel voor gehele getallen als voor breuken. Ten behoeve van kooplieden gaat vanden Hoecke uitvoerig in op de kennis van maten en gewichten en van de verschillende munten. Hierop volgt een lange reeks vraagstukken, opgelost met de regel van drieën, de regel van de valse onderstelling of met andere methodes. Dan wordt het rekenen met wortelvormen geleerd. Hierbij beperkt vanden Hoecke zich niet tot kwadraat- en kubiekwortels, maar werkt hij ook meer algemeen met n-de wortels. Een stukje is gewijd aan de theorie van de proporties. Hij wijst op het belang ervan voor het berekenen van boldriehoeken in de astronomie, en geeft een voorbeeld ontleend aan de Almagest van Ptolemaeus. Aan de ‘regule cos’ of algebra wijdt vanden Hoecke 44 bladzijden. Hij omschrijft die wetenschap als volgt: ‘die cos dat is die rekeninghe van eenen dingh’. ‘Ding’ is de vertaling van het Italiaanse ‘cosa’, dat staat voor de onbekende. In Duitsland werd dit tot ‘Coss’ omgevormd en hier onder de vorm ‘cos’ overgenomen. Begonnen wordt met het rekenen met algebraïsche vormen. Dan volgt het oplossen van vergelijkingen van de eerste en de tweede graad en van vergelijkingen die, door het invoeren van een hulponbekende, tot tweedegraadsvergelijkingen kunnen herleid worden. Ook stelsels van lineaire vergelijkingen worden behandeld. Vanden Hoecke gebruikt een duidelijke en handige notatie voor de machten van de onbekende en voor het aangeven van de wortelexponent. Voor het eerst in de Nederlanden verschijnen hier de tekens + en - voor optellen en aftrekken of voor het aangeven van positieve en negatieve getallen.

Een sonderlinghe boeck eindigt met drie korte traktaatjes, het eerste over de vizierroede, dan iets over tijdrekening en het maken van kalenders. Het laatste is ‘een cleyn tractaet aengaende de practike vanden landmeten’. Het begint met enkele gegevens over de gebruikelijke landmaten. Daarna wordt geleerd hoe men de oppervlakte van veelhoekige landerijen kan berekenen. Vanden Hoecke 's duidelijke en betrouwbare uiteenzetting betekent een grote vooruitgang, vergeleken met de verwarde en niet zelden onjuiste regels in van der Noots boekje over geometrie.

Vanden Hoecke 's Arithmetica is zeker geen origineel werk. Hij erkent ruiterlijk in de proloog van zijn boek dat het werd samengesteld met het beste uit diverse werken, waaronder Latijnse, Duitse, Italiaanse en Franse. Uit nader onderzoek blijkt dat hij vooral uit de volgende werken heeft geput: Grammateus' Rechenbuchlin, Etienne de la Roche's Larismethique en Rudolffs Behend unnd hübsch Rechnung. Hele stukken uit deze drie werken zijn gewoon vertaald overgenomen. In het bijzonder het deel over algebra is grotendeels aan Rudolff ontleend.

Wel brengt vanden Hoecke een belangrijke wijziging aan: hij vervangt de oude cossische tekens voor de machten van de onbekende door de veel duidelijker en bruikbaarder notatie die hij overneemt uit Grammateus' Rechenbuchlin. Onder de gebruikte bronnen is vermoedelijk ook Pacioli's Summa di Arithmetica en een astronomisch werk: Johann Stöfflers Ephemeridum Opus (Tübingen, 1531).

Van Een sonderlinghe boeck verscheen in 1545 een tweede editie, eveneens bij Simon Cock te Antwerpen, maar met een enigszins gewijzigde titel: In Arithmetica een sonderlinge excellent boeck.

[p. 118]

▪ Wiskunde in dienst van landmeters en cartografen

Ongeveer even oud als Gielis vanden Hoecke was Jacob van Deventer (1500-1575), die op 24 april 1520 als student te Leuven werd ingeschreven. Hij volgde er de lessen van filosofie en studeerde daarna geneeskunde. Al vroeg moet hij zich hebben toegelegd op de landmeetkunde en het vervaardigen van kaarten. Op grond van zijn landmeetkundige en cartografische vaardigheden werd hem omstreeks 1540 de titel van Keizerlijk Geograaf verleend. Over Jacob van Deventers werkwijze bij de opmetingen op het terrein is weinig of niets bekend. Onderzoek van zijn kaarten bewijst hun zuiver meetkundige grondslag, berustende op hoekmeting. Van Deventers kennis van de wiskunde stond ongetwijfeld op een veel hoger peil dan wat in toenmalige werkjes over toegepaste geometrie en landmeetkunde te vinden was.

Beter ingelicht zijn we over het leven en het werk van Jacob van Deventers tijdgenoot Gemma Frisius. Geboren op 8 december 1508 te Dokkum in Friesland, kwam hij als zeventienjarige in 1526 naar Leuven, waar hij de studies in de artesfaculteit aanvatte. In maart 1528 was hij ‘magister artium’. Enkele jaren later vatte hij de studie aan van de geneeskunde. Op 30 augustus 1536 promoveerde hij tot doctor in de medicijnen. Naast de uitoefening van een medische praktijk gaf hij, vermoedelijk sinds 1539 en zeker vanaf 1542, ook les over geneeskunde. Zijn grootste verdienste ligt echter op het gebied van de wiskunde, astronomie, landmeetkunde en cartografie.

Over Gemma Frisius' activiteit gedurende zijn studietijd zijn we slechts matig ingelicht. Het eerste teken van zijn belangstelling voor wiskunde en astronomie is de publicatie in 1529 van een licht gewijzigde uitgave van de Cosmographia van de Beierse geograaf Petrus Apianus (1495-1552). Vier jaar later kwam er een heruitgave, aangevuld met een kort maar merkwaardig werkje met als titel Libellus de locorum describendorum ratione. Het is een handleiding voor het opnemen van regionale kaarten, steunend op het meten van hoeken. In het derde hoofdstuk leert Frisius hoe men de afstand tot een ontoegankelijk punt kan vinden, gebruikmakend van de gelijkvormigheid van driehoeken en de theorie van de verhoudingen. Hij geeft de gang van de berekeningen, maar geen bewijs. Wel houdt hij er één ter beschikking van ieder die er

Portret van een man (Gemma Frisius), vermoedelijk van de hand van Maarten van Heemskerk. Rotterdam, Museum Boymans - Van Beuningen, Inv. n^o 1347. © M.B.V.B. ▪

naar vraagt. Nergens wordt in de eerste uitgave van de Libellus verwezen naar het gebruik van goniometrische tabellen. Eerst in latere uitgaven, beginnende met die van 1540, noteert hij aan het einde van het werkje dat hij met opzet zwijgt over het gebruik van sinustafels, omdat dit niet tot de gebruikelijke methodes van de kosmografie (lees geografie) schijnt te behoren, maar thuishoort in meer wetenschappelijke beschouwingen.

In nauw verband met zijn bijdragen tot de landmeetkunde en de mathematische geografie staat de belangstelling van Gemma Frisius voor het verbeteren en vervaardigen van mathematische instrumenten. Getuige hiervan zijn werkje Usus Annuli Astronomici, over het gebruik van de astronomische ring. Hoewel geschreven in 1534, is de oudste gepubliceerde tekst hiervan te vinden in de uitgave Antwerpen 1539

[p. 119]

van Apianus' Cosmographia. Hij leert er onder meer hoe men met dit instrument hoogten en afstanden kan bepalen. Hierbij gebruikt hij nergens goniometrische tafels. Dit is wel het geval in zijn De radio astronomico et geometrico liber uit 1545, waarin hij een soort verbeterde jakobsstaf beschrijft en toepast bij allerlei geometrische, landmeetkundige of astronomische metingen. We ontmoeten hier een Gemma Frisius die duidelijk vertrouwd is met de trigonometrie zoals ze wordt uiteengezet door Johannes Regiomontanus (1436-1476) in zijn De triangulis omnimodis libri quin-

Gemma Frisius, Usus Annuli Astronomici, Antwerpen, 1539. Foto's uit privé-bezit ▪

que (Nurenberg, 1533). Hierin wordt de trigonometrie voor het eerst als een zelfstandige tak van de wiskunde behandeld. Ook de door Regiomontanus berekende tangenstafel neemt Frisius op in zijn Radio astronomico. Uit dit werkje blijkt nog dat hij tot de allereerste lezers heeft behoord van Copernicus' De Revolutionibus orbium caelestium, verschenen in 1543. Enkele keren verwijst hij naar het mathematische deel in boek 1 van dit werk.

Het enige zuiver mathematische werk dat Gemma Frisius publiceerde is zijn Arithmeticae practicae methodus, verschenen te Antwerpen in 1540. Het is opgedragen aan Willem van Rethy, aan wie ook Gielis vanden Hoecke drie jaar voordien zijn Arithmetica had opgedragen. Alle gebruikelijke onderwerpen worden er op bondige maar klare en duidelijke manier behandeld. Het boek sluit met een aantal toepassingen op het berekenen van de oppervlakte van driehoeken of de inhoud van bol en kubus. Gemma Frisius noteert hierbij dat hij er van afziet de gegeven regels te bewijzen, omdat ze een niet geringe meetkundige kennis onderstellen. Hij wil dit bewaren voor een afzonderlijk werk over praktische geometrie, dat echter nooit is verschenen. Gemma Frisius' Arihmetica werd een ongewoon succes. Meer dan zeventig uitgaven zijn bekend, waaronder vertalingen in het Frans en in het Italiaans. Enkele malen zinspeelt Gemma Frisius in zijn Arihmetica op wat hij de wonderlijke algebra noemt. Hij hoopt, met Gods hulp, daarover nog iets te publiceren, tenzij, wat hij verwacht, iemand anders hem voor is.

We wezen er reeds op dat in de eerste decennia van de 16de eeuw te Leuven in elk van de vier pedagogieën van de artesfaculteit wel lessen over aritmetica werden gegeven, maar dat de geometrie werd verwaarloosd. Ook privaat onderricht in de mathematische wetenschappen werd er omstreeks 1530 niet gegeven. Frisius schijnt de eerste te zijn die hiermee omstreeks 1540 is begonnen. Onder de toehoorders vinden we Gerard Mercator, die hierover vele jaren later, in een brief van 3 maart 1581 aan Wolfgang Haller in Zürich, schrijft dat hij weinig profijt haalde uit de lessen van Frisius over de theorie der planeten, omdat hij niets afwist van geometrie. Frisius gaf hem de raad Johannes Vögelins Elementale geometricum (Wenen, 1528) te bestuderen, een elementair leerboekje met de belangrijkste stellingen over vlakke meetkunde uit Euclides' Elementen. Wat hij niet verstond, liet hij zich

[p. 120]

uitleggen door Frisius. Dit stelde hem in staat na korte tijd de zes eerste boeken van Euclides te begrijpen.

De belangstelling binnen het Leuvense universitaire milieu voor astronomie, geografie en cartografie stimuleerde de vraag naar onderricht in wiskunde dat dieper ging dan wat in de artesfaculteit werd gegeven. Maar ook uit een andere hoek groeide belangstelling voor de mathematische wetenschappen. De humanistische beweging rond het Collegium Trilingue richtte zich aanvankelijk vooral op de vorming van taal en stijl en op het zo zuiver mogelijk schrijven en spreken van Latijn en Grieks. De ideale weg was de studie van de literatuur overgeleverd uit de Oudheid. Geleidelijk breidde de beweging zich ook uit tot andere gebieden, waaronder de mathematische wetenschappen. Een echo hiervan klinkt door in een oratio, rond 1540 te Leuven gehouden als inleiding op een reeks lessen over Euclides, door de medicus Justus Velsius (1502-1581). Hij publiceerde de tekst in 1544 te Straatsburg onder de titel: De Mathematicarum Disciplinarum vario usu dignitateque. Het werkje is opgedragen aan de Spaanse astronoom Juan de Rojas (16de eeuw), die rond de jaren 1540 in Leuven verbleef en er de lessen van Gemma Frisius volgde. In zijn rede beklemtoont Velsius de absolute noodzaak de oudere auteurs te bestuderen om tot een solide kennis van de wiskunde te komen. Hij vermeldt in het bijzonder Euclides, Archimedes, Apollonius, Nicomachus, Ptolemaeus en Proclus onder de Grieken, onder de Latijnen Boëthius, Vitelo en Jordanus Nemorarius, naast de meer recente Georg Peurbach en diens leerling Johannes Regiomontanus. Van zijn plannen heeft Velsius te Leuven niets kunnen verwezenlijken. Reeds voor 1540 verliet hij de Brabantse stad, waarschijnlijk uit vrees voor de inquisitie. Van dan af werd zijn leven een voortdurend zwerven. Hij overleed in 1581, waar is niet bekend.

In de jaren na 1545 heeft ook een Arnould de Lens te Leuven onderwijs in geometrie verstrekt aan studerenden in de artes. Hij publiceerde zijn lessen in 1565 te Antwerpen onder de titel In Geometrica Elementa Eisagoge. Het is een keuze van theorema's uit Euclides Elementen, die nuttig zijn bij bewijsvoeringen in geometrie. Op de titelpagina van zijn werkje stelt de Lens zich voor als ‘Medicus ac Mathematicus’. Ten onrechte werd hij tot nu toe geïdentificeerd met de Arnoldus Lencaeus die als lijfarts van tsaar Ivan IV omkwam in 1571 bij de verwoesting van Moskou door de Krim-Tartaren. Arnould de Lens was afkomstig uit Beloeil in Henegouwen. Hij overleed voor of in 1570.

Ook studenten zetten zich in om hun jongere collega's te helpen bij de studie van de wiskunde. In 1545 verscheen te Leuven een werkje met als titel Arithmeticoe practicoe libri quatuor. De auteur, Anathole Des Barres, een jonge edelman geboren in 1524 of 1525 te Salins in de Franche-Comté, werd op jeugdige leeftijd naar Leuven gezonden, waar hij filosofie en misschien ook rechten studeerde. Hoogstwaarschijnlijk leerde hij wiskunde bij Gemma Frisius. Reeds op de titelpagina laat hij weten dat zijn werk bestemd is voor de ijverige jeugd, en dat het werd samengelezen uit de beste auteurs. Gemma Frisius is duidelijk zijn belangrijkste bron geweest.

Bij het overlijden van Gemma Frisius in 1558 was de bloeiperiode van de mathematische wetenschappen rond de Leuvense universiteit reeds voorbij. Het onderwijs van de wiskunde in de vier colleges van de artesfaculteit schijnt in de loop van de jaren nog te zijn afgezwakt. De statuten van 1567-68 vermelden onder de verplichte vakken voor de mathesis alleen nog de aritmetica en de astronomie. Concrete gegevens over de situatie in 1568 bleven bewaard in een rapport van de rector bestemd voor koning Filips II. Hieruit blijkt dat alleen nog in de pedagogie Het Varken meetkunde werd onderwezen. In 't Kasteel gebruikte men de Arithmetica van de Zwitserse humanist Henricus Glareanus, en in De Valk die van Gemma Frisius. Misschien wel om aan die onbevredigende toestand te verhelpen, werd in 1563 door het Leuvense stadsmagistraat - weliswaar tegen de zin van de universiteit en de artesfaculteit - een publieke cursus mathematica opgericht. De lessen werden van 1565 tot 1569 gegeven door Johannes Stadius. Nadat door de Staten van Brabant de cursus tot een koninklijke fundatie was bevorderd, werd in 1569 Petrus Beausard als eerste koninklijke professor in de wiskunde benoemd. Beausard was in 1520 te Leuven geboren. Van 1559 tot aan zijn benoeming te Leuven was hij stadsdokter te Middelburg. Voor zijn studenten schreef hij een Arithmetices praxis (Leuven, 1573). Het is naar inhoud en opbouw een nabootsing van Gemma Frisius' Arithmeticae practicae methodus. Naast aritmetica doceerde Beausard ook geometrie. Hiervoor gebruikte hij als handboek Arnould de Lens' In Geometrica Elementa Eisagoge. Na de dood van Beausard in 1578 bleef de koninklijke leerstoel voor wiskunde onbezet.

[p. 121]

Medeoorzaak was ongetwijfeld de benarde toestand waarin de stad en de universiteit waren terechtgekomen ten gevolge van oorlog, bezetting, plundering en pest. De universiteit kwam ongeveer stil te liggen en vele studenten en professoren verlieten Leuven om ergens anders een veiliger werkkring te vinden.

▪ Mathematici uit de Zuidelijke Nederlanden in den vreemde

Reeds vroeg hebben kunstenaars en geleerden uit onze streken hun kunnen en kennis ver buiten de landsgrenzen uitgedragen en onderwezen. Paulus van Middelburg (1445-1533) werd omstreeks 1479 door de Venetiaanse Republiek uitgenodigd om in Padua astronomie te onderwijzen. Judocus Clichthove, geboren te Nieuwpoort in 1472 en overleden te Chartres in 1543, trok, na studies te Leuven, naar Parijs om er zich te vervolmaken. In samenwerking met zijn leraar Jacques Lefèvre d'Etaple (ca. 1455-1537) publiceerde hij met commentaar Boëthius' Arithmetica en de Algorismus van Sacrobosco. Die trend zette zich door in de 16de eeuw, en we zien hoe verschillende mathematici, vaak om zeer uiteenlopende redenen, hun vaderland verlieten en in den vreemde hun wetenschappelijk werk voortzetten.

Een van hen was Johannes Stadius, geboren te Loenhout op 1 mei 1527. Na studies aan de Leuvense universiteit vinden we hem te Antwerpen, vanwaar hij in augustus 1554 vertrok naar Turijn. Twee jaar later was hij terug in Brussel, waar hij astronomische waarnemingen verrichtte. In 1556 verschenen te Keulen zijn Ephemerides novae et exactae, met een lovend voorwoord van Gemma Frisius. Vanaf 1559 verbleef Stadius te Luik aan het hof van de prins-bisschop Robrecht van Berghen. Hoe lang hij er bleef is niet duidelijk, maar zeker niet tot na 1562. In 1565 werd Stadius benoemd tot professor van wiskunde en oude geschiedenis aan de Leuvense universiteit. Ondertussen waren de Spaanse Nederlanden in 1562 te Douai een tweede universiteit rijker geworden. In 1570 begon men er ook het onderwijs van de mathematica te organiseren. In afwachting van een definitieve benoeming inviteerde men een aantal professoren ‘es ars mathématique’, om een deel van het onderwijs te verzorgen. Het waren, naast Stadius, de Fries Phicdagus, de Duitser Johannes Stenius en de Schot Jacob Cheyneius. Het was uiteindelijk deze laatste die in 1572 op de leerstoel mathematica werd benoemd. Stadius zwierf ondertussen van de ene stad naar de andere, van Antwerpen naar Gent, en dan naar Brugge. In 1576 was hij in Parijs, waar hij deelnam aan een concours tot het begeven van een leerstoel wiskunde aan het Collège Royal. In 1568 had de bekende anti-aristoteliaan Petrus Ramus (1515-1572), sinds 1551 ‘lecteur royal’ in wiskunde, een testament gemaakt, waarin hij het grootste deel van zijn vermogen bestemde voor een nieuw te stichten leerstoel in wiskunde binnen het Collège. Hij stipuleerde dat er elke drie jaar zowel de zuiver mathematische vakken als de astronomie zouden behandeld worden. De kandidaten moesten Grieks kennen en op de hoogte zijn van de niet-mathematische vrije kunsten. Om de drie jaar zou een concours worden gehouden, waarvoor iedere wiskundige die aan de genoemde eisen voldeed, uit welk land dan ook, zou kunnen inschrijven. Na de dood van Ramus op 26 augustus 1572 werd diens testament niet direct tot uitvoering gebracht. Pas op 15 juli 1576 werd voor het eerst een examen tot het begeven van de Ramusleerstoel ingericht. Er waren drie kandidaten: Maurice Bressieu (1546-1617), Guillaume Postel (1505-1581) en Stadius. De leerstoel werd uiteindelijk toevertrouwd aan Bressieu, maar op grond van zijn prestaties werd ook Stadius nog hetzelfde jaar benoemd tot ‘lecteur royal’, met dezelfde bezoldiging als de andere koninklijke professoren. Slechts drie jaar heeft Stadius mathematica kunnen onderwijzen aan het Collège Royal: hij overleed te Parijs op 17 juni 1579.

De belangstelling van Stadius ging vooral uit naar de astronomie. Zijn enige specifiek mathematische publicatie is een bewerking van Ramus' Arithmetica, verschenen te Parijs in 1577. Ze werd herdrukt in 1581 te Parijs met als titel Arithmeticae libri duo a Io. Stadio recognita, en nogmaals te Leiden in 1581.

Een bijzondere figuur in het corps van de 16de-eeuwse mathematici is Jean Taisnier, geboren op 2 september 1508 te Ath in Henegouwen. Over zijn leven weten we niet veel meer dan wat hij, niet zonder enige overdrijving, ons meedeelt in zijn werken. Op de titelpagina's van zijn werken presenteert hij zich als uitstekend wiskundige, doctor in de beide rechten, bekroond poëet en voortreffelijk musicus. Uit de opdracht van enkele van zijn werken vernemen we dat hij in verschillende Italiaanse steden, hij vermeldt Rome, Ferrara, Bologna, Padua, Firenze, Palermo en Venetië, publieke lessen heeft gegeven over mathematica.

[p. 122]

Wanneer hij is overleden is niet bekend; waarschijnlijk in 1562 of niet lang erna.

Onder de werken van Taisnier zijn er een viertal die handelen over toegepaste wiskunde. Men leert er het gebruik van mathematische instrumenten en hun toepassing in de astronomie en de landmeetkunde. Hoogten, lengten of diepten worden bepaald met de methode van de gelijkvormige driehoeken. De overige werken van Taisnier, en in het bijzonder zijn groot Opus mathematicum (Keulen, 1562), hebben weinig of niets met wiskunde te maken, maar handelen over astrologie, chiromantie, theoretische en praktische muziek, magnetisme, enz. Alleen in zijn Opusculum de Natura Magnetis (Keulen, 1562) vindt men een betrekkelijk uitvoerig mathematisch fragment. Taisnier betwist er de opvatting van Aristoteles, dat een rechte lijn niet kan vergeleken worden met kromme lijnen. Hij verwijst naar Archimedes' werk Over de Cirkelmeting, en construeert een figuur begrensd door bogen van parabolen, die gelijke oppervlakte heeft als een door rechte lijnen begrensde figuur. Taisniers kennis van de klassieke mathematische literatuur blijkt niet alleen uit de talrijke verwijzingen naar Euclides, maar ook uit aanhalingen uit verschillende werken van Archimedes en verwijzingen naar Apollonius' Konika.

Van bij het prilste begin van de Hervorming hadden diverse religieuze stromingen aanhang gevonden in de grote Brabantse en Vlaamse steden, evenals in Doornik en Valenciennes. Ondanks de vele plakkaten die sedert Karel V tegen de ketters waren uitgevaardigd, verspreidde de Hervorming zich versneld na 1550. Het repressieve optreden van de regering bracht een vlucht op gang naar Frankrijk, Engeland en de westelijke Duitse territoria. Eén van die uitwijkelingen was de medicus Hendrik vander Broeck, beter bekend onder zijn gelatiniseerde naam Henricus Brucaeus. Hij was in 1531 te Aalst geboren, waar zijn vader schepen was. De eerste beginselen van de klassieke opleiding ontving hij te Gent, waarna hij voor verdere studie naar Parijs werd gezonden. Aan het Collège Royal volgde hij de lessen van Petrus Ramus. Na een driejarig verblijf aan de Parijse universiteit, keerde hij terug naar Vlaanderen en wijdde zich te Brugge aan het onderwijs van de jeugd. Lang bleef hij er niet. Hij trok naar Rome, waar hij privaat onderwijs gaf in wiskunde. Wat hij hiermee verdiende, stelde hem in staat in Bologna medicijnen te studeren. Hij promoveerde er in 1557 tot doctor in de wijsbegeerte en de geneeskunde. Zeker in 1561 was hij terug in zijn geboortestad Aalst, waar hij benoemd werd tot stadsarts en schepen. In 1565 werd hij lijfarts van Margaretha van Parma (1522-1586), landvoogdes der Nederlanden. Op aanbeveling van de Rostockse linguïst en poëet Nathan Chytraeus (1543-1598) riep hertog Johann Albrecht van Mecklenburg (1525-1576) Brucaeus naar Rostock om er aan de universiteit wiskunde en geneeskunde te onderwijzen. In juli 1567 werd hij er op de academische rol ingeschreven als ‘doctor Henricus Brucaeus, artis medicae et mathematicum Professor Rostochii’. Naast geneeskunde behelsde zijn leeropdracht de gehele wiskunde, dit is zowel aritmetica en geometrie, als astronomie en zelfs muziek. Over astronomie publiceerde Brucaeus De Motu primo libri tres (Rostock, 1575). Dit werkje wordt ingeleid met enkele begrippen uit de geometrie. Verschillende problemen over boldriehoeken worden er met behulp van trigonometrie opgelost. Boek III bevat een Brevis explicatio doctrinae sinuum, samen met een sinustafel. Een zuiver mathematisch werk is zijn Mathematicarum exercitationum libri duo (Rostock, 1575). In boek I wordt de theorie van de verhoudingen en de evenredigheden behandeld; boek II is gewijd aan de algebra.

Brucaeus' belangstelling voor astronomie werd zeker gestimuleerd door Tycho Brahe (1546-1601), met wie hij vriendschappelijke betrekkingen onderhield. Ze hadden elkaar vermoedelijk voor het eerst ontmoet en leren kennen in de loop van 1567, toen Tycho Brahe in Rostock verbleef en er studeerde. Henricus Brucaeus, humanist in hart en nieren en verdienstelijk mathematicus, overleed te Rostock in 1593.

Wanneer Brucaeus in 1567 in Rostock arriveerde, vond hij er een sinds enkele jaren ingeburgerde landgenoot, de medicus Levinus Baten of Battus. Diens vader, Bartholomeus Baten, omstreeks 1515 te Aalst geboren, was al vroeg aanhanger van de Hervorming geworden. Hiervoor vervolgd en enkele malen in de gevangenis geworpen, vestigde hij zich te Gent, waar hij een tiental jaren woonde. Toen ook hier de situatie te gevaarlijk werd, week hij met zijn hele gezin uit en vestigde zich omstreeks 1555 in Rostock. Levinus Battus is waarschijnlijk, nog voor 1540, te Aalst geboren. Voor de familie het land verliet, zou hij te Antwerpen onderwijs in wis- en sterrenkunde hebben gekregen van Johannes Stadius. In januari 1556 werd hij ingeschreven in de universiteitsregisters van Rostock. Drie jaar later promoveerde hij tot ‘magister artium’ aan de

[p. 123]

universiteit van Wittenberg. In 1560 werd hij, als professor van wiskunde, opgenomen in de Rostocker artesfaculteit. Vluchtend voor de pest en de oorlog die Rostock teisterden, trok hij in 1565 naar Italië. Hij zou er in Venetië tot doctor in de geneeskunde gepromoveerd zijn. Terug in Rostock, benoemde hertog Ulrich hem tot professor in de medicijnen en stelde hem aan tot zijn lijfarts. Als professor, zowel in geneeskunde als van ‘matheseos et artium’, had Battus wel een zeer zware opdracht. Hij gaf lessen, zowel over algemene astronomie, als over bijzondere onderwerpen als zons- en maansverduisteringen, verder over aritmetica - waarbij hij Gemma Frisius' Arithmeticae practicae methodus gebruikte - algebra en geometrie. Toen Tycho Brahe in de jaren 1566-68 te Rostock studeerde, woonde hij een tijdlang in bij Battus. Beide geleerden bleven ook later in nauwe betrekking met elkaar. Levinus Battus overleed te Rostock op 11 april 1591.

▪ Wiskunde in de volkstaal

De economische ontwikkeling in de Nederlanden is vooral in de decennia na 1530 gekenmerkt door een grote expansieve fase. Het meest markante verschijnsel hierin is de snelle groei van Antwerpen. De stad ontwikkelde zich tot één van de grootste markten in de wereld. Een gevolg hiervan was een steeds grotere complexiteit van de financiële en handelsverrichtingen, en een stijgende nood aan goede boekhoudsystemen. Voor de rekenmeesters bracht dit een nieuwe opgave mee: naast het onderwijs van rekenen en meetkunde werd ook het onderricht in het boekhouden steeds belangrijker. De plaats die Antwerpen als handelscentrum had verworven, had als bijkomend gevolg dat ook drukkers er zich bij voorkeur kwamen vestigen. Met de komst van Christoffel Plantijn (1520-1589) in 1555 en de stichting van zijn drukkerij kwamen de uitgeversactiviteiten er tot een internationaal hoogtepunt. Ook de natuurwetenschappen en het onderwijs van de wiskunde hebben hiervan geprofiteerd. Vooral vanaf 1540 merkt men een snel stijgend aantal publicaties van mathematische werkjes in de volkstaal, het overgrote deel bij Antwerpse drukkers. Ze zijn bedoeld als leerboek en de inhoud is meestal vrij eenvoudig. Dat ze aan een behoefte voldeden en er interesse voor bestond bewijzen de talrijke herdrukken.

Op 27 augustus 1547 werd aan de Antwerpse drukker Jan Roelants een gezamenlijk privilegie verleend voor ‘het prenten oft doen prenten, vercoopen ende distribueren den tijt van drij Jaren naestcomende’ van vier verschillende werken, waaronder twee meetkundige traktaten. Eén ervan was de reeds hoger vermelde herdruk van Die waerachtige const der Geometrien van Thomas van der Noot. Het andere kreeg als titel Een sonderlinghe profytelijck boeck, aenghaende de Conste ende practijcke van Geometrien, onlancx in Francoys beschreven by Meester Charles de Bouvelles, Canonick van Noyon. Charles de Bouvelles werd omstreeks 1470 te Saucourt (Picardië) geboren; hij overleed te Noyon circa 1553. Het juist genoemde werk is de vertaling van zijn Livre singulier et utile touchant l'art et pratique de géometrie, gedrukt te Parijs in 1542.

Tot de meest productieve 16de-eeuwse auteurs van leerboeken van wiskunde behoort zeker de uit Duitsland afkomstige Valentin Mennher. Hij werd omstreeks 1521 geboren te Kempten in Beieren. Waarschijnlijk woonde hij een tijd in Augsburg, vanwaar hij naar Antwerpen kwam, waar hij op 16 augustus 1549 poorter werd. Dat jaar werd hij ook opgenomen in de Sint-Ambrosiusgilde van de Antwerpse schoolmeesters. Naast verschillende traktaten over boekhouden publiceerde hij tussen 1550 en zijn overlijden in 1570 of 1571 diverse rekenboeken, op één Duits boek na alle in het Frans geschreven. Mennhers eerste rekenboek verscheen in 1550 met als titel Practique brifve pour cyfrer et tenir Livres de Compte touchant le Principal train de Marchandise. Voor zijn ‘lieben Landtsmennern den hoch Deutschen’ publiceerde hij in 1560 in hun taal een Arithmetica Practice. Zijn meest uitvoerig werk is de in 1565 verschenen Practicque pour brievement apprendre à ciffrer, & tenir livre de comptes, avec la regle de coss, & geometrie. Het bestaat, zoals de titel aangeeft, uit vier delen: rekenkunde, boekhouden, regel cos of algebra en meetkunde. Meetkundige onderwerpen komen ook reeds voor in Mennhers Livre d'Arithmeticque, contenant plusieurs belles questions et demandes, bien propres et utiles à tous Marchans uit 1561. Het is een verzameling van honderd vraagstukken, waarvan alleen het ‘Facit’ of de uitkomst wordt gegeven. De eerste 47 opgaven zijn van aritmetische aard; de oplossing van de overige vraagstukken steunt op het gebruik van sinustafels. Geheel gewijd aan de theorie van boldriehoeken en de toepassingen ervan in de geografie, de astronomie of de constructie van zonnewijzers is de Practicque des Triangles Spheriques, des Distances sur

[p. 124]

le Globe, des Horloges, Umbres, & autres ingenieuses & nouvelles questions Mathematicques, gedrukt bij Gilles Copenius te Antwerpen in 1564.

Willem Raets, afkomstig uit Maastricht, vestigde zich als koopman te Antwerpen. Hij publiceerde er in 1566 Arithmetica. Die fundamenten seer grondelyck verclaert, ende met veel schoonder questien geillustreert. Het jaar daarop volgde een handboekje voor wijnroeiers met als titel Practyck om lichtelyck te leeren visieren alle vaten metter wisselroede. Raets zelf deed herhaalde pogingen om als officieel wijnroeier door de stad te worden aangesteld, maar slaagde niet in de opgelegde proeven.

Van de Spaanse aanwezigheid te Antwerpen en van de internationale betekenis van de stad als uitgeverscentrum getuigt de publicatie in 1567 van een Spaans werk over wiskunde: Libro de Algebra en Arithmetica y Geometria. De auteur is de bekende Portugese geleerde Pedro Nuñez (1502-1578), ook wel Nonius genoemd. Hij was professor van wiskunde aan de universiteit van Coimbra en kosmograaf van de koning van Portugal. Oorspronkelijk schreef hij zijn werk in het Portugees, maar om het een zo groot mogelijke verspreiding te geven, vertaalde hij het in het Castiliaans en liet hij het in Antwerpen drukken.

In 1569 bezorgde de Antwerpse drukker Jan van Ghelen nog een herdruk van Thomas van der Noots rekenboekje uit 1508. Hetzelfde jaar verscheen te Brugge bij Pieter de Clerck een Cijfer-bouck, Inhoudende vele nieuwe, fraye, ende gherievighe Practijcken van Arithmetica, met vele meer andere zonderlijnghe zaken. De auteur, Adriaan vander Gucht, was inwoner van Brugge en schoolmeester aldaar. In de Franse opdracht van zijn boek ‘Aux vertueus et honorables Seigneurs les Marchants de la ville de Bruges’ bekent hij dat hij veel heeft ontleend aan andere werken. Bij nader toezien blijkt dat één van zijn belangrijkste bronnen Thomas van der Noots reeds meer dan zestig jaar oude rekenboekje is geweest. Hele passages zijn er woordelijk uit overgenomen.

Eduard Leon Mellema uit Leeuwarden werd op 2 december 1569 als poorter te Antwerpen ingeschreven. Hij was geboren in 1544 als zoon van burgemeester Leeuwe Mellema. Te Antwerpen publiceerde hij een tweedelige Arithmetique compose de plusieurs inventions & problemes nouveaux. Uit het eerste deel, verschenen in 1582 en opgedragen aan het stadsbestuur van Aken, vernemen we dat Mellema, voor hij

Portret van Valentin Mennher. Foto uit privé-bezit ▪

zich te Antwerpen vestigde, in Aken onderwijs had gegeven in Latijn en Frans, en bovendien in aritmetica, algebra en geometrie. Vier jaar later, bij het verschijnen van het tweede deel in 1586, blijkt Mellema te zijn verhuisd naar Haarlem, waar hij schoolmeester was. Wel noemt hij zich nog ‘citoien d'Anvers’. Zijn herhaalde verandering van woonplaats hangt ongetwijfeld samen met het feit dat hij de Hervorming was toegedaan. Zijn vertrek uit Aken wijt hij namelijk zelf aan de ‘malcontens papaux’.

Speciaal geschreven voor het onderricht van de koopman zijn de rekenboeken van Anthoni Smyters, rekenmeester, maar ook taal- en letterkundige. Hij werd omstreeks 1545 te Antwerpen geboren. In december 1566 werd hij opgenomen in de schoolmeestersgilde van Sint-Ambrosius. In 1580 publiceerde hij te Antwerpen een eerste rekenboek, Les fondemens d' Arithmetique, dat in 1589 werd herdrukt. Lijk zovelen voor hem verliet Smyters omstreeks 1580 met zijn familie de Zuidelijke Nederlanden om de ‘verdervighe inlantsche oorloghe’ te ontvluchten en ‘om met gheruster conscientie in vrijdom der Religie te moghen leven’. Hij vestigde zich te Amsterdam, waar hem,

[p. 125]

waarschijnlijk in 1593, admissie werd verleend ‘openbaerlijck te mogen doceren ende Schole op te rechten’. In 1600 verscheen nog van zijn hand te Rotterdam L' Arithmetique, laquelle contient les computations de plusieurs questions, necessaires à tous Marchands, Trafiqueurs et Amateurs de ceste science. Een Nederlandse uitgave, Arithmetica. Dat is: de Rekenkonste, in twee delen, volgde in 1609-10, eveneens te Rotterdam.

Onder de Antwerpse schoolmeesters, auteurs van elementaire rekenboekjes, vinden we ook nog Bernard Stockmans, Martin vanden Dijcke en Jan de Raeymaker. Stockmans, geboren te Antwerpen, werd op 17 december 1572 als schoolmeester ingeschreven in de Antwerpse gilde. Hij week later uit naar Dordrecht, waar hij vanaf 1588 als Frans schoolmeester was gevestigd. In 1589 publiceerde hij een Arithmetica ofte Cyfferboeck, dat tot in de 17de eeuw herhaalde malen werd herdrukt. Op dezelfde dag als Stockmans werd Martin vanden Dijcke opgenomen in de Antwerpse schoolmeestersgilde. Hij was toen 23 jaar oud en onderwees aritmetica en boekhouden. In 1591 gaf hij een Chijfer-boeck uit en in 1600 een Instructie om de Wijnroede ende Peghelstock te maken. Hetzelfde jaar verscheen nog van hem La vraye reigle d'arithmetique. Jan of Hans de Raeymaker publiceerde in de jaren 1580 te Antwerpen een Traicté d' Arithmétique contenant les cincq espèces, avec la regle de Trois et la Practique. Het werd, samen met de Nederlandse vertaling, Cyffer-Boeck in-houdende de vyf specien met den Reghel van dryen ende de practycke, tot in de 17de eeuw herhaalde malen herdrukt.

Het eerste zuiver mathematische werk dat te Luik werd gedrukt, verscheen in 1604 onder de titel Institution de l'arithmétique avec les gettons et la croye. Het werd samengesteld door Gilles Guillon (ca. 1575-ca. 1620), die zichzelf voorstelt als ‘Pasteur de S. Marguerite, pres la Cite de Liege’. Hier en daar voegt de auteur in zijn betoog een aanval in tegen de ketters. Blijkbaar richt hij zich vooral tegen Eduard Leon Mellema. Guillon verontschuldigt zich voor het dooreen mengen van wiskunde en religie, maar hij acht het nodig ‘om als tegengif te dienen tegen de boosaardigheid van Leon Mellema, die onder voorwendsel de aritmetica te verklaren een omzwerving inlast met de bedoeling door zijn irritatie en godslastering de Roomse Kerk omver te werpen’. In 1607 wisselde Guillon zijn Luikse pastorie voor Rome, waar hij zich verder ging bekwamen in wiskunde bij de beroemde Christoph Clavius, professor aan het Collegium Romanum. In 1610 was hij terug in Luik. Uit Rome had hij Clavius' Algebra (1608) meegebracht. Hij zette zich aan 't vertalen en publiceerde in 1612 te Luik bij Leonard Streel L'Algebre de Christophe Clavius, sommairement recueillie, et traduite du Latin par Gille Guillon.

▪ Coignet en Stevin: ingenieurs en mathematici

Twee auteurs die over wiskunde schreven in de volkstaal zijn tot nu toe onvermeld gebleven; niet omdat hun werk onbelangrijk is, maar omdat het van een heel ander niveau is. Beiden brachten het tot ingenieur en mathematicus in dienst van hun land: de ene, Michiel Coignet, in dienst van aartshertog Albrecht in de Zuidelijke Spaanse Nederlanden, de andere, Simon Stevin, leermeester van prins Maurits van Oranje in het Noorden.

Michiel Coignet werd in 1549 te Antwerpen geboren. Zijn vader vervaardigde astronomische instrumenten. Zo kwam de jonge Coignet al heel vroeg in aanraking met de mathematica. Misschien heeft zijn vader hem wel de eerste beginselen van die wetenschap bijgebracht.

Hoe hij er zich verder in bekwaamde is niet bekend. In 1568-69 - Coignet was toen negentien - werd hij aanvaard als schoolmeester in het gild. Toen reeds onderwees hij mathematica en Frans. Vanaf 1572 verstrekte Coignet ook onderricht in wiskunde aan de hogere officieren van het Spaanse hof. Rond diezelfde tijd werd hij door de stadsmagistraat van Antwerpen aangesteld tot wijnroeier.

De eerste publicatie van Coignet dateert uit 1573. Het is een verbeterde en sterk vermeerderde uitgave van een rekenboek van Valentin Mennher met als titel Livre d'Arithmetique, contenant plusieurs belles questions & demandes, propres et utiles à tous ceux qui hantent la Trafique de Marchandise. Nog hetzelfde jaar verscheen Cent questions ingenieuses et recreatives, pour delecter et aguiser l'entendement, de feu V. Menher Allemand. Souldées et amplifiées par les raisons geometriques requises à icelles par Michiel Coignet. Coignet geeft hierin de volledige oplossing van de honderd vraagstukken opgegeven door Mennher in zijn Livre d' Arithmetique van 1561. Als inleiding worden enkele theorema's uit de trigonometrie vermeld.

[p. 126]

In 1580 bezorgde Coignet een nieuwe uitgave van een rekenboek van Willem Raets onder de titel Arithmetica oft een niew Cyfferboeck...Met noch een Tractaet vande Wisselroede. Het werd nogmaals herdrukt in 1597.

Het is vooral met zijn Nieuwe onderwysinghe op de principaelste punten der zeevaert, toegevoegd aan het werk De Zee-Vaert (Antwerpen, 1580) van Petrus de Medina (1493-1567), dat Coignet bekendheid verwierf. Ook als cartograaf was Coignet werkzaam. We beperken ons hier echter tot zijn bijdragen tot de wiskunde.

In de jaren 1587-88 schreef de toen drieëntwintigjarige Galilei een korte studie over het bepalen van het zwaartepunt van een afgeknotte parabolische conoïde. Gepubliceerd werd het eerst veel later, in 1638, als appendix bij zijn Discorsi e Dimostrazioni matematiche, intorno à due nuove scienze. Op één of andere manier, misschien langs Christoph Clavius en de Antwerpse jezuïeten om, moet een kopie in handen van Abraham Ortelius gekomen zijn, die ze doorspeelde aan Coignet. Deze schreef hierover op 31 maart 1588 een brief aan Galilei, waarin hij zijn bewondering uitspreekt over de prestatie van de jonge geleerde. Uit de brief blijkt dat ook Coignet zich met het probleem had beziggehouden, maar hij geeft toe dat Galilei's oplossing beter is dan de zijne. Terloops klaagt Coignet er over dat de ongelukkige oorlogen die de Nederlanden teisteren de beoefening van de vrije kunsten belemmeren, zodat men met moeite iemand vindt die er zich mee bezighoudt. Wel vermeldt hij een zekere ‘Coloniensis, nomine Ludolpho’, die hem onlangs enkele geometrische problemen voorlegde. Bedoeld is Ludolf van Ceulen (1540-1610), van wie Coignet denkt dat hij afkomstig is uit Keulen. Eén van de problemen, dat hij zelf oploste met behulp van algebra, legt hij voor aan Galilei.

Een onderwerp dat erg in de belangstelling stond aan het einde van de 16de eeuw is de trigonometrie en het berekenen van sinus-, tangens- en secanstafels. De eerste volledig decimale sinustafel werd berekend door Johannes Regiomontanus in 1468, en voor het eerst uitgegeven in 1541. De eerste volledig nieuwe berekening van sinus- en tangenstafels werd uitgevoerd door Georg Joachim Rheticus (1514-1576) en gepubliceerd in 1596 door Valentinus Otto in het Opus Palatinum de Triangulis. Dat ook Coignet goed vertrouwd was met trigonometrie en het berekenen van goniometrische tafels, blijkt uit een bewaard gebleven handschrift uit 1610-12, dat een drietal traktaatjes bevat waarin verschillende aspecten van de goniometrie en de trigonometrie worden behandeld. Het is een soort handboek, dat Coignet schreef voor een zekere kapitein Thomas Francquin. Het begint met een Traicté des Sinus, contenant un abregé pour faire les tables des Sinus. Voor het berekenen van koorden in een cirkel volgt Coignet de methode die Ptolemaeus aangeeft in boek I van zijn Almagest. Hij steunt bovendien op het werk van Regiomontanus over het samenstellen van sinustafels. Het tweede traktaat is een zeer modern aandoend leerboek van vlakke driehoeksmeting. Het derde handelt over de pantometer, een door Coignet uitgedacht instrument. Het is een proportionaalpasser waarmee men allerlei problemen uit de praktische wiskunde mechanisch kan oplossen. Een uitvoerige beschrijving van de constructie van de pantometer en van de toepassingen ervan bleef bewaard in een aantal handschriften. Het is waarschijnlijk Coignets pantometer die Galilei de inspiratie bezorgde voor de constructie van wat hij zijn ‘compasso geometrico et militare’ noemde.

Coignet overleed in 1621, 74 jaar oud. Uit wat bewaard bleef van zijn geschriften blijkt hij een uitstekend leraar, vertrouwd met de mathematische kennis van zijn tijd. Hij was ook een uitmuntend practicus, die zijn theoretische kennis wist bruikbaar te maken voor de landmeter, vestingbouwer of militaire tacticus.

Simon Stevin werd te Brugge geboren in 1548. Over zijn jeugd en opleiding is niets bekend. Een tijdlang had hij een betrekking als boekhouder en kassier te Antwerpen. In 1577 was hij klerk op het belastingkantoor van de Vrije van Brugge. Vanaf 1581 was hij in Leiden, waar hij op 16 februari 1583 werd ingeschreven aan de universiteit als ‘Simon Stevinus brugensis’. Zeker omstreeks 1593 stond hij in dienst van prins Maurits van Nassau, waarschijnlijk met de titel ingenieur. Rond die tijd is ook hun gemeenschappelijke beoefening van de wiskunde, de natuurwetenschappen en de krijgskunde te situeren, waaruit Stevins meest omvangrijk werk, zijn Wisconstighe Ghedachtenissen, is gegroeid.

Het eerste werk dat Stevin publiceerde is Tafelen van Interest, midtsgaders de constructie der selver. Het werd bij Christoffel Plantijn te Antwerpen gedrukt in 1582. Stevins bijdragen tot de wiskunde vindt men in de volgende werken: Problemata Geometrica (Antwerpen,

[p. 127]

Simon Stevin, De Thiende, Leiden, 1585. Voorpagina en optelling. Foto's uit privé-bezit ▪

zonder jaartal, maar waarschijnlijk uit 1583), De Thiende (Leiden, 1585), L'Arithmetique (Leiden, 1585), Appendice Algebraique (Leiden, 1594) en in delen van Wisconstighe Ghedachtenissen (Leiden, 1605 en 1608).

Het bekendste van die werken is wel De Thiende, waarvan de ondertitel luidt: leerende door onghehoorde lichticheyt allen rekeningen onder den menschen noodich vallende afveerdighen door heele ghetalen sonder ghebrokenen. Dit bescheiden werkje van amper 36 bladzijden bevat de eerste systematische uiteenzetting over decimale breuken en hun gebruik. In een Aenhangsel bepleit Stevin de invoering van de decimale indeling van alle maten, gewichten en munten. Eerst meer dan twee eeuwen later zou dit door de Franse Revolutie worden verwezenlijkt.

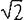
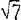
L'Arithmetique met het appendix La Practique d'Arithmetique heeft volop het karakter van een uitgebreid leerboek van aritmetica en algebra. Stevin begint met enkele interessante beschouwingen over het getalbegrip. Hij bestrijdt de sinds de Grieken geldende opvattingen dat I geen getal is, en dat het getal een discontinue grootheid is. Verder is hij van mening dat vormen als of even aanvaardbare getallen zijn als 2 of 7, en dat hieraan niets absurds of onredelijks is. Zoals gebruikelijk was in de 16de eeuw, beschouwt Stevin de algebra nog als een onderdeel of een bijzondere regel van de aritmetica. Voor het aangeven van de macht van de onbekende gebruikt Stevin een systeem dat ontleend is aan Raffaele Bombelli's Algebra (Bologna, 1572), en dat in wezen equivalent is met dat gebruikt door Gielis vanden Hoecke. Uitvoerig wordt het oplossen van lineaire en vierkantsvergelijkingen behandeld, en - voor het eerst in de Nederlanden - ook de derde- en vierdegraadsvergelijkingen. L'Arithmetique sluit met een lange reeks opgaven en met als toemaat een bewerking van de eerste vier hoeken van Diophantes' Arithmetica, het eerste en belangrijkste Griekse werk over algebra.

Een originele bijdrage tot het oplossen van algebraïsche vergelijkingen geeft Stevin in zijn slechts zes bladzijden tellende Appendice Algebraique, contenant regle generale de toutes equations, gedrukt bij Frans van Ravelingen te Leiden in 1594. Hij ontwikkelt er een benaderingsmethode voor de wortels van vergelijkingen van willekeurige graad.

In La Pratique d' Arithmetique komen de praktische toepassingen aan de beurt. Men vindt er de verschil-

[p. 128]

Simon Stevin, L'Arithmétique, Leiden, 1585. Voorpagina en theorema. Foto's uit privé-bezit ▪

lende regels uit de traditionele rekenboekjes terug: de regel van drieën, de regel van vijven, de gezelschapsregel, de ‘regula falsi’, de intrestregel, enz. In een Traicte des incommensurables grandeurs aan het einde van het werk geeft Stevin een herwerking van het moeilijke en beruchte tiende boek van Euclides' Elementen.

Het enige werk dat Stevin in het Latijn publiceerde is zijn Problemata Geometrica. Het is een zuiver wetenschappelijk werk, geheel in de geest van Euclides' Elementen. Vooral interessant is het deel waar hij handelt over de vijf regelmatige veelvlakken en over halfregelmatige veelvlakken. Dit zijn convexe veelvlakken, waarvan alle zijvlakken regelmatige maar niet alle onderling congruente veelhoeken zijn, en alle veelvlakshoeken aan de hoekpunten onderling congruent zijn. Zeven dergelijke veelvlakken werden reeds door Albrecht Dürer (1471-1528) beschreven in zijn Underweysung der messung mit dem zirckel und richtscheyt (Nurenberg, 1525). Stevin geeft er nog drie andere. Hij toont ook hoe sommige ontstaan uit de afknotting van regelmatige veelvlakken.

In het eerste deel van de Wisconstighe Ghedachtenissen, onder de titel Van de Driehouckhandel, behandelt Stevin de goniometrie, samen met de vlakke en sferische trigonometrie. Hij toont aan hoe men sinus-, tangens- en secanstafels berekent. De tafels die hij opneemt zijn ontleend aan Regiomontanus of aan Erasmus Reinholds Primus Liber Tabularum Directionum (Tübingen, 1554).

Praktische meetkunde behandelt Stevin in het tweede deel van zijn Wisconstighe Ghedachtenissen onder de titel Van de Meetdaet. Allerlei instrumenten, zowel voor het tekenen op papier als voor metingen op het terrein, worden besproken.

Onder de mathematische bijdragen die Stevin schreef voor prins Maurits dient nog zijn leerboek over perspectief vermeld te worden. Men vindt het in deel twee van de Wisconstighe Ghedachtenissen onder de titel Van de Verschaeuwing, een Nederlands woord dat Stevin vormde als vertaling van ‘scenographia’. In het voorwoord schrijft hij dat prins Maurits, die in staat was grondplannen of vooraanzichten van vestingen te

[p. 129]

lezen en te tekenen, het nuttig vond zich ook te oefenen in een derde manier van tekenen, namelijk de perspectief of het schilderen, om hiermee beter zijn inzichten aan anderen te kunnen meedelen. Hij ging hiervoor te rade bij de beste meesters in de schilderkunst, maar vond dat hun schetsen alleen op gissingen en louter op het oog steunden. Hij wenste exact de perspectief van elk voorwerp te kunnen tekenen, en dit met kennis van de gronden en hun mathematische bewijzen. Daarom is Stevin de belangrijkste schrijvers over dit onderwerp gaan raadplegen, en schreef hij daarover, in zijn eigen stijl, dit zuiver mathematisch traktaat.

▪ Adriaan van Roomen

Adriaan van Roomen of Romanus, zoals hij naar de gewoonte van zijn tijd zijn naam latiniseerde, werd op 29 september 1561 te Antwerpen geboren (en niet te Leuven, zoals meestal wordt aangenomen). Hij studeerde bij de jezuïeten te Keulen en daarna aan de Keulse universiteit, waar hij de studie van de geneeskunde aanvatte, die hij voortzette te Leuven en in Italië. In 1586 was hij professor aan de Leuvense universiteit, waar hij naast geneeskunde ook wiskunde onderwees. Het was vooral dit laatste vak waarnaar zijn belangstelling uitging. In een brief van 11 mei 1592 aan Christoph Clavius in Rome vertelt van Roomen één en ander over de beoefening van de mathematica in de Nederlanden. Hij schrijft dat er maar weinigen zijn die belangstelling tonen voor die moeilijke wetenschap. Onder degenen over wie hij iets weet, schijnen vooral Simon Stevin en Ludolf van Ceulen uit te blinken. De eerste kent hij uit zijn werken, de tweede uit wat over hem wordt gezegd en uit de briefwisseling die hij met hem voert. Van Roomen vermeldt ook het een jaar te voren verschenen werk Triangulorum Geometriae libri quatuor van Filip van Lansbergen. Hij karakteriseert het als bondig, maar goed geschreven. Van Lansbergen werd te Gent geboren in 1561. Wegens de godsdiensttroebelen waren zijn ouders in 1566 verplicht uit te wijken, eerst naar Frankrijk, daarna naar Engeland, waar hij theologie en wiskunde studeerde. Na zijn terugkeer rond 1579 nam hij een werkzaam aandeel in de kerkhervorming. In 1580 was hij predikant te Antwerpen. Hij bleef er tot de overgave van de stad in augustus 1585 door Marnix van Sint-Aldegonde aan Farnese hem verplichtte de Zuidelijke Nederlanden te verlaten. Van 1586 tot 1613 was hij predikant te Goes in Zeeland, waarna hij zich in Middelburg vestigde. Hij overleed er in 1632. Als wetenschapper hield hij zich vooral bezig met astronomie. Zoals menig tijdgenoot heeft ook van Lansbergen meegedaan aan de competitie voor de beste benadering van het getal π. In 1610 publiceerde hij hierover zijn Cyclometriae novae libri II, waarin hij beweert een betere benadering te hebben gevonden dan Ludolf van Ceulen.

In dezelfde brief aan Clavius bericht van Roomen ook over zijn eigen mathematische studies. Hij oefent zich in het berekenen van goniometrische tafels, en beschikt reeds over sinus-, tangens- en secanstafels nauwkeurig in zestien decimalen, maar dit slechts voor bogen om de drie graden. Hij is ook bezig de hele theorie van de boldriehoeken te verwerken in tabellen.

Van Roomens eerste zuiver wiskundige publicatie is zijn Ideae Mathematicae Pars prima, sive Methodus Polygonorum, gedrukt te Leuven bij Masius en verschenen in 1593. Hij draagt het op aan Clavius en geeft ook hier enkele aanduidingen over zijn wiskundige studies. Het is zijn bedoeling zich vooral bezig te houden met die gebieden waarin tot nu toe weinig werd gepresteerd. Hiertoe behoort de ‘doctrina polygonorum’, dit is de studie van de regelmatige veelhoeken, met in het bijzonder de berekening van hun zijden in functie van de straal van de omschreven cirkel. Hiervoor vond van Roomen reeds drie methoden, waarvan er één gebruikmaakt van algebraïsche vergelijkingen. Blijkbaar had hij reeds in 1590, onafhankelijk van François Viète (1540-1603), de relatie ontdekt die bestaat tussen de koorde van een boog α en de koorde van de boog n α (n een natuurlijk getal). Is de koorde van n α gegeven, dan levert die relatie een vergelijking van de n-de graad op, een zogenaamde hoekdelingsvergelijking, die de koorde van α als wortel heeft. Van Roomen bekent dat, voor n groter dan 4, het hem nog niet gelukt is die vergelijkingen op te lossen, maar dat hij ze naar zijn vriend Ludolf van Ceulen zond, die beloofde dit voor hem te doen. De eerste resultaten van zijn berekeningen publiceerde hij in de vier boeken van zijn Ideae Mathematicae. Van de vier sinds de Oudheid bekende regelmatige veelhoeken, de drie-, vier-, vijf- en vijftienhoek, en van de veelhoeken die er uit ontstaan door herhaalde verdubbeling van het aantal zijden, geeft hij de zijden in 32 decimalen nauwkeurig, als men de straal van de omgeschreven

[p. 130]

cirkel als eenheid neemt. De berekeningen zet hij door tot aan de veelhoek met 15 x 2⁶⁰ zijden. Als nevenresultaat vindt hij het getal π nauwkeurig in zestien decimalen. Van Roomen hoopt zijn verdere ontdekkingen over zijden van regelmatige veelhoeken te publiceren in nog een tiental boeken. Die plannen heeft hij echter niet kunnen verwezenlijken, afgezien van enkele fragmenten, verschenen onder andere titels. Zo publiceerde hij in 1602 de zijde van de regelmatige dertighoek in vele decimalen nauwkeurig, en in 1609, onder de titel Mathematicae Analyseos Triumphus of Triomf van de Mathematische Analyse, de zijde van de regelmatige negenhoek in 108 decimalen. In dit laatste werkje, dat van Roomen op eigen kosten publiceerde, staan alle berekeningen in extenso afgedrukt. Het resultaat is een boekje van 25 bladzijden met niets anders dan cijfers.

Alhoewel de mathematische inhoud van de Ideae Mathematicae onbeduidend is, heeft het werkje zich toch een plaats weten te veroveren in de geschiedenis van de wiskunde dankzij een uitdaging, gericht tot alle mathematici van de wereld. Het is een vergelijking van de 45ste graad, waarvan de oplossing wordt gevraagd. De Franse diplomaat - en in zijn vrije tijd mathematicus - François Viète herkende onmiddellijk de hoekdelingsvergelijking die het verband aangeeft tussen de koorde van een boog α en de koorde van de boog 45 α. De oplossing publiceerde hij onder de titel Ad Problema quod omnibus Mathematicis totius orbis construendum proposuit Adrianus Romanus Responsum (Parijs, 1595). Op zijn beurt legde Viète een probleem ter oplossing voor aan van Roomen: een cirkel te construeren, die drie gegeven cirkels raakt. Van Roomen antwoordde hierop met zijn Problema Apolloniacum quo datis tribus circulis, quaeritur quartus eos contingens (Würzburg, 1596).

Ondertussen had van Roomen in 1593 Leuven verlaten en een benoeming aanvaard aan de kort ervoor opgerichte universiteit van Würzburg. Zijn opdracht was het onderwijs van de geneeskunde, maar zijn belangstelling bleef wel in de eerste plaats uitgaan naar de wiskunde.

In 1594 publiceerde de beroemde Franse filoloog Justus Joseph Scaliger (1540-1609), professor te Leiden, een werk over de cirkelmeting onder de titel Cyclometrica Elementa duo. Hierin tracht hij te bewijzen dat Archimedes' benadering van het getal π onjuist is, en stelt hij een nieuwe, door hem gevonden benadering in de plaats. Onmiddellijk werd hem door verschillende mathematici gewezen op fouten in zijn werk. Als eerste kwam Ludolf van Ceulen die, nog geen twee weken na het verschijnen van het werk, aan Scaliger de raad gaf het in te houden en zo zijn eer te vrijwaren. Die welgemeende raad beantwoordde Scaliger alleen maar met bijtende spot. Toen van Roomen die onheuse behandeling van zijn vriend vernam, reageerde ook hij, en liet hij zijn kritiek door Franciscus Raphelengius, de uitgever van het werk, overmaken aan Scaliger. Deze bleef echter doof voor alle waarschuwingen. Nog in hetzelfde jaar 1594 liet hij een Appendix ad Cyclometrica sua drukken, waarin hij zijn werk verdedigt tegen wat hij ‘kwaadwillige critici’ noemt. Hij zond een exemplaar aan van Roomen, samen met een brief waarin men onder meer leest dat degenen die zijn beweringen niet aanvaarden, óf zijn werk niet begrijpen, óf van slechte wil zijn. Bij zoveel onwil kon ook van Roomen niet langer zwijgen. Hij achtte het nodig eens en voorgoed Scaligers paralogismen publiek aan de kaak te stellen, en publiceerde daarom in 1597 zijn In Archimedis Circuli dimensionem Expositio et Analysis. Apologia pro Archimede ad clariss. virum Josephum Scaligerum, Orontium Finoeum et Raymarum Ursum. Het eerste deel is een uitgave van de Griekse tekst van Archimedes' Cirkelmeting, met een Latijnse vertaling en een uitvoerige analyse. Het tweede deel is een apologie van Archimedes, waarin Scaligers bezwaren tegen diens methode worden ontzenuwd. Deel drie begint met een overzicht van de controverse rond Scaligers Cyclometrica Elementa. Daarna weerlegt van Roomen in tien dialogen de vermeende cirkelkwadraturen van Orontius Finaeus, Simon van der Eycke, Raymarus Ursus en uiteindelijk die van Scaliger. Van Roomen introduceert in dit werk de originele idee van een algemene theorie over grootheden: een geheel van begrippen, axioma's, relaties en theorema's, geldig zowel voor aritmetische en geometrische als voor andere soorten grootheden. Het is een soort abstracte algebra avant la lettre, die hij ‘Prima Mathematica’ noemt, en die dient als basis voor zowel de aritmetica als de geometrie.

Op de idee van de ‘Prima Mathematica’ komt van Roomen terug in een werk dat spijtig genoeg onvoltooid is gebleven, maar waarover we toch iets moeten zeggen. Door bemiddeling van de Praagse geleerde Thaddeus Hajek (1525-1600) kwam van Roomen in het bezit van een handschrift met een Latijnse versie

[p. 131]

van de Algebra van de Arabische wiskundige al-Khwarizmi (ca. 780-ca. 850). Hij besloot het werk uit te geven, voorzien van commentaar. De tekst moet reeds in 1600 of kort erna in handen geweest zijn van de Würzburgse drukker Georg Fleischmann. Begonnen werd met zetten en drukken, maar dit werd om één of andere reden voortijdig gestaakt. Slechts 72 bladzijden kwamen klaar, de rest is nooit verschenen. Er is geen titelpagina, noch opdracht of voorwoord, maar de tekst begint onmiddellijk met van Roomens inleiding onder de titel In Mahumedis Arabis Algebram Prolegomena. Eerst komen enkele algemene beschouwingen over de naam, het object en het nut van de algebra. Dan volgt een soort geschiedenis van de algebra onder de vorm van lijsten van auteurs die er over schreven. Na die inleiding begint de eigenlijke publicatie van al-Khwarizmi's werk onder de titel Liber Algebroe et Almucabula de quaestionibus arithmeticis et geometricis. Van Roomen geeft de eerste twee regels van het werk en begint dan aan het eerste deel van zijn commentaar, die loopt over zestien bladzijden. Hij geeft er wat hij de beginselen van de algebra noemt: definities, axioma's, postulaten, theorema's. Wat we hier krijgen is niets anders dan de verdere uitwerking van zijn idee van de ‘Prima Mathematica’. Het vol-

Portret van Justus Joseph Scaliger. In: Isaac Bullart, Académie des Sciences et des Arts, Brussel, 1695. © B.U.L. ▪

gende fragment uit al-Khwarizmi's werk, een halve bladzijde lang, introduceert het indo-arabische decimale positietalstelsel. Als commentaar geeft van Roomen een beschrijving van het systeem. In het derde fragment uit al-Khwarizmi worden de begrippen ‘wortel’ voor de onbepaalde grootheid x en ‘kwadraat’ voor x² ingevoerd. Vanaf hier gaat het dan mis met van Roomens commentaar. Aan de hand van volledig uitgewerkte voorbeelden leert hij de opeenvolgende machten van een getal berekenen en de 2de, 3de, 4de, 5de,...wortel trekken. Daarop volgt een uitvoerige theorie over machtsverheffing en worteltrekking. Zijn methode berust op de ontwikkeling van (a + b)ⁿ. Om bij het rekenen vaak voorkomende bewerkingen niet telkens te moeten herhalen, geeft hij twee uitgebreide tabellen, één met de eerste 33 machten van de getallen 1 tot 9, en één met de coëfficiënten van (a + b)ⁿ voor n gaande van 2 tot 69. Dit alles levert bladzijden en bladzijden cijfers. Op bladzijde 72, de laatste die werd gedrukt, kondigt van Roomen nog een aantal voorbeelden van machtsverheffing en worteltrekking aan. Hij merkt op dat sommige van die bewerkingen zo omvangrijk zijn, dat ze acht of negen bladzijden beslaan, die op een speciale manier moeten gedrukt worden. Waarschijnlijk is dit de druppel geweest die de emmer deed overlopen en de drukker deed besluiten ermee te stoppen. Van Roomens liefde voor monsterberekeningen is waarschijnlijk de oorzaak dat het interessante en waardevolle dat hij over algebra te vertellen had, ons onthouden werd.

Van Roomen schreef niet alleen over wiskunde, maar ook over astronomie, fysica, meteorologie, geografie, chronologie, geneeskunde en allerlei andere onderwerpen als pyrotechnie, farmacologie en botanica. Als humanist en mathematicus stond hij in betrekking met vele geleerden, onder wie Justus Lipsius, Rembert Dodoens, Ulisse Aldrovandi, Jan Brozek, Christoph Clavius, Johann Kepler en Tycho Brahe. Als medicus kan men hem eren als de grondlegger van het medisch onderwijs aan de universiteit van Würzburg. Nadat hij er tien jaar had gewerkt, vroeg hij in maart 1603 de toelating voor lange tijd afwezig te zijn om rust te zoeken in zijn vaderland. Kort daarop was hij in Leuven, waar hij twee jaar bleef. De volgende jaren vinden we hem afwisselend in Würzburg en Leuven. In 1607 bood hij zijn ontslag aan als professor. Tussen 1610 en 1612 verbleef hij in de Poolse stad Zamosc, waar hij Thomas Zamojski (1595-1638), zoon van de beroemde

[p. 132]

Poolse staatsman Jan Zamojski (1541-1605), onderwijs gaf in wiskunde. Van Roomen overleed op 4 mei 1615 in Mainz, op weg naar Spa, waar hij nog genezing hoopte te vinden.

▪ Onderwijs van de wiskunde in de 17de eeuw

Na het vertrek van Adriaan van Roomen uit Leuven in 1593 schijnt de belangstelling voor de mathematische wetenschappen er tot een dieptepunt te zijn gedaald. Sinds de dood van Beausard in 1578 was de koninklijke leerstoel voor wiskunde onbezet gebleven. Eerst in 1610 werd opnieuw een titularis benoemd, de Mechelaar Jan Storms of Sturmius (1559-1650). Hij was toen vijftig en zou nog gedurende 36 jaar de leerstoel bezet houden. Ondertussen liet hij zich in 1634, hij was toen vijfenzeventig, nog benoemen tot professor in de geneeskunde. Dit lange professoraat heeft het onderwijs van de wiskunde zeker niet bevorderd. Omstreeks 1638, Sturmius was toen bijna tachtig, volgden nog hoogstens twee of drie studenten zijn lessen. Over wiskunde schreef hij De accurate circuli dimensione et quadratura, cum sylvula epigrammatum, aenig-

Portret van Jan Zamojski. In: Isaac Bullart, Académie des Sciences et des Arts, Brussel, 1695. © B.U.L. ▪

matum, aliorumque versuum de numeris, ad animum partim instruendum, partim recreandum inventis (Leuven, 1633). Het is een onbenullig werkje, geschreven in verzen, dat met de ‘nauwkeurige cirkelkwadratuur’ niets te maken heeft.

Misschien wel om de aandacht te vestigen op die onaanvaardbare situatie verscheen in 1638 een anoniem pamflet, als nieuwjaarsgift voor 1639 aangeboden aan alle mathematici van de Leuvense universiteit. Het bevat drie opgaven, die alle betrekking hebben op het oplossen van vergelijkingen of stelsels van vergelijkingen. Ze staan in direct verband met de uitdaging die Adriaan van Roomen in 1593 richtte tot alle mathematici van de wereld. Dat de opsteller van het pamflet weinig verwacht van de Leuvense professoren blijkt duidelijk uit de slotzin: ‘Wie zal dit lezen? Misschien twee, misschien ook niemand. Schandelijk en jammer’.

Misschien is het pamflet toch niet helemaal zonder effect gebleven, want nog in de loop van 1639 werd een poging ondernomen om de situatie te verbeteren door de aanstelling van Gerard van Gutschoven (1615-1668) als suppleant van Sturmius. Het resultaat was dat het aantal studenten in de cursus wiskunde weer ging stijgen. Van Gutschoven verliet echter reeds het volgende jaar Leuven, om zich te Antwerpen te vestigen, de leerstoel wiskunde zo goed als vacant achterlatend. In 1646 nam Sturmius eindelijk ontslag als ‘professor regius’ in de mathesis en werd Gerard van Gutschoven in zijn plaats benoemd. Van Gutschoven had in Leuven geneeskunde gestudeerd. Een tijdlang verbleef hij in de Noordelijke Nederlanden, waar hij in persoonlijk contact kwam met Descartes. Hij werd een fervent voorstander van de cartesiaanse filosofie, en was ook vertrouwd met Descartes' Géométrie. René de Sluse vermeldt in een brief van 18 augustus 1662 aan Christiaan Huygens een vierdegraadskromme die hem door van Gutschoven werd gesuggereerd. Voor zijn studenten schreef hij een beknopt rekenboekje, Arithmeticae practicae regulae brevissimae (Leuven, 1654). Postuum verscheen nog Arithmeticae virgularis seu tabulae pythagoricae mobilis elucidatio (Leuven, 1673) over het gebruik van de door John Neper uitgedachte rekenstaafjes. In een anoniem manuscript, waarschijnlijk in van Gutschovens hand, bevinden zich uitgebreide versies van de hierboven genoemde werkjes. Het bevat verder een traktaatje De Perspectiva, grotendeels ontleend aan Stevin, en

[p. 133]

Gerard van Gutschoven, De Perspectiva. Handschrift. Foto uit privé-bezit ▪

een stukje over ‘den talstock’, een gegradueerd instrument dat kan gebruikt worden bij het richten van mortiergeschut of bij het bepalen van hoogten.

Weinig is geweten over het onderwijs van de wiskunde te Douai aan de tweede universiteit in de Zuidelijke Nederlanden. In 1620 werd de jezuïet Charles Malapert er benoemd op de leerstoel wiskunde. Hij zag het levenslicht te Bergen in 1581, onderwees filosofie te Pont-à-Mousson en wiskunde in Polen en te Douai. Wanneer Filips IV het Colegio Imperial van de jezuïeten te Madrid tot universiteit verhief, werd Malapert er in 1629 benoemd tot professor in de mathematica. Hij overleed echter in Vittoria, op weg naar Madrid, op 5 november 1630. Malapert is vooral bekend als Latijns dichter en astronoom. Voor zijn studenten publiceerde hij een bewerking van de eerste zes boeken van Euclides' Elementen onder de titel Euclidis Elementorum libri sex priores. Quorum demonstrationes tum alibi sparsim, tum maximè libro quinto ad faciliorem captum accomodavit (Douai, 1620, 1625, 1633). In hetzelfde jaar verscheen ook zijn Arithmeticae practicae brevi Institutio. In qua nova ratio multiplicandi et dividendi per tabulam Pythagoricam & alia non passim obvia explicantur (Douai, 1620, 1626). Met de nieuwe methode van vermenigvuldigen en delen, aangekondigd in de titel, bedoelt Malapert het gebruik van wat hij de tabula Pythagorica mobilis noemt, dit zijn rekenstaafjes zoals ze worden beschreven door John Neper in zijn Rabdologiae seu numerationis per virgulas libri duo (Edinburg, 1617). Malapert vermeldt Neper niet, en het is ook niet zeker of hij zijn idee aan hem ontleende. Het is even goed mogelijk dat hij werd geïnspireerd door het werk van de Luikse ingenieur Jean Gallé (ca. 1580-ca. 1636), die in zijn Nouveau Epitome d'Arithmétique (Luik, 1616) een door hem gevonden rekenmethode met staafjes aankondigt. Een volledige uiteenzetting van zijn methode gaf hij eerst in zijn Nouvelle invention d'apprendre l'arithmétique par le moyen de dix petits batons, avec l'unzième servant à l'extraction des racinnes quarées et cubes (Parijs, 1635).

Met Gallé zijn we beland in Luik, waar sinds 1614 het college van de Engelse jezuïeten was gevestigd. Jonge jezuïeten studeerden er filosofie en theologie. Tot het filosofisch curriculum behoorden ook de mathematische wetenschappen. De meest bekende onder de

[p. 134]

professoren is ongetwijfeld pater Francis Hall of Line (1595-1675), meestal met zijn Latijnse naam Linus aangeduid. Hij kwam naar Luik in 1630 om er wiskunde en Hebreeuws te doceren. Bekendheid verwierf hij vooral als ontwerper van zonnewijzers en - in de laatste jaren van zijn leven - door zijn discussie met de jonge Newton over de kleurentheorie. Als wiskundige mengde hij zich een paar maal in betwistingen rond mislukte cirkelkwadraturen. Voor het eerst in 1657 in verband met pater Gregorius a Sancto Vincentio's pogingen om het probleem op te lossen (zie volgend nummer). Een tweede gelegenheid bood het verschijnen van Exercitatio de Geometria Indivisibilium et Proportione Spiralis ad Circulum (Londen, 1658) van Thomas de Albis, gelatiniseerde naam van de Engelse wiskundige Thomas White (1588-1680). Vermoedelijk op vraag van René de Sluse weerlegt Linus de erin voorkomende cirkelkwadratuur in zijn De Pseudoquadratura circuli Dom. Thomae Witi (Londen, 1659). White antwoordde met een Apologia pro doctrina sua ad calumniatores (Londen, 1660), waarop Linus weer reageerde met een Refutation of the attempt to square the circle (Londen, 1660).

Enige gegevens over de inhoud van het wiskundeonderwijs in het college geeft pater John Keynes (ca. 1625-1697), die er een tijdlang studieprefect en later rector was. Het bericht dateert uit 1685, en stelt de zaken misschien wat te mooi voor, maar geldt voor een groot deel ook reeds voor de periode waarin Linus er wiskunde doceerde. Men vangt aan met aritmetica en geometrie. Perspectief wordt onderwezen als een deel van de optica. Ook de algebra ontbreekt niet, evenmin als de methode van de ‘indivisibilia’, naast verschillende geleerde onderwerpen uit de Konika van Apollonius en uit het werk van meer recente auteurs.

Onder de docenten wiskunde in het laatste kwart van de 17de eeuw en het begin van de 18de eeuw waren nog de paters Edward Slaughter (1655-1729) en Jacob Gooden (1670-1730). De eerste publiceerde Arithmetica methodicè et succinte tradita (Luik, 1702). Van de tweede hebben we Trigonometria plana et sphaerica cum selectis ex geometria et astronomia problematis (Luik, 1704).

Naast de universiteiten van Leuven en Douai en het college van de Engelse jezuïeten te Luik was er in de Zuidelijke Nederlanden nog een vierde centrum - en niet het minste - waar wiskunde werd onderwezen. Hieraan is het volgende nummer gewijd.

▪ De wiskundeschool van de Vlaamse jezuïeten

In april 1606 richtte Carolus Scribani (1561-1629), rector van de jezuïetengemeenschap te Antwerpen, een petitie tot de magistraat van de stad om te mogen beschikken over een leegstaand huis, om er het nogal in het nauw zittende jezuïetencollege in onder te brengen. Hij ondersteunde zijn vraag met de belofte later een speciale school voor wiskunde te openen. De vraag van Scribani werd ingewilligd, maar van de school kwam voorlopig niets. Te Antwerpen verbleef toen pater Frans Aguilon, geboren te Brussel in 1567. Naast de vele opdrachten die hij te vervullen had, en zijn werk als architect bij de bouw van de Antwerpse jezuïetenkerk, was hij ook actief op het terrein van de wetenschap. In 1613 verscheen bij de Plantijnse drukkerij zijn Opticorum libri sex, een prachtig in folio met een frontispies en zes vignetten getekend door Rubens. In de boeken IV en V vindt men reeds een aantal zuiver wiskundige lemma's, die moeten dienen als basis voor de geometrische optica. Ook het zesde en laatste boek, dat ongeveer een derde van het hele werk beslaat, is zuiver mathematisch. Het behandelt de geometrische theorie van de projecties. In de inleiding van zijn werk belooft Aguilon de zes boeken over optica te laten volgen door vier over catoptrica en nog enkele over dioptrica. Ook zinspeelt hij op een traktaat over kegelsneden dat hij zinnens is te schrijven. Niets van deze publicaties werd echter verwezenlijkt. Wel bleef een handschrift van Aguilon bewaard, thans in de Koninklijke Bibliotheek te Brussel, met een reeks lemma's die misschien als voorbereiding van de beloofde werken moesten dienen. Drie onderwerpen worden er behandeld. Het eerste is het reeds uit de Oudheid stammende probleem van een hoek in drie gelijke delen te verdelen. Hierop volgt een reeks lemma's over de harmonische dubbelverhouding of de verdeling van een lijnstuk in uiterste en middelste reden. Het laatste stuk bevat een vijftigtal lemma's over de ellips.

In december 1615 arriveerde pater Gregorius a Sancto Vincentio te Antwerpen. Hij was te Brugge geboren in 1584. In oktober 1605 trad hij te Rome in het noviciaat van de jezuïeten. Naast filosofie en theologie, studeerde hij wiskunde in het Collegium Romanum, waar hij de twee vooraanstaande mathematici Christoph Clavius en Christoph Grienberger leerde

[p. 135]

kennen. Sancto Vincentio was de geschikte man om, samen met Aguilon, het oude maar nooit vergeten plan van lessen over wiskunde te verwezenlijken. Aguilon overleed echter reeds in maart 1617, amper 51 jaar oud. In de herfst van dat jaar startte Sancto Vincentio eindelijk de cursus wiskunde, die niet alleen bestemd was voor jezuïeten, maar ook openstond voor externe geïnteresseerden. Reeds in 1621 verhuisde de school voor wiskunde naar Leuven, waar Sancto Vincentio zijn onderwijs voortzette tot 1625.

Reeds te Antwerpen had Sancto Vincentio zijn wetenschappelijk onderzoek aangevat, hierin geïnspireerd door het werk van Aguilon. De meest vruchtbare periode van zijn leven, gekenmerkt door meer dan één mathematische ontdekking, waren echter de jaren die hij te Leuven doorbracht. Met een nieuwe door hem uitgedachte infinitesimaalmethode geloofde hij uiteindelijk de sleutel te hebben gevonden voor de oplossing van het eeuwenoude probleem van de cirkelkwadratuur. Aan de generaal van de jezuïetenorde, Mutius Vitelleschi (1563-1645), vroeg hij toelating om de resultaten van zijn onderzoek te publiceren. Sancto Vincentio kreeg de raad zijn handschrift naar Rome te zenden, om het te laten onderzoeken door Christoph Grienberger, de opvolger van Clavius aan het Romeins College. Met de hulp van enkele medewerkers, onder wie zijn vroegere leerlingen Ignatius Der Kennis, Willem Boelmans en Theodorus Moretus, werden de nodige teksten klaargemaakt en begin 1625 naar Rome gezonden. Een definitief oordeel kon echter ook Grienberger niet geven, maar hij zag er wel wat in. Vitelleschi bleef echter voorzichtig en schreef op 19 april 1625 aan Florent de Montmorency (1580-?), overste van de provincie Flandro-Belgica, Sancto Vincentio naar Rome te sturen, om daar samen met Grienberger de zaak verder te onderzoeken. Zowat anderhalf jaar werkte Sancto Vincentio er aan het ordenen en aanvullen van zijn werk. Hierover brengt Grienberger verslag uit aan Vitelleschi in een brief van 11 oktober 1627: voorlopig schijnt de cirkelkwadratuur er nog niet in te zitten, maar de geschriften van Sancto Vincentio bevatten zoveel originele ideeën, die, wanneer ze gepubliceerd worden, de bewondering van de geleerden zullen afdwingen. Een toelating tot publicatie kwam er voorlopig niet.

Einde 1627 keerde Sancto Vincentio terug naar de Nederlanden. Hij bleef er slechts kort, want op vraag van keizer Ferdinand II werd hij in 1628 naar Praag gezonden. Ondertussen was koning Filips IV van Spanje in onderhandeling met de generaal van de jezuïeten om een professor voor wiskunde te bekomen voor het Colegio Imperial te Madrid. Amper geïnstalleerd te Praag kreeg Sancto Vincentio bericht dat hij in Madrid benoemd was, maar, getroffen door een beroerte, was hij in de onmogelijkheid te vertrekken. Zijn zwakke gezondheid verplichtte hem een helper te vragen. Hij stelde twee van zijn vroegere leerlingen voor: Theodoor Moretus, of, indien deze niet beschikbaar was, Jan-Karel della Faille. Laatstgenoemde werd in Sancto Vincentio's plaats naar Madrid gezonden. Moretus kreeg de opdracht Sancto Vincentio te gaan helpen. Hij arriveerde in Praag in de loop van 1629. Maar reeds in 1631 maakte de inname van Praag door de Zweden een einde aan zijn werk. Sancto Vincentio keerde terug naar Vlaanderen. Hij zou er tot aan zijn dood verblijven in het jezuïetencollege te Gent. Bij de plundering van Praag ging een deel van zijn manuscripten verloren. De rest werd gered door zijn confrater, pater Rodericus de Arriaga (1592-1667), die ze naar Wenen in veiligheid bracht. Het duurde echter tot 1641 voor Sancto Vincentio ze terug in zijn bezit kreeg. Met de sinds 1625 voorhanden zijnde teksten werd begonnen aan de definitieve redactie van zijn groot werk over de cirkelkwadratuur. In 1646 was het eindelijk klaar en kon het drukken beginnen. Het verscheen het jaar daarop bij Joannes en Jacobius Meursius te Antwerpen. Het is een groot in folio van meer dan 1.250 bladzijden. Op de prachtige titelpagina leest men: Problema Austriacum Plus Ultra Quadratura Circuli. Meestal wordt het werk aangegeven met de voortitel op het eerste blad: Opus Geometricum Quadratura Circuli et Sectionum Coni Decem libris comprehensum. Alvorens dieper in te gaan op de inhoud van dit werk en op de invloed ervan, blikken we even terug om kennis te maken met enkele van Sancto Vincentio's leerlingen.

Tot de allereerste studenten van Gregorius a Sancto Vincentio te Antwerpen behoorde Jan-Karel della Faille, telg uit een bekende koopmansfamilie. Hij werd geboren te Antwerpen op 1 maart 1597. In september 1613 trad hij in bij de jezuïeten. Gedurende drie op elkaar volgende jaren, van 1617 tot 1620, volgde hij de lessen van wiskunde. In 1620 verdedigde hij met brio een aantal mathematische thesissen. Nog datzelfde jaar werd hij naar Dôle gezonden om er theologie te studeren, maar hij kreeg tegelijk de opdracht

[p. 136]

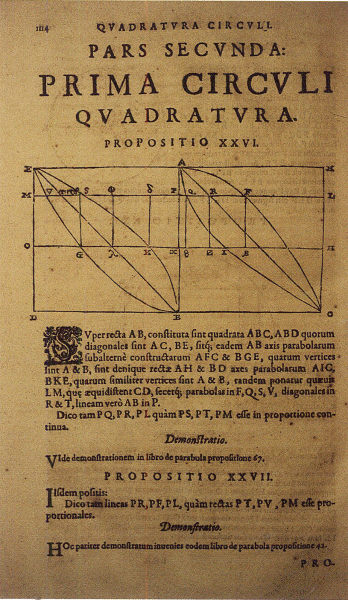
Gregorius a Saneto Vincentio, Opus Geametricum Quadratura Circuli el Sectionum Coni Decem libris comprehensum, Antwerpen, 1647. Foto uit privé-bezit ▪

wiskunde te doceren. In 1626 was hij in Leuven, waar hij de lessen overnam van Saneto Vincentio, die vertrokken was naar Rome. Nadat de benoeming van deze laatste als professor van wiskunde aan het Colegio Imperial te Madrid niet kon doorgaan, werd della Faille in zijn plaats gezonden. Omstreeks 1645 stelde Filips IV pater della Faille aan als preceptor van zijn natuurlijke zoon Don Juan van Oostenrijk. Toen deze laatste benoemd werd tot commandant van de vloot, bekwam hij van zijn vader dat pater della Faille in zijn dienst bleef. Della Faille vergezelde Don Juan op zijn tochten naar Sicilië en Napels, en later naar Barcelona, waar hij op 4 november 1652 overleed.

Afgezien van Theses Mechanicae, die hij in 1625 door studenten te Dôle liet verdedigen, publiceerde della Faille slechts één werk, zijn Theoremata de Centro Gravitatis Partium Circuli et Ellipsis (Antwerpen, 1632). In dit werkje van slechts 53 bladzijden bepaalt della Faille het zwaartepunt van cirkelsegmenten en cirkelsectoren en toont hij bovendien hoe die resultaten kunnen worden uitgebreid tot segmenten of sectoren van ellipsen. Het is systematisch opgebouwd naar het voorbeeld en volgens de methode die Archimedes gebruikt in zijn geschrift Over het evenwicht van vlakke figuren en over zwaartepunten.

Ignatius Der Kennis (1598-1656) volgde wiskunde bij Sancto Vincentio in de jaren 1618-20. Later hielp hij in Leuven de teksten klaarmaken die in 1625 naar Grienberger werden gezonden. Hij onderwees er gedurende twee jaar wiskunde aan externe studenten.

Vermelden we nog Jacobus Durand (1598-1644), die de lessen van wiskunde volgde in de periode 1619-20.

[p. 137]

Antoon van Dyck, portret van Pater Jan-Karel della Faille, S.J. Brussel, Koninklijke Musea voor Schone Kunsten van België. © K.M.S.K.B. ▪

In 1627 werd hij naar Gratz gezonden om er zowel wiskunde als theologie te onderwijzen. Voor zijn studenten schreef hij een handboek over geometrie en trigonometrie, gesteund op werken van Grienberger en Clavius.

Van Sancto Vincentio's leerlingen uit de Leuvense periode komt als eerste Willem Boelmans, geboren te Maastricht in 1603. Hij had een belangrijk aandeel in de redactie van de documenten die in 1624-25 naar Rome werden gezonden. Nadat della Faille naar Madrid was vertrokken, nam Boelmans zijn taak als professor van wiskunde over. Op 8 en 9 augustus 1634 organiseerde hij een plechtige academische zitting, waarop hij door enkele studenten, onder wie Andreas Tacquet, een aantal theses uit de geometrie, de aritmetica, de optica, enz. liet verdedigen. Het programma dat bij die gelegenheid werd gedrukt, een brochure van 28 bladzijden, getuigt van het hoog niveau van Boelmans onderwijs. Onder de zuiver mathematische thesissen vinden we, in verband met de drie beroemde problemen uit de Oudheid, volgende stellingen: met de konchoïde, de cissoïde en de parabool kan het probleem van de verdubbeling van de kubus worden opgelost; met de konchoïde, de hyperbool en de kwadratrix

[p. 138]

kan een boog in drie gelijke delen worden verdeeld, en met de kwadratrix is de cirkelkwadratuur te verwezenlijken. Verder vinden we echo's van de discussie rond de vraag of een hoek een kwantiteit is of niet, en of uitdrukkingen als getallen zijn. Wegens zijn zwakke gezondheid gaf Boelmans na twee jaar het onderwijs op. Hij overleed reeds in 1638.

Theodorus Moretus, te Antwerpen geboren in 1602, volgde gedurende een jaar de lessen van Sancto Vincentio, waarschijnlijk in 1622-23. Als zijn medewerker schreef hij een aantal teksten die bestemd waren voor Grienberger in Rome. In 1628 werd hij naar Münster gezonden om er wiskunde te doceren, maar reeds in 1630 werd hem opgedragen naar Praag te reizen om er Sancto Vincentio na zijn beroerte te assisteren. Na de val van de stad in 1631 week hij uit naar Olmutz. Van 1634 tot 1642 doceerde hij wiskunde aan het Collegium Clementinum te Praag en later, vanaf 1660, aan het jezuïetencollege te Breslau, waar hij overleed in november 1667.

De laatste van Sancto Vincentio's leerlingen over wie we iets moeten meedelen is Jan Ciermans uit 's-Hertogenbosch. In 1637 volgde hij, na een onderbreking van de lessen gedurende twee jaar, Boelmans op als professor van wiskunde te Leuven. In 1640, ter gelegenheid van het eeuwfeest van de Sociëteit van Jezus, publiceerde Ciermans een samenvatting van de cursus die hij dat jaar gaf. De behandelde materie wordt ingedeeld per maand, beginnende met oktober en eindigend met september, met in elke maand drie weken. In het Ad Lectorem merkt Ciermans op dat alle behandelde onderwerpen, hoe verschillend ze ook zijn, iets te maken hebben met oorlogsvoering. Zo buitengewoon is dit niet, want de meeste van zijn studenten waren jongelui die zich op een militaire carrière voorbereidden. De zuivere wiskunde wordt behandeld gedurende de eerste twee maanden. De stof is als volgt verdeeld over zes weken:

Oktober. Geometrie.

1.	De elementen van meetkunde.
2.	Over de contact- of raakhoek.
3.	Over de instrumenten gebruikt in de geometrie.

November. Aritmetica.

1.	Over de verschillende soorten getallen.
2.	Het praktisch rekenen.
3.	Over sinus, tangens, enz.

Het onderwerp dat behandeld wordt in de tweede week van oktober houdt verband met de discussies rond het begrip hoek en de vraag of een hoek al of niet een kwantiteit is. Ze ontstonden rond de contact- of raakhoek, gevormd door een cirkel en een raaklijn. Bij de behandeling van het getalbegrip in de eerste week van november keert Ciermans zich tegen Stevins opvatting dat het getal een continue grootheid is. Hij verwerpt eveneens diens mening dat 1 een getal is, dit op grond van Euclides' definitie: getal is uit eenheden samengestelde veelheid. Hij handelt verder over breuken, figurale getallen, priemgetallen, perfecte getallen en over verhoudingen. Een merkwaardige opmerking vindt men in de Problemata aan het einde van de eerste week van november. Ciermans schrijft er dat hij een rekenmachine construeerde die werkt met radertjes en waarmee men met de grootste nauwkeurigheid kan vermenigvuldigen en delen.

Alles samen heeft Ciermans' onderwijs veel weg van wat tot het programma van een opleiding aan een militaire academie behoort. Dat hij zich speciaal ook voor militaire architectuur en vestingbouw interesseerde, bewijzen de thesissen die hij in juni 1641 te Antwerpen liet verdedigen.

In dat zelfde jaar 1641 werd Ciermans aangeduid om naar de missie in China te vertrekken. Hij reisde naar Lissabon om daar in te schepen. In afwachting van het vertrek gaf hij les in wiskunde en wetenschappen aan het college Santo Antão. Men deed ook een beroep op zijn hulp bij het bouwen en verbeteren van de vestingen aan de Portugese grens. Uiteindelijk engageerde Ciermans zich in het leger, wat resulteerde in zijn uitwijzing uit de Sociëteit. Hij sneuvelde op 20 juni 1648 bij een aanval op de stad Olivenza.

Keren we nu terug naar 1647 en Gregorius a Sancto Vincentio's groot Opus geometricum. Het hele werk is opgesteld in de stijl van de grote mathematici uit de Oudheid: Euclides en vooral Archimedes en Apollonius. Alle bewijzen verlopen zuiver geometrisch, zonder enig gebruik van symbolen of formules. Van algebra is er geen spoor. Dit alles maakt de lezing van het werk niet eenvoudig. Bij de beoordeling moet men echter rekening houden met het feit dat het eerst twee decennia na zijn ontstaan werd gedrukt en daardoor - wat de vorm betreft - bij zijn verschijnen reeds grotendeels achterhaald was. Men bedenke slechts dat Descartes' Géométrie tien jaar ervoor was verschenen.

Het allereerste waar de aandacht van de geleerde wereld naartoe ging, was de vraag in hoever de vier cirkelkwadraturen in het tiende boek gelukt waren.

[p. 139]

De eerste gepubliceerde reactie kwam van pater Mersenne (1588-1648). In zijn Novarum Observationum physico-mathematicarum tomus III (Parijs, 1647) wijdt hij een paragraaf aan de cirkelkwadratuur. Hij beweert er dat Sancto Vincentio niets anders doet dan dit probleem herleiden tot het volgende nog moeilijker probleem: gegeven drie rationale of irrationale grootheden, en van twee ervan ook de logaritme, langs meetkundige weg de logaritme van de derde vinden. Een volgende reactie kwam van de jonge Christiaan Huygens (1629-1695). In een brief van oktober 1651 aan Sancto Vincentio drukt hij zijn twijfel uit over de juistheid van een propositie in

Jan Ciermans, Disciplinae mathematicae, 1640. Foto's uit privé-bezit ▪

boek X, en hij vraagt of hij zijn bemerkingen mag publiceren. Nog voor het einde van het jaar verschijnen ze in zijn Theoremata de Quadratura hyperboles, ellipsi et circuli ex dato portionum gravitatis centro. Quibus subiuncta est ἐξέτασιϛ Cyclometrioe Cl. Viri G. a Sancto Vincentio, editae anno 1647 (Leiden, 1651). In juli van dat jaar was Christiaan Huygens met zijn vader in België en hij bezocht bij die gelegenheid Sancto Vincentio te Gent. Later schrijft hij hierover aan Andreas Tacquet dat het onderhoud niets opleverde en dat Sancto Vincentio blijft pogen zijn kwadratuur te verdedigen. Eveneens in 1651 verscheen een kritiek van de Pool Alexis Sylvius in zijn werk Lunae circulares periodi seu cycli...Adiunctum quoque est Examen circuli quarundam propositionum Quadraturae circuli R.P. Gregorii a Sancto Vincentio (Lesna, 1651).

Drie jaar later, in 1654, mengde de Franse jezuïet Vincent Leotaud (1596-1672) zich in de discussie met een Examen circuli quadraturae hactenus editarum celeberrimae, quam Apollonius alter, magno illo Pergoeo non minor Geometra, R.P. Gregorius a Sancto Vincentio S.J. exposuit (Lyon, 1654). Zoals blijkt uit de titel bewonderde Leotaud Sancto Vincentio als mathematicus, maar hij had niettemin belangrijke bezwaren tegen diens cirkelkwadraturen. Het volgende jaar kwam er nog een aanval van de Deense geleerde Marcus Meibom (1621-1710) in zijn werk De proportionibus dialogus (Kopenhagen, 1655). Bovendien circuleerde er in dat zelfde jaar een kritiek van de Franse astronoom Adrien Auzout (1622-1691), waarvan echter geen exemplaar schijnt bewaard te zijn gebleven.

Op al deze kritieken heeft Gregorius a Sancto Vincentio zelf nooit publiek gereageerd. Zijn verdediging heeft hij aan anderen overgelaten. Wel heeft hij hen daarbij geïnspireerd en geholpen. Een antwoord op Mersennes kritiek kwam van Sancto Vincentio's ordegenoot Alfons Antoon de Sarassa (1617-1667). In zijn Solutio Problematis a R.P. Marino Mersenne propositi (Antwerpen, 1649) tracht hij een oplossing te geven voor het door Mersenne gestelde probleem. Het tweede deel van zijn werk wijdt hij aan de moeilijkheid die de oorzaak is van de mislukking van de cirkelkwadraturen, namelijk de eigenaardige wijze waarop Sancto Vincentio de som maakt van verhoudingen. De Sarassa geeft toe dat hij bij het schrijven van dit antwoord werd geholpen door Sancto Vincentio.

[p. 140]

Een poging de tweede cirkelkwadratuur van Sancto Vincentio te verdedigen leverde Godefridus Aloysius Kinner a Löwenthurn (1610-?) in zijn Elucidatio Geometrico Problematis Austriaci sive Quadratura Circuli detectoe per G. a Sancto Vincentio (Praag, 1653). Ook hij maakte gebruik van materiaal dat Sancto Vincentio hem had gegeven.

In zijn correspondentie, onder meer met Huygens, en in gesprekken verwees Sancto Vincentio enkele malen naar zijn leerling Aynscom, die een herwerkte uitgave van de cirkelkwadraturen aan het voorbereiden was. Franciscus Xaverius Aynscom (1620-1660) was in 1638 ingetreden in de Sociëteit. Hij volgde de lessen van Sancto Vincentio te Gent in de jaren 1654-56. Het aangekondigde werk verscheen eindelijk in 1656 te Antwerpen met als titel Expositio ac Deductio Geometrico Quadraturarum Circuli R.P. Gregorio a Sancto Vincentio. Aynscom tracht er de vier cirkelkwadraturen uit Sancto Vincentio's Opus op punt te stellen en de opwerpingen van Huygens, Leotaud, Meibom en Auzout te ontkrachten. Hij had echter een vooraf verloren zaak te verdedigen. Reeds in oktober kwam hierop nog een antwoord van Huygens. Daarmee eindigden de discussies rond Sancto Vincentio's cirkelkwadraturen, afgezien van nog een late reactie van Leotaud, zeven jaar na het verschijnen van Aynscoms werk.

Het koppig weigeren van Sancto Vincentio om zijn vergissingen toe te geven wekte stilaan ergernis op, onder meer bij Huygens, Tacquet en vooral bij Linus. Deze schreef op 21 februari 1657 een brief aan Goswin Nickel, de generaal van de jezuïeten, waarin hij suggereert Sancto Vincentio te verbieden nog verder te redetwisten, ‘omdat anders onze vijanden zullen beweren dat het onze aard is, eenmaal we iets hebben beweerd, het ook steeds te blijven verdedigen, zelfs nadat we overtuigd werden dat het fout is’. Nickels antwoord was kort: ‘Men kan van mij niet verwachten tijd te vinden om mathematische kwesties te onderzoeken’.

Uiteindelijk is Sancto Vincentio wel zelf gaan twijfelen aan zijn kwadraturen en heeft hij zijn aandacht gericht op andere problemen. De laatste jaren van zijn leven hield hij zich bezig met een ander beroemd probleem, de verdubbeling van de kubus, of - wat daarmee nauw verbonden is - het bepalen van twee middelevenredigen tussen twee gegeven grootheden. Eind 1665 kreeg hij toelating hierover een werk te publiceren. Het verschijnen ervan heeft hij echter niet meer mogen beleven. Hij overleed te Gent op 27 januari 1667. Aan het nagelaten handschrift werden nog enkele verbeteringen aangebracht. Joachim van Papenbroek (1639-1694), de laatste leerling van Sancto Vincentio, zorgde voor het drukken van het werk. Het verscheen in 1668 te Antwerpen als Opus Posthumum ad Mesolabum.

De ongelukkige cirkelkwadraturen in Sancto Vincentio's Opus Geometricum hebben als gevolg gehad dat de rest van het werk minder aandacht heeft gekregen dan het werkelijk verdiende. De invloed ervan beperkte zich aanvankelijk tot de kleine kring van zijn medewerkers en verdedigers. Het bevat nochtans een aantal belangrijke ontdekkingen, die door enkele van de beste onder zijn jongere tijdgenoten werden herkend en gewaardeerd. Daaronder zijn de sommering van oneindige geometrische reeksen, de relatie tussen de archimedische spiraal en de parabool, het verband tussen de oppervlakte onder de hyperbool en de logaritmen, en vooral de eerste streng geometrische integratiemethode. Langs Leibniz om heeft het Opus een niet te onderschatten invloed uitgeoefend op de ontwikkeling van de infinitesimaalanalyse.

Keren we nogmaals terug naar Leuven en de school van wiskunde. Over de jaren na het vertrek van Ciermans in 1641 is niets belangrijks te melden. Einde 1645 verhuisde de wiskundeschool naar Antwerpen. Het onderwijs werd toevertrouwd aan de Antwerpenaar Andreas Tacquet. Hij had in de jaren 1633-34 en 1634-35 te Leuven de lessen van Boelmans gevolgd. In de herfst van 1649 keerde Tacquet samen met de wiskundeschool terug naar Leuven. In de jaren 1650, 1651 en 1652 organiseerde hij, naar het voorbeeld van zijn voorgangers, academische zittingen, waarop door één van zijn studenten een aantal thesissen werd verdedigd. Onder de behandelde onderwerpen vinden we onder meer de cycloïde, de driedeling van een hoek en nogmaals het probleem van de raakhoek. Er is ook kritiek op de methode van de ‘indivisibilia’.

Ondertussen was in 1651 Tacquets Cylindricorum et Annularium libri IV verschenen. In dit werk bewijst hij een aantal eigenschappen van cilinders en ringen, kundig gebruikmakend van de infinitesimaalmethodes van Sancto Vincentio. Zoals de regels van de Sociëteit het voorschreven, zond Tacquet een exemplaar naar Rome. Pater Goswin Nickel dankte hem en stelde voor dat hij een cursus wiskunde zou schrijven, geschikt voor gebruik in de colleges van de Sociëteit. Tacquet

[p. 141]

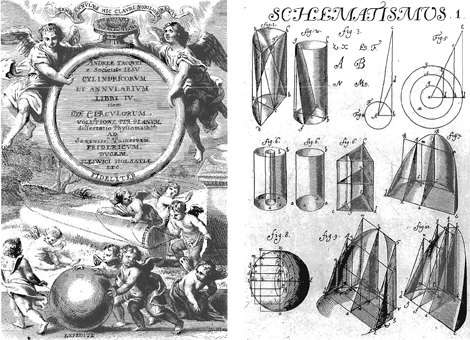
Andreas Tacquet, Cylindricorum et Annularium Libri IV, Antwerpen, 1651. Foto uit privé-bezit ▪

zette zich aan het werk en in 1654 verschenen zijn Elemenca Geometriae planae ac solidae, en twee jaar later de Arithmeticae theoria et praxis. De Elementen van Meetkunde geven de boeken I tot VI, XI en XII van Euclides, maar met wijzigingen in tal van bewijzen. Als toemaat geeft Tacquet een aantal proposities ontleend aan Archimedes' Cirkelmeting en aan diens werk Over bol en cilinder. Tacquets handboek voor meetkunde kende een ongehoord succes en bleef in gebruik tot ver in de 18de eeuw. Aangevuld met nota's van William Whiston (1667-1745), opvolger van Newton als ‘Lucasian Professor’ in Cambridge, werd het daar als officieel handboek voor meetkunde gebruikt. Het werd vertaald in het Engels en het Italiaans, en in 1739-45 verscheen te Sint-Petersburg nog een Russische versie.

Het eerste deel van Tacquets Arithmetica behandelt de theoretische aritmetica. Het is een bewerking van de boeken VII, VIII en IX van Euclides' Elementen. Het tweede deel, veruit het omvangrijkste, is gewijd aan de praktische rekenkunde. In het Ad Lectorem kondigt Tacquet aan dat hij zich niet zal beperken tot het formuleren van de verschillende regels, maar ze ook zal bewijzen. Hij voegt er aan toe dat, voor zover hij het weet, dit nog nooit eerder door iemand werd gedaan. Terloops vermeldt hij ook de algebra. Hij stelt hierover een publicatie in het vooruitzicht, maar die is er niet gekomen.

Einde 1559 verhuisde Tacquet samen met de wiskundeschool weer naar Antwerpen. In dat zelfde jaar verscheen een aanvulling op zijn werk over cilinders en ringen onder de titel Cylindricorum et Annularium liber quintus. Tacquet overleed te Antwerpen op 22 december 1660, nog geen vijftig jaar oud. Een aantal nagelaten geschriften werd door pater Hendrik de Prince, zijn laatste leerling, uitgegeven onder de titel Opera Mathematica (Antwerpen, Jacob Meursius, 1669). Het volumineuze werk begint met een uitvoerig traktaat over astronomie, met aan het slot een inleiding in de sferische trigonometrie. Hierop volgt een praktische geometrie, hoofdzakelijk een traktaat over vlakke driehoeksmeting met toepassingen in de landmeetkunde. Verder zijn er traktaten over optica, catoptrica en krijgsbouwkunde. Het volume sluit met een

[p. 142]

heruitgave van de vijf boeken over cilinders en ringen. Een tweede uitgave van deze Opera verscheen te Antwerpen in 1707 bij Henricus Cornelius Verdussen.

Alvorens definitief afscheid te nemen van Tacquet moeten we nog één, van zijn leerlingen vermelden: de Brusselaar Gilles-François de Gottignies (1630-1689). Voor hij intrad in de Sociëteit van Jezus in november 1653 had hij gedurende twee jaar aan de Leuvense artesfaculteit gestudeerd, en daarna gedurende drie jaar de lessen van wiskunde bij Tacquet gevolgd. Voor de studie van de theologie werd hij naar Rome gezonden, waar hij de rest van zijn leven heeft doorgebracht. In 1662 werd hij benoemd op de leerstoel wiskunde aan het Collegium Romanum. Voor zijn studenten schreef hij Elementa Geometrioe planae (Rome, 1669), een eigenaardig werkje waarin hij zich sterk afzet tegen de door Euclides gevolgde methode. Daarnaast publiceerde hij vier werkjes over wat hij ‘logistica’ noemt, maar wat niets anders dan algebra is. Als eerste komt Logistica sive Scientia circa quamlibet quantitatem demonstrative discurrens (Rome, 1675). In de opdracht aan de lezer zet Gottignies uiteen welk soort wetenschap de ‘logistica’ is. Het is een geheel van proposities die gelden voor elk soort grootheid, zowel voor aritmetische als geometrische of nog andere. Dergelijke proposities noemt Gottignies algemene proposities. Ze vormen samen de ‘Mathematica universalis’ of algemene mathematica. Dit is een wetenschap die uitgaat van eigen grondbeginselen, onafhankelijk van de geometrie, alleen de principes van de elementaire aritmetica onderstellende. De ‘Mathematica universalis’ herinnert sterk aan de ‘Mathesis Prima’ van Adriaan van Roomen en het is niet onmogelijk en zelfs waarschijnlijk dat Gottignies zijn idee aan diens werk heeft ontleend. Als inleiding tot de ‘logistica’ schreef hij Arithmetica Introductio ad Logisticam (Rome, 1676). Een uiteenzetting van de algemene mathesis volgde drie jaar later: Universae Mathesis servientes Logisticae Clavis (Rome, 1679). Acht jaar later verscheen nog een groot in folio, waarin Gottignies de inhoud van de voorgaande werken herwerkt en uitbreidt: Logistica Universalis. Sive Mathematica Gottiniana amplectens Arithmeticae, Geometriae aliarumque partium Matheseos Elemanta (Napels, 1687).

Na de dood van Tacquet in 1660 was er gedurende vijf jaar geen professor voor wiskunde. Eerst in 1665 werd Ignatius de Jonghe (1632-1692) uit Beveren-Waas benoemd te Antwerpen, post die hij behield tot 1670. Gedurende die periode werd de cursus ontdubbeld en Hendrik de Prince onderwees te Leuven van 1667 tot 1669. Van dan af constateert men een langzame teleurgang van de door Gregorius a Sancto Vincentio begonnen speciale leergang wiskunde. Rond 1690 was hij geheel verdwenen. Een laatste vrucht ervan verscheen in 1688: Ignatius de Jonghe's Geometrica Inquisitio in parabolas numero et specie infinitas et iisdem congenitas hyperbolas ac praecipue in quadraturam hyperbolae Apollonianae, een werk over parabolen en hyperbolen van willekeurige orde en hun kwadratuur.

▪ René-François de Sluse

Opvallend in het werk ontstaan uit de wiskundeschool van de Vlaamse jezuïeten, is de verwaarlozing en afwezigheid van de algebra. Stijl en methode staan nog geheel in de geometrische traditie van de Griekse mathematici. Een heel andere benadering vinden we bij mathematici als Viète, van Roomen en Descartes. De algebra krijgt in hun werk een belangrijke plaats en wordt met succes toegepast als analytisch instrument, ook in de geometrie. In deze groep situeert zich ook de laatste mathematicus van betekenis uit onze gewesten in de 17de eeuw: René-François de Sluse. Hij werd op 2 juli 1622 te Visé in het prinsbisdom Luik geboren. Van 1638 tot 1642 studeerde hij te Leuven en daarna te Rome, waar hij op 8 oktober 1643 promoveerde tot doctor in de rechten. Hij bleef er verschillende jaren, zich verder bekwamend in talen, wiskunde en astronomie. Zijn installatie in 1650 als kanunnik in het kapittel van de Sint-Lambertuskathedraal te Luik verplichtte hem Rome, met zijn bloeiend wetenschappelijk leven, vaarwel te zeggen. Directe gegevens over Sluses mathematische activiteit gedurende zijn verblijf in Italië zijn er niet, maar men mag aannemen dat hij zich in die jaren heeft ingewerkt in de meest recente en belangrijkste mathematische literatuur, in het bijzonder in de werken van Viète, Cavalieri, Torricelli, en vooral in de Géométrie van Descartes. Uit die tijd en uit de eerste jaren te Luik dateren zijn onderzoekingen over de constructie van de wortels van kubische vergelijkingen en zijn eerste methode voor de constructie van raaklijnen aan krommen.

In brieven, onder meer aan Huygens, klaagt Sluse herhaalde malen over de povere wetenschappelijke belangstelling te Luik, ‘een stad waar boeken die

[p. 143]

Portret van René François de Sluse. Visé, Musée de Visé. © C.A.L. ▪

handelen over wiskunde zeldzaam zijn, en waar die wetenschap als dood is en onbekend, en zelfs veracht wordt’. Soelaas in zijn wetenschappelijk isolement bracht zijn vriendschap met Gerard van Gutschoven en vooral, vanaf 1657, zijn correspondentie met enkele van de meest vooraanstaande geleerden van zijn tijd, in het bijzonder met Pascal Huygens. Problemen werden uitgewisseld. Sluse nam actief deel aan de mathematische actualiteit en deelde de resultaten mee van zijn onderzoek over de veralgemeende cycloïde, over spiralen en andere krommen. Aangemoedigd door zijn correspondenten, die zijn werk apprecieerden, publiceerde hij in 1659 zijn eerste mathematisch werk, de Mesolabum, over de constructie van twee middelevenredigen tussen twee gegeven lijnstukken. Hij lost het probleem op met behulp van een cirkel en een ellips of een hyperbool, en dat op oneindig veel manieren. Hij toont bovendien hoe men, met dezelfde middelen en volgens dezelfde methode, de wortels van kubische vergelijkingen kan

René-François de Sluse, Mesolobum, Luik, 1668. © B.U.L. ▪

construeren. Het werkje is puur geometrisch, geheel in de stijl van de ouden, zonder enig gebruik van algebra. Hoe hij die constructies vond, verraadt Sluse niet. Wel belooft hij in het ‘Aan de Lezer’ dat, indien zijn werkje gunstig wordt onthaald, hij later zijn methode, samen met andere vondsten, aan het oordeel van de lezer zal onderwerpen.

Gedurende enkele jaren werkte Sluse verder, maar langzaam schijnt zijn belangstelling voor wiskunde te zijn verzwakt. Pas vanaf 1667, dankzij vooral de tussenkomst van een nieuwe correspondent, Henri Oldenburg (1626-1678), secretaris van de Royal Society, ging Sluse weer actief deelnemen aan het mathematisch leven. In 1668 bezorgde hij een nieuwe uitgave van zijn Mesolabum, ditmaal aangevuld met de beloofde analyse, waarin hij uiteenzet hoe hij langs algebraïsche weg tot de constructies is gekomen. In de bijgevoegde Miscellanea behandelt hij nog een aantal onderwerpen die niet direct iets te maken hebben met het voorgaande, onder meer over spiralen, de

[p. 144]

kwadratuur van krommen, maxima en minima, buigpunten van krommen, zwaartepunten, enz.

Een probleem waarmee Sluse sinds lang bezig was, is de constructie van raaklijnen aan algebraïsche krommen. Einde 1671 meldde hij aan Oldenburg dat hij hiervoor over een ‘korte en gemakkelijke regel’ beschikte, die hij zinnens was te publiceren. Het duurde echter nog tot januari 1673 voor hij de regel meedeelde aan Oldenburg, die zorgde voor publicatie in de Philosophical Transactions. Dit is de laatste bijdrage geweest van Sluse tot de wiskunde. De volle bekroning van zijn wetenschappelijk werk volgde in 1674 met zijn benoeming tot lid van de Royal Society.

De gepubliceerde werken van Sluse vertegenwoordigen slechts een klein deel van zijn bijdragen tot de wiskunde. Om hem ten volle te leren kennen is een grondige studie nodig van de handschriften die hij heeft nagelaten, en die thans berusten in de Bibliothèque Nationale te Parijs. Naast onderwerpen behandeld in zijn Mesolabum, vindt men er bijdragen over combinatoriek, onbepaalde vergelijkingen, rectificatie van krommen, enz. Sluse overleed te Luik op 19 maart 1685. Met hem doofde in onze streken ook alle belangstelling uit voor wiskunde, en dit op het ogenblik dat zich voor deze wetenschap een gans nieuw tijdperk aankondigde.