De mechanisering van het wereldbeeld
(1950)–E.J. Dijksterhuis–
[pagina 319]
| |||||||||||||
A. Nicolaus CopernicusGa naar eind12. De vereniging van vernieuwing en behoud, die zo kenmerkend is voor de wijze waarop ingrijpende veranderingen in het natuurwetenschappelijk denken zich plegen te voltrekken en die door den vaak gebruikten term omwenteling zo slecht wordt uitgedrukt, komt bij geen enkele grote figuur uit de wetenschapsgeschiedenis duidelijker tot uiting dan bij Copernicus. Met hem begint een nieuwe tijd, maar men moet dit vooral niet zo verstaan, dat hij tabula rasa zou hebben gemaakt van de begrippen en methoden waarmee de astronomie door de eeuwen heen gewerkt had, dat hij de gelegenheid zou hebben gehad, zich eens onbevangen tegenover de sterrenwereld te plaatsen, als ware hij de eerste die haar denkend beschouwde. Veel meer dan het nieuwe valt in zijn werk het oude op, de ganse traditionele stijl der Griekse astronomie, haar manier om problemen te stellen, haar methode om ze op te lossen. Men weet, hem lezende, dat men te maken heeft met het in 1543 verschenen werk van een Pruisischen astronoom, maar, als men afziet van de toepassing van trigonometrische rekenwijzen, vindt men er niets in, dat niet even goed in de tweede eeuw na Christus door een opvolger van Ptolemaios geschreven zou kunnen zijn. Na een stilstand van circa veertien eeuwen zet zich de ontwikkeling van de astronomie te Frauenburg voort op het punt, waarop zij te Alexandria was blijven staan. Copernicus brengt in het stelsel van Ptolemaios twee principiële wijzigingen aan, die in wezen beide een terugkeer naar oudere Griekse denkbeelden beduiden: hij neemt aan, dat de aarde in beweging verkeert en hij maakt ernst met het Platonisch voorschrift, dat de hemelverschijnselen moeten worden gered enkel met eenparige cirkelbewegingen. Ptolemaios had het eerste op physische gronden verworpen, hoewel hij er de astronomische bruikbaarheid van inzag (I: 79) en zich aan het tweede ondanks physische bezwaren niet gebonden geacht, toen hij kans zag, door het invoeren van vereffeningspunten de aansluiting van de theorie aan de waarneming te verbeteren (I: 73). Copernicus past zijn physisch denken aan de leer der bewegende aarde aan, maar voelt zich daardoor juist versterkt in de principiële verwerping van iedere afwijking van de eenparigheid in de bewegingen der hemellichamen, zoals de theorie van het vereffeningspunt die in feite toch met zich meebracht. Achteraf gezien lijkt de eerste wijziging oneindig belangrijker dan de tweede: in de eerste herkent men een gedachte van blijvende waarde, die spreekwoordelijk zou worden voor iedere radicale standpuntsverandering; in de tweede ziet men niet meer dan een technisch detail van een reeds lang opgegeven theorie. Copernicus zelf dacht er anders over: wanneer hij aan het eind van zijn jaren nog eens zijn levenswerk overziet, be- | |||||||||||||
[pagina 320]
| |||||||||||||
schouwt hij als de grootste winst die het voor de astronomie heeft opgeleverd, niet de veranderde positie van de zon in het heelal en de daaruit voortvloeiende vereenvoudiging van het wereldbeeld, maar de afschaffing van het punctum aequansGa naar eind2, de verzoening van de zonde tegen den geest der Platonische wijsbegeerte, die Ptolemaios te kwader ure begaan had. Wie het denken van Copernicus werkelijk wil begrijpen, mag over deze uitlating evenmin heenlezen als hij, Goethe bestuderend, na mag laten er aandacht aan te schenken, dat deze op hogen leeftijd meer waarde blijkt te hechten aan zijn prestaties op het gebied van de kleurentheorie dan aan zijn literaire productieGa naar eind3. 3. Het werk De Revolutionibus bestaat uit twee gedeelten, die onderling sterk verschillen in doelstelling, aard en betekenis. Het eerste wordt uitsluitend gevormd door het eerste van de zes boeken, waarin het gehele werk verdeeld is. Het is bestemd voor den algemenen lezer en geeft een zeer bevattelijke, sterk vereenvoudigde schets van het nieuwe wereldstelsel, waarin echter ook de wijsgerige gronden waarop het berust, worden ontwikkeld. Het tweede, de boeken II-VI omvattend, is geschreven voor beroepsastronomen; het geeft in streng wetenschappelijken vorm de zeer gecompliceerde details van het stelsel en vormt daardoor lectuur van eenzelfden graad van moeilijkheid als de Almagest (die Copernicus oorspronkelijk ook als model voor zijn eigen werk heeft willen gebruiken). Wij kunnen hier uiteraard op dat tweede deel niet ingaan. Over het eerste alleen te spreken zou echter kunnen verleiden tot een schromelijke onderschatting van den door Copernicus verrichten arbeid en tot een onjuiste voorstelling over wat na hem nog in de astronomie te doen overbleef. We zullen dus na de behandeling van den vereenvoudigden vorm van het stelsel toch ook nog iets over de werkelijke uitvoering moeten zeggen. 4. De inzet van Boek I verloopt met zijn argumenten voor den bolvorm van het heelal, de hemellichamen en de aarde geheel in de Aristotelisch-Ptolemaeische spheer. Nieuw, maar ook nog geheel in Grieksen denkstijl is dan echter de gedachte, dat een bolvormig lichaam van nature een eenparige rotatie om een van zijn middellijnen moet uitvoeren. In de plaats van het religieuse motief, dat Plato er toe gedreven had, aan hemellichamen slechts eenparige cirkelbewegingen toe te staan (iedere onregelmatigheid zou in strijd zijn met den aard van het goddelijke) en van het physische, dat Aristoteles zijn eis had doen overnemen (de zijnsvorm van de vijfde essentie sluit eenparige cirkelbeweging in) treedt nu dus een van mathematischen aard: de bewegingstoestand vloeit voort uit den geometrischen vorm. Aan den bolvorm van de aarde is dus voor Copernicus haar dagelijkse aswenteling even onverbrekelijk verbonden als voor Ptolemaios haar rust in het wereldcentrum het aan haar physische constitutie geweest was. De ene stelling is zoveel waard als de andere en het is dan ook geen wonder, dat de argumenten waarmee Copernicus de redeneringen van | |||||||||||||
[pagina 321]
| |||||||||||||
den Almagest bestrijdt, slechts overtuigend zijn voor wie niet meer overtuigd behoeft te worden. Als de aarde draaide, had Ptolemaios gezegd, zou ze wegens de grote omwentelingssnelheid uit elkaar moeten spatten. Maar Uw hemel dan, vraagt Copernicus, waarvan de punten toch een nog veel grotere snelheid zouden bezitten, is die dan wel bestand tegen dat wentelen? Bovendien, de beweging die ik aan de aarde toeken, wordt haar niet opgedrongen, zoals de draaiing aan een wentelend wiel en men behoeft dus niet bang te zijn voor de centrifugale verschijnselen die het wiel vertoont. Waarop Ptolemaios natuurlijk zou hebben kunnen antwoorden, dat er dan ook geen reden is om zich bezorgd te maken over den draaienden hemel, die immers ook van nature ronddraait en die bovendien helemaal niet uit aardse materie bestaat. Stuk voor stuk bespreekt Copernicus ook de argumenten die we Ptolemaios tegen de onderstelling van een dagelijkse aswenteling hebben horen aanvoeren (I: 79) en die betrekking hadden op het gedrag van wolken, vogels en opgeworpen lichamen: met de aarde wentelt de binnenste schil van den dampkring rond en alles wat zich daarin bevindt, deelt van nature in haar beweging. De buitenste schil echter rust met den hemel en daarom gedragen de kometen, die zich daarin bevinden, zich, wat op- en ondergaan betreft, geheel als de echte hemellichamen. De gelijkwaardigheid der beide standpunten komt ook tot uiting in de opvatting die de beide partijen van zwaarte hebben: voor Ptolemaios is dit, evenals voor Aristoteles, een streven naar het wereldcentrum, voor Copernicus echter een streven naar vereniging met het gelijksoortige. Bij Ptolemaios valt een zwaar lichaam naar de aarde toe omdat het zodoende zo dicht mogelijk het wereldcentrum, dat het zou willen bereiken, benadert. Bij Copernicus doet het hetzelfde om zich te kunnen verenigen met het geheel waartoe het behoort. Wanneer de aarde eens verplaatst werd naar de maanspheer en men liet in de buurt ervan een zwaar lichaam los, dan zou dit volgens Copernicus naar de aarde in haar nieuwen stand vallen en niet, zoals Aristoteles wilde, toch naar het nu aardloze wereldcentrum gaan. 5. Tot zover staat er in De Revolutionibus niets, wat men niet ook in het Traité du Ciel et du Monde van Oresme zou hebben kunnen lezen en ook in den uitleg, dat de dagelijkse aswenteling der aarde inderdaad de dagelijkse hemeldraaiing kan verklaren, gaat Copernicus niet boven zijn scholastieken voorganger uit. Dat wordt echter anders, wanneer hij over de jaarlijkse beweging van de aarde begint te spreken. Dat zij bestaat, kan hij natuurlijk niet bewijzen, ten hoogste door een analogieredenering aannemelijk maken: wanneer in het stelsel van Ptolemaios aan de zon, de maan en de planeten, alle lichamen, die door de zwaarte (opgevat als een streven tot vereniging van het gelijksoortige) in bolvorm zijn samengekomen, verscheidene cirkelbewegingen tegelijk worden toegekend, waarom zou dan niet ook de aarde behalve haar aswenteling nog andere bewegingen kunnen uitvoeren? Nemen we nu aan, dat zij in een jaar om de Zon draait | |||||||||||||
[pagina 322]
| |||||||||||||
en dat de planeten Mercurius, Venus, Mars, Jupiter en Saturnus dat, elk in hun eigen omloopstijd, ook doen, dan blijkt, dat er een wereldstelsel tot stand komt dat eenvoudiger en harmonischer is dan dat van Ptalemaios en die beide kenmerken zijn sterke waarborgen voor de waarheid ervan. Copernicus zet slechts zeer beknopt uiteen, dat de meest opvallende verschijnselen van de zons- en de planetenbeweging zich inderdaad door deze nieuwe hypothese òf evengoed òf beter laten redden dan in het stelsel van Ptolemaios. Wanneer we ons beperken tot den vereenvoudigden vorm waarin we dit laatste (in I: 76) hebben weergegeven en voor het Copernicaanse de eveneens vereenvoudigde gedaante gebruiken waarin het in Boek I geschetst wordt, kunnen we de mogelijkheid om van het ene op het andere stelsel over te gaan, als volgt inzien. 6. We tonen eerst aan, dat door invoering van twee aanvullende hypothesen het stelsel van Ptolemaios een vorm verkrijgt, die als een tussenstadium in den overgang tot het Copernicaanse te beschouwen is. We herinneren daartoe eerst aan den eigenaardigen samenhang die in het stelsel van Ptolemaios bestaat tussen de bewegingen van de planeten en die van de zon en waarop Regiomontanus nog kort geleden opnieuw de aandacht had gevestigd: voor een binnen-planeet ligt het epicykelmiddelpunt op de lijn aarde-zon, voor een buitenplaneet is de epicykelvoerstraal evenwijdig aan deze lijn. Verder merken we op, dat de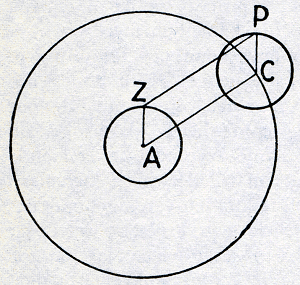 Fig. 14. Overgang van het planetenstelsel van Ptolemaios op dat
van Tycho Brahe. Inplaats van te zeggen, dat de zon Z om de aarde A draait en de planeet P om het, een cirkel om A
doorlopend, centrum C, kan men zeggen, dat Z om A en P om
Z draait.
waarneming wel de verhouding leert kennen van de stralen van epicykel en deferens, maar dat er niets uit is af te leiden over hun absolute waarden. Men kan een van de twee dus nog vrij kiezen; we maken hiervan gebruik in de volgende twee aanvullende hypothesen:
De eerste onderstelling is geen andere, dan die reeds door Herakleides gemaakt was en die de gehele Middeleeuwen door als Aegyptische hypothese bekend was gebleven. Zij zegt eenvoudig, dat de binnenplaneten om de zon wentelen. De draagwijdte van de tweede blijkt, wanneer we de nieuwe situatie voor een buitenplaneet in tekening brengen. Zij (Fig. 14) A de aarde, Z de zon, C het epicykelmiddelpunt en P de planeet. | |||||||||||||
[pagina 323]
| |||||||||||||
Ondersteld is dus CP
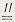 AZ. Vierhoek ACPZ is dus een parallelogram en dus is ook
ZP
AZ. Vierhoek ACPZ is dus een parallelogram en dus is ook
ZP
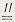 AC. We kunnen dus de beweging van de planeet ook
omschrijven door te zeggen, dat hij een epicykel doorloopt met straal ZP en dat de zonsbaan de deferens daarvoor is. Ook de
buitenplaneten draaien dus om de zon. We zullen zien, dat de hiermee
verkregen tussenvorm tussen de stelsels van Ptolemaios en Copernicus
inderdaad in de geschiedenis der astronomie is voorgekomen, maar eerst na
Copernicus; het is namelijk de (eveneens vereenvoudigde) gedaante van het
door Tycho Brahe voorgestelde wereldbeeld (IV: 21).
AC. We kunnen dus de beweging van de planeet ook
omschrijven door te zeggen, dat hij een epicykel doorloopt met straal ZP en dat de zonsbaan de deferens daarvoor is. Ook de
buitenplaneten draaien dus om de zon. We zullen zien, dat de hiermee
verkregen tussenvorm tussen de stelsels van Ptolemaios en Copernicus
inderdaad in de geschiedenis der astronomie is voorgekomen, maar eerst na
Copernicus; het is namelijk de (eveneens vereenvoudigde) gedaante van het
door Tycho Brahe voorgestelde wereldbeeld (IV: 21).
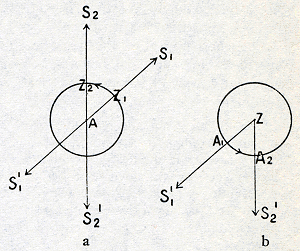 Fig. 15. Overgang van het geocentrische op het heliocentrische
standpunt. Inplaats van te zeggen, dat de zon Z om de
aarde A draait, kan men zeggen, dat de aarde in
denzelfden zin een cirkel om Z doorloopt.
De definitieve overgang op het stelsel van Copernicus komt nu tot stand als men overweegt, dat het voor de waarneming op hetzelfde neerkomt, of Z een cirkel om A beschrijft of dat A in denzelfden tijd een even groten cirkel om Z in dezelfde richting doorloopt. Ziet namelijk in Fig. 15a de aarde A de zon Z op de tijdstippen t1 en t2 opv. in de richting van de sterren S1 en S2, dan ziet de zon de aarde op diezelfde tijdstippen opv. in de richting van de sterren S'1 en S'2. Dit zelfde effect wordt echter ook bereikt in Fig. 15b, waarin de aarde om de zon wentelt. Hiermee zijn we nu echter op het vereenvoudigde stelsel van Copernicus uitgekomen: mèt de planeten wentelt de aarde om de zon; zij is evengoed een hemellichaam als zij. Het is duidelijk, dat deze wijziging van standpunt voor de zonsbeweging weliswaar geen, maar voor de planetenbeweging een zeer aanzienlijke vereenvoudiging betekent. Zij redt immers met één slag de tweede ongelijkheden van alle planetenbewegingen en ontneemt er dus de meest opvallende onregelmatigheid, de periodiek terugkerende retrograde beweging, aan. De epicykelbeweging, waardoor Ptolemaios deze onregelmatigheid had verklaard, blijkt niets anders te zijn dan de afspiegeling van de jaarlijkse aardbeweging om de zon in het gedrag der planeten. 7. De hiermee bereikte vereenvoudiging van het wereldbeeld blijkt nu voor Copernicus wel het eigenlijke doorslaggevende argument voor de juistheid van zijn theorie te zijn geweest. Dat de zon het centrum van de wereld vormt, wordt gewaarborgd door de ordelijke wijze waarop de | |||||||||||||
[pagina 324]
| |||||||||||||
planeten nu binnen de onbeweeglijke buitenste spheer gerangschikt zijn: zij bewegen zich, alle in dezelfde richting, in concentrische banen met hoeksnelheden die met toenemenden afstand tot het centrum gestadig geringer worden, een voorstelling die harmonischer en aesthetischer is dan die van planetenspheren die met gestadig afnemende hoeksnelheid Oostwaarts draaien binnen een sterrenspheer die met een zeer veel grotere hoeksnelheid Westwaarts wentelt, en die daarom ook beter de waarheid benadert. In een beroemd geworden passage van het tiende hoofdstuk betoogt Copernicus nog eens, dat in dit schoon geordende wereldstelsel de zon nergens anders een haar waardige plaats zou kunnen innemen dan in het centrum: In het midden van alle hemellichamen zetelt de Zon. Wie zou in dezen prachtigen tempel deze lamp op een andere of betere plaats kunnen zetten dan van waaruit ze alles gelijktijdig verlichten kan? Waarlijk niet ten onrechte hebben sommigen haar het licht der wereld, anderen haar geest, weer anderen haar heerser genoemd. Trismegistos noemt haar den zichtbaren God, de Electra van Sophokles de alziende. Zo inderdaad als zetelend op een koninklijken troon bestuurt de Zon het geslacht der sterren, die haar omgeven. 8. Men kan zich levendig voorstellen, dat iemand die van De Revolutionibus niet meer dan het eerste boek gelezen heeft en nu het stelsel van Copernicus meent te kennen, er gemakkelijk toe komt, juichtonen aan te heffen om de ontzaglijke vereenvoudiging die door de heliocentrische hypothese in de astronomie is teweeg gebracht, en zich te verwonderen, dat niet iedereen gaarne bereid was, het nieuwe wereldstelsel als het enig ware te aanvaarden. Een ogenblik van bezinning leert echter al spoedig, dat in het eerste Boek nooit meer gedaan kan zijn dan het trekken van de grote lijnen en dat het eigenlijke astronomische werk, de wiskundige voorstelling van de waargenomen bewegingen, nog moet beginnen. Vooreerst wat de zon betreft: de in dit boek gegeven voorstelling, dat de aarde in een jaar eenparig een cirkel om de zon beschrijft, is voor de Griekse astronomie aequivalent met de onderstelling, dat de zon in een jaar eenparig een cirkel om de aarde doorloopt. De Grieken hadden echter al ettelijke eeuwen voor Ptolemaios ontdekt, dat deze onderstelling niet met de feiten klopt: de jaargetijden zouden dan namelijk alle even lang moeten zijn en dat bleek niet het geval te zijn. Daarom had Hipparchos reeds een excentrische zonsbeweging ingevoerd. Het is duidelijk, dat Copernicus zijn eenvoudige hypothese ook door een meer gecompliceerde zal moeten vervangen. Dan wat de planeten aangaat: door de hypothese, dat de aarde zich om de zon beweegt, was wel de tweede ongelijkheid van de planetenbeweging gered, maar was aan de eerste nog niets gedaan. Om deze te verklaren, had Ptolemaios zich echter gedwongen gezien, af te wijken van het Plato- | |||||||||||||
[pagina 325]
| |||||||||||||
nisch axioma, vereffeningspunten in te voeren en dus in feite niet-een-parige bewegingen toe te laten. Copernicus wijst dezen uitweg principieel af, maar hoe zal hij nu de eerste ongelijkheid redden? En ten slotte de maan. Hiervoor maakt het niets uit, of de zon om de aarde of de aarde om de zon loopt, want zij blijft toch altijd om de aarde bewegen. Om die beweging wiskundig voor te stellen, had Ptolemaios de verfijndste hulpmiddelen van de Griekse astronomie te baat moeten nemen en het was hem ondanks het zeer gecompliceerde bewegingsstelsel dat hii er voor in elkaar had gezet, nog maar ten dele gelukt. Copernicus stond nu echter voor precies dezelfde taak. 9. Over dit alles wordt in Boek I echter niet gerept. Daarom begaat men een schromelijke onbillijkheid, wanneer men den harmonischen eenvoud van het hierin geschetste ideale wereldbeeld plaatst tegenover de volle complicatie van het reële stelsel van Ptolemaios, op grond waarvan tafels voor de bewegingen van zon, maan en planeten berekend waren, waaruit hun plaatsen aan den hemel konden worden afgeleid. Het is een onbillijkheid, waarvan Copernicus zelf zich niet geheel vrijhoudt, waar hij het heeft over de welhaast oneindige veelheid van cirkels, die in den Almagest worden aangetroffen en die hij vermijden kanGa naar eind4. De invoering van de aardbeweging om de zon heeft nooit meer dan vijf epicykels overbodig kunnen maken. Vergelijking der beide stelsels heeft pas zin, wanneer men ook van het Copernicaanse de uitwerking kent en de prestaties op het gebied van tafelberekening kan overzien. Voorzover de nieuw te berekenen tafels beter zullen zijn dan de Alfonsinische, die op het stelsel van Ptolemaios gebaseerd waren, zullen ze dit echter niet te danken hebben aan de heliocentrische hypothese als zodanig, maar alleen aan de betere qualiteit van de detailstructuur van het nieuwe stelsel. Door invoering van een ander coördinatenstelsel kan men namelijk de wiskundige voorstelling van een waargenomen beweging wel eenvoudiger, maar niet nauwkeuriger maken. 10. Men ontmoet van tijd tot tijd in de literatuur over de historische ontwikkeling van de astronomie uitingen van verbazing, bedroefdheid of ergernis, dat Copernicus, na het Ptolemaeïsche juk te hebben afgeschud, zoals men dan rhetorisch zegt, en na de ijdele subtiliteiten van zijn bizarre bouwsel te hebben weggevaagd, zelf weer is teruggevallen, zoals dat dan heet, in de oude dwalingen door ook weer met epicykels te gaan werkenGa naar eind5 (excenters ontkomen gewoonlijk aan de kritiek, omdat men deze minder onnatuurlijk, d.w.z. gemakkelijker in een mechanisch model realiseerbaar, vindt). Dat is een volkomen onjuiste opvatting. Vooreerst was het stelsel van Ptolemaios niet in denzelfden zin een juk, als waarin men de Aristotelische physica in de zestiende eeuw zo kon betitelen, maar een zeer geslaagde poging om met de beschikbare hulpmiddelen de waargenomen astronomische verschijnselen wiskundig voor te stellen in een coördinatenstelsel, waarvan de oorsprong in het aardcentrum lag; vervolgens doet het | |||||||||||||
[pagina 326]
| |||||||||||||
stelsel van Copernicus ondanks de vereenvoudiging in het redden van de tweede ongelijkheid der planetenbeweging in complicatie nauwelijks voor dat van Ptolemaios onder en kan er ook niet veel voor onderdoen, omdat de weer te geven bewegingen nu eenmaal hoogst onregelmatig zijn; en ten slotte was de wiskunde in de zestiende eeuw wel verder gekomen dan in de Oudheid op het gebied der trigonometrie, zodat de berekeningen uit de boldriehoeksmeting vlotter konden verlopen, maar had ze in de meetkunde het oude peil nog niet weer bereikt en was ze in de algebra nog lang niet ver genoeg gevorderd om de mogelijkheid van een analytische uitdrukking der hemelbewegingen met behulp van reeksontwikkelingen zelfs maar te kunnen doen vermoeden. II. Dat dus in de boeken II-VI weer excenters en epicykels voorkomen, mag niet de minste reden tot verwondering zijn. Wat eerder verbazing kan wekken, is dat Copernicus zich, voordat hij met de behandeling van zon, maan en planeten begint, de uiterste moeite geeft om de ongelijkheid in de praecessie, die aanleiding had gegeven tot de theorie van de trepidatie (II: 16), en de saeculaire vermindering van de helling van de ecliptica die men meende op te merken, door de onderstelling van twee onafhankelijke oscillatorische bewegingen van de aardas te redden; hoewel toch het feitenmateriaal dat hiervoor ter beschikking stond, lang niet volledig en exact genoeg was om zo gedetailleerde constructies te wettigen. Dat hij ze toch ging uitvoeren, vormt een typerend symptoom van het onbeperkte vertrouwen dat hij in de nauwkeurigheid en de integriteit van zijn voorgangers in de astronomie steldeGa naar eind6; hij heeft hun theorieën, waar hij dat nodig vond, durven verwerpen, maar den moed, aan hun waarnemingen te twijfelen, heeft hij nooit bezeten. Hij achtte zich dus verplicht, zijn theorieën zo in te richten, dat alle overgeleverde observaties er in pasten en dat heeft hem speciaal in zake de praecessie veel overbodige moeite bezorgd. Eerst tegen het eind van zijn leven heeft hij het niet ongerechtvaardigde vermoeden uitgesproken, dat althans Ptolemaios zijn waarnemingen misschien wel eens enigszins heeft gefatsoeneerd om ze beter met zijn theorie te laten overeenstemmenGa naar eind7. Wij kunnen hier Copernicus evenmin in de details van zijn vernuftige praecessie-theorie volgen als we uiteen kunnen zetten, hoe hij dan verder met excenters en epicykels de bewegingen van de aarde, de maan en de planeten weergeeft. 12. Wel willen we nog opmerken, dat, nu het stelsel wordt uitgewerkt, de zon er helemaal niet de allesbeheersende positie in blijkt te bekleden die wij in het tiende hoofdstuk van Boek I in zo hooggestemde bewoordingen hoorden schetsen. Het centrale punt waarin alle absidenlijnen van de planetenbanen elkaar snijden, blijkt het lege mathematische centrum van de aardbaan te zijn. De zon staat ergens ter zijde en doet niets anders dan het geheel verlichten. En de term heliocentrisch, waarmee we het Copernicaanse stelsel plegen aan te duiden, drukt er den eigenlijken aard | |||||||||||||
[pagina 327]
| |||||||||||||
nog veel minder van uit dan het Ptolemaeïsche in strikten zin geocentrisch mag heten. Nu heeft men wel eens den term heliocentrisch willen rechtvaardigen door er op te wijzen, dat de zon het centrum van de spheer der vaste sterren is. Echter heeft Simon Stevin, aan wien wij een helderen commentaar en een vurige verdediging van het stelsel van Copernicus danken, reeds opgemerktGa naar eind8, dat deze zegswijze geen zin heeft. Om namelijk te ontkomen aan het onmiddellijk tegen zijn theorie aangevoerde en volkomen gewettigde bezwaar, dat de jaarlijkse aardbeweging om de zon zich even goed zou moeten afspiegelen in het gedrag der vaste sterren als ze het doet in dat der planeten en dat we de sterren dus jaarlijks gesloten banen zouden. moeten zien doorlopen (het later inderdaad ontdekte en toen sterk voor het stelsel pleitende verschijnsel van de parallaxis) had Copernicus moeten aannemen, dat de sterrenspheer zo ver van ons verwijderd is, dat we van dit verschijnsel niets merken; de aardbaan moet daartoe, vergeleken met deze spheer, als een punt zijn; dan heeft het echter geen zin, van de binnen de aardbaan gelegen punten eerder het ene dan het andere als centrum van de sterrenspheer of van het heelal te beschouwen. 13. Ondanks een verschil van mening over de toelaatbare constructiemiddelen is de gehele denkspheer waarin de opbouw van De Revolutionibus wordt uitgevoerd, zo zeer dezelfde als die van den Almagest, dat de lezing ook dezelfde vraag doet rijzen als het werk van Ptolemaios altijd gewekt had: wat is nu eigenlijk de bedoeling van al deze vernuftig in elkaar gezette bewegingsstelsels? Zijn het mathematische analysen van de wijze waarop de hemellichamen zich gedragen; moet men dus, om een vergelijking aan de moderne wiskunde te ontlenen, in deze ontleding van een waargenomen beweging in eenvoudige componenten iets soortgelijks zien als in de voorstelling van een willekeurige functie door een som van sinusfuncties? Of wil de auteur beweren, dat er in de ruimte in feite voor ons onzichtbare mechanismen werkzaam zijn, waarin de beschreven bewegingen worden uitgevoerd, maar waarvan wij alleen het uiteindelijk resultaat waarnemen? Men had deze vraag ten aanzien van Ptolemaios ook altijd wel gesteld, maar ze kreeg nu een veel dringender strekking. Voorheen betrof ze alleen de hemelruimte, die we niet door directe ervaring kennen; nu gold ze de aarde, die onze eigen verblijfplaats is. En hiervoor nam ze den vorm van een niet te ontwijken dilemma aan: is de onderstelde aardbeweging een mathematische fictie of houdt Copernicus vol, dat de aarde niet rust in het centrum van de wereld, maar zich zowel om haar as als om de zon beweegt? 14. De eerste lezers van De Revolutionibus heeft dit dilemma niet behoeven te verontrusten. Aan het eigenlijke werk gaat namelijk een voorrede vooraf, getiteld Aan den lezer, over de hypothesen van dit werk, waarin | |||||||||||||
[pagina 328]
| |||||||||||||
wordt meegedeeld, dat de auteur alleen de aan een astronoom toevallende taak heeft willen volbrengen, met behulp van hypothesen de hemelbewegingen berekenbaar te maken, maar dat het opstellen van die hypothesen helemaal niet de bewering insluit, dat zij ook waar, zelfs niet, dat zij ook maar waarschijnlijk zijn. De astronomie kan nu eenmaal op dit punt niets zekers leren; wie de onderstellingen, die zij voor een ander doel maakt, voor waarheid houdt, zal dommer van haar heen gaan dan hij gekomen is. Het is later gebleken, dat deze voorrede afkomstig is van den Luthersen theoloog Osiander, die toezicht op het drukken van het werk had uitgeoefend en die blijkbaar op deze wijze de bezwaren tegen het nieuwe stelsel die men verwachten kon, heeft willen ondervangen en den strijd die er om gevoerd zou worden, heeft trachten te voorkomen. In den kring van de naaste aanhangers van Copernicus heeft het grote verontwaardiging gewekt, dat zijn theorie van de aardbeweging als een mathematische fictie zonder enige realiteitsaanspraak werd voorgesteld, inplaats van als een uitdrukking van de ware toedracht van zaken en Osiander heeft dan ook dadelijk den naam gekregen en tot in de twintigste eeuw toe behouden van een falsaris, die de ware bedoelingen van den auteur van een aan zijn zorgen toevertrouwd werk uit domperse motieven opzettelijk vervalst zou hebben weergegeven. 15. Tegenwoordig beoordeelt men hem echter wel andersGa naar eind9: vooreerst is de opvatting van doel en draagwijdte van een mathematisch-physische theorie die aan zijn beschouwingen ten grondslag ligt, alleszins houdbaar: men kan inderdaad op goede gronden van mening zijn, dat zulk een theorie doet wat men van haar verwachten mag, wanneer zij er in slaagt, een mathematisch gedachtenstelsel te construeren waarvan de resultaten kloppen met reeds uitgevoerde metingen en door nieuwe waarnemingen bevestigd worden. Vervolgens is het lang niet zeker, dat zijn voorrede door Copernicus wel met dezelfde verontwaardiging zou zijn afgewezen, als waarmee zijn vrienden er na zijn dood op hebben gereageerd. Wèl door den Copernicus, die het eerste Boek van De Revolutionibus heeft geschreven en die er blijkbaar vast van overtuigd is, dat het zin heeft om te zeggen, dat de zon in rust verkeert en de aarde niet en die bovendien ook zeker meent te weten, hoe deze zich beweegt. Maar de auteur der Boeken II-VI zou toch wel heel moeilijk hebben kunnen volhouden, dat hij over de daarin ontwikkelde theorieën anders dacht dan Osiander. Hij maakt immers in zo ruime mate gebruik van de vrijheid om waargenomen afwijkingen van een eenvoudige theorie te redden door er nog maar weer een epicykel bij te nemen; hij zet ook zo onbevangen uiteen, hoe soms eenzelfde verschijnsel door geheel verschillende hypothesen kan worden gered zonder ook maar een poging te doen, om uit te maken, welke onderstelling physisch het meest aannemelijk is; en hij komt, met name bij de planeet Mercurius, tot zo ingewikkelde bewegingscombinaties, dat hij ze | |||||||||||||
[pagina 329]
| |||||||||||||
onmogelijk als physisch in de ruimte gerealiseerd kan hebben beschouwd. Wanneer men deze boeken leest met de beginselverklaring van Osiander in de gedachten, voelt men nergens de minste tegenstrijdigheid. Het is in dit verband veelzeggend, dat Copernicus op een door Osiander gedaan voorstel, een voorrede van de bedoelde strekking op te nemen, niet geantwoord schijnt te hebbenGa naar eind10. Wat zou hij ook hebben moeten antwoorden, daar hij toch moeilijk voor de aardbeweging de physische realiteit kon opeisen die hij aan zijn constructies voor de bewegingen der andere planeten ten duidelijkste niet toekende? Het is Kepler al opgevallen, dat Copernicus speculerend een heel andere is dan Copernicus rekenendGa naar eind11; het is juist de tegenstelling, die we boven tussen den auteur van Boek I en dien van de rest van het werk gemaakt hebben. 16. Ten slotte echter kan men voor de bedoelingen die Osiander blijkbaar tot het schrijven van zijn voorrede hebben gebracht, moeilijk anders dan waardering gevoelen. Het denkbeeld van de dubbele aardbeweging druiste zo zeer in tegen de overheersende, gelijkelijk in geloof en wetenschap wortelende wereldbeschouwing en het kon, voorzover het meer wilde zijn dan een mathematische fictie ter vereenvoudiging van de berekeningen der astronomie, op zo weinig werkelijk overtuigende argumenten bogen, dat men grote moeilijkheden kon verwachten, zodra het buiten de kringen der beroepsastronomen bekend zou worden en daar een onderwerp van discussie zou gaan uitmaken. Er was alles voor te zeggen, het eerst maar eens door de beoefenaren der wetenschappelijke astronomie te laten bestuderen en de resultaten waartoe het voerde, aan de waarneming te laten toetsen, en dat kon niet beter verwezenlijkt worden dan door voorlopig maar op het strikt technisch-astronomische karakter, dat de nieuwe leer toch ongetwijfeld ook bezat, den nadruk te leggen. Wanneer men de opdracht aan Paus Paulus III leest, waarmee het werk begint, krijgt men den indruk, dat dit toch ook wel met de wensen van den schrijver moet hebben gestrookt. Hij zegt daarin immers zelf, dat hij, vooruitziend dat zijn theorie voor onzinnig zal worden uitgekreten en dat er allerlei mensen over zullen meepraten die haar niet kunnen beoordelen, er over gedacht heeft, haar volgens de gewoonte der Pythagoraeërs alleen aan enkele ingewijden en dan nog slechts mondeling mee te delen. Eerst op aandringen van bevriende zijde is hij tot publicatie overgegaan. En in de bekend geworden woorden Mathemata mathematicis scribuntur (Over wiskundige, d.w.z. astronomische dingen wordt voor mathematici geschreven) geeft hij duidelijk aan, welke lezers hij zich wenst. De voorrede van Osiander kon de vervulling van dien wens alleen maar bevorderen. 17. Wij willen thans de behandeling van Copernicus besluiten met de behandeling van twee vragen die naar aanleiding van zijn optreden gesteld plegen te worden, die naar de mate van zijn originaliteit en die naar de gevolgen die de publicatie van zijn werk gehad heeft. Over zijn oorspronkelijkheid kan men tegenwoordig wel eens in twijfe- | |||||||||||||
[pagina 330]
| |||||||||||||
lenden toon horen sprekenGa naar eind12 en de door wetenschapshistorici altijd zo naarstig bedreven jacht op z.g. voorlopers schijnt wel eens de strekking te vertonen, dien twijfel te versterken. Men wijst dan op Pythagoraeïsche theorieën, waarin de aarde bewegend gedacht werd, op Herakleides en Aristarchos, op Oresme, Cusanus, Leonardo da Vinci; men noemt zelfs Calcagnini en vindt bij Regiomontanus en den Bolognesen astronoom Domenico Maria da Novara, waarmee Copernicus in zijn Italiaansen studietijd is omgegaan, althans aanwijzingen voor een op handen zijnde vernieuwing van het astronomisch denken. Zulke onderzoekingen zijn natuurlijk altijd de moeite waard en de aanspraken waartoe ze voeren, mogen dan ook niet altijd voldoende gefundeerd zijn, zo lijdt het toch b.v. in het bijzonder geen twijfel, dat Aristarchos de mogelijkheid heeft ingezien, door een dubbele aardbeweging zowel de dagelijkse hemelbeweging als een deel van de bewegingsverschijnselen van de zon en de planeten ten opzichte van de vaste sterren te redden (I: 78) en evenmin, dat Oresme de theorie van de aswenteling behandeld heeft op een wijze, die Copernicus niet meer behoefde te verbeteren (II: 149). Zoals het echter bij voorlopersstudies vaak gaat, is ook in het geval van Copernicus het uiteindelijk resultaat, dat de verdienste die een voltooier zich door zijn werk verwerft, groter blijkt te worden bij iedere ontdekking van iemand, die vóór hem verwante ideeën koesterde en ze niet in een daad omzette. Het krijgen van vernuftige invallen is voor den bloei der wetenschap natuurlijk volstrekt onmisbaar, het overwegen van mogelijkheden, hoe men een verschijnsel zou kunnen verklaren of een theorie zou kunnen opzetten, steeds van belang en vaak vruchtbaar. Maar men moet nooit vergeten, dat de daden waardoor de wetenschap groeit, verricht worden door hen die in een vaak jarenlang voortgezetten ingespannen arbeid de moeilijkheden die altijd optreden wanneer een gelukkige gedachte moet worden uitgebouwd tot een volledig denksysteem, overwinnen, hun invallen tot voltooide theorieën uitbreiden en van mogelijkheden werkelijkheden maken. Met hen vergeleken zijn voorlopers mensen die wel voelden, welken weg ze moesten inslaan, maar dat om welke reden dan ook niet deden of er ontijdig halt op hielden. 18. De gevolgen die het optreden van Copernicus gehad heeft, eerst voor de astronomie, daarna voor de natuurwetenschap in het algemeen en ten slotte voor het gehele menselijke denken zijn diep ingrijpend geweestGa naar eind13. Men is hem steeds intuïtief blijven beschouwen als den vernieuwer bij uitnemendheid, zelfs wel eens ten koste van het inzicht in de sterke bindingen waarmee het verleden hem in den algemenen stijl van zijn denken en in sommige concrete voorstellingen is blijven vasthouden, en zonder dat men steeds voldoende onderscheid heeft gemaakt tussen den invloed van zijn eigen werk en dat van de voortzetters en voltooiers van de door hem wel ingeleide, maar niet tot het einde toe voltrokken vernieuwing. Copernicaanse wending is sedert KantGa naar eind14 een staan- | |||||||||||||
[pagina 331]
| |||||||||||||
de uitdrukking geworden voor een radicale standpuntsverandering en 1543 geldt in de wetenschapsgeschiedenis als het eigenlijke grensjaar tussen de Middeleeuwen en den Nieuwen Tijd. 19. Wanneer men tot de zestiende eeuw zelf teruggaat, bespeurt men spoedig, dat de uitwerking van zijn daad, hoe sterk ze later ook gevoeld zou worden, zich aanvankelijk slechts weinig bemerkbaar maakt en eerst ongeveer een halve eeuw na zijn dood een duidelijken vorm begint aan te nemen. Men kan wel al spoedig in verscheidene landen astronomen aantreffen die zich tot zijn aanhangers verklaren, maar daarnaast blijven anderen zijn stelsel verwerpen, zonder dat ze daarom als vakman de minderen behoeven te zijn van de volgelingen. Het komt ook voor, dat men hem hoog prijst om zijn verdiensten voor de astronomie en gaarne gebruik maakt van de z.g. Prutenische tafels, die Erasmus Reinhold op grond van zijn theorieën berekend had, maar daaraan geen enkele uiting van adhaesie aan de heliocentrische gedachte verbindt. Na wat wij boven gezegd hebben over de tegenstelling tussen de twee stukken, waarin De Revolutionibus te verdelen is, zal het duidelijk zijn, dat dit een alleszins mogelijke houding is. Zelfs is ze, merkwaardig genoeg, in overeenstemming met een gedragslijn, die Copernicus zelf zich aanvankelijk voorgesteld had te volgen, namelijk wel nieuwe tafels te berekenen, en te publiceren, maar er niet bij te zeggen, op grond van welke hypothesen ze waren samengesteldGa naar eind15. De Prutenische tafels vormen eigenlijk het enige onmiddellijke (d.w.z. zonder medewerking van andere vernieuwers bewerkte) en het eerste algemeen opgemerkte gevolg van de publicatie van De Revolutionibus. Zij waren in vele opzichten beter dan de Alfonsinische, maar ze overtroffen deze toch niet zozeer als men onwillekeurig verwacht, wanneer men nalaat zich goed in de historische situatie te verplaatsen en de vernieuwing der astronomie reeds voltrokken waant, toen ze nog maar nauwelijks begonnen was. Dat dit moeilijk anders had kunnen zijn, hebben we boven reeds ten dele toegelicht: de invoering van het heliocentrische wereldbeeld als zodanig kon niet tot grotere nauwkeurigheid van de planetentafels leiden; deze kon alleen het gevolg zijn van een meer geslaagde voorstelling der waargenomen posities door de ontworpen bewegingsstelsels of van een verbetering in die posities zelf en voor dat laatste waren nieuwe en nauwkeuriger waarnemingen nodig. In dit opzicht stond Copernicus er echter, toen hij met zijn werk begon, niet noemenswaard beter voor dan Ptolemaios, terwijl hij zelf te weinig observator was om het ontbrekende door eigen activiteit aan te vullen. Dat hangt waarschijnlijk weer met den aard van zijn wetenschappelijke visie op de natuur samen. Overtuigd als hij is van den eenvoud en de harmonie van den bouw der sterrenwereld, is hij tevreden met het minimum aan waarnemingen dat voor de bepaling van een ideaal bewegingsstelsel voldoende is. Wat enerzijds inspirerend werkte, stond anderzijds de vereiste empirische instelling in den weg. | |||||||||||||
[pagina 332]
| |||||||||||||
Hier wordt duidelijk, waaraan de astronomie na Copernicus allereerst behoefte had: verzameling van een omvangrijker en nauwkeuriger observatiemateriaal en als onmisbare voorwaarde daarvoor, verbetering van de astronomische waarnemingskunst. Zij heeft het geluk gehad, juist toen zij hem nodig had, in de persoon van den Deensen astronoom Tycho Brahe den man te zien verschijnen, die beide verlangens zou bevredigen. | |||||||||||||
B. Tycho BraheGa naar eind1620. In de twintig jaren die Tycho in zijn sterrenwacht Uraniborg op het eiland Hven heeft kunnen doorbrengen, heeft hij met behulp van verbeterde of nieuwe instrumenten en dank zij een ongeëvenaarde observatiekunst de waarnemende astronomie tot een voorheen ongekende en voor de uitvinding der kijkers ook niet weer bereikte hoogte opgevoerd. Welke zijn toestellenGa naar eind17 en meetmethoden waren en welke waarnemingen hij ermee deed, kunnen we in verband met het technisch karakter van het onderwerp hier evenmin uiteenzetten als we hebben kunnen ingaan op de theoretische onderzoekingen van Copernicus. We moeten dus volstaan met enkele mededelingen over de resultaten die hij er mee bereikt heeft. Deze bestaan in de verbetering van verscheidene astronomische constanten, de ontdekking van twee nieuwe ongelijkheden in de maanbeweging, aanmerkelijk nauwkeuriger maan- en zonnetafels dan tot dusver hadden bestaan, een catalogus van 1000 vaste sterren met nieuw gemeten waarden van lengte en breedte, tafels voor atmospherische refractie, het bewijs, dat kometen niet, zoals men nog algemeen meende, atmospherische verschijnselen zijn en ten slotte een zeer omvangrijk materiaal van waargenomen planeetposities, dat, toen hij in 1597 van Hven vertrok, nog op bewerking wachtte. Tycho zelf zou met deze opsomming ongetwijfeld niet tevreden zijn geweest en er als eerste en voornaamste punt aan hebben toegevoegd: een nieuw theoretisch wereldbeeld, dat de voordelen van de stelsels van Ptolemaios en Copernicus verenigt en beider nadelen vermijdt. Hoewel namelijk zijn begaafdheid veel meer op het terrein van instrumentmaken en observeren lag dan op dat der theoretische constructie, heeft hij zich altijd sterk tot het laatste aangetrokken gevoeld en het als zijn eigenlijke levenstaak beschouwd, niet alleen door zijn waarnemingen de middelen ter bereiking van het doel der astronomie ter beschikking te stellen, maar dit doel ook zelf te verwezenlijken. 21. Tycho was een veel te scherpzinnig astronoom om niet in te zien, welk een aanzienlijke vereenvoudiging de overgang op het heliocentrische standpunt in het wereldbeeld bracht, maar hij was aan den anderen kant nog te zeer bevangen in de Aristotelische denkwijze om zich te kunnen onttrekken aan den invloed van de argumenten tegen de mogelijkheid van een aardbeweging die we door Ptolemaios hebben horen aanvoeren | |||||||||||||
[pagina 333]
| |||||||||||||
(I: 79) en door Oresme en Copernicus weerleggen (II: 149; IV: 4). Hij voegt er in een briefwisseling met den Copernicaans gezinden astronoom RothmannGa naar eind18 een aan toe, dat grote bekendheid zou verwerven: als de aarde van West naar Oost draaide, zou een kanon dat naar het Westen gericht was, aan een kogel een veel grotere schootsverheid moeten meedelen, dan wanneer het Oostwaarts schoot. Immers in het eerste geval komt de aarde den kogel als het ware tegemoet, terwijl deze haar in het tweede moet inhalen. En op het tegenargument, dat het kanon en dus ook de kogel delen in de natuurlijke beweging der aarde, antwoordt hij met het voor de Aristotelische natuurbeschouwing essentiële bezwaar, dat het ondenkbaar is, dat deze natuurlijke beweging en de uiterst gedwongen beweging die de explosie van de lading aan het projectiel meedeelt, samen zouden kunnen bestaan, zonder elkaar te hinderen. Ten slotte is hij met de overgrote meerderheid van zijn tijdgenoten van mening, dat het stelsel van Copernicus in strijd is met het Christelijk geloof. Hij hoopt nu een uitweg uit het dilemma te vinden door den overgang van Ptolemaios naar Copernicus slechts voor de helft mee te maken en dus te blijven staan bij de voorstelling, die wij (in IV: 6) als tussenstadium hebben leren kennen: met Copernicus laat hij de planeten om de zon wentelen (nauwkeuriger: om centra in de nabijheid van de zon), maar met Ptolemaios handhaaft hij de centrale positie van de aarde. 22. Tycho is er nooit in geslaagd, dit stelsel, dat hem zeer ter harte ging, verder te brengen dan tot den rang van een vernuftig in elkaar gezette denkbaarheid in den trant van de stelsels van Eudoxos, Herakleides en Aristarchos. Hij heeft het nooit uitgewerkt tot een volledige theorie van de bewegingen van zon, maan en planeten, zoals Ptolemaios en Copernicus die hadden gegeven, tot een theorie waarop nieuwe planetentafels konden worden gebaseerd en die daarin aan de waarneming kon worden getoetst. De oorzaak daarvan ligt waarschijnlijk ten dele wel in een tekort aan theoretische begaafdheid; er was echter ook nog een andere invloed werkzaam, die het hoe langer hoe moeilijker maakte, de waargenomen verschijnselen met de hulpmiddelen der oude astronomie, met excenters, epicykels en de weer in ere herstelde vereffeningspunten, te redden. Die invloed ging van hem zelf uit: zolang men het met Copernicus als hoogste ideaal had gezien, de planeetposities weer te geven met een nauwkeurigheid van tien boogminuten, hadden zich heel wat afwijkingen tussen theorie en waarneming laten verdoezelen. Toen echter Tycho de nauwkeurigheidsgrens van de metingen omlaag had weten te drukken tot twee boogminuten en soms zelfs tot een minuut of tot dertig seconden en hij dus van de theoretische verstelseling deze zelfde mate van nauwkeurigheid in de aansluiting aan de waarneming moest gaan eisen, namen de moeilijkheden van de kinematische afbeelding gestadig toe; het bleek al spoedig nodig te zijn, de excentriciteiten van de planetenbanen veranderlijk te denken en hun afmetingen pulserend te laten variëren en nog wilde de | |||||||||||||
[pagina 334]
| |||||||||||||
aansluiting aan de waarneming niet gelukken. Tycho streefde een ideaal na, dat hij door zijn eigen werk hoe langer hoe onbereikbaarder maakte. Er zou een jonger genie nodig zijn, minder geremd door traditie, rijker aan phantasie en onversaagder in het denken, om dezen vicieusen cirkel te verbreken. Weer heeft de astronomie het geluk gehad, op het juiste ogenblik den man te zien verschijnen, waaraan ze behoefte had. We zullen over hem dadelijk uitvoerig spreken en zullen dan zien, dat hij het door Tycho verzamelde materiaal gebruikt heeft om niet Tycho's eigen ideaal, maar dat van Copernicus tot definitieve voltooiing te brengen en algemeen te doen aanvaarden. 23. Opnieuw komt hier de wonderlijke trek in Tycho's levenslot tot uiting, dat hij rechtstreeks of middellijk door zijn werk als astronoom steeds weer heeft bijgedragen tot de overwinning van denkbeelden die het geestelijk klimaat waarin hij zelf leefde en dat hem dierbaar was, hielpen verstoren. Door zijn waarnemingen over de Nova van 1572 en de kometen van 1577 en latere jaren bewees hij, dat dit verschijnselen aan den sterrenhemel waren en schokte daardoor het Aristotelisch dogma van de onveranderlijkheid van den hemel. In zijn streven, de bestaande planetenstelsels te verbeteren, voerde hij de methodiek die er aan ten grondslag lag en die voor hem de enig denkbare was, ad absurdum. En hij verschafte ten slotte aan Kepler de wapenen om een wereldstelsel dat hij zelf verwierp, boven zijn eigen stelsel te laten zegevieren. 24. Zelfs in een zo globale schets van Tycho's wetenschappelijke persoonlijkheid als we hier slechts kunnen geven, mag een opmerking over zijn alchemistische en astrologische denkbeelden niet ontbreken. Waar ze precies uit bestonden, kan in het midden blijven; dat hij ze bezat is echter niet onbelangrijk voor het inzicht in het werk dat hij als astronoom verricht heeft. Hij vermoedt namelijk een essentiëlen samenhang van het onderzoek naar de eigenschappen der ondermaanse materie met dat van de sterren en hij leeft in de overtuiging van een wezenlijk verband tussen de hemelverschijnselen en het gebeuren op aarde. Op grond van het eerste is hij altijd, soms zelfs ten koste van zijn werk als astronoom, de chemie blijven beoefenen; op Uraniborg trof men niet alleen een astronomisch observatorium aan, maar ook een scheikundig laboratorium. En het tweede heeft hem, ondanks de scherpe veroordeling die hij over de practijken der sterrenwichelarij heeft uitgesproken, altijd tot een adept van een ideëel verstane astrologie gemaakt. In beide facetten van zijn denken komt het diep gewortelde, in oorsprong stoïcijnse kosmologische geloof in den innerlijken samenhang van al het bestaande tot uiting, dat voor zovele grote natuuronderzoekers een bron van inspiratie geweest is. Tycho heeft dit geloof zelf op zinrijke wijze verbeeld in een tweetal vignetten, waarmee in een van zijn werken titel- en sluitblad versierd zijn. Op het ene ziet men hem leunend tegen een globe met een passer in de hand en omhoog kijkend naar den hemel, met het randschrift Suspicien- | |||||||||||||
[pagina 335]
| |||||||||||||
do despicio (omhoog blikkend zie ik omlaag); op het andere heeft hij den blik op een chemisch apparaat gericht; om zijn arm is een slang (symbool van de eveneens door astrologische overtuigingen beheerste geneeskunst) gewonden en de zinspreuk luidt: Despiciendo suspicio (omlaag ziende kijk ik omhoog)Ga naar eind19. In moderne termen vertaald: de astronomie kan bijdragen leveren tot de atoomtheorie en de laatste helpt de processen die zich in de sterren afspelen, begrijpen. | |||||||||||||
C. Johannes KeplerGa naar eind2025. Johannes Kepler werd in 1599 assistent van Tycho, die inmiddels Uraniborg verlaten had en te Praag een toevlucht bij Keizer Rudolf II gevonden had. Hij bezat reeds naam als astronoom op grond van een in 1596 gepubliceerd werkje, Mysterium Cosmographicum, waarin hij een poging had gedaan, om in het Copernicaans geordende planetenstelsel regelmaat te ontdekken en daardoor tevens te verklaren, waarom er juist zes planeten bestaan (de vijf van ouds bekende en de aarde). Een van de consequenties van de Copernicaanse hypothese was geweest, dat de verhoudingen van de afstanden van de verschillende planeten tot de zon bekend waren geworden, zodat men een model op schaal van het stelsel kon construeren. Dat dit mogelijk was, wordt duidelijk als men bedenkt, dat bij Ptolemaios reeds de verhouding van de stralen van epicykel en deferens voor iedere planeet uit de waarneming kon worden afgeleid en dat de overgang van zijn stekel op het Copernicaanse voltrokken kan worden door voor een binnenplaneet de deferens te laten samenvallen met en voor een buitenplaneet den epicykel congruent te maken aan de baan van de zon om de aarde. Men kan dus in het eerste geval den epicykelstraal en in het tweede den straal van den deferens uitdrukken in den afstand aarde-zon als eenheid, maar heeft dan ook juist de afstanden van alle planeten tot de zon gevonden. Kepler had nu in 1595 de ingeving ontvangen, dat het aantal zes der planeten samen moest hangen met het feit, dat er juist vijf regelmatige veelvlakken zijn en dat er een verband moest bestaan tussen hun afstanden tot de zon en de stralen van de om- en ingeschreven bollen van die veelvlakken. Deze ingeving volgend kwam hij tot het volgende inzicht in de structuur van het stelsel: Wanneer men in de Saturnusspheer (d.i. dus de bol om de zon als middelpunt, waarop de baan van Saturnus ligt) een hexaëder beschrijft, zal de ingeschreven bol daarvan de Jupiterspheer zijn. Beschrijft men hierin een tetraëder en daarin weer een bol, dan verkrijgt men de Marsspheer en wanneer men, zo doorgaande, opv. den dodecaëder, den icosaëder en den octaëder gebruikt, vindt men als ingeschreven bollen opv. de spheren van de Aarde, van Venus en van Mercurius. Dat er juist zes | |||||||||||||
[pagina 336]
| |||||||||||||
planeten zijn, volgt dus uit het feit, dat zes concentrische bollen juist het aantal tussenruimten leveren, waarin vijf regelmatige veelvlakken op de beschreven manier geplaatst kunnen worden. Kepler is overtuigd, dat dit geen toeval kan zijn en dat hij inderdaad een tip heeft opgelicht van den sluier, die het goddelijk scheppingsplan voor het mensenoog verhult. 26. Men behoeft zich niet lang af te vragen, in welke geestelijke atmospheer wij hier verkeren. De overtuiging van een mathematisch beschrijfbare structuur van de wereld, theologisch geformuleerd als het geloof, dat God zich bij de schepping van de wereld door wiskundige overwegingen heeft laten leiden, de onwrikbare zekerheid, dat eenvoud tevens een kenmerk van waarheid is en dat het wiskundig eenvoudige identiek is met het harmonisch-aesthetische, het partij trekken ten slotte van het opvallende feit, dat er juist vijf veelvlakken bestaan, die aan de hoogste eisen van regelmatigheid voldoen en die dus noodzakelijk iets met de ware wereldstructuur te maken moeten hebben, het zijn alles onmiskenbare symptomen van de Pythagoraeïsch-Platonische wereldbeschouwing, die hier zo levend blijkt te zijn als ooit. Het is de denkstijl van den Timaios, die na in een ononderbroken, zij het ook soms onzichtbaar wordende traditie de gehele Middeleeuwen door de overheersing van het Aristotelisme te hebben getrotseerd, in de zestiende eeuw weer tot volle ontplooiing komt. 27. Er is echter intussen een nieuw element ingekomen, dat er voor de ontwikkeling der natuurwetenschap eerst de volle waarde aan geeft. Intuïtieve inzichten in het innerlijke der natuur lopen altijd de kans, wel bekoorlijk, maar niettemin onvruchtbaar te zijn; of ze inderdaad iets van waarheid bevatten, kan alleen de empirische controle leren en de phantasie, die voor de wetenschap een zo onmisbaar element vormt, kan toch nooit zonder wantrouwen worden aangezien. Nu is er wellicht nooit een natuuronderzoeker geweest, die zo rijk aan ingevingen was als Kepler en die er tegelijk zo kritisch tegenover stond, wiens phantasie een zo hoge vlucht nam en wiens hoofd er zo koel bij bleef, die zich zo kon laten meeslepen door zijn verbeelding en die dan zo nuchter en geduldig kon gaan zitten narekenen, of het ook houdbaar was wat ze hem voortoverde. Eerst deze combinatie van bezieling en exactheid heeft het Pythagoraeïsme waarlijk vruchtbaar gemaakt en de wiskundige mystiek in den dienst der wetenschap gesteld. 28. Aan Kepler's onhoudbaar gebleken phantasie van den samenhang tussen het planetenstelsel en de Platonische lichamen (even onhoudbaar als het verband, dat Plato zelf tussen vier van hen en de atoomvormen der elementen had willen leggen (I: 17)) dankt de astronomie een van de vruchtbaarste contacten die ooit tussen twee van haar beoefenaren gelegd zijn. Zijn ingeving uitwerkend zag Kepler zich genoodzaakt, rekening te houden met de excentriciteiten van de planetenbanen en dus de mathematische spheren die hij eerst om en in de opvolgende polyeders beschreven had, te vervangen door concentrische bolschalen van een zo- | |||||||||||||
[pagina 337]
| |||||||||||||
danige dikte, dat de excenter er, aan beide oppervlakken rakend, plaats in kon vinden. Daartoe moest hij echter over de juiste waarden van deze excentriciteiten beschikken en er was niemand die hem daarover beter kon inlichten dan de reeds lang in geheel Europa als observator beroemde Tycho. En zo is dan als vrucht van Kepler's zelfkritiek en accuratesse de relatie tot stand gekomen waaraan de astronomie haar definitieve hervorming te danken zou krijgen. 29. Wij moeten in dit werk het biographisch element zozeer op den achtergrond houden, dat we niet kunnen spreken over de menselijke moeilijkheden die den omgang tussen twee zo markante en verschillend geaarde persoonlijkheden, den autoritairen Tycho en zijn veel jongeren, uiterlijk bescheiden maar, als het er op aankwam, verrassend zelfbewusten assistent in den weg hebben gestaan. We beperken ons tot de zuiver wetenschappelijke geschilpunten die hun samenwerking belemmerden. Vooreerst was Kepler overtuigd Copernicaan en voelde niets voor het compromisstelsel dat Tycho zo dierbaar was en dat deze nog op zijn sterfbed in zijn aandacht zou aanbevelenGa naar eind21; en vervolgens - men moet zich in het denken van den tijd verplaatsen om de draagwijdte van het meningsverschil te beseffen - had Kepler overwegende bezwaren tegen de bijkomstige positie die de zon zowel in het stelsel van Tycho als in dat van Copernicus innam. Beiden hadden de absidenlijnen van alle planetenbanen elkaar laten snijden in een mathematisch punt in de nabijheid van de zon en aan deze zelf geen andere dan een optische functie toegekend: zij verlicht het planetenstelsel, maar bestuurt het niet. Dat nu - het is opnieuw een voorbeeld, hoe sterk de invloed kan zijn dien supra-rationele voorstellingen in de meest exacte wetenschappen kunnen uitoefenen - is voor Kepler op religieuse gronden onaanvaardbaar; de verering die hij de zon toedraagt, staat het niet toe. De zon is voor hem niet alleen licht- maar ook krachtbron voor de wereld; de bewegingen der planeten hebben niet alleen om haar en in haar licht, maar ook door haar toedoen plaats. Hij drukt dit in een mystieken vorm uit door de drieheid van zon, sterrenspheer en de wereldruimte tussen beide te vergelijken met de H. Drieëenheid, waarbij de zon als rustend centrum en krachtbron met den Vader overeenstemt, de spheer der vaste sterren, die door haar rust ruimte schept voor de bewegingen der planeten, met den Zoon, die immers ook de schepping voortbrengt en in stand houdt, en de bewegende kracht van de zon, die zich in de binnenruimte van het heelal uitbreidt, met den H. Geest. Dat lijkt misschien gezocht, onvruchtbaar en onbelangrijk. Maar het gaat er niet zozeer om, wat een beschouwing als deze een hedendaagsen lezer zegt als om wat ze voor Kepler's eigen denken betekend kan hebben. In zijn geest liggen mystiek, wiskunde, astronomie en physica vlak bij elkaar, ja door elkaar heen. Den overgang van het wereldbeeld naar de H. Drieëenheid voltrekt hij zonder de minste moeite en het is geenszins | |||||||||||||
[pagina 338]
| |||||||||||||
ondenkbaar, dat de gelijkenis die hij tussen beide ziet, hem mede heeft geïnspireerd tot een van zijn vruchtbaarste denkbeelden, de opvatting van de zon als causa efficiëns van de planetenbeweging. 30. Voorlopig was hij echter aan de uitwerking van dit denkbeeld nog niet toe, maar stond hij voor de concrete taak, uit Tycho's metingen van posities van Mars een bewegingsstelsel voor deze planeet af te leiden. Van de moeilijkheden die hij bij de uitvoering van dit werk te overwinnen heeft gehad en die hem jarenlang bezig hebben gehouden, zijn we nauwkeurig op de hoogte. Kepler heeft namelijk, in deze geheel afwijkend van de antieke mathematische traditie, de gewoonte, den lezer deelgenoot te maken van al de overleggingen die hem tot het uiteindelijke resultaat van zijn onderzoek hebben gevoerd, maar dat dan ook zo volledig te doen, dat hij hem geen detail spaart en even omstandig verhaalt, welke dwaalwegen hij bewandeld heeft en hoe hij daarvan is teruggekomen als hoe hij ten slotte de waarheid toch nog heeft achterhaald. Van de wijze, waarop hij de juiste toedracht van de Marsbeweging op het spoor is gekomen, brengt hij in het bijzonder in zijn grootste werk, de Astronomia Nova, een uitvoerig verslag uit, dat, voor wie den moed heeft zich er in te verdiepen, een fascinerend relaas blijkt te bevatten van opgewekte en weer teleurgestelde verwachtingen, van nieuwe pogingen en nieuwe ontgoochelingen, van ergernis om wat later domheden bleken, van onmenselijk rekenwerk en steeds door van een koppig volhouden in de vaste overtuiging dat eenmaal uit Tycho's getallenreeksen de schone en eenvoudige waarheid zal oplichten, een ware worsteling met den Engel, die ten slotte zijn zegen ook niet onthoudt. Het voert tot in de hoogste regionen van de toenmalige wetenschap en er kan daarom geen sprake van zijn, het hier na te vertellen. Maar aan den anderen kant: wij staan hier voor een der belangrijkste gebeurtenissen uit de geschiedenis van het denken, misschien wel het meest eigenlijke keerpunt van de vernieuwing, die het thema van dit boek vormt; daarom willen we trachten, hier althans de grote lijn van het uitgevoerde onderzoek te laten zien en zo een indruk te geven van wat zich tussen het jaar 1601, waarin Kepler na Tycho's dood voor het eerst de vrije beschikking over de Mars-waarnemingen kreeg en het jaar 1609, waarin de Astronomia Nova verscheen, in zijn vurigen en nuchteren, phantastischen en exacten geest heeft afgespeeld. 31. Het leek aanvankelijk zo eenvoudig: er waren observaties in overvloed beschikbaar en de toe te passen methode was bekend. Men moest proberen, een excentrische beweging te verzinnen waarin de waargenomen posities pasten en, als dat niet gelukte, het opnieuw beproeven met verdeelde excentriciteit, d.w.z. door ook een vereffeningspunt aan te nemen (I: 73). Dat bracht een omvangrijk rekenwerk met zich mee, maar dat schrikte Kepler niet af en hij hoopte dan ook in enkele maanden klaar te zullen komen. Die verwachting werd al dadelijk beschaamd. Er waren eerst technische moeilijkheden te overwinnen, die samenhingen | |||||||||||||
[pagina 339]
| |||||||||||||
met het boven behandelde meningsverschil over de positie van de zon, en ook daarna bleek de berekening (die nog geheel zonder logarithmen moest worden uitgevoerd) zo moeilijk te zijn, dat eerst na enkele jaren een hypothese tot stand was gebracht waardoor zich de gebruikte Marsposities met een nauwkeurigheid van twee boogminuten lieten voorstellen. Het ontworpen beeld bestond uit het volgende: de planeet doorloopt (Fig. 16) een excenter met verdeelde excentriciteit. Het middelpunt daarvan is C; de zon staat in Z. V, zo op de lijn der absiden gelegen, dat CV=ZC, is het vereffeningspunt. De verhouding van CZ tot den straal van den cirkel bedraagt 0,0566. Het aphelium ligt in Leo 28° 48′ 55″, d.w.z. de zon ziet het punt Q aan den hemel in een punt met astronomische lengte 148° 48′ 55″. 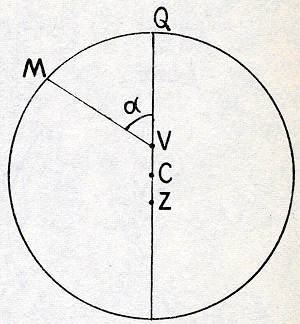 Fig. 16. Keplers eerste voorstelling van de beweging van Mars (Hypothesis vacaria). C: baancentrum. Z: zon. V: vereffeningspunt. CZ =
CV.M: Mars. α verandert evenredig met den tijd,
verstreken na doorgang van de planeet door het aphelium Q. λQ = 148°
48′ 55″. CZ/CQ
= e =0,09264
32. Dat was een resultaat, waarmee de meest veeleisende astronoom zich tevreden had kunnen verklaren en dat de stoutste verwachtingen van Copernicus overtroffen zou hebben. Maar Kepler is nooit tevreden; zijn instinct waarschuwt hem steeds, niet te snel te menen, dat het einddoel al bereikt is. Weliswaar werden alle gebruikte Marsposities met een bevredigende nauwkeurigheid voorgesteld, maar deze lagen alle òf bij een van de absiden òf ongeveer 90° daarvan verwijderd. Hij ging daarom ter controle ook eens voor gevallen, waarin die afstand 45° of 135° bedroeg, berekende en waargenomen posities vergelijken en vond toen een afwijking van acht boogminuten. Dit was voor hem een voldoende grond om de gehele theorie op te geven. Ptolemaiosen Copernicus, bij wie de nauwkeurigheidsgrens bij tien minuten lag, zouden een afwijking van acht minuten zonder bezwaar als bevestiging van de juistheid van hun onderstellingen hebben kunnen beschouwen, maar, aldus Kepler in de befaamde slotwoorden van het 19e hoofdstuk: ons, wien God's goedheid in Tycho Brahe een allerzorgvuldigsten observator heeft geschonken, door wiens waarnemingen de fout van 8′ in de volgens Ptolemaeus uitgevoerde berekeningen in het licht wordt gesteld, past het, met een dankbaar gemoed deze weldaad Gods te erkennen en er gebruik van te maken. Laten we ons dus moeite geven om, steunend op de | |||||||||||||
[pagina 340]
| |||||||||||||
bewijsgronden voor de onjuistheid van de gemaakte onderstellingen, uiteindelijk den waren vorm van de hemelbewegingen op het spoor te komen. Ik zal zelf naar mijn vermogen in het volgende op dezen weg voortgaan... Deze acht minuten alleen hebben dus den weg gewezen naar de totale hervorming der astronomie; zij zijn de bouwstof geworden voor een groot deel van dit werk.33. Op dit punt gekomen, laat Kepler eerst de constructie van de Marsbaan rusten en stelt een minutieus onderzoek in naar de juiste toedracht van de beweging van de aarde om de zon. Daar deze beweging zich immers volgens de theorie van Copernicus afspiegelt in de tweede ongelijkheid van de planetenbeweging, zullen de onvolkomenheden van de theorie der aardbeweging zich als het ware voortplanten in die van de planetenbeweging. Met behulp van een geniale nieuwe methode om de relatieve afstanden van de aarde tot de zon te bepalen (hij slaagt er in, de aardbaan in gedachten van een vast punt van de Marsbaan uit te observeren) kan hij aantonen, dat ook voor de aarde de excentriciteit verdeeld moet worden, dat ook haar baan een vereffeningspunt bezit. Weer geldt 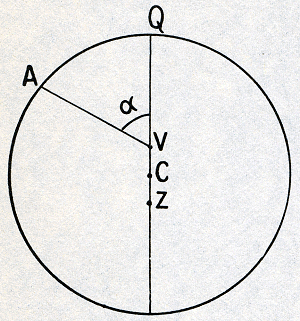 Fig. 17. Keplers voorstelling van de beweging van de Aarde. Z: zon. V: vereffeningspunt. C: baancentrum. A: Aarde. CZ = CV. α verandert evenredig met den
tijd, verstreken na doorgang van de aarde door het aphelium Q. λQ =
95° 30′ CZ/CQ = e = 0,018
(Fig. 17), met dezelfde betekenis der letters als boven (alleen is de planeet P nu door de aarde A vervangen.) CV = CZ, terwijl nu CZ/CQ = 0,009 en hetaphelium Q op een lengte van 185° 30′ ligt. 34. Tot zover is er nog niets geschreven, dat ook niet in den Almagest zou hebben kunnen staan. Maar Kepler durft nu een consequentie aan die Ptolemaios wel had kunnen, maar nooit heeft durven trekken. Trachtte deze, als hij een vereffeningspunt gebruikte, door invoering van een vereffeningscirkel te verbloemen, dat in feite een niet-eenparige cirkelbeweging was ingevoerd en dus het Platonisch axioma grovelijk was geschonden, Kepler neemt deze conclusie onbekommerd voor zijn rekening en verdiept zich liever in de vraag naar de wijze, waarop de snelheid bij het doorlopen van de baan verandert dan dat hij voor het feit der verandering de ogen zou sluiten. Hij bewijst eerst bij benadering, dat de | |||||||||||||
[pagina 341]
| |||||||||||||
lineaire snelheden in het perihelium en het aphelium zich omgekeerd verhouden als de afstanden van deze punten tot de zon en breidt dit eenvoudige resultaat door een stoutmoedige, maar ongerechtvaardigde generalisering tot alle punten van de baan uit. Hij komt zo tot de voor alle planeten algemeen geldig gedachte betrekking, dat voerstraal en snelheid omgekeerd evenredig met elkaar zijn; we zullen deze (onjuiste) wet verder de stralenwet noemen. Het thans bereikte punt in de ontwikkeling laat zich samenvatten in de volgende twee uitspraken:
35. Kepler's gehele constructie is tot dusver zuiver kinematisch geweest en is dus even goed verenigbaar met de door Osiander verdedigde mathematische opvatting, dat van de opgestelde hypothese niet meer verlangd wordt dan dat de resultaten waartoe ze voert met de waarneming zullen overeenstemmen, als met de realistische, dat zij de ware toedracht van het verloop der bewegingen moet uitdrukken. Welke van deze twee zienswijzen Keplers eigene was, blijft bij de lectuur van zijn werken niet lang verborgen. Met overtuiging stelt hij zich op het tweede standpunt, dat, naar hij meent, ook dat van Copernicus is geweest, en hij keurt dan ook de voorrede van Osiander volstrekt af. Van een hypothese wordt niet alleen bruikbaarheid, maar ook waarheid verlangd en wanneer eenzelfde verschijnsel door twee verschillende hypothesen gered blijkt te kunnen worden, moet men physische of metaphysische argumenten trachten op te sporen om uit te maken, welke van deze twee in de natuur in feite is gerealiseerd of aan te tonen, dat ze geen van beide waarheid bevatten. Wij hebben boven reeds een der kriteria leren kennen, met behulp waarvan Kepler dergelijke beslissingen wil treffen: eenvoud van quantitatieve relatie, synoniem met harmonie, is het kenmerk van waarheid; het stelsel van Copernicus verdient de voorkeur boven dat van Ptolemaios, omdat het een overzichtelijker, het gevoel voor orde en regelmaat meer bevredigend wereldbeeld levert. 36. Hier komt nu echter in de Astronomia Nova een nieuwe overweging bij, die in den volledigen titel van het werk reeds staat aangekondigd. Die titel luidt, voorzover hij hier ter zake doet: Astronomia Nova ΑΙΤΙΟΛΟΓΗΤΟΣ seu Physica Coelestis, d.w.z. Nieuwe Astronomie, naar oorzaken behandeld, of Physica des Hemels. Deze titel beduit een program: Kepler zal zich niet tevreden stellen met de kinematische beschrijving van het verloop der gebeurtenissen aan den hemel, maar hij zal trachten, ook de oorzaken op het spoor te komen waardoor zij in het leven worden geroepen; aan de kinematica zal hij een dynamica des hemels toevoegen. Deze opvatting van zijn taak hangt natuurlijk nauw samen met het | |||||||||||||
[pagina 342]
| |||||||||||||
realistische standpunt dat hij ten aanzien van het wezen van een astronomische hypothese inneemt. Wanneer men wil verklaren, hoe het komt, dat iets gebeurt, zal men toch eerst zeker moeten weten, dat het gebeurt. Het heeft weinig zin te vragen naar de oorzaken die een zeker bewegingsstelsel in het leven zouden kunnen roepen, wanneer men dat stelsel niet beschouwt als een uitdrukking van de realiteit, maar als een mathematische fictie, die in staat stelt, door berekening resultaten te bereiken die tegen empirische controle bestand zijn. Tenzij men die oorzaken ook als mathematische ficties opvat, hetgeen een houdbaar, maar niet Kepler's standpunt is. Omgekeerd zal de overtuiging, dat een kinematisch beeld de ware toedracht weergeeft, des te sterker worden, naarmate men het beter causaal kan verklaren. 37. Zoals blijken zal, is Kepler er niet in geslaagd, voor de dynamica der planetenbeweging resultaten van blijvende waarde te bereiken. Dat neemt niet weg, dat de beschouwingen die hij naar aanleiding van de stralenwet over de oorzaken van de hierdoor gekarakteriseerde planetenbeweging houdt, historisch van het allerhoogste belang zijn. Want, als we afzien van de toepassing van het impetusbegrip op de bewegingen van hemelspheren die we bij de Parijse Terministen aantroffen (II: 112), wordt hier de eerste stap gezet op een weg, die tot een der allerbelangrijkste resultaten der klassieke natuurwetenschap, de mechanica des hemels, zal voeren. En er zijn weinig plaatsen in de geschiedenis der wetenschap aan te wijzen, waar men van zo nabij een ingrijpende richtingsverandering in het denken - en nog wel een die met het thema van dit boek ten nauwste verband houdt - kan gadeslaan. Waar die verandering uit bestaat, wordt wellicht het allerduidelijkst door Kepler zelf gezegd in een van de aantekeningen, die hij in de tweede uitgave van het Mysterium Cosmographicum (1631) aan den tekst van 1596 heeft toegevoegd. Hij had in het tweede hoofdstuk naar aanleiding van het feit, dat de lineaire snelheid van een planeet met toenemenden afstand tot de zon kleiner wordt, geschrevenGa naar eind22: Wij moeten dus een van de volgende twee feiten vaststellen: òf de bewegende zielen (der planeten) zijn des te zwakker, naarmate zij verder van de zon verwijderd zijn òf er huist slechts één bewegende ziel in het centrum van alle banen, t.w. de Zon, die een lichaam des te heftiger aandrijft, naarmate het dichter bij is, maar die bij de verder verwijderde wegens den afstand en de (hiermee samenhangende) verzwakking van vermogen, krachteloos wordt. In 1623 voegt hij hier deze noot aan toeGa naar eind23: Wanneer men inplaats van ziel(anima) het woord kracht(vis) zet, heeft men precies het principe, waarop de physica des hemels in de Marscommentaren (d.i. de Astronomia Nova) is opgebouwd. 38. Het gaat hier slechts om de vervanging van een woord door een ander, maar deze beide woorden vertegenwoordigen geheel verschillende | |||||||||||||
[pagina 343]
| |||||||||||||
denkrichtingen. Vis lezen waar eerst anima stond betekent een animistische zienswijze voor een mechanistische opgeven. Kepler wil, zoals hij het elders uitdrukt, de natuur niet langer zien instar divini animalis (als een goddelijk bezield wezen), maar instar horologii (als een uurwerk)Ga naar eind24. Aanvankelijk had hij op het voetspoor van J.C. Scaliger, wiens Exercitationes Exotericae hij in zijn jeugd met grote aandacht had bestudeerdGa naar eind25, de Stoïcijnse opvatting gehuldigd, dat een planeet een intelligentie of geest (mens) bezit, die hem in staat stelt, bewust zijn weg door de hemelruimte te vinden. De in de Middeleeuwen overheersende voorstelling van hemelse intelligenties, die de spheren waaraan de planeetlichamen bevestigd zijn bewegen, was onhoudbaar gebleken, toen Tycho uit zijn waarnemingen over kometen had afgeleid, dat deze in hun loop al die spheren zouden moeten doorboren, maar de animistische grondgedachte had die weerlegging van haar gebruikelijke uitwerking overleefd en was, zoals blijkt, zelfs in sterkeren vorm dan ooit te voren aanvaard. 39. Nauwgezet als steeds, was Kepler zich nu echter gaan verdiepen in de vraag, hoe zulk een planeetgeest het wel aan zou moeten leggen, om uit eigen inzicht zijn lichaam de ingewikkelde bewegingen te laten volbrengen die het volgens de astronomie uitvoert en dit leidde reeds in de eenvoudigste gevallen tot aanzienlijke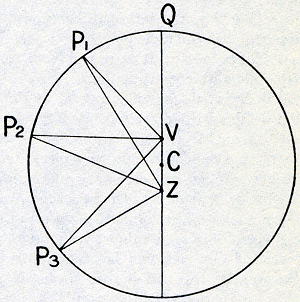 Fig. 18. De planeetgeest moet zijn lichaam zo bewegen, dat de
juiste afstanden tot Z in acht worden genomen,
terwijl CPi constant moet zijn
en ∠ QVPi eenparig
moet veranderen.
moeilijkheden. Wanneer de baan een eenvoudige excenter is, wanneer dus de planeet (Fig. 18) eenparig een cirkel doorloopt om C als centrum, terwijl de zon in Z staat, kan men zich desnoods nog voorstellen, dat de geest, het lichaam eenparig voortstuwend, telkens zorgt voor de juiste afstanden P1Z, P2Z, P3Z enz., door op de schijnbare middellijn van Z te letten en dat hij er zodoende in slaagt, het op een constanten afstand van het onzichtbare mathematische punt C te houden. Bij verdeling der excentriciteit wordt dat echter al veel moeilijker, omdat hij dan den veranderlijken afstand tot Z zo moet combineren met de veranderlijke lineaire snelheid, dat daaruit een constante afstand tot C resulteert. En bij een epicyclische beweging wordt het helemaal onbegrijpelijk, hoe het mathematische | |||||||||||||
[pagina 344]
| |||||||||||||
epicykelcentrum, waarin geen geest kan huizen, er in slaagt, al dan niet eenparig den deferens te doorlopen. 40. Dit alles wordt in Hoofdstuk II van de Astronomia Nova uitvoerig overwogen, maar daarmee is de zaak nog lang niet afgedaan. Kepler komt er nog herhaaldelijk op terug en geeft het denkbeeld, dat hem blijkbaar na aan het hart lag, slechts schoorvoetend en niet na nog een tijdlang de mogelijkheid van een van buiten af te verlenen steun te hebben toegelaten, op. Dat hij het ten slotte laat varen, geschiedt vooral onder den indruk van de eenvoudige quantitatief formuleerbare relatie die hij in de stralenwet uitspreekt en die onweerstaanbaar de gedachte aan een hefboomwerking volgens de Aristotelische opvatting opwekt. De planeet wordt des te langzamer bewogen, schijnt dus des te zwaarder te zijn, naarmate zij verder van de zon verwijderd is; een gewicht aan een hefboom lijkt ook des te zwaarder (d.w.z. werkt des te sterker), naarmate het verder van het steunpunt afhangt. Heeft het nu wel zin, in het eerste geval een bewuste intelligentie in de planeet, in de zon of in beide aan te nemen en deze in het tweede niet toe te kennen aan het juk en de gewichten die er aanhangen? Wanneer we de gedragingen van den hefboom toeschrijven aan de werking van zekere natuurkrachten, die de Schepper in Zijn schepping werkzaam heeft gesteld en onveranderd in stand houdt waarom dan niet de bewegingen der hemellichamen? 41. Dit betoog heeft natuurlijk voor een getrouwen volgeling van Aristoteles niets overtuigends: hemel en aarde verschillen zo wezenlijk van elkaar, dat analogieredeneringen als de bovenstaande volstrekt ongeoorloofd zijn. Minder rechtzinnige aanhangers hadden dit bezwaar al niet meer gevoeld: we zagen immers de Parijse Terministen hun door aardse bewegingsverschijnselen geïnspireerd impetusbegrip onbekommerd op de bewegingen van de hemelspheren toepassen. En sedert Copernicus de aarde als een planeet had leren beschouwen, was de oude tegenstelling tussen het hemelse en het ondermaanse tot in den grond verstoord. Hoe zal men een verschil in aard kunnen volhouden, als er geen ruimtelijk onderscheid meer is? Ontdaan van het beschermend omhulsel, dat Osiander in zijn voorrede er over had geworpen, niet langer op te vatten als mathematische fictie, maar optredend met volle aanspraak, de reële structuur der wereld weer te geven, openbaart het stelsel van Copernicus onverbloemd de vernietigende, uitwerking die het op de traditionele wereldbeschouwing heeft. 42. Kepler vervangt dus ziel door kracht. Verandert daarmee nu werkelijk veel? In zekeren zin natuurlijk niet. Ziel is een onbekend agens, waarvan het bestaan wordt aangenomen om zekere gedragingen van levende lichamen te verklaren. Kracht is een onbekend agens, waarvan het bestaan wordt aangenomen om zekere gedragingen van levenloze lichamen te verklaren. Vast staan in beide gevallen alleen de gedragingen. Men verkrijgt geen dieper of juister inzicht door hun onbekende oorzaak met een of anderen naam te gaan benoemen. | |||||||||||||
[pagina 345]
| |||||||||||||
In een anderen zin verandert er heel veel. Wanneer men de bewegingen der planeten inplaats van aan een ziel aan een kracht gaat toeschrijven, geeft men te kennen, dat men ze wil beschouwen als levenloze lichamen en dat ze dus vallen onder de hiervoor geldende wettelijkheid, die die der mechanica is. Zou men gaan spreken over de intelligentie van een hefboom, dan zou men daardoor uitdrukking geven aan den wens, dit toestel te beschouwen als een bewust levend wezen, dat dus onder de daarvoor heersende wettelijkheid, die der psychologie, valt. In beide gevallen schept men eenheid, waar verscheidenheid was en dat kan zeer bevorderlijk zijn voor het wetenschappelijk denken. In Kepler's tijd bestond er een mechanica die voldoende ontwikkeld was om het probleem der planetenbeweging aan te durven en die, voorzover die moed overmoed bleek te zijn, zich al spoedig tot de hoogte van haar taak zou opwerken. Er bestond geen psychologie die iets met de gedragingen van een balans zou hebben weten te beginnen. Kepler deed dus een eersten stap in de goede richting toen hij in de theorie der planetenbeweging vis ging zeggen inplaats van anima, niet omdat het eerste woord iets kon verklaren, wat het tweede niet verklaren kon (in feite verklaarden ze geen van beide iets), maar omdat het gebruik van het eerste een aankondiging was van het streven, na te gaan wat men met behulp van de mechanica van de planetenbeweging kon leren verstaan. 43. Men kan hier in een dubbelen zin van mechanisering spreken, al naar men deze onderschikking van de hemelbewegingen aan de wetenschap der mechanica op het oog heeft of nadruk legt op de opvatting der wereld als een door een bovenwereldlijke intelligentie bewust geconstrueerde machine. Geen van beide opvattingen sluit echter naar Kepler's inzicht in, dat de hemellichamen levenloos zouden moeten zijn. Aan de Aarde is hij althans altijd een vegetatieve ziel blijven toekennenGa naar eind26. In de Astronomia Nova wordt daarvan echter afgezien. 44. De proclamering van de mechanistische opvatting van de planetenbeweging, die het woord vis inhoudt, beduidde natuurlijk nog niet meer dan de opstelling van een werkprogram. Kepler stond voor de taak, nader aan te geven, welke krachten het waren die de bewegingen der planeten beheersten en volgens welke wetten zij werkten. Daar krachten echter onbekende agentia zijn, kon dat alleen maar geschieden door te verwijzen naar analoge gevallen of door een specifieke kracht ad hoc in te voeren. Kepler doet het eerste. Onder den indruk van de lectuur van het in 1600 verschenen werk De Magnete van den Engelsen medicus William Gilbert (waarover meer in IV: 172-182) schetst hij een magnetische theorie van het planetenstelsel. 45. Hij ontleent daartoe aan Gilbert de opvatting van de aarde als een grote magneet en breidt deze uit op de andere planeten en de zon. Het magnetisme van de zon wordt gedacht geconcentreerd te zijn in cirkelvormige vezels langs het vlak van de ecliptica. Hieruit wordt nu volgens | |||||||||||||
[pagina 346]
| |||||||||||||
een voorstelling, die we reeds uit de lichttheorieën van Grosseteste en Bacon kennen (II: 73), een immateriële species straalsgewijs uitgezonden. Een wenteling, die de zon om een as loodrecht op de ecliptica uitvoert (een anticipatie van de enkele jaren later door Scheiner inderdaad ontdekte aswenteling van de zon) brengt nu deze species in draaiende beweging en deze roterende species grijpt nu de planeten aan, die door hun traagheid anders in rust zouden blijven, en sleept ze met zich mee. Daar zij alle magneten zijn, houden hun assen op kleine langzame schommelingen na een vasten stand in de ruimte. Daar de species slechts in een vlak wordt uitgestraald en zich dus over cirkels van aangroeienden diameter uitbreidt, de omtrekken van die cirkels echter met de diameters evenredig zijn, vermindert haar dichtheid omgekeerd evenredig met de eerste macht van den afstand tot de zon en niet met de tweede, zoals bij ruimtelijke uitbreiding het geval zou zijn. De bewegende kracht die op de planeten werkt, neemt dus in dezelfde verhouding af en, daar volgens de grondwet der (nog steeds) peripatetische dynamica de kracht evenredig is met de snelheid die ze veroorzaakt, is dus de snelheid van de planeet omgekeerd evenredig met haar afstand tot de zon. Hiermee is de stralenwet voor elke planeet dynamisch afgeleid. 46. Het is natuurlijk niet moeilijk, de onhoudbaarheid van deze afleiding aan te tonen. Kepler identificeert voor de aarde de magnetische en de geographische polen, houdt dus den op kleine schommelingen na onveranderlijken stand van de aardas in de ruimte voor hetzelfde verschijnsel als den onveranderlijken stand van een magneetnaald die op aarde in een kring wordt rondgedragen. Hij mist het inzicht, dat traagheid der materie in haar algemenen vorm in een volharden in een bewegingstoestand bestaat en dat volharden in rust slechts een bijzonder geval daarvan is. En ten slotte past hij een onjuiste dynamische grondwet toe en komt tot een resultaat dat niet algemeen geldig is. En het grootste probleem blijft natuurlijk, hoe het komt, dat niet iedere planeet een cirkel om de zon als centrum beschrijft. En toch: we staan hier aan den oorsprong van de mechanica des hemels, een tak van de natuurwetenschap die meer dan een andere de richting heeft aangegeven waarin zij zich als geheel zou ontwikkelen, het ideaal heeft opgesteld dat zij voor ogen zou houden, de atmospheer heeft bepaald waarin zij verder zou leven. De dynamische behandeling van de hemelverschijnselen doet hier, in de eerste jaren van de zeventiende eeuw, haar eerste onzekere schreden; voordat de eeuw zou aflopen, zou zij onder leiding van Newton het doel dat Kepler voor ogen had gezweefd, bereikt hebben. Wat Kepler het meest weerhouden heeft om op dit gebied meer dan eerste schreden te doen, is vooral de beperktheid van zijn traagheids-inzicht geweest. Inertie - het woord is door hem ingevoerd - is voor hem alleen traagheid in den zin van het gewone spraakgebruik: zelf niets doen, | |||||||||||||
[pagina 347]
| |||||||||||||
in rust willen blijven. Rust eist evenmin een oorzaak als duisternis; het zijn geen zijnden, maar privaties van zijn. Beweging echter kan evenmin zonder oorzaak ontstaan en in stand worden gehouden als licht. 47. Deze opvatting brengt natuurlijk moeilijkheden met zich mee, wanneer het er om gaat - en Kepler stond voor die taak in een briefwisseling met den astronoom Fabricius - te antwoorden op de bekende physische tegenwerpingen tegen het denkbeeld van een bewegende aarde en wel speciaal op het argument van het Oostelijk of Westelijk gerichte kanon, dat Tycho als nieuw element in de discussie had gebracht. Op grond van zijn traagheidsbeginsel kan hij niet instemmen met de opvatting van Copernicus, dat alle aardse lichamen, dus ook wolken, vogels, een opgeworpen steen, van nature in de aardbeweging delen; hij heeft behoefte, een reëlen physischen band te zien die hen daartoe dwingt. Deze wordt echter geleverd door de magnetische attractie die de aarde op alle lichamen uitoefent. Ieder voorwerp dat zich op zekeren afstand van het aardoppervlak bevindt, is te beschouwen als top van een aan de aarde rakenden kegel, die binnen zijn mantel al de banden insluit die het lichaam aan de aarde binden en die het dwingen, met haar mee te draaien. De resultante van de krachten die zij uitoefenen, is verticaal omlaag gericht en daardoor kost het moeite, het lichaam omhoog te bewegen. Geeft men het echter een zijdelingsen stoot, dan verzet zich altijd slechts een gedeelte der bindingen en een ander gedeelte werkt mee. Voorkeur voor een richting is er niet en daarom hangt de schootsverheid ook niet van de richting af. Wanneer de aantrekkende krachten er niet waren, zou het Aristotelische argument van den opgeworpen en weer terugvallenden steen ook al beslissend tegen de aardbeweging geweest zijn; de steen volgt tijdens zijn verticale beweging de aarde alleen, omdat zij hem zo stevig vasthoudt. Hij zou het niet meer geheel kunnen doen, wanneer hij op grotere hoogte kwam waar de aantrekkingskracht verzwakt is; om deze reden is de omloopstijd van de maan ook zoveel groter dan een dag. 48. Het verdient nog opmerking, dat, hoewel Kepler altijd spreekt van de kracht waarmee de aarde een lichaam aantrekt (de toevoeging van het adjectief magnetisch heeft natuurlijk geen enkele betekenis en dient alleen om er een schijn van bekendheid aan te geven) hij toch wel een wederzijdse attractie op het oog heeft. De aarde en een steen daarbuiten ondergaan beide den invloed van de natuurkracht die er naar streeft, ze te verenigen. Vertoont zijn denkbeeld in zoverre dus verwantschap met de latere gravitatietheorie van Newton, zo wijkt het er principieel van af, doordat de krachten die de lichamen ondervinden, niet onderling gelijk worden gedacht. Zij verhouden zich als de moles der lichamen, welk woord hier hoeveelheid materie schijnt te betekenen en dus het best door massa zou kunnen worden weergegeven. Wanneer de twee lichamen de gelegenheid krijgen, zich te bewegen, verenigen zij zich in een punt, dat het verbindingslijnstuk van hun centra verdeelt in stukken, die zich om- | |||||||||||||
[pagina 348]
| |||||||||||||
gekeerd verhouden als de massa's. Het is niet moeilijk in te zien, welke dynamische gedachtengang tot deze bewering kan hebben geleid: de toegevoegde opmerking, dat de verhouding dezelfde is als bij een balans, wekt het vermoeden, dat zij slechts op deze analogie steunt. 49. Intussen is door deze uitweiding de kinematische behandeling van de Marsbeweging onderbroken. Haar hervattend blijft Kepler voorlopig werken met de onjuist bevonden hypothese van IV: 31 (thans hypothesis vicaria (plaatsvervangende hypothese genaamd), omdat deze althans benaderde Mars-posities oplevert. Hij stelt hiervoor nu het fundamentele probleem aan de orde dat iedere planetentheorie, wil zij ooit tot samenstelling van tafels komen, noodzakelijk zal moeten kunnen oplossen, nl. de berekening van de positie van een planeet op een gegeven tijdstip. Om deze te kunnen geven, moet hij (Fig. 19) het verband kennen tussen den boog QP die sedert het passeren van het aphelium Q doorlopen is en den daaraan besteden tijd. 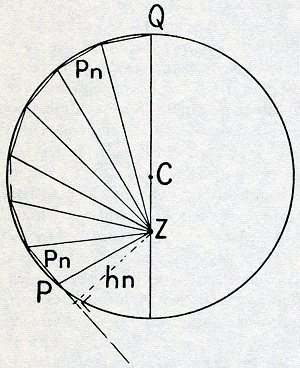 Fig. 19. De planeet P doorloopt een cirkel om C als middelpunt zo, dat de lineaire snelheid,
omgekeerd evenredig is met den afstand tot Z. Kan men
nu de oppervlakte van het perk QZP als een maat
beschouwen voor den tijd die verstreken is sedert den doorgang van de
planeet door het aphelium Q?
50. Dat was een vraagstuk dat de krachten van Kepler en van alle andere wiskundigen van een tijd die nog geen analytische meetkunde en geen infinitesimaalrekening kende, verre te boven ging en hij kan dan ook niet meer doen dan het formuleren en de mathematici aansporen, de oplossing ervan te zoeken. Het ligt echter niet in zijn aard, zich door dergelijke moeilijkheden te laten ophouden en waar de exacte oplossing niet mogelijk is, zoekt hij een benaderde. Hij overweegt dat, daar de snelheid in een punt P van de baan volgens de stralenwet omgekeerd evenredig is met den voerstraal ZP, de tijd die aan een baanelement besteed wordt, er recht evenredig mee moet zijn en dus bij geschikte keuze van eenheden door dien voerstraal kan worden voorgesteld en hij vraagt zich nu af, of niet de totale tijd die voor het doorlopen van den boog QP nodig is, zou kunnen worden aangegeven door de oppervlakte van het perk QZP, beschouwd als de som van al zijn voerstralen. Hij beroept zich daartoe op Archimedes, die een cirkelsector als som van al zijn stralen zou hebben opgevat, maar hij is een | |||||||||||||
[pagina 349]
| |||||||||||||
veel te goed wiskundige om niet te beseffen, dat dit
beroep niet opgaat, omdat de cirkelstralen CA in Fig. 20
wèl, maar de voerstralen ZP in Fig. 19 niet
loodrecht op den cirkelomtrek staan. Inderdaad: beschrijft men in bg QP van Fig. 20 een regelmatig gebroken lijnstuk met n-zijden pn en een
apothema rn, dan is de oppervlakte van
sector QCP de limiet van de som van de oppervlakten der
driehoeken, die C tot top en de lijnstukken pn tot basis hebben, dus van ½
n . pnrn, als
n tot oneindig nadert. Voor die som kan men schrijven
½ pn Σ rn en nu de zegswijze, dat de sector
de som van al zijn stralen is, opvatten als een onstrenge uitdrukking voor
het feit, dat rn nadert tot den straal
van den cirkel; immers Σ rn
kan als benadering van de som van een groot aantal 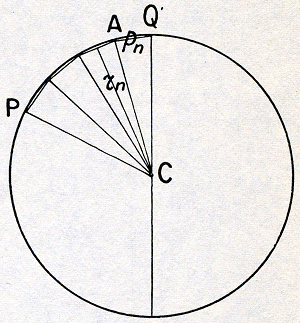 Fig. 20. In welken zin men in tegenstelling tot Fig. 19 de
oppervlakte van den cirkelsector QCP als de som
van al zijn stralen CA beschouwen kan.
stralen worden beschouwd. In Fig. 19 kan men ook de oppervlakte van het perk QZP wel beschouwen als de limiet van de som van de oppervlakten van driehoeken met top Z en basis pn, maar deze driehoeken zijn niet gelijkbenig. Zijn hun hoogten hi (i = 1...n), dan wordt de som ½ pn Σ̄ hi, maar nu nadert hi niet tot een van de zijden van den driehoek, maar tot den afstand van Z tot een raaklijn van den cirkel, zodat Σ hi nooit als benaderde som van voerstralen kan worden gelezen. 51. Maar nu volgt een typisch Keplerachtige stap: het is wiskundig weliswaar onhoudbaar, maar we zullen toch maar bij wijze van benadering de oppervlakte van het perk QZP als een maat beschouwen voor den tijd, waarin de voerstraal uit Z het perk doorlopen heeft. Hiermee heeft Kepler de wet verkregen die men tegenwoordig zijn tweede pleegt te noemen, omdat zij beschouwd wordt als aanvulling van de eerste, die zegt, dat de planeet een ellips doorloopt met de zon in een der brandpunten. Zij is echter eerder ontdekt en wel voor een cirkelbeweging met verdeelde excentriciteit als een benadering voor een exacte berekening op grond van de stralenwet. Kepler komt op haar afleiding niet meer terug en neemt haar onveranderd over, wanneer hij later tot de conclusie komt, dat de ware baanvorm die van een ellips is. Intussen is nu de uitdrukking voor den tijd t, waarin de planeet bg QP doorloopt, heel eenvoudig geworden. Immers (Fig. 21): | |||||||||||||
[pagina 350]
| |||||||||||||
opp. perk QZP = opp. sector QCP + opp. Δ CZP. Is nu CP = 1, CZ = e, ∠ PCQ = β (genaamd excentrische anomalie), dan blijkt: opp. perk QZP = ½ β + ½ e sin β. Wordt de gehele baan in den tijd T doorlopen, dan geldt dus:
Stellen wij nu β + e sin β = α, dan is hiermee een rekengrootheid ingevoerd, genaamd middelbare anomalie, die evenredig met den tijd verandert en die de benadering voorstelt van ∠ QVM in de hypothesis vicaria (Fig. 16). 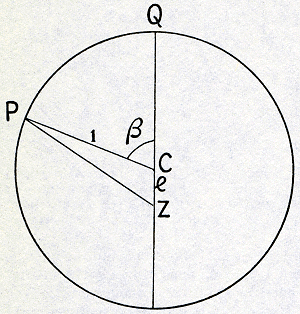 Fig. 21. Afleiding van de betrekking tussen den boog QP, dien de planeet P sedert den doorgang
door het aphelium Q heeft doorlopen en den daaraan
besteden tijd. Deze tijd wordt voorgesteld door de oppervlakte van het
perk QZP. ∠QZP = v. PZ = ρ
De astronomie verlangt echter niet zozeer bij een gegeven positie van de planeet het tijdstip te berekenen waarop zij haar bereikt, als wel omgekeerd, voor een gegeven waarde van den tijd de waarde van β te vinden die de plaats bepaalt. Nu volgt uit t de middelbare anomalie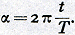 . Men moet nu β vinden uit de vergelijking: . Men moet nu β vinden uit de vergelijking:
β + e sin β = α die in de wiskunde den naam van vergelijking van Kepler heeft gekregen. De oplossing van deze transcendente vergelijking levert moeilijkheden op, die de vermogens van de 16e-eeuwse wiskunde verre te boven gaan. Denkt men echter een benaderde waarde voor β gevonden, dan wordt de positie van de planeet bepaald door de formules:
waarvan de eerste den afstand tot Z leert kennen en de tweede den hoek v (ware anomalie), die uitdrukt, hoever Z P van het aphelium Q af ziet en die, daar de heliocentrische lengte van het aphelium bekend is, dus ook de heliocentrische lengte van de planeet bepaalt. | |||||||||||||
[pagina 351]
| |||||||||||||
52. Wij zagen boven reeds, dat Kepler de eerste was, die openlijk durfde afwijken van dat deel van het Platonisch axioma, waarin van alle bewegingen van hemellichamen eenparigheid wordt geëist. Aan het andere, dat slechts cirkelvormige banen toelaat, heeft ook hij tot dusver nog niet getornd. Bij de voortzetting van zijn berekeningen ziet hij zich daartoe echter ook gedwongen. Hij had namelijk bij de toepassing van de boven vermelde methode ter bepaling van de afstanden Aarde-Zon tegelijk een aantal afstanden Mars-Zon kunnen bepalen, terwijl de hypothesis vicaria hem met voldoende nauwkeurigheid de bijbehorende heliocentrische posities van de planeet leerde kennen. Nu kan men uit drie dergelijke waardenparen de ligging van het aphelium en de excentriciteit van de cirkelvormig onderstelde Marsbaan vinden. Als steeds wantrouwend tegen zijn eigen resultaten voert Kepler die berekening voor verschillende drietallen uit en vindt telkens andere uitkomsten. Hieruit trekt hij nu de conclusie, dat de Marsbaan geen cirkel kan zijn, waardoor hij het Platonisch axioma in zijn vollen omvang verwerpt. De astronomie werd hiermee ontdaan van een leidraad die, na lang een heilzame steun te zijn geweest, langzamerhand in een knellenden band was ontaard. Voorlopig bleef ze er echter wel enigszins stuurloos door achter. 53. Kepler stelt nu eerst op grond van lange berekeningen vast, in welken zin de baan van een cirkel afwijkt. Het blijkt, dat de verschillen in de afstanden die uit waarnemingen berekend zijn en die uit de tot dusver aanvaarde hypothese volgen, des te groter zijn, naarmate de planeet verder van de absiden afligt en wel zo, dat de baan zijdelings ingedeukt is en dus den vorm van een ovaal heeft. 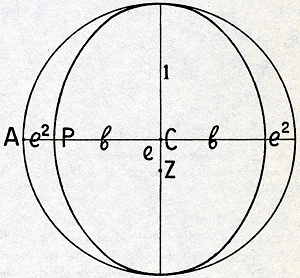 Fig. 22. Benadering van den ovalen vorm van de Marsbaan door een
ellips, die het lijnstuk perihelium-aphelium tot grote as (2a) heeft. Voor a = 1 is de kleine as (2b) bepaald door b = 1 - e2, waarin e2 = 0,00858.
Op dit punt grijpt de dynamische beschouwingswijze weer in. Kepler tracht een physische oorzaak te vinden van het tot dusver onverklaard gebleven feit, dat de planeet, aangegrepen door de van de zon uitstralende en met haar ronddraaiende species niet eenvoudig met constante snelheid een cirkel om de zon doorloopt. Hij vindt deze in een eigen inwendig bewegend vermogen van de planeet, waardoor zij een epicykel beschrijft om een punt dat niet eenparig om | |||||||||||||
[pagina 352]
| |||||||||||||
de zon draait. De resulterende baan blijkt nu inderdaad een ovalen vorm te hebben. Door nu opnieuw op zeer vrijmoedige wijze deze voorstelling te combineren met de hypothesis vicaria komt Kepler tot een meetkundige constructie van deze ovaal, maar ondervindt onoverkomelijke moeilijkheden, als hij hierop nu de perkenwet, die oppervlakteberekeningen vereist, wil toepassen. Hij vervangt haar nu bij benadering door een ellips (Fig. 22), waarvan de grote as samenvalt met het lijnstuk perihelium-aphelium, terwijl de kleine as de breedte van de ovaal in het midden aangeeft. Heeft de halve lange as a de waarde 1, dan blijkt de halve korte as b = 1 - e2 te zijn. De grootste breedte van het maantje tussen de ellips en den cirkel, die de lange as tot diameter heeft, is dus e2 = 0,00858. 54. Weer niet gerust op de uitkomst controleert hij haar door negentien afstanden Mars-Zon te berekenen in posities die zo regelmatig mogelijk over de baan verspreid liggen. Bij vergelijking met de elliptische benadering van de ovaal blijkt echter, dat ze er slechts bij zouden passen, wanneer de breedte van het maantje 0,00429 was. 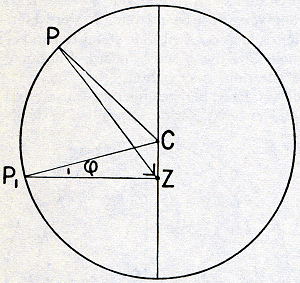 Fig. 23. De optische vereffening (∠ CPZ) bereikt haar maximum wanneer P in P1 is (P1Z
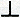 CZ). φ = 5° 18′.
secφ = 1,00429.
CZ). φ = 5° 18′.
secφ = 1,00429.Op dit punt kwam hem een toeval te hulp, zoals alleen aan iemand die zich geheel in een probleem heeft vastgebeten, te beurt valt. Bij de berekening van Marsposities volgens de hypothesis vicaria had hij nog al eens te maken met de maximale waarde van de z.g. optische vereffening, d.i. de hoek tussen de richtingen CP en ZP (Fig. 23). Deze bereikt haar |maximum φ in den stand P1 van de planeet, waarin ZP1  CZ en bedraagt dan voor Mars 5° 18′.
Nu had hij op een zeker ogenblik den secans van dezen hoek nodig en deze
bleek 1,00429 te bedragen, dus een mantisse te hebben, die juist de breedte
van het maantje aangaf. ‘Toen ik dit zag,’ schrijft
hijGa naar eind27, ‘was het mij of ik uit den
slaap gewekt werd en een nieuw licht zag en ik ben als volgt gaan
redeneren:’
CZ en bedraagt dan voor Mars 5° 18′.
Nu had hij op een zeker ogenblik den secans van dezen hoek nodig en deze
bleek 1,00429 te bedragen, dus een mantisse te hebben, die juist de breedte
van het maantje aangaf. ‘Toen ik dit zag,’ schrijft
hijGa naar eind27, ‘was het mij of ik uit den
slaap gewekt werd en een nieuw licht zag en ik ben als volgt gaan
redeneren:’
In de gecorrigeerde ovaal (Fig. 22) moet CA/CP = 1,00429 zijnGa naar voetnoot* en dit blijkt sec φ te zijn; dus is CP = CA. cos φ. Denk deze betrekking nu geldig (Fig. 24) tussen de afstanden van Z tot alle punten Pc van de | |||||||||||||
[pagina 353]
| |||||||||||||
werkelijke baan en tot de op ZPc liggende punten P van den cirkel met dien verstande, dat φ voor iedere richting de optische vereffening aangeeft, dan vindt men als afstandsformule: ρ = ZPc = ZP cos φ = PM = = 1 + e. cos β.  Fig. 24. Verbetering van de benadering van Fig. 22. ZPc = ZP cos
φ.
Het bleek nu bij narekenen, dat de berekende afstanden hiermee heel goed klopten, zodat er nu dus zekerheid bestond over de twee betrekkingen: ρ = 1 + e cos β (1)Na nu voor de bepaling van den waren baanvorm nog allerlei tijdrovende dwaalwegen te hebben ingeslagen, waarop we hem niet zullen volgen, komt Kepler op het achteraf voor de hand liggende denkbeeld, de ovaal niet te benaderen door een ellips met b = 1 - e2, die een tweemaal te breed maantje gaf, maar door een ellips met b = 1 - ½ e2. Dat bleek met de waargenomen posities goed te kloppen. 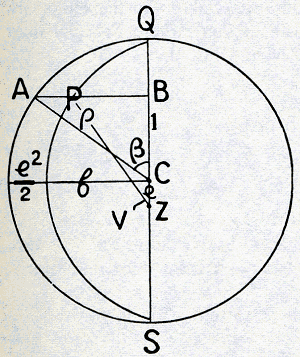 Fig. 25. Definitieve voorstelling van de Marsbaan door een
ellips, waarvan voor a = 1, b =
1 - e2/2 (e2 = 0,00858). Men trekke nog de lijn
ZA.
Echter bleef het verband tussen deze hypothese over den baanvorm en de afstandsformule (1) nog duister. Kepler vertelt, dat hij hierover heeft nagedacht pene usque ad insaniamGa naar eind28 (om er bijna gek van te worden), totdat hem op eens de schellen van de ogen vielen en hij inzag, dat de formule (1) juist bij deze ellips paste. Wij zullen de moeizame redenering, waardoor hij dit bewijst, als volgt vereenvoudigd weergeven (Fig. 25). Denk de ellips verkregen door alle ordinaten loodrecht QS in de verhouding b (= 1 - ½ e2) te verkleinen en de excentrische anomalie β geinterpreteerd als ∠ QCA, dan blijkt uit de figuur: | |||||||||||||
[pagina 354]
| |||||||||||||
ZB = ρ cos v = ZC + CB = e + cos β waaruit door quadrateren en optellen volgt: ρ2 = e2 + 2 e cos β + cos2 β +Verwaarlozen we nu bij het quadrateren van 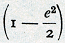 de vierde macht van e, dan vinden we: de vierde macht van e, dan vinden we:
ρ2 = (1 + e cos β)2, dus inderdaad: ρ = 1 + e cos β. Het is nu nog van belang te weten, waar de brandpunten van de ellips liggen. Hun afstand tot het centrum wordt bepaald door: c2 = 1 - b2 = 1 - als we weer de vierde macht van e verwaarlozen. Dus is c = e, d.w.z. een der brandpunten valt in de zon. 55. Ten slotte moet nog worden nagegaan, hoe het nu met de perkenwet staat. We berekenen hiertoe (Fig. 25) de oppervlakte van het ellipsperk ZQP door het te beschouwen als ontstaan uit het cirkelperk ZQA door ordinaatverkorting in de verhouding b. Men vindt dan Opp. ZQP = b . opp. ZQA = b (opp. Δ ZCA + opp. sector QCA) = b (½ e sin β + ½ β) = ½ b α. Dus geldt: 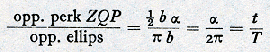 wanneer t de tijd is, waarin de planeet van Q naar P komt en T de omloopstijd. Het blijkt dus, dat het perk weer een maat voor den tijd is, dus dat de perkenwet geldt. De gehele theorie is ten slotte samen te vatten in de formules: α = β + e sin β waarin Voor een gegeven tijdstip t kent men α. De vergelijking (1) moet dan β leveren. Met behulp van (β) berekent men uit (2) den afstand tot de zon | |||||||||||||
[pagina 355]
| |||||||||||||
en daarna uit (3) de ware anomalie, waaruit de heliocentrische positie volgt. In woorden laat zich het verkregen resultaat uitdrukken in de eerste twee wetten van Kepler:
In deze wetten is de gehele kinematica van de planetenbeweging samengevat. 56. Dit boek is ongetwijfeld geen handboek voor de geschiedenis der theoretische astronomie. Wij hebben er echter prijs op gesteld, den lezer althans een indruk te geven (meer dan een indruk is het niet) van de wijze, waarop Kepler zijn wetten heeft gevonden, omdat we hier als het ware de deur die de zaal der antieke en middeleeuwse natuurwetenschap van die der klassieke scheidt, op haar hengsels zien draaien en we met den man die haar opende in de nieuw ontsloten denkruimte kunnen binnentreden. Wat is het nieuwe, dat we er opmerken? Niet in de eerste plaats resultaten die sterk van het oude afwijken, maar voor alles een methode die dat heel duidelijk doet. Haar voornaamste kenmerken zijn:
Wij merken hier nog bij op, dat de in 2) genoemde zelfstandigheid van de natuurwetenschap ten aanzien van philosophie en theologie als wetenschappen beschouwd natuurlijk niet insluit, dat het denken onafhankelijk zou zijn geworden van metaphysische of godsdienstige overtuigingen, maar alleen, dat deze in de wetenschapsbeoefening als zodanig geen functie meer mogen vervullen. Dat er van onafhankelijkheid geen sprake is, kan niemand ons beter leren dan Kepler, die voortdurend zowel in de voorstellingen van de Christelijke geloofsleer als in de denkbeelden van de Pythagoraeïsche getallenmystiek inspiratie voor zijn wetenschappelijk werk zoekt en vindt. 57. De ontdekkingsgeschiedenis van Kepler's eerste twee wetten heeft behalve haar historische betekenis ook een psychologische, omdat zij zo duidelijk de wonderlijke mengeling van rationele en irrationele momenten toont, waaruit grote wetenschappelijke vondsten in den regel voortkomen. Het ging, zoals in onze korte schets al reeds voldoende duidelijk geworden zal zijn, waarlijk niet steeds volgens de regelen der logische kunst in zijn werk. Er werden heel wat sprongen gemaakt die redelijk niet te verant- | |||||||||||||
[pagina 356]
| |||||||||||||
woorden waren, de wiskunde bleek inderdaad wel heel vaak giskunde te zijn en de phantasie scheen het soms geheel van het wetenschappelijk denken te winnen. Maar ten slotte had de koele redelijke kritiek toch het laatste woord en het uiteindelijk resultaat is als een voltooid bouwwerk, waarin niets meer herinnert aan de onordelijkheid die er nog een paar dagen geleden in viel aan te treffen. Of misschien toch iets. Kepler is na de formulering van de perkenwet toch altijd overtuigd gebleven van de geldigheid van de stralenwet (waarvan hij immers een dynamische afleiding meende te bezitten en die hij daardoor in haar wezen meende te begrijpen) en hij heeft de eerste altijd slechts beschouwd en gebruikt als een benadering van de tweede. In werkelijkheid is de relatie juist andersom. De perkenwet is te formuleren als omgekeerde evenredigheid tussen de lineaire snelheid en den afstand van de Zon tot de raaklijn waarlangs de snelheid gericht is; bij kleine waarden van de excentriciteit, zoals alle planetenbanen die bezitten, verschilt de doorlopen ellips echter weinig van den cirkel en haar brandpunt valt bijna met het centrum samen, zodat de voerstraal van de Zon naar een punt van de kromme als benadering kan gelden voor haar afstand tot de raaklijn in dat punt. 58. De eerste twee wetten, die door generalisering al spoedig voor iedere planeet geldig werden verklaard, leren alleen iets over de beweging van elke planeet afzonderlijk. Tien jaar na hun publicatie heeft Kepler ze aangevuld met een derde wet, die verband legt tussen den omloopstijd van een planeet en de halve grote as van haar baan en die dus pas het systeem leert kennen dat het planetenstelsel als geheel beheerst. Zij spreekt uit, dat er voor alle planeten een constante verhouding bestaat tussen de tweede macht van den omloopstijd en de derde macht van de halve grote as en ze geeft dus tot op zekere hoogte een antwoord op de vraag naar het verband tussen de afstanden van de verschillende planeten tot de zon, die Kepler in 1597 in het Mysterium Cosmographicum gesteld had en opgelost meende te hebben. De derde wet komt voor in het in 1619 verschenen werk Harmonice Mundi, maar zij heeft eigenlijk met den inhoud van dit werk weinig te maken en ze is ook pas ontdekt, toen het al voltooid wasGa naar eind29. Zij komt voor in een overzicht over de planetentheorie, dat als inleiding dient voor de definitieve beschouwingen over den samenhang tussen de bewegingen der planeten en het systeem der muzikale harmonieën; ze wordt hierin zonder een poging tot nadere verklaring eenvoudig op grond van door Tycho verrichte metingen als een empirisch feit vastgesteld; op de dan volgende beschouwingen heeft ze geen invloed, omdat daarin wel de waarden van de omloopstijden en de halve grote assen voor de verschillende planeten voorkomen, maar niet de betrekking tussen deze grootheden, die de wet uitdrukt. 59. Voor de astronomie was de ontdekking van de derde wet een feit | |||||||||||||
[pagina 357]
| |||||||||||||
van grote historische betekenis en voor Kepler's leven was ze van uitzonderlijk belang, omdat ze de definitieve bevestiging bracht van zijn vermoeden, dat er een mathematisch uitdrukbare structuur van het planetenstelsel moest bestaan. Reeds in het Mysterium Cosmographicum had hij zich bezig gehouden met de vraag naar het verband tussen omloopstijd en afstand tot de zon en in de bijna twintig jaren die sindsdien verstreken waren, had de vraag hem nooit losgelaten. Evenals dat bij vorige gelegenheden het geval was geweest, bracht het nieuwe inzicht hem ook nu in een toestand van extase. Hij spreekt van heilige razernij en van een onzegbare verrukking over de aanschouwing der hemelse harmonieënGa naar eind30. In een later werk, Epitome Astronomiae Copernicanae, heeft hij nog moeite gedaan, een physischen grondslag voor de derde wet te vinden, maar zonder succesGa naar eind31. De opzet van dit boek geeft ons geen aanleiding over het werk Harmonice Mundi zelf te spreken. Het is in zijn lange en phantastische beschouwingen over de mathematische harmonieën die door de bewegingen der planeten worden geconstitueerd, uiterst belangwekkend voor de kennis van Kepler's veelzijdige en nooit geheel te doorgronden persoonlijkheid en bezit ook grote waarde voor de ontwikkelingsgeschiedenis der Pythagoraeïsche wereldbeschouwing, maar het heeft op het aspect der klassieke natuurwetenschap dat het onderwerp van dit boek vormt, geen merkbaren invloed uitgeoefend. Hetzelfde geldt voor Kepler's astrologische theorieën. |
|


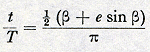 of
of 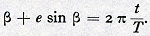
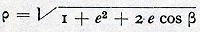 en ρ cos v = e + cos
β
en ρ cos v = e + cos
β