Jongens en wetenschap. Deel 1

Het stukgesneden Lint

Als je uit een stuk papier omheteven welk figuur zó uitknipt, dat de schaar van een punt vertrekkend tot datzelfde punt terugkeert, dan twijfelt er niemand aan, dat je uiteindelijk steeds twee stukken papier in handen hebben zal. Het spreekt van zelf, dal dit ook geldt voor holle lichamen of cylinders, als je ze zó vaneensnijdt, dat de schaar steeds naar haar vertrekpunt terugkeert. Er is nochtans een merkwaardige uitzondering op die algemene regel. In één enkel geval immers, kan een stuk papier volledig in twee worden doorgesneden, terwijl de einduitkomst een onverdeeld geheel blijft. Probeer het maar eens zelf. Je neemt een stuk papier en je snijdt er een lint uit, waarvan je de twee uiteinden aan elkaar kleeft. Dit doe je echter niet op de gewone wijze, zodat je een regelmatige papierring krijgt, daar de



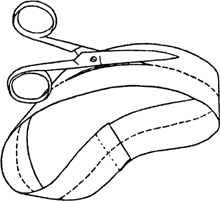
beide uiteinden van het lint elkander op dezelfde zijde raken. Je moet het heel anders doen en namelijk zo, dal je het eene eind van het lint omdraait, vooraleer het aanhetandere eind gekleefd wordt. Dan krijg je een papierring, die een vorm heeft, zoals die hiernaast staat afgebeeld. Nu snijd je het lint overlangs door, maar je volgt zeer nauwkeurig de streepjeslijn, zoals ze op ons figuur voorkomt, tot je het punt hebt bereikt van waaruit je vertrokken bent. De uitslag zal je verrassen, want niet twee linten, wel echter één enkel lint, en dan nog uit één stuk, zal je ten slotte in handen hebben.