Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden

(1878)–David Bierens de Haan– rechtenstatus

BOUWSTOFFEN VOOR DE GESCHIEDENIS der WIS- EN NATUURKUNDIGE WETENSCHAPPEN IN DE NEDERLANDEN. door D. BIERENS DE HAAN.

XIII. Handschrift van Franciscus van Schooten.

1. Onder de talrijke, prachtige en belangrijke feestgaven, die de Leidsche Hoogeschool ter gelegenheid van haar driehonderd-jarig bestaan, den 8^sten Februarij 1875, ontving, behoort een folioband met den rugtitel

Mathemati-(sche)
wercken doo(r)
f. van schoot(en).

Dit is een geschenk van ons medelid j.g. de hoop scheffer; het is merkwaardig voor de geschiedenis der wetenschappen van dien tijd, omstreeks 1620. De gever houdt het doorloopende schrift, waarmede ook een nader te vermelden tusschen-titel voorkomt, voor eigenhandig: het keurige schoonschrift op de 52 eerste bladzijden voor dat van een onder van schooten's leerlingen. Zijne meening, als zoude het eerste schrift gemakkelijk als zijn eigen hand kunnen geconstateerd worden, door middel van het Album Civium Academicorum, is niet bevestigd, omdat onze van schooten nimmer Rector Magnificus is geweest. Het is mij ook niet mogen gelukken, in de verzamelingen aan onze Bibliotheek een handschrift of brief van onzen van schooten in handen te krijgen, ter vergelijking. Toch

ben ik het met den gever eens, dat dit werk waarschijnlijk grootendeels eigenhandig door van schooten, den vader, is ter neder geschreven.

Verder deelt de gever nog mede, dat hij het boek in 1854 geërfd heeft van zijnen oom j. de hoop; deze in 1822 van zijne nicht maria kruijer; en deze laatste wederom van haren neef matthijs vet. Laatstgenoemde was in 1744 geboren, en verzamelde eene bibliotheek, ook over wiskunde; uit deze bibliotheek was dit handschrift bewaard gebleven om de prentjes, die er in voorkomen. De genealogie van dit werk gaat dus eene eeuw terug, verder niet.

2. Wat vooreerst den schrijver aangaat, Mr. franciscus van schooten, deze werd in 1581 te Leiden geboren, waar hij 11 December 1646 stierf. Na den dood van ludolf van ceulen in 1610 (zie Bouwstoffen N^o. VIII) nam hij diens hollandsche lessen in wiskunde waar, en werd in 1615 tot hoogleeraar alhier aangesteld; deze betrekking bekleedde hij tot zijn dood, en werd toen door franciscus van schooten, zijn zoon en naamgenoot, opgevolgd. In het jaar 1627 gaf hij uit Tabulae Sinuum Tangentium Secantium in 8^o.Ga naar eind1)*, waarvan ik nog bezit een herdruk door j.j. stampioen van 1632 te RotterdamGa naar eind2), van 1683 te BrusselGa naar eind3), alsmede eene fransche vertaling van dezen herdrukGa naar eind4), eindelijk een druk te Rouen van 1672Ga naar eind5). In den eersten druk zegt hij.

‘Heb || daerom de selve voor eenighen || tijt tot mijn particulier gebruyck, || met groote moeyte uyt haer dif- || ferentien ghecorrigeert, alsoo dat || ick seecker houde gheen eenighe || faute daer in te zijn. Daerom, en || door begeerte van eenighe lief- || hebbers, heb niet connen naelaten, || de selve door den druck ghemeen || te maecken, in welcke mede zoo || nau en sorghvuldigh is ghelet, dat || daer door van der selver seecker- || heyt niet en is te twijfelen.’

Vandaar de, helaas niet onbetwiste, roem van nauwkeurigheid bij deze tafels.

Verder gaf hij uit ‘de 15 Boecken der Elementen van Euclidis,’ waarvan ik slechts een tweede uitgave bezit door J(acob) v(an) L(eest) te Amsterdam in 1662 bezorgdGa naar eind6). Eindelijk nog ‘Roozenkrans te Dordrecht, 1623 in 4^o.’

Hij was ook ingenieur in dienst van Hunne Hoogmogenden; en dat hij een goed teekenaar en graveur was, bewijst o.a. het door hem vervaardigde portret van renatus des-cartes, voorkomende in diens Principia Philosophiae te Amsterdam, 1660 in 4^o.Ga naar eind7). Dit portret toch bevat als randschrift, rondom het ovaal,

‘Renatvs Des Cartes, Dominvs de perron, natvs Hagae Tvronvm, Anno. M.D.XCVI. vltimo die martii.’ In de vier hoeken van het kader leest men ‘Franciscus à’ ‘Schooten Pr. Mat.’ ‘ad vivum delineavit’ ‘et fecit. Anno 1644.’ Daaronder een vers van ‘Constantini Hvgenii Fly.’

3. En thans hebben wij genoeg gegevens, om over te gaan tot de beschrijving van ons handschrift.

Het bevat 512 bladzijden, groot folio, waarvan de 301 eerste gepagineerd; bij de 153 eerste zijn de vier marges met roode lijnen afgesneden. De 52 eerste bladzijden zijn grootendeels met eene fraaie hand in het net geschreven; daartusschen komen enkele toevoegsels voor van dezelfde hand, met donkerder inkt, die men van af bladz. 54 ontmoet. Mede van diezelfde hand is, hetgeen men leest als titel op bladz. 285:

‘Begonnen den 25^en november || Anō 1622 door Frans van Schooten || proffessor der Fortificatien en || Dependerende scientien in̄ universiteyt || tot leyden.’

Een enkele maal, bijv. op bladz. 111, vindt men een andere hand daartusschen; dit zijn denkelijk toevoegsels uit lateren tijd.

Uit dit alles mag men met den gever wel besluiten, dat het een handschrift is van frans van schooten zelven.

Dit wordt nog bevestigd door de inrichting van het boek zelve. Het is niet doorloopend volgeschreven, maar van tijd tot tijd komen er hoofden voor boven aan de bladzijden; daarop volgt dan de tekst, maar er blijven soms nog verscheidene bladzijden wit Soms ook volgen op die hoofden nog eerst eenige bladzijden wit. Het schijnt daaruit te blijken, dat het boek eerst allengs is volgeschreven tot den tegenwoordigen toestand; ook is er niet een bepaalde volgorde te bespeuren tusschen de werkstukken, die onder een zelfde hoofd voorkomen. Men verkrijgt dus den indruk, dat het gediend heeft, als eene verzameling adversaria tot gebruik bij te geven lessen. Slaat men nu het

oog op den straks vermelden datum, 25 Nov. 1622, dan wijzen ook deze omstandigheden er op, dat het boek door f. van schooten, bij zijne lessen werd gebruikt. En daarmede komen goed overeen de keurige prentjes, waarmede de figuren soms zijn geïllustreerd, zie bijv. 136-169; zij wijzen op een geoefend teekenaar, zooals van schooten was. Voor ons hebben zij te meer waarde, omdat zij, naar de overlevering, het middel zijn geweest, om dit boek uit de vergetelheid te bewaren.

4. De inhoud van dit handschrift volge nu.

blz. 1. ‘Extractie Des quadraet wortel:’

Voorbeeld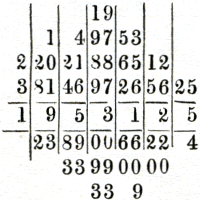

waarbij alle cijfers, behalve die van de ‘sijde’ doorgestreept zijn.

blz. 4. ‘Extractie Des Cubiq wortel.’

Voorbeeld

blz. 7. ‘Vande Tiende Getallen.’

Hij gebruikt deze notatie ‘346,875 3’, om aan te duiden dat er drie decimalen zijn.

blz. 16. ‘Fondamenten van Geometrie.’ Difinitien [1-32] (Tusschen de bladz 16 en 17 is er een blad uitgesneden.)

blz. 23. ‘Gemene Bekentenissen’ [Axiomata 1-16].

blz. 25. ‘Volgen de propositien’ [1^e Bouckx, Prop. 4-6, 13, 8, 15, 16, 18-21, 26, 27, 29, 32-35, 37, 41, 43, 47].

blz. 36. ‘2^en Bouckx.’ Prop. 1, 3-6, 9, 10, 7.

blz. 44. ‘3^en Bouckx.’ Prop. 3, 16, 20, 22, 31, 32, 35, 36.

blz. 47. ‘Des 6^en Bouckx.’ Prop. 1-4, 8, 14, 16, 19. De bladzijden 53, 54 zijn wit.

blz. 55. ‘Van t'Gebruyck des passers en Liniaels || Te Weeten, Hoemen door deselue alle geometrische Fygueren, || linien en Houcken, maecken en vinden sal’ Etc. || (Bladz. 62-64 wit). De laatste werkstukken luiden: Hoemen Beschrijven sal een slanghtrek, een geometrische Rose.

blz. 73. ‘Transformatie van Fygueren, Te weeten Hoemen || allerley Rechtlinische Fygueren veranderen sal in sodanige || Form alsmen Begeert.’

blz. 76. ‘Additie in Fygueren.’

blz. 78. ‘Subtractie in Fygueren.’

blz. 80. ‘Multiplicatie in Fygueren.’

blz. 83. ‘Divisie in Fygueren.’ Het laatste werkstuk leert een cirkel, wiens inhoud 12 is, te verdeelen in drie cirkels, wier inhouden zijn 3, 4, 5.

blz. 92. ‘Practijck des Landmeetens || Te weeten Hoemen alle Formen van Beganglicke || landen met de Roede Meeten, Ende door getallen || wtreeckenen sal.’

De werkstukken op bladz. 108, 109, 110, zijn alleen geconstrueerd, niet berekend, zooals de vorige dit waren. Het werkstuk op blz. 111 is van de vroeger vermelde latere hand. Bladz. 112 is wit.

blz. 113. ‘Vant gebruyck der Tafelen Sinus Tangens || en Secans, te weeten hoemen door deselue || alle Onbeganglicke distantien, Hooghten || en Diepten meeten sal.’

Schrijver gebruikt hier vijf decimalen, maar geen decimaal-teeken achter den index.

blz. 135. ‘Exempelen vant Meeten van || allerley Hoochten En Diepten.’

De werkstukken op bladz. 140, 141, 142, 148, 149, zijn

niet afgewerkt. Bladz. 171-173 zijn wit. Bij verschillende werkstukken is de constructie met andere inkt geschreven, dan de berekening, die dus later is bijgevoegd; doch altijd met dezelfde hand. Het is in deze afdeeling, dat de prentjes voorkomen.

blz. 173. ‘Meetinge van onbeganglicke landen, || Door 't gebruyck der tafelen, Sinus, Tangens, || Secans.’ Het werkstuk op bladz. 190 is niet afgemaakt.

blz. 191. ‘Meetinge van Circkels en Circkelstucken.’ Bovenaan staat een cirkel, met de twee grenzen van het getal π in 35 decimalen, op dezelfde wijze als de figuur op de titel-plaat van ludolf van ceulen's ‘vanden Cirkel. Delf 1596 in folio’ (zie Bouwstoffen, N^o. VIII).

blz. 198. ‘Deelingen van Allerley Formen van Landen.’ Bladz. 221, 222 wit.

blz. 223. ‘Metingen van Onbeganglicke landen sonder || t'gebruyck der Tafelen.’ Blz. 241, 242 wit.

blz. 243. ‘Meetingen van Allerley Formen van Corpora || Als van Aerde, Steen, Hout, Water, Iser, Etc.’ Hier verdeelt hij de maten als volgt:

Cubiq Roede, Este	Cubiq Duim
Schijfvoet ofte Schacht	Schijfgrein
Riemvoet	Riemgrein
Cubiq voet	Cubiq Grein
Schijfduim
Riemduim

waarbij ieder volgende maat het tiende deel der vorige is, ‘Na de ordre der Tiendegetallen’, namelijk Grein, Duim, Voet Bladz. 254, 256, 260, 262, 268, 270-278 zijn wit.

blz. 279. ‘Vant wijn Roeijen, of Meeten van allerley vaten grootte’. Bladz 282-284 wit.

blz. 285 bovenaan. ‘Begonnen den 25en nouember || Anō 1622 door Frans van Schooten || proffessor der Fortificatien En || Dependerende scientien in Vniversiteyt tot leyden.’ Verder is deze bladzijde wit, even als 286.

blz. 287. ‘Diffinitien 1-42.’ Bladz. 293 wit, 294-297 constructien.

blz. 298. ‘Vant maecken der Regulare Fygueren met den || passer En liniael, opt papier.’

blz. (304) zonder pagineering. ‘Manier Hoemen Opt veldt een Irregulaer || Bolwerck afsteecken sal.’ Bladz. (307)-(314), (322), (324), (326), (328), (336), (338), (340) wit. De overige bladzijden bevatten teekeningen van bolwerken, hetzij opgeteekend, hetzij in schets.

blz. (341). ‘Manier Hoemen een Irregulare plaets ofte oude stadt || welcke men Begeert te fortificeeren, Inden grondt sal leggen || Ofte een perfeckte Afteickeningh daervan maecken sal. || Mede te Bereeckenen hoe groot deselve sy.’

Bladz. (342)-(352), (354), (356)-(358), (360), (362), (364), (366), (368), (370), (372), (374), (376), (378), (380), (382), (384), (386), (388), (390), (392)-(396), (398), (400), (402)-(404), (406), (408), (410), (412), (414), (416)-(418), (420)-(422), (424), (426), (428), (430), (432)-(434) wit; de overige bevatten teekeningen zonder tekst, hetzij in schets, hetzij meer of minder opgeteekend en gewasschen.

blz. 435. ‘Batterien’ (met potlood) (436), (438), (440), (444), (452), (454), (458), (459), (462), (464), (466), (468), (470), (472), (474), (476), (478), (480)-(486), (493), (495), (497), (499), (500), (505), (506), (511), (512) wit. Bladz. (488)-(491), (501)-(504) en (507)-(510) bevatten tekst en berekeningen; de overige alleen teekeningen, of slechts in schets, of ook meer of minder opgeteekend en gewasschen. Bij bladz. (477) staat met potlood, maar altijd van dezelfde hand, ‘leger voor gulick.’

5. Uit de voorgaande beschrijving volgt duidelijk genoeg, dat het werk, dat voor mij ligt, niet op eens, maar slechts van lieverlede ontstaan is; dat het niet alleen bestemd was voor opteekening ten eigen nutte, maar wel degelijk, om den inhoud ook aan anderen mede te deelen. Brengt men dit in verband met den reeds besproken datum, dan mag men zich gerechtigd houden tot het besluit, dat het voor des schrijvers lessen of collegien heeft gediend. En dat wij dus den welwillenden gever dank mogen heeten, dat hij dit bewijs van ijverige wetenschappelijke werkzaamheid van den hoogleeraar frans van schooten aan de Leidsche Hoogeschool als feestgave heeft willen schenken.

6. Na zijn dood werd deze franciscus van schooten op-

gevolgd door zijn zoon en naamgenoot franciscus van schooten, die professor bleef tot aan zijnen dood 30 Mei 1660. Hij maakte zich vooral beroemd door de invoering niet alleen van de methode van descartes in ons land: maar inzonderheid door zijne uitgaven van de wiskunde van descartes. De eerste was zijne ‘Geometria à Renato des Cartes van 1649’ in 4^o.Ga naar eind8) met de Noten van florimond de beaune, en zijne eigene Commentarii, benevens een Additamentum. De tweede druk van 1659, in twee deelen, 4^o.Ga naar eind9), bevatte echter veel meer; tusschen de Commentarius en het Additamentum voegde van schooten in een Appendix de cubicarum aequationum resolutione; na het Additamentum komen nu twee brieven van den Burgemeester johannes hudde en een van hendrik van heuraet. En het tweede deel bevat ‘de Principia Matheseos Universalis seu Introductio ad geometriae methodum Renati des Cartes’, de tweede druk, [de eerste druk was in het jaar 1651 afzonderlijk verschenenGa naar eind10)], en daarvan twee Tractatus posthumi van florimond de beaune (die, zoo als ook uit de opdracht blijkt, 27 Sept. 1601 geboren, den 19^den Augustus 1652 overleden was). Beide stukken zijn van de hand van erasmus bartholinus caspari fil.; de voorrede van het eerste is gedateerd ‘Scribebam Leidae, || Anno CIƆIƆCL. || Calend. Jun.’ hij was toen student te Leiden; die van het tweede ‘Hafniae, Anno || CIƆIƆCLVII’, toen hij Medicinae & Mathematum Professor Regius publicus in Academia Hafniensi was geworden.

Uit dezen tweeden druk zoude, wat den titel betreft, waarop de naam van frans van schooten niet voorkomt; - en evenzeer wat de ‘Lectori S.’ aangaat - schijnen te blijken, dat bartholinus de schrijver was. In die voorrede toch deelt bartholinus mede, dat hij dit werk naar de lessen van fr. van schooten, met zijn goedkeuring, en na zijn onderzoek schreef; ‘postquam ad hasce oras, Academiam Illustrem, || quae Leidae est, accessi, Vir Celeberrimus atque Doctissimus || Franciscus à Schooten, Matheseos ibidem Professor publicus, || me Artem Analyticam, hancque Methodum, tam eximiâ fide || docuit... non modò veniam (de elementis hisce evulgandis) hujus zeli impetravi, sed & eam || huminitatem, ut omnia perlegere & examinare haud grava- || tus fuerit, lucemque ingenii & consilii sui porrigere’. Maar op de beide

Catalogi, voor de beide deelen gedrukt, staat er: ‘francisci a schooten, Principia Matheseos Universalis’ en op de laatste bladz. 48 staat aan het hoofd: franciscus à, schooten || ad lectorem, en daarin geeft deze de ‘menda’ van dit werk zelf, en tevens die van zijne ‘Exercitationes’ van het jaar 1657; alsof het werk hemzelven toekwam. Wendt men zich echter tot de eerste uitgaaf [zie Noot (10)], dan vindt men daar ‘Francisci à Schooten Principia - edita ab Er. Bartholino, Casp. Fil.’; overigens bijna hetzelfde voorwerk en dezelfde tekst, als bij de ‘Editio secunda’. Men mag het er dus voor honden, dat de ‘Principia’ het werk zijn van frans van schooten, maar dat zij door erasmus bartholinus zijn ‘edita of conscripta’, bijv. naar de lessen of het dicteeren van van schooten zijn opgeteekend.

Daarop volgen in de verzameling de Elementa curvarum linearum van johannes de witt, 2 Libri; en eindelijk een Tractatus posthumus van frans van schooten De Concinnandis demonstrationibus geometricis ex calculo Algebraico; hetwelk door zijn broeder petrus van schooten in het licht werd gegeven.

Behalve dezen arbeid gaf hij uit in 1657 zijne ‘Exercitationum Mathematicarum, Libri V’Ga naar eind11): welk boek ook in het nederlandsch in het jaar 1659 verscheen ‘Mathematische Oefeningen, in V Boucken’Ga naar eind12), waarvan er eene nieuwe titeluitgaaf in 1660 uitkwamGa naar eind13). Van deze vijf boeken zijn de voorredens in het latijn (en ook in het hollandsch) gedateerd, van het eerste, 12 Sept. 1656, van het tweede, 15 December 1656, van het derde, 1 Januari 1657; die van het vijfde draagt geen datum; die van het vierde is gedateerd 1 Nov. 1646. Van dit laatste boek bestaat er dan ook een vroeger afzonderlijke uitgaaf ‘De organica Conicarum Sectionum in plano descriptione Tractatus.’ Lugd. Bat. 1646 in 4^o.Ga naar eind14).

7. De zoo straks genoemde broeder petrus van schooten was geboren 22 Febr. 1634, was reeds een jaar lang lector in de wiskunde, toen hij zijne broeder frans opvolgde in 1661: in 1669 verkreeg hij verlof, om ook in het latijn te onderwijzen; hij bleef professor tot aan zijn dood, 30 September 1679. Het is mij niet bekend, dat hij iets heeft uitgegeven, dan het bovengenoemd werk van zijn broeder frans.

Deze drie van schootens, de vader zoowel als de beide zoons, waren geplaatst aan de Ingenieurschool, opgericht in het jaar 1600 (zie Bouwstoffen N^o. VIII), en waaraan ludolf van ceulen de eerste hoogleeraar was; te zamen onderwezen zij dus aan die school zeventig jaren.

Maart 1875.

Naschrift.

8. Hoezeer door mij geene moeite was gespaard, om eene gelegenheid te zoeken tot het identifieeren van het handschrift van franciscus van schooten den vader, in het behandelde MSS, mogt mij dit niet gelukken; tot ik onlangs van mijnen ambtgenoot Prof enschedé te Groningen vernam, dat aan de bibliotheek zijner Akademie, eene reeks MSS. van de familie van schooten voorhanden waren, waarvan hier de opgaaf moge volgen.

Een MSS. van f.a. schooten, gedat. 5 Dec. 1632, bevattende:
Demonstratio Constructionis quatuor Ovalium.
Oplossing der Cubische Aequatien door de Parabel en Hyperbola.
Problemata uit de Lessen van Prof. Golius en Otterlo.
Aanmerkingen op de beschrijving der Parabola en Hyperbola, volgens Descartes.
Aanmerkingen over verscheidene Problemata van Apollonius, Archimedes, &c.
Clavis Mathematica.
Specimen Arithmeticum et Algebraicum.
De grootste gemeene maat.
Van de gebrokene getallen.
De Genesi et Analysi Potestatum, &c.
Over de Wortels eener Cubische Aequatie.
Verschillende Regelen, om te bepalen, welke getallen quadraat of cubicq zijn.
Compendium Musicae.
Doctrina Prostaphaeretica.
Trigonometria Logarithmica.

II.	MSS. van fr. à schooten bevat: Matheseos universalis. Lib. I. Ratio et proportio. Lib. II. De Symmetria et Asymmetria. Lib. III. De Analysi Mathematica. Lib. IV. Pars altera de Arithmetica.
III.	Verschillende stukken van Diophantes Alexandrinus, uitgewerkt door fr. à schooten.
IV.	Verschillende uitgewerkte stukken van fr. à schooten over de Algebra.
V.	Lessen van f. van schooten over Arithmetica.
VI.	f. van schooten, Verhandeling over de Arithmetica.
VII.	Lessen, gehouden door f. van schooten, 9 Dec. 1655, over de Natuur, constructie en 't gebruik der Logarithmische Tafelen van Briggs en Vlacq.
VIII.	Eene volledige verhandeling over de Sphaerische Drieboeksmeting van f. van schooten, door zijn broeder. Hierbij vele Astronomische Problemata.
IX.	Kompleet Tractaat over de Arithmetica en een groot gedeelte der Algebra, behelzende de laatste Voorlezingen van Prof. fr. van schooten, die 30 Mei 1660 overleden is, en door zijn broeder p. van schooten is opgevolgd.
X.	MSS. van f. à schooten, waarbij Aanteekeningen van p. van schooten, gedat. April 1656, bevat: Arithmetique ou l'art à chiffrer. Tabulae Logarithmicae &c. in het Nederduitsch. Deeling der figuren door evenwijdige linien zamengesteld. Fundamenta quibus usus fuit fr. à schooten. Eene Verhandeling over de Fortificatie.
XI.	p. à schooten et f. à schooten. Ad locos planos et solidos. Appendix ad Isagogen topicam, continens Solutionem problematum solidorum per locos. De Tangentibus Linearum Curvarum. De Centro gravitatis parabolici Conoidis. Extrait d'une lettre du 15 Juin 1636 au P. Mersenne &c. Propositio per quatuor puncta Parabolam describere.

Problema 10 Nov. 1642: invenire cylindrum maximi ambitus in sphaera.

XII.

petrus van schooten (Prof. te Leiden) a^o 1655, verschillende verhandelingen.

1^o.	Figurae ceteraque quae desiderantur in L. II. Geographiae B. Vareni.
2^o.	Guido Ubaldi Planisphaeriorum universalium Theorica. Dit handschrift heeft aan het einde: ‘Scripsit petrus à schooten, Hagae Comitis, Anno 1665,’ waaruit zoude volgen, dat hij toen te 's Gravenhage woonde.

XIII.

Oplossing van verschillende Geometrische en Algebraische Vraagstukken, door p. van schooten.

XIV.

Specimen Problematum algebraicorum sectionumque, quae in cono effici possunt, auctore p. van schooten.

XV.

De Cos-rekening, benevens eene Verhandeling over de Irrationale grootheden. Door p. van schooten.

XVI.

Euclidis Elementa van petrus van schooten.

9. Het handschrift N^o. I heb ik door de welwillendheid van bovengenoemden Hoogleeraar kunnen gebruiken, tot vermeld doel.

In den aanvang bleef dit Handschrift N^o. I weigerachtig, omdat daarin meer dan ééne hand scheen voor te komen; maar een nauwgezetter onderzoek bracht mij eindelijk op het spoor. Aan het einde toch van het Compendium Musicae staat:

‘Bredae Brabantinorum pridie Calendas || Januarias anni MDCXVIII completo.’

Daaronder met andere hand

‘cum ageret (ni fallor) annum 21_num.

Scripsit haec pro domino Zecmanno Scholo Dordra- || cenae moderatore, nunc temporis cum primum in has regiones venisset, et ex Schola Flechiana in Gallia ubi studuisset, sortitus esset, ut ibi multas || se incumberet. Mansit autem Bre- || dae per 15 menses unde in Germaniam discessit || dum intestina bella ibi orirentur: ut mihi ipse || narravit. ||

Habentur et Libri in Bibliotheca Flechiana sua || manu notati et Collegio donati, nam ibidem moris || est quemquam non egredi scholam qui non donarit || ipsae Bibliothecae librum aliquem.’

Deze bijzonderheden kunnen alleen slaan op renatus descartes, en zij strooken dan ook geheel met hetgeen van zijn

reizend en trekkend leven bekend is; waartoe dan het bovenstaande eene misschien nog onbekende bijzonderheid oplevert. De sprekende (of schrijvende) persoon [ut mihi ipse narravit] is dus zonder twijfel onze franciscus van schooten: derhalve ziet men hier zijne hand.

En nu is deze kleine, geleerde hand volstrekt ongelijkvormig aan het groote klerkachtige schrift, dat eerst in het Leidsche MSS. voor de hand van van schooten gehouden werd.

Het blijkt dus dat het in dit opstel beschreven handschrift van van schooten - hoewel zeer waarschrijnlijk door hemzelven opgesteld, en van tijd tot tijd vermeerderd, - niet door hemzelven is geschreven; maar dat hij daartoe twee verschillende schrijvers achtereen gebruikte; dit laatste blijkt daaruit, dat in het eerste gedeelte (blz. 1-52), met een staande letter geschreven, later aanmerkingen zijn ingelascht, geschreven met meer loopende hand.

10. Maar het onderzoek van het Groningsche Handschrift N^o. I leerde mij nog meer. Vooreerst vond ik daarin onder het hoofd, Caput. XII, ‘de genesi et Analisy potestatum &c.’ een manier om den vierkantswortel te trekken uit een irrationeel quadrinomium. De bewerking luidt dus

Extraheert den quadraetwortel uit 108 - √1200 + √2000 - √60

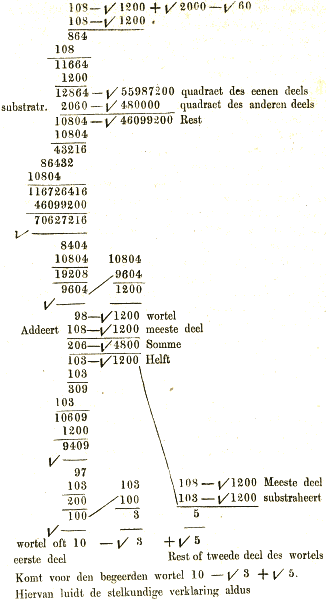Komt voor den begeerden wortel 10 - √3 + √5.

Hiervan luidt de stelkundige verklaring aldus

Zoek a + √b + √c uit (a + √b + √c)² = (a² + b + c) +

+ 2a√b + 2a√c + 2√bc = R².

Neem daartoe

P⁴ = (a² + b + c + 2a√b)² - (2a√c + 2√bc)² =

= [(a² + b + c)² + 4a²b - (4a²c + 4bc)] +

+ [(a² + b + c) 4a√b - 8ac√b] =

= [(a² + b - c)² + 4a²b] + [(a² + b - c) 4a√b].

Om hieruit den wortel te trekken zij verder

Q³ = [(a² + b - c)² + 4a²b]² - [(a² + b - c) 4a√b]² =

= [(a² + b - c)² + 4a²b + (a² + b - c) 4a√b] ×

× [(a² + b - c)² + 4a²b - (a² + b - c) 4a√b] =

= [a² + b - c + 2a√b]² [a² + b - c - 2a√b]² =

= [(a² + b - c)² - 4a²b]²

dus Q = (a² + b - c)² - 4a²b.

Neem hiervan som en verschil met het rationele deel van P⁴, dan komt er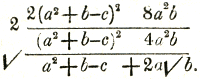

Tel hierbij de beide eerste termen van R²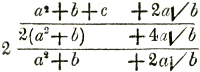

op de gewone wijze vindt men hier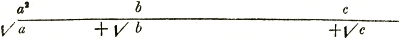

is dus de wortel, waarvan men was uitgegaan.

11. Vooral belangrijk kwam mij de oplossing voor van een vraagstuk door twee loodrechte projectie-vlakken, als in de beschrijvende meetkunde, zooals men hier in 1632 zeker niet zoude verwachten.

Dit stuk komt voor onder het hoofd: ‘Over de wortels eener Cubische Aequatie’, en luidt aldus.

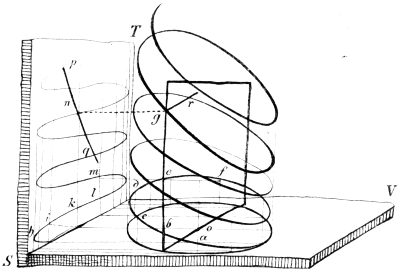
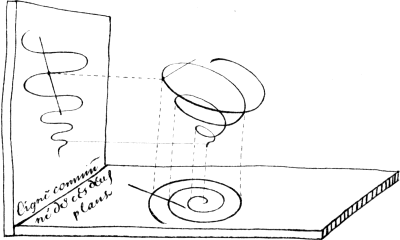
Ex Descartio, quot radices in cubicis aequationibus || occurrunt, tot plurimum problema admittit casus. || Sub primo genere linearum curuarum continentur circulus || Parabola, Hyperbola, Ellipsis, sub secundo genere || comprehendentur, Conchoidis vulgaris, parabola || descripta ex motu alterius alicujus, et rectae lineae || et catena nempe quae eodem modo describuntur per || intersectionem rectae lineae et aliae cuius libet coni sec- || tionis, ut circuli, Hyperbolae et Ellipseos. Et qaem- || admodum circulus linearum curuarnm primi generis prima est atque || simplicissima, sic item conchoides quae ortum suum || habent ex circulo curuarum secundi generis, prima || ést atque simplicissima. Rursus, quoniam circulus || non soluit omnia problemata solida et quadrato-qua || dratica, sic item conchoides non omnia soluit pro- || blemata surdesolida, et quadrato cubica et rursus ut || parabola soluit omnia problemata cubica et quadratocu- || bica (quae ad cubica reduci possunt) sic item parabola || secundi generis soluit omnia problemata surdesolida || et quadrato-cubica (quae ad surdesolida reduci possunt)’. ||

Eene nieuwe bladzijde begint met figuur 1. Daaronder

‘In plano S V, proponatur cilindrus quidam, cuius basis circulus circa O constructus, et in cuius super- || fitie descripta sit helix cilindrica a, b, c, d, e, f, g. Datum || jam sit punctum g in Helice et oporteat ducere rec- || tam lineam, per punctum g quae secet Helicem ad ad rec- || tos angulos (ut g r). Erigatur planum aliquod S T ad || rectos angulos, ipsi plano S V, in quo ab infinitis || punctis helicis ut a, b, c, d, e &c. demittantur perpendicu- || lares ah, bi, ch, dl, em et gn. Haec igitur perpen- || diculares cum in plano S T describant etiam aliam quam- || dam Helicem, ut h, i, k, l, m, n &c. Ducatur in plano || S T per n punctum recta p n q secans hanc helicam ad || rectos angalos, et intelligatur planum infinitum, transiens per || rectas p n q et n g, quod secet planum infinitum duc || tum per g b, (quae quidem perpendicularis est ad basin circu- || li) et b o (quae ab hoc puncto b ducitur per centrum cir- || culi O) secundum rectam lineam g r. Dico rectam || g r secare Helicem a b c d &c ad rectos angulos. At- || que in tali sensu intelligenda sunt posteriora verba Libri secundi’.

Eene nieuwe bladzijde begint met figuur 2. Daaronder

‘Aliquando in utraque parte aequationis non sunt || aequales dimensiones et fit quando unitas deter- || minata subintelligitur, fitque breuitatis causa, o- || riginem sumens ex progressioni, quod saepe in cubicis || aequationibus accidit ut in parabola, ubi plurimum || distantia verticis a foco pro unitate sumitur.’

12. In hetzelfde handschrift N^o. I, is vooraan nog eene bibliographische zeldzaamheid ingeplakt, een dier wiskunstige vraagstukken, die eenige wiskundige aan de liefhebbers ter oplossing voorstelde. Dit is een ‘Problema astromonicum et geometricum door Johan Stampioen’Ga naar eind15) gedrukt in plano, met eene plaat in kopergravure. Aan den kant is door van schooten de oplossing geschreven, althans tot zekere hoogte aangegeven.

Februari 1877.

eind1)*: Tabvlae || sinvvm || tanentivm || secantivm, || ad Radium 10 000000; || Met 't gebruyck der selve in || Rechtlinische Triangulen, || Door Fr. van Schooten || Professor Matheseos || tot Leyden. || Vignette: eene meetkundige figuur voor de constructie der goniometrische lijnen. || Tot Amsterdam, || Bij Willem J. Blauw || in de Sonnewyser. || 1627 || in 8^o. klein formaat.

A-O, 216 bladz. niet gepagineerd,

bevatten de titel, die geheel gegraveerd en met zinnebeeldige figuren versierd is, ‘Korte || instrvctie || deser tafelen’ (12 bladz.), dan: Canon || sinvvm, || tangentive || et || secantivm. || Ad Radium. || 10000000.

in 7 decimalen (181 bladz.).

In verso. ‘Van 't ghebruyck der Ta- || felen in 't ineten der platte || Triangulen’. 31 bladz.

eind2): * Tabvlae || Sinvvm || Tangentivm et Secantivm, || ad Radium 10000000; || Met 't gebruych der selver in Rechtlinische || triangulen, Door Fr. van Schootē || gecorrigeert, || Ende in 't cort by gevoecht, d'ontbindinghe || der Sphaerischer-Triangulen, met noch || eenige Constige Geometrische, ende || Polygonaelsche questien. || Door j.j. stampioen de Jonge; || vignette als boven. || Tot Rotterdam || bij de Weduwe van Matthys bastiaenss. op 't Steyger, in 12^o.
De titel is gegraveerd, doch verschilt van dien voor het boekje in noot (1).
A-K, 236 bladz., niet gepagineerd,
is op dezelfde wijze ingericht als het vorige boekje, behalve dat het voorwerk 10 bladz. en het achterwerk 45 bladz. telt.
Daarachter volgt
Kort || By-voeghsel || der || Sphaerischer || Triangulen. || Door || J.J. Stampioenivm; || Iuniorem; Mathematicum. || Vignette: eene meetkundige figuur, die voorkomt op de 28^ste bladz. || Tot Rotterdam, || By de Weduwe van Matthys || Bastiaensz, Boeck-verkooper, Op 't || Steyger, in Josephus, 1632, in 12^o.
A-C, 10 bladz. zonder paginatuur.
In verso van den titel, een vers van J.J. Paep ‘Aen den Gheleerden, Konst- || rycken Ionghelingh; || Johan Stampioen.’
Dit boekjebegint aldus:
‘Dv verder verhaelt zynde, de || uyt-rekeningh der recht-lini- || scher triangulen; ende dat ten || deele door 't gebruyck der vo- || renen beschreven tafelen.'’
waaruit blijkt, dat het werkelijk behoort bij de eerst beschreven tafels, en dat deze dus evenzeer in 1632 zijn gedrukt.

eind3): *Tabulae || sinuum || tangentivm || et || secantivm || Ad Radium 10,000,000. || Met 't gebruyck der selve in Recht- || linische Triangulen. || Door || Franciscus van Schoten || Professor Matheseos tot Leyden. || Van nieuws volgens de correcste || Exemplaria over-sien ende || verbetert. || Tot Brussel, || By Lambert Marchant, || in den goeden Herder. || M. DC. LXXXIII. in 12^o.
A-I, 228 bladz., zonder paginatuur: met dezelfde inrichting als in Noot (1), met 12, 181, 35 bladz.
Tegenover den uitgeschreven gedrukten titel, vindt men een gegraveerden, met de woorden:
Tabvlae || sinvvm || tangentivm || secantivm || ad Radium 100000000 || cvm || Trigonometria || Triangulorum planorum || Studio || Francisci Schoten || Math. Prof. Lugd. Bat. || Vignette: dezelfde meetkundige figuur || Brvxellis || Apud Lambrtum || Marchant || sub signo || Boni pastoris. || 1683.

eind4): *Tables || de sinus || Tangentes || et Secantes || Ad Radium 10000000. || Avec une methode de resoudre tres-fa- || cilement par leur moyen tous les || Triangles Rectilignes & || Spheriques. || Par || Francois Schoten || Professeur de Mathematique en || t'Vniversité de Leyden. || Reveuës & exactement Corrigées || en cette Edition, || a Brusselles, || Chez Lambert Marhant, || Libraire au Maché aux Herbes. || M. DC. LXXXIII. in 12^o.
A-I, 224 bladz.
De tekst is Fransch, maar de verdeeling is weder dezelfde met 12, 181, 31 bladz.
Er is een gegraveerde titel volkomen gelijk aan die in ht werk van Noot (3).

eind5): * Table|| des Sinus || des Tangentes || et Secantes || povr le Rayon || 10000000. || Par. Fr. de Schoten. || Vignette als bij Noot (1) || A. Roüen || chez || David Berthelin || et || Jacques Lucas || Rüe || aux Juifs. 1672. || Avec Privilege du Roy. in 12^o.
A-T, 250 bladz. zonder paginatuur.
De titel is weder eene gravure, doch veel grover dan de voorgaande: de tekst is fransch; de inrichting is dezelfde in 12, 181, 47 bladz.

eind6): * De 15 Boecken der || Elementen || Van Euclidis, || Met korte verklaringen eeni- || ger Propositien. || Uyt het Latyn Overgeset, || Door Frans van Schoten, || in sijn leven Professer Matheseos der || Hooge Schoole tot Leyden. || En nu vergroot door J.V.L. met || het sesthiende Boeck van Christophoro || Clavio, trouwelyck uyt Latyn Vertaelt, || ende met een Aenhangsel der Fonda- || menten vande Mathematische Namen || ende Coracteren (sic) verryckt, in dese const || gebruyckelyck tot gerief der Aencomelingen. || t'Amsterdam, || By Jacob van Leest, op 't Water in de || Blaeuwe Kroon. 1662. in 12^o.
VIII bladz. zonder pagineering, bevatten titel, en opdracht aan ‘Den E: ende Godtvruchtighen || welgeleerden Jonghman Justo || Bonardo student Matheseo, || weuscht (sic) J.V.L. Geluck || en Salicheyt lang le- || ven, en Salich || sterven.’

A-L. Bladz. 1-243. bevatten Bouck I-XVI. (bladz. 1-199).

bladz. 200-208. ‘Fondamenten vande Mathematische const.’

bladz. 209-243. ‘.Aenhang op de 15 Boucken || Euclidis.

eind7): * Renati || des- cartes || principia || philosophae. || Nunc demum hac Editione diligenter reco- || gnita, & mendis expurgata, || Vignette; Minerva met een boom en het devies: ne extra oleas. || Amstelodami, || Apud Ludovicum & Danielem Elsevírios, || Anno cIƆ, IƆcLVI. || Cum Privilegiis. || in 4^o.
44 bladz. bevatten vóór den titel een fransche titel:
‘ Renati || des-cartes || opera || philosophica. || editio tertia. || Nunc demum hac Editione diligente recognita, || & mendis expurgata.’
de ‘Contenta’ de ‘Typographvs || ad lectorem.’ || en het portret.
Na de Titel volgt het ‘Privilege’ van Frankryk, de opdracht aan ‘Elisabethae. || Frederici Bohemiae Regis, || ... || Filiae natu maximae.’ (6 blz.), de ‘Epistola Avthoris’. (15 bladz.) en de ‘Index’ (13 bladz.).

A-Ee, bladz. 1-222.

Dan een nieuwe titel en index (16 bladz.).

a-hh. bladz. 1-248.

Dan een nieuwe titel en voorwerk (24 bladz.)

A-M. bladz. 1-92.

Index. 4 bladz.

eind8): * Geometria, || à || Renato des Cartes || Anno 1637 Gallicè edita; nunc autem || Cum Notis || Florimondi de Beavne, || In Curiâ Blaesen si Consilarii Regii, || In linguam Latinam versa, & commenta- || riis illustrata, || Operâ atque studio || Francisci à Schooten, || Leydensis, in Academiâ Lugduno-Batavâ, Matheseos || Professoris, Belgicè docentis. || Vignette: een spittende landman, met het motto: ‘Fac et spera’. || Lvgdvni Batavorvm, || Ex Officinâ Joannis Maire. || CIƆIƆCXLIX. in. 4^o.
XII blz. (niet gepagineerd) bevat titel, opdracht aan ‘Elisabethae, || Friderici Bohemiae regis, Comitis Palatini, & Electoris Sacri Ro- || mani Imperii, filiae natu || maximae’ (4 bladz.) gedateerd ‘Dabam Leydae, XII Kal. Julii, || Anni CIƆIƆCXLIX’; dan ‘Lectori Benevolo’ (3 blz.) Index (3 blz.).

A-P, blz. 1-118. Libri I-III.

P-X, blz. 119-161. Florimondi de Beavne || in geometram || Renati des Cartes || Notae breves.

X-Oo, blz. 162-294. Francisci à Schooten || in geometram || Renati des Cartes || Commentarii.

Oo-Vu, blz. 295-336. Additamentum. De laatste bladzijde bevat de ‘Errata’.

Daarop twee bladzijden (niet gepagineerd) met verbeteringen.

eind9): * Geometria, || à || Renato des Cartes || Anno 1637 Gallicè edita; postea autem || Unà cum Notis || Florimondi de Beavne, || In Curia Blesensi Consilarii Regii, Gallicè conscriptis in || Latinam linguam versa, & Commentariis illustrata, || Operâ atque studio || Francisci à Schooten, || in. Acad. Lugd. Batava Matheseos Professoris. || Nunc demum ab eodem diligenter recognita, locupletioribus Commentariis || instructa, multisque egregiis accessionibus, tam ad uberiorem expli- || cationem, quàm ad ampliandam hujus Geometriae ex- || cellentiam facientibus, exornata, || Quorum omnium Catalogum paginav ersa exhibet || Vignette: Minerva onder olijfboom met de spreuk ‘ne extra oleas. || Amstelaedami Apud Ludovicum & Danielem Elzevirios, || CIƆIƆCLIX. in 4^o.
XII blz. voorwerk, hetzelfde als in het vorige werk. Tegenover den titel een fraai portret van Descartes, gegraveerd door van Schooten, hetzelfde als voorkomt in het boek van Noot (7). In verso van het portret, een fransche titel
Renati || des-Cartes || Geometria. || Editio Secunda. || Multis accessionibus exornata, & plus alterâ || sui parte adaucta. In verso van den titel de Catalogvs || eorum, || Quae hoc Opere continentur. ||

[blz 1-106]. Renati des Cartes Geometria, tribus libris com- || prehensa.

[blz. 107-142]. Florimondi de Beavne in illam Notae Breves.

[blz. 143-344]. Francisci à Schooten in eandem Commentarii, || recogniti & aucti.

[blz. 345-368]. ejusdem Appendix, de Cubicarum Aequationum || Resolutione.

[blz. 369-400]. ejusdem Additamentum. in quo continetur solu- || tio artificiosissima difficilis cujusdam Problematis; || & Generalis Regula de extrahendis quibuscunque || Radicibus Binomiis.

[blz. 401-405: een begeleidende brief voor de twee volgende van Johannes Hvdde, gedateerd ‘Amstelaedami ipsis || Calendis Aprilis 1658’].

[blz. 406 - 506, 507-516]. Johannis Huddenii Epistolae duae, quarum altera || de Aequationum Reductione, altera de Maximis & Minimis || agit.

[blz. 517-520]. Henrici van Heuraet Epistola, de Curvarum || Linearum in Rectas transmutatione.

Hetgeen tusschen de haakjes [ ] voorkomt, staat niet in den ‘Catalogus’.
Dit eerste deel bevat vel A-Ttt.
Het tweede deel bevat vier stukken, die ook in den voorgaanden Catalogus, en op nieuw in een catalogus aan het hoofd van dit tweede deel worden aangegeven; maar ieder heeft vervolgens een afzonderlijken titel. Vooreerst de titel:
Principia || matheseos || vniversalis, || sev || introductio || ad || geometriae methodvm || Renati des Cartes || Conscripta ab || Er. Bartholinus, Casp. Fil. || Editio Secunda, priore correctior. || vignette, als bij het eerste deel. || Amstelaedami, || Apud Ludovicum & Danielem Elzevirios, || CIƆIƆCLXI.
XIV bladz. (zonder pagineering) bevatten de opdracht (10 blz.) gedateerd ‘Leidae || Anno CIƆIƆCL. || Calend. Jun.’ dan Lectori s. (4 blz.)

A-F. blz. 1-48. De laatste bladzijde heeft tot titel Franciscus à Schooten || ad lectorem’, waarin hij de ‘menda’ opgeeft voor dit werk en zijne ‘Exercitationes van 1657’.

Daarop de titel.

De || aequationum || Natura, Constitutione, & Limitibus || Opuscula Duo. Incoepta à || Florimondo de Beavne, || in Curia Blesensi Consiliario Regio: || Absoluta verò & post mortem ejus edita || ab || Erasmio Bartholino, || Medicinae & Mathematum in Regia Academia || Hafniensi Professore publico. || Vignette, als boven || Amstelaedami, || Apud Ludovicum & Danielem Elzevirios, || CIƆIƆCLIX.

G, H blz. 49-63 (niet gepagineerd) bevatten opdracht aan ‘Joachim Gersdorph’ (5 blz.) gedateerd ‘Hafniae Anno || CIƆIƆCLVII’. Epistola praeliminaris || ad Clarissimum Virum || Claudium Hardy (16 blz.) Florimondi de Beaune || Praefatio (1 blz.).

Dan H-T blz. 63-152. Het boek zelf, afgebroken door een brief van Er. Bartholinus aan Franciscus à, Schooten, blz. 117-120 (niet gepagineerd).

Dan de titel.

Johannis de Witt || elementa || curvarum || linearum: || Edita || Operâ Francisci à Schooten, || in Academia Lugduno-Batava Matheseos || Professoris. || Vignette, als boven || Amstelaedami. || Apud Ludovicum & Danielem Elzevirios, || CIƆIƆCLIX.

V. blz. 153-158. Brief van Johannes de Witt aan Fr. à Schooten (3 blz.)

V-Tt blz. 159-340. Het werk in twee boeken.

Daarop de titel.

Francisci à Schooten, || Leidensis, || dum viveret in Academia Lugduno-Batava || Matheseos Professoris, || Tractatus || de || concinnandis || demonstrationibus || geometricis || ex Calculo Algebraïco. || In lucem editus || à || Petro à Schooten || Francisci Fratre || Vignette, als boven || Amstelaedami, || Apud Ludovicum & Danielem Elzevirios, || CIƆIƆCLXI.

VII blz. 341-344. Opdracht door P. van Schooten aan de Curatoren der Leidsche Hoogeschool.

Xx-Ggg blz. 345-420. Het werk zelf.

blz. 421 (niet gepagineerd). Errata.

blz. 422 (niet gepagineerd). Lectori Benevolo || J. Hudde S.P.

blz. 423-424. Twee verzen één latijn, één grieksch.

eind10): Francisci à Schooten || principia || mathaeseos || vniversalis || sev || introductio || ad || geometriae methodum || Renati des Cartes, || edita ab || Er. Bartholino, Casp. Fil. || Vignette: de tuinman met olijfboom en omschrift. ‘Non solus’ || Lvgd. Batav. || Ex Officinâ Elseviriorum. || CIƆIƆCLI in 4^o.
XVI bladz. (zonder pagineering) bevat de opdracht. D. Christiano Thomae, || Toparchae in Stavgard (10 blz.) gedateerd, ‘Leidae || Anno CIƆIƆCL || Calend. Jun.’ De Praefatio in haec principia, et || de modo legendi || geometriam (4 bldz.) gedateerd ‘Leidae, Anno || Christi CIƆIƆCL Postridie Non. Maii’.
Met verkorting der beide laatste bladzijden, komt dit stuk in de Editio secunda voor als het ‘Lectori S.’. Beide stukken zijn van Erasmius Bartholinus.
A-F blz. 1-46.

eind11): * Francini à Schooten || exercitationvm || mathematicarum || libri quinque. || I. Propositionum Arithmeticarum et Geome- || tricarum Centuria || II. Constructio Problematum Simplicium Geo- || metricorum, || III. Apolionii Pergaei Loca Plana restituta. || IV. Organica Conicarum Sectionum in plano || descriptio. || V. Sectiones Miscellaneae triginta. || Quibus accedit Christiani Huge ii Tractatus, || de Ratiociniis in Aleae Ludo. in 4^o.
A-Xxx, blz. 1-534.
Ieder dezer vijf stukken heeft een afzonderlijken titel met een afzonderlijk jaartal.

I.

1657. VIII blz. (zonder pagineering). Opdracht aan het Hof van Holland, Zeeland en West-Friesland; gedateerd ‘Idibus Septembris. Anno || CIƆIƆCLVI.’
blz. 1-112, het werk zelf.

II.

1656. blz. 114-118. Opdracht aan de Curatoren van de Academie te Leiden; blz. 119 -122, ‘Praefatio ad Lectorem;’ blz. 123-190 het werk zelf.

III.

1656. blz. 193-196. Brief aan Petrus Chanuto, gedateerd ‘Kalendis Januariis Anni CIƆIƆCLVII’; blz. 197-202 ‘Praefatio ad Lectorem.’ blz. 203-292 het werk zelf.

IV.

1657. blz. 294-296 (niet gepagineerd). Opdracht aan de Curatoren voornoemd, gedateerd ‘Kal. Novemb. MDCXLVI’; blz. 297-302. Praefatio ad Lectorem; blz. 303-368 het werk zelf.

V.

1657. blz. 371-272. Brief aan Johannes Walbeeck; blz. 373-516 het werk zelf.

blz. 517-518. ‘Ad Lectorem.’

blz. 519-520. Brief van Christiaen Hugenius aan Fr. Schotenius gedateerd: ‘Hagae Comitum. 27 April 1657.’

blz. 521-534. De ratiociniis in ludo aleae.

1 blz. wit. de ‘Errata.’

Op ieder titel komt als vignette voor een olijfboom met tuinman en bijschrift. ‘Non solus.’ Daaronder
‘Lvgd. Batav. || Ex Officina Johannis Elsevirii. || Academiae Typographi.

eind12): * Eerste Bouck || der || mathematische || oeffeningen, || Begrijpende || Vijftigh Arithmetische, en Vijftigh || Geometrische Voorstellen. || Door || Franciscvs van Schooten, || Professor Matheseos in de Vniversiteyt tot Leyden. || Vignette: drukkersornament || t'Amsterdam, || Bij Gerrit van Goedesbergh, || Boeck-verkooper op 't Water/ in de Delfsche Bijbel/ tegen || over de Nieuwe-Brugh. || Anno 1659. 4^o.
A, VIII. blz. (niet gepagineerd), bevat opdracht (6 blz.). Daarop
‘Francisci van Schooten || mathematische || oefffningen, || Begrepen in vijf Boecken. || I. Verhandeling van vijftig Arithmetische en vijftig Geometrische || Voorstellen. || II. Ontbinding der simpele Meet-konstige Werck-stucken. || III. Apollonii Pergaei herstelde Vlacke Plaetsen. || IV. Tuych-werckelycke beschrijving der Kegel-sneden op een || vlack. || V. Dertich Af-deelingen van gemengde stoffe. || Waer by gevougt is een Tractaet/ handelende van Reeckening || in Speelen van Geluck. || Door d' Heer || Christianus Hugenius. || Desen Druck vermeerdert met een korte verhandeling van || de Fondamenten || der || Perspective.

B-Ffff blz. 11-544.

blz. 11-112. bevat dit ‘Eerste Bouck’.

blz. 113-182. ‘Tweede Bouck’.

blz. 183-273, ‘Derde Bouck’.

blz. 273-342. ‘Vierde Bouck’.

blz. 343-484. ‘Vijfde Bouck’.

blz. 485-500. ‘Van Rekeningh in spelen van geluck’.

blz. 501-543. ‘Tractaet der Perspective’.

blz. 544. ‘Faulten’.

Aan het slot staat
‘Tot Leyden || Gedruckt by || Severin Matthijsz. || By de St. Pieters Kerck, in de Wereldt vol Drucks, 1660.’

eind13): * Hetzelfde werk met dezelfde titels en tekst. Alleen komt het jaartal 1659 in plaats van 1660.

eind14): * Francisci à Schooten || leydensis, || de || organica || conicarum sectionum || in plano descriptione, || tractatus. || geometricis, opticis; || Praesertim verò || gnomonicis & mechanicis || utilis. || Cui subnexa est Appendix, de Cubicarum || Aequationum resolutione. || Vignette dezelfde als bij Noot (11). || Lvgd. Batavor. || Ex Officinâ Elseviriorum, || A^o. cIɔ Iɔ cxcvi. in 4^o.
XVI blz. (niet gepagineerd) bevat opdracht ‘Illustris Academiae || Lvgdvno Batavae Cvratoribvs’ gedateerd ‘Leydae, Kal. Novembr. Anni MDCXLVI’ ‘de Praefatio || ad || Lectorem’ (10 blz.).

A-M. bls. 1-90. het werk zelf.

M-P. blz. 91-117. Appendix.

eind15): Problemata || astronomicvm || et || geometricum || voor-gestelt. || Door Johan Stampioen de Jonghe Mathematicus || Resideerende in 's Gravenhaghe || aende || Vytgevers van het Antwerpsch || Vraegh-stvck.
Deze titel staat aan het hoofd van een vel in plano. Daaronder een op koper gegraveerd plaatje, voorstellende een viertal heeren, naast drie stokken van verschillende lengte, wier voetpunten een driehoek A B C vormen. Daaronder het vraagstuk
‘SYnde in den Lenten tijt, een Stierman, op een onbekende plaetse in een effen Hori- || zontael ofte Water-pas velt, op eenen morgenstont, als de Sonne klaer was schy- || nende, heeft daer drie stocken van ongelycken lengte op-gherecht in de Loot- || rye. Eerstelick, merckende de schaduwe van den stock A. bevondt die te eyndi- || ghen in B, alsoo, dat A B lanck was 33 voeten. Een weinigh tydts daer na de Sonne || wat hoogher zijnde, heeft de schaduwe van den stock A bevonden te eindighen in C [met potlood is bijgevoegd: ten derden die van B in C]. Ten || vierden soo quam de schaduwe van B te eyndighen in A. Ten laetsten de Sonne wederom || wat verloopende, soo quam de schaduwe van den stock C te eyndighen in A. Den dach ver- || loopen zynde heeft de uyterste vande drie Koninghen staende op het beelt van Orion in || eene rechte lynie water-pas bevonden; Ende van stonden aen ghemerckt, dat het binnenste der || vier Planeetjens, die om Jupiter loopen Eclipseerde. Vraghe? op wat Polus hoogte, op wat || dagh van t' Jaer, op wat ure dat de Son elcke male geobserveerdt is, ende oock hoe verre de || stocken van den anderen stonden. Midtschaders oock de ware lenghte van de selve plaetse || Als de stock A langck is 6 voet. B 18 voet, ende C 8 voeten. || Antwoordt.’

Vorige Volgende