Journal tenu par Isaac Beeckman de 1604 à 1634. Tome 1: 1604-1619

[p. 353]

Appendices

[p. 354]

I Etudes sur la chainette

Nous avons remarqué que déjà Stevin s'était occupé des conditions d'équilibre d'un polygone funiculaire ouvert, dont Beeckman semble avoir tiré le problème de la chainette (ci-dessus pp. 43-44 et 45). Les notes, dans lesquelles celui-ci revient sur le sujet, se trouvent dans le Journal à fol. 159verso et 160recto, faisant suite à une note datée du 20 avril 1620. Cependant ces notes sont suivies à leur tour de copies des écrits de Descartes sur le paradoxe hydrostatique (fol. 160verso-162recto), sur la chute des corps (fol. 162recto-162verso) et du Compendium Musicae (fol. 163recto-178verso), c'est à dire des pièces datant de la fin de 1618. Comme nous l'avons remarqué (cf. notre Note sur le Manuscrit), il faut supposer que c'était bien longtemps après la date de leur composition que Beeckman remit les originaux de ces derniers documents à son copiste et à l'èpoque que celui-ci avait terminé sa copie des notes dressées avant le 20 avril 1620. Ainsi leur copie fut continuée à la fin du cahier qui renferme ces notes, interrompant cependant l'ordre chronologique des notes personnelles continuées dans un cahier nouveau. Nous croyons donc pouvoir admet re que les notes suivantes datent également de la fin de 1618 ou même d'une époque antérieure. Aussi Descartes nous apprend que Beeckman lui proposait le problème de la chainette environ vers la fin de l'année 1618¹⁾.

Nos documents ne donnent pas un exposé de la disposition des figures; peut-être aussi le copiste n'a pas reçu toutes les pièces regardant le sujet²⁾. Dans ces deux documents l'auteur avait l'intention de prouver que la courbe considerée soit une parabole, comme on le croyait alors souvent. Albert Girard en faisant mention de la chai-

1) Cf. sa note reproduite ci-dessous p. 362.

2) La disposition des figures semble dirigée par le raisonnement suivant: Le point H (voir la figure première) est sollicité par trois forces: le poids L, la tension de HC et cellede HF, les deux dernières forces étant représentées par les lignes HC et HF. Ces forces sont en équilibre; il en résulte que les projections horizontales des tensions en chaque point sont égales (donc HF = GC (non tirée) et ainsi pour les points C etc.). Le quadrilatère CHFG constitue le parallélogramme des forces. Le triangle rectangle GHF a pour côtés les deux tensions agissant sur H et la force HG égale au poids L (polygone de Varignon). Aux points C, etc., on retrouve les proportions HF: GF = CG : CH = DE : DC. La figure se constitue donc comme suit: Dressez le triangle GHF. Tirez GC parallèle à HF et HC parallèle à FG, ce qui fait trouver le point. C. Puis on fait CE = HG, l'on tire ED parallèle à HC et CD parallèle à HE, ce qui fait trouver le point D etc. On peut ajouter: tg GFH = HG : HF = poids du fragment H: tension en HF = longueur du fragment H: certaine constante a; ceci donne pour la chainette tg α = s/a, ce qui exprime sa propriété géometrique.

[p. 355]

nette, relate¹⁾ que Stevin avait bien vu que les cordes ‘ne sont pas en lignes droites estant estenduës, sinon que la seule corde perpendiculaire à l'horizon; car les autres cordes lasches ou fort estenduës, sont lignes paraboliques (comme j'ay autrefois demonstré environ l'an 1617), ainsi que je demonstreray cy-après à la fin du corollaire suivant, ce qui viendra icy fort à propos pour l'ornement de cette Spartostatique’²⁾. On sait que Galilée, dans son ouvrage de 1638, croyait également que la courbe en question était une parabole³⁾. Vers 1643 Mersenne s'informa sur la courbe chez ses correspondants et c'était en 1646 que Christiaen Huygens lui envoya la preuve qu'elle a ses propriétés spéciales. Plus tard encore les Bernouilli prouvèrent son identité avec la Velaria (profil de la forme d'une voile poussée par le vent).

1) Les Oeuvres mathématiques de Simon Stevin de Bruges etc. Le tout reveu et augmenté par Albert Girard, Samielois, mathematicien. A Leyde, chez Bonaventure et Abraham Elzevier, imprimeurs ordinaires de l' Université. Anno CIƆ.IƆ.CXXXIV. - t. IV, p. 508.

2) Girard ne tint pas promesse, en écrivant au lieu indiqué: ‘N'ayant pas le loisir toutefois de mettre icy la copie de ma demonstration entiere, je la donneray une autre fois au public, avec mes autres oeuvres, moyennant l'aide de Dieu, lorsque la recherche des sciences sera plus recommendable qu'elle n'est à present.’

3) Discorsi (Leiden, 1638), pp. 146 et 285-286.

[p. 356]

⁺

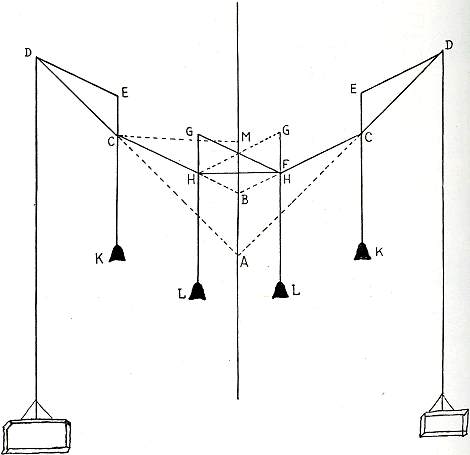Fig. 72.

La figure du manuscrit, dressée par le copiste, est très défectueuse. Les lignes verticales ne sont pas équidistantes et les lignes DE point parallèles aux lignes HC; les lignes HB et CA ne sont pas dans le prolongement de CH et DC. Les deux poids L sont attachès à des cordes beaucoup plus courtes que celles des poids K, ainsi que les poids L se trouvent très près des lignes CA. Nous avons restitué la figure d'après les indications données ci-dessus p. 354, n. 2, en gardant la forme des poids aux extremités pour imiter l'aspect de la figure du manuscrit.

+ Fol. 159^v

[p. 357]

⁺

⁺Maeckt een koorcle DCHHCD ende laet HH en GC^a) even groot zyn ende hanght aen H en C even swaer gewichten, ende treckt de linie AB doort midden van HH, ende treckt CH ende DC voorwaerts tot aen AB.

Ick segge dat de sonnestrale^b) evenwydich vallende met AB, wederomsteuten sal^c) boven de linie CH.

Laet AB recht nederwaerts hangen naer het middelpunt van het aerdtryck, soo sal ECK daert aenhanght, evenwydich syn met AB ende verstrecken voor de sonnestralen. Ist dan dat de linie ECK vallende op DCA den hoeck ECD grooter maeckt dan den hoeck ACB, is, soo steut de strale EC boven CH, want sy maeckt int steuten sulck eenen hoeck als int vallen op deselve linie.

Dat den hoeck DCE grooter is dan ACB bewys ick aldus. Treckt van E de lynie ED evenwydigh met CH ende maeckt HG soo groot als CE ende treckt GF oock evenwydigh met CH. Nu gelyck hem heeft^d) de swaerte, die op CE kompt^e), tot die op GH compt^f), soo heeft hem CE tot GH^g); <ende>^h) wederom: gelyck de swaerte op HG komendeⁱ⁾, tot die op FG komende^k), soo heeft hem HG tot FG. Maer de swaerte, die op CE kompt, is soo groot als de swaerte die op HG kompt; soo is dan GF soo groot als GH^l). Deselve reden heeft oock CE tot GF^m). Soo syn dan CE endeⁿ⁾ GH^o) ende GF even groot. Maer dewyle GF in den dryhoeck GHF altyt over den rechthoeck staet, so is GF altyt grooter dan GH, ende daerom oock DE altyt grooter dan CE. Maer den hoeck DCE is soo groot als den hoek CAB ende BCA gelyck EDC^p) ende den hoeck ECD^q) grooter dan den hoeck CDE; soo is dan oock den hoeck ECD grooter dan den hoeck ACB.

Soo sal dan de strale EC, steutende, eenen grooteren hoeck maecken met CA dan ACB, sal derhalven boven CH wederom steuten in M, twelck is als ghy CM ende AM even groot maeckt te zyn¹⁾.

+ Fol. 159^v

+ Chorda ex duobus tabulati locis dependens, quam lineam describat quaesitum.

a) le ms porte: HH en HC.

b) sonnestralen.

c) sall.

d) hen heeft.

e) kompt is soo groot, mais soo groot barré.

f) op CH kompt.

g) tot CH.

h) ende manque.

i) op CEG komende.

k) FG komen.

l) als CH.

m) CE tot DE.

n) DE ende.

o) CH.

p) gelyck FDC.

q) den hoeck EDC.

1) Ainsi le rayon tombant par la verticale GF refléchira tellement par un point M′ de l'axe BA que M′F = M′B, et ainsi pour les autres rayons. Or l'auteur avait dû démontrer ici que tous ces points M, M′ etc., coincident dans un seul point, comme il l'admet selon la figure suivante et le texte qui s'y rapporte. Cette démonstration nous ne l'avons pas. En admettant que tous les rayons tombant parallèlement à l'axe AB, refléchissent par le même point M, l'auteur a voulu sans daute remarquer que ceci est une des propriétés de la parabole, en établissant ainsi la nature parabolique de la courbe considerée.

[p. 358]

⁺

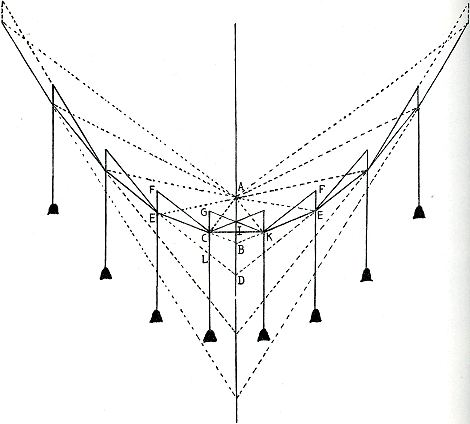Fig. 73.

Dans le manuscrit cette figure aussi est très défectueuse. Par exemple les lignes GC, EF, etc. ne sont point égales. Plusieurs lignes pointillées ne se trouvent pas dans l'allongement des lignes tirées. D'ailleurs il y a à droite et à gauche des lignes pointillées et presque verticales, qui ne joignent pas des points et dont on ne reconnait pas la signification.

+ Fol. 160^r

[p. 359]

⁺

Ut CA ad CE/BE, sic AEC ad EAC/EAB. E¹⁾.

<Ergo:>^a) Ut CE ad EB, aut EL ad ED, sic^b) EAC ad EAB²⁾.

Ut GC ad GK, sic IB ad CB, et Ut GC ad GK, sic FE ad EC,

Ergo:

Ut IB ad CB, sic FE ad EC,

Ergo:

Ut FE ad EC, sic IB ad CB,

Ergo:

Ut EC et³⁾ IB ad IB, sic EC et³) CB ad CB.

At

Ut DB ad IB, sic EC et³) CB ad CB,

(nam ut EB ad BD, sic GK ad GC, et Ut GK ad GC, sic CB ad BI)^c),

Ergo FE et³) IB aequalia sunt DB.

+ Fol. 160^r

1) La seconde proportionalité implique que AC = AB, c'est à dire qu'il existe pour le rayon GC une propriété analogue à celle qui a été démontrée, dans le document précédent, pour le rayon EC (ici FE). En mettant en compte ce que nous avons dit dans la note à la page 357, le point A correspond donc avec le point M de la figure précédente.

a) Ergo omis.

b) ut CE aut EL ad EB aut ED sic.

2) Il faut lire ici et dans la ligne précédente, au lieu de AEC, EAC ct EAB, les sinus de ces angles. Ceci est peut-être indiqué par la lettre E qui termine la ligne précédente. Nous avons rencontré la suppression du mot ‘sinus’ en tels cas chez des mathématiciens excellents de cette époque.

3) C'est à dire: ‘augmenté de’.

c) pas de parenthèses. - Les lignes 1 et 2 sont écrites à gauche de la ligne verticale AB de la figure, les lignes 3-13 à droite de cette verticale.

[p. 360]

II Notes de Descartes

Dans ses notes rédigées à la fin de 1618 à Breda, Beeckman avait fait mention plusieurs fois de Descartes. Comme son ami, Descartes rédigea à, la même époque une série de notes qu'il donna le titre de ‘Parnassus’. Après la mort de Descartes, à Stockholm en 1650 on trouva le recueil comprenant ces notes¹⁾; avec les autres manuscrits, le recueil fut remis à Clerselier, à Paris, qui préparait l'édition de divers papiers. C'est chez Clerselier que Leibniz put consulter, en 1676, le recueil cité, dont il emporta une copie en Allemagne. Cette copie, conservée à la Bibliothèque d'Hanovre, fut utilisée et publiée en 1859 par Foucher de Careil²⁾. Malheureusement elle se perdit, ainsi que MM. Adam et Tannery, les éditeurs de la dernière édition des oeuvres du philosophe, devaient se contenter de reproduire le texte donné par Foucher de Careil, dont ils corrigeaient cependant plusieurs fautes de lecture. C'est à leur édition que nous empruntons le texte suivant des notes de Descartes³⁾ qui peuvent compléter les relations de Beeckman.

Contigit mihi ante paucos dies familiaritate uti ingeniosissimi viri⁴⁾ qui talem mihi quaestionem proposuit:

Lapis, ajebat⁵⁾, descendit ab A ad B unâ horâ; attrahitur autem a Terrâ perpetuò eâdem vi, nec quid deperdit ab illâ celeritate quae illi impressa est priori attractione:

1) L'inventaire de Stockholm porte: ‘Un petit registre en parchemin, quotté en dedans de la couverture: Anno 1619 Kalendis Januarii, où se trouvent premièrement iS feuillets de considérations mathématiques sous un tiltre ‘Parnassus’ (Oeuvres de Descartes, ed. Adam et Tannery, t. X (1908), p. 7).

2) Oeuvres inédites de Descartes (Paris, 1859-1860), pp. 14-28.

3) Oeuvres de Descartes, t. X (1908), pp. 219-228.

4) Beeckman, cf. ci-dessus p. 237.

5) Pour le problème de la chute des graves, cf. ci-dessus pp. 44, 174 et 260-265, et l'écrit plus étendu que Descartes remit à Beeckman et que nous reproduirons au t. IV.

[p. 361]

quod enim in vacuo movetur, semper moveri existimabat. Quaeritur: quo tempore tale spatium percurrat.

Solvi quaestionem. In triangulo isoscele rectangulo, ABC spatium <motum>^a)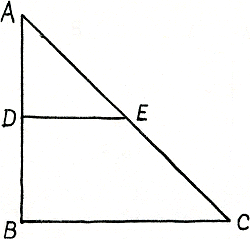

Fig. 74.

repraesentat; inaequalitas spatij à puncto A ad basim BC, motûs inaequalitatem. Igitur AD percurritur tempore quod ADE repraesentat: DB verò tempore, quod DEBC repraesentat; ubi est notandum minus spatium tardiorem motum repraesentare. Est autem AED tertia pars DEBC¹⁾; ergo triplò tardiùs percurret AD quàm DB.

Aliter autem proponi potest haec quaestio, ita ut semper vis attractiva Terrae aequalis sit illi quae primo momento fuit: nova producitur, priore^b) remanente. Tunc quaestio solvetur in pyramide²⁾.

Ut autem hujus scientiae fundamenta jaciam, motus ubique aequalis lineâ repraesentabitur, vel superficie rectangulâ, vel parallelogrammo, vel parallelopipedo; quod augetur ab unâ causâ, triangulo; a duabus, pyramide, ut supra; a tribus, alijs figuris.

Fig. 75.

Ex his infinitae quaestiones solventur. Verbi gratiâ, lapis in aere descendit viresque acquirit eundo³⁾. Quandonam incipiet aequali celeritate moveri?⁴⁾.

Quod solvetur, haec linea repraesentet gravitatem lapidis in primo instanti: curvatura linearum AEG et CFH inaequalitates motûs: à puncto enim E, F, aequaliter moveri incipiet, quia AEG non est curva nisi ab A ad E; ab E ad G est recta.

Item, si fax accensa in aere descendat, ut etiam ignis magna levitas de gravitate aliquid tollat, cùm levitatis quantitas sit nota.

Item, etiam gravitatis totius facis et aeris impedimentum, si quaeratur quo in-

a) motum omis.

1) Note de Leibniz: ‘Si AD dimidia ipsius DB’ (à lire: AB, et non DB).

b) priori.

2) Si l'on admet un accroissement constant de la force attractive avec le temps, ainsi que les chemins parcourus deviennent proportionnels à la troisième puissance du temps, on peut représenter ces chemins par le volume d'un pyramide.

3) Virgile, Aen., IV, vs. 175.

4) Pour la question du point d'égalité introduit par Beeckman, cf. ci-dessus pp. 150, 174, 263-264, 264-265 et 267-268.

[p. 362]

stanti celerrimè descendat et quo instanti non descendat; ubi etiam notum esse oportet, quid de face singulis momentis comburatur.

Aliaeque innumerae quaestiones sunt ex geometricâ pariter et mathematicâ pro-

Fig. 76.

gressione. Ad talia pertinet quaestio de reditu redituum¹⁾. G.v., mutuò accepi AB; post tempus AC, debeo CD; post tempus AE debebam tantùm EF, si BFD ducta sit linea proportionum. Linea proportionum cum quadratrice conjungenda: oritur enim <quadratrix> ex duobus motibus sibi non subordinatis, circulari et recto²⁾. Petijt à me Isaacus Middelburgensis an funis acb affixus clavis a, b, sectionis

Fig. 77.

conicae partem describat³⁾. Quod non licet per otium nunc disquirere.

Idem suspicatur⁴⁾ nervos in testudine eò celeriùs moveri quò acutiores sunt, ita ut duos motûs edat octava acutior, dum unum gravior; item quinta acutior 1½ etc.

Idem advertit⁵⁾ quare in motu projectorum, quae è manu exeunt per vim

Fig. 78.

circularem, statim ad motum rectum deflectant. Quòd scilicet pars aa majorem describat circulum quàm bb, ideòque celeriùs movetur: unde fit ut, dum è manu exit, partem b praecedat et eam post se trahat.

Unde sequitur aliquid projici posse circulariter hoc modo: à puncto e pendeat pondus a, agiteturque liberè per circulum abcd; quia omnes partes ponderis aequaliter moventur, ideò si funis ea frangatur, pergit moveri circulariter. Id licebit experiri, si in aquam decidat.

1) Pour cette question de ‘l'intérêt de l'intérêt’, cf. la fin de l'écrit de Descartes sur la chute des graves qu'il remit à Beeckman et qu'on trouvera au t. IV.

2) Cf. ci-dessus p. 43 et 44 et la lettre de Descartes à Beeckman du 26 mars 1619.

3) Pour la chainette cf. ci-dessus pp. 47 et 354 sqq.

4) Cf. ci-dessus p. 269 et les lieux indiqués dans les notes 1 et 3.

5) Cf. ci-dessus pp. 167, 253-255 et 256-257.

[p. 363]

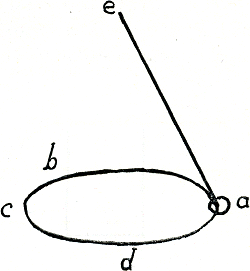Fig. 79.

Idem me monet aquam congelatam plus loci occupare quàm solutam¹⁾. Idem expertus est glaciem in medio vasis rariorem esse quàm in extremitatibus; quod fit, inquit²⁾, quia spiritûs ignei qui locum occupant, initio à frigore ad medium vasis detra-huntur; unde tandem, cùm exeunt, etiam frigore impellente, locum in medio vacuum relinquunt. Imò etiam glaciem sublevant, cùm exeunt. Unde fit ut majorem locum occupet glacies quàm aqua.

Idem quoque dixit acûs in his regionibus fieri tam acutas, ut monetam argenteam perforent; et tam tenues, ut aquae supernatent³⁾. Quid fieri posse existimo; parvae enim res ejusdem materiae non tam facilè aquam dividunt quàm magnae, quòd sola superficies aquam premit, quae major est proportione in exiguo corpore quàm in magno⁴⁾.

⁺Pour toucher une mandoline exactement, selon mes regles de musique⁵⁾, il faut diviser l'espace depuis le sillet, jusqu'au chevalet en 192 parties egales pour le A; en oster 12 et mettre le B, puis 18 pour le C, 2 pour le D, 16 pour le E, et 9 pour le F; puis accorder les cordes alternativement à la quinte et à la quarte, comme on fait ordinairement. Le C et le D serviront pour le re mobile, et toute musique se pourra jouer sur cette mandoline, pourvu qu'il n'y ait point de diezes irreguliers aux cordes non destinees aux muances⁶⁾.

Si partant de Bucolia⁷⁾, on veut aller en Chemnis ou quelque autre port de l'Egypte que ce soit, il faut remarquer exactement, avant que de partir, en quel endroit Pythius et Pythias sont opposés l'un à l'autre à l'embouchure du Nil; puis après en quelque lieu que ce soit, si l'on veut trouver son chemin, il faut regarder seulement où est Pythias et de quelles servantes de Psyché elle est accompagnee; car par ce moyen, connoissant combien elle est eloignee du lieu où elle estoit à Bucolia, on trouve son chemin⁸⁾.

1) Cf. ci-dessus pp. 21-22, 60, 61, 155, 215 et 281.

2) Cf. ci-dessus p. 60.

3) Cf. ci-dessus pp. 233-234.

4) Cf. la théorème de Beeckman énoncé ci-dessus pp. 31, l17, 171, 175. et ailleurs.

+ Instrument de musique fait avec une précision mathematique.

5) Cf. ci-dessus p. 246. On retrouve les chiffres que Descartes mentionne ici, dans une table qu'il donna dans son Compendium Musicae (Oeuvres, ed. Adam et Tannery, t. X (1908), p. 153.

6) Si et si bémol. L'instrument n'était destiné qu'à jouer des compositions du genre diatonique, sans aucun mélange de tons chromatiques.

7) Les termes cachés sont expliqués par Leibniz: ‘Bucolia, lieu de départ; Egypte, globe de la Terre; embouchure du Nil, lieu de départ; Pythius et Pythias et : les servantes de Psyché, les fixes.

8) Pour le problème des longitudes sur mer, cf. ci-dessus pp. 33-34, 48-49 et 106-107, et les lettres de Descartes à Beeckman du 26 mars et du 23 avril 1619 au t. IV.

[p. 364]

Petiit è Stevino¹⁾ Isaacus Middelburgensis quomodo aqua gravitet in fundo vasis b aeque ac in fundo vasis c et a. Item, totum vas c non magis gravitet quàm a cujus pondus medium affixum est et immobilè.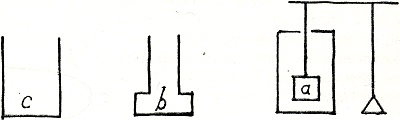

Fig. 80.

Respondi aquam aequaliter pellere omnia circumquaque corpora, quibus sublatis aeque descendit, si aliqua pars fundi aperiatur, atque fiet in vase c. Ergo aeque premit fundum.

Objicitur, si pars inferior vasis b et c aperiatur simul, aquam in c magis descensuram quàm in b, quoniam est naturalis modus celeritatis in descensu aquae qui deberet excedi ab aquâ exsistente in tubo vasis b, ut repleret locum relictum ab inferiore aquâ.

Ubi respondeo inde sequi in motu semper minus celeriter descendere aquam vasis b quàm c; atqui gravitatio non è motu sumitur, sed ab inclinatione ad descensum in ultimo instanti ante motum, ubi nulla est ratio celeritatis²⁾.

1) De Beghinselen des waterwichts (Leyden, 1586), ou dans l'édition des oeuvres, dont Beeckman se sert: Vierde stuck der Wisconstighe Ghedachtnissen van de Weeghconst. Inhoudende etc. (cf. ci-dessus p. 3). Beschreven deur Simon Stevin van Brugghe. Tot Leyden, By Ian Bouwensz. woonende op de Hoogelantsche Kerckgraft. Anno CIƆ.IƆ.CV, pp. 133-135 et 163-166.

2) Pour la démonstration de Descartes du paradoxe hydrostatique, cf. l'écrit étendu qu'il remit aussi à Beeckman et que nous reproduirons au t. IV. Cf. aussi ci-dessus pp. 305-306.