De macht van het woord

Een selectie uit het taalkundig werk van D.M. Bakker

[p. 88]

Volgorde van taalelementen; enkele preliminaire opmerkingen

1

Stel dat de volgende reeksen gegeven zijn:

(1)	I	O
(2)	O	I

Ik kan uit dit gegeven opmaken dat I en O van plaats kunnen verwisselen, permuteren. Ik kan ook zeggen, dat I zowel links als rechts van O kan staan, of dat O zowel rechts als links van I kan voorkomen. Ik kan ook veronderstellen, dat (1) en (2) het resultaat zijn van weglating van het eerste resp. het laatste element van de reeks O I O. En op vele andere manieren kan ik nog het reeksonderscheid weergeven dat door (1) en (2) wordt aangegeven.

Over deze formuleringen is heel wat te zeggen, hoe weinig problematisch ze op het eerste gezicht ook mogen schijnen. Ik wijs er allereerst op, dat de I's en de O's die erin voorkomen, niet dezelfde zijn als de I's en de O's in (1) en (2). Het lijkt een triviale bezigheid, te signaleren wat iedereen met eigen ogen kan zien. Belangrijker is echter, dat met de I's en de O's die in de formuleringen van permutatiemogelijkheden en -resultaten voorkomen, andersoortige elementen bedoeld moeten zijn dan de I's en de O's die in (1) en (2) voorkomen. Want de I die vóór de O in (1) staat, is een andere I dan de I achter de O in (2). Daaruit volgt, dat de I in (1) nooit door plaatsverwisseling achter de O in (2) terecht kan zijn gekomen. Voor verwisseling is immers noodzakelijk, dat de verwisselende elementen hun identiteit bewaren; en de I en O van (1) zijn niet dezelfde als de I en O van (2).

Al wordt dan ook in de bedoelde formulering gehandeld over andersoortige elementen, toch hebben ze wel degelijk betrekking op (1) en (2). Om dit te illustreren, wil ik een voorbeeld gebruiken. Stel ik heb twee kort na elkaar genomen foto's, één waarop A links van B staat en één waarop A rechts van B staat. Foto 1 heeft de afbeeldingen A₁ en B₁ van A en B, foto 2 de afbeeldingen B₂ en A₂. A₁ kan niet van plaats verwisselen met B₁, A₂ niet met B₂. Maar de afgebeelde personen, A en B, hebben wel degelijk van plaats verwisseld. Wat ik van de afbeeldingen niet kan zeggen, geldt wèl voor de afgebeelden. Men zou kunnen tegenwerpen, dat we de foto's in tweeën kunnen knippen en aldus bijvoorbeeld de volgende afbeeldingsreeksen maken:

[p. 89]

(3)	A1	B1	B1	A1
	A1	B2	B2	A1	(De onderstreepte reeksen stellen de oorspronkelijke foto's voor)
	A2	B1	B1	A2
	A2	B2	B2	A2

Deze mogelijkheid is natuurlijk niet te loochenen. Maar haar bestaan kan niet gelden als bewijs tegen onze stelling dat de elementen A₁, B₁, A₂ en B₂ niet van plaats kunnen verwisselen. De reeksen A₁ B₁ en B₂ A₂ zijn vastleggingen van een bepaalde reeksopstelling van A en B op een bepaald moment; als zodanig vormen ze vaste reeksen. De niet onderstreepte reeksen van (3) zijn vastleggingen niet van bepaalde reeksopstellingen van A en B, maar van elementen A₁, B₁, A₂ en B₂; dit zijn afbeeldingen van personen en als zodanig onderscheiden van de personen A en B. Aangezien nu de identiteit van wat blijkens (3) permuteert (de vier fotohelften) een andere is dan van wat blijkens de beide foto's kan permuteren: de personen A en B, moeten we besluiten dat de permutaties onder (3) gegeven geen bewijs zijn voor de permutabiliteit van A₁ en B₁, B₂ en A₂ als afbeeldingen van A en B.

Op dezelfde wijze geldt, dat we de formuleringen van permutatiemogelijkheden en -resultaten wel degelijk op I en O van toepassing kunnen verklaren, maar dat we erop bedacht moeten zijn, dat we, sprekend van verwisseling van I en O, handelen over entiteiten die tot de I's en O's in (1) en (2) staan als afgebeelden tot afbeeldingen. Met dit verschil echter: de afgebeelde personen zijn zichtbaar, wat er aan de I's en O's in (1) en (2) beantwoordt, is als zodanig ‘onzichtbaar’.

2

Moge deze vergelijking met foto's van wat er bij (1,2) aan de orde is verhelderend zijn, we zouden weer spoedig in het duister tasten als we niet tegelijk het verschil tussen beide gevallen onderkenden. De personen A en B kunnen van plaats ruilen, evenals we losse voorwerpen stuivertje kunnen laten wisselen. Maar de I en O kunnen dat niet. Dit is zonneklaar voor wat betreft getypte varianten van (1) en (2): de types die tegen lint en papier worden aangeslagen, maken deel uit van een type-arm, die geen los voorwerp is en dus niet van plaats kan verwisselen met iets anders (als alles goed is). Wat wel van plaats (of liever: tijdstip) kan wisselen is het aanslaan van I resp.O.

Het met de hand schrijven van beide reeksen is een moeilijker te beschrijven procedure, waarvan we de belangrijkste trekken echter op het spoor kunnen komen door vast te stellen, welke de condities zijn voor het aanslaan van types op een schrijfmachine. Wat bedoeld op het papier verschijnt, beantwoordt aan een normatief beeld in onze geest. Om zover te komen moet ik de toets opzoeken waarvan ik weet dat het aanslaan ervan het gewenste effect oplevert, òf omdat het gewenste teken erop staat, òf

[p. 90]

omdat hij een bepaalde positie op het bord inneemt (blind tikken). Op analoge wijze produceren we met pen of potlood d.m.v. bewegingen met hand en arm figuren, die beantwoorden aan hetzelfde normatieve beeld. Zoals bekend is de structuur van dit beeld uitermate complex; de ‘token’ vormen vertonen een grote mate van variabiliteit ten opzichte van het normatieve beeld, en men kan de vraag stellen of er niet meer dan één normatief beeld van een letter bestaat en of bijgevolg de lettervorm uiteindelijk niet ‘beeldloos’ is. Als dit inderdaad het geval zou zijn, bestaat er des te minder aanleiding aan te nemen, dat de ‘mentale’ lettertypes reeds in de geest gerangschikt zouden zijn tot reeksen en dat deze reeksen op papier zouden worden nagebootst. Met andere woorden, er is in onze redenering zoals we die tot dusver hebben gevoerd, niets dat ervoor pleit de mentale ‘types’ de eigenschp van permutabiliteit toe te kennen, die de boven vermelde personen en losse voorwerpen bezitten. Men kan met evenveel recht veronderstellen dat ze zelf niet zozeer in enige volgorde worden geplaatst als wel in een bepaalde (tijds)volgorde ‘gerealiseerd’, net zoals de types van de schrijfmachine in een bepaalde (tijds)volgorde worden aangeslagen.

3

Wat geldt voor realisaties van letters, kan ook gelden voor mondelinge of schriftelijke realisaties van woorden en woordgroepen. Ook hier onzekerheid over de vraag, of de normatieve mentale pendanten van gerealiseerde woorden en woordgroepen al of niet in een bepaalde volgorde gerangschikt zijn, vooraleer ze worden gerealiseerd. In de volgende syntactische groepen:

(4)	Jan slaapt
(5)	slaapt Jan

hebben we te maken met twee taaluitingen, die ieder twee realisaties van een woord bevatten. Deze woordrealisaties zijn impermutabel; zeker bij de gesproken taal valt dit op. Zoals de I's en O's uit (1) en (2) realisaties zijn van de ‘onzichtbare’ I en O, zo zijn de woordrealisaties ook realisaties van onzichtbare ‘dingen’. Althans, dat zou op grond van het bovenstaande de conclusie moeten zijn. We zouden dan kunnen zeggen, dat de waarneembare realisaties verwerkelijkingen zijn van elementen van de langue, ‘woorden’ genaamd, evenals de klanken realisaties zijn van fonemen. Zo althans zou het in een niet-generatieve structuralistische gedachtengang kunnen worden geformuleerd. Maar we kunnen niet uitmaken, of de ‘mentale’ woorden en woordgroepen, alvorens gerealiseerd te worden, in de menselijke geest al of niet in reeksvorm zijn gezet. Nog minder kunnen we nagaan, of de taalelementen, indien ze al voor realisatie in de geest in reeksvorm zijn gezet, vóórdien serieel ongeordend in de geest aanwezig waren dan wel reeds in een bepaalde ‘basisvolgorde’ gegeven. En nog hachelijker wordt

[p. 91]

het, te speculeren over de vraag, of taalelementen, alvorens in een bepaalde basisvolgorde gerangschikt te zijn of zich aan te bieden, al of niet serieel geordend waren.

4

Bovenstaande overwegingen heb ik niet omwille van henzelf willen meedelen. Ik heb ze nodig om er de aandacht op te vestigen, hoe snel we ons schuldig zouden kunnen maken aan onverantwoorde metaforiek, wanneer we termen als ‘rechte volgorde’, ‘basisvolgorde’, ‘inversie’, ‘permutatie’, en dergelijke gebruiken. Hetzelfde geldt voor termen als ‘additie’, ‘deletie’, en ‘commutatie’ (‘substitutie’), voorzover daarmee op reeksverschillen wordt gedoeld. Als het onmogelijk is te zeggen dat (4) een permutatie is van (5) of omgekeerd, en als het even onmogelijk is te zeggen of de ‘mentale’ woorden en woordgroepen vóór realisatie wel of niet in reeksvormen gegeven zijn, dan ontbreekt ons elke mogelijkheid om van ‘permutatie’ te spreken anders dan in overdrachtelijke zin voorzover het althans de elementen betreft wier reekseigenschappen wij bestuderen. De realisaties van woorden en woordgroepen zijn aantoonbaar niet, hun mentale pendanten zijn niet aantoonbaar vatbaar voor veranderingen als door de termen ‘inversie’, ‘permutatie’, ‘additie’, ‘deletie’ en ‘commutatie’ of ‘substitutie’ aangeduid. Terzake van (4) en (5) is de sterkst mogelijke uitspraak, dat in (4), Jan, in (5) slaapt ter linkerzijde is gerealiseerd, hetgeen slechts suggereert wat in feite alleen vast te stellen is van de mondelinge pendanten van (4) en (5), namelijk dat Jan resp. slaapt het eerste zijn gerealiseerd. Noem ik nu (4) en (5) omkeringen van elkaar, dan kan ik daarmee slechts duiden op een proces dat zich voltrekt voor het geestesoog van de taalbeschouwer: hij stelt de zaken voor alsof de realisaties van Jan en slaapt van plaats verwisselen. De taalbeschouwer behoeft, om van ‘omkering’ te spreken, niet perse een taalwetenschappelijk beschouwer te zijn; ook de niet linguistisch geschoolde taalgebruiker kan, zij het alleen taalgebruik beschouwend, denkend over zijn taalgebruik en dat van anderen de term ‘omkering’ laten vallen, terwijl er van geen enkele omkering aantoonbaar sprake is in het object van beschouwing. Ook de in het begin van deze paragraaf genoemde termen zijn slechts zinvol als aanduiding van het resultaat van intralinguale (of, maar dat laat ik verder buiten beschouwing, interlinguale) vergelijking, eventueel wetenschappelijke vergelijking; ze zijn ongevaarlijk zolang we ons ervan bewust zijn dat ze in letterlijke zin slechts hierop kunnen doelen: het is immers niet aantoonbaar, dat de taalgebruiker permuteert, deleert en substitueert, en evenmin dat het taalsysteem zelf overeenkomstige regels kent; transformatieregels zijn dienvolgens niet meer dan vastlegging van resultaten van wetenschappelijke vergelijking. Een ‘basisvolgorde’ is niet meer dan een geschikt uitgangspunt voor de formulering van andere reeksen; een transformatieregel niet meer dan een aanduiding voor een taalkundige collega, hoe hij, vanuit een basisvolgorde, andere reeksen kan bouwen. Dergelijke regels zijn kenmerkend

[p. 92]

voor een grammatica van een taalkundige, zij zijn dat niet noodzakelijkerwijze, en indien wèl, hoogstens indirect, voor de ‘grammaticale’ organisatie van een taal.

5

We hebben al gezien dat Jan c.q. slaapt in (4) een geheel ander element is dan Jan c.q. slaapt in (5). Hierop nadrukkelijk te wijzen, heeft ook een voordeel wat betreft de beschrijving van de intonatiemogelijkheden voor mondelinge pendanten van (4) en (5): intonationeel verschillen de twee realisaties van Jan en slaapt van elkaar en, zoals bekend, interfereren intonatieverschijnselen veelvuldig met volgordeverschijnselen. Bovendien is het bedoelde onderscheid een sleutel tot het verstaan van samentrekkingsverschijnselen (Bakker 1968:74). Niettemin kunnen we (4) en (5) beschrijven als permutaties van elkaar. Wat er dan permuteert zijn uiteraard geen elementen uit één der beide zinnen; het zijn abstracte elementen, objecten van de verbeelding van de taalbeschouwer en ook slechts daarin bestaand; elementen die slechts gedacht worden en waaraan die eigenschappen worden toegekend welke de Jan's resp. de slaapt's uit (4) en (5) gemeen hebben. De identiteit van het abstracte element berust dus in de gemeenschappelijke trek(ken) van de overeenkomstige elementen van (4) en (5). De abstractie is uiteraard alleen gewettigd indien die gemeenschappelijke trek of trekken belangrijk genoeg zijn. Gelijkheid van fonematische op bouw op zich is, gezien de potentiële ambiguïteit van taalelementen, niet voldoende; gelijkheid in betekenis, een gelijke plaatsing in een gelijke syntactische verbinding is daarenboven noodzakelijk. Gemeten aan deze maatstaven zijn de volgende zinnen niet op te vatten als permutaties van elkaar:

(6)	Jan heeft nog lang niet geslapen
(7)	Jan heeft nog niet lang geslapen

Niet altijd, in feite slechts zelden, zijn we in staat bedoelde abstracte elementen te vormen anders dan op grond van vooralsnog nauwelijks te expliciteren, voor-wetenschappelijke, zij het niet voor-taalbeschouwelijke intuïties. De simpele bewering, dat Jan in (4) en in (5) ‘onderwerp’ is kan nog steeds niet worden gemotiveerd, is misschien wel in het geheel niet motiveerbaar.

Desondanks menen we operaties als ‘permutatie’ etc. zinvol te kunnen uitvoeren. Ik zal zeker niet bestrijden dat dit mogelijk is, maar wil er wel op wijzen, dat de weinig expliciete werkwijze, die we toepassen ter vast-stelling van de identiteit der permuterende elementen, het gevaar inhoudt, dat de hantering van de daarbij gebruikte maatstaven en die maatstaven zelf zonder dat we het merken aan veranderlijkheid onderhevig kunnen zijn; waarbij dan nog als extra probleem komt het gevaar van willekeur in de qualificatie van gemeenschappelijke kenmerken van overeenkomstige elemen-

[p. 93]

ten als ‘belangrijk’. De zinnen:

(8)	Hij ging zitten op de bank
(9)	Hij ging op de bank zitten

lijken permutaties van elkaar. Toch is het mogelijk een redenering op te zetten, volgens welke ze dat niet zijn: op de bank in (8) is een toevoeging bij Hij ging zitten en op de bank in (9) is een toevoeging, zo men wil een bepaling, bij zitten. De vraag: wat ging hij doen? wordt in (8) beantwoord met: zitten (en wel op de bank) en in (9) met: op de bank zitten. Een subtiel onderscheid, zal men zeggen. Maar waar halen we het recht vandaan te ontkennen dat op de bank in (8) anders functioneert dan in (9), of van dit functionele verschil te abstraheren?

6

Permutatie en permutatie is twee. Reeksen kunnen worden gedefinieerd in termen van nabuurschapsrelaties, maar ook en bovendien, in termen van links-rechtsordening. Zowel in A B C als in C B A is B de buur van A en C; de permutatie tast de nabuurschapsrelatie niet aan. Deze wordt pas veranderd, als ik bijvoorbeeld A B C permuteer tot C A B. Dan is B geen buur meer van C. Let ik alleen op nabuurschapsrelaties, dan zijn A B C en C B A aan elkaar gelijk; voer ik bovendien rechtslinksordening in, dan zijn ze dat niet. Gewoonlijk houdt men zich in de taalkunde bezig met linksrechts permutaties, en maakt men er geen punt van of de permutaties al dan niet de nabuurschapsrelaties veranderen. Ik wil hierop geen kritiek oefenen, maar alleen laten zien dat wat we gewoonlijk doen, reeds een keuze inhoudt.

Permutatie komt neer op rotatie van elementen. Het verdient de aandacht, dat niet perse de elementen behoeven te roteren; het kan ook voorkomen dat het punt, ten opzichte waarvan elementen als links c.q. rechts zijn gedefinieerd, roteert, terwijl de elementen ‘op hun plaats’ blijven:

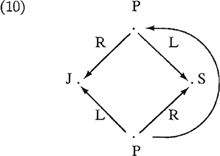
J: Jan
S: slaapt
P: punt ten opzichte waarvan J en S links dan wel rechts zijn
L: links
R: rechts

Een linksrechtspermutatie is dus een verandering in de onderlinge plaats van de permuterende elementen en/of het (verzwegen) oriëntatiepunt. Per-

[p. 94]

mutatie is dus een ingewikkelder operatie dan eenvoudig naar links c.q. rechts verplaatsen. Het is mogelijk dat het geen bezwaar oplevert te werken met een versimpelde opvatting van het begrip ‘permutatie’; in ieder geval kan het nooit kwaad dit te weten.

7

In de transformationeel-generatieve grammatica worden permutaties gewoonlijk door middel van transformaties ingevoerd, die al of niet opereren op een basisvolgorde, in de zin van uitgangsreeks voor permutaties in de dieptestructuur. Zoals we zagen, is een ‘basisvolgorde’ niet meer dan een geschikt uitgangspunt voor permutaties; we dienen ons ervan te weerhouden, hypotheses op te stellen over de bouw van de taal of de geest van de taalgebruiker, alleen maar op grond van het feit dat we een handig uitgang-spunt voor permutaties hebben. In deze basisvolgorde is, bij een linksrechts geordende dieptestructuur, de linksrechtsplaats van elk element gegeven. Elke permutatie moet apart worden verantwoord: zo moeten de volgende zinnen:

(11)	Hij heeft vandaag niets erover gezegd
(12)	Hij heeft vandaag er niets over gezegd
(13)	Hij heeft er vandaag niets over gezegd

gerelateerd worden door bijv. een dubbele toepassing van Er-hopping. Dit bokspringen kan vermeden worden door aan te nemen, dat alle leden van een permutatiegroep vrij kunnen permuteren, behoudens restricties, die in dien zin kunnen worden geformuleerd, dat bepaalde elementen niet met elkaar van plaats kunnen verwisselen, m.a.w. een vaste volgorde hebben en dus reeksen vormen van niet voor permutatie vatbare elementen. Argument voor vrije permutatie is allereerst, dat transformatieregels als Er-hopping, overbodig worden, en dat men kan volstaan met iets als V-plaatsing, een topicalisatieregel, en misschien nog een enkele meer (waaronder eventueel ‘PP over V’, zie hieronder). Een tweede argument is dat volgorde in permutatiegroepen lang niet altijd de functie der delen definieert; als men - voor het notationele gemak - bij de formulering van dieptestructuurregels ‘doet alsof’ dit wel het geval is, kan men daar later last van krijgen in de vorm van T-regels die permutaties (en wel stuk voor stuk) moeten bewerkstelligen.

Permutabele delen zijn niet alleen woordgroepen en woorden, ook woorddelen kunnen als zodanig optreden. Beschouwen we de volgende gevallen:

(14)	Jan slaapt
(15)	slaapt Jan?
(16)	je werkt
(17)	werk je

[p. 95]

dan blijkt dan (16) en (17) niet zonder meer permutaties van dezelfde elementen kunnen worden genoemd: werkt is niet identiek aan werk. Onderscheiden we nu binnen werkt een werkwoordsstam, -werk-, en een uitgang t, dan kunnen we de permutaties die blijkens (16,17), als we letten op het parallellisme met (14,15), in weerwil van het verschil tussen werkt en werk toch kunnen worden geformuleerd als volgt noteren:

(18)	je -werk-
(19)	-werk- je

Dit houdt in dat ik naast woorden en andere fatische elementen ook woord-delen, i.c. werkwoordsstammen, ga erkennen als permutabele elementen. Dit geeft bepaalde voordelen. Zo kan ik met behulp van een restrictie:

(20)	boeken_____-lees-

de volgende gevallen beschrijven:

(21a)	boeken lezen is fijn (: *lezen boeken)
(21b)	(wat heb je gedaan?) boeken gelezen (: *gelezen boeken)
(21c)	al boeken lezend, kun je een hoop opsteken (: *lezend boeken)
(21d)	ik wil boeken lezen (: *lezen boeken)
(21e)	ik heb boeken gelezen (: *gelezen boeken)
(21f)	ik houd ermee op, boeken te lezen (: *te lezen boeken)
(21g)	.....dat ik boeken lees (: *lees boeken)
(21h)	je moet tijd hebben om boeken te lezen (: *om te lezen boeken)

De onderstaande zinnen passen er niet in:

(22a)	ik lees boeken
(22b)	lees ik boeken?

Om deze gevallen te verklaren in overeenstemming met reeks (20), moeten we het begrip ‘persoonsvorm’ in de beschrijving invoeren. We kunnen dan vaststellen, dat de persoonsvorm hetzij op de eerste, hetzij op de tweede plaats in de persoonsvormconstructie staat, hetzij elders (in de zgn. afhankelijke zin). Maakt de stam van het kernwerkwoord (in de zin van Van Bakel 1969:204) deel uit van de persoonsvorm, dan volgt hij de volgorderegels, die voor de persoonsvorm gelden en verlaat dus eventueel de plaats die hij volgens vaststellingen als (20) heeft (verg. Koster 1974).

Terzake van de volgende zinnen:

(22c)	boeken lees ik
(22d)	boeken wil ik lezen

[p. 96]

(22e)

lezen wil ik boeken

kan worden afgeleid dat een restrictie, iets uitgebreider geformuleerd dan in (20):

(23)	ik__ boeken___ -lees-

niet uitsluit dat men zowel boeken als een woord dat -lees- bevat (in casu een infinitief) uit de reeks kan halen en vooraan zetten. Overigens blijft dan de reeks gehandhaafd:

(24a)	boeken ik _____ Φ ________ -lees-
(24b)	-lees- ik ___ boeken ___ Φ

De zin (22c) wordt dan gevormd op basis van de plaatsingsregels geldend voor de stam, wanneer hij in de persoonsvorm is opgenomen, èn op basis van vooraanplaatsing van één der elementen uit reeks (23).

Uit de combinatie van:

(25a)	ik__ het boek_____ -veroordeel-
(25b)	ik__ daar_____ mee_ -veroordeel-

volgen rechtstreeks deze combinaties:

(26a)	(dat) ik daarmee	het boek	-veroordeel-
(26b)	(dat) ik	het boek daarmee	-veroordeel-
(26c)	(dat) ik daar	het boek	mee	-veroordeel-

Al deze combinaties zijn acceptabel in de omgangstaal. Helaas echter maakt (25b) de volgende zin niet mogelijk:

(27)	(dat) ik het boek veroordeel daarmee

Deze zin vereist een regel, volgens welke -mee alleen na veroordeel kan staan als daar- er onmiddellijk aan voorafgaat. Het is me nog niet duidelijk of deze regel de vorm van ‘PP over V’ moet hebben. De reeks (25b) maakt echter wel duidelijk het verschijnsel van ‘weving’ (verg. Bakker 1974): één en dezelfde syntactische structuur kan op verschillende wijzen worden gerealiseerd, mits als (20), (23), (25a, 25b) worden gerespecteerd. Het blijft echter voor mij een open vraag of in het geval van (26a, 26b, 26c) de volgordeverschillen al of niet significant zijn. In ieder geval kan men nimmer in het algemeen discussiëren over de relevantie van een bepaalde volgorde: men moet onderscheid maken tussen verschillende soorten relevantie, al naar gelang van doelstellingen die met bepaalde volgordes worden gediend. Zo is het verschil tussen (26a, 26b, 26c) irrelevant voorzover het

[p. 97]

de uitdrukking betreft van de syntactische structuur; maar het is wellicht in een ander opzicht wèl relevant. Assumptie van relevantie in absolute zin lijkt mij in het algemeen, maar zeker hier aanleiding te geven tot veel vruchteloos discussiëren.

8

Samenvattend merk ik het volgende op.

1.	De besproken omzettingen in volgorde zijn in ieder geval taalbeschouwelijke operaties.
2.	De permuterende elementen zijn abstracte elementen.
3.	De identiteit van deze elementen wordt vooralsnog veelal vastgesteld op grond van niet-expliciete kriteria.
4.	Assumptie van een in principe vrije volgorde kàn leiden tot een reductie van omzettingsregels in vergelijking met de gangbare transformationeel-generatieve grammatica.
5.	Er bestaan binnen permutatiegroepen restricties die formuleerbaar zijn als reeksen niet permuterende elementen.
6.	Eén van die vaste reeksen (en wel een belangrijke) is subject_____object_____hoofdwerkwoordsstam (deze lijkt op SOV).
7.	Het is niet aantoonbaar, dat omzettingen en ‘basisvolgordes’ als de besprokene iets anders zijn dan wetenschappelijke constructies; dat ze in deze vorm taalregels zijn, verlangt onafhankelijke argumentatie; dat ze mentale processen c.q. inhouden weerspiegelen, moet eveneens nog bewezen worden.

In de huiver, die prof. Van Es steeds heeft gevoeld voor een volstrekt systematische grammatica, meen ik een zelfde beduchtheid waar te nemen als ook ik bespeur voor de bedreiging van een juiste visie op het object van taalonderzoek, een bedreiging die ontstaat wanneer de wetenschap haar grenzen zou overschrijden. In dit gevoel van verwantschap zij hem dit opstel, onder grote waardering voor zijn taalwetenschappelijke arbeid, opgedragen.

Literatuur

Bakker, D.M. (1968)	Samentrekking in Nederlandse syntactische groepen. Leiden.
Bakker, D.M. (1974)	‘Zinnen als reeksen: een vergelijkende standpuntbepaling’. In: De nieuwe taalgids 67, blz. 265-78.

[p. 98]

Koster, J. (1973/4)	‘Het werkwoord als spiegelcentrum’. In: Spektator 3, blz. 601-18.
Rijpma, E., F.G. Schuringa (1969)	Nederlandse spraakkunst, bewerkt door dr. Jan van Bakel. Groningen, 22e dr.